七年级下册数学应用题和几何题100道(最新整理)

七年级下册数学应用问题和几何题100道第一部分：数学应用问题（50道）1. 某商店有100个苹果，每天卖出5个，问几天能卖完？2. 一本书的原价是80元，打6折后的价格是多少？3. 小明父亲的年龄是35岁，小明的年龄是他父亲的1/5，问小明几岁？4. 一个长方形的长度是10厘米，宽度是4厘米，计算它的面积和周长。

5. 爸爸给小明的压岁钱是200元，小明花了其中的1/4买了一本书，还剩多少钱？6. 小华每天早上骑自行车去学校，单程需要15分钟，问他来回一共要多长时间？7. 小红家离学校有3千米，她每天步行去学校，速度是每小时4千米，问她需要多长时间到达学校？8. 小明购买了一台电视机，原价是2000元，经过砍价后，他以8折的价格购买了它，他花了多少钱？9. 一家超市里面，水果有苹果、橙子和香蕉，苹果有24个，橙子是苹果的3/4，香蕉是橙子的2倍，问超市里面一共有多少个水果？10. 甲、乙两个人合作做一件工作，甲能独立完成这个工作需要6天，乙能独立完成这个工作需要8天，问他们合作完成这个工作需要多少天？...（依次类推）第二部分：几何题（50道）51. 把一个长方形切成4个同样大小的正方形，每个正方形的边长是10厘米，那么原来长方形的周长是多少？52. 一个正方形的边长是8厘米，计算它的面积和周长。

53. 一个圆的半径是5厘米，计算它的面积和周长。

54. 一条边长为12厘米的正三角形，计算它的周长。

55. 一个矩形的长是10厘米，宽是6厘米，计算它的面积和周长。

56. 一条边长为9厘米的正六边形，计算它的周长。

57. 一个长方体的长是5厘米，宽是3厘米，高是4厘米，计算它的体积和表面积。

58. 一个圆柱体的底面半径是3厘米，高是8厘米，计算它的体积和表面积。

59. 一个圆锥体的底面半径是6厘米，高是10厘米，计算它的体积和表面积。

60. 一个球的半径是7厘米，计算它的体积和表面积。

...（依次类推）本文档包含50道数学应用问题和50道几何题，帮助七年级学生进行数学应用和几何的练习。

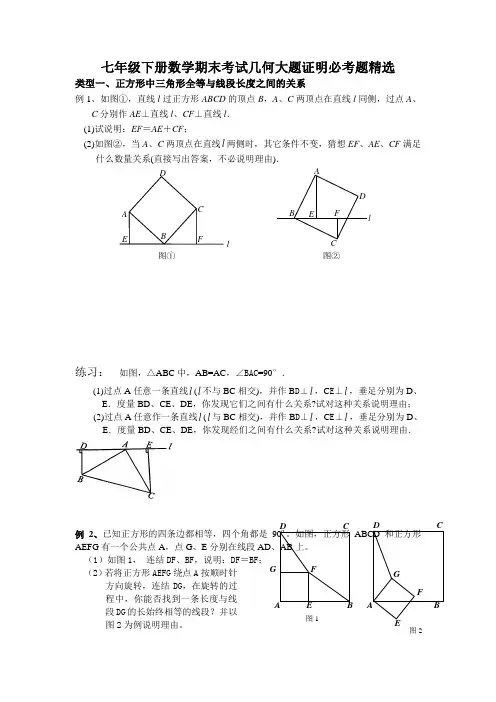
图①DA EC B Fl图②ABEF C lD 七年级下册数学期末考试几何大题证明必考题精选类型一、正方形中三角形全等与线段长度之间的关系例1、如图①，直线l 过正方形ABCD 的顶点B ，A 、C 两顶点在直线l 同侧，过点A 、C 分别作AE ⊥直线l 、CF ⊥直线l ． (1)试说明：EF ＝AE ＋CF ；(2)如图②，当A 、C 两顶点在直线l 两侧时，其它条件不变，猜想EF 、AE 、CF 满足什么数量关系(直接写出答案，不必说明理由)．练习： 如图，△ABC 中，AB=AC ，∠BAC =90°．(1)过点A 任意一条直线l (l 不与BC 相交)，并作B D ⊥l ，C E ⊥l ，垂足分别为D 、E ．度量BD 、CE 、DE ，你发现它们之间有什么关系?试对这种关系说明理由； (2)过点A 任意作一条直线l (l 与BC 相交)，并作B D ⊥l ，C E ⊥l ，垂足分别为D 、E ．度量BD 、CE 、DE ，你发现经们之间有什么关系?试对这种关系说明理由．例2、已知正方形的四条边都相等，四个角都是90º。

如图，正方形ABCD 和正方形AEFG 有一个公共点A ，点G 、E 分别在线段AD 、AB 上。

（1）如图1， 连结DF 、BF ，说明：DF ＝BF ；（2）若将正方形AEFG 绕点A 按顺时针方向旋转，连结DG ，在旋转的过程中，你能否找到一条长度与线段DG 的长始终相等的线段？并以图2为例说明理由。

A EB 图1D CG FA BD C GFE 图2练习：如图，正方形ABCD 的边CD 在正方形ECGF 的边CE 上，B 、C 、G 三点在一条直线上，且边长分别为2和3，在BG 上截取GP ＝2，连结AP 、PF. （1）观察猜想AP 与PF 之间的大小关系，并说明理由.（2）图中是否存在通过旋转、平移、反射等变换能够互相重合的两个三角形？若存在，请说明变换过程；若不存在，请说明理由.（3）若把这个图形沿着PA 、PF 剪成三块，请你把它们拼成一个大正方形，在原图上（1）BD 与CE 相等吗？请说明理由．（2）你能求出BD 与CE 的夹角∠BFC 的度数吗？（3）若将已知条件改为：四边形ABCD 与四边形AEFG 都是正方形，例3、正方形四边条边都相等，四个角都是90．如图，已知正方形ABCD 在直线MN 的上方，BC 在直线MN 上，点E 是直线MN 上一点，以AE 为边在直线MN 的上方作正方形AEFG ．（1）如图1，当点E 在线段BC 上（不与点B 、C 重合）时： ①判断△ADG 与△ABE 是否全等，并说明理由；②过点F 作FH ⊥MN ，垂足为点H ，观察并猜测线段BE 与线段CH 的数量关系，并说明理由；（2）如图2，当点E 在射线CN 上（不与点C 重合）时： ①判断△ADG 与△ABE 是否全等，不需说明理由；F B②过点F 作FH ⊥MN ，垂足为点H ，已知GD ＝4，求△CFH 的面积．练习：如图1，四边形ABCD 是正方形，G 是CD 边上的一个点(点G 与C 、D 不重合)，以CG 为一边作正方形CEFG ，连结BG ，DE ．（1）如图1，说明BG= DE 的理由（2）将图1中的正方形CEFG 绕着点C 按顺时针方向旋转任意角度α，得到如图2．请你猜想①BG= DE 是否仍然成立？②BG 与DE 位置关系？并选取图2验证你的猜想．类型二、探究题例1、如图，已知等边△A B C 和点P ，设点P 到△A B C 三边A B 、A C 、B C （或其延长线）的距离分别为h 1、h 2、h 3，△A B C 的高为h ．在图（1）中，点P 是边B C 的中点，此时h 3=0，可得结论：h h h h =++321． 在图（2）--（5）中，点P 分别在线段M C 上、M C 延长线上、△A B C 内、△A B C图 2FG D A 图 1F D A外．（1）请探究：图（2）--（5）中， h 1、h 2、h 3、h 之间的关系；（直接写出结论）（2）证明图（2）所得结论； （3）证明图（4）所得结论． （4）（附加题2分）在图（6）中，若四边形R B C S 是等腰梯形，∠B =∠C =60o ， R S =n ，B C =m ，点P 在梯形内，且点P 到四边B R 、R S 、S C 、C B 的距离分别是h 1、h 2、h 3、h 4，桥形的高为h ，则h 1、h 2、h 3、h 4、h 之间的关系为： ；图（4）与图（6）中的等式有何关系？练习：1、如图，在△ABC 中，AB=AC ，P 为底边上任意一点，PE ⊥AB ，PF ⊥AC ，BD ⊥AC.（1）求证：PE+PF=BD ；（2）若点P 是底边BC 的延长线上一点，其余条件不变，（1）中的结论还成立吗？如果成立，请说明理由；如果不成立，请画出图形，并探究它们的关系.2、如图，已知△ABC 三边长相等，和点P ，设点P 到△ABC 三边AB 、AC 、BC （或其延长线）的距离分别为h 1、h 2、h 3，△ABC 的高为h ．在图（1）中， 点P 是边BC 的中点，由S △ABP+S △ACP=S △ABC 得，h BC h AC h AB ⋅=⋅+⋅21212121可得h h h =+21A B C D EP A B C DE P M(3) A B C D EP M (2) A B C D EM (P ) (1) A B C D E P M(5)C B APDEFC B E 又因为h 3=0，所以：h h h h =++321．图（2）~（5）中，点P 分别在线段MC 上、MC 延长线上、△ABC 内、△ABC 外．（1）请探究：图（2）~（5）中，h 1、h 2、h 3、h 之间的关系；⑵ ⑶ ⑷ ⑸ （2）说明图（2）所得结论为什么是正确的；例2、已知△ABC 是等边三角形，将一块含30角的直角三角板DEF 如图1放置，当点E 与点B 重合时，点A 恰好落在三角板的斜边DF 上. （1）AC=CF 吗? 为什么?（2）让三角板在BC 上向右平行移动，在三角板平行移动的过程中，(如图2)是否存在与线段EB 始终相等的线段（设AB ，AC 与三角板斜边的交点分别为G ，H ）？如果存在，请指出这条线段，并证明；如果不存在，请说明理由.(B)CE F图1ABC DEP ABCDEPM(3)ABCDE P M (2)ABCDEM (P ) (1)练习：1、如图1，一等腰直角三角尺GEF （∠EGF=90°,∠GEF=∠GFE=45°,GE=GF ）的两条直角边与正方形ABCD 的两条边分别重合在一起．现正方形ABCD 保持不动，将三角尺GEF 绕斜边EF 的中点O （点O 也是BD 中点）按顺时针方向旋转．（1）如图2，当EF 与AB 相交于点M ，GF 与BD 相交于点N 时，通过观察或测量BM ，FN 的长度，猜想BM ，FN 相等吗？并说明理由；（2）若三角尺GEF 旋转到如图3所示的位置时，线段FE 的延长线与AB 的延长线相交于点M ，线段BD 的延长线与GF 的延长线相交于点N ，此时，（1）中的猜想还成立吗？请说明理由．2、已知：△ABC 为等边三角形，M 是BC 延长线上一点，直角三角尺的一条直角边经过点A ，且60º角的顶点E 在BC 上滑动，（点E 不与点B 、C 重合），斜边∠ACM 的平分线CF 交于点F（1）如图（1）当点B 在BC 边得中点位置时（6分） ○1猜想AE 与BF 满足的数量关系是 。

追及问题姐姐步行速度是75米/分，妹妹步行速度是45米/分。

在妹妹出发20分钟后，姐姐出发去追妹妹。

问：多少分钟后能追上？2.小张和小王，分别从甲乙两地出发步行，1小时30分后，小张走了甲乙两地距离的一半多1.5千米，此时与小王相遇。

小王的速度是3.7千米/小时，那么小张的速度是多少？3.甲乙两车从同一地点出发，沿着同一公路追赶前面的一个骑车人。

甲乙两车分别用10分钟、6分钟追上骑车人。

已知甲车速度是24千米/小时，乙车速度是30千米/小时，问两车出发时相距多少千米？4.一支部队排成1.2千米队行军，在队尾的张明要与在最前面的营长联系，他用6分钟时间追上了营长。

为了回到队尾，在追上营长的地方等待了18分钟。

如果他从最前头跑步回到队尾，那么用多少时间？5.甲乙两车分别从两地同时相向开出。

快车经过8小时到达乙地，慢车经过10小时到达甲地。

（1）相遇时，乙车行了360千米。

求两地距离。

（2）相遇时，乙离目的地还有360千米。

求两地距离。

（3）相遇时，乙比甲多行360千米。

求两地距离。

（4）两车在离中点处360千米相遇，求两地距离。

（5）5分钟后两车又相距360千米。

求两地距离。

6.家离图书馆4.8千米，弟弟从家出发以60米/分速度步行去图书馆。

15分钟后，哥哥骑自行车从家出发去追赶弟弟，自行车的速度是240米/分。

问：（1）哥哥在离家多远处追上弟弟？（2）哥哥追上弟弟后不久到达图书馆，又马上折回，过不久与弟弟相遇，那么相遇处离图书馆多少千米？环行跑道问题1.小张和小王各自以一定的速度在周长为500米的跑道上跑步。

小王每分跑180米。

①小张和小王同时从一个地点出发，反向而行，75秒钟后两人相遇，求小张的速度？②小张和小王同时从一个地点出发，沿同一方向跑步，经过多少分钟两人第一次相遇？2.在600米环行跑道上，兄妹两同时从同一起点都按逆时针跑，每隔12分两人相遇一次；若两人反向跑，则每隔4分两人相遇一次。

七年级数学下几何与代数练习题
练一（几何）
1. 在平面直角坐标系中，A(2, 3)和B(6, 5)是两个点，求线段AB的长度。

2. 勾股定理：已知直角三角形的两个直角边长分别为3cm和4cm，求斜边的长度。

3. 一个平面上有一个正方形，已知其边长为5cm，求正方形的周长和面积。

练二（代数）
1. 已知x = 2，求下列代数式的值：
a) 2x^2 - 3x + 1
b) x^3 - 4x^2 + 5x - 2
2. 已知y = -3，求下列代数式的值：
a) 3y^2 + 2y - 1
b) y^3 - 2y^2 - 3y + 4
3. 计算下列代数式的值：
a) 2(x + 3) - 3
b) 4(x - 2)^2 + 2(x - 2) + 1
练三（几何与代数综合）
1. 已知直角三角形的斜边长度为10cm，其中一条直角边的长
度为6cm，求另一条直角边的长度。

2. 设正方形的周长为20cm，求正方形的面积。

3. 如果一个矩形的长是5cm，宽是3cm，求矩形的周长和面积。

练四（几何与代数综合）
1. 已知直角三角形的斜边长度为13cm，其中一条直角边的长
度为5cm，求另一条直角边的长度。

2. 计算下列代数式的值：
a) (x + 3)(x - 2)
b) (2x + 1)^2
3. 如果一个矩形的长是7cm，宽是4cm，求矩形的周长和面积。

七年级下册数学应用题和几何题100道追及问题姐姐步行速度是75米/分，妹妹步行速度是45米/分。

在妹妹出发20分钟后，姐姐出发去追妹妹。

问：多少分钟后能追上？2.小张和小王，分别从甲乙两地出发步行，1小时30分后，小张走了甲乙两地距离的一半多1.5千米，此时与小王相遇。

小王的速度是3.7千米/小时，那么小张的速度是多少？3.甲乙两车从同一地点出发，沿着同一公路追赶前面的一个骑车人。

甲乙两车分别用10分钟、6分钟追上骑车人。

已知甲车速度是24千米/小时，乙车速度是30千米/小时，问两车出发时相距多少千米？4.一支部队排成1.2千米队行军，在队尾的张明要与在最前面的营长联系，他用6分钟时间追上了营长。

为了回到队尾，在追上营长的地方等待了18分钟。

如果他从最前头跑步回到队尾，那么用多少时间？5.甲乙两车分别从两地同时相向开出。

快车经过8小时到达乙地，慢车经过10小时到达甲地。

（1）相遇时，乙车行了360千米。

求两地距离。

（2）相遇时，乙离目的地还有360千米。

求两地距离。

（3）相遇时，乙比甲多行360千米。

求两地距离。

（4）两车在离中点处360千米相遇，求两地距离。

（5）5分钟后两车又相距360千米。

求两地距离。

6.家离图书馆4.8千米，弟弟从家出发以60米/分速度步行去图书馆。

15分钟后，哥哥骑自行车从家出发去追赶弟弟，自行车的速度是240米/分。

问：（1）哥哥在离家多远处追上弟弟？（2）哥哥追上弟弟后不久到达图书馆，又马上折回，过不久与弟弟相遇，那么相遇处离图书馆多少千米？环行跑道问题1.小张和小王各自以一定的速度在周长为500米的跑道上跑步。

小王每分跑180米。

①小张和小王同时从一个地点出发，反向而行，75秒钟后两人相遇，求小张的速度？②小张和小王同时从一个地点出发，沿同一方向跑步，经过多少分钟两人第一次相遇？2.在600米环行跑道上，兄妹两同时从同一起点都按逆时针跑，每隔12分两人相遇一次；若两人反向跑，则每隔4分两人相遇一次。

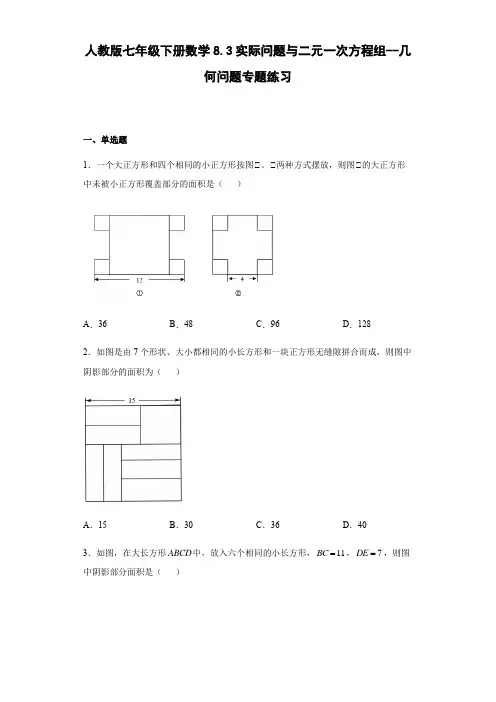
人教版七年级下册数学8.3实际问题与二元一次方程组--几何问题专题练习一、单选题1．一个大正方形和四个相同的小正方形按图①、①两种方式摆放，则图①的大正方形中未被小正方形覆盖部分的面积是（ ）A ．36B ．48C ．96D ．128 2．如图是由7个形状、大小都相同的小长方形和一块正方形无缝隙拼合而成，则图中阴影部分的面积为（ ）A ．15B ．30C ．36D ．40 3．如图，在大长方形ABCD 中，放入六个相同的小长方形，11BC =，7DE =，则图中阴影部分面积是（ ）A．53B．52C．51D．504．如图，在长为50米．宽为30米的矩形方地上，沿平行于矩形各边的方向分割出三个完全相同的小矩形草坪，问：小矩形草坪的长和宽各为多少米？设小矩形草坪的长为x米，宽为y米，则可列方程组为（）A．250,230x yx y+=⎧⎨+=⎩B．350,230x yx y-=⎧⎨+=⎩C．250,230x yy x+=⎧⎨+=⎩D．30,250x yx y+=⎧⎨+=⎩5．如图，宽为50cm的长方形图案由10个相同的小长方形拼成，其中一个小长方形的面积为（）A．2400cm B．2500cm C．2600cm D．2700cm6．把图1中的菱形沿对角线分成四个全等的直角三角形，将这四个直角三角形分别拼成如图2，图3所示的正方形，则图1中菱形的面积为（）A．6B．24C．26D．127．用5个大小相同的小长方形拼成了如图所示的大长方形，若大长方形的周长是28,则每个小长方形的周长是()A．12B．14C．13D．168．把如图折成正方体后，若相对面所对应的值相等，那么x-3y的值为（）A．-2B．-1C．0D．1二、填空题9．如图，将左侧所示的6个大小、形状完全相同的小长方形放置在右侧的大长方形中，所标尺寸如图所图中含有阴影部分的总面积为________．10．如图，宽为50cm的长方形图案由10个大小一样的小长方形拼成，则小长方形的周长为______cm．11．如图，长方形中放置9个形状、大小都相同的小长方形，则图中阴影部分面积为________．12．利用两块完全一样的长方体木块测量一张桌子的高度，首先按图①所示的方式放置，再交换两木块的位置，按图①所示的方式放置．测量的数据如图，则桌子的高度等于______．13．如图①，一个长为2a，宽为2b的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块全等的小长方形，然后按照图①那样拼成一个面积为49的大正方形，若中间小正方形的面积为1，则a＝______、b＝_____．14．一个长方形的长减少3cm，同时宽增加2cm，就成为一个正方形，并且这两个图形的面积相等，则原长方形的长是_____，宽是_____．15．如图所示，是由截面相同的长方形墙砖粘贴的部分墙面，根据图中信息可得每块墙砖的截面面积是__________2cm．16．如图，长方形空地的长为10m，宽为8m，沿平行于长方形边的方向分割出三个形状、大小完全一样的小长方形花圃（阴影部分），则其中一个小长方形的面积为_____m2．三、解答题17．某长方形的周长是44cm，若宽的3倍比长多6cm，则该长方形的长和宽各是多少？18．已知一个长方形，若它的长增加4cm，宽减少1cm，则面积保持不变；若它的长减少2cm，宽增加1cm，则面积仍保持不变. 求这个长方形的面积.19．学校为了提高绿化品位，美化环境，准备将一块周长为76m的长方形草地，设计分成长和宽分别相等的9块小长方形，（放置位置如图所示），种上各种花卉．经市场预测，绿化每平方米造价约为108元．（1）求出每一个小长方形的长和宽．（2）请计算完成这项绿化工程预计投入资金多少元？20．光大中学的领导要装修学校的食堂，决定采用如图的图案铺地面，该图案是用8块相同的长方形地砖拼成一个大的长方形，发现学校食堂地面需要拼成的大的长方形共300个，请计算食堂地面的面积．参考答案：1．B2．C3．C4．A5．A6．D7．A8．B9．6810．10011．8212．75cm13．4314．9cm4cm15．11216．817．长方形的长和宽分别为15cm和7cm．18．这个长方形的面积是242cm.19．（1）每个小长方形的长和宽分别是10米、4米；（2）完成这块绿化工程预计投入资金为38880元．20．食堂地面的面积是2162m．。

七年级下学期几何专题一、精心选一选，慧眼识金！1.过五边形的一个顶点可作（）条对角线A.1B.2C.3D.42.三角形的三个内角( )A、至少有两个锐角B、至少有一个直角C、至多有两个钝角D、至少有一个钝角3.下列图形中具有稳定性的是( )A、菱形B、钝角三角形C、长方形D、正方形4．下列图形中，是属于轴对称图形的是（）A. B. C. D.●5．如图：BE、CF是ABC∆的角平分线，0∠，A＝40则=∠BDC（ D ）11065 C. 095 D. 0A．050 B. 06.以下列长度的三条线段为边，不能组成三角形的是（）A．4，4，5 B．3，2，5 C．3，12，13 D．6，8，107. 下列说法：①等边三角形是等腰三角形；②在三角形中至少有二个锐角；③三角形的一个外角等于两个内角的和；④钝角三角形的三条高相交于三角形外一点，其中正确的个数有（）A、1个B、2个C、3个D、4个8. 下列图形：①角；②线段；③等腰三角形；④等边三角形；⑤平行四边形中是轴对称图形的个数是（）A、1个B、2个C、 3个D、4个9.平面内三条直线最少有（）个交点A.3B.2C.1D.0●10.已知Rt△ABC，∠A=30°，则∠B=（ C ）A.60°B.90°C.60°或90°D.30°11.如图，由AB∥CD，能推出正确结论的是( B ) A 、∠1=∠2 B 、∠3=∠4 C 、∠A=∠C D 、AD∥BC12.下列命题为真命题的是（ D ） A.内错角相等B.点到直线的距离即为点到直线的垂线段C.如果∠A+∠B+∠C=180°，那么∠A 、∠B 、∠C 互补D.同一平面内，垂直于同一直线的两直线平行。

13.用同一种下列形状的图形地砖不能进行平面镶嵌的是（ C ） A.正三角形 B.长方形 C.正八边形 D.正六边形14.当多边形的边数增加时，其外角和( C ) A 、增加 B 、减少 C 、不变 D 、不能确定● 15.已知：一光线沿平行于AB经镜面AC 、AB 反射后，如图所示， 若∠A=40°则∠MNA=（ B ） A.90° B.100° C.60° D.80°● 16.已知：如图B 处在A 处的南偏西40C 处在A 处的南偏东15°方向上，C 处在B 处的北偏东80°方向，则∠ACB=（ B ）A.90°B.85°C.40°D.60° 17.若一个三角形中的其中一个外角等于与它相邻的内角，则此三角形是( A ) A 、直角三角形 B 、锐角三角形 C 、钝角三角形 D 、无法确定18.点到直线的距离是指这点到这条直线的( D )A 、垂线段B 、垂线C 、垂线的长度D 、垂线段的长度二、巧心填一填，一锤定音!19.已知∠a 的对顶角是58°，则∠a=______。

七年级下学期数学几何阶段测试题一、选择题：（每题3分，共30分）1．下面有4个汽车标志图案，其中是轴对称图形的是（）A．②③④ B．①③④ C．①②④ D．①②③2．小华在电话中问小明：“已知一个三角形三边长分别是4，9，12，如何求这个三角形的面积？”小明提示说：“可通过作最长边上的高来求解．”小华根据小明的提示作出的图形正确的是（）A. B. C. D.3．小华在镜中看到身后墙上的钟，你认为实际时间最接近8点的是（）A． B． C． D．4、在△ABC所在的平面内存在一点P，它到A、B、C三点的距离都相等，那么点P一定是（）A．△ABC三边中垂线的交点 B．△ABC三边上高线的交点C．△ABC三内角平分线的交点 D．△ABC三条中线的中点5．△ABC中，AC=5，中线AD=7，则AB边的取值范围是（）A．1＜AB＜29 B．9＜AB＜19 C．5＜AB＜19 D．4＜AB＜24 6．已知：如图，下列三角形中，AB=AC，则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是（）A．①③④ B．①②③④ C．①②④ D．①③9题图 11题图 12题图 13题图8题图 7题图 7．如图，在一个规格为6×12（即6×12个小正方形）的球台上，有两个小球A ，B ．若击打小球A ，经过球台边的反弹后，恰好击中小球B ，那么小球A 击出时，应瞄准球台边上的点（ ） A ．P 1 B ．P 2 C ．P 3 D ．P 48．如图，在Rt △ABC 中，∠ACB=90°，∠BAC=30°，∠ACB 的平分线与∠ABC 的外角平分线交于E 点，连接AE ，则∠CEA 是（ ）A ．15°B ．20°C ．30°D ．35°9．如图，已知∠AOB=40°，点P 关于OA 、OB 的对称点分别为C 、D ，CD 交OA 、OB 于M 、N 两点，则∠MPN 的度数是（ ）A ．70°B ．80°C ．90°D ．100°10．如图，C 为线段AE 上一动点（不与A 、E 重合），在AE 同侧分别作正三角形ABC 和正三角形CDE ，AD 与BE 交于点O ，AD 与BC 交于点P ，BE 与CD 交于点Q ，连接PQ 、OC ，以下五个结论：①AD=BE ；②PQ ∥AE ；③AP=BQ ；④DE=DP ；⑤∠AOE=120°；⑥OC 平分∠AOE 。

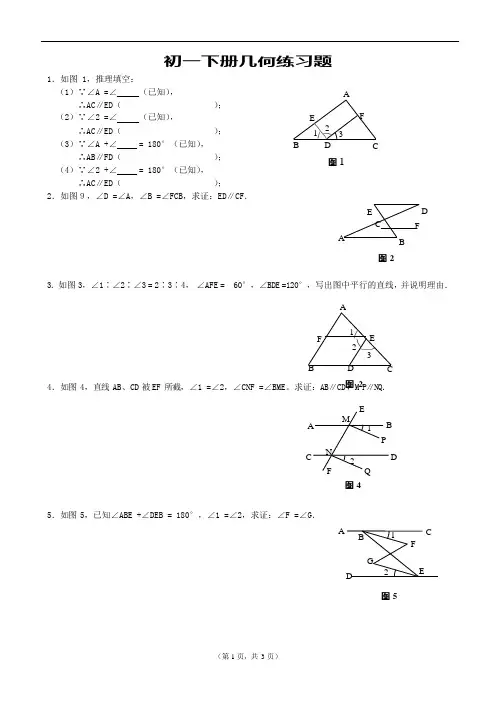
初一下册几何练习题1．如图 1，推理填空： （1）∵∠A =∠ （已知），A∴AC∥ED（ ）； （2）∵∠2 =∠ （已知），E F ∴AC∥ED（ ）； （3）∵∠A +∠ = 180°（已知），∴AB∥FD（ ）； （4）∵∠2 +∠ = 180°（已知），∴AC∥ED（ ）；2．如图９，∠D =∠A，∠B =∠FCB，求证：ED∥CF．1 2 3BD图 1ACE D CF图 23．如图 3，∠1∶∠2∶∠3 = 2∶3∶4， ∠AFE = 60°，∠BDE =120°，写出图中平行的直线，并说明理由．ABDC4．如图 4，直线 AB 、CD 被 EF 所截，∠1 =∠2，∠CNF =∠BME。

求证：AB∥CD 图，M 2P∥NQ．EAM1 BPCN 2DFQ图 45．如图 5，已知∠ABE +∠DEB = 180°，∠1 =∠2，求证：∠F =∠G．AB 1C FGD2 E图 51 F2 E36．如图 10，DE∥BC，∠D∶∠DBC = 2∶1，∠1 =∠2，求∠DEB 的度数．D E21B C图67.如图 11，已知AB∥CD，试再添上一个条件，使∠1 =∠2成立．（要求给出两个以上答案，并选择其中一个加以证明）A 1 BEFC 2 D图78.如图12，∠ABD和∠BDC的平分线交于E，BE 交CD 于点F，∠1+∠2 =90°．求证：（1）AB∥CD；（2）∠2 +∠3 = 90°．A B123C F D图89.已知：如图：∠AHF＋∠FMD＝180°，GH 平分∠AHM，MN 平分∠DMH。

求证：GH∥MN。

图910.已知：如图，，，且.求证：EC∥DF.11.如图，∠B＝∠E，AB＝EF，BD＝EC，那么△ABC与△FED全等吗？为什么？．12.如图, 已知点A C、B、D、在同一直线上, AM=CN, BM=DN, ∠M=∠N, 试说明: AC=BD.13.如图所示, 已知AB=DC, AE=DF, CE=BF, 试说明: AF=DE.14.11、如图，在△ABC和△DBC中，∠1=∠2，∠3=∠4，P 是BC 上任一点。

七年级下册数学应用题和几何题道HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】追及问题姐姐步行速度是75米/分，妹妹步行速度是45米/分。

在妹妹出发20分钟后，姐姐出发去追妹妹。

问：多少分钟后能追上？2.小张和小王，分别从甲乙两地出发步行，1小时30分后，小张走了甲乙两地距离的一半多千米，此时与小王相遇。

小王的速度是千米/小时，那么小张的速度是多少？3.甲乙两车从同一地点出发，沿着同一公路追赶前面的一个骑车人。

甲乙两车分别用10分钟、6分钟追上骑车人。

已知甲车速度是24千米/小时，乙车速度是30千米/小时，问两车出发时相距多少千米？4.一支部队排成千米队行军，在队尾的张明要与在最前面的营长联系，他用6分钟时间追上了营长。

为了回到队尾，在追上营长的地方等待了18分钟。

如果他从最前头跑步回到队尾，那么用多少时间？5.甲乙两车分别从两地同时相向开出。

快车经过8小时到达乙地，慢车经过10小时到达甲地。

（1）相遇时，乙车行了360千米。

求两地距离。

（2）相遇时，乙离目的地还有360千米。

求两地距离。

（3）相遇时，乙比甲多行360千米。

求两地距离。

（4）两车在离中点处360千米相遇，求两地距离。

（5）5分钟后两车又相距360千米。

求两地距离。

6.家离图书馆千米，弟弟从家出发以60米/分速度步行去图书馆。

15分钟后，哥哥骑自行车从家出发去追赶弟弟，自行车的速度是240米/分。

问：（1）哥哥在离家多远处追上弟弟？（2）哥哥追上弟弟后不久到达图书馆，又马上折回，过不久与弟弟相遇，那么相遇处离图书馆多少千米？环行跑道问题1.小张和小王各自以一定的速度在周长为500米的跑道上跑步。

小王每分跑180米。

①小张和小王同时从一个地点出发，反向而行，75秒钟后两人相遇，求小张的速度？②小张和小王同时从一个地点出发，沿同一方向跑步，经过多少分钟两人第一次相遇？2.在600米环行跑道上，兄妹两同时从同一起点都按逆时针跑，每隔12分两人相遇一次；若两人反向跑，则每隔4分两人相遇一次。