测距电离层延迟误差分析.

ds
电离层对相位和码伪距观测值的影响大小（近似）相等，符号相反。
Ne 为电子密度(electrons/m3)且为正值，因此对码伪距的延迟量 g为正 （延迟）、对相位观测值的延迟 p为负（提前）。
3.1 电离层误差(IV)
电离层延迟与总电子含量（TEC）
1）TEC总电子含量（Total Elctron Content）
在天顶方向上的延迟量约为2m，并且随着站星视线天顶距的增加而增 大。对于卫星高度角仅有几度的卫星，GPS信号的电离层延迟可以达到 数m。
一般来讲，对流层延迟与温度、气压、湿度以及GPS天线的位置有关。
3.2 对流层误差(II)
对流层延迟与大气折射
1）折射指数与折射率
折射指数 n （refractive index）
4）提供的卫星轨道精度较差，目前约为 ~ 1 m。
brdc2090.07n
2.1 卫星轨道误差(III)
精密星历
1）主要由IGS （International GNSS Service）提供；
2）以一定的时间间隔给出卫星在空间的三维坐标及其运动
速度，由用户进行内插后求得观测时刻 ti 卫星在空间的位 置及运动速度；
R -- 改正项
测站高H 和卫星天顶距z 的列表函数，可通过插值得到。
3.2 对流层误差(III)（续）
在模型中，可以使用气压、温度、湿度的实测值，或者使用由 标准大气模型得到的值，公式如下：
H0 0m
P0 1013.25mbar
T0 18 C
Rh0 50%
P P0 1 0.000226(H H0 ) 5.225 T T0 0.0065(H H0 )

卫星钟差可通过下式得到改正：
ts a0 a1(t t0 ) a2 (t t0 )2
式中t0为一参考历元，系数a0、a1、a2分别表示钟在t0时刻 的钟差、钟速及钟速的变率。这些数值由卫星的地面控制 系统根据前一段时间的跟踪资料和GPS标准时推算出来， 并通过卫星的导航电文提供给用户。
经上述钟差改正后，各卫星钟之间的同步差可 保持在20ns以内，由此引起的等效距离偏差不超过 6m。卫星钟差或经改正后的残差，在相对定位中可 通过差分法在一次求差中得到消除。
相对定位：
利用两站的同步观测资料进行相对定位时，由于星历误 差对两站的影响具有很强的相关性，所以在求坐标差时，共 同的影响可自行消去，从而获得高精度的相对坐标。根据一 次观测的结果，可以导出星历误差对定位影响的估算式为：
由卫星星历误差所引起的基线误差
卫星星历误差
基线长
卫星至测站的距离
3）削弱星历误差的方法：
卫星钟差是GPS卫星上所安装的原子钟 的钟面时与GPS标准时间的误差。
卫星钟采用的是GPS 时，但尽管GPS卫星均设 有高精度的原子钟（铷钟和铯钟），它们与理想的 GPS时之间仍存在着难以避免的频率偏差或频率漂 移，也包含钟的随机误差。这些偏差总量在1ms以 内，由此引起的等效距离可达300km。
对流层延迟的90%是由大气中干 燥气体引起的，称为干分量；其 余10%是由水汽引起的，称为湿 分量。由于大气层中的水汽分布 在时间和空间上变化很大，其折 射误差很难准确预测，所以湿分 量成为限制对流层延迟改正精度 的主要因素。
◆对流层对信号的影响与信号的高度角有关， 在天顶方向，信号穿过对流层的路线最短，其 时延值约为2.3m，随着天顶距的增加，时延也 加大，在地面方向最大，约为20m。 这对于 GPS导航和低精度定位而言可以满足其精度要 求，所以此时可以不考虑该项误差。但对高、 中精度的定位测量而言，则必须顾及对流层误 差，尤其是它对垂直分量影响较大，如果对流 层天顶时延有1cm的误差，则将导致垂直分量 产生3cm的误差。

GNSS测量误差的来源与分析方法研究近年来，全球导航卫星系统(GNSS)在现代测量与导航领域起到了至关重要的作用。

然而，由于各种误差的存在，GNSS测量结果往往无法完全准确。

因此，深入研究GNSS测量误差的来源和分析方法对于提高测量精度、减少误差具有重要意义。

一、GNSS测量误差的来源由于GNSS测量受到多种因素的影响，导致测量误差的产生。

这些误差可以分为系统误差和随机误差两类。

1. 系统误差系统误差是由GNSS系统自身的特性引起的误差。

比如，钟差误差、电离层延迟、大气湿延迟等。

首先，由于卫星钟的频率稳定性有限，卫星钟差引起的误差是非常常见的。

其次，由于电离层对电磁波的传播具有一定的影响，导致信号传播路径长度发生变化，进而引起测量误差。

此外，大气中的湿度也会对信号传播产生影响，从而引起大气湿延迟误差。

2. 随机误差随机误差是一种无规律的误差，很难被准确预测。

随机误差的来源包括多路径效应、多普勒频率偏移、观测器误差等。

首先，多路径效应是由信号在传播过程中遇到反射、绕射等导致信号路径变化的现象，导致信号到达接收器的时间有所延迟。

这会造成测量结果的误差。

其次，多普勒频率偏移是由于卫星与接收机之间的相对运动引起的，这也会对测量结果产生一定的影响。

此外，观测器自身的误差，如观测器钟差、观测器天线相位中心偏差等也是随机误差的重要来源。

二、GNSS测量误差的分析方法为了准确分析GNSS测量误差，科学有效的分析方法显得非常重要。

下面将介绍几种常用的分析方法。

1. 差分测量差分测量是通过测量两个或多个接收器之间的相对位置差异，排除掉公共误差，从而获得较高精度的定位结果。

相对于单点测量，差分测量能够有效消除大部分系统误差和一部分随机误差，提高测量精度。

此外，差分测量还可以用于解决一些特殊的测量需求，如动态测量、快速初始化等。

2. 卡尔曼滤波卡尔曼滤波是一种常用的状态估计方法，广泛应用于GNSS测量数据分析。

其基本思想是通过不断更新系统状态，利用历史观测数据来进行误差补偿，从而提高定位精度。

区域电离层建模摘要：电离层延迟误差是GPS 定位中的一项重要误差源，自从2000年5月美国取消了SA 政策后，电离层延迟误差改正显得尤为重要。

通常我们都是选取合适的模型来消除电离层，本文的目的就是系统性论述电离层常用模型，已经对某个特定区域进行TEC 建模的方法，并用数据进行了验证。

关键字：电离层；误差；TEC ；建模 引言电离层是高度在60-1000km 间的大气层，当GPS 卫星所发射的信号穿过电离层时，其传播速度会发生变化，变化程度取决于电离层中的电子密度和信号频率，从而使得信号的传播时间't ∆乘上真空中的光速c 后所得到的距离'ρ不等于从信号源至接收机的几何距离ρ，其造成的误差一般在白天可达15m ，夜晚可达3m ；在天顶方向最大可达50m ，在水平方向最大可达150m ，因此必须对电离层延迟加以改正。

一、电离层介绍电离层是一种含有较高密度电子的弥散性介质，电磁波在电离层中的传播速度G V 与群折射率G n 为：)28.401(2--==f N C n Cv e GG 式中，e N 表示电子密度（电子数/3m ），f 为信号的频率（Hz ），C 为真空中的光速。

在进行伪据测量时，P 码以群速度G V 在电离层中传播，若伪据测量中测得信号的传播时间为t ∆，那么卫星值接收机的真正距离ρ为：ds N f C ds N fCt C dtV s e s e tG ⎰⎰⎰-=-∆==∆''2228.4028.40ρρ 由上式可以看出，电离层延迟的大小与电离层中的电子密度（TEC ），令⎰=se dSN TEC则我们称TEC 为总电子含量。

它表示沿着卫星信号传播路径s 对电子密度e N 进行积分。

由此可见电离层改正的大小主要取决于信号传播路径上电子总量和信号频率。

由公式可知，伪据测量中的电离层群延迟改正g )(ion ∆为：TEC fG ion 24028.0)()(-=∆米 式中，TEC 以1610个电子/3m 为单位，信号频率f 以GHz 为单位，其电离层延迟改正分别为：TECm TEC m L ion L ion 267286.0)()(162292.0)()(21=∆=∆根据电离层特性，TEC 主要集中在电离层的F 层，他在300km~500km 达到最大值，因此我们假定F 层的某一个高度处，所有的自由电子大部分都集中在一个厚度为无限薄的球壳上，距离地面约为375km ，此即电离层单层模型SLM 。

张 文 山
（ 哈尔滨市勘察测绘 研究院 ， 黑龙江 哈尔滨 １各种主要误 差来源、 Ｐ 特点及影响 ， 出减小或消除误 差的解决方法。 提
文 献 标 识 码 ： Ｂ 文 章编 号 ： ７ ５ ６ （０ ８ ０ ０ ｌ ０ １ ２～ ８７ ２ ０ ）３— １０— ２ ６
关 键 词 ： Ｐ ； 差 ； 度 Ｇ Ｓ误 精 中图 分 类 号 ：２ ８ ４ Ｐ ２ ．
Ｅｒ ｏ ａ ｙ ｉ ｎ ｎ ｒ ｌｏ ｒ ｒ Ａｎ ｌ ｓｓ ａ ｄ Ｃｏ ｔ ｏ ｆＧＰＳ Ｓ ｒ ｅ ｉ ｇ ｕ ｖ ｙｎ
Ｚ ＨＡＮＧ Ｗ ｅ —ｓ ａｌ ｎ ｈｌ
施。
定 的卫 星并不能 完全消 除星 历误差 。
但是 ， 于位 置相距 较 近 的用户 ， 因为 星历 误 差 而 对 会
具 有几 乎相 同的误 差范 围 ， 因此 ， 采用 差分 观 测的 方法 基 本 上可 以消除 星历误差 。 ２ 卫 星钟差 ： 指预 报 的 卫 星钟 差 。众 所 周 知 ， Ｐ ） 是 ＧＳ 基 于单 程测 距 ， 主要 取 决 于预 报 的卫 星 钟 。卫 星 钟 差 它 对 Ｃ Ａ码用 户和 Ｐ码 用 户 是 相 同 的 ， 且 此 影 响 同方 向 ／ 并 无 关 。这在采 用 差 分改 正 技 术 时 很有 用 ， 部 差 分 站 同 全 用户 观测值都 含有 相 等 的钟差 。卫 星 钟差 的 主要 误差 源
是 Ｓ 但从 ２ ０ Ａ， ０ ０年 ５月 １日起 美 国取 消 了该 项 限 制 措 施。
ｌ 误 差 来 源 及影 响
Ｇ Ｓ测 量误差 产生 的主要 来 源可 分 为三 大部 分 ： Ｐ Ｐ ＧＳ
１２ Ｇ Ｓ ． Ｐ 信号 的传输误差
１ 电离 层误 差 ： 由于 电离 层效 应 引 起 的观 测 值 的 ） 是 误差 。它 与沿卫 星和用 户接 收 机视 线 方 向上 的电子 密度 有关 ， 垂直 方 向上 延迟值 在 夜 间平 均可 达 ３ｍ 左右 ， 在 白 天 可达 １ 在低 仰角情 况下分 别可 达 ９ｍ 和 ４ 在 反 ５ｍ， ５ｍ， 常 时期这个 值还会 加 大 。为 了削 弱 电离 层 延迟所 引起 的 定 位精度 损失 ， 长 基准 测 量 中用 双 频 接 收 机 采 集 Ｇ Ｓ 在 Ｐ 数 据 ， 观测成 果 进行 实 时 电离 层 延迟 改正 ， 以获得很 对 可

GNSS测量中常见误差源及其校正方法导语：全球卫星导航系统（GNSS）已经成为现代测量和定位领域中不可或缺的技术工具。

然而，由于各种因素的干扰，GNSS测量结果可能会出现误差。

本文将讨论一些常见的GNSS测量误差源以及相应的校正方法。

一、信号传播误差在GNSS测量中，信号从卫星到接收机的传播过程中会受到大气层、多径效应等因素的影响，从而引入误差。

其中，大气层误差是最主要的误差源之一。

大气层中的水蒸气、电离层密度等因素会影响信号的传播速度和路径，进而引起测量结果的偏差。

校正大气层误差的方法包括双频差分测量和大气层模型计算。

二、钟差误差GNSS卫星上的原子钟是精确度非常高的，但是由于各种因素的影响，例如温度、空间辐射等，钟差误差仍然无法避免。

钟差误差会导致接收机收到的卫星信号的到达时间产生偏差，进而影响测量结果的准确性。

为了校正钟差误差，常见的方法是利用双频差分测量或者接收机内部的钟差模型进行补偿。

三、多路径误差多径效应是由于信号在传播过程中，同时经过直射路径和反射路径，造成接收机接收到多个信号，从而引起测量结果偏差的现象。

这种误差特别突出在城市环境或者山区等多反射面的地形中。

为了解决多路径误差，一种常见的方法是使用反射面特征分析技术，提高接收机的可靠度和抗干扰能力。

四、动态误差GNSS测量的准确性在很大程度上取决于接收机和测量对象的相对运动状态。

动态误差主要来自于运动的加速度、速度等变化过程中引起的信号多普勒效应、载波缺失等问题。

对于动态误差的校正，可以通过使用惯性测量单元（IMU）配合GNSS仪器进行联合定位，从而提高定位的精度和稳定性。

五、卫星几何误差卫星几何误差是由于卫星的位置分布、卫星与接收机的相对位置等因素引起的。

当卫星几何配置良好时，测量误差较小，但当卫星分布较差或者接收机与卫星的角度较小时，测量误差将增大。

为了解决卫星几何误差问题，可以通过使用多频多系统的GNSS接收机，提高系统的可靠性。

GPS定位误差的产生原因分析与减小方法引言：在现代社会，全球定位系统（Global Positioning System，GPS）已经成为了人们生活中不可或缺的一部分。

无论是导航、交通监控还是地理信息系统等领域都离不开GPS定位技术。

然而，随着GPS定位的广泛应用，人们也逐渐发现定位误差问题的存在。

本文将从GPS定位误差产生的原因入手，探讨解决这一问题的方法。

一、GPS定位误差的原因分析：1. GPS系统误差：GPS系统本身存在着一些系统误差，例如卫星钟差、伪距观测误差、大气延迟等。

这些误差会直接影响到GPS定位的准确性。

2. 空间几何因素：GPS定位需要至少4颗卫星进行定位计算，卫星的位置和空间几何分布对定位精度有着重要影响。

当卫星分布不均匀或存在遮挡物时，会导致定位误差增大。

3. 电离层和大气影响：电离层和大气中的湿度、温度等因素都会对GPS信号产生影响，导致信号传播延迟或折射，从而引起定位误差。

4. 载波相位等伪距测量误差：GPS定位是通过测量卫星发射的信号和接收器接收的信号之间的时间差来计算位置的。

然而，由于载波相位的波长较短，测量精度更高，但受到多普勒效应的影响，会产生伪距测量误差。

二、减小GPS定位误差的方法：1. 多路径效应抑制：多路径效应是指GPS信号在传播过程中发生反射、散射等现象，致使接收器接收到多个信号，在信号合成过程中引入误差。

为了减小多路径效应，可以利用天线设计和信号处理技术，选择适合的接收天线和增加抗多路径干扰的算法。

2. 差分定位：差分定位是通过引入一个参考站与基准站的距离进行辅助定位，利用参考站的精确位置和信号传播速度信息来对GPS定位结果进行修正。

差分定位可以大幅度减小系统误差和信号传播误差的影响，提高定位精度。

3. 增加卫星数量和分布：通过增加卫星数量和改善卫星的空间分布，可以提高GPS定位的可见卫星数目和几何配置，从而减小定位误差。

可以使用卫星信噪比、可视卫星数等指标来优选卫星，并避开存在遮挡物的区域。

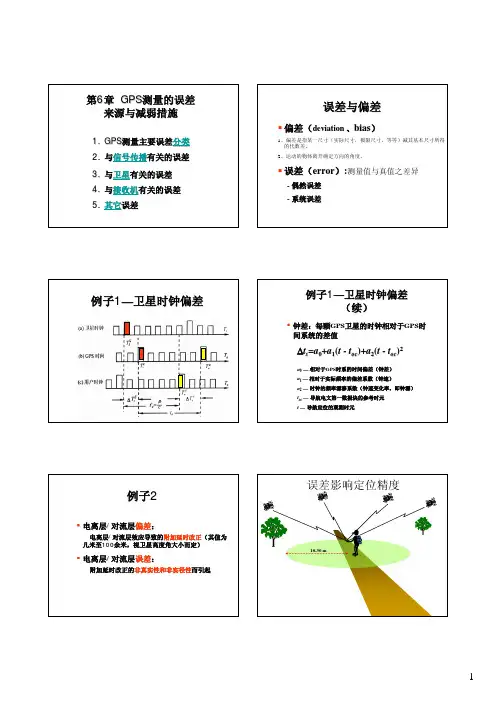
误差影响定位精度10-30 m接收机天线相位中心的偏移和变化消除或消弱各种误差影响的方法①•模型改正法–原理：利用模型计算出误差影响的大小，直接对观测值进行修正–适用情况：对误差的特性、机制及产生原因有较深刻了解，能建立理论或经验公式–所针对的误差源•相对论效应•电离层延迟•对流层延迟•卫星钟差–限制：有些误差难以模型化改正后的观测值=原始观测值+模型改正•求差法–原理：通过观测值间一定方式的相互求差，消去或消弱求差观测值中所包含的相同或相似的误差影响–适用情况：误差具有较强的空间、时间或其它类型的相关性。

–所针对的误差源•电离层延迟•对流层延迟•卫星轨道误差•…–限制：空间相关性将随着测站间距离的增加而减弱消除或消弱各种误差影响的方法②消除或消弱各种误差影响的方法③•参数法–原理：采用参数估计的方法，将系统性偏差求定出来–适用情况：几乎适用于任何的情况–限制：不能同时将所有影响均作为参数来估计消除或消弱各种误差影响的方法④•回避法–原理：选择合适的观测地点，避开易产生误差的环境；采用特殊的观测方法；采用特殊的硬件设备，消除或减弱误差的影响–适用情况：对误差产生的条件及原因有所了解；具有特殊的设备。

–所针对的误差源•电磁波干扰•多路径效应–限制：无法完全避免误差的影响，具有一定的盲目性6.1 GPS测量误差分类及对距离测量的影响与信号传播有关的误差与卫星有关的误差与接收机有关的误差其它误差•对流层折射•电离层折射•多路径效应•星历误差•卫星钟差•相对论效应•接收机钟差•位置误差•天线相位中心的偏差及变化•各通道间的信号延迟误差•地球潮汐1.5-15m1.5-15m1.5-5m1. m6.2 与信号传播有关的误差电离层折射对流层折射多路径误差电离层中的气体分子由于大气折射效应）利用电离层改正)(2cos P T t P-π∑3ϕαDC =5ns T P =14hαn 和βn ：由导航tropion N δρδρλ++- 6.2.2对流层折射▪离地面高度40km 以下的大气层，是一种非电离大气层。

卫星导航接收机定位误差分析摘要：卫星导航接收机主要功能是进行位置结算为用户提供精确位置信息，同时兼具授时功能。

定位精度是导航接收机最为重要的一项指标，定位精度越高说明接收机解算出的位置坐标与接收机当前真实位置坐标之间的差距就越小。

影响卫星导航接收机定位误差的因素主要有三个方面，分别是卫星相关误差、空间传播相关误差以及用户设备误差。

本文针对不同情况下的卫星导航接收机的误差进行分析和总结，并且给出了一些可行的误差处理对策。

关键词：卫星导航；接收机；误差分析1、卫星导航接收机定位误差分析1.1、卫星相关误差分析卫星星历主要用于描述导航星的特定位置及其在宇宙中的空速。

卫星星历也可以称为两行轨道数据，具体来说，其是一种表达式，主要用于对描述卫星的具体位置以及飞行速度。

卫星星历在在卫星时间、坐标以及方位等等多个数值的测定上，需要结合开普勒定律，在多年的应用中已经形成了较高的精度。

卫星星历是由地面监控站跟踪监测卫星来求得的，但是卫星在运行时，会受到多个摄动力的影响，但是仅仅应用地面监控站又不易测定其中的作用规律，所以这样看来，星历预报也会产生一定的误差。

星历计算过程中所产生的卫星空间位置和实际位置之间的差距则是卫星星历误差，也可以称为时钟钟差。

1.2、信号传播误差（1）电离层误差。

电离层是指距离地面60千米或以上的大气层，这部分大气大多处于电离状态，所以存在大量的电子和离子，会影响到无线电波传播速度，从而出现折射以及反射问题。

卫星的信号在通过电离层时，信号路径会出现一定的扭曲，相应地，传播和速度也无法完全维持原样，所以信号的传播时间并不能完全代表距离，这样引起的误差就称为电离折射层误差。

（2）对流层误差。

对流层是指高度为40km以下的大气，对流层构成了大气质量的绝大多数，质量大约占据了99%。

该区域的大气密度高，运行情况也较为复杂，所以信号传播速度以及路径都会造成一定的影响。

1.3、接收机设备的误差卫星导航系统要求导航星座和导航接收机之间的时钟也必须同步，两者之间的差称为接收机的时钟差。

GPS接收机伪码测距方法及误差分析夏俊【摘要】根据全球定位系统(GPS)的信号特点,介绍了GPS接收机利用L1频段C/A码进行伪码测距的原理和方法,提出了一种简单、易行的位同步环设计方法,并与传统设计方案进行了对比.最后,对影响伪距测量值的因素进行了讨论,给出了误差计算的方法,分析了对测距精度的影响.【期刊名称】《电讯技术》【年(卷),期】2010(050)008【总页数】4页(P26-29)【关键词】GPS接收机;伪码测距;位同步;电路设计;误差分析【作者】夏俊【作者单位】成都天奥信息科技有限公司,成都,611731【正文语种】中文【中图分类】P228;V5561 引言全球定位系统(GPS)的不断完善使得GPS接收机在导航定位中得到了广泛的应用。

要实现导航定位，必须获得卫星到接收机的距离。

GPS通过测量信号从位置已知的发射源(卫星)发出至到达用户接收机所经历的时间，乘以信号的速度(光速)，便得到从发射源到接收机的距离[1]。

GPS卫星信号包含有数据码D(t)、测距码(C/A码和P码)和载波(L1和L2)3种成分。

C/A码是伪码，码的速率是1.023 MHz，码长1 023位，周期为1 ms。

C/A 码具有很好的自相关性和很弱的互相关性，每一颗卫星有一种固定的C/A码。

接收机可以利用码的自相关性和互相关性对不同的卫星信号进行接收。

导航电文，即包含导航信息的数据码，是二进制编码文件按规定格式组成的数据帧，有严格的时间标记。

根据GPS卫星信号的特点，利用伪随机码的相关技术测距，实现比较简单，被广泛采用。

本文阐述了GPS接收机伪码测距原理，介绍了测距方法，详细分析了伪码测距的误差。

实际应用证明，本文提出的伪距测量方法相比传统方法更简单、便捷。

2 伪距的测量2.1 伪距定义到卫星i的伪距(单位m)定义如下：ρi=c[TR(n)-TTi(n)](1)式中，c=299 792 458 m/s为光速，TR(n)表示与GPS接收机时钟第n历元相对应的接收时刻(单位s)；TTi(n)表示基于卫星i时钟的发射时刻(单位s)。

卫星导航系统的误差分析与校正在当今的科技时代，卫星导航系统已经成为我们日常生活中不可或缺的一部分。

无论是出行导航、物流运输，还是地质勘探、农业生产等领域，都离不开卫星导航系统的精准定位服务。

然而，卫星导航系统并非完美无缺，其存在着一定的误差。

为了更好地利用卫星导航系统，提高定位精度，对其误差进行分析与校正就显得尤为重要。

卫星导航系统的误差来源多种多样，大致可以分为三类：与卫星相关的误差、与信号传播有关的误差以及与接收机相关的误差。

首先，与卫星相关的误差主要包括卫星星历误差和卫星钟误差。

卫星星历是描述卫星运行轨道的一组参数，由于卫星在太空中受到各种引力和非引力的影响，其实际运行轨道与预测的星历可能存在偏差，从而导致定位误差。

卫星钟误差则是由于卫星上的原子钟与地面标准时间存在差异而产生的。

尽管卫星钟的精度已经非常高，但微小的时间偏差在经过距离计算后仍可能导致较大的定位误差。

其次，信号传播过程中的误差也不可忽视。

电离层延迟是其中的一个重要因素。

当卫星信号穿过电离层时，电离层中的自由电子会使信号的传播速度发生变化，从而导致信号传播时间的测量出现误差。

对流层延迟同样会影响信号传播。

对流层中的水汽和大气压力的变化会使信号的传播路径发生弯曲，进而造成定位误差。

多路径效应也是常见的问题。

当卫星信号到达接收机时，可能会通过多条不同的路径，例如建筑物反射、水面反射等，这些不同路径的信号相互叠加，会干扰接收机对主信号的准确测量。

最后，接收机自身也可能引入误差。

接收机的钟差就是一个例子，接收机内部的时钟与卫星钟不同步，会导致时间测量的误差。

此外，接收机的位置误差、天线相位中心偏差等也会对定位结果产生影响。

为了减小这些误差，提高卫星导航系统的定位精度，科学家们采取了一系列的校正方法。

针对卫星星历误差和卫星钟误差，地面控制站会对卫星进行持续监测，并通过上传修正参数来对卫星的轨道和时钟进行修正。

同时，利用多个地面监测站组成的监测网，可以更加精确地确定卫星的位置和时钟偏差，从而提高星历和钟差的精度。

全球定位系统测量的误差分析与校正方法全球定位系统（Global Positioning System, GPS）是一项广泛应用于航海、航空、交通、军事等领域的全球导航卫星系统。

然而，由于各种因素的影响，GPS测量的定位结果可能存在一定的误差。

因此，进行误差分析与校正是提高GPS定位精度的关键。

本文将从GPS接收机误差、大气延迟误差和卫星系统误差三个方面探讨全球定位系统测量的误差分析与校正方法。

GPS接收机误差是GPS定位误差中的一个重要组成部分。

接收机的硬件和软件设计不尽相同，从而导致接收机的性能差异。

常见的误差包括钟差误差、多路径效应误差和接收机噪声误差。

钟差误差是由于接收机内部的时间标准与卫星时间标准之间存在微小差异而产生的。

解决方法可以通过接收机校准或使用精密钟件进行补偿。

多路径效应误差是由于信号在传播过程中发生反射或折射而导致的，造成接收机接收到多个信号，产生干扰和延迟。

采用天线切换、消除阴影区域或利用接收机软件滤波等方法可以减小多路径效应误差。

接收机噪声误差是由于接收机自身电路和放大器的噪声引起的，可以通过接收机硬件的升级或降低接收机工作温度来减小。

大气延迟是导致GPS定位误差的另一个主要因素。

GPS信号传播过程中，会受到大气层的影响，引起信号的传播速度变化，从而导致定位误差。

大气延迟误差主要包括对流层延迟和电离层延迟。

对流层延迟是由于大气中不同折射率导致信号传播速度的变化，可以通过接收机观测多颗卫星来消除对流层延迟误差。

电离层延迟是因为电离层中自由电子的存在导致信号的相位发生变化，采用双频接收机的技术可以减小电离层延迟误差。

卫星系统误差是GPS定位误差的另一个重要组成部分。

卫星时钟误差、星历误差和卫星几何分布误差都会对GPS定位结果产生影响。

卫星时钟误差是由于卫星时钟的不精确造成的，可以通过接收机观测多颗卫星进行校准。

星历误差是由于卫星轨道参数估计不准确而导致的，可以使用差分定位或采用改进的星历算法来消除。

rtk点位中误差计算RTK点位中误差计算RTK（Real-Time Kinematic）是一种实时运动定位技术，通过接收卫星导航系统的信号，利用测距原理实现对移动物体的精确定位。

在RTK定位中，误差是不可避免的，而误差的计算对于定位精度的评估和改进至关重要。

误差来源主要包括卫星信号误差、接收机误差、大气误差、多路径误差等。

为了准确计算RTK点位中的误差，我们需要了解各个误差来源，并采取相应的措施进行校正。

下面将详细介绍各个误差来源以及相应的误差计算方法。

1. 卫星信号误差卫星信号误差主要包括钟差误差、星历误差、轨道误差等。

这些误差会导致卫星定位信号与真实位置之间存在一定的偏差。

对于这些误差，我们可以通过接收多颗卫星的信号进行差分处理，消除或减小其影响。

2. 接收机误差接收机误差包括接收机的硬件误差和信号处理误差。

硬件误差主要来自于接收机内部的时钟精度、频率稳定性等因素，而信号处理误差则与接收机的算法和处理能力有关。

为了减小接收机误差，可以选择高精度的接收机设备，并进行相关的校准和调试。

3. 大气误差大气误差主要包括电离层延迟、对流层延迟等。

这些误差会导致卫星信号在穿过大气层时发生折射，从而影响定位的精度。

为了消除大气误差的影响，可以通过接收多颗卫星的信号进行差分定位，利用差分信号计算出大气误差，并进行相应的校正。

4. 多路径误差多路径误差是指卫星信号在传播过程中遇到障碍物后，发生反射、绕射等现象导致的误差。

这种误差会导致接收机接收到来自不同路径的信号，从而影响定位的准确性。

为了减小多路径误差，可以选择合适的接收机天线，避免信号的反射和绕射，或者通过信号处理算法进行多路径抑制。

对于以上各个误差来源，我们可以通过以下方法来计算RTK点位中的误差：1. 静态定位法静态定位法是通过静止不动的方式进行定位，利用接收到的卫星信号进行测量和计算。

通过记录一段时间内的观测数据，并进行差分处理，可以得到相对较为准确的定位结果。

北斗卫星导航系统URE与定位精度分析贾蕊溪;董绪荣;尚晨;王军【摘要】Beidou satellite navigation system has possessed a regional passive navigation capability. In order to study the po-sitioning accuracy of Beidou system in the case of currently available constellations,the calculation model of the user equivalent range error(UERE)and accuracy assessment method combining dilution of precision(DOP)value is analyzed in this paper. By using the above method and the actual data,the static positioning accuracy in a period of time of Beidou system and GPS sys-tem is compared and analyzed. The analysis result indicates that,during this period,Beidou system positioning accuracy error is less than 5 m in the horizontal direction and 15 m in height direction.%北斗卫星导航系统已具有区域无源导航能力，为了研究当前可用星座情况下的系统定位精度，首先分析用户等效测距误差（UERE）结合精度因子（DOP）值的精度评估方法计算模型，然后利用上述方法采用实际数据对比分析了北斗卫星导航系统和GPS系统一段时间内的静态定位精度。

m
•利用同步观测值求差：当观测站间的距离较近（小于20km）时，卫星信号到达不同观测站的路径相近，s通过同步求差，残差不超过
10-6。
数字分析表明，上述残差对GPS的影响最大可达70ns，对卫星钟速的影响可达，显然此影响对精密定位不能忽略。
在GPS定位中，除了上述各种误差外，卫星钟和接收机钟震荡器的随机误差、大气折射模型和卫星轨道摄动模型误差、地球潮汐以及
GPS测量的误差来源
§观测量的误差来源及其影响
1.误差的分类 GPS定位中，影响观测量精度的主要误差来源分为三类：
•与卫星有关的误差。
•与信号传播有关的误差。
•与接收设备有关的误差。
为了便于理解，通常均把各种误差的影响投影到站星距 离上，以相应的距离误差表示，称为等效距离误差。
测码伪距的等效距离误差/m
•引入相应的未知参数，在数据处理中联同其它未知参数一并求解。
卫星的轨道误差是当前GPS定位的重要误差来源之一。
W a （2）卫星轨道偏差（星历误差）：
（3）载波相位观测的整周未知数
m
f c f W ga (1R) 在狭义和广义相对论的综合影响下，卫星频率的变化为： 目前，通过导航电文所得的卫星轨道信息，相2应的位置误2差约200-40路设计。
•利用同步观测值求差：当观测站间的距离较近（小于20km）时，卫星信号到达不同观测站的路径相近，通过同步求差，残差不超过
不可避免地存在钟差和漂移，偏差总量约在 内，引起 1 ms 10-6。
在GPS定位中，除了上述各种误差外，卫星钟和接收机钟震荡器的随机误差、大气折射模型和卫星轨道摄动模型误差、地球潮汐以及
5.0-10.0 2.0 1.2 0.5 5.5-10.3
7.5 0.5 7.5

2 2 2 σ0 = ( a b c ( 6) 3σ 1 ) +( 3 σ2 ) +( 3σ 3) 若 σ1 =σ2 = σ3 , 三 频一 阶修 正 后观 测噪 声 放大 倍
数为 m3 =
2 2 2 a 3 +b 3 +c 3
( 7)
4 应用
以 G a l i l e o 卫星导航定位 系统为例 , 其四个 典型载 波的 中心频率值及相应调 制方式下的测距噪声如表 1 所示 [ 4] 。 根据公式 ( 2) ～ ( 7)分 析不同修 正方法 和不同 频率组 合等多种情 况下 电 离层 延迟 修 正中 伪距 观 测噪 声 的影 响 , 结果见表 2。 其中 , 放大后的伪距噪声指表 1 中相应频点的
( 2)
( 3) 3. 2 三频修正 三频观测 的频 点 为 f 1 , f 2 , f 3 , 对应 的 伪距 观 测量 为
m1 =
2 2 a +b 1 1
第 4 期 王梦丽等 三种电离层延迟多频修正算法的比较 ρ , ρ , ρ 。 假 设三 个伪 距 观 测量 的 观测 噪 声为 n 、n , 1 2 3 1 2
3 三种电离层延迟多频修正算法
双频修正采 用两个 频点 的数据 , 能够修 正电 离层 效应 的一阶项 ;三频 修正 采用三 个频 点的数 据 , 能够 修正 电离 层效应的一 阶项和 二阶 项 , 也可 以只修 正到 一阶项 , 本文 分别定义为三频二阶修 正和三频一阶修正 [ 2 , 3 ] 。 3. 1 双频修正 双频观测的频点为 f 1 , f 2 , 对应的伪距观测量为 ρ 1 , ρ 2 。 假设两个伪距观测量 的观测噪声 为 n 、 n , 且 E [ n ] = 1 2 1 2 2 2 2 0, E [n [n [n [n 1 ] =σ 1 , E 2] =0, E 2 ] =σ2 , E 1n 2] =0。 忽略电离层延迟二阶及 以上各项 , 伪距观测量可以表示为 A 1 ρ ,( i= 1, 2) i =ρ 0 + 2 +n i f i 双频修正后伪距 ρ 0 的估计值 ρ 0 =a 1ρ 1 +b 1ρ 2 其中 , 2 f 1 a 1 = 2 2 f f 12 2 f 2 b 1 = 2 2 f f 12 的噪声 ( 均方差 ) 放大为 ρ 0

GPS定位误差的产生原因分析与减小方法导言全球定位系统（GPS）已成为现代社会中广泛应用于导航、地理测量和定位等领域的重要技术。

然而，在使用GPS时，我们常会遇到定位误差的问题。

本文将分析GPS定位误差产生的原因，并探讨减小定位误差的方法。

一、多普勒效应引起的频率偏移误差GPS定位是通过接收来自卫星的信号并测量其到达时间来确定位置的。

然而，卫星和接收器之间的运动会引起多普勒效应，导致接收器测量的信号频率偏离真实频率。

这会导致接收器估计的距离与实际距离之间存在误差。

为了减小多普勒效应带来的误差，可以采用快速信号处理算法和精确的频率模型来纠正频率偏移。

二、大气延迟引起的距离误差GPS信号在穿过大气层时会受到大气延迟的影响，从而导致接收器估计的距离与实际距离之间存在偏差。

大气延迟主要由电离层延迟和对流层延迟组成。

为了减小大气延迟带来的误差，可以通过使用多频信号进行差分定位、引入大气误差模型进行修正以及使用增强的大气改正模型来提高定位精度。

三、钟差引起的时间误差卫星和接收器的时钟不可能完全同步，这会导致接收器估计的时间与实际时间之间存在差异。

这个差异会引起接收器估计的距离与实际距离之间的误差。

为了减小时钟差带来的误差，可以使用差分定位技术来修正时间误差，并利用接收器内部的时间校准机制来提高时钟的准确性。

四、多径效应引起的信号衰减误差当GPS信号在传播过程中发生反射或折射时，会产生多径效应，导致接收器接收到的信号变弱或出现多个传播路径，从而影响定位精度。

为了减小多径效应带来的误差，可以采用抗多径干扰技术，如采用天线阵列、时延估计和信号处理算法等来抑制多径干扰。

五、精度限制引起的测量误差GPS接收器自身的精度限制也会导致定位误差。

接收器的硬件设计和信号处理算法的精度限制都会影响最终的定位精度。

为了减小精度限制带来的误差，可以采用高精度的接收器硬件设计和先进的信号处理算法，以提高定位的准确性。

六、综合多种减小误差方法为了进一步提高GPS定位的精度，可以综合应用上述减小误差的方法。