立体的相贯线画法指导
- 格式:ppt
- 大小:1.42 MB
- 文档页数:48
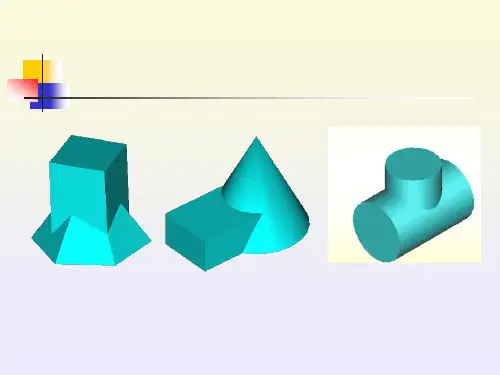

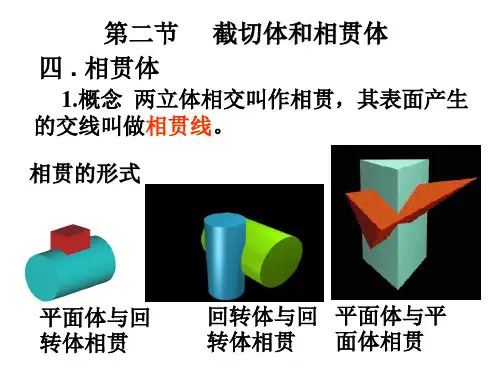


第十一章立体的相贯线§11-1概述§11-2平面立体与平面立体相贯§11-3平面立体与曲面立体相贯§11-4曲面立体与曲面立体相贯§11-1概述1.相贯线——两立体表面的交线。
相贯线是两立体表面的共有线,相贯线上的点是两立体表面的共有点。
2.相贯线的性质——是两立体表面的共有线,相贯线上的点是两立体表面的共有点。
3.相贯线的形式——随着立体形状、大小和相对位置的不同而不同。
§11-2 平面立体与平面立体相贯一、两平面立体的相贯线二、求两平面立体相贯线的方法三、相贯线可见性的判别原则四、例题一、两平面立体的相贯线两平面立体的相贯线是两立体表面的共有线,相贯线上的点是两立体表面的共有点。
二、求两平面立体相贯线的方法第一种方法求各侧棱对另一形体表面的交线,然后把位于形体1同一侧棱面又位于形体2同一侧棱面上的两点,依次连接起来。
第二种方法求一形体各侧棱面与另一形体各侧棱面的交线。
三、相贯线可见性的判别原则只有位于两形体都可见的侧面上的交线,才是可见的。
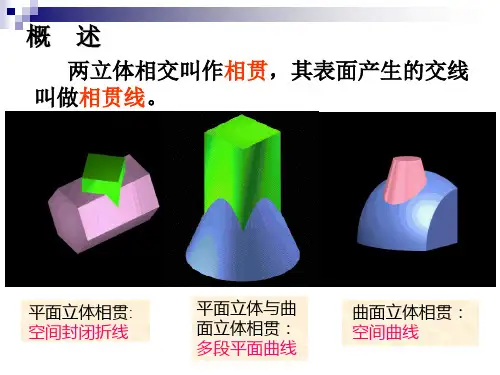
例题平面立体与平面立体相贯1平面立体与平面立体相贯2平面立体与平面立体相贯3平面立体与平面立体相贯4屋脊线斜脊线天沟线平面立体与平面立体相贯5§11-3平面立体与曲面立体相贯平面立体与曲面立体相贯时,相贯线由若干段平面曲线或平面曲线和直线组成。
各段平面曲线或直线,就是平面体上各侧面截割曲面所得的截交线。
每一段平面曲线或直线的转折点,就是平面体的侧棱与曲面体表面的交点。
例题平面立体与曲面立体相贯1a" aa" aa" a平面立体与曲面立体相贯4平面立体与曲面立体相贯5平面立体与曲面立体相贯6平面立体与曲面立体相贯7平面立体与曲面立体相贯8平面立体与曲面立体相贯9平面立体与曲面立体相贯10§11-4 两曲面立体相贯一、两曲面立体相贯线的性质二、相贯线的三种基本形式三、两曲面立体相贯线的求法四、相贯线上共有点的求法五、例题六、相贯线的特殊情况一、相贯线的性质1 、一般情况下,相贯线为封闭的空间曲线。
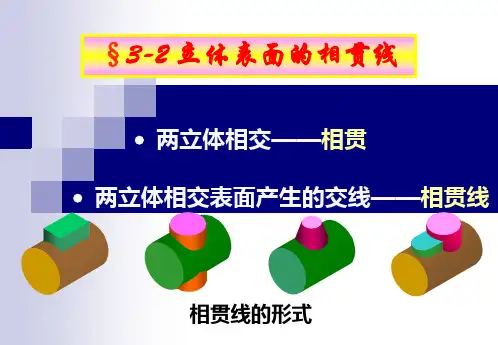



第五节 两曲面立体的相贯线[Intersection of Two Curved Surface Solids]两曲面体的相贯线,一般是封闭的空间曲线。
此类相贯线在建筑形体中常常会遇到,例如图5-19所示,它是由一系列柱面相贯所形成的屋顶。
组成相贯线的所有点,均为两曲面体表面的共有点。
因此求相贯线时,要先求出一系列的共有点,然后用曲线板依次连接所求各点,即得相贯线。
求共有点时,应先求出相贯线上的特殊点,即最高、最低、最左、最右、最前、最后及转向轮廓线上的点等,然后再求出其上的一般位置点。
一、求相贯线常用的两种方法 [Two Commonly Used Methods to Find Intersection Line ](一) 利用曲面的积聚投影,用表面取点法作出相贯线相交两曲面之一,如果有一个投影具有积聚性,就可以利用该曲面的积聚性投影作出两曲面的一系列公有点,然后连成相贯线。
因为如果有一个曲面的某投影具有积聚性,相贯线在此投影面上的投影就已知,求相贯线的其余投影,实质上就是根据这一已知投影在另一立体的表面取点。
因此,此法也叫表面取点法。
例5-10 已知两半圆柱屋面相交,求它们的交线,如图5-20所示。
投影分析:由图5-20可知:屋面的大拱是半圆柱面,小拱则也是半圆柱面。
前者素线垂直于W 面,后者素线垂直于V 面,两拱轴线相交且平行于H 面。
相贯线是一段空间曲线,其V 面投影重影在小圆柱的V 面投影上,W 面投影重影在大拱的W 面投影上,相贯线的H 面投影为曲线,可通过求出相贯线上一系列的点而作出。
图5-19由柱面相贯构成的屋面作图步骤(图5-20):(1) 求特殊点。
最高点A 是小圆柱最高素线与大拱的交点,最低、最前点B 、C (也 是最左、最右点),是小圆柱最左、最右素线与大拱最前素线的交点。
它们的三投影均可直接求得。
(2) 求一般点E 、F 。
在相贯线V 面投影的半圆周上任取点e ′和f ′。