不确定性

如何在不确定性下做出明确的判断？在生活中，我们经常会遇到各种不确定性的情况，如未知的风险、未知的未来等等，这些不确定性因素容易对我们的决策产生影响，使我们难以做出明确的判断。

但是，如何在不确定性下做出明确的判断呢？本文将介绍几种应对不确定性的策略。

一、收集信息在面对不确定性的情况时，我们应该首先收集尽可能多的信息来降低不确定性。

通过收集信息，可以了解到更多的细节和背景信息，从而更好地了解问题的本质。

收集信息可以通过多种形式实现，如查阅资料、咨询专业人士、探求相关的经验等等。

二、分析概率通过概率分析，可以更好地了解未知的风险或事件发生的可能性。

这种方法适用于需要权衡多种因素的情况，通过分析每种因素的发生概率，可以得到更清晰的决策。

三、制定计划在不确定性的情况下，制定计划可帮助我们更好地应对突发情况。

计划制定需要合理地评估未来可能出现的情况，根据预测的情况，制定相应的应对措施，以最小的代价应对最坏的情况。

四、多方面考虑在决策时，我们不应只关注一方面的因素，而应全面考虑。

从经济学的角度，应该考虑成本与效益，从法律的角度，应该考虑是否符合规定等。

全面考虑可能使决策的质量更高，层次更清晰，更利于长远发展。

五、自我反省在做出决策后，我们应该对自己的决策进行反省。

通过反思，可以了解自己的决策思路是否合理，是否有失误之处，对于下次做出决策是具有参考意义的。

总之，在不确定性下做出明确的判断需要运用多种策略，如收集信息、分析概率、制定计划、多方面考虑和自我反省。

仅靠单方面的思考往往会导致偏颇的决策，因此我们应该注重多元思考，在对未来做出决策之前，了解问题的本质和潜在风险，根据实际情况综合考虑，尽量得出更准确、更合理的结论。

不确定性原理和测不准性不确定性原理和测不准性是量子物理学中的两个基本概念。

不确定性原理指的是，在某些情况下，我们无法同时准确地测量一个粒子的位置和动量。

测不准性是指，无论我们如何精密地测量一个粒子的位置或速度，我们都会存在一定的测量误差。

这些概念为量子力学的基本思想提供了重要的支持。

不确定性原理最初是由德国著名物理学家海森堡在1927年提出的。

他认为，在对一个粒子的位置和动量进行测量时，它们之间存在固有的不确定性。

具体来说，如果我们精确地测量了一个粒子的位置，那么它的动量就会变得不确定，反之亦然。

其背后的原因是，在量子力学中，测量本身会对待测系统产生干扰，这个干扰的大小与测量的精度成正比。

因此，在测量的过程中，测量设备和待测系统之间无可避免地会发生相互作用，导致求解粒子位置和动量的过程变得复杂。

实际上，不确定性原理已经被实验证实。

例如，我们可以通过强制粒子到一个非常小的区域内，并观察它的位置和速度的变化。

这个过程中，我们就会发现，当我们测量位置时，速度变得不确定，否则测量速度，位置就变得不确定。

因此，不确定性原理无疑是量子力学中最基础的原理之一。

它告诉我们，世界上并不存在完全可预测的物体。

这就是说，即使我们了解了粒子的所有属性，我们仍旧无法完全预测它在某一时刻的状态。

不确定性原理的含义是什么？我们可以从物理意义上解读这个原理。

首先，不确定性原理阐述了量子物理学中物理量的局部性质，这意味着测量一个粒子的属性并不能反映出整个系统的性质。

其次，不确定性原理还告诉我们，粒子的位置和动量测量值不是独立的。

这是因为，在测量位置时，我们使系统的状态发生了变化，从而影响了测量动量的程序。

因此，如果我们任何一个物理量变得越精确，它就会对其他物理量的测量产生更大的影响。

不确定性原理是量子力学的基础之一，它揭示了自然界中的局限性。

但是，实验界越来越关注的是测不准性问题，即我们是否可以准确地测量一个量子系统的位置或动量。

不确定性原理概述：不确定性原理是量子力学中的基本原理之一，由德国物理学家海森堡于1927年提出。

该原理指出，在量子力学中，无法同时准确确定粒子的位置和动量，或者说粒子的位置和动量具有一定的不确定性。

不确定性原理改变了人们对物理世界的认识，揭示了微观世界的本质。

1. 不确定性原理的基本概念不确定性原理包括位置-动量不确定性原理和能量-时间不确定性原理两个方面。

位置-动量不确定性原理指出，粒子的位置和动量不能同时被准确测量，其测量结果存在一定的不确定性。

能量-时间不确定性原理则表明，粒子的能量和存在时间也存在一定的不确定性。

2. 位置-动量不确定性原理位置-动量不确定性原理可以用数学表达式来描述，即Δx·Δp ≥ h/2π，其中Δx为位置的不确定度，Δp为动量的不确定度，h为普朗克常数。

这意味着，当我们试图准确测量粒子的位置时，其动量的不确定度会增大；反之，当我们试图准确测量粒子的动量时，其位置的不确定度会增大。

3. 能量-时间不确定性原理能量-时间不确定性原理可以用数学表达式来描述，即ΔE·Δt ≥ h/2π，其中ΔE为能量的不确定度，Δt为时间的不确定度。

这意味着，当我们试图准确测量粒子的能量时，其存在时间的不确定度会增大；反之，当我们试图准确测量粒子的存在时间时，其能量的不确定度会增大。

4. 不确定性原理的实验验证不确定性原理的实验验证是通过一系列精密的实验来观察和测量微观粒子的行为得出的。

例如，双缝干涉实验就是一种经典的实验，通过在射出粒子的路径上设置两个狭缝，观察粒子在屏幕上形成的干涉条纹，从而验证了不确定性原理。

5. 不确定性原理的意义和应用不确定性原理的提出对物理学产生了深远的影响。

它揭示了微观世界的本质，推翻了经典物理学中对粒子位置和动量的确定性认识。

不确定性原理也被广泛应用于量子力学的研究和技术应用中，如量子计算、量子通信等领域。

6. 不确定性原理的局限性不确定性原理并不意味着我们无法获得任何关于粒子位置和动量的信息，而是指在某一时刻上我们无法同时准确获得它们的值。

在不确定性中寻找确定性
不确定性是指未来的不可知,也就是说在做出一个决策之前你无法准确预测它会发生什么. 确定性是指已经知道了结果,而且这种结果已经被事先明确规定下来了(如数学上的定理).所以从本质上讲,确定性和不确定性没有区别,只是表现形式不同罢了.
当然我们说“不确定”并非意味着绝对的不可能,只要掌握好时机,合适的时候去做正确的事情还是很有把握的!但“不确定”毕竟是客观存在的,所以为了避免盲目地冒险,人类才需要寻找相应的方法或者工具来帮助自己更加精确、快速地达到既定目标。

因此,寻求确定性是人类行动中永恒的主题。

在实际操作过程中,通常将不确定性分成两部分:第一部分是外界环境带给我们的不确定性;第二部分则是由于我们内心造成的不确定性。

1、确定性与不确定性都属于随机变量,其统计特征完全相反,即均服从正态分布,都是连续型随机变量,都遵循概率论基础。

2、确定性与不确定性又各有侧重点。

3、确定性强调稳定性,注重长期趋势,偏向于宏观研究;不确定性强调波动性,注重短期走势,偏向于微观研究。

4、不确定性与风险是紧密联系的,高度关注不确定性问题,积极防范和化解风险隐患,努力提升抵御风险挑战的能力。

5、在市场交易活动中,投资者必须充分认识到不确定性的危害及影响,树立起风险管理意识,建立健康良好的心态。

唯一确定的，就是不确定性人生充满了变数，充满了不确定性。

我们总是想要在不确定的世界中寻找一些确定性，然而唯一确定的，就是不确定性本身。

这种悖论似乎让人感到迷茫，但也正是这种迷茫，让我们更加珍惜每一刻，更加珍惜身边的人和事物，更加努力地前行。

不确定性是人生的常态，无论是个人发展还是世界的变迁，都充满了各种变数。

在这个充满了挑战和机遇的时代，我们需要学会接受和适应不确定性，而不是试图逃避或者抗拒。

在人生的道路上，我们会面对各种抉择和挑战，我们需要学会在不确定的情况下做出决策，把握机会，迎接挑战。

不确定性也是激励人们前行的动力。

正因为不确定性，我们才会充满期待地去面对未来，才会更加珍惜眼前的幸福和快乐。

在经历过种种变数和挫折之后，我们更加明白生命的可贵，更加懂得珍惜每一个美好的瞬间。

正是不确定性让我们不停地前行，不停地探索，不停地创新。

正是不确定性造就了我们今天所看到的世界，助力我们不断进步。

不确定性也会给我们带来困惑和焦虑。

在面对不确定的未来时，我们往往难以预测和控制一切。

这时，我们需要学会放下焦虑，从容面对不确定性，接受它的存在。

只有在接受不确定性的基础上，我们才能更加淡定地思考和行动，更加理智地做出决策。

不确定性还会让我们更加谦卑。

当我们意识到自己并不能完全掌控未来时，我们就会更加谦卑地对待周围的人和事物，更加珍惜眼前的幸福。

我们会明白，每一个瞬间都是宝贵的，每一次相遇都是意义非凡的。

正是不确定性，让我们更加懂得珍惜眼前的一切，更加感恩拥有的每一份美好。

面对不确定的未来，我们需要保持乐观。

即使种种困难和挑战都会在我们前行的路上出现，我们也要相信，只要我们坚定信念、勇敢面对，就一定能够克服一切困难，迎接未来的挑战。

乐观的态度和积极的心态，是面对不确定性时的最好武器。

为了更好地面对不确定性，我们也需要有所准备。

我们可以通过不断学习和提升自己的能力，来增强应对不确定性的能力。

只有当我们不断丰富自己的知识和技能，提高自己的素养和能力时，我们才能更加从容地面对不确定的未来，更加灵活地应对各种挑战。

关于不确定性的心得体会关于不确定性的心得体会不确定性是生活中无法避免的一部分。

无论我们多么努力地计划和预测，总会面临各种意外和变化。

在面对不确定性时，我们往往会感到焦虑和困惑。

然而，我在经历了一些不确定性的时候，逐渐认识到了它的价值和意义。

下面是我对于不确定性的一些心得体会。

首先，不确定性是人生的一种常态。

没有谁能掌控自己的未来或预测一切的结果。

就像法国哲学家布莱兹·帕斯卡曾说过的：“人的生命始终是一场赌博”。

我们所能做的就是接受这个事实，以一种积极的态度去面对它。

不确定性的存在使得我们的生活充满了变数和挑战，它促使我们寻找新的解决方案和适应新的环境，从而让我们不断成长和进步。

其次，不确定性是一种机遇。

虽然我们常常希望一切都能按照我们的计划进行，但如果一切事情都是确定的，生活将会变得乏味和缺少挑战。

不确定性让我们有机会去尝试新的事物，发现新的可能性。

它激发了我们的创造力和想象力，让我们能够突破自己的局限，实现个人和职业的成长。

第三，不确定性教会了我学会适应和调整。

当我们面对不确定的情况时，往往会感到困惑和无助。

但正是这种不确定性推动着我们寻找更好的解决方案和方法来适应新的情况。

我们需要灵活地调整自己的计划和目标，不断适应环境的变化。

这样的经历让我在遇到挫折和困难时更加坚韧，更好地适应各种变化。

此外，不确定性也教会了我珍惜当下。

当我们意识到未来的结果是无法预测的时候，我们会更加珍惜当前的时刻。

我们会更加关注眼前的事情，真正体验生活的乐趣。

这样的心态让我更加积极地面对每一天，享受生活中的各种美好和精彩。

最后，不确定性让我成为一个更有耐心和坚韧的人。

当我们面临不确定的情况时，往往需要等待并持续努力。

这个过程需要耐心和勇气，因为我们永远无法预测结果会是怎样的。

但正是在这个等待和努力的过程中，我们能够锻炼自己的决心和坚韧，不轻易放弃。

总而言之，不确定性是我们人生中必然存在的一部分。

它让我们面对各种挑战和变化，激发我们的创造力和想象力，让我们能够适应新的情况，并珍惜每一刻。

如何处理测量中的不确定性问题测量是科学研究和应用中不可或缺的一部分，它提供了实验数据以支持理论验证、质量控制和决策制定。

然而，测量结果往往是不确定的，即使使用最先进的仪器和精确的方法进行测量。

因此，正确处理测量中的不确定性问题对于保证数据的可靠性和正确性至关重要。

在处理测量中的不确定性问题时，首先需要理解不确定性的来源。

测量不确定性可以来自多个方面，包括仪器本身的精度和准确度、操作者的技术能力、环境条件的影响以及测量过程中存在的随机误差和系统误差等。

因此，要准确评估和处理测量中的不确定性，必须对测量过程中的各种因素进行全面考虑。

其次，为了处理测量中的不确定性问题，一个最基本的步骤是建立合适的测量模型。

测量模型可以帮助我们了解测量结果与测量对象之间的关系，并揭示不确定性的来源。

在建立测量模型时，需要充分考虑到测量对象的特性以及测量过程中可能存在的误差源。

通过建立合理的模型，可以明确测量的目的和需求，并为后续的不确定度评估和处理提供基础。

然后，在评估测量不确定性时，我们需要使用适当的统计方法和工具。

常用的方法包括重复测量法、回归分析、方差分析等。

通过对重复测量数据进行统计分析，可以得到一组统计特征，如平均值、标准差和置信区间等。

这些统计特征提供了对测量结果的描述和定量评估，帮助我们确定测量结果的可靠性和精确度。

除了统计方法，我们还可以使用不确定度扩展法来处理测量中的不确定性。

不确定度扩展法是一种基于误差传递规则的方法，将各个测量量的不确定度通过数学运算进行组合，得到最终的测量结果的不确定度。

这种方法可以很好地反映不同误差源对最终结果的影响，并为后续的决策和分析提供可靠的依据。

此外，在处理测量中的不确定性问题时，我们还可以借鉴同行评议、国际比对和标准参照物等方法。

同行评议是一种通过与其他实验室进行交流和对比的方式，验证和确认测量结果的准确性和可靠性。

国际比对是一种通过参与国际标准化组织组织的国际比对活动，将本实验室的测量结果与其他实验室的结果进行对比和评估。

不确定性分析范文不确定性分析是决策科学中的一个重要工具，用于评估决策中各种不确定因素对结果的影响和可能性的量化分析。

不确定性是指在决策过程中，由于信息缺乏、环境变化等原因导致的不能确定决策结果的情况。

不确定性分析旨在帮助决策者更好地理解和应对不确定性，提供可靠的决策依据。

不确定性分析包括定性和定量两个层面。

定性分析主要通过专家经验、判断和集体智慧等方法，对不确定因素进行分类、描述和评估，并从中挖掘潜在风险和机会。

定量分析则是在定性分析的基础上，通过数学模型、统计分析等方法，对不确定因素的可能性、影响程度、相关关系等进行量化分析，以求得更准确的决策结果。

不确定性分析的关键是对不确定因素的合理识别和评估。

其中，数据收集和分析是不确定性分析的基础，它需要收集和整理与决策有关的各类数据，并通过统计分析等方法对数据进行处理和挖掘。

在数据收集和分析的基础上，决策者可以借助各种工具和方法对不确定性进行模拟和预测，以评估不同决策方案的风险和机会。

在不确定性分析中，常用的工具和方法有：1.方差分析：用于比较不同因素对结果的影响，以确定主要影响因素，并探索其变化对结果的影响程度。

2.鱼骨图：用于找出问题的根本原因，从而采取相应的改进措施，减少不确定性因素的影响。

3.模拟分析：通过构建数学模型和运行大量的随机试验，模拟和预测不同决策方案的结果，并获得相应的概率分布。

4.概率分布：用于描述和模拟不确定因素的可能性，如正态分布、均匀分布、指数分布等。

5.假设检验：通过对不确定因素的样本数据进行统计分析，检验不确定因素的假设，从而评估其对决策结果的影响。

不确定性分析的结果可以帮助决策者更好地理解和应对不确定性，做出相应的措施和决策调整。

同时，不确定性分析还可以为决策提供多种方案，并根据不同方案的不确定性程度，通过风险评估和风险管理等方法，为决策提供相应的风险控制措施和优化方案。

不确定性分析在实践中广泛应用于金融、投资、工程、环境管理等各个领域。

不确定性分析不确定性分析是一种在决策过程中考虑不确定性因素的方法。

在现实生活中，无论是个人还是组织都面临着各种不确定性的风险，包括经济波动、市场需求变化、自然灾害等。

因此，通过进行不确定性分析，可以帮助我们更好地理解和评估不确定性，并为决策提供更全面和准确的信息支持。

一、不确定性分析的定义与目的不确定性分析是指对未来可能发生的不确定情况进行分析和评估的方法。

其主要目的是通过定量或定性的方式，分析和评估不确定性因素对决策结果的潜在影响，以此为基础做出合理、可信的决策。

不确定性分析可以帮助我们识别潜在的风险和机会，规划风险控制和应对策略，提高决策的可靠性和可持续性。

二、不确定性分析的方法和工具1. 概率分析：概率分析是一种通过收集历史数据、构建概率分布函数等方式，对不确定性因素进行量化评估的方法。

通过统计学方法，我们可以计算出不同事件发生的概率，从而确定不同决策结果的可能性。

常用的概率分布包括正态分布、泊松分布等。

2. 场景分析：场景分析是一种通过构建多种可能性的情景，评估每种情景下的决策结果的方法。

通过制定不同的假设和条件，我们可以模拟和研究不同情景下的决策结果，以此为基础制定相应的风险管理和决策策略。

3. 灵敏度分析：灵敏度分析是一种通过改变不确定性因素的数值，观察决策结果的变化情况，评估不确定性因素对决策结果的敏感性的方法。

通过灵敏度分析，我们可以确定哪些因素对决策结果影响最大，从而有针对性地控制和优化决策过程。

三、不确定性分析的应用领域不确定性分析在各个领域都有广泛的应用，以下是一些典型的应用领域：1. 金融风险管理：在金融领域，不确定性分析可以帮助机构评估投资风险、市场波动等因素对投资组合的影响，为投资决策提供科学依据。

2. 项目管理：在项目管理中，不确定性分析可以帮助项目经理评估项目进度、成本等因素的不确定性，规划项目风险管理和资源分配策略。

3. 生产运营：在生产运营中，不确定性分析可以帮助企业评估市场需求、原材料供应等不确定性因素对生产计划和库存策略的影响，提高运营效率和灵活性。

不确定性原理生活中的应用1. 什么是不确定性原理？不确定性原理（Uncertainty Principle）是量子力学中的基本原理之一，由德国物理学家海森堡于1927年提出。

它表明，在量子尺度下，存在着测量某个粒子的位置和动量同时精确的限制，也就是说，我们无法同时准确测量一个粒子的位置和动量。

2. 不确定性原理的数学表达式根据不确定性原理的数学表达式，我们可以得知：Δx × Δx≥ ℏ/2其中，Δx表示位置的不确定度，Δx表示动量的不确定度，ℏ表示约化普朗克常量（约等于6.63×10^-34 J·s）。

3. 不确定性原理在生活中的应用尽管不确定性原理最初是由物理学家提出的，但它却在我们的日常生活中有着广泛的应用。

以下是一些不确定性原理在生活中的应用示例：3.1. 光学显微镜光学显微镜是生物学、医学等领域中常用的实验工具。

在显微镜下观察细胞、微生物等微观物体时，由于光的特性，我们无法同时确定物体的位置和速度。

即使使用了更先进的显微镜技术，也会受到不确定性原理的限制。

3.2. 粒子物理实验在粒子物理实验中，科学家们使用粒子加速器等设备对微观粒子进行观测和研究。

然而，由于不确定性原理的存在，他们只能间接地探测粒子的一些属性，如位置和动量，并且无法同时确定它们的准确值。

3.3. 化学反应速率在化学反应中，反应速率是一个重要的指标。

然而，不确定性原理告诉我们，我们无法同时准确测量反应物的位置和动量，因此在实际观测和测量过程中，我们只能得到近似的结果。

这就解释了为什么有些实验数据会有一定的测量误差。

3.4. 量子计算机量子计算是一种基于量子力学的新型计算方式，有着巨大的潜力和应用前景。

然而，由于不确定性原理的存在，量子计算机在进行计算时也受到一定的限制。

科学家们正在努力解决这个问题，以提高量子计算机的稳定性和可靠性。

3.5. 音频和视频压缩在数字音频和视频压缩中，我们常常使用离散余弦变换（Discrete Cosine Transform）等算法来实现数据的压缩。

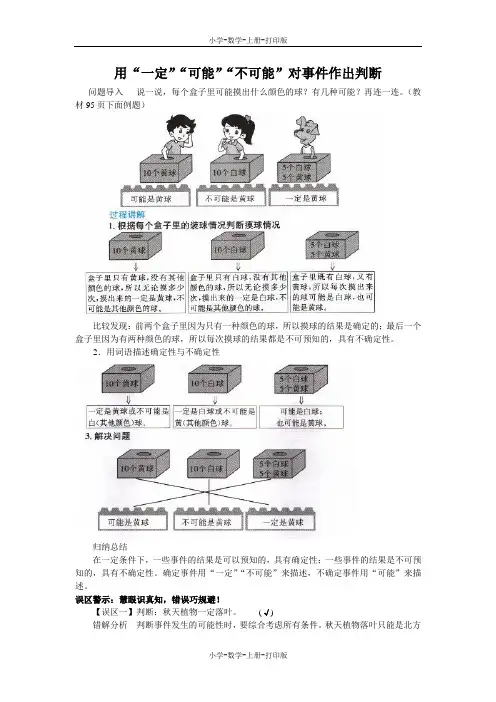
用“一定”“可能”“不可能”对事件作出判断
问题导入说一说，每个盒子里可能摸出什么颜色的球？有几种可能？再连一连。

（教材95页下面例题）
比较发现：前两个盒子里因为只有一种颜色的球，所以摸球的结果是确定的；最后一个盒子里因为有两种颜色的球，所以每次摸球的结果都是不可预知的，具有不确定性。

2．用词语描述确定性与不确定性
归纳总结
在一定条件下，一些事件的结果是可以预知的，具有确定性；一些事件的结果是不可预知的，具有不确定性。

确定事件用“一定”“不可能”来描述，不确定事件用“可能”来描述。

误区警示：慧眼识真知，错误巧规避！
【误区一】判断：秋天植物一定落叶。

(√)
错解分析判断事件发生的可能性时，要综合考虑所有条件。

秋天植物落叶只能是北方
一些植物的现象，不能说一定落叶，一些常绿植物秋冬两季是不落叶的。

错解改正×
温馨提示判断事件发生的可能性，一定要综合考虑各种情况。

【误区二】判断：哈尔滨连续下了两天的雪，明天不可能再下雪了。

(√)错解分析虽然下了两天的雪，但第三天的天气情况仍具有不确定性，可能下雪，也可能不下雪。

错解改正×
温馨提示有些事件发生的结果是不确定的，并不受前几次结果的影响。

如何处理不确定性和复杂性在日常生活和工作中，我们经常会面对一些不确定和复杂的情况。

处理这些情况需要一定的技巧和策略。

本文将从不确定性和复杂性的本质、影响和处理方法三个方面，探讨如何处理不确定和复杂的情况。

一、不确定性和复杂性的本质不确定性是指人们对过去和未来的认识不够清晰，缺乏准确的信息和预测能力。

它在我们的生活和工作中无处不在，比如未来会发生什么事情、自己的职业规划、市场走势等。

一些因素比如多个因素的交织、自然变化、社会现象的复杂性等，增加了不确定性。

复杂性指的是一组相互关联且互相影响的因素的数量和结构。

它也是一些因素相互影响的结果。

复杂性使得某些问题变得难以解决，因为任何单一的想法或解决方案都无法涵盖所有可能性。

二、不确定性和复杂性的影响不确定性和复杂性造成的影响主要包括以下两个方面：1.决策制定困难不确定性和复杂性使得决策制定变得困难。

因为很难预测未来，制定的决策往往会受到影响因素的多样性。

这会导致决策的结果不是最优的，可能会导致财务和时间上的损失。

2.缺乏计划的准确性在面对不确定性和复杂性的情况下，缺乏准确的计划往往会导致一些意想不到的后果。

可能会导致计划流产，无法按计划完成任务，并增加了成本和时间等不必要的开销。

三、处理不确定性和复杂性的方法尽管不确定性和复杂性构成了一定的挑战，但我们也可以采取一些方法来应对这些问题。

1.了解和识别不确定性和复杂性的来源了解和识别不确定性和复杂性的来源是处理这类情况的基本要求。

这样能够给出一个清晰的层次和参照来对复杂和不确定的影响进行积极的纠正和管理。

2.建立有效的意识和沟通体系有效的意识和沟通体系可以协助管理复杂性和不确定性的依据。

这些体系可以提高相互之间的意识和理解，保证信息的及时和有效传递。

同时，还能够建立一个快速响应和消除不确定性和复杂性的机制。

3.灵活和创新的思考灵活和创新的思考能够协助人们在制定方案时更好地适应变化的不确定和复杂性。

例如，采用敏捷方法论，能够在面对不确定性和复杂性时，快速地进行迭代和反馈，从而促进了项目的成功。

不确定性分析方法有不确定性是指在决策或评估时，存在一定的不确定性或风险。

在现代社会中，不确定性已成为各种决策的日常伴侣，因此我们需要一套方法来分析和应对它。

在本文中，将介绍一些常见的不确定性分析方法。

1. 探索性数据分析（EDA）EDA是对数据集的探索性分析，旨在发现数据的特征、漏洞、畸变、异常值等。

通过EDA，我们可以更好地了解数据并推断数据的规律。

这对于理解不确定性很有帮助，因为如果我们可以发现数据背后的特征和规律，我们就可以更好地评估未来可能的情况。

2. 蒙特卡洛模拟蒙特卡洛模拟是一种基于概率的模拟方法，旨在通过模拟大量随机事件来评估可能的结果。

一个典型的蒙特卡洛模拟包含三个主要组成部分：确定输入参数、建立模型和运行模拟。

在确定输入参数时，需要考虑可能的不确定性。

然后在建立模型时，将可能的不确定性纳入考虑，进行模拟。

最后，我们可以使用模拟结果来评估不确定性。

3. 场景分析场景分析是一种定量和定性方法，旨在评估一系列可能的情况。

在场景分析中，我们定义一组关键参数或变量，在不同的参数或变量值下运行模型。

这样可以得到多个场景的模拟结果。

通过比较不同场景的结果，我们可以评估可能的不确定性情况。

4. 灵敏度分析灵敏度分析是评估模型参数对输出结果的敏感性的一种方法。

在灵敏度分析中，我们通过改变输入参数或变量的值来评估输出结果的变化情况。

通过分析变化的大小和方式，我们可以评估可能的不确定性。

5. 探索性情境分析情境分析是针对复杂和不确定环境的一种方法，旨在评估在未来可能的情况下，可能出现的不确定性。

情境分析通常分为两个阶段：第一阶段是探索性分析，旨在收集信息和了解情境，第二阶段是操作性分析，旨在确定行动方案和评估可能的结果。

6. 决策树分析决策树分析是一种图形化分析方法，旨在帮助我们更好地理解决策的影响和可能的结果。

在决策树分析中，我们定义关键因素和可能的结果，然后绘制出一棵树。

通过分析决策树的某些节点，我们可以评估决策的可能结果和不确定性。

不确定性原理展现的哲学。

不确定性原理被认为是一种哲学观点，它指出，世界上几乎每一
件事，通过客观观测，都不可能完全确定其结果。

这是由于物理定律
和人类观察的限制。

不确定性原理表明，生活中几乎所有的结果都是不确定的。

就物
理学而言，不确定原理说明，大多数物理定律对于极小的物理运动
（比如原子）不适用。

这意味着，虽然科学家们可以预测物理的某种
结果，但这些结果可能是有限的，而且他们永远不知道物理系统可能
会发生什么。

在看待人类行为方面，不确定性原理也表明了一些包含容忍含义
的观点，例如，即使我们不知道可能发生的情况，我们仍然应该尝试
去把握它。

其中的一个原因是，即使我们的行动会有一定的不确定性，但是我们仍有可能通过赋予我们的行动更好的结果，用我们最好的可
能进行改变。

而在人类的努力与天生自然之间，不确定性原理的含义是：即使
人类的努力无法给予完美的结果，天生的规律也无法完全理解。

两者
都在不断变化，这就是不确定性原理提示我们的道理。

因此，每个人都应该把握机会，尽力在每一个时刻都尽量好，虽
然结果不能完全被控制，但也要在变幻的环境中闯出自己的一片天地。

不确定性原理不确定性原理是量子力学中的一个基本原理，由德国物理学家海森堡于1927年提出。

它指出，对于微观粒子，无论是位置还是动量，我们都无法同时知道它们的精确数值。

也就是说，我们无法同时确定一个微观粒子的位置和动量，这种不确定性是固有的，不是由于我们的测量方法不够精确所导致的。

这一原理的提出颠覆了经典物理学中对于微观粒子运动的认识，揭示了微观世界的奇妙之处。

不确定性原理的重要性在于，它限制了我们对微观世界的认识和理解。

在日常生活中，我们习惯于通过测量来获取物体的位置和动量，然而在微观世界中，这种测量是不可行的。

不确定性原理的数学表达形式为ΔxΔp≥ℏ/2，其中Δx代表位置不确定度，Δp代表动量不确定度，ℏ代表普朗克常数。

这个不等式告诉我们，位置和动量的不确定度乘积不会小于普朗克常数的一半。

这意味着，当我们试图减小对粒子位置的测量不确定度时，粒子的动量测量不确定度会增大；反之亦然。

这种相互制约的关系揭示了微观世界的本质。

不确定性原理的提出对量子力学的发展产生了深远影响。

它揭示了自然界中的一种固有规律，也挑战了人们对于物理世界的直观认识。

在科学研究和技术应用中，不确定性原理的影响也是不可忽视的。

例如，在核物理实验中，科学家们必须考虑到不确定性原理的限制，以避免误解实验结果。

除了在物理学领域，不确定性原理的思想也深刻影响了哲学和认识论。

它提醒人们，我们对于自然界的认识总是有限的，存在着无法逾越的局限。

这种谦卑的态度也让人更加谨慎地对待对于世界的认识和理解。

总之，不确定性原理是量子力学中的一个基本原理，揭示了微观世界的奇妙之处。

它限制了我们对微观粒子的位置和动量的认识，也深刻影响了科学、哲学和认识论。

不确定性原理的提出开启了人们对于自然界本质的探索之旅，也提醒我们，对于世界的认识永远是有限的。

管理中的不确定性及其系统分析框架作为现代社会的重要组成部分，管理在组织运作中扮演着关键的角色。

然而，管理过程中常常面临各种不确定性的挑战，这对组织的运行和发展带来了许多难题。

本文将从不确定性的角度出发，探讨管理中的不确定性及其系统分析框架。

一、不确定性的定义及其类型不确定性是指在面对未知或不可预测的因素时，人们对事物或事件结果的无法确定程度。

在管理中，不确定性常常表现为以下几种类型：1. 外部环境不确定性：指组织所处的外部环境存在变化、不可预测或难以控制的因素，例如政策变化、市场变动、竞争压力等。

2. 内部环境不确定性：指组织内部的因素存在不稳定性或变动性，例如组织架构调整、人员流动、技术变革等。

3. 信息不确定性：指管理者在做决策时，由于信息的不完全性或不准确性而导致对结果的不确定性。

4. 时间不确定性：指由于未来的发展是无法预测的，因此在管理过程中也存在时间上的不确定性。

二、管理中的不确定性对组织的影响管理中的不确定性对组织的影响是多方面的，包括以下几个方面：1. 决策难度增加：由于不确定性的存在，管理者在制定决策时往往无法准确地预测结果，增加了决策的难度。

2. 组织运营风险增加：不确定性会给组织的运营带来风险，可能导致组织面临竞争失败、市场波动、财务困境等问题。

3. 战略调整需求增加：面对变化多端的环境，组织需要频繁调整战略以适应外部和内部环境的变化。

4. 决策效果不确定：决策的结果在不确定性的环境下往往难以准确预测，可能出现预期与实际差异较大的情况。

三、管理中的不确定性系统分析框架为了更好地应对管理中的不确定性，我们可以采用系统分析框架来进行管理。

1. 环境分析：对外部环境进行全面、准确的分析，了解市场动态、竞争态势、政策规定等因素对组织产生的不确定性影响。

2. 内部分析：全面了解组织内部的情况，了解组织架构、核心能力、人员结构等因素对组织稳定性和不确定性的影响。

3. 信息收集与处理：建立完善的信息收集机制，关注市场变化、技术发展、竞争动态等，及时掌握信息以应对不确定性。

简述实践标准的确定性和不确定性
1、坚持实践标准是确定性和不确定性的统一，就是在真理标准问题上坚持了辨证法，实践标准的确定性（绝对性）是指：第一、实践是检验真理的唯一标准，此外，再没有别的标准；
第二、无限发展着的实践对一切认识都能做出确定的检验。

2、实践标准的不确定性（相对性）是指：
第一、实践有着自身的局限性，它不能对现有的一切认识都做出确定的检验；
第二、在一定发展阶段上，经过实践证实的真理，还需要继续接受新的实践的检验。

3、坚持实践标准，绝对性和相对性的统一，既要反对夸大实践标准的绝对性，否认相对性的绝对主义，又要反对夸大实践标准的相对性，否认绝对性的相对主义，主观唯心主义和不可知论。