全站仪三角高程的精度分析及应用

随着全站仪在工程测量中的普及，使用既可任意置站，又可减少误差来源，同时还无需每次量取仪器高及棱镜高度的棱镜跟踪杆配合全站仪测量高程方法，已愈发受到广大测量人员青睐。

通过已有工程实例证明，无量高全站仪三角高程测量法可使测量精度进一步提高、施测速度更快，特别适合于复杂环境下工程的应用。

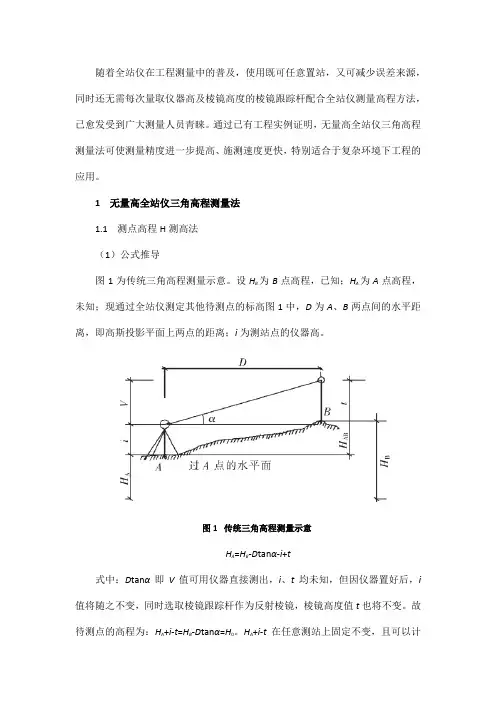
1 无量高全站仪三角高程测量法1.1 测点高程H测高法（1）公式推导图1为传统三角高程测量示意。

设HB为B点高程，已知；H A为A点高程，未知；现通过全站仪测定其他待测点的标高图1中，D为A、B两点间的水平距离，即高斯投影平面上两点的距离；i为测站点的仪器高。

图1 传统三角高程测量示意H A=H B-D tanα-i+t式中：D tanα即V值可用仪器直接测出，i、t均未知，但因仪器置好后，i 值将随之不变，同时选取棱镜跟踪杆作为反射棱镜，棱镜高度值t也将不变。

故待测点的高程为：HA+i-t=H B-D tanα=H0。

H A+i-t在任意测站上固定不变，且可以计算出其测站点高程H0。

故有H求= H0+D'tanα'+i-t。

式中：H求为待测点高程；D'为测站点到待测点的水平距离；α'为测站点到待测点的观测垂直角。

当i=0、t=0时，H求= H0+D'tanα'。

（2）操作过程1）选择与已知高程点通视的位置将仪器任意置点。

2）测出V值，计算出H0。

3）重新设定仪器测站点高程为H0，且设置仪器高及棱镜高为0。

4）照准待测点，测出其高程。

1.2 借高三维Z坐标测高法（1）公式推导借高三维Z坐标值测高法测量如图2所示，B=BM为后视点B的高程代号。

假设B点的高程H；已知，C点的高程HC未知，A点为任意置站点，通过全站仪测定C点的高程HC。

图2 借高三维Z坐标值测高法测量示意由Z坐标测量原理可知：Z B=Z A+D tanα+i-t式中：D tanα即V值可以用仪器直接测出，测出V值后将仪器中仪高值i改设为（t-D tanα）值、将测站点ZA坐标设置为基准点高点H B。

三角高程测量代替四等水准测量在实际工程中的应用目前，在实际工程中，三角高程测量已经开始代替四等水准测量，成为常用的测量方法之一。

以下是三角高程测量代替四等水准测量在实际工程中的应用的相关内容。

1. 精度要求高：相比起四等水准测量，三角高程测量的精度更高。

尤其是在大型工程项目中，如高速公路、铁路、桥梁等的建设中，对高程的精度和稳定性要求非常高。

三角高程测量在这些工程中广泛应用，可以提供更准确的高程数据，确保工程的施工质量。

2. 测量效率高：相比起四等水准测量，在实际工程中，三角高程测量的测量效率更高。

这是由于三角高程测量通常采用全站仪等现代化仪器，可以快速测量多个站点的高程，而不需要像四等水准测量那样每次只能测量一个站点。

三角高程测量可以在短时间内获得大量的高程数据，提高工程的测量效率。

3. 数据处理方便：在三角高程测量中，高程数据可以直接通过仪器进行记录和存储，然后通过计算机软件进行数据处理和分析。

与四等水准测量相比，三角高程测量的数据处理更为方便快捷，可以自动化处理大量的数据，从而减少了人工处理的工作量，并提高了数据处理的准确性。

4. 测量范围广：三角高程测量的测量范围更广。

四等水准测量通常只适用于相对较小的范围，而且需要进行大量的平差工作。

相反，三角高程测量可以在较大范围内进行测量，不需要进行大量的平差工作，节省了时间和人力资源。

在大范围的工程项目中，三角高程测量更加适用。

5. 前期准备工作较少：相比起四等水准测量，三角高程测量在前期准备工作上较少。

四等水准测量需要进行控制点的选择、等高线的描绘等作业，而在三角高程测量中，只需要选择测量站点和测量角度即可，减少了前期准备工作的工作量。

三角高程测量在实际工程中逐渐代替四等水准测量的应用越来越广泛。

它具有高精度、高效率、方便的数据处理、适应大范围的测量和少量的前期准备工作等优点。

随着技术的不断发展，相信三角高程测量在实际工程中的应用将会越来越广泛。

中点单觇法三角高程测量及其精度分析0 前言目前，随着测距技术的发展，精度的提高，以及测距仪、全站仪的普及，三角高程测量作为高程控制测量的一种有效手段，正逐步受到广大测绘工作者的青睐。

在三角高程测量方法中，现阶段主要采用的是直返觇法——用往返观测测定相邻点的高差的方法；而应用中点单觇法（在两置觇点中间安置仪器测定觇点间高差的方法）的人却较少。

虽然直返觇法在建立平面控制网的同时，为求这些待定平面点的高程而建立三角高程控制网时较为方便，但由于平面控制点大多建在制高点上，用其作为高程控制点，使用较为不便，一般平面控制网与高程控制网均分开布设，高程点布设在利于保存、使用的地方，此时运用中点单觇法来进行三角高程测量，较之直返觇法有较强的灵活性与实用性。

中点单觇法三角高程测量有以下几个特点：a 测站不需对中，不需量取仪器高；b 采用适当方法，可不量取觇标高；c 测站选在中部时，可减弱大气折光的影响；d 减少劳动强度、提高作业速度等。

1 中点单觇法三角高程测量原理及精度分析1.1 高差计算公式的推导如图1所示，为求A、B两点间的高差，将全站仪置于A、B两点大致中间位置的D点处，则图1故A点至B点的高差为：式中：s——经气象改正后的斜距；z——天顶距的观测值；V——觇标高；R——测区地球平均曲率半径；K——大气折光系数。

由于前、后视高差观测是在相近条件下进行的，可认为其折光系数，kA≈kB，令kA=kB=k，代入式（3）得：中点单觇法三角高差测量时，每一测站均应独立施测两次，满足要求后，取其平均值作为最后成果，即式中：h′AB——第一次观测高差；h″AB——第二次观测高差。

由上述可知，中点单觇法三角高差测量时，不需对中和量取仪器高。

1.2 中误差计算式对式(4)进行全微分，得：由于式(6)等号右边前四项括号中的第二项较小、相对于第一项而言，可忽略不计，并顾及DA=sAsinzA、DB=sBsinzB，则得：运用误差传播定律，考虑到观测量之间相互独立，得：由于采用中点单觇法进行三角高程测量时，仪器大致在两置觇点的中部且一般距离较短，则可近似认为m2sA=m2sB=m2s；并顾及m2zA=m2zB=m2z，m2vA=m2vB=m2v，由上式可得：式中：mh——中点单觇法三角高差的中误差；ms——测边中误差；mz——天顶距观测中误差；mk——大气折光系数测定中误差；mv——觇标高量取中误差；Z——天顶距的观测值；D——水平距离，D=s·cosz；R——测区地球平均曲率半径；ρ——取206265″.则，高差平均值的中误差为：1.3 精度分析及结论设ms=±10 mm、mz=±1.8″、mk=±0.05、mv=±1 mm，取不同的平距D和天顶距Z，按式(10)计算高差平均值的中误差，结果列于表1中。

三角高程测量原理误差分析及应用三角高程测量是一种常用的地理测量方法，用于测量地球表面上任意两点之间的高差。

它的原理基于三角形的几何性质，通过测量三角形的边长和角度来计算出高程差。

误差分析是对测量结果进行评估和分析，以确定测量结果的可靠性和精度。

三角高程测量在工程测量、地形测量和地理信息系统等领域有广泛的应用。

三角高程测量的原理是基于几何三角形的性质。

在三角形中，已知两边长度和夹角时，可以通过正弦定理求得第三边的长度。

在实际应用中，使用测量仪器（如全站仪、水准仪）测量两个点的水平距离和夹角，然后根据几何关系计算出两点之间的高差。

对于三角高程测量的误差分析，需要对各种误差进行综合评估和处理。

首先要进行误差源的分析和估计，确定各个误差源对测量结果的影响程度。

然后通过合适的数理统计方法对误差进行处理，例如最小二乘法、平差方法等，以提高测量结果的准确性和可靠性。

最后，通过误差传递的计算，评估最终测量结果的误差范围和可信度。

三角高程测量在地理测量和工程测量中有广泛的应用。

地理测量方面，可以通过三角高程测量来测量地球表面的高程特征，生成数字高程模型，用于地形分析和地图制作。

在工程测量方面，三角高程测量被用于测量任意两点间的高差，如建筑物、道路和管道等的高程差，以支持工程设计和建设。

另外，在地理信息系统中，三角高程测量可以用于数据融合和质量控制，提高地理数据的精度和准确性。

总结而言，三角高程测量是一种常用的地理测量方法，利用三角形的几何性质来测量地表上任意两点的高差。

在测量过程中会存在各种误差，需要进行误差分析和处理，以提高测量结果的准确性和可靠性。

三角高程测量在地理测量和工程测量中有广泛应用，可以用于生成数字高程模型、工程设计和数据质量控制等领域。

全站仪三角高程测量方法全站仪是一种先进的测量仪器，具有测量水平角、垂直角和斜距的功能，因此在进行三角高程测量时，可以采用以下方法：1. 三角高程测量原理：三角高程测量是利用三角学原理进行测量的方法。

当我们在地面上选择三个测站，并测量出它们之间的水平角、垂直角和斜距时，根据三角关系可以计算出这些测站的高程。

2. 选择测站：在进行三角高程测量时，首先需要选择三个测站，并保证这三个测站之间形成一个合理的三角形。

测站的选择要考虑到其位置相对固定和稳定，同时要满足仪器观测范围的要求。

3. 测量水平角：使用全站仪测量水平角的方法有两种：反射测量和直接测量。

反射测量是将反光棱镜放置在测站上，然后使用全站仪对反射棱镜进行测量，得到水平角的数据。

直接测量是将全站仪直接对准目标，通过全站仪内置的水平角读数装置进行测量。

4. 测量垂直角：全站仪可以通过照准测量和激光测量两种方法来测量垂直角。

照准测量是将全站仪对准目标，然后通过全站仪内置的图像传感器来读取目标的中轴线，从而获得垂直角的数据。

激光测量是利用全站仪内置的激光器向目标发射激光束，然后通过在目标接收到光线的位置上读取垂直角的数据。

5. 测量斜距：通过使用全站仪的测距仪，可以实时测量出目标与测站之间的水平距离或斜距。

全站仪的测距仪可以通过使用红外线或激光技术来测量距离，并将测得的数据显示在仪器的屏幕上。

6. 计算高程：当我们完成三个测站的水平角、垂直角和斜距的测量后，可以利用三角关系计算出测站的高程。

常用的计算方法有正算法和反算法。

正算法是已知两个测站的高程和一个介于它们之间的斜距，通过三角关系计算出第三个测站的高程。

反算法是已知两个测站的高程和一个测站的高程，通过三角关系计算出这个测站到其他两个测站的斜距。

总结：全站仪的三角高程测量方法包括选择测站、测量水平角、测量垂直角、测量斜距和计算高程。

通过合理的测站选择和准确的观测操作，可以获得高精度的三角高程测量数据，从而为工程测量和地形测量提供可靠的高程数据支持。

南方NTS-372R全站仪精密三角高程测量应用摘要:本文根据全站仪三角高程原理，探讨了用南方NTS-372R全站仪进行三角高程测量的方法并对精度进行了分析，总结了减弱误差的方法及提高精度的措施。

关键词:三角高程;全站仪;精度分析Abstract: Based on the principle of total station triangle elevation discussed with the South NTS-372R Total Station trigonometric leveling method and accuracy are analyzed, summarized and reduced error method to improve the accuracy of the measure.Keywords: triangle elevation; Total Station; precision analysis一、引言传统高程控制网的建立使用水准仪进行水准测量。

而对于地面高低起伏较大或用水准仪测量不便的地区，应用受到很大的限制。

随着测量技术的高速发展，全站仪测距和测角精度大为提高，全站仪三角测量得到广泛应用。

本文结合南方NTS-372R全站仪，对三角高程测量进行了精度分析三角高程测量的原理和方法，应用误差传播定律，对南方NTS-372R全站仪三角高程测量进行了精度分析。

探讨了南方NTS-372R全站仪三角高程在一定范围内代替等级水准的可行性。

二、三角高程测量原理三角高程测量是根据观测两点之间的高度角及斜距来计算两点间高差的，两点间高差为:。

（1）式中：S为两点间斜距；a为垂直角；K为大气垂直折光系数；i为测站点仪器高；v为观测目标高；R为地球曲率半径。

由式1可以看出，三角高程测量两点高差的精度受到两点间斜距的量取精度、两点间竖直角的观测精度、大气折光、仪器高及棱镜高量取精度的影响。

全站仪高程导线测量精度分析摘要：针对全站仪三角高程导线测量代替三等水准测量问题，采用精密测量技术施测了全站仪高程导线。

以每千米高差偶然中误差和全中误差作为精度衡量指标，分析全站仪高程导线测量精度。

实验结果表明，全站仪高程导线测量每千米高差偶然中误差达到2.959 mm，每千米高差全中误差达到5.762 mm，符合三等水准测量精度要求。

基于精密施测的全站仪高程导线测量代替三等水准测量是可行的，且全站仪高程导线测量效率高，地形普适性强，具有三、四等水准测量无可比拟的优势。

关键词：全站仪；水准测量；观测误差；三角高程导线测量0引言传统水准测量是高程测量的最可靠方法，按精度划分可分为一、二、三、四等水准测量[1]。

等级水准测量虽然测量精度高，但也有诸多不足，如外业工作量大，视距差不能过大，速度相对较慢，而且受视野等因素的局限，有时部分测段水准测量难以进行[2]。

随着测绘技术的不断发展，传统的水准测量出现了替代方法，目前，电磁波三角高程测量正逐渐替代四等水准测量[3]，替代三等水准测量也在讨论之中，如柴华、姜启鹏等人采用电磁波三角高程测量代替三等水准测量，并推证了三等水准测量可以被三角高程替代[4,5]，近年来，甚至出现了二等水准测量的替代方法，如孔宁等人利用精密三角高程测量代替二等水准测量，取得了近似替代精度[6]，张恒等人利用精密三角高程代替二等水跨河准测量，得到了令人满意的成果[7]。

本文利用高精度全站仪布设高程导线，分析全站仪三角高程导线测量代替三等水准测量的可行性。

1全站仪高程导线测量原理1.1代替三等水准测量可行性测定地面待测点的高程的常用方法是水准测量、经纬仪三角高程测量和全站仪高程测量，这些方法中水准测量的精度最高，但是它施测时受限较多，适用于平坦区域高程测量，经纬仪三角高程测量虽然适用于山区，但是由于测距精度较低，导致高程测量精度相对较低，全站仪具有较高的测距测角精度，且测量速度快，适宜于各类复杂地形，所以研究全站仪高程导线测量精度能否达到等级水准测量精度十分必要。

全站仪三角高程测量方法及精度分析【摘要】测量工作对工程施工来讲有着重要影响，在建筑业、市政行业等多方面全站仪三角高程测量都发挥了重要作用，其相对于其他高程测量更加精准、高效，下面文章结合工程案例对全站仪三角高程测量方法及精度进行分析。

【Abstract】Surveying work has an important impact on engineering construction. It plays an important role in building industry, Municipal Industry and other aspects of total station trigonometric elevation survey. Compared with other elevation surveys, it is more accurate and efficient. The following article combines engineering cases to analyze the total station trigonometric elevation survey method and its accuracy.【关键词】全站仪；三角测量；高程测量；测量方法【Keywords】Total Station; Triangle Measurement; Elevation Measurement; Measurement Method1引言目前随着我国的科学技术在不断的发展，高精度全站仪在各个方面都已经得到了很大的提高，高精度全站仪的快速发展为目前我国的高程测量打下了坚实的基础，在一定程度上为了能够更好的促进测量的水平，要进一步提升高程测量的技术和方法。

2全站仪三角高程测量方法第一，单向观测：单向观测方法是通过已知的高程来对未知的高程进行有效确定的方法，在对未知高程点进行测量时，需要首先对已知高程点与未知高程点的高差进行一定程度的观测，然后在已知的高程点之上设置全站仪，并将全站仪的高度进行测量并记录；在未知高程点之上设置反射棱镜，同样需要测量反射棱镜的高度并记录。

浅谈全站仪中的三角高程测量2012-6-9 自己的一点体会吧 ，希望能给大家带来一点帮助，谢谢首先了解三角高程原理：原理：Ha+i=Hb+v-SsinA(A有正负之分。

Ha标示测站点高程，i表示仪器高，hb：待测的高程v标示棱镜高，s：斜距，s：垂直角)原理搞清楚了，用全站仪测量会比较方便。

比如在地形测量中。

比如你不知道测站点的高程，就可以灵活运用三角高程的原理：1， 你直接设置测站点的高程为0，目的只是测量高程，所以后视的步骤都可以随便后视的。

然后输入棱镜高：1.35m 380.00，你测量的是100，所以你测站点的高程为：380-（100-0）=370，记住千万要看清楚仪器上的高程，仪器实质上是运用三角高程测量的原理制动算出来的，所以你不必为原理而纳闷，知道这一点很重要。

（我以前就犯了个这样的错误，我以为仪器没有减去棱镜与仪器搞得差值，所以错了，当时我就没有想明白。

原因是以前一般都没有用这个全站仪测量高程吧（精度低）。

全站仪不后视的方法另外我给大家讲个我自己刚发现的,可能好多人都知道可能还是有道友不知道这个小窍门。

全站仪测量三维坐标的时候不是要后视吗？就要后视点的坐标或是方位角。

一般都要人拿着棱镜去后视照准的，我有个方法可以不用人去后视点立棱镜，而且是在转点的情况下都可以。

区域（地形测量）用的多。

说明：你在一个点测完能测量的点位了，就得转点测量D1不能测到的点位。

你就得布置转点ZD1，ZD2…..方法步骤：你直接在D1测量布置ZD1，测量其三维坐标并记下HR1(右角，记住不能是左角)，——你在ZD1安置好仪器并输入三维坐标——该后视了，你直接输入后视点的坐标，仪器上显示是否照准后视点并有HR的值你转动仪器使得HR=HR1±180(当HR1小于180°取+，当HR1大于180°取- 。

)——你也可以检验下大概方位对不，因为他的后视点就是D1. { 这个就是反方位角的原理及用处吧。

全站仪三角高程测量方法全站仪三角高程测量是一种常见的测量方法，它是利用全站仪的功能完成的。

全站仪是一种先进的测量仪器，可以同时测量水平角、垂直角和斜距，具有高精度和高效率的特点。

三角高程测量是通过测量三角形的角度和边长来计算出待测点的高程。

全站仪三角高程测量的步骤如下：1. 建立三角测量网：首先，需要在待测区域内建立起一定数量的控制点，这些控制点要能够互相看见，形成一个闭合的三角形控制网。

控制点的位置可以根据地形和实际需求来选择，一般要选取在地势较高且不易遮挡的地方。

2. 选择目标点：选择待测点，即需要测量高程的点。

目标点的选择要考虑到测量的准确性和可行性，一般要选择在可观测的控制点旁边，以保证测量的精度。

3. 进行观测：使用全站仪观测待测点与控制点之间的角度和斜距。

观测时，首先要对控制点进行测量，测量控制点的位置和高程，以确定其空间坐标。

然后，将全站仪转至待测点，观测待测点与控制点之间的角度和斜距。

观测时，要注意保持仪器的水平和垂直，控制观测的时间和操作使其尽量减小。

4. 数据处理：观测完成后，需要对观测数据进行处理。

处理的主要内容包括角度观测值的平差、斜距观测值的平差和高程计算。

角度观测值的平差可以使用三角闭合平差法或最小二乘法进行，斜距观测值的平差可以使用杆长观测法或三边观测法进行平差。

在计算高程时，需要使用三角形的高程计算公式，结合已知的控制点高程和测得的控制点与待测点之间的高差，来计算待测点的高程值。

5. 矫正高程：为了提高测量的精度，需要对观测到的高程进行矫正。

主要的矫正方式有大地水准面、大地水准面高差改正、六参数高差改正等。

根据实际情况，选择合适的矫正方法进行矫正。

全站仪三角高程测量方法具有测量精度高、操作简便、测量效率高的特点，因此被广泛应用于各种测量工程中。

但是，在实际测量中，还需要注意一些技术要点，如全站仪的校准、观测时的操作规范、数据处理的准确性等，以确保测量结果的准确性和可靠性。