计算流体力学与油藏数值模拟技术的联系与区别

数学模型建立及求解
以平面油水系统为例
建立数学模型
建立一套描述油藏流体渗流的偏微分方程组 。完整的数学模型包括定解条件（初始条件 和边界条件）。
建立数值模型
偏微分 方程组
非线性有限 差分方程组
线性代数 方程组
离散化
线性化
建立计算机模型 将各种数学模型的计算方法编制成计
算机程序，用计算机计算各种结果。
油相基本流动方程：
ok ro k o B S o w o q ~ o t B o o So
水相基本流动方程：
wkrw k w B S w w w q ~ w t B w w Sw
油水渗流的数学模型 （续）
3. 状态方程 即辅助方程
SoSw1 Pc(Sw)PoPwf(Sw)
（续）
专题和机理问题的研究
对比注水、注气和天然枯竭开采动态 研究各种注水方式的效果 研究井距、井网对油藏动态的影响 研究不同开发层系油藏动态 研究不同开发方案的指标 研究单井产量对采收率的影响
油藏数值模拟应用
（续）
专题和机理问题的研究(续)
研究注水速度对产油量和采收率的影响 研究油藏平面性质和层间非均质性对油藏动态的影响 验证油藏的面积和地质储量 检验油藏数据 为谈判和开发提供必要的数据
Vo kkrooSwP
Vwkkrw wSwP
油水渗流的数学模型 （续）
2. 连续性方程 连续性方程代表的是质量守恒定律，即：对于地层中任意的单元体，
在一定的时间间隔△t过后，流入的量减去流出的量，等于单元体内增加 的量。写成广义坐标形式为：
t
油水渗流的数学模型 （续）
2. 连续性方程（续）
把油水运动方程带入连续性方程中，同时考虑存在生产油井或注水 井，则可在方程中增加一个产量项：

生产指数控制着单井流量开始下 降的时间，对预测单井的动态意
义较大。
开始
油藏原始平衡状态检查（零流量模拟） 拟合油田平均压力 拟合单井压力 拟合油田综合含水率 拟合单井含水率
油藏压力已经拟合好了？ 拟合井底压力 结束
生产史拟合
3、可修改的参数
可以单个的或集体的改变几个参数。通常按下述范 围进行修改： 1、岩石数据的修改：
4、 在初始化（initialization）时，计算油藏每一层的静压力 剃度，并给每一个网格赋每一相的饱和度值
给定初始化数据的方法
给定平衡区数据：
平衡区数据被用来初始化 饱和度分布、基准深度的压 力及压力梯度。
用枚举的方式给出每一个 单元的初始饱和度及压力。
一、油藏数值模拟技术
（一）基本概念及作用 （二）所需的数据及准备方法 （三）模型初始化方法 （四）生产史拟合技术 （五）动态预测技术
平衡区---概念及作用
概念：
在原始状况下，认为在同一个 平衡区中的流体的静力学是平衡 的。
作用：
用于定义油藏初始条件下的 每一个网格单元的压力、饱和度 值。
平衡区---初始平衡计算（一）
初始压力计算：
原始水分布
也可以在PROPS 部分中使用 SWATINIT 定义每 个单元的原始含 水饱和度值。
在每个区域，需要设置最大、最小及临界饱 和度值。
用于定义过渡带的饱和度。
岩石数据
岩石数据是特定的岩心分析试验的结果， 该数据用于： 设置每一流体相的最大、最小饱和度，该 值用于定义平衡区的相饱和度。 定义过渡带的范围及属性。 描述各相在网格块间流动时的动态表现。
数据准备方法
1、网格描述 2、PVT分析 3、岩心分析 4、平衡区 5、油藏工程方法 6、数据文件实例

流体力学在油藏工程中的应用一、引言流体力学是研究液体和气体在静力学和动力学下的力学行为的学科，广泛应用于各个领域。

在油藏工程中，流体力学扮演着重要的角色。

本文将探讨流体力学在油藏工程中的应用，并分析其对油藏开发和管理的重要性。

二、油藏工程概述油藏工程是与藏有石油和天然气等自然资源相关的一门工程学科。

在石油勘探、开发以及生产过程中，油藏工程起着至关重要的作用。

其中，流体力学是油藏工程中不可或缺的一环。

三、流体力学在油藏工程中的应用流体力学在油藏工程中的应用广泛而多样，主要包括以下几个方面：1. 压力传递和分布分析压力传递和分布对于油藏的管理至关重要。

通过流体力学中的模型和理论，可以准确分析油藏中的压力传递和分布规律。

这有助于确定油藏内部的压力变化情况，进而预测和优化油藏的开发方案。

2. 流体流动规律研究流体力学可以帮助研究油藏中流体的流动规律。

通过建立相应的数学模型，可以揭示油藏中的流体流动速度、流量、压力变化等关键因素。

这些研究成果可以指导工程师进行合理的油藏开发和生产设计。

3. 油藏改造和增产通过流体力学的方法，可以研究和模拟油藏中的渗流过程，进而提出有效的油藏改造和增产方案。

例如，通过注入压裂液体或增聚剂来改变油藏的渗透性和流动性，从而提高油井的采油效果。

4. 油藏储量估算流体力学的应用还包括油藏储量的估算。

通过分析油藏的渗透性、孔隙度、流体性质等参数，可以利用流体力学的方法来预测油藏中的石油或天然气储量。

这对于资源评估和投资决策至关重要。

四、流体力学在油藏工程中的重要性流体力学在油藏工程中的应用对油藏的开发和管理具有重要的意义。

它可以提供准确的数据和指导，优化油藏的开发方案，提高采油效率。

同时，通过对油藏中流体流动规律的研究，可以帮助工程师更好地理解油藏的特性和动态变化，从而制定更科学的管理策略。

五、结论综上所述，流体力学在油藏工程中扮演着重要的角色。

通过流体力学的理论和方法，可以对油藏进行深入研究，提供有力的支持和指导。

计算流体力学和流体力学的区别摘要：1.计算流体力学与流体力学的定义与区别2.计算流体力学的基本原理和方法3.计算流体力学在实际应用中的优势和局限性4.我国在计算流体力学领域的发展和成果正文：计算流体力学与流体力学是密切相关但又有所区别的两个领域。

为了更好地理解这两个概念，我们首先来了解它们的定义和特点。

流体力学是研究流体在不同条件下运动和变形的物理学分支。

它涵盖了广泛的研究领域，如流体动力学、流体静力学、湍流理论等。

流体力学在许多工程领域具有重要的应用价值，如航空航天、水利、建筑、生物医学等。

而计算流体力学则是在流体力学的基础上，利用计算机和数值方法对流体运动进行模拟和研究的一门学科。

它将计算机科学、数学和流体力学相结合，通过求解流体运动方程组，模拟流体在不同条件下的运动状态和特性。

计算流体力学的发展，使得研究人员能够更深入地探讨流体力学的理论和应用，为实际工程问题提供更为精确的解决方案。

计算流体力学的基本原理和方法主要包括以下几点：1.建立流体运动方程：根据流体力学的理论，建立描述流体运动的偏微分方程组。

2.离散化：将连续的流体域划分为若干个离散的网格，以便于数值求解。

3.数值求解：采用适当的数值方法（如有限差分法、有限元法等）对离散化的方程组进行求解。

4.结果分析与后处理：对求解得到的结果进行分析，提取流体的运动特性，如速度、压力等。

此外，还可以通过后处理技术对结果进行可视化，以便于观察和分析。

计算流体力学在实际应用中具有显著的优势，如：1.提高设计效率：通过计算流体力学的方法，可以快速地评估不同设计方案的流体动力学性能，从而优化设计。

2.降低试验成本：计算流体力学可以替代部分实际试验，节省试验成本和时间。

然而，计算流体力学也存在一定的局限性，如：1.计算机资源需求高：计算流体力学需要大量的计算资源和时间，尤其是在处理复杂的三维问题和高速流体运动时。

2.模型和数值方法的局限性：计算流体力学的结果依赖于所采用的模型和数值方法，不同的模型和数值方法可能导致不同的结果。

油田油藏数值模拟技术的研究与应用油田油藏是我国的重要能源资源之一，其开采和管理对于国家经济的发展具有极其重要的作用。

而油田油藏数值模拟技术则是现代油田油藏管理的重要工具之一。

本文将会从油田油藏数值模拟技术的基本原理、模拟方法以及应用案例等方面进行探讨。

1. 油田油藏数值模拟技术的基本原理油田油藏数值模拟技术是基于理论模型的油藏动态分析方法，其基本原理是将油藏的数学模型转换为计算机的数值模型，利用适当的计算方法，对油藏动态进行精细的模拟计算。

油藏的数学模型通常包括地质学、储层物理性质、流体性质等多个方面的参数，数值模拟的目标就是通过计算机模拟得出油藏内部的流动状态、压力分布以及物质的运移规律等信息，为油田采油作业的优化和管理提供依据。

2. 油田油藏数值模拟技术的模拟方法油田油藏数值模拟主要包括三个步骤：建模、数值解法与模拟计算。

建模是模拟的第一步，要求对油藏地质结构、储层参数等进行精细化的描述和建模，以便进行后续的计算分析。

数值解法则是决定油藏动态计算精度与计算速度的关键因素，常用的数值方法包括有限差分法、有限元法、谱元法等。

在模拟计算过程中，还需要对计算结果进行验证和校正，保证模拟结果的准确性与可靠性。

3. 油田油藏数值模拟技术的应用案例油田油藏数值模拟技术作为现代油藏开采与管理的重要工具，其应用范围涉及到石油勘探开发、油藏评价和采油设计等多个方面。

以下列举几个优秀的应用案例：案例一：东淮低渗透油田强化采油模拟东淮低渗透油田是我国重要的石油资源产区之一，其塔河油田采油难度大，生产水油比较高，在此前提下，利用油藏数值模拟技术，进行强化采油模拟分析。

结果显示，通过有针对性的采油方式，采出潜在储量约1.2亿桶，取得了卓越的技术经济效益。

案例二：渤海湾盆地高压气藏开发数值模拟渤海湾盆地是我国主要的天然气区之一，其中高压气藏开发难度大，需采用先进的技术手段进行分析。

因此，借助油藏数值模拟技术的建模与数值解法，对高压气藏进行了模拟计算，为盆地的开发提供了实用的技术支持，有效地提高了勘探的效率和开采的质量。

流体力学在石油储运中的应用引言流体力学是研究流体在运动和静止状态下力学规律的学科。

石油储运作为石油工业的重要环节之一，对流体力学的应用有着重要意义。

本文将重点介绍流体力学在石油储运中的应用，并分析其在提高石油储运效率、降低损耗和保证安全性方面的作用。

1. 管道输油的流体力学分析管道输油是石油储运的主要方式之一。

流体力学分析可以帮助我们确定管道输油的最佳方法。

通过分析油液在管道内的流动速度、流量、压力和摩擦等参数，可以合理设计管道的直径、长度和曲线半径，以降低能量损失和压力下降，并保证油液的有效输送和储存。

2. 液体泵的流体力学设计液体泵在石油储运中起到了关键作用。

流体力学的应用可以帮助我们设计出高效、稳定的液体泵。

通过分析泵的叶片形状、叶片间隙和泵的转速等参数，可以确定最佳的泵参数，以提高泵的工作效率和吸排油量，并减少能源消耗和泵的磨损。

3. 隔膜阀的流体力学优化隔膜阀在石油储运中广泛使用，它具有自动控制和阻隔液体的特点。

流体力学的分析可以帮助我们优化隔膜阀的设计。

通过分析阀门的开启和关闭速度、液体的流速和压力等参数，可以确定最佳的阀门尺寸、材料和结构，以提高阀门的密封性和工作效率，并减少泄漏和压力损失。

4. 储油罐的流体力学模拟储油罐是石油储运过程中重要的设备之一。

流体力学模拟可以帮助我们了解储油罐内油液的流动和压力分布情况。

通过模拟油液的流动速度、油液和罐壁的摩擦力等参数，可以优化储油罐的结构和材料，以提高油液的贮存稳定性和防止爆炸和泄漏的风险。

5. 流体力学在石油泄漏应急响应中的应用石油泄漏是石油储运过程中常见的事故之一。

流体力学的应用可以帮助我们预测泄漏液体的扩散和传播规律，以便采取相应的应急措施。

通过模拟泄漏液体的流速、流量和环境条件等参数，可以确定最佳的应急响应方案，以最大限度地减少泄漏对环境和人体健康的危害。

结论流体力学在石油储运中的应用是必不可少的。

通过流体力学的分析和优化，可以提高石油储运的效率，降低能源消耗和损耗，保证石油储运的安全性。

流体力学中的数值模拟与应用流体力学是一门研究流体运动规律和流体力学性质的科学，包括流体静力学和流体动力学两个方面。

流体力学应用广泛，如气体动力学、水力学、气象学等领域。

本文将着重介绍流体力学中的数值模拟及其应用。

一、数值模拟数值模拟是一种通过计算机模拟流体等物理现象的方法，通常采用计算流体动力学（CFD）方法来实现。

CFD模拟涉及到流体力学、数值分析、计算机科学和编程等多个领域。

1. 基本原理运用数值方法，将物理问题转换为数值问题，对流场进行数值求解。

其中最重要的是Navier-Stokes方程组，它是描述不可压缩流体动力学的基本方程。

Navier-Stokes方程组分为连续性方程和动量方程两个部分。

连续性方程描述了质量守恒，动量方程描述了动量守恒。

对于不同的物理问题，还需要加入适当的边界条件和物理参数等。

2. 数值方法常用的CFD数值方法有有限体积法、有限元法、谱方法、边界元法等。

其中，有限体积法是最常用的方法，它的特点是离散区域简单，应用广泛。

3. 软件工具目前使用最多的CFD软件工具包括ANSYS Fluent、OpenFOAM、Star-CCM+、COMSOL Multiphysics等。

这些工具包括了多种物理模型和数值方法，能够应用到各种工程领域中。

二、应用领域数值模拟在工程应用中具有重要的作用，可以帮助工程师和科学家更好地理解物理现象，预测实验结果，并进行优化。

以下是几个CFD在流体力学中的应用领域：1. 汽车工程CFD模拟可以帮助汽车设计师预测汽车性能和气动外观。

如在汽车的外形设计上，可以通过CFD模拟预测空气阻力对车辆速度和燃油经济性的影响。

在引擎设计中，CFD模拟可以预测燃烧过程中的热传导、气流动力学和挥发物扩散等。

2. 船舶工程在船舶工程中，CFD模拟可以用来预测船体的水动力性能，包括船速、抗拒力、侧向力和推力等。

同时，CFD模拟还可以分析船舶的安全性和稳定性，优化船体结构和舵型设计。

油藏数值模拟
油藏数值模拟是应用计算机研究油气藏中多相流 体渗流规律的数值计算方法，它能够解决油气藏开发 过程中难以解析求解的极为复杂的渗流及工程问题， 是评价和优化油气藏开发方案的有力工具。近年来随 着偏微分方程数值解法的发展和高速、大容量电子计 算机的更新换代，油藏数值模拟方法日趋成熟，建立 和发展了一系列功能丰富的应用软件，在油气田开发 中得以广泛应用，成为提高油气田开发科学决策水平 的重要技术。
油藏数值模拟的主要步骤
一、明确油藏工程问题
在模拟开始的时候，根据油藏的实际开发情况和所研究的问题，进一步 具体明确模拟的目的和要求，要解决那些问题？实际否？划算吗？
二、选择模型
要根据油藏渗流机理的正确分析和所研究的问题，考虑流体性质（气、凝 析气、挥发油、黑油、稠油）开采条件、注入流体（蒸汽、气、化学剂） 等选择合适的模型。
解决油田开发决策问题，预测投资的时候做。 在编制油田开发方案时，对比开发方案时做。 开发后，在研究油田开采机理和评价提高采收率方法等需
要答案而一般常规计算解决不了问题的时候做。
油藏数值模拟主要内容和基本过程
一、油藏数值模拟的主要内容
油藏数值模拟：数学模型—数值模型（离散-线性方程组-求解）—计 算机模型 1、数学模型：建立一套描述油藏渗流的偏微分方程组，加上方程组的 辅助方程和初始条件和边界条件。 2、数值模型：首先离散化偏微分方程转化为有限差分方程组，然后将 其非线性系数线性化，得到线性代数方程组，再通过线性方程组解法求 得所要求的未知量。（压力、饱和度、温度、组分等）的分布和变化。 3、计算机模型：将各种数学模型的计算方法编制成计算机程序，利用 计算机计算各种结果。
数学模拟
在六十年代（电子计算机问世）以后，数学模拟逐渐发 展并占据主导地位。 在一定的定解条件下，通过求解描述某一物理过程的数学 方程组（数学模型）来研究其物理变化规律的方法。 数学模型不是一个实体模型，而是从物理现象中抽象出来。 同一个物理概念，可以建立不同的数学模型。

油藏数值模拟原理1.地质数值建模：首先需要建立一个准确的地质模型。

地质模型是以地质数据为基础构建的地下储层的数值模型，包括储层的几何形状、岩石性态、孔隙结构和渗透性等参数。

这个模型需要提供关键的地下信息，如沉积相、构造、岩性、孔隙度等，在实际中通常通过地震数据、钻井岩芯数据等多种地质勘探技术获取。

2.模拟网格划分：建立地质模型后，需要将其分割为一系列小的网格单元。

网格划分可以是规则的也可以是非规则的，最常用的划分方法是用四面体网格或六面体网格。

这些网格单元将成为模拟的基本单元，用于描述油藏中流体的运移和渗流。

3.二相流模型：油藏中通常存在着多个相的流体，如油、水、气等。

为了精确地描述不同流体相的运移和相互作用，需要采用适当的二相流模型。

最常用的模型是饱和度-渗透率模型，即根据饱和度确定渗透率，进而计算不同流体相的渗透率。

4.质量守恒和动量守恒方程：通过对油藏中的质量守恒和动量守恒进行数值解析，可以获得流体在油藏中的运动和分布信息。

质量守恒方程通常写为连续性方程，用于描述质量的积累和消耗；动量守恒方程则描述了流体在不同流动条件下的运动和力学特性。

5.边界条件和初始条件：在模拟中，需要给定适当的边界条件和初始条件。

边界条件是指油藏与外界环境的物理和化学交换，如油藏与井筒之间的流体交换；初始条件则是指模拟开始时的油藏状态，通常需要通过历史数据或合理的估算确定。

6.数值求解方法：为了求解复杂的守恒方程组，需要采用数值方法进行计算。

常用的数值求解方法包括有限差分法、有限元法和有限体积法等。

这些方法将连续的守恒方程离散化为代数方程组，并通过迭代求解来获得数值解。

7.模拟结果评估：最后，需要对模拟结果进行评估和分析。

通过比较模拟结果与实际观测数据的吻合程度，可以评价模拟的可靠性和准确性。

如果模拟结果与实际相吻合，那么可以利用模型进行进一步的预测和优化决策。

总之，油藏数值模拟的原理是基于数值计算方法对油藏中的流体运移和渗流进行模拟和分析。

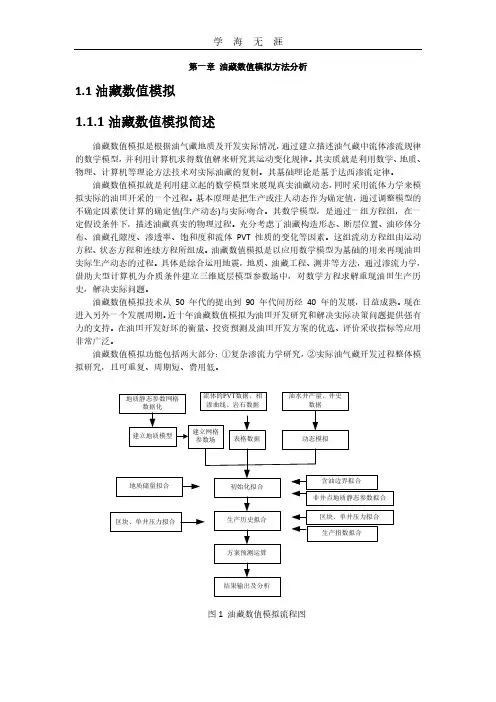
第一章油藏数值模拟方法分析1.1油藏数值模拟1.1.1油藏数值模拟简述油藏数值模拟是根据油气藏地质及开发实际情况，通过建立描述油气藏中流体渗流规律的数学模型，并利用计算机求得数值解来研究其运动变化规律。

其实质就是利用数学、地质、物理、计算机等理论方法技术对实际油藏的复制。

其基础理论是基于达西渗流定律。

油藏数值模拟就是利用建立起的数学模型来展现真实油藏动态，同时采用流体力学来模拟实际的油田开采的一个过程。

基本原理是把生产或注人动态作为确定值，通过调整模型的不确定因素使计算的确定值(生产动态)与实际吻合。

其数学模型，是通过一组方程组，在一定假设条件下，描述油藏真实的物理过程。

充分考虑了油藏构造形态、断层位置、油砂体分布、油藏孔隙度、渗透率、饱和度和流体PVT性质的变化等因素。

这组流动方程组由运动方程、状态方程和连续方程所组成。

油藏数值模拟是以应用数学模型为基础的用来再现油田实际生产动态的过程。

具体是综合运用地震，地质、油藏工程、测井等方法，通过渗流力学，借助大型计算机为介质条件建立三维底层模型参数场中，对数学方程求解重现油田生产历史，解决实际问题。

油藏数值模拟技术从50 年代的提出到90 年代间历经40 年的发展，日益成熟。

现在进入另外一个发展周期。

近十年油藏数值模拟为油田开发研究和解决实际决策问题提供强有力的支持。

在油田开发好坏的衡量、投资预测及油田开发方案的优选、评价采收指标等应用非常广泛。

油藏数值模拟功能包括两大部分：①复杂渗流力学研究，②实际油气藏开发过程整体模拟研究，且可重复、周期短、费用低。

图1 油藏数值模拟流程图1.1.2油藏数值模拟的类型油藏数值模拟类型的划分方法有多种，划分时最常用的标准是油藏类型、需要模拟的油藏流体类型和目标油藏中发生的开采过程，也可以根据油气藏特性及开发时需要处理的各种各样的复杂问题而设定，油气藏特性和油气性质不同，选择的模型也不同，还可以根据油藏数值模拟模型所使用的坐标系、空间维数和相态数来划分。

计算流体力学在石油工程中的应用随着石油工程领域的不断发展，计算流体力学（CFD）技术已经成为了不可或缺的一部分。

CFD是一种通过计算机解决流体力学问题的技术，通过建立数学模型，使用数值方法求解流体力学基本方程组，最终得到流场、温度场、压力场等物理量的分布及变化规律的一种技术。

石油工程领域中对流体流动、传热和化学反应等问题的研究离不开CFD技术的支持。

石油工程中的流体动力学问题石油工程中涉及到的流体动力学问题十分复杂。

在油田地质勘探、钻井、油藏开采、油气输送等领域，流体动力学问题都是需要解决的重要问题。

例如，在油藏开采过程中，液体、气体从高压区域移动到低压区域，会产生物质交换、速度变化等复杂的流动和传热现象。

这对于油田开采的效率和安全都有着至关重要的影响。

CFD在石油工程中的应用1. 油藏开采优化CFD技术可以用于模拟油藏开采过程中的复杂流体动力学现象，包括套压、油藏压力变化、水力压裂、注水等。

通过CFD模拟，可以对油藏开采过程进行优化，提高采收率、减少生产成本和环境污染。

2. 油井钻造孔在油井钻造孔过程中，CFD技术可以模拟钻头与地层之间的摩擦力、钻井液的泵入和回流、土屑的运移以及井壁稳定等问题。

通过CFD模拟，可以预测切削力、钻头绕行、回流速度和排出口位置等，提高钻井效率和井筒完整度。

3. 管道输送管道输送是石油工程中常见的一种运输方式。

CFD技术可以模拟管道中流体的运动状态、沉积、腐蚀等问题，预测管道的流变性、排放物的质量和运输效率等。

同时，CFD还可以用于管道设计和优化，提高输送效率和经济性。

4. 炼油过程的优化在炼油过程中，CFD技术可以模拟各个装置的流动、传热和化学反应过程，包括加热炉、蒸馏塔、反应器等。

通过CFD模拟，可以提高炼油装置的效率，减少能源消耗和二氧化碳排放，同时也有利于炼油工艺的优化和改进。

5. 垃圾焚烧CFD技术还可以应用于垃圾焚烧等领域。

在垃圾焚烧过程中，CFD技术可以模拟物料的流动、燃烧过程等，并对燃烧反应和废气排放进行优化和改进。

油藏数值模拟的发展概况和发展方向
向量化
70年代 标量计算，又称串行运算，即一个时刻内只进行一对 数据计算。
80年代 可以用向量计算机进行向量计算，即一个时刻内可使两 个数组内各因素同时进行计算，也可以是一个数和一个数组内的各因素 同时计算。
工作站前后处理
前处理：井点静态参数输入； 网格自动剖分、增减； 网格数据自动形成； 等值图件绘制。
• 油田开发前期 作规划方案 • 油田开发初期 作初步方案 • 油田开发中期 作调整方案 • 油田开发后期 作IOR、EOR方案
第二节
油藏数值模拟的 主要内容和步骤
• 油藏数值模拟的主要内容 •油藏数值模拟的步骤
油藏数值模拟的主要内容和步骤
一、主要内容
• 数学模型（Mathematical Model） • 数值模型（Numerical Model） • 计算机模型（Computer Model）
前后处理
动态存储分配
多模型一体化
二.八十年代油藏数值模拟进展
八十年代，油藏数值模拟已经进入工业化应用阶段，随着工业化进程， 即应用的拓宽和计算机的发展，则必然在模型、解法及前后处理等方面有较 大的发展。归纳起来有十个方面进展。
●模型方面
状态方程的组分模型 该模型涉及到： 组分模型：组分的质量守恒方程。 状态方程：不同压力、温度下的相态. 数值模拟将烃类组分的相态与地下的渗流力学问题有机地结合起来。 该模型可用于模拟： 凝析气田开发； 凝析气田的循环注气； 回收气藏中的自凝析油； 高收缩挥发性原油的开采； 注co2 或者N2的非混相驱或近混相驱
油藏数值模拟的基本概念
模拟：描述或实现油藏开发的动态变化过程（仿真）。
物理模拟：采油物理实体的办法 岩心试验、单管模型、平板模型试验等 数学模拟：采用数学描述的方法 数学模型、模型求解

油藏数值模拟技术与应用
常晓平
河南油田勘探开发研究院
一、油藏数值模拟技术 二、油藏数值模拟的主流软件及发展方向 三、实例
一、油藏数值模拟技术
（一）基本概念及作用 （二）所需的数据及准备方法 （三）模型初始化方法 （四）生产史拟合技术 （五）动态预测技术
油藏数值模拟技术是一门将油田开发重大 决策纳入严格科学轨道的关键技术。
差越大
6
inj1
(二) 网格设计的发展阶段
3、PEBI网格：1999 ——
可模拟任何几何形状的油藏 用k-PEBI网格处理油藏的各向异性 加密网格与基础网格能够自动耦合 收敛速度快稳定性高误差极小 正交极小加速算法(Orthomin)
网格设计方法的发展阶段
3、PEBI网格：1999 ——
更具 灵活性
在垂向上网格分层基于： 1、可得的层面数据。 2、渗透性随深度的变化。 3、影响垂向上流动的隔挡：
如泥岩夹层的影响程度 及范围等。
优点：夹层描述精确； 弱点：网格多，占用空间
大；容易与流量相关的导致 不收敛问题
优点：网格少，省空间；与 流量相关的不收敛问题较少。
弱点：垂向上描述较粗，需
花较大的功夫调整垂向传导 率
网格描述
(三) 网格的类型及描述方法
到目前主要有三种网格类型： 块中心、角点及PEBI网格。
网格几何描述
块中心网格：
给出DX、DY、 DZ及深度
角点网格：需
要指定组成每一 个网格的四条坐
标线坐标 （COORD）及八
个角点的深度
块中心网格描述倾斜构造
在块中心网格系统， 虽然相邻网格的深度 错开，但ECLIPSE 还是认为其间是相连 的，有流动发生。
网格描述

流体力学数值模拟流体力学数值模拟指根据一定的数学模型和物理假设，运用计算机对流体运动进行仿真模拟的技术。

它是流体力学研究中的重要分支，广泛应用于航空航天、能源工程、交通运输、环境保护、生物医学等领域。

一、背景随着计算机技术和数值计算方法的不断进步，流体力学数值模拟已经成为研究流体动力学的重要手段。

相对于实验方法，数值模拟可以更加便捷地得出流体的状态和特性，保存数据用于后续分析和优化。

此外，数值模拟还可以对流体中的微观现象进行模拟，尤其是对于无法进行实验的状况，数值模拟成为了唯一的手段。

二、数值模拟的基本方法数值模拟的基本方法可以分为以下四个步骤：1.选择数学模型与边界条件在模拟过程中，首先要根据实际问题的特点，选择合适的数学模型并制定边界条件。

例如，在研究飞机空气动力学问题时，流体可以近似视为粘性不可压缩的流体，因此可以采用Navier-Stokes方程组，并给出边界条件，比如空气在飞机表面的流动情况、飞机尾迹等等。

2.离散数学模型，建立差分或者有限元法数值模型在确定数学模型和边界条件后，需要将模型离散化，建立一个数值模型来进行求解。

常用的数值计算方法有有限差分法、有限元法、谱方法等。

例如采用有限差分法对Navier-Stokes方程进行离散化处理得到一组代数方程组，通常采用迭代求解方法来计算这组方程。

3.确定计算方法和求解方案确定计算方法和求解方案是建立在数学模型和边界条件之上的。

需要通过对问题的探究，选择最佳的求解方法和计算方案。

此外，还需要考虑数值计算中的数值稳定性、精确度、计算效率等因素，以便找到最优方案。

4.计算并分析结果最后，需要通过计算机实现计算并分析结果，验证模型的可靠性。

在进行结果分析时，需要关注流场的各个物理量的变化规律，以及流体运动的特性和本质。

最终的目标是得到一组可靠的流体动力学数据，为优化实际问题提供依据。

三、数值模拟的应用流体力学数值模拟广泛应用于航空航天、能源工程、交通运输、环境保护、生物医学等领域。

高速 大容量计算机问世
硬件飞速发展
油藏模拟国内外发展概况（国外）
80年代末-90年代：油藏模拟向全隐式、向量化发展
差分解法：全隐式、SEQ、AIM
计算技
数值解法： SOR、D4、 ILUC、RSVP
术迅猛发展、
模型技术：自适应技术、局部网格加密
计算方法大量 推出
技术、自动拟合技术、工作站一体化 技术、水平井技术、复杂油田模拟技术
五、灵敏度试验
将影响油田开发指标（产量、压力、含水、油气比）的地质静态资 料、流体资料和特殊岩心分析资料人为地加以变化，输入计算机程序 中，观察他们对开发指标的影响，从中找出影响比较大的性质参数， 对这一参数应尽量取准。
六、历史拟合
用已知的地质、流体性质和特殊岩心分析资料和实际的 生产历史动态资料（产量或井底压力随时间变化），输入计 算机程序中，将计算结果和实际观测和测定的开发指标（油 层压力和综合含水）相比较，若发现两者有相当大的差异， 则说明我们用的资料与实际油田资料差异较大，可根据灵敏 度试验结果逐步修改输入数据，使计算结果与实际结果一致， 这就是历史拟合。
目前已有各种各样的模型，且已经都很成熟且已经形成计算机软件。
1、黑油模型
2、组份模型
3、热采模型
4、三元复合驱模型 5、聚合物模型
6、双重介质模型
三、模拟策略方法
既要解决提出的油藏工程问题，又要具体地模型化，如： 1、全油田整体模拟还是部分模拟； 2、区块模拟还是井组模拟； 3、整体模拟中是一次整体模拟还是分区模拟； 4、一次模拟还是分阶段模拟。
九、报告的形成
分析整理模拟结果，提出建议，形成报告。
油藏数值模拟应用
油田初期开发方案
实施方案的可行性评价 选择井网、开发层系、井数和井位 选择注水方式 对比不同的产量效果 油藏和流体性质的敏感性研究

名词解释:1油藏模拟：是用油藏模型来研究油藏的各种物理性质和流体在其中的流动规律，以便更好地认识油层，作出正确的评价，确定合理的开发方案和提高采收率的措施。

2 数值模型：用离散化方法将偏微分方程组转化为有限查分方程组，将其非线性系数线性化，得到线性方程组，然后求解。

3 油藏数值模拟：用数值方法求解油藏数学方程组，就是油藏数值模拟。

4 动态预测:在历史拟合的基础上对未来的开发指标进行计算。

5 黑油模型：黑油模型是简化的组份模型。

烃类系统只考虑两个组份:“油”组份是地层油经微分蒸发后在大气压的残存液（即黑油），而“气”组份是剩余的流体。

水相与其他两相不发生质量转移；气可以从油中出入，但油不能汽化为气相。

6 适定问题：一个问题的解存在，唯一且稳定时就称问题为适定问题。

7 三相流模型：描述有三相流体同时流动的数学模型。

8 三维模型：描述油藏流体沿三个方向上同时发生流动的数学模型。

9 气藏模型：描述天然气气藏的数学模型，有的气藏只有天然气的存在，而有的气藏不仅有天然气存在还有水存在。

10 离散化：离散化就是把整体分割为若干单元来处理。

11 有限差分法：有限差分法是对网格范围内的各点求解。

即原先表示连续的、足够光滑函数的偏微分方程，被一套对每个离散点的、与该点近似解有关的代数方程组所取代。

12 块中心网格：用网格分割成小块的中心来表示小块坐标。

13 一阶向前查商:对于函数p(x,t) ,x p p x p ii ∆-=∂∂+1 为一阶向前查商。

14 截断误差：当微商用查商表示时，把泰勒级数的余项截断，由于截断了泰勒级数的余项所产生的误差称为截断误差。

15 网格节点：网格的交点称为节点。

16 显式处理：在n+1时刻求解方程组时，若其系数直接用n 时刻的值，为显式处理。

17不均匀网格：为了模拟油藏的实际情况，划分网格时，在靠近井的附近网格取密一些，而沿径相外逐渐稀疏，这种网格称为不均匀网格。

18 IMPES 方法：是指隐式求解压力方程，显式求解饱和度方法。