模拟退火算法及其改进_蒋龙聪

余弦退火算法
余弦退火算法（Cosine Annealing）是一种改进的模拟退火算法，它可以有效地帮助机器学习者提高模型的性能。

它具有很好的优化性能，可以有效地减少训练模型时的时间和计算资源消耗。

余弦退火算法可以用来优化深度学习模型的参数。

它的基本原理是：使用余弦函数来控制模型的学习率，使其在训练过程中具有指数衰减的特性，从而达到模型性能的最优化。

余弦退火算法的工作原理是：首先，设定初始学习率，然后通过余弦函数对学习率进行衰减，逐渐降低学习率，从而达到最优化的效果。

当学习率衰减至一定程度，模型就可以达到最优解。

余弦退火算法的优点是：它可以有效地控制学习率的衰减，使模型更容易收敛到最优解。

另外，它还可以帮助模型在训练过程中更加稳定，减少模型波动的可能性。

除此之外，余弦退火算法也可以用于更新模型参数，使模型更加精确。

当模型收敛至最优解时，可以使用余弦函数来更新模型参数，从而获得更准确的模型结果。

总而言之，余弦退火算法是一种改进的模拟退火算法，它可以帮助机器学习者更有效地优化深度学习模型，并有效地提高模型性能。

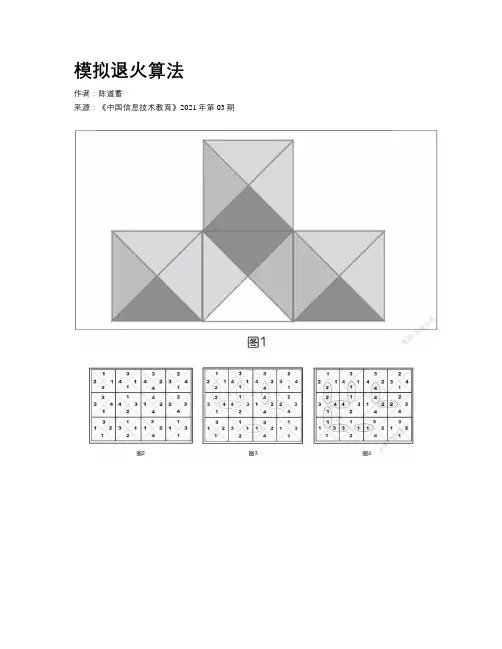
模拟退火算法作者：陈道蓄来源：《中国信息技术教育》2021年第03期“人工智能”無疑是当前最流行的词语之一。

不过现在能看到的智能应用技术，包括机器学习，基本上还无法得到脑科学等研究成果的直接支撑。

这些应用的成功在很大程度上还是依赖于计算机科学技术领域内的算法创新。

下面，我们以一种智力游戏为例，让读者体会应用层面上的“智能”背后的算法支撑。

● 涂色方块拼接游戏在平面上的矩形框内有m×n个小方块，按照m行n列排放。

每个方块面上被两条对角线分为四个三角形区域，每个三角形可以从四种颜色中任选一种着色。

（如图1所示，在后面的讨论与算法实现中用数字表示颜色）给定一种排列，相邻方块邻接边两侧的三角区域颜色可能相同也可能不同（如图2）。

任意给定的m×n个方块在矩形框中按某种排列构成游戏的一次输入，对其内部任意边界线段（不包括贴框的边），若两侧的三角形颜色相同则记1分。

玩家每一步可任选两个方块相互交换位置（也称“置换”），但不可旋转，通过置换操作争取尽可能的高分。

置换次数并无限制。

（显然，内部边界线段数是可能的最高分）图2所示是一个3×4的例子。

本文约定：输入中的每个小方块用集合{1，2，3，4}中元素构成的一个四元组表示。

从顶部起始，按照顺时针方向标示相应三角区中的颜色，如图2中第一行输入是（1，1，2，2），（3，1，1，4），（3，2，4，4），（2，4，1，3）。

这个例子很小，不难看出其得分值为6，如图3所示。

同样也不难看出如果交换最下面一行中第1和第4个小方块，则得到如图4所示的布局，分值增加为8。

但即便是这么小的例子，我们也不易确定如何能进一步提高分值，更难以确定达到多少就是最优解。

12个小方块可能的排列有12！种。

这个值大约为4.8亿。

想用穷尽的方法确认最优解显然不容易。

笔者在笔记本电脑中尝试执行100万次简单循环大约消耗8秒的CPU时间，由此可以推想将12！种可能的排列扫描一遍大约耗时1个小时。

模拟退⽕算法和遗传算法爬⼭算法在介绍这两种算法前，先介绍⼀下爬⼭算法。

爬⼭算法是⼀种简单的贪⼼搜索算法，该算法每次从当前解的临近解空间中选择⼀个最优解作为当前解，直到达到⼀个局部最优解。

爬⼭算法实现很简单，其主要缺点是会陷⼊局部最优解，⽽不⼀定能搜索到全局最优解。

如图1所⽰：假设C点为当前解，爬⼭算法搜索到A点这个局部最优解就会停⽌搜索，因为在A点⽆论向那个⽅向⼩幅度移动都不能得到更优的解。

模拟退⽕算法(SA)为了解决局部最优解问题， 1983年，Kirkpatrick等提出了模拟退⽕算法（SA）能有效的解决局部最优解问题。

模拟退⽕其实也是⼀种贪⼼算法，但是它的搜索过程引⼊了随机因素。

模拟退⽕算法以⼀定的概率来接受⼀个⽐当前解要差的解，因此有可能会跳出这个局部的最优解，达到全局的最优解。

算法介绍我们知道在分⼦和原⼦的世界中，能量越⼤，意味着分⼦和原⼦越不稳定，当能量越低时，原⼦越稳定。

“退⽕”是物理学术语，指对物体加温在冷却的过程。

模拟退⽕算法来源于晶体冷却的过程，如果固体不处于最低能量状态，给固体加热再冷却，随着温度缓慢下降，固体中的原⼦按照⼀定形状排列，形成⾼密度、低能量的有规则晶体，对应于算法中的全局最优解。

⽽如果温度下降过快，可能导致原⼦缺少⾜够的时间排列成晶体的结构，结果产⽣了具有较⾼能量的⾮晶体，这就是局部最优解。

因此就可以根据退⽕的过程，给其在增加⼀点能量，然后在冷却，如果增加能量，跳出了局部最优解，这本次退⽕就是成功的。

算法原理模拟退⽕算法包含两个部分即Metropolis算法和退⽕过程。

Metropolis算法就是如何在局部最优解的情况下让其跳出来，是退⽕的基础。

1953年Metropolis提出重要性采样⽅法，即以概率来接受新状态，⽽不是使⽤完全确定的规则，称为Metropolis准则。

状态转换规则温度很低时，材料以很⼤概率进⼊最⼩能量状态模拟退⽕寻优⽅法注意事项理论上，降温过程要⾜够缓慢，使得在每⼀温度下达到热平衡。

三维装箱问题是一类经典的组合优化问题，在计算机科学和工程等领域中具有广泛的应用。

解决这个问题可以采用混合遗传模拟退火算法，其基本过程如下：
1. 初始化种群
初始时，生成一组随机的箱子序列，并将它们作为初始种群。

2. 选择操作
根据每个箱子的适应度（即“剩余体积”或“填装率”），从当前种群中选择一些个体作为父代进入下一步的交叉操作。

3. 交叉操作
选定两个父代，根据某种交叉算法将它们的部分染色体进行交换，形成新的子代个体。

4. 变异操作
从产生的子代个体中，按照一定概率随机地选择一个箱子进行变异。

变异操作包括修改该箱子的位置、角度或大小等。

5. 模拟退火操作
对变异后的子代个体进行一定次数的模拟退火操作，以达到全局最优解。

6. 更新操作
根据产生的新个体和当前的种群，更新选择出下一代种群。

7. 终止条件
当达到指定迭代次数或者找到符合要求的最优解时，停止搜索。

通过以上操作，混合遗传模拟退火算法可以逐步寻找最优解，解决三维装箱问题。

需要注意的是，如何定义“适应度”函数是影响算法效果的关键因素，需要仔细考虑和调节。

同时，由于该问题具有很高的复杂性，算法的具体实现还需要根据具体情况进行一些调整和优化。

模拟退火算法及其改进
刘怀亮
【期刊名称】《广州大学学报（自然科学版）》
【年(卷),期】2005(4)6
【摘要】介绍了模拟退火算法的背景、原理和具体实现方法,分析了它的不足之处,讨论了它的改进措施,并进行了仿真实验验证.
【总页数】4页(P503-506)
【作者】刘怀亮
【作者单位】广州大学,信息与机电工程学院,广东,广州,510006
【正文语种】中文
【中图分类】TP15
【相关文献】
1.基于模拟退火算法改进粒子群算法优化数学函数 [J], 朱焕雄
2.基于改进模拟退火算法的虚拟机调度优化方法 [J], 宋杨
3.求解带序列相关准备时间双边装配线平衡问题的改进模拟退火算法 [J], 赵瀚明;唐秋华;蒙凯;李梓响;张子凯
4.基于OWA算子改进模拟退火算法的路线规划研究 [J], 赵人行;郭旭萌;霍俊生;赵景林
5.基于改进模拟退火算法的登机口分配问题 [J], 谢维;关嘉欣;周游;朱文斌
因版权原因，仅展示原文概要，查看原文内容请购买。

模拟退火算法与遗传算法
模拟退火算法（Simulated Annealing，SA）和遗传算法（Genetic Algorithms，GA）是两种常用的优化算法，分别简要介绍如下：
1. 模拟退火算法（Simulated Annealing，SA）：模拟退火是一种基于物理退火原理的优化算法。

该算法在搜索过程中，根据某一概率接受一个比当前解要差的解，因此有可能会跳出局部最优解，达到全局最优解。

它的优点是能够在全局范围内搜索到最优解，具有较好的鲁棒性，适用于多峰值、非线性、离散、连续等问题的优化。

在求解组合优化问题和离散优化问题上模拟退火表现良好。

2. 遗传算法（Genetic Algorithms，GA）：遗传算法是一种基于自然选择和遗传学原理的优化算法。

它通过模拟生物进化过程中的自然选择和遗传机制，如选择、交叉、变异等操作，在解空间内搜索最优解。

遗传算法具有较好的全局搜索能力，能够处理复杂的、非线性的、离散的优化问题。

在求解连续函数优化问题和组合优化问题上表现良好。

总之，模拟退火算法和遗传算法都是非常有效的优化算法，各有其适用范围和优点。

在实际应用中，可以根据问题的类型和特点选择合适的算法进行优化求解。

模拟退火算法介绍模拟退火算法（Simulated Annealing，SA）是一种基于蒙特卡洛方法的优化算法，由Kirkpatrick等人于1983年提出。

它模拟了固体物体从高温到低温时退火的过程，通过模拟这一过程来寻找问题的最优解。

首先，模拟退火算法需要生成一个初始解。

初始解是随机生成的，它代表了问题的一个可能解。

初始解的生成可以采用随机数生成方法，或者使用其他启发式算法生成。

然后，算法需要定义一个邻域结构来解空间。

邻域结构定义了问题的解的相邻解之间的关系。

在退火算法中，邻域结构是动态变化的，随着算法的进行，邻域结构会不断调整以适应的需求。

在退火准则方面，模拟退火算法使用了一个“接受准则”来决定是否接受一个邻域解。

接受准则基于Metropolis准则，它比较了当前解和邻域解之间的差异以及温度参数。

如果邻域解的质量更好，那么就接受它；否则，以一定的概率接受较差的解。

这个概率与温度成正比，随着温度降低，接受较差解的概率逐渐减小。

在算法的每个迭代中，温度参数会随着迭代次数逐渐降低，这意味着算法逐渐从随机转变为局部。

温度参数的降低速率决定了算法的接受较差解的概率的减小速率。

温度参数的决定是关键，它通常是一个退火函数的参数，根据经验选择。

总的来说，模拟退火算法是一种随机化的优化算法，通过模拟物理退火过程，在解空间时能够克服局部最优解，从而寻找全局最优解。

它的应用范围广泛，涵盖了诸多领域，如组合优化、图像处理、网络设计等。

但是，模拟退火算法的收敛速度相对较慢，需要很多次迭代才能找到最优解，因此在实际应用中需要根据具体问题进行合适的调整和优化。

模拟退火算法及其在最优化中的应用随着计算机科学的不断发展，求解模型的最优解已成为一项重要课题。

而对于许多实际问题来说，求解最优解是一个 NP 难问题。

因此，人们常常使用各种算法来解决这些问题。

模拟退火算法作为一种求解 NP 难问题的启发式算法，越来越受到学术界和工业界的关注。

一、模拟退火算法的原理模拟退火算法源于统计物理学中的模拟物理过程。

它的核心思想是以一定的概率接受比当前状态差的解，为了避免陷入局部最优解，随着时间的推移逐渐减小概率。

在求解问题时，模拟退火算法首先会随机选择一个初始解，然后根据一定的规则来生成邻域解。

接下来，算法会计算这个邻域解与当前最优解之间的差距，如果邻域解更优，那么它就成为新的最优解；否则，按照一定的概率接受它，以避免陷入局部最优解。

这个概率与当前的温度有关。

在初始阶段，温度非常高，此时概率极大，那么算法就更有可能接受一个比最优解差的解。

但随着时间的推移，温度越来越低，概率就越来越小，这时算法的行为就趋向于贪心算法，只会接受更优的解。

二、模拟退火在最优化中的应用模拟退火算法广泛应用于组合优化问题，如图形着色、旅行商问题、背包问题等。

它也可以用于解决连续优化问题，如函数最大值或最小值的求解。

在实践过程中，模拟退火算法已经被证明是一种有效、高效的求解方法。

下面我们以图形着色问题为例来说明模拟退火算法的应用。

给定一个图 $G=(V,E)$，要求每个顶点 $v_i \in V$ 都染上一种颜色，使得相邻的两个点不会被染上相同的颜色。

这就是图形着色问题，也是一个 NP 难问题。

对于这个问题，我们可以用模拟退火算法来求解。

首先我们随机给每个顶点染上一种颜色，然后计算与当前方案不同的解，每次取这些解中最优的一个。

如果这个解比当前最优的解更优，那么它成为新的最优解。

否则，以一定的概率接受新的解，以避免陷入局部最优解。

在实际应用中，我们通常将温度初始值设为一个稍大于 1 的常数，然后进行一定的迭代次数，直到温度降到一个极小值。

模拟退火优化算法曲线
模拟退火是一种全局优化算法，最初是受到固体退火过程的启发而提出的。

它通过模拟固体退火时的分子运动过程来寻找问题的全局最优解。

这种优化算法通常用于解决组合优化问题，如旅行商问题、装箱问题等。

在模拟退火算法中，曲线通常指的是优化过程中目标函数值随着迭代次数的变化曲线。

这条曲线可以反映出算法在搜索过程中的收敛情况，以及最终找到的解的质量。

通常情况下，曲线会呈现出逐渐下降并趋于稳定的趋势，但也有可能会出现震荡或者突然上升的情况，这可能意味着算法陷入了局部最优解而无法跳出。

从算法角度来看，模拟退火算法通过控制退火温度、接受概率等参数来调节搜索过程，从而在全局范围内寻找最优解。

曲线的形状可以反映出这些参数对算法性能的影响，对于调参和优化算法性能有一定的指导意义。

另外，从应用角度来看，曲线也可以反映出模拟退火算法在不同问题上的表现。

不同类型的优化问题可能会对算法的性能提出不同的要求，因此对于特定问题，曲线的形状可能会有所不同。

总的来说，曲线在模拟退火算法中扮演着重要的角色，它可以帮助我们了解算法的收敛情况和性能表现，从而指导我们对算法的调参和优化，以及对特定问题的应用。

物流配送路径优化车辆路径规划算法的研究与改进一、引言物流配送是现代经济发展中不可或缺的一环，对于提高效率、降低成本具有重要意义。

而车辆路径规划算法在优化物流配送中扮演着关键角色。

本文旨在研究与改进物流配送路径优化车辆路径规划算法，以提高配送效率和降低成本。

二、传统算法的不足传统的车辆路径规划算法一般采用贪婪算法、遗传算法等，虽然在某些情况下能够得到可行的解，但存在以下不足之处：1. 时间复杂度高：在处理大规模数据时，传统算法往往需要较长的计算时间，导致配送时间延长。

2. 缺乏灵活性：传统算法对于各种配送场景的适应能力较差，不能高效应对复杂的实际情况。

3. 没有考虑实时交通状况：传统算法无法根据实时交通状况进行动态调整，无法最大程度地缩短配送时间。

三、现有算法的研究与改进针对传统算法的不足，研究者们提出了一些改进和创新的算法，以期能够更好地应对物流配送路径优化的需求。

1. 基于模拟退火算法的路径规划算法改进模拟退火算法是一种基于概率统计的全局优化算法，通过模拟金属的退火过程来搜索最优解。

研究者们将模拟退火算法应用于车辆路径规划中，并对其做了一些改进。

例如，引入动态邻域搜索策略，提高了算法的收敛速度和解的质量。

2. 基于蚁群算法的路径规划算法改进蚁群算法是一种群体智能算法，模拟了蚂蚁在寻找食物过程中的行为。

研究者们将蚁群算法应用于车辆路径规划中，并对其进行了改进。

例如，通过引入启发式信息素计算方法，提高了算法的收敛速度和路径的优化程度。

3. 基于深度学习的路径规划算法改进深度学习是近年来兴起的一种机器学习方法，通过多层次的神经网络模型实现对数据的自动学习和表征。

研究者们将深度学习应用于车辆路径规划中，并融合实时交通数据，提出了一些改进的算法。

例如，通过训练神经网络模型，使得算法能够根据实时交通状况进行动态路径调整，从而有效降低配送时间。

四、算法的实验与应用为了验证改进算法的有效性，研究者们进行了大量实验和应用。

求解三维装箱问题的混合遗传模拟退火算法一、本文概述装箱问题，也称为装箱优化问题，是一类广泛存在于现实生活中的组合优化问题。

特别是在物流、工业工程、计算机科学等领域，装箱问题以其高度的复杂性和实际应用价值而备受关注。

其中，三维装箱问题更是因其涉及物品的三维形状和空间利用率的优化而显得尤为复杂。

近年来，随着智能优化算法的发展，遗传算法和模拟退火算法等启发式搜索算法在求解此类问题上展现出了强大的潜力。

本文旨在探讨一种结合遗传算法和模拟退火算法的混合算法，以求解三维装箱问题。

我们将首先介绍三维装箱问题的定义、特点以及求解难度，然后详细阐述混合遗传模拟退火算法的设计原理、实现过程以及关键参数的选择。

通过对比实验和结果分析，我们将验证该混合算法在求解三维装箱问题上的有效性和优越性。

本文的主要内容包括：三维装箱问题的数学模型及求解难点分析；混合遗传模拟退火算法的设计和实现；算法性能的实验验证与对比分析；以及结论与展望。

通过本文的研究，我们期望能为三维装箱问题的求解提供一种新的有效方法，并为相关领域的实际应用提供理论支持和实践指导。

二、相关理论基础三维装箱问题（Three-Dimensional Bin Packing Problem,3D-BPP）是一个经典的组合优化问题，涉及到如何将一组不同尺寸的三维物体有效地放入有限数量的容器中，同时尽可能减少容器的使用数量。

由于该问题的复杂性，传统的数学方法往往难以在合理的时间内找到最优解，因此，启发式算法和元启发式算法在求解此类问题上显示出其独特的优势。

遗传算法（Genetic Algorithm, GA）是一种基于自然选择和遗传学原理的优化搜索算法。

它通过模拟生物进化过程中的选择、交叉、变异等操作，在问题的解空间中寻找最优解。

遗传算法具有较强的全局搜索能力，但容易陷入局部最优解，导致搜索效率降低。

模拟退火算法（Simulated Annealing, SA）则是一种基于物理退火过程的优化算法。

模拟退火算法适用范围
一、简介
模拟退火算法（Simulated Annealing，简称SA）是由Kirkpatrick 等人于1983年提出的一种算法，它模拟了物理体系经历温度变化后的退火（annealing）过程，其目标是求解全局最优解。

它是一种基于概率算法，在过程中通过概率来决定接受下一步解。

通过模拟物理体系的退火过程系，模拟退火算法在局部最优解时，可以避免过早“著陷”于局部解，最终到最优解。

二、适用范围
（1）模拟退火算法可以用于解决多目标优化问题，其特点是可以把多目标优化问题转换成单目标优化问题来解决；
（2）模拟退火算法可以用于可解复杂优化问题，可以解决非线性、不可解析、禁忌等复杂的优化问题；
（3）模拟退火算法可以用于求解非凸优化问题，可以解决存在局部最优解的优化问题；
（4）模拟退火算法还可以应用于模式识别、图像处理、机器视觉、智能控制等领域来解决复杂的问题；
（5）模拟退火算法还可以应用于求解组合优化问题。

模拟退火算法的原理及算法在优化问题上的应用共3篇模拟退火算法的原理及算法在优化问题上的应用1模拟退火算法的原理及算法在优化问题上的应用随着计算机科学的发展，越来越多的计算问题需要用到优化算法来得到最优解，而模拟退火算法（Simulated Annealing）是一种常用的优化算法之一。

本文将介绍模拟退火算法的原理，以及它在优化问题上的应用。

一、模拟退火算法的原理模拟退火算法最早由Kirkpatrick等人在1983年提出，是一种启发式优化算法。

其思想来源于固态物理学中的模拟退火过程，也就是将物质加热后缓慢冷却的过程。

这个过程中，原子系统会从高温状态演变到低温状态，从而达到低能量状态。

模拟退火算法的基本思路是从一个初状态开始，通过改变状态来不断寻找更优的解，直到达到最优解或者达到一定的停机条件。

其核心思想是在搜索过程中不断接受差解，以避免被困在局部最优解。

具体来说，模拟退火算法主要包含以下几个步骤：1. 随机初始化一个状态。

2. 初始化一个温度T，T越高，搜索过程越接受差解。

3. 在当前状态的附近随机生成一个新状态。

4. 计算当前状态与新状态的差异性，如果新状态更优则接受新状态，否则以一定的概率接受新状态。

5. 降低温度，温度降低的速度越来越慢，直到温度降到结束条件。

6. 如果结束条件没有满足，继续从第三步开始。

模拟退火算法的核心在于如何根据当前温度，以一定的概率接受差解，这就需要引入Metropolis准则：P(solution_i→solution_j) = min{1, exp((Ei - Ej) / T)},其中P(solution_i→solution_j) 为从解i转移到解j的概率，Ei为当前解的能量，Ej为新解的能量，T为温度。

通过Metropolis准则，模拟退火算法在搜索过程中可以接受一定的差解，从而避免陷入局部最优解。

二、模拟退火算法在优化问题上的应用模拟退火算法可以应用到很多优化问题中，例如旅行商问题、最大割问题等。

模拟退火算法参数1. 引言模拟退火算法是一种基于物理退火过程的随机优化算法，起源于物理学中的固体物理领域。

随着计算机技术的不断发展，在各个领域中得到了广泛的应用，如最优化问题、图论、组合优化等。

在模拟退火算法中，其优化过程就是一个随机“走山”过程，通过控制温度来决定搜寻方向，从而获得全局最优解。

因此，在使用模拟退火算法时，不同参数的设置会对整个算法的结果产生重要影响，本文将会对模拟退火算法中的参数进行探讨和分析。

2. 参数说明模拟退火算法的三个主要参数是初始温度、降温速率和终止温度，下面分别进行介绍。

初始温度初始温度是指模拟退火算法开始时的温度大小。

初始温度应该足够高，以便算法能够跳出当前局部最优解进入到全局最优解的搜索空间。

但如果初始温度过高，则可能会造成算法的不稳定性，使其无法达到全局最优解。

那么如何设置初始温度呢？通常的做法是通过试验，逐步增加初始温度，直到算法在较短时间内可以找到较优解。

理论上，初始温度越大，算法越容易发现更优解，但也会增加算法的运行时间和内存消耗。

降温速率降温速率是指模拟退火算法中温度降低的速度，这是控制算法搜索速度的关键参数。

降温速率越小，算法搜索的步骤越多，但时间也越长；降温速率越大，算法搜索步骤较少，但搜索的深度可能不够。

降温速率的选择应该适当，一般是根据问题的复杂程度来进行选择。

对于相对简单的问题，可以适当加快降温速率，而对于比较复杂的问题，则应该选择较慢的降温速率。

终止温度终止温度是指模拟退火算法搜索过程中最终允许的温度。

当算法达到终止温度时，算法退火结束，产生的解即为最优解，此时不进行搜索。

通常，终止温度应该足够低，以确保搜索空间充分被搜寻到。

终止温度的大小一般取决于问题的复杂性和降温速率的选择。

较高的终止温度会导致算法没有足够的时间来搜索全局最优解，而较低的终止温度会使算法更容易落入局部最优解。

3. 参数调整方法对于模拟退火算法，参数的选择不同会对算法的收敛和优化结果产生重大影响。