各种振动分析诊断案例
- 格式:ppt
- 大小:18.46 MB
- 文档页数:76

桥梁结构的振动特性与实践案例分析桥梁结构是现代社会重要的基础设施,它们承载着交通运输的重任,保障着人们的出行安全和经济的发展。
然而,桥梁结构的振动特性对于其稳定性和安全性具有重要影响。
因此,深入了解桥梁结构的振动特性,并通过实践案例分析来探讨解决方法,对于提高桥梁工程的质量和安全性具有重要意义。
首先,桥梁结构的振动特性是指在受到外界激励或自身系统内部激励下,结构会发生振动。
振动特性包括振动频率、振动模态和振动幅值等参数。
振动频率是指桥梁结构在特定的条件下的振动周期,它与结构的刚度和质量密切相关。
振动模态是指桥梁结构在不同振动频率下的振动形态,它与结构的固有频率和振动模态形式有关。
振动幅值是指桥梁结构振动的幅度大小,它与激励的力度和结构的阻尼特性有关。
其次,桥梁结构的振动特性会对结构的稳定性和安全性产生影响。
当桥梁受到外界激励(如风荷载、地震等)时,如果结构的振动频率与激励频率接近甚至相同,就会出现共振现象。
共振会导致结构振幅增大,从而可能引起结构的破坏和倒塌。
此外,结构的振动还会导致桥梁的舒适性下降,对行人和车辆的安全造成威胁。
针对桥梁结构的振动问题,我们可以采取一系列的措施来保障桥梁的稳定性和安全性。
首先,通过结构设计和分析,合理选择结构材料和断面形状,提高桥梁的抗振能力。
其次,进行结构的振动监测与评估,了解结构的振动性能,及时采取相应的措施,如增加阻尼器、加强刚度等。
同时,制定科学合理的维护养护计划,及时发现和修复结构的损伤,防止进一步的振动放大。
本文将通过实践案例分析来探讨桥梁结构的振动特性及其对结构的影响。
以北京市某桥梁为例,该桥梁于1990年建成,经过多年的使用,出现了明显的振动问题。
通过实测数据和有限元分析,我们发现该桥梁的固有频率与甚至接近风荷载频率,导致桥梁受到风荷载时出现共振现象,振幅增大,威胁到行车安全。
因此,我们采取了增加阻尼器和加强结构刚度的措施,在不改变原有结构的情况下有效控制了振动问题。

单自由度振动系统的运动方程解析解的应用案例分析单自由度振动系统是机械工程中非常重要的一类振动系统。
它的运动方程可用解析解表示,这在许多实际问题的解决中发挥着重要作用。
本文将通过分析两个应用案例,展示单自由度振动系统运动方程解析解的实际应用。
案例一:弹簧振子考虑一个弹簧振子系统,由一个质量为m的物体通过一个弹簧与固定支撑相连。
假设摩擦系数为零,物体只有沿水平方向的振动。
根据牛顿第二定律可以得到以下运动方程:m a=−aa其中a是物体的加速度,k是弹簧的劲度系数,x是物体的位移。
通过简单的求解可以得到该系统的解析解为:a = a cos(a_0 t + a)其中A和a分别是振幅和相位,a_0 是系统的固有角频率,有关常数可以通过初始条件来确定。
这个方程给出了振子在任意时间点的位移,通过振幅和相位可以描述振动的特征。
在实际应用中,我们可以利用这个方程来分析弹簧振子的运动规律,如计算特定时刻的位移、速度和加速度等。
案例二:简谐受迫振动考虑一个简谐受迫振动系统,它除了由弹簧力驱动外,还受到外部激励力F(t)的作用。
运动方程可以表示为:m a=−aa +F(t)其中F(t)是外部激励力的函数形式,可以是任意周期性函数。
在这种情况下,运动方程没有解析解,但我们可以通过变换方法将其转化为解析解出现的形式。
一个常见的方法是利用复指数形式的解,并通过计算使运动方程等号两边的实部和虚部相等。
通过求解可以得到:a = a cos(a_0 t + a) + a_p其中a_p是该系统的稳态解,表示受迫振动的特定解,由外部激励力决定,A和a是自由振动的振幅和相位。
这个方程描述了受迫振动系统的运动,可以用于分析系统在不同激励力下的响应,如共振频率、相位差等。
总结起来,单自由度振动系统运动方程解析解的应用案例分析有助于我们深入理解振动系统的运动行为。
通过解析解,我们可以更好地预测和控制系统的振动特性,为相关工程问题提供解决思路。
![电厂旋转机械设备振动问题处理案例分析_张学延[1]](https://uimg.taocdn.com/bfad575bf7ec4afe04a1df84.webp)
的问题[1-6]。
尽管随着振动监测系统越来越广泛的应用[7],使得更容易捕捉到反映振动故障根源的特征参数,而且振动故障诊断技术日臻成熟,然而,正确理解并使用好这些技术解决现场出现的振动问题不仅需要扎实的理论知识,而且需要现场诊断经验的持续积累。
如果忽视了一些重要的振动现象和特征,就可能无法查找到真正的故障原因。
有时即使确定了振动故障原因,但如果没有根据现场具体情况,提出有效的解决方案,则只能取得事倍功半的效果,甚至达不到任何效果。
本文通过介绍近几年对某汽轮机、发电机、凝结水泵驱动电机和脱硫增压风机振动问题处理过程的案例分析,说明振动故障诊断和治理技术的实际应用及效果。
这些故障涉及轴承失效、发电机匝间短路、结构共振和不稳定质量不平衡。
1某660MW 汽轮机低压转子突发性振动诊断和处理1.1设备简介及振动特点某机组汽轮机系哈尔滨汽轮机厂生产的6601.2振动故障诊断及处理最初怀疑低压Ⅰ转子上有部件逐渐脱落或出现局部动静碰磨使转子产生热弯曲进而导致振动爬升。
但在4号轴承轴振增大的同时,其轴承座振动几乎没有增大,同时相邻的3、5号轴承轴振也没有增大,这一现象在逻辑上无法解释。
还有观点认为可能是4号轴承轴振测量系统出现问题,但一般同一轴承2个轴振测点同时出现测量数据偏差的可能性较小。
随后检查低压Ⅰ转子末级叶收稿日期:2015-04-26作者简介:张学延(1962—),男,重庆人,研究员,长期从事汽轮发电机组振动故障诊断和治理工作。
图1低压Ⅰ转子4号轴承X 、Y 方向轴振趋势Fig.1Shaft vibration trend in X and Y directions atBearing 4of LP Rotor Ⅰ发电第8期片等未发现异常及检查振动测量系统无误后机组冲转。
在冲转过程中,转速达到1200r/min 后4号轴承X 、Y 方向轴振动快速增大,转速最高冲至1540r/min 时振动已达400μm 以上而跳机(Bode曲线见图2)。


非线性系统的实际应用案例非线性系统在现代科学与技术中有着广泛的应用,涉及到各个领域,如机械、自动控制、生态学、神经科学等等。
在本文中,我们将介绍一些非线性系统的实际应用案例,并力图从中探讨非线性系统的工程问题和特性。
一、喷气发动机振动分析喷气发动机是现代航空发展的主要推动力,而它的结构十分复杂,有许多非线性振动的现象。
因此,正确地分析和诊断其振动特性就显得十分必要。
以一具喷气发动机为例,德国学者L. RICHTER在其论文中分析了其在运行过程中的振动特性,结果表明该发动机的非线性动力分析对于研究其振动动态行为有明显的促进作用。
通过对喷气发动机的振动分析,不仅可以对其结构及特性进行诊断,还可以为改进设计提供更加清晰的思路。
二、生态系统的动态模拟生态学是研究生物群落及其环境相互作用的一门学科。
当生态系统变化时,非线性动力学便成为研究这种复杂性的重要工具。
在一些生态系统研究中,如重构同化指数、广义线性模型等,非线性系统模型的应用相当明显。
通过对生态系统的动态模拟,科学家不仅可以深入了解其内部机制,还可以为制定可持续的经济发展方案提供依据。
三、神经控制系统设计随着工业智能化的发展,神经控制系统应用越来越广泛。
与传统PID控制系统不同的是,神经控制系统能够模拟人的智能思维,对于建模非线性系统尤为有效。
例如,通过神经网络结构,可以模拟汽车转向、加速、制动等非线性系统,对于提升车辆性能有着积极的作用。
此外,神经控制系统还可以用于医学领域,如针灸、手术机器人等,都有着明显的非线性动力学性质。
四、机器人行走控制机器人在现代制造业中发挥着越来越重要的作用,而其行走控制则是重点问题。
由于机器人的结构变化以及外部环境干扰等因素,机器人行走控制是一个非线性系统问题。
在控制模型优化和状态预判等方面,非线性系统的方法优于传统线性方法。
例如,一个名为“空中蹦床”的机器人模型,通过非线性分析建立行走控制模型,使其在精准地控制脚部力量的同时能够更加灵活地执行任务。

前言S8000系统为阿尔斯通创为实技术发展(深圳)有限公司开发的新一代大型旋转机械状态监测系统,该系统现已被越来越多的石化、电力、冶金企业所使用,并成为设备管理人员对大机组管理、诊断的得力助手。
本案例集收集了近三年内,使用S8000系统进行的部分诊断案例,并按案例类别进行了大概的整理,供各企业设备管理人员参考;由于原诊断报告篇幅过长,在本案例集中对原报告进行了一些删剪,以方便阅读,如需对某案例进行更详细了解,请与创为实公司联系;由于我们的水平有限,可能的失误难免存在,欢迎批评指正。
阿尔斯通创为实技术发展(深圳)有限公司2007年9月目 录1 叶片断裂类案例 (1)2 油膜涡动类故障 (35)3 磨擦类故障 (56)4 垢层脱落故障 (64)5 电气干扰类故障 (74)6 动平衡不良类 (88)7 通过相关性分析发现工艺量设置类问题 (95)8 转子热弯曲 (102)1叶片断裂类案例1.1某厂04年09月27日空压机断叶片故障诊断分析故障状态描述:此厂空气压缩机组K1202/KT1202于2004年9月27日发生空压机驱动透平振动突然增大事故,以下把故障发生过程中各图谱的变化情况列举如下:通频值振动趋势图(2004-09-27 12:01:5至2004-09-27 15:36:5的历史数据和灵敏监测数据)从上面的趋势图上可以很清楚的看出,该机组在9月27日的12:18:09时振动瞬间突发性升高,同时,振动的相位也发生了明显的变化,其振动能量主要是集中表现在工作频率上。
这些都意味着透平转子出现了故障,产生了极大的不平衡。
126V035A波形频谱图(事故发生瞬间的整个过程)上图为某一测点事故发生瞬间整个过程的波形频谱图,从图中可以看到转子物质脱落前的4个周期的振动波形、脱落开始的瞬间波形变化以及脱落后的振动慢慢趋于稳定的系列过程,这一瞬间不仅其振动的幅值有大幅度的增大,而且其相位的变化也较明显。
透平入口事故发生瞬间的轴心轨迹图诊断分析结果:通过对S8000系统所捕捉到的数据的分析,我们认为这次故障是因为透平转子上有部件掉落,如叶片突然断裂或围带、拉筋、铆钉脱落,因而瞬间造成了一个很大的不平衡,引起振动在短时间内突然上升。

振动信号的小波变换与故障诊断振动信号在机械设备故障诊断中起着重要的作用。
为了从振动信号中获得有用的信息并准确诊断故障,小波变换被广泛应用于振动信号的分析与诊断中。
本文将介绍振动信号的小波变换原理及其在故障诊断中的应用。
一、小波变换原理小波变换是一种时频分析方法,能够将信号在时域和频域上进行局部分析。
相比傅里叶变换,小波变换具有时域分辨率高、频域分辨率可变的优点,适用于非平稳信号的分析与处理。
小波变换的数学表达式为:\[WT(f,a)=\int_{-\infty}^{\infty}x(t)\Psi^*\left(\frac{t-a}{f}\right)dt\]其中,\(x(t)\)为原始信号,\(\Psi(t)\)为小波基函数,\(a\)为时间平移参数,\(f\)为尺度参数。
通过调整小波基函数的尺度参数和平移参数,可以实现对信号的局部分析。
二、振动信号的小波变换分析振动信号通常包含多个频率和幅值变化较大的成分,对其进行小波变换可以更好地揭示故障特征。
以下是几个常用的小波变换分析方法。
1. 连续小波变换(CWT)连续小波变换是最基本的小波变换方法,它能够对信号在不同尺度下的频率成分进行分析。
CWT的实质是将信号与小波基函数进行卷积运算,得到时频图谱,展示了信号在不同时间和频率上的能量分布情况。
2. 离散小波变换(DWT)离散小波变换是对连续小波变换的离散化处理,通过多级滤波和下采样操作将信号进行分解与重构。
DWT可实现信号的多尺度分解与重构,从而提取出信号在不同频段的特征。
3. 小波包变换(WPT)小波包变换是对DWT的扩展,通过允许更多的分解方式,提高了信号的频域分辨率。
小波包变换能够更加精细地分析信号的频域特性,对于复杂信号的故障诊断具有更好的效果。
三、振动信号的故障诊断应用振动信号的小波变换在故障诊断中有着广泛的应用。
以下是几个典型的案例。
1. 轴承故障诊断轴承故障通常表现为冲击、摩擦和失效等特征,在振动信号中可以清晰地表现出来。

蚀性气体或液体需要做好防护措施。
同时,由于控制系统含有精密仪器,安装前,还需要对这些仪器仪表进行质量检验和精度校准,保证计量时的准确度,并加装必需的保护装置,保障人身和设备安全,保障电气设备可靠运行。
安装完成后,需要对设备进行合理地维护,针对设备缺陷有有效的应对方案,同时保证设备检修的及时性和效率,提高电力系统的可靠性和稳定性。
参考文献[1]齐书可.电气设备自动化控制中PLC技术的应用研究[J].科技经济市场,2019(1):4-5.[2]李建奇.电气设备自动控制系统中的PLC技术运用[J].无线互联科技,2018,15(24):131-132,135.[3]徐小燕.电气设备的自动控制设计[J].科技资讯,2018,16(33):57-58.[4]董敏.电气设备安装及调试过程中质量控制措施[J].低碳世界,2018(11):38-39.[5]王辉.关于电气调试中电子电路的干扰问题分析[J].计算机产品与流通,2018(9):73.[6]王维平.变电站的电气设备安装和调试经验谈[J].智能城市,2018,4(17):149-150.〔编辑叶允菁〕转动设备振动频谱分析案例韩国良(大庆炼化公司电仪运行中心,黑龙江大庆163000)摘要:旋转机械广泛应用振动信号进行诊断的方法不仅简便可行,而且经过不断实践、研究,积累的经验和技术已经比较成熟。
当一台设备发生振动故障时,为了准确快速地寻找故障原因,解决振动问题,就需要采集振动信号,运用频谱分析方法来进行分析。
本文通过一些实际案例来说明如何进行振动频率分析、故障诊断、处理。
关键词:频谱;不平衡;不对中;基础刚性不足中图分类号:TQ053文献标识码:B DOI:10.16621/ki.issn1001-0599.2019.07D.1350引言在化工生产中由机械振动引起的设备损坏率很高,设备损坏的严重程度又与振动的大小有直接关系。
而振动信号中又包含着丰富的设备状态信息,通过振动采集设备可以采集到设备振动的时域波形,再通过傅里叶变换转换成频域谱图,通过频域谱图就可以发现一些设备运行的特征频率,不同的特征频率往往对应着一定的故障类别。

振动大实例与原因分析 Company number:【0089WT-8898YT-W8CCB-BUUT-202108】1倍频振动大除了动平衡还应检查什么据统计,有19%的设备振动来自动不平衡即一倍频,而产生动不平衡有很多原因。
现场测量的许多频谱结果也多与机器的一倍频有关系,下面仅就一倍频振动增大的原因进行分析。
一、单一一倍频信号转子不平衡振动的时域波形为正弦波,频率为转子工作频率,径向振动大。
频谱图中基频有稳定的高峰,谐波能量集中于基频,其他倍频振幅较小。
当振动频率小于固有频率时,基频振幅随转速增大而增大;当振动频率大于固有频率时,转速增加振幅趋于一个较小的稳定值;当振动频率接近固有频率时机器发生共振,振幅具有最大峰值。
由于通常轴承水平方向的刚度小,振动幅值较大,使轴心轨迹成为椭圆形。
振动强烈程度对工作转速的变化很敏感。
1.力不平衡频谱特征为振动波形接近正弦波,轴心轨迹近似圆形;振动以径向为主,一般水平方向幅值大于垂直方向;振幅与转速平方成正比,振动频率为一倍频;相位稳定,两个轴承处相位接近,同一轴承水平方向和垂直方向的相位差接近90度。
2.偶不平衡频谱特征为振动波形接近正弦波,轴心轨迹近似圆形;在两个轴承处均产生较大的振动,不平衡严重时,还会产生较大的轴向振动;振幅与转速平方成正比,振动频率以一倍频为主,有时也会有二、三倍频成分;振动相位稳定,两个轴承处相位相差180度。
3.动不平衡频谱特征为振动波形接近正弦波,轴心轨迹近似圆形;振动以径向为主,振幅与转速平方成正比,频率以一倍频为主;振动相位稳定,两个轴承处相位接近。
4.外力作用下(旋转)产生的共振各个零部件、结构件在外力作用下所产生的固有共振为自激振动,其频率与不同的结构对应,即刚度不同引起的不同共振。
频谱特征为时域波形为正弦波,振动频率以一倍频为主。
二、相关一倍频信号1.转子永久弯曲振动类似于动不平衡和不对中,以一倍转频为主,也会产生二倍转频振动;振动随转速增加很快;通常振幅稳定,轴向振动较大,两支承处相位相差180度。

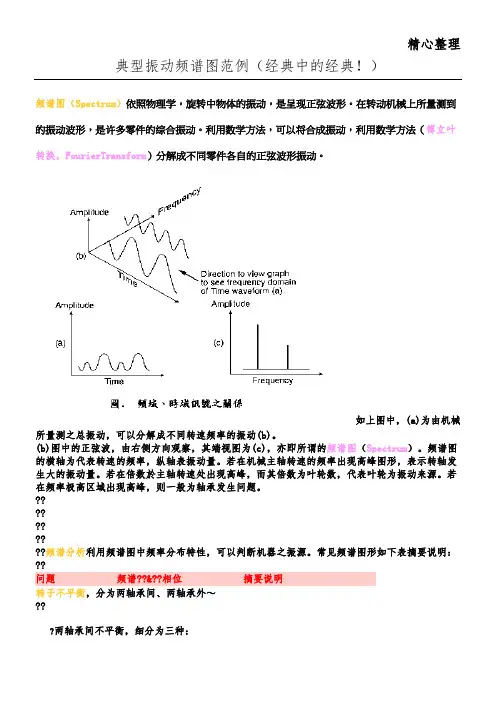
精心整理典型振动频谱图范例(经典中的经典!)频谱图(Spectrum)依照物理学,旋转中物体的振动,是呈现正弦波形。
在转动机械上所量测到的振动波形,是许多零件的综合振动。
利用数学方法,可以将合成振动,利用数学方法(傅立叶转换,FourierTransform)分解成不同零件各自的正弦波形振动。
(b)??????????频谱分析利用频谱图中频率分布特性,可以判断机器之振源。
常见频谱图形如下表摘要说明:转子不平衡,分为两轴承间、两轴承外~??两轴承间不平衡,细分为三种:1.静不平衡StaticUnblance ?振动频率为1倍转速(1×RPM)。
?径向振动大,轴向小。
?两轴承径向呈同相(InPhase)运动,两相角相差0°,同轴承垂直与水平相位差90°。
2.∙径向振动大,轴向有可能大。
3.∙∙∙∙偏心转子(EccentricRotor ) ∙之直线振动。
∙振动频率出现在1倍转速(1×RPM)。
∙同轴承垂直或水平相位差180°或90°。
轴弯曲?会产生大的轴向振动。
?两轴承间之相位相差180°。
转子对心不良,分为联轴器、轴承两类~??∙联轴器两端,再细分为角度与平行两种:1.角度不对心∙会产生大的轴向振动。
∙频率出现在1×、2×、3×...等,严重时会出现更高频之谐波。
∙在联轴器两端之相位差180°反向。
2.1.2.3.平轴承1.油漩2.轴承间隙过大?振频出现於1×、2×、3×...等,甚至有更高频之谐波。
传动皮带1.皮带松动、损坏∙皮带振动频率低於轴转速,通常会有1、2、3...倍之皮带振动频率出现。
∙2倍之皮带振动频率通常为主振动频率。
2.皮带对心不良?会导致很高之轴向振动。
?振频出现於1倍之主动轮或从动轮之转速。
转子摩擦RotorRub ∙与机械松动之频谱类似。
振动与冲击1. 引言振动与冲击是物理学中一个重要的研究领域,涉及到许多物理现象和工程应用。
振动指的是物体或系统在一定时间范围内往复运动的现象,而冲击则是突然产生的、短暂而强烈的外力作用于物体的现象。
振动和冲击都是自然界和生活中经常遇到的现象,深入研究和理解振动与冲击对于工程设计、结构优化和故障分析等方面有重要的意义。
2. 振动的基本概念和特性振动是物体或系统在时间上的往复运动。
振动的基本特性包括频率、振幅和周期。
频率是指在单位时间内振动的次数,单位为赫兹(Hz)。
振幅是指振动过程中物体或系统离开平衡位置的最大位移,通常用米(m)来表示。
周期是指物体或系统完成一个完整振动循环所需要的时间,单位为秒(s)。
振动的类型可以分为自由振动和强迫振动。
自由振动是指物体或系统在无外力作用下的振动,其频率由物体的固有特性决定。
而强迫振动是指物体或系统在受到外力作用下的振动,其频率和外力的特性有关。
3. 振动的应用振动在各个领域和行业都有着广泛的应用。
以下是一些典型的振动应用案例:3.1 振动传感器振动传感器是一种能够测量和监测物体振动的设备。
它广泛应用于机械设备、航空航天、汽车工业等领域。
振动传感器可以帮助监测机械设备的运行状况,及时发现故障和异常振动,以保证设备的正常运行和安全性。
3.2 振动控制振动控制是通过采用各种技术手段来减小或消除振动对系统和结构的影响。
例如,通过安装阻尼器或减振器来减小机械设备产生的振动;通过调整车辆的悬挂系统来降低行驶时的振动。
3.3 振动测试与分析振动测试与分析是通过测量物体或系统的振动响应,来了解其结构、性能和健康状况的一种方法。
通过振动测试和分析,可以识别出结构的固有频率、模态分布和故障状态,从而为工程优化和故障诊断提供依据。
4. 冲击的基本概念和特性冲击是指突然产生的、短暂而强烈的外力作用于物体的现象。
冲击的特性包括幅度、持续时间和冲击力。
幅度是指冲击产生的位移或形变,通常用米(m)来表示。
同步振动和异步振动分析比较研究同步振动和异步振动是机械系统中常见的两种振动形式。
在这篇文章中,我们将会分析和比较这两种振动的性质、影响以及应用。
一、同步振动同步振动是指机械系统的振动频率与其激励源频率相同。
它通常发生在由单个激波源激励的机械系统中,例如电动机的转子、风扇和蒸汽轮机。
当机械系统与其激励源的频率相同或接近时,系统的振动将会增强,并且可能会导致系统的损坏,例如锈蚀、磨损和疲劳。
同步振动的一个重要特征是其频率相对于机械系统来说是稳定的。
这意味着如果激励源的频率变化,机械系统也会相应地改变其振动频率。
同步振动还可以导致机械系统失去稳定性,这可能会导致机械系统的崩溃。
二、异步振动异步振动是指机械系统的振动频率与其激励源频率不同。
它通常发生在由多个激波源激励的机械系统中,例如汽车发动机、风力涡轮机和液体输送系统。
当机械系统与其激励源的频率不同或不稳定时,系统的振动可能会减弱,也可能会变得更加复杂和难以预测。
异步振动的一个重要特征是其频率相对于机械系统来说是变化的。
这意味着即使激励源的频率变化,机械系统的振动频率也可能不会改变。
异步振动可能会导致机械系统产生各种不同频率的振动,这可能会导致机械系统出现共振、谐振等问题。
三、同步振动和异步振动的比较同步振动和异步振动虽然是机械系统中常见的振动形式,但它们在性质、影响和应用方面存在明显的差异。
下面是它们的比较:1.性质:同步振动的频率相对稳定,而异步振动的频率相对变化。
2.影响:同步振动可能导致机械系统失去稳定性;异步振动可能导致机械系统产生各种不同频率的振动。
3.应用:同步振动可用于机械系统的调谐和正常运行;异步振动可用于机械系统的故障检测和故障分析。
四、应用案例同步振动和异步振动的应用范围非常广泛,下面是一些应用案例:1.风力涡轮机:风力涡轮机是一种异步振动的机械系统,它的振动频率与风速和斜纹轮的转速有关。
通过监测和分析它的振动,可以检测到机械系统中的故障,例如轴承磨损、齿轮磨损等。