全站仪三角高程测量精度分析
- 格式:doc
- 大小:685.00 KB
- 文档页数:32



jiaoshi三角高程随全站仪使用越来越普及,三角高程广泛用于工程测量的各个阶段.它的精度在一定情况下是可以代替水准高程的.大家做过什么样的三角高程呢?在测量过程中我们要注意些什么呢?使用不同的仪器进行三角高程测量的计算不完全一样,为什么呢?这主是测距仪与十字丝是否同轴的原因引起的。
在用徕卡系列的仪器进行三角高程测量时,由于仪器测距仪的中心与十字丝中心是同轴的,所以计算的角度和距离都不用进行测距仪与十字丝中心的改正!其它的测量距仪就要进行类似的改正。
FZFZFZ1968三角高程的高差计算原理公式,(不考虑球差改正)h=S*tgα+i-v其误差计算公式mh=√( ms*sinα)^2+(S*mα*cosα/ρ)^2+ mi^2+mv^2 2楼从中我们可以看出三角高程的误差主要是垂直角的大小、垂直角的测量误差、距离的长短在实地测量时一定要注意垂直角的观测精度,他对高差精度的影响最大,如果是用全站仪观测,更要注意,多观测几个回合是非常有必要的三角高程测量示意图jiaoshi水电水利工程施工测量规范(DL/T5173-2003)中的误差公式与你的公式略有不同,公式如下:m h=√( ms*sinα)^2+(S*mα*cosα/ρ)^2+ mi^2+mv^2+D^4/4R^2*mk^2增加了一个大气折光系统测量误差。
考虑球差高差计算公式是:h=S*cosZ+i-v+(1-K)S^2/2/R*SIN^2Z上式中:Z:归算到测距时的天顶距(度)K:大气折光系数(0.08至0.14)R:平均曲率半径6369000M另:在三角高程的计算时一定要考虑地球曲率和大气折光对高差的改正!下面两个点是我们做过的两个导线点,观测数据如下:站A测B:S=1187.98米,天顶距:95度58分18秒站B测A:S=1187.9768米,天顶距:84度02分8秒棱镜与仪器同高,如果按2楼的公式计算往返高差相差14.9厘米.FZFZFZ1968在三角高程的计算时要考虑地球曲率和大气折光对高差的改正是对的,但不是一定,至于你说的你所测的一对数据按我写的公式计算往返高差相差14.9厘米,我认为这绝不是因为没有经过两差改正的原因,那你按经过两差改正的高差分别又是多少呢,请你把完整的计算过程写出来,让看看到底经过改正和没有经过改正的高差分别相差jiaoshi站A测B:S=1187.98米,天顶距:95度58分18秒站B测A:S=1187.9768米,天顶距:84度02分8秒棱镜高与仪器高均相同高度一、用公式:h=S*tgα+i-v计算站A测B:GC=-123.5935米站B测A:GC=123.4444米相差:-0.1491米二、用公式:h=S*cosZ+i-v+(1-K)S^2/2/R*SIN^2Z站A测B:GC=-123.4981米站B测A:GC=123.4824米相差:-0.0157米计算说明:1、天顶距及斜距均采用TCR702进行测量,天顶距无需进行归算,斜距的温度与气压改正由全站仪完成;2、表中K值取0.13。

全站仪三角高程测量的方法与误差分析本科毕业论文全站仪通过发射一束可见光束,测量激光束从仪器到目标反射点的时间,并通过时间差计算出仪器与目标点之间的距离。
三角高程测量是利用全站仪的水平角和垂直角的测量结果,结合已知的基线长度,通过三角形计算出目标点的高程。
1.设置仪器:将全站仪放置在测站点上,确保仪器的水平和垂直准星位于同一平面上。
2.瞄准目标点:通过望远镜瞄准需要测量高程的目标点。
3.测量水平角:通过全站仪记录目标点与两个已知点的水平角。
4.测量垂直角:通过全站仪记录目标点与水平面的垂直角。
5.计算高程:根据测量的水平角和垂直角以及已知基线长度,通过三角形计算出目标点的高程。
6.数据处理:根据多次测量的结果,进行数据平差处理,获得更准确的测量结果。
在全站仪三角高程测量中,需要考虑的误差主要包括仪器误差、自然因素和操作误差。
仪器误差包括仪器刻度误差、指向误差和折射误差等,可以通过定期校准仪器和使用精确的仪器控制误差。
自然因素包括大气折射、大地水准曲率和大地水准面偏差等,可以通过校正和补偿来减小误差。
操作误差主要包括读数误差、瞄准误差和放样误差等,可以通过培训和规范操作来减小误差。
为了进一步分析误差,可以采用误差理论进行误差分析。
误差理论可以通过误差传播法则计算最终测量结果的误差范围。
同时,可以通过实验和模拟等方法验证误差分析的有效性,并提出改进测量方法和减小误差的措施。
综上所述,全站仪三角高程测量是一种常用的测量方法,能够提供准确的高程数据。
在实际测量中,需要注意仪器的校准和控制、自然因素的校正和补偿,以及规范的操作。
通过误差分析,可以评估测量结果的准确性,并提出改进测量方法和减小误差的建议,从而提高测量的可靠性和准确性。



中点单觇法三角高程测量及其精度分析0 前言目前,随着测距技术的发展,精度的提高,以及测距仪、全站仪的普及,三角高程测量作为高程控制测量的一种有效手段,正逐步受到广大测绘工作者的青睐。
在三角高程测量方法中,现阶段主要采用的是直返觇法——用往返观测测定相邻点的高差的方法;而应用中点单觇法(在两置觇点中间安置仪器测定觇点间高差的方法)的人却较少。
虽然直返觇法在建立平面控制网的同时,为求这些待定平面点的高程而建立三角高程控制网时较为方便,但由于平面控制点大多建在制高点上,用其作为高程控制点,使用较为不便,一般平面控制网与高程控制网均分开布设,高程点布设在利于保存、使用的地方,此时运用中点单觇法来进行三角高程测量,较之直返觇法有较强的灵活性与实用性。
中点单觇法三角高程测量有以下几个特点:a 测站不需对中,不需量取仪器高;b 采用适当方法,可不量取觇标高;c 测站选在中部时,可减弱大气折光的影响;d 减少劳动强度、提高作业速度等。
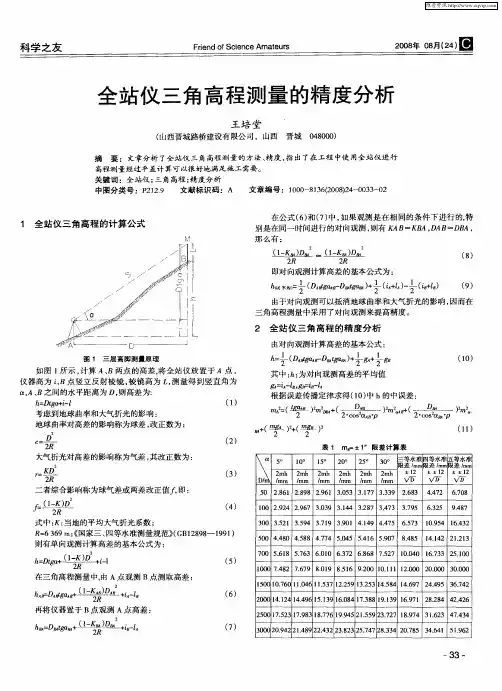
1 中点单觇法三角高程测量原理及精度分析1.1 高差计算公式的推导如图1所示,为求A、B两点间的高差,将全站仪置于A、B两点大致中间位置的D点处,则图1故A点至B点的高差为:式中:s——经气象改正后的斜距;z——天顶距的观测值;V——觇标高;R——测区地球平均曲率半径;K——大气折光系数。
由于前、后视高差观测是在相近条件下进行的,可认为其折光系数,kA≈kB,令kA=kB=k,代入式(3)得:中点单觇法三角高差测量时,每一测站均应独立施测两次,满足要求后,取其平均值作为最后成果,即式中:h′AB——第一次观测高差;h″AB——第二次观测高差。
由上述可知,中点单觇法三角高差测量时,不需对中和量取仪器高。
1.2 中误差计算式对式(4)进行全微分,得:由于式(6)等号右边前四项括号中的第二项较小、相对于第一项而言,可忽略不计,并顾及DA=sAsinzA、DB=sBsinzB,则得:运用误差传播定律,考虑到观测量之间相互独立,得:由于采用中点单觇法进行三角高程测量时,仪器大致在两置觇点的中部且一般距离较短,则可近似认为m2sA=m2sB=m2s;并顾及m2zA=m2zB=m2z,m2vA=m2vB=m2v,由上式可得:式中:mh——中点单觇法三角高差的中误差;ms——测边中误差;mz——天顶距观测中误差;mk——大气折光系数测定中误差;mv——觇标高量取中误差;Z——天顶距的观测值;D——水平距离,D=s·cosz;R——测区地球平均曲率半径;ρ——取206265″.则,高差平均值的中误差为:1.3 精度分析及结论设ms=±10 mm、mz=±1.8″、mk=±0.05、mv=±1 mm,取不同的平距D和天顶距Z,按式(10)计算高差平均值的中误差,结果列于表1中。



工程测量中三角高程测量的误差分析及解决方法戚忠中国水利水电第四工程局有限公司测绘中心,青海西宁,邮编810007一引言一直以来,为保证精度,高等级高程测量都采用几何水准的方法。
而在某些特定环境下,几何水准往往会耗费大量的人力、物力,且受地形等条件因素影响较大!鉴于几何水准在某些特定情形下无法进行的问题,探讨如何提高三角高程测量的精度,以保证其测量成果的可行性和可靠性,使得三角高程测量成果足以替代几何水准。
随着高精度全站仪的问世,结合合理的方式、方法,运用三角高程替代几何水准测量是切实可行的。
三角高程代替几何水准可以解决跨河水准及高边坡、危险地段无法进行精密几何水准测量的难题,保障危险地段测量人员和仪器设备的安全,提高了工作效率,降低了测量成本。
二三角高程测量误差分析常见的三角高程测量有单向观测法、中间法和对象观测法,对向观测法可以消除部分误差,故在三角高程测量中采用较为广泛。
对向观测法三角高程测量的高差公式为:(1)式中:D为两点问的距离;a为垂直角;为往返测大气垂直折光系数差;i为仪器高;v为目标高; R为地球曲率半径(6370 km);为垂线偏差非线性变化量;令。
对式(1)微分,则由误差传播定律可得高差中误差:(2) 由式(2)可知影响三角高程测量精度主要有:1.竖直角(或天顶距)、2.距离、3.仪器高、4.目标高、5.球气差。
第1、2项可以通过试验观测数据分析选择精度合适的仪器及其配套的反光棱镜、温度计、气压表等,我们选择的是徕卡TCA2003及其配套的单棱镜、国产机械通风干湿温度计、盒式气压计;第3、4项,一般要求建立稳定的观测墩和强制对中装置,采用游标卡尺在基座3个方向量取,使3个方向量取的校差小于0.2 mm,并在测前、测后进行2次量测;第5项球气差也就是大气折光差,也是本课题的研究重点。
三减弱大气折光差的方法和措施大气折光差:是电磁波经过大气层时,由于传播路径产生弯曲及传播速度发生变化而引起观测方向或距离的误差。
第33卷第6期2010年12月测绘与空间地理信息G E O M A TI C S&S PA T I A L l N FO R M A T I O N T E C H N O L O G YV01.33.N O.6D ec.,2010浅谈三角高程测量方法及精度分析崔克忠(吉林省地理信息工程院。
吉林长春130051)摘要:分析了一般的三角高程测量方法的局限性,在实践中总结了一种便捷的三角高程测量的新方法。
同时还论证了用三角高程测量代替三、四等水准测量的理论依据,并采用全站仪任意置站的方法,测量时不必量取仪器高、棱镜高,既减少了三角高程的误差来源,又加快了施测速度。
关键词:三角高程;精度;操作方法;论证中图分类号:P224.2文献标识码:B文章编号:1672—5867(2010)06—0215—02N ew M et hod of T r i gonom et r i c L evel i ng and A ccur acy A nal ys i sC U I K e—z hong(Ji l i n I n st i t ut e of G eom at i cs E ngi neer i ng,C han gchun130051,C hi na)A b s t ra c t:Thi s pape r ana l yz es t he ge ne r al l i m i t at i on s of t r i gon om e t r i c l eve l i ng m et h od,s um m ed up i n pr act i ce a new conveni ent m et h—od of t r i gon om e t r i c l ev el i ng.I t al s o de m ons t r a t e s t he t heor et i ca l basi s of usi ng t r i gonom et r i c l eve l i ng i ns t ead of l evel m ea s u r e m e n t.U-s i ng t he m et h od of any on e s et po i nt by t o t al s ta t ion,i t i s not ne ce ssa r y t o m e as ur e t he hei g ht of i n st r u m en t and pr i sm,w hi c h not oll l y r educ es t he t r i gon om e t r i c l eve l i ng er r or sou r ces,but al s o acc el er at es t he sur veyi ng s peed.K e y w o r ds:t r i gon om e t r i c l ev el i ng;acc ur acy;oper at i on m e t ho d;di s cus si o n0引言1三角高程测量原理及精度城市规划是城市建设和发展的龙头,城市测绘是规划编制和管理的基础。