1.板块模型

板块模型新发现
本文旨在介绍最新的关于板块模型的研究发现。

尽管我们不会具体总结内容，但以下是一些主要发现的简要概述：
1. 基本定义
- 板块模型是地壳运动和地球板块演化的理论框架。

- 板块是地球表面的巨大岩石块，包括大陆和海洋地壳。

- 板块模型解释了地震、火山活动和山脉形成等地质现象。

2. 新发现
- 最新的研究表明，板块模型中的板块并非完全固定不动的。

- 板块的边界会发生微小的相对运动，但这种运动常常被忽略或难以观测。

- 通过先进的地震监测和地球科学技术，研究人员发现了更多微小板块的存在。

- 这些微小板块可能对地质演化和板块动力学有重要影响。

3. 影响和意义
- 更深入地了解板块模型的微小运动，有助于我们对地球的演化和地质活动有更全面的理解。

- 这些新发现可能改变我们对板块模型的观点和解释现有的地质现象的方式。

- 对于地震预测和地质灾害风险评估，了解板块模型的微小运动非常重要。

4. 研究挑战和未来展望
- 进一步研究板块模型的微小运动仍然面临许多挑战。

- 需要更多的观测数据、模拟研究和地质测试来验证这些发现的准确性和可重复性。

- 从事板块模型研究的科学家们将继续努力，以更好地理解地壳运动的本质。

以上是关于板块模型的最新研究发现的简要介绍。

这些发现对于地球科学领域将产生重要的影响，并希望能够激发更多相关研究的兴趣与探索。

板块模型学案一、板块模型的简介在物理学中，板块模型是一种常见且重要的模型，用于研究不同物体之间的相对运动和相互作用力。

板块模型通常涉及两个或多个相互接触的物体，它们在水平或倾斜的表面上运动。

板块模型的应用范围非常广泛，从简单的力学问题到复杂的工程实际都有所涉及。

例如，在工业生产中的传送带运输、车辆的制动系统，以及日常生活中的滑板运动等场景中，都能看到板块模型的身影。

二、板块模型的基本要素1、物体的质量物体的质量是决定其运动状态和受力情况的重要因素。

质量越大，物体的惯性越大，改变其运动状态就越困难。

2、接触面的摩擦力摩擦力在板块模型中起着关键作用。

摩擦力的大小和方向取决于接触面的性质、物体之间的压力以及相对运动的情况。

3、外力的作用外部施加的力可以改变物体的运动状态。

例如，推动或拉动其中一个物体，或者施加一个倾斜的力等。

三、板块模型的常见类型1、无摩擦力的板块模型在这种情况下，物体之间的接触面非常光滑，没有摩擦力的作用。

此时，物体的运动主要取决于外力和它们自身的惯性。

2、有摩擦力的板块模型这是更常见的情况，摩擦力的存在会影响物体的运动速度和相对位置。

根据摩擦力的性质（静摩擦力或动摩擦力），物体的运动状态会有所不同。

3、多个物体的板块模型可能涉及两个以上的物体相互接触和作用，分析起来会更加复杂，需要综合考虑每个物体的受力和运动情况。

四、板块模型的解题思路1、确定研究对象首先要明确我们要研究的是哪个或哪些物体，将它们从系统中分离出来进行单独分析。

2、进行受力分析画出每个研究对象所受到的力，包括重力、支持力、摩擦力、外力等，并确定力的方向和大小。

3、建立运动方程根据牛顿第二定律，结合物体的受力情况，建立运动方程。

如果是多个物体，还需要考虑它们之间的相互作用力。

4、求解方程通过数学方法求解所建立的方程，得到物体的加速度、速度、位移等物理量。

五、板块模型的实例分析例 1：在水平光滑的表面上，有一个质量为 M 的大木板，上面放置一个质量为 m 的小木块。

板块模型高考知识点【正文】板块模型是高考物理中的一个重要知识点，主要用于解决题目中涉及到的平衡、稳定性和力的分析问题。

它是一种简化和抽象的模型，通过将物体分解为多个部分，从而更好地理解和研究物体的运动特性。

一、板块模型的基本原理板块模型的基本思想是将物体分解为若干个小块，每个小块都带有自己的质量、形状和位置等特征。

这些小块之间存在相互作用力，通过分析这些力的平衡和合成，就可以得到整个物体的运动情况。

以平衡为例，我们可以将物体划分为若干个平行小块，每个小块都受到重力和支持力的作用。

通过分析每个小块的受力情况，可以确定物体是否处于平衡状态。

这种分块分析的方法可以大大简化问题，使其更易于处理。

二、板块模型的应用板块模型在解决高考物理题中起到了重要的作用。

例如，在研究斜面上物体的运动时，我们可以将斜面分解为水平和竖直两个方向的小块，从而分析物体受力和速度的关系。

此外，板块模型还可以用于分析各种力的合成和分解问题。

例如，对于一个悬挂在天花板上的物体，我们可以将其划分为水平和竖直方向的两个小块，从而分析其受力的方向和大小。

三、板块模型的特点板块模型具有一定的抽象性和简化性。

它不需要考虑物体的具体形状和内部结构，而只需要关注物体的整体特性和相互作用。

这使得板块模型在解决一些复杂问题时非常有效，并且可以应用于不同的情况和条件。

此外，板块模型还可以灵活应用于不同的题型和考点。

无论是平衡问题、稳定性问题还是力的合成问题，都可以采用板块模型来解决。

这种统一的思维框架能够帮助我们更好地理解物理问题的本质，提高解题的能力。

总结：板块模型是解决高考物理题中的常用工具，它通过将物体分解为若干小块，分析小块之间的相互作用力，从而帮助我们理解和解决复杂的运动问题。

板块模型具有简化、抽象的特点，可以应用于不同的情况和考点，对于提高物理解题的能力具有重要意义。

通过学习板块模型，我们可以更好地理解和掌握高考物理中涉及的平衡、稳定性和力的分析问题。

高中物理必修一·板块模型全文共四篇示例，供您参考第一篇示例：高中物理必修一《板块模型》是学生在学习中的一个重要内容，它主要是用来帮助学生更好地理解物质的构成和运动规律。

在板块模型中，我们将物质分为不可再分的基本粒子和由基本粒子构成的原子、分子、离子和晶体等不同层次。

通过板块模型，我们可以更好地理解物质的性质和各种自然现象。

第一部分，介绍板块模型的基本概念。

板块模型是一种物质结构的模型，它将物质分为不可再分的基本粒子和由基本粒子构成的不同层次的结构。

基本粒子包括电子、质子、中子等，它们构成了原子，而原子又构成了分子、离子和晶体等物质结构。

通过这种层次分解的方式，我们可以更好地理解物质的组成和性质。

第二部分，探讨板块模型在物质结构和性质方面的应用。

板块模型可以帮助我们更好地理解物质的结构和性质。

通过对原子结构的理解，我们可以解释元素的周期表规律和原子的化学性质。

通过对分子结构的理解，我们可以理解不同物质之间的相互关系，比如共价键、离子键和金属键等。

通过对晶体结构的理解，我们可以解释晶体的性质和各种晶体的特点。

第三部分，探讨板块模型在自然现象和技术应用方面的意义。

板块模型的理论可以帮助我们更好地理解各种自然现象和技术应用。

通过对电子结构和电子运动的理解，我们可以解释电流、电场和电磁感应等电学现象。

通过对分子结构和分子运动的理解，我们可以解释物质的热性质和热力学定律。

板块模型的理论也可以应用在材料科学、电子工程和能源技术等方面，为各种技术应用提供理论基础。

第四部分，总结板块模型对学生的重要性。

通过学习板块模型，学生不仅可以更好地理解物质的结构和性质，还可以培养科学思维和分析问题的能力。

板块模型的理论也为学生将来从事科学研究和工程技术提供了扎实的理论基础。

学生应该认真学习板块模型，并将其运用到实际的学习和生活中。

高中物理必修一《板块模型》是一个重要的知识点，它可以帮助学生更好地理解物质结构和性质，促进科学思维和分析问题的能力的培养，并在自然现象和技术应用方面发挥着重要的作用。

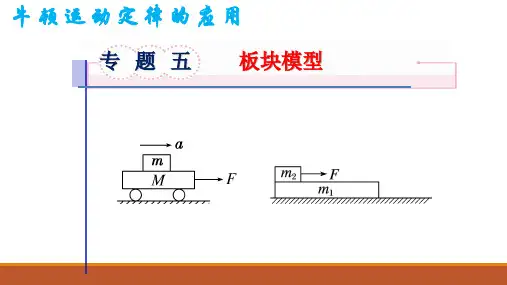
高中物理板块模型知识点总结一、板块模型的基本概念。

1. 板块模型组成。

- 板块模型通常由一个或多个滑块（可视为质点）和木板组成。

滑块和木板之间存在着摩擦力等相互作用，并且它们在一个平面上运动，这个平面可能是光滑的，也可能存在摩擦力。

2. 研究对象的选取。

- 在板块模型中，我们既可以单独选取滑块或木板作为研究对象，也可以将滑块和木板整体作为研究对象。

当研究它们之间的相对运动时，往往需要分别分析滑块和木板的受力情况；当整体的外力情况比较明确，且不涉及它们之间的内部摩擦力做功等问题时，可以采用整体法。

二、受力分析。

1. 滑块的受力。

- 滑块受到重力G = mg（其中m为滑块质量，g为重力加速度）。

- 如果滑块在木板上滑动，它受到木板对它的摩擦力。

当滑块相对木板滑动时，摩擦力为滑动摩擦力f=μ N，其中μ为动摩擦因数，N为滑块与木板间的正压力（在水平面上N = mg）。

如果滑块有相对木板运动的趋势但未滑动，则受到静摩擦力，静摩擦力的大小根据牛顿第二定律结合物体的运动状态求解，其方向与相对运动趋势方向相反。

2. 木板的受力。

- 木板同样受到重力G'=M g（M为木板质量）。

- 它受到滑块对它的摩擦力，大小与滑块受到的摩擦力相等，方向相反（根据牛顿第三定律）。

如果木板放在水平面上，还受到水平面的支持力F_N=(m + M)g（整体法分析时），若水平面不光滑，木板还受到水平面的摩擦力。

三、运动分析。

1. 加速度的计算。

- 根据牛顿第二定律F = ma计算滑块和木板的加速度。

- 对于滑块，例如受到水平拉力F和摩擦力f时，其加速度a_1=(F - f)/(m)（假设拉力方向与摩擦力方向相反）。

- 对于木板，若受到滑块的摩擦力f和其他外力F'（如水平面的摩擦力等），其加速度a_2=(f+F')/(M)。

2. 相对运动情况。

- 当滑块和木板的加速度不同时，它们之间就会产生相对运动。

判断相对运动的方向可以通过比较它们加速度的大小和方向。

板块模型规律总结一、板块模型是啥。

板块模型呢，就是那种有两个或者多个板块放在一起的物理模型啦。

就好像是几个小伙伴排排坐，不过它们之间可是有着各种奇妙的物理关系哦。

你可以想象成是几块木板叠在一起，或者是一块木板在另一块木板上滑动这样的情况。

这种模型在物理学习里可是相当重要的，就像游戏里的关键关卡一样，掌握了它，好多物理问题都能迎刃而解呢。

二、受力分析是关键。

在研究板块模型的时候呀，受力分析简直就是我们的秘密武器。

对于每个板块，我们都得仔仔细细地看看它受到哪些力的作用。

比如说重力，这个大家都很熟悉啦，就像地球爷爷拉着板块不让它们飞走一样。

还有摩擦力呢，这个摩擦力可调皮了，它有时候是板块运动的阻碍，有时候又像是板块运动的小助手。

当两个板块相对静止的时候，它们之间的摩擦力是静摩擦力，这个静摩擦力的大小会根据情况变化，就像一个会自适应的小助手。

要是板块相对滑动了，那就变成滑动摩擦力啦，滑动摩擦力有它自己的计算公式，就像一个有固定规则的小怪兽。

而且呀，板块还可能受到外力的作用呢。

这个外力就像是从外面来的一个小捣蛋鬼，推动或者拉动着板块。

比如说，你用手推一个木板，这个推力就是外力啦。

在做受力分析的时候，我们可不能把这些力给弄丢了，得像数家珍一样，一个一个地把它们找出来。

三、运动状态要搞清。

板块的运动状态也是超级重要的一部分。

板块可能是静止的，就像一个安静睡觉的小宝贝。

也可能是做匀速直线运动，这就像是一个听话的小朋友沿着直线稳稳地走路。

还有可能是做变速运动呢，这个时候板块就像一个调皮的小猴子，一会儿快一会儿慢。

当板块相对静止的时候，我们要根据它们整体的受力情况来判断它们的状态。

如果整体受力平衡，那它们就会安安静静地待着。

要是板块相对滑动了，我们就得分别考虑每个板块的加速度啦。

加速度就像是板块运动的小指挥，告诉板块是该加速还是减速。

比如说，一个木板在粗糙的地面上滑动，由于受到摩擦力的作用，它就会有一个加速度，这个加速度会让它的速度慢慢改变。

最全板块模型总结引言在现代管理学中，板块模型是一种常用的分析方法，通过将企业或组织分成不同的功能模块来进行研究和管理。

板块模型的应用可以帮助企业更好地理解组织结构，优化业务流程，提高效率和生产力。

本文将对最常见的板块模型进行总结和归纳，并对其应用进行分析和评价。

1. 功能模块板块模型功能模块板块模型是最常见和基础的一种板块模型。

它将企业的各种功能分为不同的模块，如生产、销售、市场营销、人力资源等。

每个模块负责特定的职能或任务，相互之间具有一定的依赖关系和协作关系。

1.1 生产模块生产模块负责产品的制造和加工过程。

它包括原材料采购、生产计划、生产线管理等。

生产模块的目标是提高生产效率和产品质量，降低生产成本，实现生产过程的优化。

1.2 销售模块销售模块负责产品的销售和市场拓展。

它包括市场调研、销售策略制定、销售渠道管理等。

销售模块的目标是扩大销售规模，提高销售额，增强市场竞争力。

1.3 市场营销模块市场营销模块负责企业的市场推广和品牌建设。

它包括市场定位、品牌推广、市场公关等。

市场营销模块的目标是提高品牌知名度，吸引更多的目标客户，推动销售增长。

1.4 人力资源模块人力资源模块负责企业的人力资源管理和员工培训。

它包括招聘、培训、绩效评估等。

人力资源模块的目标是提高员工的绩效和满意度，确保企业人力资源的合理配置。

2. 流程模块板块模型流程模块板块模型将企业的业务流程进行划分和管理。

它以流程为核心，将企业的各个环节划分为不同的模块，通过流程的优化和改进，提高工作效率和质量。

2.1 采购流程模块采购流程模块包括物料采购、供应商管理、采购订单等。

它的目标是提高采购效率，降低采购成本，确保供应链的稳定和可靠。

2.2 生产流程模块生产流程模块包括生产计划、物料加工、质量控制等。

它的目标是提高生产效率和产品质量，降低生产成本，实现生产过程的优化。

2.3 销售流程模块销售流程模块包括市场开发、订单管理、售后服务等。