模型构建专题 相似三角形中的基本模型

专题09相似三角形中的基本模型-对角互补模型相似三角形在中考数学几何模块中占据着重要地位。

相似三角形与其它知识点结合以综合题的形式呈现，其变化很多，难度大，是中考的常考题型。

如果大家平时注重解题方法，熟练掌握基本解题模型，再遇到该类问题就信心更足了。

本专题就对角互补模型进行梳理及对应试题分析，方便掌握。

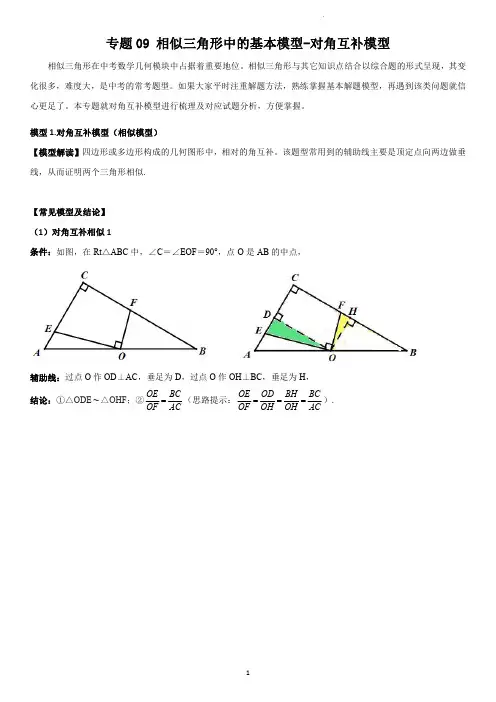
模型1.对角互补模型（相似模型）【模型解读】四边形或多边形构成的几何图形中，相对的角互补。

该题型常用到的辅助线主要是顶定点向两边做垂线，从而证明两个三角形相似.【常见模型及结论】（1）对角互补相似1条件：如图，在Rt△ABC中，∠C＝∠EOF＝90°，点O是AB的中点，辅助线：过点O作OD⊥AC D，过点O作OH⊥BC，垂足为H，结论：①△ODE∼△OHF；②OE BCOF AC=（思路提示：OE OD BH BCOF OH OH AC===）.（2）对角互补相似2条件：如图，已知∠AOB ＝∠DCE ＝90°，∠BOC ＝α.辅助线：作法1：如图1，过点C 作CF ⊥OA ，垂足为F ，过点C 作CG ⊥OB ，垂足为G ；结论：①△ECG ∼△DCF ；②CE ＝CD·tan α.（思路提示：CE CG CD CF =，CF =OG ，在Rt △COG 中，CG tan OGα=）辅助线：作法2：如图2，过点C 作CF ⊥OC ，交OB 于F ；结论：①△CFE ∼△COD ；②CE ＝CD·tan α.（思路提示：CE CF tan CD CO α==，在Rt △OCF 中，CF tan OC α=）（3）对角互补相似3条件：已知如图，四边形ABCD 中，∠B+∠D=180°辅助线：过点D 作DE ⊥BA ，垂足为E ，过点D 作DF ⊥BC ，垂足为F ；结论：①△DAE ∼△DCF ；②ABCD 四点共圆。

例1．（2022·黑龙江·鸡西九年级期末）如图，在Rt ABC 中，90ABC ∠=︒，6AB =，8BC =，在Rt MPN △中，90MPN ∠=︒，点P 在AC 上，PM 交AB 于点E ，PN 交BC 于点F ，当2PE PF =时，AP 的长为（）A ．4B ．6C ．245D ．256例3．（2022·江西·吉水县九年级期末）【问题情境】如图①，直角三角板ABC中，∠C＝90°，AC＝BC，将一个用足够长的细铁丝制作的直角的顶点D放在直角三角板ABC的斜边AB上，再将该直角绕点D旋转，并使其两边分别与三角板的AC边、BC边交于P、Q两点．【问题探究】（1）在旋转过程中，①如图2，当AD＝BD时，线段DP、DQ的数量关系是（）A、DP＜DQB、DP＝DQC、DP＞DQD、无法确定②如图3，当AD＝2BD时，线段DP、DQ有何数量关系？并说明理由．③根据你对①、②的探究结果，试写出当AD＝nBD时，DP、DQ满足的数量关系为（直接写出结论，不必证明）。

相似三角形12种基本模型证明相似三角形是指拥有相同形状但不同大小的三角形。

在三角形中，如果它们的对应角度相等，那么它们就是相似三角形。

相似三角形一般用比例关系表示。

下面是相似三角形12种基本模型的证明：1. AAA相似模型如果两个三角形的三个角分别相等，则它们是相似的。

证明：三角形的三个角之和为180度。

如果两个三角形的三个角分别相等，那么它们的三个角和也相等，即这两个三角形的三个角和相等，因此它们是相似的。

2. AA相似模型如果两个三角形中有两个对应角相等，则它们是相似的。

证明：假设两个三角形的对应角分别为A和A’，B和B’，C和C’。

由于A和A’相等，B和B’相等，那么它们的第三个对应角C和C’也必须相等。

因此，这两个三角形的三个角分别相等，它们是相似的。

3. SSS相似模型如果两个三角形的三条边分别成比例，则它们是相似的。

证明：假设两个三角形的三条边为a, b, c和a’, b’, c’。

由于它们是成比例的，即a/a’= b/b’= c/c’，那么它们的三边比例相等，即它们是相似的。

4. SAS相似模型如果两个三角形中有两条边成比例，且夹角相等，则它们是相似的。

证明：假设两个三角形的两条边为a, b和a’, b’，夹角为C和C’。

由于它们是成比例的，即a/a’= b/b’，那么它们的三边比例相等。

又由于它们的夹角相等，即C = C’，因此它们是相似的。

5. ASA相似模型如果两个三角形中有两个角相等，且它们对应的两条边成比例，则它们是相似的。

证明：假设两个三角形的两个对应角分别为A和A’，B和B’，且对应的两条边分别为a, a’和b, b’。

由于它们的两条边成比例，即a/a’= b/b’，那么它们的三边比例相等。

又由于它们的两个角相等，即A = A’，因此它们是相似的。

6. HL相似模型如果两个三角形中有一条边和一条斜边分别成比例，且这两条边夹角相等，则它们是相似的。

证明：假设两个三角形的一条边为b，斜边为c，且夹角为C，另一个三角形的一条边为b’，斜边为c’，且夹角为C’。

全等与相似三角形中的基本模型之十字架模型几何学是数学的一个重要分支，研究的是形状、大小和相对位置等几何对象的性质和变换。

在初中几何学中，十字模型就是综合了上述知识的一个重要模型。

本专题就十字模型相关的考点作梳理，帮助学生更好地理解和掌握。

模型1.矩形的十字架模型(相似模型)矩形的十字架模型：矩形相对两边上的任意两点联结的线段是互相垂直的，此时这两条线段的的比等于矩形的两边之比。

通过平移线段构造基本图形，再借助相似三角形和平行四边的性质求得线段间的比例关系。

如图1，在矩形ABCD中，若E是AB上的点，且DE⊥AC，则DEAC=BCAB.如图2，在矩形ABCD中，若E、F分别是AB、CD上的点，且EF⊥AC，则EFAC=BCAB.如图3，在矩形ABCD中，若E、F、M、N分别是AB、CD、AD、BC上的点，且EF⊥MN，则EFMN=BCAB.1(23·24上·成都市·九年级期中)如图，把边长为AB=6，BC=8的矩形ABCD对折，使点B和D重合，求折痕MN的长．2(22·23下·河北·九年级期中)如图，在矩形ABCD中，E、F、G、H分别为AD、BC、AB、CD边上的点，当EF⊥GH时，证明：EF:GH=AB:BC．3(22·23下·湖北·九年级期中)在矩形纸片ABCD 中AB =5，AD =3，点E 、F 在矩形的边上，连接EF ，将纸片沿EF 折叠，点D 的对应点为点P ．(1)如图①，若点P 在边AB 上，当点P 与点A 重合时，则∠DEF =°，当点E 与点A 重合时，则∠DEF =°．(2)如图②，若点P 在边AB 上，且点E 、F 分别在AD 、DC 边上，则线段AP 的取值范围是；(3)如图③，若点F 与点C 重合，点E 在AD 上，线段BA 、PF 交于点M ，且AM =DE ，求线段AE 的长度．4(江苏2022-2023学年九年级上学期期中数学试题)某数学课外兴趣小组成员在研究下面三个有联系的问题，请你帮助他们解决：(1)如图1，矩形ABCD 中，AB =8，BC =6，将矩形对折，使得点B 、点D 重叠，折痕为EF ，过点F 作AB 的垂线交AB 于点G ，求EF 的长；(2)如图2，矩形ABCD 中，AB =a ，BC =b ，点E ，F 分别在AB ，DC上，点G ，H 分别在AD ，BC 上且EF ⊥GH ，求EFGH的值；(3)如图3，四边形ABCD 中，∠ABC =90°，AB =AD =8，BC =CD =4，AM ⊥DN ，点M ，N 分别在边BC ，AB 上，求DNAM的值．模型2.三角形的十字架模型(全等+相似模型)1)等边三角形中的斜十字模型(全等+相似)：如图1，已知等边△ABC ，BD =EC (或CD =AE )，则①AD =BE ，②AD 和BE 夹角为60°，③△ADB ∽△BDF ∽△BEC 。

模型构建专题：相似三角形的基本模型的构建——熟知需要用相似来解决的图形◆模型一“A”字型1．(2016·贵阳中考)如图，在△ABC中，DE∥BC，ADAB＝13，BC＝12，则DE的长是（）A．3 B．4 C．5 D．6第1题图第2题图2．如图，正方形CDEF内接于Rt△ABC，点D，E，F分别在边AC，AB和BC上，当AD ＝2，BF＝3时，正方形CDEF 的面积是______.◆模型二“X”字型3．如图，在▱ABCD中，点E是边AD的中点，EC交对角线BD于点F，则EF：FC等于（）A．3∶2 B．3∶1 C．1∶1 D．1∶2第3题图第4题图4．如图，点F是矩形ABCD 的边CD上一点，射线BF交AD 的延长线于点E，则下列结论错误的是（）A.EDBC＝EFFBB.DEAD＝DFABC.BCDE＝CFDFD.BFBE＝BCAE◆模型三旋转型5．(2017·滦县模拟)如图，已知∠1＝∠2，那么添加下列一个条件后，仍无法判定△ABC ∽△ADE的是（）A．∠C＝∠E B．∠B ＝∠ADEC.ABAD＝ACAED.ABAD＝BCDE◆模型四“子母”型(大三角形中包含小三角形)6．(2016·安徽中考)如图，在△ABC中，AD是中线，BC＝8，∠B＝∠DAC，则线段AC的长为（）A．4 B．42C．6 D．4 3第6题图第7题图7．如图，在△ABC中，点D，E分别在AB，AC上，∠AED ＝∠B，那么下列各式中一定正确的是（）A．AE·AC＝AD·ABB．CE·CA＝BD·ABC．AC·AD＝AE·ABD．AE·EC＝AD·DB◆模型五垂直型8．如图，在△ABC中，∠ACB＝90°，CD⊥AB于点D，则图中相似三角形共有【方法14】（）A．1对 B．2对 C．3对 D．4对第8题图第9题图9．如图，在矩形ABCD中，M是BC边上且与B，C不重合的点，点P是射线AM上的点，若以A，P，D为顶点的三角形与△ABM相似，则这样的点P 有_______个．◆模型六一线三等角型10．如图，AB⊥BD，ED⊥CD，C是线段BD的中点，且AC ⊥CE，ED＝1，BD＝4，那么AB ＝________.第10题图第11题图11．如图，在边长为9的正三角形ABC中，BD＝3，∠ADE ＝60°，则AE的长为_______.【方法14】模型构建专题：相似三角形的基本模型的构建答案1．B 2.6 3.D 4.B 5.D 6.B 7.A 8.C9．2 解析：∵四边形ABCD 是矩形，∴BC∥AD，∴∠DAP ＝∠AMB.若△APD与△ABM相似，则①DP⊥AM；②P为AM与DC延长线的交点．故这样的点P有2个．10．411．7 解析：∵△ABC为等边三角形，∴∠B＝∠C＝60°，AB＝BC＝AC＝9.∵BD＝3，∴CD＝BC－BD＝9－3＝6.∵∠ADC＝∠B＋∠BAD＝∠ADE ＋∠CDE，∠ADE＝∠B＝60°，∴∠BAD＝∠CDE，∴△ABD∽△DCE，∴ABDC＝BDCE，即96＝3CE，解得CE＝2，∴AE＝9－2＝7.构建数学的知识网络学习数学,重要的是要构建一个数学的知识网络,将单一的知识都串联起来,这样有助于对综合型题目的解答。

专题10 相似三角形的基本六大模型考点一 （双）A 字型相似考点二 （双）8字型相似考点三 母子型相似考点四 旋转相似考点五 K 字型相似 考点六 三角形内接矩形考点一 （双）A 字型相似【答案】见解析【分析】根据已知线段长度求出【详解】证明：在△ABC∵824ABAE==，63ACAD=【答案】（1）见详解；（2）见详解【分析】（1）由题意易得AD AE BD EC=（2）由（1）及题意可知AD AF BD EF=考点二 （双）8字型相似1．（2022·福建·福州华伦中学八年级期中）如图，在平行四边形ABCD 中，E 为CD 上一点，连接AE 、BD ，且AE 、BD 交于点F ，DEF S △：9ABF S =V ：49，则DE ：DC =（ ）A ．2：5B ．2：3C ．3：7D ．3：4【答案】C 【分析】根据平行四边形的性质得到DC ∥AB ，DC =AB ，得到△DFE :△ABF ，根据相似三角形的性质计算即可．【详解】∵四边形ABCD 是平行四边形，∴AB CD ∥，AB DC =，∵E 为DC 上一点，∴DE BA∥∴DEF V :ABF V ，3【答案】2【答案】（1）见解析；（2）见解析【分析】（1）利用平行四边形的性质得AB=CD，AB∥CD，再证明四边形BECD为平行四边形得到BD∥CE，根据相似三角形的判定方法，由CM∥DB可判断△BND∽△CNM；（2）先利用AD2=AB•AF可证明△ADB∽△AFD，则∠1=∠F，再根据平行线的性质得∠F=∠4，∠2=∠3，所以∠3=∠4，加上∠NMC=∠CMD，于是可判断△MNC∽△MCD，所以MC：MD=CN：CD，然后利用CD=AB和比例的性质即可得到结论．【详解】证明：（1）∵四边形ABCD是平行四边形，∴AB=CD，AB∥CD，而BE=AB，∴BE=CD，而BE∥CD，∴四边形BECD为平行四边形，∴BD∥CE，∵CM∥DB，∴△BND∽△CNM；（2）∵AD2=AB•AF，∴AD：AB=AF：AD，而∠DAB=∠FAD，∴△ADB∽△AFD，∴∠1=∠F，∵CD∥AF，BD∥CE，∴∠F=∠4，∠2=∠3，∴∠3=∠4，而∠NMC=∠CMD，∴△MNC∽△MCD，∴MC：MD=CN：CD，∴MC•CD=MD•CN，而CD=AB，∴CM•AB=DM•CN．【点睛】本题考查了三角形相似的判定与性质：在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形．在运用相似三角形的性质时主要利用相似比计算线段的长．也考查了平行四边形的判定与性质．考点三母子型相似(1)求证：△ABC∽△BDC．(2)若∠C＝90°，BC＝2，求AB的长．【答案】(1)见解析；(2)4．【分析】（1）先证明∠A＝∠DBA，进而得到∠A＝∠CBD，再根据∠C＝∠C，即可证明△ABC∽△BDC；（2）根据∠C＝90°得到∠A＋∠ABC＝90°，根据（1）得到∠A =∠ABD＝∠CBD，即可求出∠A＝30°，即可求出AB＝4．（1）证明：如图，∵AD＝BD，∴∠A＝∠DBA，∵BD平分∠ABC交AC于点D，∴∠CBD＝∠DBA，∴∠A＝∠CBD，∵∠C＝∠C，∴△ABC∽△BDC；（2）解：如图，∵∠C＝90°，∴∠A＋∠ABC＝90°，由（1）得∴∠A =∠ABD＝∠CBD，∴∠A＋∠ABD＋∠CBD＝3∠A＝90°，∴∠A＝30°，考点四旋转相似（3）如图，过A 作AF ⊥EC ，由题意可知Rt △ABC∽Rt △AED ，∠BAC ＝∠EAD ＝90°，然后根据相似三角形的性质及题意易证△BAE ∽△CAD ，最后根据勾股定理及等积法进行求解即可．【详解】解：（1）在Rt △ABC 中，AB ＝AC ，∴∠B ＝∠ACB ＝45°，∵∠BAC ＝∠DAE ＝90°，∴∠BAC ﹣∠DAC ＝∠DAE ﹣∠DAC ，即∠BAD ＝∠CAE ，在△BAD 和△CAE 中，AB AC BAD CAE AD AE =ìïÐ=Ðíï=î，∴△BAD ≌△CAE （SAS ），∴BD ＝CE ，∠B ＝∠ACE ＝45°，∵∠ACB ＝45°，∴∠BCE ＝45°+45°＝90°，故答案为：BD ＝CE ，BD ⊥CE ；（2）BD ⊥CE ，理由：如图2，连接BD ，∵在Rt △ABC 和Rt △ADE 中，AB ＝AC ，AD ＝AE ，∠AEC ＝45°，∵∠CAB ＝∠DAE ＝90°，∴∠BAD ＝∠CAE ，∵AC ＝AB ，AE ＝AD ，∴△CEA ≌△BDA （SAS ），∴∠BDA ＝∠AEC ＝45°，∴∠BDE ＝∠ADB +∠ADE ＝90°，∴BD ⊥CE ；（3）如图3，过A 作AF ⊥EC ，考点五K字型相似1．（2021·湖南长沙·九年级专题练习）如图，在矩形ABCD中，BC＝6，AB＝2，Rt△BEF的顶点E在边CD【点睛】本题是三角形综合题，主要考查了三角形相似的性质和判定，勾股定理，判断相似是解决本题的关键，求CE是本题的难点．考点六三角形内接矩形。

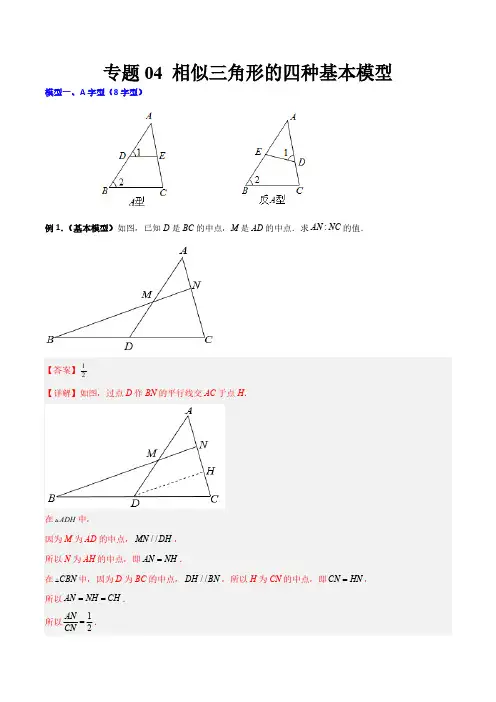
专题04 相似三角形的四种基本模型模型一、A字型（8字型）AN NC的值．例1．（基本模型）如图，已知D是BC的中点，M是AD的中点．求:例2．（培优）如图，ABC V 中，点D 在AC 边上，且1902BDC ABD Ð=+Ðo ．（1）求证：DB AB =；（2）点E 在BC 边上，连接AE 交BD 于点F ，且AFD ABC Ð=Ð，BE CD =，求ACB Ð的度数．（3）在（2）的条件下，若16BC =，ABF V 的周长等于30，求AF 的长．【变式训练1】如图，点O是△ABC边BC上一点，过点O的直线分别交AB，AC所在直线于点M，N，且AB AM＝m，ACAN＝n．（1）若点O是线段BC中点．①求证：m+n＝2；②求mn的最大值；（2）若COOB＝k（k≠0）求m，n之间的关系（用含k的代数式表示）．【变式训练2】矩形ABCD中，AB＝8，AD＝12．将矩形折叠，使点A落在点P处，折痕为DE．（1）如图①，若点P恰好在边BC上，连接AP，求APDE的值；（2）如图②，若E是AB的中点，EP的延长线交BC于点F，求BF的长．模型二、X （8）字型X 字型（平行） 反X 字型（不平行）例1．（基本模型）已知：如图，在△ABC 中，点D 、E 分别在边AB 、AC 上，DE ∥BC ，点F 在边AB 上，BC 2=BF•BA ，CF 与DE 相交于点G ．（1）求证：DF•AB=BC•DG ；（2）当点E 为AC 中点时，求证：2DF•EG=AF•DG ．【答案】（1）证明见解析；（2）证明见解析．【详解】证明：（1）∵BC 2=BF•BA ，∴BC ：BF=BA ：BC ，而∠ABC=∠CBF ，∴BAC BCF V V ∽，例2．（培优）如图1，ΔABC中，AB=AC，点D在BA的延长线上，点E在BC上，DE=DC，点F是DE 与AC的交点．（1）求证：∠BDE=∠ACD；（2）若DE=2DF，过点E作EG//AC交AB于点G，求证：AB=2AG；（3）将“点D在BA的延长线上，点E在BC上”改为“点D在AB上，点E在CB的延长线上”，“点F是DE 与AC的交点”改为“点F是ED的延长线与AC的交点”，其它条件不变，如图2．①求证：AB·BE=AD·BC；②若DE=4DF，请直接写出SΔABC:SΔDEC的值．【答案】（1）见解析；（2）见解析；（3）①见解析；②16:15．【详解】（1）证明：∵AC=AB，∴∠ACB=∠B，∵DC=DE，【变式训练1】 如图，正方形ABCD 的边长为12，点E 是射线BC 上的一个动点，连接AE 并延长，交射线DC 于点F ，将ABE △沿直线AE 翻折，点B 落在点B ¢处．（1）当1BE CE=时，如图1，延长AB ¢，交CD 于点M ，①CF 的长为________；②求证：AM FM =．（2）当点B ¢恰好落在对角线AC 上时，如图2，此时CF 的长为________；BE CE=________； （3）当3BE CE =时，求DAB ¢Ð的正弦值．【变式训练2】如图1，在矩形ABCO中，OA＝8，OC＝6，D，E分别是AB，BC上一点，AD＝2，CE＝3，OE与CD相交于点F．（1）求证：OE⊥CD；（2）如图2，点G是CD的中点，延长OG交BC于H，求CH的长．【变式训练3】已知：矩形ABCD中，AB＝6，BC＝8，点P是线段AD上一点，连接CP，点E在对角线AC上（不与点A，C重合），∠CPE＝∠ACB，PE的延长线与BC交于点F．（1）如图1，当AP＝2时，求CF的长；（2）如图2，当PF⊥BC时，求AP的长；（3）当△PFC是等腰三角形时，求AP的长．模型三、子母型已知：∠ 1=∠2；结论：△ACD ∽△ABCDAC B 12例1．（基本模型）如图，在△ABC中，点D在BC边上，点E在AC边上，且AD＝AB，∠DEC＝∠B．（1）求证：△AED∽△ADC；（2）若AE＝1，EC＝3，求AB的长．例2.（培优）在Rt△ABC中，∠ACB=90°，点D为AB上一点．（1）如图1，若CD⊥AB，求证：AC2=AD·AB；（2）如图2，若AC=BC，EF⊥CD交CD于H，交AC于F，且49FHHE=，求ADBD的值；（3）如图3，若AC=BC，点H在CD上，∠AHD=45°，CH=3DH，则tan∠ACH的值为________．【变式训练1】在矩形ABCD 中，4AB =，3BC =，E 是AB 边上一点，EF CE ^交AD 于点F ，过点E 作AEH BEC Ð=Ð，交射线FD 于点H ，交射线CD 于点N ．（1）如图a ，当点H 与点F 重合时，求BE 的长．（2）如图b ，当点H 在线段FD 上时，设BE x =，DN y =，求y 与x 之间的函数关系式，并写出它的定义域．△相似时，求线段DN的长．（3）连接AC，当FHEV与AEC2Ð=Ð，设②若FHE ECA【变式训练2】如图，锐角△ABC中，CD，BE分别是AB，AC边上的高，垂足为D，E．（1）求证：△ACD∽△ABE；（2）若将点D，E连接起来，则△AED和△ABC能相似吗？说说你的理由．【答案】（1）见详解；（2）相似，理由见详解；【详解】证明：（1）∵CD，BE分别是AB，AC边上的高，∴∠ADC＝∠AEB＝90°．∵∠A＝∠A，∴△ACD∽△ABE（2）连接DE，∵△ACD∽△ABE,∴AD：AE＝AC：AB．∴AD：AC＝AE：AB．∵∠A＝∠A．∴△AED∽△ABC，【变式训练3】已知正方形ABCD的边长为4，点E在边BC上，点F在边CD上，且CF BE=，AE和BF交于点G．（1）如图，求证：①AE BF=^②AE BF（2）连接CG并延长交AB于点H，①若点E为BC的中点（如图），求BH的长．②若点E在BC边上滑动（不与点,B C重合），当CG取得最小值时，求BE的长．模型四、旋转型例1．（基本模型）在同一平面内，如图①，将两个全等的等腰直角三角形摆放在一起，点A 为公共顶点，90BAC AED Ð=Ð=°．如图②，若△ABC 固定不动，把△ADE 绕点A 逆时针旋转，使AD 、AE 与边BC 的交点分别为M 、N 点M 不与点B 重合，点N 不与点C 重合．【探究】求证：BAN CMA ∽△△．【应用】已知等腰直角三角形的斜边长为4．(1)BN CM ×的值为______．(2)若BM CN =，则MN 的长为______．例2．（培优）【问题发现】如图1，在Rt△ABC中，∠BAC＝90°，AB＝AC，D为斜边BC上一点（不与点B，C重合），将线段AD绕点A顺时针旋转90°得到AE，连接EC，则线段BD与CE的数量关系是______，位置关系是______；【探究证明】如图2，在Rt△ABC和Rt△ADE中，∠BAC＝∠DAE＝90°，AB＝AC，AD＝AE，将△ADE绕点A旋转，当点C，D，E在同一条直线上时，BD与CE具有怎样的位置关系，说明理由；【拓展延伸】如图3，在Rt△BCD中，∠BCD＝90°，BC＝2CD＝4，过点C作CA⊥BD于A．将△ACD绕点A顺时针旋转，点C的对应点为点E．设旋转角∠CAE为a（0°＜a＜360°），当C，D，E在同一条直线上时，画出图形，并求出线段BE的长度．根据题意可知，Rt△ABC∽AB AC AB AE在Rt△ACD中，CD边上的高【变式训练1】如图，等腰三角形ABC和等腰三角形ADE，其中AB＝AC，AD＝AE．(1)如图1，若∠BAC＝90°，当C、D、E共线时，AD的延长线AF⊥BC交BC于点F，则∠ACE＝______；(2)如图2，连接CD、BE，延长ED交BC于点F，若点F是BC的中点，∠BAC＝∠DAE，证明：AD⊥CD；(3)如图3，延长DC到点M，连接BM，使得∠ABM＋∠ACM＝180°，延长ED、BM交于点N，连接AN，若∠BAC＝2∠NAD，请写出∠ADM、∠DAE它们之间的数量关系，并写出证明过程．【答案】(1)22.5°；(2)见解析(3)∠DAE+2∠ADM=180°，详见解析【解析】（1）解：∵△ABC为等腰三角形，∠BAC=90°，∴∠ABC=∠ACB=45°，由三角形外角性质知，∠ADE=∠ACE+∠DAC，∠AED=∠ECB+∠B，∵AD=AE，∴∠ADE=∠AED，∴∠ACE+∠DAC=∠ECB+∠B，∵AF⊥BC，∴∠BAF=∠CAD=45°，∴∠ACE=∠BCE，又∠ACB=45°，∴∠ACE=22.5°，故答案为：22.5°．（2）解：连接AF，过A作AH⊥EF于H，如图所示，∵∠BAC=∠DAE，AD=AE，AB=AC，∴∠CAF=∠BAF=∠DAH=∠EAH，∵∠BAC =∠QAN ，∴∠QAC =∠BAN ，∵∠ABM +∠ACM =180°，∠ACM +∠ACQ =180°【变式训练2】［问题发现］(1)如图1，在Rt △ABC 中，AB AC =，90BAC Ð=°，点D 为BC 的中点，以CD 为一边作正方形CDEF ，点E 与点A 重合，已知ACF BCE D D ∽．请直接写出线段BE 与AF 的数量关系；［实验研究］(2)在（1）的条件下，将正方形CDEF绕点C旋转至如图2所示的位置，连接BE，CE，AF．请猜想线段BE 和AF的数量关系，并证明你的结论；［结论运用］D的面积为8，当正方形CDEF旋转到B，E，F三点共线时，请求出线(3)在（1）（2）的条件下，若ABC段AF的长．模型五、一线三垂直型例1．（模型探究）【感知】如图①，在四边形ABCD 中，点P 在边AB 上（点P 不与点A 、B 重合），90A B DPC Ð=Ð=Ð=°．易证DAP PBC △△∽．（不需要证明）【探究】如图②，在四边形ABCD 中，点P 在边AB 上（点P 不与点A 、B 重合），A B DPC Ð=Ð=Ð．若4PD =，8PC =，6BC =，求AP 的长．【拓展】如图③，在ABC V 中，8AC BC ==，12AB =，点P 在边AB 上（点P 不与点A 、B 重合），连结EDC B AED C B AE D C B ACP ，作CPE A Ð=Ð，PE 与边BC 交于点E ，当CPE △是等腰三角形时，直接写出AP 的长．例2．（培优）问题提出（1）如图1，在矩形ABCD 中，4cm AB =，点E 为AB 的中点，点F 在BC 上，过点E 作//EG BC 交FD 于点G ．若5cm EG =，则EFD △的面积为_________．问题探究（2）如图2，在矩形ABCD 中，6cm,9cm AB BC ==，点P 是AD 边上一动点，点Q 是CD 的中点将．ABP △沿着BP 折叠，点A 的对应点是A ¢，将QDP △沿着PQ 折叠，点D 的对应点是D ¢．请问是否存在这样的点P ，使得点P 、A ¢、D ¢在同一条直线上？若存在，求出此时AP 的长度；若不存在，请说明理由．问题解决（3）某精密仪器厂接到生产一种特殊四边形金属部件的任务，部件要求：如图3，在四边形ABCD 中，4cm BC =，点D 到BC 的距离为5cm,AD CD ^，且CD =．若过点D 作//BC MN ，过点A 作MN 的垂线，交MN 于点E ，交CB 的延长线于点H ，过点C 作CF MN ^于点F ，连接AC ．设AE 的长为(cm)x ，四边形ABCD 的面积为()2cm y ．①根据题意求出y 与x 之间的函数关系式；②在满足要求和保证质量的前提下，仪器厂希望造价最低．已知这种金属材料每平方厘米造价60元，请你帮忙求出这种四边形金属部件每个的造价最低费用． 1.73)»由题意得：5CF EH ==．∵AD CD ^，∴90EDA CDF Ð+Ð=°．∵CF MN ^，【变式训练1】问题提出：（1）如图①，矩形ABCD中，AD＝6．点E为AD的中点．点F在AB上，过点E作EG//AB交FC于点G．若EG＝7．则S△EFC＝ ．问题探究：（2）如图②．已知矩形ABCD纸片中．AB＝9，AD＝6，点P是CD边上一动点．点Q是BC的中点．将△ADP沿着AP折叠，在纸片上点D的对应点是D¢，将△QCP沿着PQ折叠．在纸片上点C的对应点是C¢．请问是否存在这样的点P．使得点P、D¢、C¢在同一条直线上？若存在，求出此时DP的长度．若不存在，请说明理由．问题解决：（3）某精密仪器厂接到生产一种特殊四边形金属部件的任务．部件要求：如图③，四边形ABCD中，AB＝4厘米，点C到AB的距离为5厘米，BC⊥CD．且BC．在满足要求和保证质量的前提下，仪器厂希望造价最低，已知这种金属材料每平方厘米造价50元．请问这种四边形金属部件每个的造价最低是多少）【答案】（1）21；（2）存在，6或3；（3）802.75元【变式训练2】如图，矩形ABCD中，AB＝1，BC＝3，点E是边BC上一个动点（不与点B、C重合），AE的垂线AF交CD的延长线于点F，点G在线段EF上，满足FG∶GE＝1∶2，设BE＝x．（1）求证：AD DF AB BE=；（2）当点G在△ADF的内部时，用x的代数式表示∠ADG的余切；（3）当∠FGD＝∠AFE时，求线段BE的长．【变式训练3】如图1和图2，在平面直角坐标系中，点C的坐标为（0，4），A是x轴上的一个动点，M是线段AC的中点．把线段AM以A为旋转中心、按顺时针方向旋转90°得到AB．过B作x轴的垂线、过点C 作y轴的垂线，两直线交于点D，直线DB交x轴于点E．设A点的横坐标为m．（1）求证：△AOC∽△BEA；（2）若m=3，则点B的坐标为　；若m=﹣3，则点B的坐标为　；（3）若m＞0，△BCD的面积为S，则m为何值时，S=6？（4）是否存在m，使得以B、C、D为顶点的三角形与△AOC相似？若存在，求此时m的值；若不存在，请说明理由．。

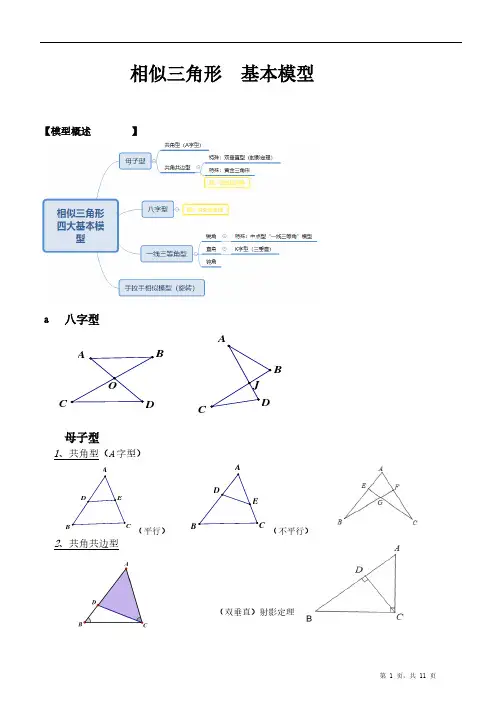
相似三角形Ⲵ基本模型
【模型概述ᙍ㔤ሬമ】
аǃ八字型
Ҽǃ母子型
1、共角型（A 字型）
（平行）
（不平行）
2、共角共边型
（双垂直）射影定理
B
C
B C
B
【典ර㓳Ґ仈】——母子型（A 型）
1．已知：如图，在Rt △ABC 中，∠C =90°，BC =2，AC =4，P 是斜边AB 上的一个动点，PD ⊥AB ，交边
AC 于点D （点D 与点A 、C 都不重合），E 是射线DC 上一点，且∠EPD =∠A ．设A
、P 两点的距离为x ，△BEP 的面积为y ． （1）求证：AE =2PE ；
（2）求y 关于x 的函数解析式，并写出它的定义域；
【典例㓳Ґ仈】——双垂直型直角三角形˖：
Rt △ABC 中，∠C =90º，CD ⊥AB 于D ，则
∽ ∽ 射影定理：
CD 2
= ·
AC 2
= ·
BC 2
= ·
A
C
B
P
D E
йǃ一线三等角相似模型
一 线 三 等 角
直角形一线三等角
（K 字型）
钝角形一线三等角
锐角形一线三等角
ഋǃ手拉手相似模型
1、定义：
两个相似且共顶点的三角形形成的图形。

2、固定结论：
将三角形顶角（头）朝上，正对读者，读者左边为着手顶点，右边为右手顶点，会得到一对新的相似三角形
ӄǃ十字架相似模型
．。

专题05 相似三角形中的基本模型--对角互补模型相似三角形在中考数学几何模块中占据着重要地位。

相似三角形与其它知识点结合以综合题的形式呈现，其变化很多，难度大，是中考的常考题型。

如果大家平时注重解题方法，熟练掌握基本解题模型，再遇到该类问题就信心更足了。

本专题就对角互补模型进行梳理及对应试题分析，方便掌握。

模型1.对角互补模型（相似模型）【模型解读】四边形或多边形构成的几何图形中，相对的角互补。

该题型常用到的辅助线主要是顶定点向两边做垂线，从而证明两个三角形相似.【常见模型及结论】1）对角互补相似1条件：如图，在Rt △ABC 中，∠C ＝∠EOF ＝90°，点O 是AB 的中点，辅助线：过点O 作OD ⊥AC ，垂足为D ，过点O 作OH ⊥BC ，垂足为H ，结论：BC AC =（思路提示：OE OD BH BC OF OH OH AC===）.2）对角互补相似2条件：如图，已知∠AOB ＝∠DCE ＝90°，∠BOC ＝α.辅助线：作法1：如图1，过点C 作CF ⊥OA ，垂足为F ，过点C 作CG ⊥OB ，垂足为G ；结论：①△ECG ∼△DCF ；②CE ＝CD ·tan α.（思路提示：CE CG CD CF=，CF =OG ，在Rt △COG 中，CG tan OGα=）辅助线：作法2：如图2，过点C 作CF ⊥OC ，交OB 于F ；结论：①△CFE ∼△COD ；②CE ＝CD ·tan α.（思路提示：CE CF tan CD CO α==，在Rt △OCF 中，CF tan OCα=）3）对角互补相似3条件：已知如图，四边形ABCD 中，∠B +∠D =180°辅助线：过点D 作DE ⊥BA ，垂足为E ，过点D 作DF ⊥BC ，垂足为F ；结论：①△DAE ∼△DCF ；②ABCD 四点共圆。

例1．（2023·重庆·九年级期中）如图，在Rt △ABC 中，∠ABC ＝90°，AB ＝3，BC ＝4，在Rt △MPN 中，∠MPN ＝90°，点P 在AC 上，PM 交AB 于点E ，PN 交BC 于点F ，当PE ＝2PF 时，AP ＝________．例2．（2023·河南南阳·九年级统考阶段练习）如图，在等腰直角ABC V 中，90ACB Ð=°，AC BC =，过点C 作射线CP AB ∥，D 为射线CP 上一点，E 在边BC 上（不与,B C 重合）且45DAE =°∠，AC 与DE 交于点O ．（1）求证：ADC AEB :△△；（2）求证：ADE ACB V :V ；（3）如果CD CE =，求证：2CD CO CA =g ．例4．（2022·山东·宁阳县九年级期末）如图1，将直角三角板放在正方形ABCD上，使三角板的直角顶点E 与正方形ABCD的顶点A重合，三角板的一边交边CD于点F，另一边交CB的延长线于点G．（1）求证：EF EG=；（2）如图2，移动三角板，使顶点E始终在正方形ABCD的对角线AC上，其他条件不变，(1)中的结论是否仍然成立？若成立，请给予证明：若不成立．请说明理由；（3）如图3，将（2）中BC=，则的“正方形ABCD”改为“矩形ABCD”，且使三角板的一边经过点B，其他条件不变，若3AB=，6EF=______．EGE为BA延长线上一点，AE＝1，连接DE，作DF⊥DE交AC延长线于点F，求AF的长；（3）类比迁移：如图3，已知在V ABC中，∠BAC＝120°，AB＝AC＝4，取BC边上中点D，连接AD，点E 为射线BA上一点（不与点A、点B重合），连接DE，将射线DE绕点D顺时针旋转30°交射线CA于点F，当AE＝4AF时，求AF的长．2．（2023·江苏扬州·八年级校考阶段练习）且AF=2BF,E为射线BC上一点,∠4．（2023·内蒙古·统考中考真题）如图，在5．（2023·浙江·九年级专题练习）如图，在BC上，(1)若D是AB中点，线上，且34ABBD=，MDNÐ6．（2023·安徽·九年级专题练习）点D是ABCV内一点，交AC于点F．7．（2023吉林九年级上学期期末数学试题）已知在Rt ABC △中，边上的一点．过点D 用射线DE DF ⊥，分别交边AB AC ，于点(1)当D 为BC 的中点，且DE AB ⊥时，如图①，DE DF=______；(2)若D 为BC 的中点，将EDF Ð绕点D 旋转到图②位置时，求DE DF 的值；(3)若改变点D 的位置，且CD m =时，如图③，则DE =______（用含m ，n 的代数式表示），则的值为，求的值；【初步感知】(1)如图1，当1n =时，兴趣小组探究得出结论：22AE BF AB +=，请写出证明过程．【深入探究】(2)①如图2，当2n =，且点F 在线段BC 上时，试探究线段AE BF AB ，，之间的数量关系，请写出结论并证明；②请通过类比、归纳、猜想，探究出线段AE BF AB ，，之间数量关系的一般结论（直接写出结论，不必证明）（1）如图1，在等边ABC V 中，D 为BC 边上一点，E 为AC 边上一点，60ADE Ð=°，AB =CE =______．问题解决：（2）如图2，ABC V 是等边三角形，D 是BC 的中点，射线DE ，AC 于点E ，F ，且120EDF Ð=°，求证：DE DF =．（3）如图3，90BAC Ð=°，6AB =，AC 的中点，射线DE ，DF 分别交AB ，AC 于点E ，F ，且90EDF Ð=°，求DE DF 的值．（2）【类比迁移】如图2，矩形ABCD 的对角线相交于点转的过程中，边A O ¢与边BC 交于点M ，边（3）【拓展应用】如图3，四边形ABCD 和四边形35BC =，BCD △是直角三角形．在A B C O ¢¢¢Y 绕点边CD 交于点N ．当ABCD Y 与A B C O ¢¢¢Y 重叠部分的面积是长．。