第四章 马科维茨投资组合理论

投资理论解析投资是指将资金投入到某种项目或资产中，以期望获得收益的行为。

投资理论则是对投资行为背后原理和方法的探索与总结。

在这篇文章中，我们将对几种常见的投资理论进行解析，以帮助读者更好地进行投资决策。

一、有效市场假说有效市场假说是由美国经济学家尤金·弗雷迪曼于20世纪60年代提出的。

该理论认为，市场上的价格反映了所有可获得的信息，投资者无法通过预测市场走势或选择优质的投资标的来获得超额收益。

因此，投资者应该采取被动投资策略，即通过指数型基金等方式来进行投资，以跟随市场波动。

二、均值-方差模型均值-方差模型是由马科维茨在1952年提出的投资组合理论。

该模型认为投资者在选择投资组合时应考虑预期收益和风险之间的均衡。

通过分析资产的收益率和方差，投资者可以找到最优的资产配置方案。

在均值-方差模型中，投资者需要根据个人的风险承受能力和投资目标来确定合适的资产配置比例，以达到最大化收益和最小化风险的目的。

三、行为金融学行为金融学是对传统金融理论的一种补充和扩展。

传统金融理论假设投资者在决策时是理性的，而行为金融学则认为投资者的决策常常受到情绪、心理偏差和群体行为等非理性因素的影响。

因此，行为金融学强调投资者应该认识到自己的行为偏差，并采取相应的措施来规避风险。

例如，投资者可以采用分散投资策略、定期检查投资组合等方式来降低非理性决策的负面影响。

四、资本资产定价模型资本资产定价模型（CAPM）是一种量化投资风险和预期收益之间关系的模型。

该模型通过衡量投资组合相对于市场的系统风险、特定风险以及预期的市场回报率，来确定一个合理的资本成本和预期收益率。

利用CAPM模型，投资者可以进行投资标的的评估和定价，以辅助投资决策。

总结：本文对几种常见的投资理论进行了解析，包括有效市场假说、均值-方差模型、行为金融学和资本资产定价模型。

这些理论为投资者提供了不同的思路和工具，以便在投资决策中更加理性地权衡风险和收益。

投资模型
在金融领域，投资模型是指为了评估和预测金融资产未来表现而构建的数学模型。

投资模型可以基于各种假设和数据，帮助投资者做出理性的决策，选择最佳的投资组合。

投资组合理论
投资组合理论是现代金融学的基石之一，提出了一个重要的概念——资产的收益与风险之间存在着正相关关系。

根据该理论，投资者应该根据不同资产类别的相关性和历史表现，构建一个有效的投资组合，以最大限度地实现预期收益，同时降低风险。

马科维茨投资组合理论
马科维茨投资组合理论是一种经典的投资模型，由美国经济学家哈里·马科维茨于20世纪50年代提出。

该理论通过数学模型来描述投资者在风险与回报之间做出权衡的过程，帮助投资者找到有效的投资组合。

投资模型的建立
建立一个有效的投资模型需要考虑多个因素，包括资产类别、历史数据、风险偏好等。

通常，投资者会利用统计分析、资产配置和风险管理等工具来构建模型，进而评估不同投资策略的盈利能力。

投资模型的应用
投资模型在实际投资中具有广泛的应用，可以帮助投资者优化资产配置，制定风险管理策略，提高投资组合的收益水平。

通过不断调整和优化模型参数，投资者可以更好地应对市场波动，并实现投资目标。

结语
投资模型是现代金融领域中一项重要的工具，它通过数学模型和统计分析帮助投资者做出理性的投资决策。

建立一个合理的投资模型需要充分考虑市场条件、投资目标和风险偏好，只有通过不断学习和实践，投资者才能在复杂的金融市场中获得成功。

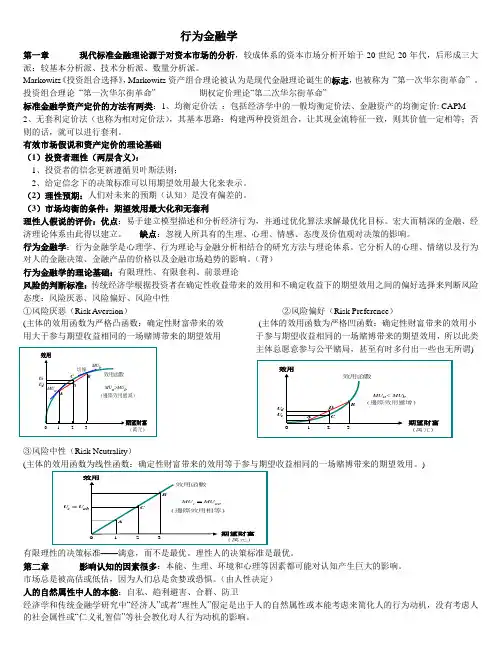
行为金融学第一章 现代标准金融理论源于对资本市场的分析，较成体系的资本市场分析开始于20世纪20年代，后形成三大派：较基本分析派、技术分析派、数量分析派。

Markowitz 《投资组合选择》，Markowitz 资产组合理论被认为是现代金融理论诞生的标志，也被称为 “第一次华尔街革命” 。

投资组合理论 “第一次华尔街革命” 期权定价理论“第二次华尔街革命”标准金融学资产定价的方法有两类：1、均衡定价法 ：包括经济学中的一般均衡定价法、金融资产的均衡定价: CAPM 2、无套利定价法（也称为相对定价法），其基本思路：构建两种投资组合，让其现金流特征一致，则其价值一定相等；否则的话，就可以进行套利。

有效市场假说和资产定价的理论基础（1）投资者理性（两层含义）：1、投资者的信念更新遵循贝叶斯法则；2、给定信念下的决策标准可以用期望效用最大化来表示。

（2）理性预期：人们对未来的预期（认知）是没有偏差的。

（3）市场均衡的条件：期望效用最大化和无套利理性人假说的评价：优点：易于建立模型描述和分析经济行为，并通过优化算法求解最优化目标。

宏大而精深的金融、经济理论体系由此得以建立。

缺点：忽视人所具有的生理、心理、情感、态度及价值观对决策的影响。

行为金融学：行为金融学是心理学、行为理论与金融分析相结合的研究方法与理论体系。

它分析人的心理、情绪以及行为对人的金融决策、金融产品的价格以及金融市场趋势的影响。

（背） 行为金融学的理论基础：有限理性、有限套利、前景理论风险的判断标准：传统经济学根据投资者在确定性收益带来的效用和不确定收益下的期望效用之间的偏好选择来判断风险态度：风险厌恶、风险偏好、风险中性①风险厌恶（Risk A version ） ②风险偏好（Risk Preference ）(主体的效用函数为严格凸函数：确定性财富带来的效 (主体的效用函数为严格凹函数：确定性财富带来的效用小 用大于参与期望收益相同的一场赌博带来的期望效用 于参与期望收益相同的一场赌博带来的期望效用，所以此类 主体总愿意参与公平赌局，甚至有时多付出一些也无所谓)③风险中性（Risk Neutrality ）(主体的效用函数为线性函数：确定性财富带来的效用等于参与期望收益相同的一场赌博带来的期望效用。

资产组合投资理论文献综述一、50年代以前的投资组合理论在马科维茨投资组合理论提出以前，分散投资的理念已经存在。

Hicks（1935）提出了“分离定理”，并解释了由于投资者有获得高收益低风险的期望,因而有对货币的需要；同时他认为和现存的价值理论一样，应构建起“货币理论”，并将风险引入分析中，因为风险将影响投资的绩效,将影响期望净收入。

Kenes（1936）和Hicks（1939）提出了风险补偿的概念，认为由于不确定性的存在，应该对不同金融产品在利率之外附加一定的风险补偿，Hicks还提出资产选择问题，认为风险可以分散。

Marschak（1938）提出了不确定条件下的序数选择理论,同时也注意到了人们往往倾向于高收益低风险等现象。

Williams（1938）提出了“分散折价模型”（Dividend Discount Model）,认为通过投资于足够多的证券,就可以消除风险,并假设总存在一个满足收益最大化和风险最小化的组合,同时能通过法律保证使得组合的事实收益和期望收益一致。

Leavens（1945）论证了分散化的好处。

随后Von Neumann（1947）应用预期效用的概念提出不确定性条件下的决策选择方法。

二、马科维茨投资组合理论及其扩展马科维茨投资组合理论是美国经济学家Markowitz（1952）发表论文《资产组合的选择》，标志着现代投资组合理论的开端。

他利用均值--方差模型分析得出通过投资组合可以有效降低风险的结论。

同时，Roy（1952）提出了“安全首要模型”（Safety-First Portfolio Theory），将投资组合的均值和方差作为一个整体来选择，尤其是他提出以极小化投资组合收益小于给定的“灾险水平”的概率作为模型的决策准则，为后来的VaR（Value at Risk）等方法提供了思路。

Tobin（1958）提出了著名的“二基金分离定理”:在允许卖空的证券组合选择问题中，每一种有效证券组合都是一种无风险资产与一种特殊的风险资产的组合。

第十二章投资组合管理本章内容概述本章主要介绍投资组合管理的基础理论和方法。

第一节介绍马科维茨均值方差模型；第二节介绍资本市场理论和CAPM模型；第三节介绍被动投资与主动投资的基本理论，包括市场有效性、被动投资、主动投资等内容；第四节介绍股票和债券投资组合的构建。

第一节现代投资组合理论一、现代投资组合理论与资本市场理论发展概述1.1952年，马科维茨在《金融杂志》上发表了一篇题为“资产组合的选择”的文章，首次提出了均值—方差模型，奠定了投资组合理论的基础，标志着现代投资组合理论的开端。

2.马科维茨用收益率的期望值来度量收益，用收益率的标准差来度量风险，推导出的结论是，投资者应该通过同时购买多种证券而不是一种证券进行分散化投资。

1990年，马科维茨凭此获得了诺贝尔经济学奖。

3.现代投资组合理论的核心思想就是把多种证券的投资组合看作是一个整体来进行分析和度量，然后把投资组合的风险分解为两部分—系统风险和非系统风险。

投资者可以通过持有多种类型的证券以达到分散非系统风险，从而进一步降低整个组合的风险。

4.现代资本市场理论的产生使关于金融问题的分析实现了从定性到定量的转变，其所涵盖的大量科学分析方法与著名的金融理论，如资产组合理论、资本资产定价模型、套利定价理论、期权定价理论以及作为它们理论基础的有效市场假说等，皆在理论界得到普遍的认可。

二、均值—方差模型概述1.投资者不仅关心投资收益率，也关心投资风险。

马科维茨投资组合理论的基本假设是投资者是厌恶风险的。

如果在两个具有相同预期收益率的证券之间进行选择，投资者会选择风险较小的。

要让投资者承担更高的风险，必须有更高的预期收益来补偿。

2.在回避风险的假定下，马科维茨建立了一个投资组合分析的模型，其要点如下：首先，投资组合具有两个相关的特征，一是预期收益率，二是各种可能的收益率围绕其预期值的偏离程度，这种偏离程度可以用方差度量。

其次，投资者将选择并持有有效的投资组合。

浅谈现代资产组合理论摘要：本文简单探讨了马科维茨的资产组合理论，介绍了资产组合理论的背景，给出了马科维茨均值-方差模型，阐述了该模型对资产投资选择的贡献。

在此基础上提出了马科维茨投资理论在实际操作中的局限性。

关键词：资产组合风险收益1.理论背景资产投资组合是投资者同时投资于多种证券，如股票、债券、银行存款等，投资组合不是券种的简单随意组合，它体现了投资者的意愿和投资者所受到的约束，即受到投资者对投资收益的权衡、投资比例的分配、投资风险的偏好等的限制。

现代资产组合理论最初是由美国经济学家哈里·马科维茨（Markowits）于1952年创立的，资产投资组合是投资者对各种风险资产的选择而形成的投资组合。

由于资产投资收入受到多种因素的影响而具有不确性，人们在投资过程中往往通过分散投资的方法来规避投资中的系统性风险和非系统性风险，实现投资效用的最大化。

资产投资组合管理的主要内容就是研究风险和收益的关系。

一般情况下风险与收益呈现正相关的关系。

即收益越高，风险越大；反之，收益越小，风险越小。

理性的投资者在风险一定的条件下，选择收益大的投资组合；在收益一定的条件下，选择风险小的资产投资组合。

马科维茨认为最佳投资组合应当是具有风险厌恶特征的投资者的无差异曲线和资产的有效边界线的交点。

威廉·夏普（Sharpe）则在其基础上提出的单指数模型，并提出以对角线模式来简化方差－协方差矩阵中的非对角线元素。

他据此建立了资本资产定价模型(CAPM)，指出无风险资产收益率与有效率风险资产组合收益率之间的连线代表了各种风险偏好的投资者组合。

根据上述理论，投资者在追求收益和厌恶风险的驱动下，会根据组合风险收益的变化调整资产组合的构成，进而会影响到市场均衡价格的形成。

2.理论主要内容马科维茨认为投资者都是风险规避者，他们不愿意陈但没有相应期望收益加以补偿的外加风险。

投资者可以用多元化的证券组合，将期望收益的离差减至最小，因此马科维茨根据一套复杂的数学方法来解决如何通过多元化的组合资产中的风险问题。

最优投资组合公式摘要：一、最优投资组合公式的概念1.投资组合的定义2.最优投资组合的概念二、最优投资组合公式的发展历程1.马科维茨投资组合理论2.夏普比率3.风险平价模型三、最优投资组合公式的应用1.资产配置2.风险管理3.投资策略制定四、最优投资组合公式的局限性与挑战1.假设条件的局限性2.计算复杂度3.投资者行为影响五、最优投资组合公式在我国的实践1.我国投资市场的特点2.最优投资组合在我国的应用3.我国投资者如何利用最优投资组合公式进行投资正文：一、最优投资组合公式的概念投资组合是指将多种资产按照一定比例组合起来进行投资的方式。

最优投资组合是指在给定风险条件下，收益最高或者在给定收益条件下，风险最低的投资组合。

二、最优投资组合公式的发展历程1.马科维茨投资组合理论：1952 年，哈里·马科维茨提出了投资组合理论，通过分散投资降低风险，同时最大化收益。

这一理论为后来的投资组合研究奠定了基础。

2.夏普比率：1964 年，威廉·夏普提出了夏普比率，用于衡量投资组合的风险调整收益。

这一指标使得投资者能够更加直观地比较不同投资组合的优劣。

3.风险平价模型：2005 年，诺奖得主罗伯特·默顿提出了风险平价模型，该模型通过等风险贡献原则来实现风险分散，提高了投资组合的风险调整收益。

三、最优投资组合公式的应用1.资产配置：投资者通过最优投资组合公式，可以确定不同资产在投资组合中的比例，以实现既定风险条件下的最优收益或者既定收益条件下的最小风险。

2.风险管理：金融机构和投资者利用最优投资组合公式，对投资组合进行风险评估和监控，有效控制潜在损失。

3.投资策略制定：通过最优投资组合公式，投资者可以制定适合自己风险承受能力和收益期望的投资策略。

四、最优投资组合公式的局限性与挑战1.假设条件的局限性：最优投资组合公式基于许多假设，如资产收益和风险的相关性、投资者风险厌恶程度等。

实际投资市场中，这些假设可能并不完全成立，从而影响最优投资组合公式的准确性。

最佳资产组合的确定1. 引言资产组合是指由多种不同类型的资产组成的投资组合。

在金融领域，资产组合管理被广泛应用于个人和机构的投资决策中，其目标是通过分散投资风险，实现最大收益。

确定最佳资产组合是投资者和资产管理公司的核心任务之一。

本文将介绍最佳资产组合的确定方法和相关的评价指标。

2. 资产组合的选择在确定最佳资产组合之前，投资者需要考虑以下几个关键因素：2.1 投资目标投资目标是决定资产组合的关键因素之一。

不同的投资目标会导致不同的投资策略和风险承受能力。

常见的投资目标包括长期资本增值、稳定收益和风险对冲等。

2.2 投资时间投资时间也是决定资产组合的重要因素之一。

投资者需要根据自己的投资时间选择合适的资产组合。

长期投资者可以更好地承受风险，选择更高风险、高回报的资产，而短期投资者则需要选择更为保守的资产。

2.3 风险承受能力投资者的风险承受能力是确定资产组合的重要指标。

风险承受能力高的投资者可以选择更高风险的资产，而风险承受能力低的投资者则需要选择更为保守的资产。

2.4 资产种类根据不同的资产种类，可以将资产分为股票、债券、房产、黄金等。

投资者需要根据自己对不同资产的了解和市场情况选择适合自己的资产组合。

3. 资产配置方法确定好投资目标、投资时间和风险承受能力后，投资者可以使用不同的资产配置方法确定最佳资产组合。

3.1 马科维茨投资组合理论马科维茨投资组合理论是由美国学者哈里·马科维茨于1952年提出的。

该理论认为，通过适当地配置不同风险和收益的资产，可以实现在给定风险水平下的最大收益。

该方法使用数学模型计算资产配置比例，并优化资产组合。

3.2 因子模型因子模型是一种基于统计分析的资产配置方法。

该方法通过研究资产收益与各种因子（如市场因子、行业因子等）之间的关系，建立数学模型来估计资产的预期收益和风险。

投资者可以根据因子模型的结果进行资产配置。

3.3 均衡风险投资策略均衡风险投资策略是一种传统的资产配置方法。