小波阈值图像降噪与MATLAB仿真设计

数字图像阈值去噪算法研究与实现摘要图像在获取和传输的过程中经常要受到噪声的污染。

噪声对图像分析有着非常重要的影响，必须在分析前去除。

所以，图像去噪成为图像分析和处理的重要技术。

传统的去噪方法不仅滤出了图像的噪声，同时使图像细节变得模糊。

小波变换是继傅琨叶变换之后的又一时频分析工具。

小波变换由于在时域频域同时具有良好的局部化性质和多分辨率分析的特点，因此不仅能满足各种去噪要求，如低通、高通、随机噪声的去除，而且与传统的去噪方法相比较，有着无可比拟的优点，成为信号分析的一个强有力的工具，被誉为分析信号的数学显微镜。

其应用包括图像预处理、图像压缩与传输、图像分析、特征提取等图像处理的很多阶段。

首先，介绍了本课题的研究目的，并介绍了目前常用的去噪方法及这些方法之间的比较。

其次，在简述了小波变换的发展历史和小波变换的基本理论知识后，对以小波为工具在数字图像处理方面进行了有益的探索。

再次，给出了小波边缘检测理论，接下来针对小波去噪的理论和方法着重进行了介绍，包括小波去噪的原理、方法和阈值去噪处理等方面的内容。

最后，对本文的工作进行了总结。

小波变换由于具有“数学显微镜”的作用，在去噪的同时能保持图像细节，得到原图像的最佳恢复。

在众多的小波去噪方法中，运用最多的是Donoho小波阈值萎缩法，但Donoho给出的阈值有“过扼杀”小波系数的倾向，重建误差较大。

本文提出基于小波变换与中值滤波相结合的方法实现了图像去噪。

该方法在去噪之前，先通过小波边缘检测确定图像边缘特征的小波系数，保留这些位置的小波系数，其不受闽值去噪影响，对其它位置的小波系数进行自适应阈值去噪，去除高斯噪声。

然后对图像进行中值滤波，去除椒盐噪声。

该算法的实验结果表明不仅能滤出图像中高斯噪声和椒盐噪声的混合噪声，而且能较好的保留图像的边缘细节，其滤波效果优于传统的图像去噪方法。

关键词：小波变换，高斯噪声，椒盐噪声，边缘检测，图像去噪ABSTRACTThe image iS often corrupted by noise in its acquisition or transmission．The noise to be removed before analysis has an important effect on image analysiS．Image～denoising is an important technology in image analysis and processingdomain．Traditional denoising methods can filter noise。

1 引 言
发动机的故障诊断需要测量多种传感器的输出信 号 。实际测试过程中测试信号中含有大量的噪声 , 这些 噪声会影响到信号的分析精度和分析结果并进一步影响 故障诊断的准确程度 。因此 , 进行信号的降噪处理是非 常必要的 。近年来 , 基于小波变换的阈值降噪方法得到 [ 12 2] 了广泛的研究和应用 。 实际应用中 ,通过实验发现不仅阈值和阈值函数的 选取是影响降噪效果的关键 , 小波分解的层数 (即尺度 )
3. 1 小波系数的去相关白化检验
则依数理统计的理论 , 其近似服从 F ( m , m ) 分布 。在原 假设条件下 ,有 2 2 2 ρ 1 +ρ 2 + … +ρ m 2 2 2 - 1 = 0 ρ ′ ′ ′ 1 +ρ 2 + … +ρ m
( 8)
^ ( m , m ) - 1 的取值较大时应 所以 ,当检验统计量 F 拒绝原假设 。这样 ,给定显著水平 α , 查自由度为 F ( m , ^(m , m ) m ) 分布表 ,得到临界值 Fα , 当实际计算结果 F
摘 要 : 小波阈值降噪算法是一种有效的从测试信号中去除噪声的方法 。通过对有用信号和噪声信号在小波空间上传播特性 的不同进行分析 ,提出了一种基于小波去相关白噪声检验的最优分解层数自适应确定算法 。该算法可以根据含噪声信号的特 点和信噪比 ,自适应的选择小波变换的最优分解层数以达到最优的降噪效果 。最后 ,在 MATLAB 环境下进行了仿真实验 ,并进 行了工程应用 。仿真实验和工程应用结果表明 ,该方法可以有效的确定合理分解层数得到最优的信噪比 。 关键词 : 小波降噪 ; 分解层数 ; 去相关 ; 白化检验 中图分类号 : O174. 2 文献标识码 : A 国家标准学科分类代码 : 520. 60

图像小波去噪去噪方法摘要：小波分析由于在时域、频域同时具有良好的局部化性质和多分辨率分析的特点，成为信号分析的一个强有力的工具。

木文首先介绍了小波分析的基木理论知识，然后介绍邻域平均法、时域频域低通滤波法、中值滤波法以及自适应平滑滤波法四种传统去噪方法，针对传统去噪方法的不足之处，提出了用小波变换和小波包对图像信号进行去噪处理。

通过Matlab仿真，得到了这两种方法的去噪效果的优缺点。

结果表明，小波包去噪方法无论是在视觉效果还是信噪比都比小波变换更好。

关键词：小波变换、小波包、图像去噪Abstract : Wavelet analysis in time domain and frequency domain due to the excellent localized properties and multi-resolution analysis of the characteristics of the signal analysis，become a powerful tool．This paper introduces the basic theories of wavelet analysis，then introduces neighborhood averaging method and time domain frequency domain low-pass filtering method，median filtering method and adaptive smoothing filtering method four traditional de-noising method，and compare to conventional de-noising method deficiency，put forward by wavelet transform and wavelet packet to deal with the noise of image signal．Through the simulation of Matlab，the advantages and disadvantages of the two methods could be demonstrated．Results show that the denoising method of wavelet packets in visual effect or signal-to-noise ratio is better than the wavelet transform．Keywords: Wavelet transform; Wavelet packet; Image de-nosing1 引言图像消噪是一种研究颇多的图像预处理技术，根据实际信号(图像是二维信号)和噪声的不同特点，人们提出了各式各样的去噪方法，其中最为直观的方法是根据噪声能景一般集中于高频，而信号频谱则分布于一个有限区间的这一特点，采用低通滤波的方法来进行去噪，例如滑动平均窗滤波、Wiener:线性滤波、中值滤波等。

小波变换的原理及m a t l a b仿真程序基于小波变换的信号降噪研究2 小波分析基本理论设Ψ(t)∈L 2( R) ( L 2( R) 表示平方可积的实数空间，即能量有限的信号空间) ， 其傅立叶变换为Ψ(t)。

当Ψ(t)满足条件[4,7]：2()R t dw w C ψψ=<∞⎰ （1）时，我们称Ψ(t)为一个基本小波或母小波，将母小波函数Ψ(t)经伸缩和平移后，就可以得到一个小波序列：,()()a b t b t aψ-= ,,0a b R a ∈≠ （2） 其中a 为伸缩因子，b 为平移因子。

对于任意的函数f(t)∈L 2( R)的连续小波变换为：,(,),()()f a b R t b W a b f f t dt aψψ-=<>=⎰（3） 其逆变换为：211()(,)()f R R t b f t W a b dadb C a aψψ+-=⎰⎰ （4） 小波变换的时频窗是可以由伸缩因子a 和平移因子b 来调节的，平移因子b,可以改变窗口在相平面时间轴上的位置，而伸缩因子b 的大小不仅能影响窗口在频率轴上的位置,还能改变窗口的形状。

小波变换对不同的频率在时域上的取样步长是可调节的，在低频时，小波变换的时间分辨率较低，频率分辨率较高：在高频时，小波变换的时间分辨率较高，而频率分辨率较低。

使用小波变换处理信号时，首先选取适当的小波函数对信号进行分解，其次对分解出的参数进行阈值处理，选取合适的阈值进行分析，最后利用处理后的参数进行逆小波变换，对信号进行重构。

3 小波降噪的原理和方法3.1 小波降噪原理从信号学的角度看 ,小波去噪是一个信号滤波的问题。

尽管在很大程度上小波去噪可以看成是低通滤波 ,但由于在去噪后 ,还能成功地保留信号特征 ,所以在这一点上又优于传统的低通滤波器。

由此可见 ,小波去噪实际上是特征提取和低通滤波的综合 ,其流程框图如图所示[6]：小波分析的重要应用之一就是用于信号消噪 ,一个含噪的一维信号模型可表示为如下形式：(k)()()S f k e k ε=+* k=0.1…….n-1 其中 ,f( k)为有用信号,s(k)为含噪声信号,e(k)为噪声,ε为噪声系数的标准偏差。

matlab小波变换信号去噪Matlab是一款非常强大的数据分析工具，其中小波变换可以应用于信号去噪的领域。

下面将详细介绍基于Matlab小波变换的信号去噪方法。

1、小波变换简介小波变换是时频分析的一种方法，它将信号分解成尺度与时间两个维度，能够保持信号的局部特征，适用于非平稳信号的分析。

小波变换的本质是将信号从时域转换到时频域，得到更加精细的频域信息，可以方便的对信号进行滤波、去噪等处理。

2、小波去噪方法小波去噪是指通过小波分析方法将噪声与信号分离并且去除的过程。

小波去噪的基本步骤是通过小波分解将信号分解成多尺度信号，然后对每一个分解系数进行阈值处理，去除一部分小于阈值的噪声信号，最后将处理后的分解系数合成原始信号。

3、基于Matlab的小波变换信号去噪实现在Matlab中，可以使用wavemenu命令进行小波变换，使用wthresh命令对小波分解系数进行阈值处理，利用waverec命令将阈值处理后的小波分解系数合成原始信号。

下面给出基于Matlab实现小波变换信号去噪的步骤：（1）读取信号，并可视化观测信号波形。

（2）通过wavedec命令将信号进行小波分解得到多个尺度系数，展示出小波分解系数。

（3）通过绘制小波系数分布直方图或者小波系数二维展示图，估计信号的噪声强度。

（4）根据阈值处理法对小波系数进行阈值处理，获得非噪声系数和噪声系数。

（5）通过waverec命令将非噪声系数合成原始信号。

（6）可视化效果，比较去噪前后信号的波形。

针对每个步骤，需要熟悉各个工具箱的使用知识。

在实际应用中，还需要根据特定的数据处理需求进行合理的参数设置。

4、总结小波去噪是一种常见的信号处理方法，在Matlab中也可以方便地实现。

通过实现基于Matlab小波变换的信号去噪，可以更好地应对复杂信号处理的需求，提高数据分析的准确性和精度。

收稿日期：2007－12－10作者简介：史振江（1979－），男，汉，河北唐山人，学士，讲师，研究方向智能检测与控制技术。

基金项目：河北省教育厅自然科学项目（Z2006442）基于MATLAB 的小波消噪仿真实现史振江１） 安建龙２） 赵玉菊１）　（石家庄铁路职业技术学院１） 河北石家庄 ０５００４１ 衡水学院２） 河北衡水 ０５３０００）　摘要：小波阈值消噪方法是利用小波变换技术对含噪信号进行分解和重构，通过对小波分解后的小波系数限定阈值来消除噪声的方法。

分析小波消噪的算法和实现步骤，并基于MATLAB 软件平台编写仿真程序。

进行光纤光栅反射信号的小波消噪仿真实验，消噪效果良好。

　关键词：小波消噪 阈值 分解 重构 光纤光栅　中图分类号：ＴＰ２７２ 文献标识码：Ａ 文章编号：1673-1816(2008)01-0063-04 １ 引言　微弱信号检测[1]是关于如何提取和测量强噪声背景下微弱信号的方法，有效的去除信号中的噪声是实现微弱信号检测的关键。

小波变换[2]是一种信号的时间、频率分析方法，具有多分辨分析的特点，是时间窗和频率窗都可以改变的时频局部化分析方法，已经广泛应用于信号消噪、信号处理、图像处理、语音识别与合成等领域。

小波消噪[3～5]的方法可以分为三类：模极大值法、相关法以及阈值方法。

其中，小波阈值消噪方法是利用小波变换技术对含噪信号进行分解和重构，通过对小波分解后的各层系数限定阈值来消除噪声的方法，因其实现简单、计算量小，取得了广泛应用。

MATLAB 即矩阵实验室，是一种建立在向量、数组和矩阵基础上，面向科学与工程计算的高级语言，它集科学计算、自动控制、信号处理、神经网络、图像处理于一体，具有极高的编程效率[6]。

其中的小波处理工具箱可以方便实现小波消噪算法，对含噪信号进行消噪处理和研究。

本文详细分析了小波消噪算法，利用MATLAB 软件编写了程序，并对光纤光栅反射谱信号进行了小波消噪仿真实验。

分类号：单击输入分类号编号：单击输入编号沈阳化工大学本科毕业论文题目：基于MATLAB小波分析的图像降噪处理院系：信息工程学院专业：通信工程班级： 1001学生姓名：田维军指导教师：郭烁论文提交日期：年月日论文答辩日期：年月日摘要本文研究的对象是加入高斯白噪声的数字信号，信号在传输或进行处理的过程中会受到噪声的影响，会影响到数字图像的质量，因此本文针对加入噪声的图像进行降噪处理，提高图像的清晰度，使得图像的质量达到最优。

为了克服传统的图像降噪方法的缺点，本文提出了小波分析的图像降噪的方法，这个方法克服了传统降噪方法的缺点，能够在很好的保留图像细节信息的前提下，更好的进行含噪图像的降噪。

小波分析降噪中的小波阈值降噪方法比较适合噪声图像的降噪处理，首先对噪声图像进行多层次的分解，然后在对噪声图像进行水平方向垂直方向以及斜线方向三个方向的阈值处理，最后对阈值处理后的图像进行图像的重构处理。

利用不同的小波基函数对噪声图像进行分解，观察利用不同的小波基函数对图像降噪的结果，通过计算信噪比和最小均方误差来判断最适合图像降噪的小波基函数，信噪比越大，最小均方误差越小则图像的降噪效果就越好，通过分析可以选择出图像降噪的最优的小波基函数。

然后在对最优的小波基函数进行不同层次的小波系数分解，也是通过计算信噪比和最小均方误差来得出小波基的最优分解层数，在最优分解层数下对噪声图像进行降噪处理效果最好。

图像最清晰，图像的质量更好，细节信息越完整。

对噪声图像进行阈值处理能够很好的对图像进行降噪处理，也能够很好的保留图像的细节信息，通过对六个小波基函数的分析，比较信噪比和最小均方误差的值可以看出bior4.4小波基降噪效果最好，在利用bior4.4小波基对图像进行了四个不同层次的分解，通过比较信噪比和最小均方误差，可知对图像进行3层的小波分解，对噪声图像的降噪效果最好。

利用以上的分析对噪声图像进行了很好的降噪效果。

关键词：小波变换，图像去噪，小波阈值，阈值函数，小波基函数，最优分解层AbstractIn the course of image processing，the collection，transformation and transmission of images are frequently affected by imaging equipments and noises in exterior environment，therefore，image quality declines．Because noises have big infection to the continuous processing of images，it has very important practical meaning to noises reduction．Image noise reduction is a widely image preprocessing of technology. It‟ s purpose is to enhance the SNR between original image and de-noised image, improve the characteristics of image. The digital image de-noise involves domains and so on optical system, microelectronic technology, computer science，mathematical analysis, it‟s a very comprehensive interdisciplinary science, now its practice application is very widespread: In the medicine, the military, art, the agriculture and all have very extensive and ripe using so on. MATLAB is one kind of highly effective engineering calculation language，in aspects and so on value computation, data processing, imagery processing, neural network, wavelet analysis all has the widespread application.Therefore, hunting for a method of denoising effectively and keeping the edge information simultaneously is a goal people have been pursuing all the time. Wavelet analysis is local analysis in the time domain and frequency domain, which represents the signal property using combination of the time domain and frequency domain ,which represents the signal property using combination of the time domain and frequency domain. It is a useful tool to analyze the unstationary signal that important multi-scale analysis to the signal by the translation and diatom of the moocher wavelet ,so it can effectively extract information from signal .Recently ,with the improvementof wavelet theory ,wavelet analysis has applied to image denoising successfully Compared with traditional methods, wavelet has incomparable advantage in image denoising. It can not only wipe off noise but also retain the image details.In this paper, wavelet threshold noise reduction, through the decomposition of the image, extracting the threshold, the final reconstructed image, wavelet threshold noise reduction coefficient of thought is a layer wavelet decomposition coefficients modulus greater than or less than a certain threshold are processed in the image obtained after the processing of digital image is reconstructed. Paper in the horizontal direction, vertical direction and diagonal direction of the threshold processing, the threshold value processing of the three directions of the image can be a good noise reduction processing. Then we discuss the quality of image noise reduction effect in the case of different wavelet bases, and in the noise reduction methods and wavelet basis in certain circumstances, to find the optimal decomposition level of wavelet coefficients obtained by the wavelet decomposition under optimal number of levels the best wavelet decomposition level image noise reduction.Key words: Wavelet Analysis; Image Denoising; Threshold; Threshold Function目录第一章绪论 (1)1.1 研究背景和意义 (1)1.2 数字图像降噪处理的简介 (4)1.3 本文研究内容 (5)第二章 MATLAB图像处理基础 (6)2.1 MATLAB简介 (6)2.1.1 MATLAB概述及发展史 (6)2.1.2 MATLAB工作环境 (7)2.2 数据类型、图像类型及转换 (8)2.2.1 数据类型 (8)2.2.2 图像类型 (9)2.2.3 图像类型转换 (10)第三章小波分析理论 (12)3.1 傅立叶变换 (12)3.1.2从傅立叶变换到小波变换 (13)3.2 小波变换 (14)3.2.1小波的基本概念 (15)3.2.2 连续小波变换 (15)3.2.3离散小波变换 (16)3.2.4小波的多分辨率分析理论 (17)3.3 常见的小波 (17)第四章应用MATLAB实现小波分析的图像降噪 (22)4.1 小波阈值降噪的概述 (22)4.2 小波阈值降噪的方法 (24)4.3 小波分析阈值降噪实例分析 (27)第五章结论 (34)参考文献 (36)致谢 (37)第一章绪论1.1 图像降噪技术的研究背景和意义图像降噪技术的研究历史非常久远，要追溯到70年代，现在每年仍有大量公发表的文献讨论这方面的问题。

基于小波变换的射线图像降噪及MATLAB 仿真作者：乔磊来源：《科技资讯》 2013年第6期乔磊(中北大学电子测试技术国家重点实验室山西太原 030051)摘要：针对射线图像噪声大、对比度低的特点，采用小波阈值法进行降噪处理。

通过利用MATLAB进行射线图像去噪仿真测试，结果表明，利用小波阈值法具有良好的降噪效果。

关键词：射线图像小波阈值阈值函数图像降噪中图分类号：TN911.73 文献标识码：A 文章编号：1672-3791(2013)02(c)-0014-01随着小波理论的不断深入研究和日益广泛的应用，小波变换以其低熵性、多分辨率、去相关性及选基灵活性等优点，成为图像去噪领域的一个重要分支和主要研究方向。

目前常用的小波图像去噪方法有基于小波变换模极大值去噪法、基于小波变换的相关去噪法及非线性小波变换阈值去噪法。

而小波阈值法是一种实现简单且计算量小的方法，具有广泛的实用性。

1 小波变换应用于图像降噪的处理过程[1](1)对含噪图像进行二维小波分解，得到一组小波系数。

应选择合适的小波基和恰当的分解层次N，然后对待处理的图像进行N层小波分解计算。

(2)对分解后的小波系数进行阈值量化处理，得到估计小波系数，使得这两个系数的差值尽可能小。

(3)根据得到的小波系数进行小波重构，从而恢复出原始图像信号，得到去噪后的图像。

2 MATLAB仿真利用Matlab对一副的加有随机噪声的射线图像分别采用传统的硬、软阈值及改进的软阈值函数进行去噪对比实验，程序中采用sym4小波对含噪图像进行2层小波分解，并使用全局阈值来进行降噪处理，实验结果如下所示。

本文进一步采用了均方误差（MSE）和峰值信噪比（PSNR）作为图像降噪效果的衡量标准，如（表1）所示。

3 结果分析小波阈值降噪法可以使图像的噪声几乎完全得到抑制,并且可以很好得保留原始信号的特征，是一种易于实现且实用效果较好的降噪方法。

通过实验可以看出，针对于射线图像的特点来说，不同的算法对图像的噪声都有一定程度的抑制，但在使用同一种阈值门限时，软阈值法的降噪效果要优于硬阈值，而改进的软阈值函数更有效得降低了均方差,提高了信噪比，其去噪后的图像边缘比较清晰，细节保持的较好，解决了抑制噪声和保留图像细节的矛盾，达到了最佳的去噪效果。

【引言】1. 背景介绍：在实际工程和科研中，数据经常受到各种噪声的干扰，因此需要对数据进行降噪处理。

2. 目的和意义：降噪处理可以使得数据更加真实可靠，有利于后续的分析和应用。

【matlab 曲线降噪的方法】3. 小波变换简介：小波变换是一种时频分析的方法，可以将信号分解为不同尺度的成分，对于曲线降噪具有很好的效果。

4. matlab中的小波变换函数：matlab提供了丰富的小波变换函数，包括连续小波变换和离散小波变换，用户可以根据具体需求选择合适的函数进行数据处理。

【matlab 曲线降噪的实现步骤】5. 数据准备：首先需要准备需要处理的数据，可以是实验采集的曲线数据，也可以是从其他渠道获取的曲线信息。

6. 选择小波函数：根据数据的特点和需求，选择合适的小波函数进行变换，常用的小波函数包括Daubechies小波、Haar小波等。

7. 对数据进行小波变换：利用matlab提供的小波变换函数，对数据进行小波分解，得到不同尺度的小波系数。

8. 降噪处理：根据小波系数的大小和分布，可以采用阈值处理、软硬阈值处理等方法对小波系数进行滤波，实现曲线的降噪处理。

9. 重构数据：经过降噪处理后，需要利用小波系数重构原始数据，得到降噪后的曲线信息。

【matlab 曲线降噪的应用实例】10. 实验数据：以某地震波形数据为例，介绍如何利用matlab的小波变换函数进行曲线降噪处理。

11. 数据分析：对比降噪前后的波形数据，分析降噪处理的效果和优势。

12. 结果展示：通过图表展示降噪前后的数据对比，直观地展现曲线降噪的效果。

【matlab 曲线降噪的注意事项】13. 参数选择：在进行小波变换和降噪处理时，需要合理选择小波函数和参数，以及阈值处理的方式和大小。

14. 原理理解：对小波变换的原理和数据特点有一定的理解，有利于选择合适的方法和优化参数。

15. 实时调试：在实际应用中，可以通过反复调试和对比分析来确定最佳的处理方案，实现最佳的降噪效果。

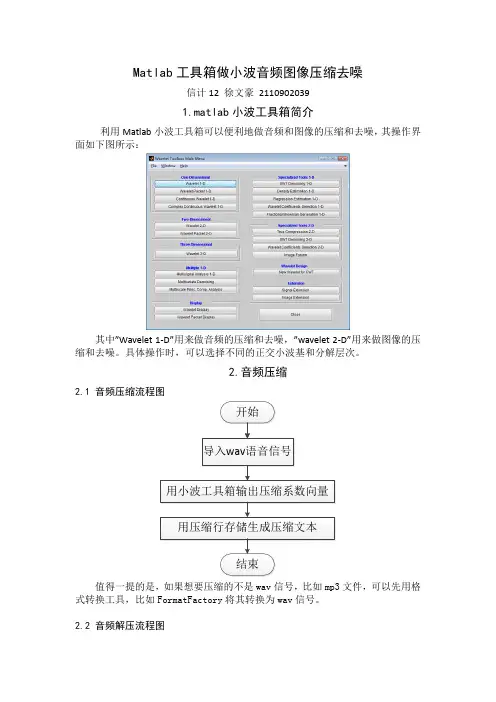
Matlab工具箱做小波音频图像压缩去噪信计12 徐文豪21109020391.matlab小波工具箱简介利用Matlab小波工具箱可以便利地做音频和图像的压缩和去噪，其操作界面如下图所示：其中”Wavelet 1-D”用来做音频的压缩和去噪，”wavelet 2-D”用来做图像的压缩和去噪。

具体操作时，可以选择不同的正交小波基和分解层次。

2.音频压缩2.1 音频压缩流程图值得一提的是，如果想要压缩的不是wav信号，比如mp3文件，可以先用格式转换工具，比如FormatFactory将其转换为wav信号。

2.2 音频解压流程图2.3 音频压缩效果比较考虑到正交小波基种类繁多，因而只比较较常用的haar、db和sym。

（1）量化音频压缩效果为了比较用不同正交小波基在不同分解层次下的压缩效果，有必要做一些量化处理。

考虑到，对同一音频信号，在取0率相同的情况下，压缩效果越好的正交小波基，其能量保留的应该越多。

因而，可先固定取0率，然后以能量保留百分比作为压缩效果的衡量指标。

（2）不同分解层次音频压缩效果比较不失一般性，考虑db4在取0率为95%的情况下在不同分解层次下的压缩效果，结果如下图：从图中可以看出，压缩效果随着分解层次的增加而增大，且增大速度先快后慢，最终压缩效果趋于稳定。

从理论上看，分解层次越多，出现小系数比率就越大，因而实验所得结果是与理论相符的。

可惜的是，在分解层次小于5时，可能是因为压缩效果已经太差，小波工具箱没给出其取0率为95%的情况，不然图像可以更加细致。

然而，也不能说分解层次越多越好，因为随着分解层次的增加，用于压缩和解压的时间会明显增加，因而这需要有一个折中。

（3）不同连续等级音频压缩效果比较对同种正交小波基，在分解层次固定时，可以比较不同连续等级对压缩效果的影响，考虑分解层次为5，取0率为95%，连续等级从1到7的db小波，结果如下图所示：从图中可以看出，随着小波基越来越连续，压缩效果是逐渐变大的，但增长速度也是先快后慢，且最终趋于平稳。

用matlab语言实现图像的小波消噪摘要本文实现了利用小波分解重构对图像进行消噪。

本次设计针对椒盐噪声，因此在滤波上，采取了对椒盐噪声最有效地中值滤波作为比较，同时采用不同类型不同噪声密度的图像上进行测试。

在消噪结果的评价上，采用PSNR以及边缘检测等进行比较。

该实验结果显示利用小波对于图像的消噪在一定程度上提高消噪效果。

关键词：小波消噪椒盐噪声中值滤波PSNR边缘检测Image Denoising in the Presence of Salt-and-Pepper Noise with MatlabAbstract：This article realize image denoising that using wavelet decomposition and reconstruction. The design for the salt and pepper noise, so take on median filter as a comparison, it is the most effective filter. I also use different noise of different types noise to testing. Using PSNR and edge detection in the evaluation of the results. The implementation show that wavelet denoising improve noise cancellation to some extent.Key words：wavelet denoising salt and pepper noise median filter PSNRedge detection目录第一章引言 (5)第二章图像的噪声及去噪2.1噪声的定义和分类 (5)2.1.1噪声的特征 (5)2.1.2噪声的来源 (6)2.2噪声的模型 (6)2.3图像去噪 (7)2.3.1图像去噪的常用方法 (7)2.3.2中值滤波 (7)2.3.3维纳滤波 (11)第三章小波分析及去噪3.1小波概述 (12)3.1.1小波分析 (12)3.1.2小波的应用 (13)3.2基本小波变换 (14)3.3常见的小波 (16)3.4小波消噪 (17)3.5小波的分解与重构 (18)3.7去噪阈值选择 (19)第四章边缘检测及图像质量判断4.1边缘检测 (20)4.2图像质量评价标准 (22)第五章设计思路及软件流程5.1设计思路 (23)5.2软件流程图 (23)第六章仿真结果比较6.1仿真效果图 (25)6.2PSNR对比结果 (26)结论 (28)致谢语 (28)参考文献 (29)附录1：程序 (30)附录2：文献 (33)附录3：翻译 (46)第一章 引言实际应用中，图像信号的产生、处理和传输都不可避免地要受到噪声的干扰，为了后续更高层次的处理，很有必要对图像信号进行去噪。

改进的小波阈值去噪方法及其在MATLAB中的仿真
李树钰
【期刊名称】《噪声与振动控制》
【年(卷),期】2010(030)002
【摘要】对比分析各种小波去噪方法,在此基础上构造一个新的阈值函数,并对阈值的选取做了一定的改进利用MATLAB软件进行信号降噪仿真实验,结果证明改进后的方法优于传统方法,取得较好的去噪效果.
【总页数】4页(P121-124)
【作者】李树钰
【作者单位】西安石油大学,机械工程学院,西安,710065
【正文语种】中文
【中图分类】TN911.72
【相关文献】
1.基于Matlab的小波阈值图像去噪方法研究 [J], 林东升
2.改进的小波阈值去噪方法在外汇市场中的应用 [J], 柳建芳;陈龙;李辰
3.一种改进小波阈值函数的图像去噪方法研究 [J], 周峡; 徐善顶
4.基于EMD和改进小波阈值的地震信号去噪方法 [J], 巨鑫;郑小鹏;武科含;周健;商冬明;徐静霞
5.基于VMD与改进小波阈值的地震信号去噪方法研究 [J], 乔云;李琼;钱浩东;宋鑫因版权原因，仅展示原文概要，查看原文内容请购买。

小波去噪的matlab程序-回复如何使用Matlab进行小波去噪。

小波去噪是数值信号处理中常用的一种方法，它可以有效地去除信号中的噪声，保留有用的信号部分。

Matlab是一个强大的数值计算和数据可视化工具，也提供了丰富的信号处理工具箱，其中包括小波去噪算法。

本文将介绍如何使用Matlab进行小波去噪，以帮助读者更好地理解和应用这一方法。

首先，我们需要定义被噪声污染的信号。

在Matlab中，可以通过生成具有噪声的信号来模拟实际应用。

以下是一段生成具有高斯白噪声的正弦信号的代码：fs = 1000; 采样频率T = 1/fs; 采样间隔L = 1000; 信号长度t = (0:L-1)*T; 时间向量f = 50; 正弦信号频率A = 0.7; 正弦信号幅度x = A*sin(2*pi*f*t); 生成正弦信号添加高斯白噪声mu = 0; 噪声均值sigma = 0.5; 噪声标准差n = sigma*randn(size(t)); 生成高斯白噪声x_noisy = x + n; 带噪声的信号上述代码中，我们生成了一个频率为50 Hz的正弦信号，并添加了均值为0、标准差为0.5的高斯白噪声。

生成的带噪声的信号存储在变量`x_noisy`中。

接下来，我们需要选择一种小波基函数以分析信号，并选择合适的小波系数阈值来进行去噪。

Matlab提供了多种小波基函数和小波系数阈值选择方法，如Daubechies小波基函数和固定阈值法、SureShrink方法等。

以下是一段使用Daubechies小波基函数和可视化小波系数阈值选择结果的代码：执行小波变换[c, l] = wavedec(x_noisy, 5, 'db4'); 小波分解可视化小波系数figure;subplot(2,1,1);plot(x_noisy);title('原始信号');subplot(2,1,2);plot(c);title('小波系数');小波系数阈值选择thr = wthrmngr('dw1ddenoLVL','penalhi',c,l); 阈值选择sorh = 's'; 阈值类型，s代表软阈值，h代表硬阈值keepapp = 1; 保留近似系数X = wdencmp('gbl',c,l,'db4',5,thr,sorh,keepapp); 小波去噪可视化去噪结果figure;subplot(2,1,1);plot(x_noisy);title('带噪声的信号');subplot(2,1,2);plot(X);title('去噪后的信号');上述代码中，我们使用了Daubechies小波基函数对信号进行了5级小波分解，并可视化了小波系数。

---------------------------------------------------------------范文最新推荐------------------------------------------------------ Matlab小波变换在图像处理中的仿真及应用+源码摘要：小波分析理论作为新的时频分析工具，在信号分析和处理中得到了很好的应用。

由于平面图像可以看成是二维信号，因此小波分析很自然地应用到了图像处理领域。

图像去噪和边缘检测是图像预处理中应用非常广泛的技术，其作用是为了提高信噪比，突出图像的期望特征，以便对其进行更高层次的处理。

由于在图像的获取和转换过程中,各类图像系统中由于传感器噪声、随机大气湍流和成像光源的散射等多方面因素都要造成图像的某些降质,使图像的分辨率和对比度产生下降,造成图像的应用性大幅降低。

针对这些情况，利用了小波变换良好的局部特性,使图像的信号通过小波变换后在频域上足够的分解,分离出了反映图像轮廓和细节的信息。

本文结合小比分析理论，借由Matlab应用程序对数字图像进行加噪、消噪、压缩、融合、平滑、增强的数字图像处理，力求保证达到预期效果。

1 / 48关键词：小波变换；小波系数；图像消噪；图像压缩；图像融合；图像增强4776Matlab based on wavelet transform in image processing in simulation and ApplicationAbstract:Wavelet analysis theory,as a new time&mdash;frequency analysis tool，has been well applied in the area of signal analysis and processing．An image is actually a two-dimensional signal．So it is natural to apply wavelet analysis to the area of image processing．Image de-noising and edge detection are two widely used technologies in image preprocessing．By enhancing SNR and highlighting expected features of image,it will be more convenient for further step of processing．Wavelet transform is more and more frequently applied to image processing according to its own advantages．In the process of image gaining and switching, because of the sensor noise, the stochastic atmospheric rapids and scattering of the image formation light - source and so on, images quality, resolution and the contrast gradient will drop, and causes---------------------------------------------------------------范文最新推荐------------------------------------------------------dramatic fall of the image application. These may create bad influence on the final recognition result. In view of this situation, this article uses the good partial characteristic of wavelet transformation, and makes the signal of image be decomposed enough in the frequency range after wavelet transformation, and separates the outline and the detail information which reflects the image. The wavelet coefficient after transforming is enhanced, then inverse transform of the wavelet coefficient is made to gain the enhanced image. The experimental result indicates that the image visual effect is improved and the image application value is enhanced.4.1.3 仿真结果264.1.4 仿真结果分析284.2 小波变换在图像压缩中的应用283 / 484.2.1 小波图像压缩的基本原理284.2.2 参数设置294.2.3 仿真结果304.2.4 仿真结果分析314.3 小波变换在图像平滑处理中的应用32 4.3.1 小波图像平滑处理的基本原理32 4.3.2 参数设置324.3.3 仿真结果334.4小波变换在图像增强中的应用344.4.1 小波图像增强的基本原理344.4.2 参数设置34---------------------------------------------------------------范文最新推荐------------------------------------------------------ 4.4.3 仿真结果354.4.3 仿真结果364.5 小波变换在图像融合中的应用364.5.1 小波图像融合的基本原理364.5.2 参数设置364.5.3 仿真结果374.6 小波变换在特定图像处理中的应用384.6.1 特定图像处理的实际意义384.6.2 小波图形用户GUI界面384.6.3 运用GUI界面对特定数字图片处理394.6.4 对特定数字图片处理的Matlab代码实现425 / 485 总结与展望47致谢48参考文献49附录50,47761 引言1.1 课题的背景及研究意义小波分析是近年来国际上掀起新潮的一个前沿研究领域，是继Fourier分析的一个突破性进展。

小波阈值图像去噪算法及MATLAR仿真实验
刘钰;马艳丽;刘艳霞
【期刊名称】《数字技术与应用》
【年(卷),期】2010(000)006
【摘要】本文研究了小波阈值图像的去噪方法,并与其它图像去噪方法进行了比较.对lena图像进行MATLAB仿真实验,得到了主观效果图和客观效果的PSNR.研究发现,小波阈值图像去噪无论主观效果还是客观效果都优于其他图像去噪方法.【总页数】2页(P122-123)
【作者】刘钰;马艳丽;刘艳霞
【作者单位】河北北方学院信息科学与工程学院,河北张家口,075000;天津大学电子信息工程学院,天津,300072;河北北方学院信息科学与工程学院,河北张家
口,075000;河北北方学院信息科学与工程学院,河北张家口,075000
【正文语种】中文
【中图分类】TP391
【相关文献】
1.一种改进的小波阈值图像去噪算法及仿真 [J], 张旗;刘辉;罗海富;罗彬;李康;
2.一种改进的小波阈值图像去噪算法及仿真 [J], 张旗;刘辉;罗海富;罗彬;李康
3.小波阈值图像去噪算法及MATLAB仿真实验 [J], 刘钰;马艳丽;刘艳霞
4.一种小波阈值函数构建的图像去噪算法研究 [J], 万庄姝;谭碧莹;段雅倩;闵钢;舒忠
5.基于小波阈值与分层深度图像去噪算法研究 [J], 陈天宇;张维忠
因版权原因，仅展示原文概要，查看原文内容请购买。

matlab小波去噪函数小波去噪是一种通过使用小波变换来减少图像或信号中噪声的技术。

在处理信号时，小波变换可以将信号分解成多个频带。

这些频带可以在不同尺度上进行分析，并且可以通过移除某些频带来提高信号的清晰度。

Matlab是一种流行的用于数学计算和数据可视化的软件。

Matlab 中有很多小波去噪函数，可以用于处理不同类型的信号和图像。

这些函数可以帮助用户快速准确地完成小波去噪的任务。

在Matlab中，最常用的小波去噪函数是wdenoise和wden。

这些函数都可以用于去除信号或图像中的噪声，并且可以通过设置参数来调整去噪的效果。

wdenoise函数可以对一维和二维信号进行去噪。

该函数使用离散小波变换来分解信号，并使用软阈值技术来减少噪声。

软阈值技术可以通过将小于某个阈值的系数设置为零来减少噪声。

这可以帮助保留信号中的重要信息，并去除噪声。

wden函数可以对一维信号进行去噪。

该函数使用小波变换和硬阈值技术来减少噪声。

硬阈值技术将小于某个阈值的系数设置为零，从而减少噪声。

与软阈值技术不同的是，硬阈值技术可能会导致信号中出现一些不连续的点。

因此，该技术更适用于信号中的高频噪声。

除了上述函数之外，Matlab中还有许多其他小波去噪函数，例如wpdencmp和modwpt。

这些函数可以帮助用户根据不同的需求进行去噪，并且可以通过设置参数来调整去噪的效果。

在使用小波去噪函数进行处理之前，用户需要了解信号或图像的特征，例如信号的频率和振幅，以及图像的亮度和对比度。

这可以帮助用户选择合适的小波去噪函数，并设置合适的参数来最大程度地减少噪声，同时保留信号或图像中的重要信息。

Matlab提供了许多小波去噪函数，可以帮助用户快速准确地处理信号和图像中的噪声。

在使用这些函数进行处理之前，用户需要了解信号或图像的特征，并选择合适的函数和参数来实现最佳的去噪效果。

基于 Matlab 实现小波阈值去噪的图像处理方法张天祥;黄小欣【摘要】概述了小波阈值去噪的基本原理，对基于 Matlab 的小波去噪函数进行了简介，并就其中的主要工作进行了详细阐述。

此外结合理论分析，进行了基于Matlab 的小波阈值去噪处理仿真实验。

为实际的图像处理过程中，小波阈值去噪方法的选择和改进提供了数据参考和依据。

%This paper summarizes the basic principles of the wavelet threshold denoising,introduces Matlab⁃based wavelet denoising function,and elaborates main tasks of wavelet threshold denoising. In addition,combined with theoretical analysis, Matlab⁃based wavelet threshold denoising processing is simulated. The paper serves as a data reference and basis for the selec⁃tion and improvement of wavelet threshold denoising method in actual image processing.【期刊名称】《现代电子技术》【年(卷),期】2013(000)005【总页数】3页(P103-105)【关键词】小波变换;图像去噪;阈值;Matlab【作者】张天祥;黄小欣【作者单位】河南省民政学校，河南郑州 450002;河南省民政学校，河南郑州450002【正文语种】中文【中图分类】TN911.73-34在产生和传输过程中数字图像会被各种噪声干扰和影响，如电子器件干扰、传感器振荡、高磁场干扰等，导致数字图像在经转换后质量有所下降，对图像的后续处理，如分割、压缩和图像理解等将造成不利的影响[1]。