最新波浪荷载计算汇总
- 格式:doc
- 大小:298.00 KB
- 文档页数:16

关于波浪超高的计算
波浪的超高对于外海建筑物的结构,标高,外力等都有很大影响.我国海港水文规范波浪对桩柱作用一节中对于静水面以上的波峰高度ηmax 的数值可以查图计算,则波浪的超高△h 可以借用△h=ηmax-H/2来计算.但波峰高度的ηmax 的图是由斯托克斯二阶波理论和椭余波理论的平均值绘制的,在实际计算中,对于有些坡偏大.有些波偏小.例如当H/d=0.3时,Ah/H 的值用椭余波理论计算的则比用规范上的ηmax 图表计算出来的大0.04,假如波面高为7m,则△h 相差28cm,显然误差太大了.我们认为用ηmax 图表计算超两是不科学的,应该按不同波浪要素对应的波浪理论来计算波浪的超高.。

波浪力的计算需要两方面理论的支持:波浪运动理论及波浪荷载计算理论。
前者研究波浪的运动,后者在已知波浪运动的前提下计算波浪对水中物体的作用。
几种常用的波浪普: 1.P-M 谱Pierson 和Moskowitz适用于无限风速发在的波浪普。
国际船模水池会议(ITTC)推荐采用这一形式的波,故也称为ITTC波谱。
JONSWAP(Joint north sea wave project).是一种频谱。
3.应力范围的长期分布模型:1.离散型模型,2.分段连续型模型,3.连续模型。
1. 离散模型:用Hs作为波高,Tz为波浪周期,定义一个余弦波。
然后用规则波理论计算作用在结构上的波浪力。
并用准静定的方法计算结构呢I的应力。
缺陷:没有将波浪作为一个随机过程来处理。
每一海况的应力范围只有一个确的数值。
因此又称为确定性模型。
2.分段连续型模型每一短期海况中,交变应力过程是一个均值为0的平稳正态过程。
综合所有海况中应力范围的短期分布,并得出各个海况出现的疲劳,就得到应力范围的长期分布,它的形式是分段连续的。
应力范围的两种短期分布模型:1.Rayleigh分布和Rice分布。
在某一海况中交变应力均值为。
应力峰值服从Rayleigh分布。
通过计算得出应力范围也服从Rayleigh分布。
3.在船舶及海洋工程结构疲劳可靠性分析中,希望应力范围的长期分布能用一个连续的分布函数来描述。
这就是应力范围长期分布的连续模型.最常用的就是Weibull分布。
4.有义波高:(significant wave height)所有波浪中波高最大的三分之一波浪的平均高度。
用Hs表示。
5.Stokes五阶波给出了波陡的量度(H/L)H/L越大,波就越陡。
当波高与波长的比值大到一定程度时,波会破碎。
6.波速=波长与频率的乘积 C=λ/T或者C=λf,其中f是频率。
或者T=2π/ω7.圆频率1.圆频率即2π秒内振动的次数,又叫角频率,和角速度的ω没有任何关系。

6.4 桥梁上部结构波浪力荷载效应计算理论6.4.1 波浪对桥面板的上托力根据流体力学理论,可得出小振幅浅水长波对静水面上波平板的理论解答。
作用在每延米平板宽度上的最大上托力为(肖小铃,2009):12zo F γ= (6.25) 式中:δ=πl /L , H 为相对波高,m ;L 为波长,m ;l 为平板在沿波浪传播方向的长度,m ;γ为水的重度,kN/m 3。
模型试验中实测的压力过程线表明,平板下除了作用有强度变化较慢的静压力以外,在波峰刚接触到平板时尚存在着历时很短(0.02~0.1 s )的冲击压力。
发生冲击压力的原因可解释为波浪遇到平板时波浪垂向动量的突然变化。
根据多家模型试验的结果,可认为冲击压强的最大值P imax ≤2γH 。
此外,国内外试验表明,当水位超过面板时,即当h 为负值时,波浪上托力将比h =0时要小。
在工程设计时,除需知道作用在桥面板底面的波浪上托力总值F zo 以及最大冲击压强P imax 外,还应知道波浪上托压力的分布图形。
根据有关模型试验的成果,可作如下规定:1)计算桥面板下的波浪上托力时,仍可以原始入射波浪要素作为依据;2)波形采用2阶有限振幅波,即式(6.22)所表示的波形;3)用原始波形计算出桥面板下各点的静水浮力,再乘压力反应系数,即为所需的波浪上托压力。
当波形已知后,静水面以上h 处桥面板底面上的静水浮力即为γ(η-h )。
考虑压力反应系数β后,可得该点波浪上托力的压强P =βγ(η-h )。
通常,当面板的λ在10 m 以下且面板与岸坡不相连时,可取β=1.5;当面板宽度较大或面板与岸坡相连时,可取β=2.0(交通部第一航务工程勘察设计院,1975)。
虽然近年来南京水利科学研究院提出了新的试验研究成果,但仍仅限于最大冲击压强P imax 和作用在水平板上的波浪上托力总值F zo ,而无波浪上托力分布图形,因此并不适用于计算底面为曲线的桥面板的波浪上托压力的分布情况。

海堤波浪越浪量常用计算方法评述
波浪越浪量是指码头堤坝上海堤护坡及防护墙所承受的波浪冲击力强度的一种参数,它是指浪高、浪周期和浪能量之间的函数关系。
常用的计算方法有Morison力法、Basson-Haig-Weinschenk(BHW)解析法、Tanimoto简化法和系数法等。
Morison力法是全球海洋工程中最常用的一种方法,它基于摩里森公式,将波浪越浪量转化为护坡及防护墙所承受的拉力、推力和弯矩。
它假定波浪在护坡及防护墙的受力方向是垂直的,在计算时可以简化波浪的长度及流速。
BHW解析法是根据Basson-Haig-Weinschenk(BHW)理论建立的一种计算方法,它假设码头及防护墙是沿着波浪的特性进行横剖面的,并建立了完整的护坡及护墙设计和分析体系。
它可以准确地计算出护坡及防护墙在越浪损坏环境下所受到的冲击力,因此,它在工程设计中应用较多。
Tanimoto简化法是基于Tanimoto简化法,将波浪越浪量的计算转化为护坡及防护墙所承受的拉力、推力和弯矩。
它假设码头及防护墙沿着波浪的特性进行横向剖面剖分,并结合Morison力计算护坡及护墙所承受的冲击力。
系数法是基于海浪、波浪谱和其他参数,将海浪能量和波浪谱转化为波浪越浪量的一种计算方法。
它一般使用简单的海浪能量计算,可以。

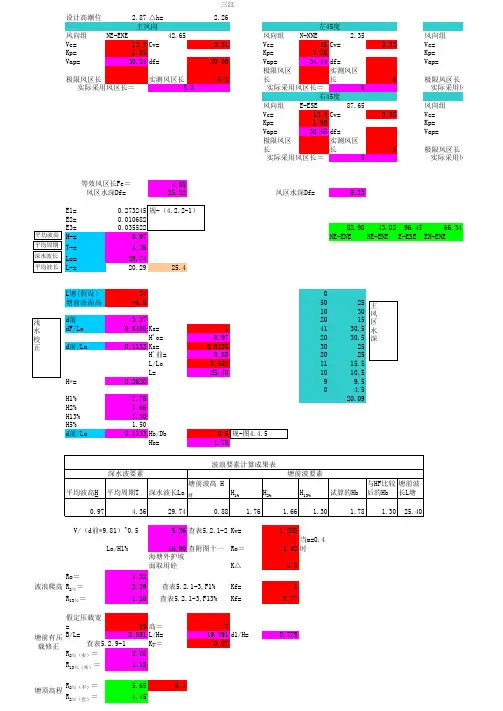
设计高潮位2.87△h= 2.26风向组NE-ENE 42.65风向组N-NNE 2.35风向组Vc=13.3Cv=0.31Vc=15Cv=0.32Vc=Kp= 1.85Kp= 1.88Kp=Vap=30.24df=20.09Vap=34.44df=Vap=极限风区长实测风区长5.2极限风区长实测风区长6极限风区长风向组E-ESE 87.65风向组Vc=12.5Cv=0.35Vc=Kp= 1.99Kp=Vap=30.55df=Vap=极限风区长实测风区长5极限风区长L塘(假设)240塘前涂面高-0.550251030d前 3.372015dF/Lo 0.8480Ks=14130.5H'o=0.972030.5d前/Lo0.1133Ks=0.91353025H'前=0.882025L/Lo 0.8541115.5L=25.401010.5H*=0.262099.504.5H1% 1.7620.09H2% 1.66H13% 1.30H5% 1.50d前/Lo0.1133Hb/DbHb=5.26查表5.2.1-2Kv= 1.285Lo/H1%16.90查附图十一Ro= 1.32当m=0.4时海塘外护坡面取用砼K△0.8Ro=1.32R 2%=2.39Kf=1R 13%=1.36Kf=0.77假定压载宽=15高=2B/L=0.591L/H=19.491d1/H=0.779Ky=0.87R 2%(实)=2.08R 13%(实)=1.18R 2%(不)= 5.65 6.1R 2%(允)=4.451.15T L=25.40H塘/d前0.3H塘/L塘0.0348A=0.0132B=27.429查表5.2.1-3,F1%查表5.2.1-3,F13%三江查表5.2.9-1塘前有压载修正塘顶高程查表6.2.2无风越浪实际采用风区长=主风向左45度5.2实际采用风区长=波浪爬高V/(d前*9.81)^0.56实际采用风区右45度实际采用风区长=5实际采用风区越顶水量q=0.00032Hc=3.23Wf=2θ=68.1986K'= 5.590越顶水量q=0.0018风速大于26.8有风越浪N-NNE 12.65风向组N-NNE 27.6515Cv=0.33Vc=15Cv=0.331.92Kp= 1.9235.15df=Vap=35.15df=实测风区长5.25极限风区长实测风区长 5.25NE-ENE 72.65风向组NE-ENE 57.6513.5Cv=0.3Vc=13.3Cv=0.31.82Kp= 1.8230.20df=Vap=29.77df=实测风区长6极限风区长实测风区长65.13180S-SSW实际采用风区长=6左15度实际采用风区长= 5.25左30度 5.25用风区长=风区水深Df=右30度右15度用风区长=6。

最新5风荷载计算汇总风荷载计算是结构设计过程中的重要内容之一,其目的是为了确定建筑物或结构物所需承受的风荷载,通过对风荷载的准确计算,可以保证建筑物或结构物的安全性和可靠性。
本文将汇总最新的5种风荷载计算方法,包括基于地表粗糙度参数的方法、数值风洞模拟的方法、统计模型的方法、模拟风场的方法以及随机信号分析的方法。
一、基于地表粗糙度参数的风荷载计算方法基于地表粗糙度参数的风荷载计算方法是基于平均最大风速和风速分布的理论模型,通过对地表粗糙度参数的确定,将风速转换为风荷载。
该方法适用于中低层建筑物和结构物的风荷载计算,适用范围广泛。
但是,该方法忽略了建筑物的形状和结构对风荷载的影响,计算结果存在一定的局限性。
二、数值风洞模拟的风荷载计算方法数值风洞模拟是通过计算流体力学方法对建筑物周围风场进行数值模拟,再根据数值模拟结果确定风荷载。
该方法考虑了建筑物的形状和结构对风荷载的影响,计算结果较为准确。
但是,该方法计算复杂、耗时较长,需要依靠计算机软件进行模拟。
三、统计模型的风荷载计算方法统计模型是通过对历史风速数据的统计分析,建立随机模型来确定风荷载。
该方法适用于大范围的结构群风荷载计算,如城市中的建筑群。
通过统计模型,可以根据地理位置、气象条件等因素确定风荷载的概率分布特性。
但是,该方法需要大量的历史数据支持,对数据的要求较高。
四、模拟风场的风荷载计算方法模拟风场是通过对大气环境的数值模拟,确定不同高度处的风速分布情况,再通过建筑物的形状和结构对风速进行修正,最终确定风荷载。
该方法综合考虑了大气环境、建筑物形状和结构对风荷载的影响,计算结果较为准确。
但是,该方法需要大量的计算资源和模型验证。
五、随机信号分析的风荷载计算方法随机信号分析是通过对风速时间序列进行傅里叶变换,得到不同频率下的风荷载谱,再综合考虑频率分布特性和风速相关特性,确定风荷载。
该方法适用于建筑物和结构物的动力响应分析,可以考虑结构的共振效应。
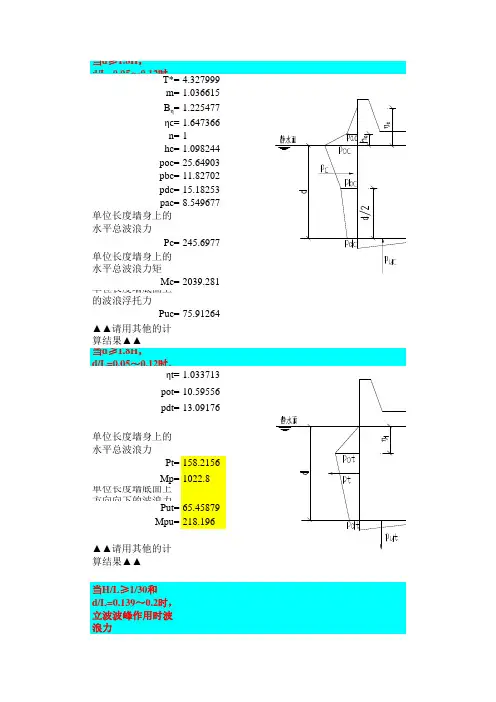


大尺度桩柱波浪力计算一览表大尺度桩柱波浪力1、极端高水位水深d = -(底面高程) + 极端高水位=+=m波长L =ma 、胸墙, 折算半径D 为:4**m D / L=/=查表惯性力系数 C M =Z 1 =+=m H / d=/=查表ηmax / H=ωt=270oZ 2 =d+ηmax-H/2=+*=m ⑴、最大总波浪力 P 、最大总波浪力矩 M max**sh()-sh()ch()-=***KN·M 29.610.13 6.96.90.3481=8914.13045.7126.929.61886.9025.0 4.6125.00.0015.052π880.17129.610.23320.6325.002.1141=1.9510.25sh=sh-88.088.0= 4.3586 2.89594.202= 2.1782 1.785126.96.9*ch2π*29.6188.02π*25.00=1.954π88.0*0.0727=0.348115.052 1.95mKN30.51=(14.0012.71)1/2=2π(-)ch()=P max =P Imax =M max =M Imax=群墩系数 K x 和附着生物修正系数 nP max ==**=M max ==**=⑵、考虑波浪浮托力作用由于两者结合紧密,故不考虑浮托力作用。
b 、整体, 折算半径D 为:4**m D / L=/=查表惯性力系数 C M =Z 1 =m⑴、计算沉箱部分的最大总波浪力 P max 、最大总波浪力矩 M max取 Z =m**sh()-sh()ch()-=0.0025.000.6892ch2π**sh88.0-1.785 2.1141= 2.895904.20288.0=KN0.6892==1.9610.25126.926.9=0=12.1141=ch2π*29.6188.014.47688 1.968914.1KNKN·M 3045.7KN KN·M11.158914.12π*2.178288.05.51-(ch = 4.20161[-(ch(0.0727(4.4718-0.3932* 4.3586-)]))-ch-ch( 1.785)88.0) 2.178288.088.0)]25.0030.5130.512π*=(12.9512.712π*88.0sh([)1/2=14.476m3.0637]1.153045.73502.60.164529.6188.00.00102516061sh2π*1KnP max KnM max π***2π(-)ch()=P max =P Imax =M max =M Imax=群墩系数 K x 和附着生物修正系数 nP max ==**=M max ==**=⑵、整体的最大总波浪力 P max 、最大总波浪力矩 M maxP max =沉箱Pmax + 胸墙 Pmax =+=M max =沉箱Mmax + 胸墙换算 Mmax=+ (/+)*=⑶、考虑波浪浮托力作用浮托力浮托力矩ωt=o z =mD / L=/=f 0 =f 1 =f 2 =f 3 =**2ch(/)ch(/)*[sin()-cos()]=**3ch(/)ch(/)*[sin()+cos()]27010473KN 104686102513502.625.003502.6104686KN·M)]1.156061(3.0637-1.785=[ 1.785*14.2016=1[2π*25.00sh(=ch2π*29.6188.0-(88.02π*KnM max KnP max 1125.00-)6970.12.8959KN·M -ch2π*3502.6910316970.1KN )]88.02025011.15KN·M9103188.02.114188.0=1.96126.9ch ]0.0088.025.002π*0.7391))1(ch( 1.785)-ch(-KN·M6.988.0*0.73914π=91031270*[1.32270-0.25](0.000)-1.32-0.000.3614.47629.61-0.251.45880.164514.4761.32KN P u =10.25 6.946061880.0088*2π*2π*KN 0.36=3705.4*14.2016-116414.476*1.45270M u =10.25 6.927088322π*29.61882π*0.00=P max =M max =2、设计高水位水深d = -(底面高程) + 设计高水位=+=m波长L =ma 、胸墙, 折算半径D 为:4**m D / L=/=查表惯性力系数 C M =Z 1 =+=m H / d=/=查表ηmax / H=ωt=270oZ 2 =d+ηmax-H/2=+*=m ⑴、最大总波浪力 P max 、最大总波浪力矩 M max**sh()-sh()ch()-=***2π(-)ch()π15.052 1.94850.17710.640.14 6.929.488514.00+KN-574.5KN·M *[(0.000)m15.052]-0.36)1/2KN·M12.71=6705.2*14.201625.00.0025.0025.0 3.5128.51=1.9410.25126.9==(6.9028.510.242=2641.428.51KN26.9*0.3035-sh2π*=sh1.8482.107525.0085.085.0ch2π*28.5185.0= 4.3615 3.09484.174= 2.1789=1.94126.94π0.3035=6225.3KN·M 6.985.0*0.0529=ch2π*28.5185.029.4885.085.0)]85.085.029.48-ch2π*2π*=1[2π*2.107525.00-(ch 4.48sh( 2.1789)85.0=P max =P Imax =M max =M Imax=群墩系数 K x 和附着生物修正系数 nP max ==**=M max ==**=⑵、考虑波浪浮托力作用由于两者结合紧密,故不考虑浮托力作用。
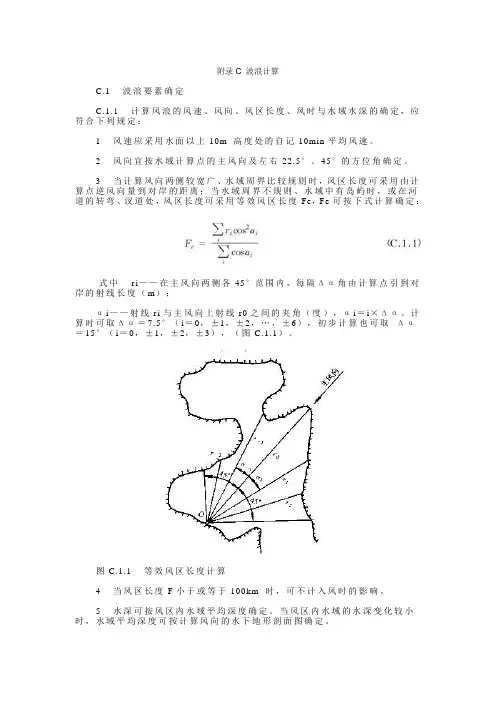
附录C 波浪计算C.1 波浪要素确定C.1.1 计算风浪的风速、风向、风区长度、风时与水域水深的确定,应符合下列规定:1 风速应采用水面以上10m 高度处的自记10min平均风速。
2 风向宜按水域计算点的主风向及左右22.5°、45°的方位角确定。
3 当计算风向两侧较宽广、水域周界比较规则时,风区长度可采用由计算点逆风向量到对岸的距离;当水域周界不规则、水域中有岛屿时,或在河道的转弯、汊道处,风区长度可采用等效风区长度Fe,Fe可按下式计算确定:式中ri——在主风向两侧各45°范围内,每隔Δα角由计算点引到对岸的射线长度(m);αi——射线ri与主风向上射线r0之间的夹角(度),αi=i×Δα。
计算时可取Δα=7.5°(i=0,±1,±2,…,±6),初步计算也可取Δα=15°(i=0,±1,±2,±3),(图C.1.1)。
图C.1.1 等效风区长度计算4 当风区长度F小于或等于100km 时,可不计入风时的影响。
5 水深可按风区内水域平均深度确定。
当风区内水域的水深变化较小时,水域平均深度可按计算风向的水下地形剖面图确定。
C.1.2 风浪要素可按下列公式计算确定:式中——平均波高(m);——平均波周期(s);V——计算风速(m/s);F——风区长度(m);d——水域的平均水深(m);g——重力加速度(9.81m/s2);tmin——风浪达到稳定状态的最小风时(s)。
C.1.3 不规则波的不同累积频率波高Hp与平均图C.1.1 等效风区长度计算波高之比值Hp/可按表C.1.3-1确定。
表C.1.3.1 不同累积频率波高换算不规则波的波周期可采用平均波周期表示,按平均波周期计算的波长L 可按下式计算,也可直接按表C.1.3-2确定。
表C.1.3.2 波长~周期~水深关系表L=f(T,d)续表 C.1.3.2C.1.4 设计波浪推算应符合下列规定:1 对河、湖堤防,设计波浪要素可采用风速推算的方法,并按本附录第C.1.2条计算确定。
浪压力计算书浪压力计算书项目名称_____________日期_____________设计者_____________校对者_____________一、基本设计资料1.依据规范及参考书目:《混凝土重力坝设计规范》(SL319-2005)《水闸设计规范》(SL265-2001)《水工建筑物荷载设计规范》(DL5077-1997)2.计算参数:建筑物位置类型:平原滨海地区计算采用的波列累积频率P = 10%迎水面前水深H = 10.800 m风区内水域平均水深H m = 10.800 m风区长度D = 530.000 m浪压力参与荷载组合类型:基本组合重现期为50年的年最大风速v o = 20.000 m/s风速的测量高度H c = 10.000 m迎水面前水域的底坡i = 1 : 1000.0二、计算依据按莆田实验站公式计算出平均波高h m(m)、平均波周期T m (s):g×h m/v o2=0.13×tanh[0.7×(g×H m/v o2)0.7]×tanh{0.0018×(g×D/v o2)0.45/[0.13×tanh(0.7×(g×H m/v o2)0.7)]}g×T m/v o=13.9×(g×h m/v o2)0.5式中:h m——平均波高(m);T m——平均波周期(s);v o——计算风速(m/s);D ——风区长度(m);H m——水域平均水深(m);g ——重力加速度,取9.81m/s2;平均波长与平均周期的关系:L m=g×T m2/2/π×tanh(2πH/L m)三、计算过程1.波长、波高计算:当浪压力参与荷载基本组合时,计算风速采用重现期为50年的年最大风速;当风速测量高度hc=10.00时,依据《混凝土重力坝设计规范》表B.6.2-1查得:风速高度修正系数Kz=1.000,计算风速vo=1.000×20.00=20.000 m/s 依据上述公式算得:平均波长L m=7.070 m,平均波高h m=0.231 m当h m/H m=0.231/10.800=0.021时,依据《混凝土重力坝设计规范》表B.6.3-1查得:h p/h m=1.697,h p=1.697×h m=1.697×0.231=0.392 m2.浪压力、弯矩计算:波浪中心线至计算水位的高度hz(m):hz=πh p2/L m×tanh-1(2πH/L m)hz=3.14×0.392/7.070×tanh-1(2×3.14×10.800/7.070)=0.068 m使波浪破碎的临界水深H cr(m):H cr=L m/4/×ln[(L m+2πh p)/(L m-2πh p)]H cr=7.070/4/×ln[(7.070+2×3.14×0.392)/(7.070-2×3.14×0.392)]=0.409 m当H=10.800≥H cr=0.409和H=10.800≥Lm/2=7.070/2时:浪压力在计算水位以下呈三角形分布,顶点位置压强p max =4.068 kPa计算高度hs=0.000m以上部分浪压力p=8.125kN/m,弯矩M =79.426kN·m/m计算高度hs=0.000m以上部分浪压力作用点与计算截面高差为9.775m。
fp mp计算公式FP MP计算公式是指计算风力系数(FP)和波浪系数(MP)的公式。
在工程中,FP MP计算公式被广泛应用于建筑物、桥梁、港口等结构的设计与施工中。
本文将介绍FP MP计算公式的原理和应用,并探讨其在工程实践中的重要性。
我们来了解一下FP MP计算公式的背景。
风力和波浪是海洋环境中两个重要的力量,它们对于海洋结构的设计和安全性具有重要影响。
FP MP计算公式的目的就是通过计算风力系数和波浪系数,来评估海洋结构受到的风力和波浪荷载。
风力系数(FP)是指风对于建筑物或其他结构物产生的力与动力压力之间的比值。
它的计算需要考虑多个因素,包括风速、风向、建筑物形状等。
一般来说,FP的计算公式可以分为两类:经验公式和数值模拟公式。
经验公式是通过实际观测数据和经验法则总结出来的,它们适用于一些简单的建筑物或常见的风场条件。
而数值模拟公式则是通过计算流体力学方法,模拟风场和建筑物之间的相互作用,得出FP的数值。
数值模拟公式更加精确,适用于复杂的建筑物和复杂的风场条件。
波浪系数(MP)是指波浪对于建筑物或其他结构物产生的力与波浪动力压力之间的比值。
与FP类似,MP的计算也需要考虑多个因素,包括波高、波长、波浪周期等。
波浪系数的计算同样可以使用经验公式和数值模拟公式。
经验公式适用于一些简单的波浪条件,而数值模拟公式适用于复杂的波浪条件。
在工程实践中,通过计算FP和MP,可以评估建筑物或其他结构物在风力和波浪作用下的受力情况。
这对于结构的设计和安全性评估非常重要。
通过合理选择FP MP计算公式,并根据具体的工程条件进行计算,可以避免结构受到过大的风力和波浪荷载,从而保证结构的安全性。
在使用FP MP计算公式时,还需要注意一些细节。
首先,计算公式的输入参数需要准确可靠,包括风速、波高等。
其次,计算过程中需要考虑不同因素的相互影响,例如风对波浪的影响。
最后,计算结果应该与实际情况进行比对,以验证计算的准确性。
静水面标高:2.28m (极端高水位);泥面标高:-10m ;桩顶标高:4.6m ;水深d :12.28m ;波高H :2.3m (极端高水位波高);波长L :123m (极端高水位波长);桩径:0.53m ;钢管桩断面积:0.22m²;速度力系数C D =1.2;惯性力系数C M =2;水的重度γ=10.25kN/m 。
波浪荷载计算经计算,H/d=2.3/12.28= 0.187<0.2,d/L=12.28/120=0.1<0.2,符合《海港水文规范》8.3.2.2及8.3.2.3条件s 规定。
根据规范8.3.2.1条,H/d=2.3/12.28=0.187,ηmax/H ≈0.62,即ηmax 约为1.43。
波浪荷载先按规范8.3.2.1条以下公式计算:(1) 波浪力速度分力212max K DH C P D D γ= 钢管桩高度断面相同,Z 1=0,Z 2= d +ηmax =12.28+1.43=13.71m 。
25.067.180-9.10-.4112328.124sh 80-12371.134sh 12304-12371.1344sh 84sh -4sh 4-412121=⨯+=⨯⨯+⨯⨯=⨯⨯⨯+⨯⨯=πππππππππL d L Z L Z L Z L Z K 钢管桩kN K DH C P D 31.4225.03.253.025.102.12212D max =⨯⨯⨯⨯==γ (2) 波浪力惯性分力22Im AHK C P M ax γ= 根据规范8.3.2.1节第(4)条,Z 1=0,Z 2= d +ηmax -H/2=12.28+1.43-2.3/2=12.56m582.0213.10706.012028.12212002sh 12056.12222sh 2122=+=⨯⨯+⨯=⨯⨯+⨯=ππππch sh L d ch L Z L Z shK ππ 22Im AHK C P M ax γ= 钢管桩kN AHK C P M ax 32582.03.222.025.10222Im =⨯⨯⨯⨯==γ根据《海港水文规范》图8.3.2.8、图8.3.2.9及图8.3.210,及H/d= 0.187,d/L=0.1,查表知35.1=α;42.1=β;25.1=p γ;4.1=M γ又根据《海港水文规范》8.3.2.2和8.3.2.3条,kN P D 82.531.435.1max =⨯=;kN P ax 75.3325.1Im =⨯=所以,kN P kN P ax D 875.15.082.5Im max =>=根据《海港水文规范》8.3.4条第(2)条,取正向水平最大总波浪力为kN P P P P D i D 42.6)82.575.325.01(82.5)25.01(22max 2max 2max max =⨯+⨯=+=。
桩基结构物波浪力的工程计算方法桩基结构物在海洋工程中具有举足轻重的地位,而波浪力是影响桩基结构物稳定性和安全性的关键因素之一。
因此,对桩基结构物波浪力的工程计算方法进行研究,对保障海洋工程的安全性和稳定性具有重要意义。
本文将围绕桩基结构物波浪力的工程计算方法展开讨论,旨在明确计算方法及其在实际工程中的应用。
桩基结构物波浪力是指海洋工程中桩基结构物受到海浪作用产生的力。
这种力的产生主要源于海浪的冲击力、海流力和重力等多种因素。
波浪力的计算公式通常根据物理力学原理进行推导,是桩基结构设计中的重要参数。
在实际工程中,波浪力的计算方法大致可分为经验法和理论法两类。
经验法主要依据实际工程数据进行拟合计算,而理论法则是基于物理力学理论进行计算。
有限元法是一种常用的数值计算方法,适用于各种复杂的工程问题。
在桩基结构物波浪力的计算中,有限元法可以将桩基和周围介质视为离散的单元体,通过对单元体进行力学分析,得到每个单元体上的力与位移关系,最终得到整个结构的应力与变形。
模拟法是通过计算机模拟海浪对桩基结构物的作用过程,从而得到结构物所受的波浪力。
这种方法需要建立海浪模型和桩基结构物模型,通过设定不同的海浪条件和结构物参数,进行大量模拟计算,最终得到不同条件下的波浪力。
为了说明上述计算方法的有效性和可行性,我们选取了一个实际案例进行详细的分析和验证。
该案例为某海上风电场桩基结构物,基础形式为单桩基础。
我们运用有限元法对该结构物进行了建模,并对其在不同海浪条件下的波浪力进行了模拟计算。
计算结果表明,在相同的海浪条件下,有限元法与模拟法得到的波浪力结果相近,证明了这两种计算方法的可靠性。
同时,通过对比分析,我们发现有限元法在处理复杂边界条件和多因素耦合问题上具有更大的优势。
本文对桩基结构物波浪力的工程计算方法进行了系统的探讨,分别介绍了经验法和理论法两种计算思路,并详细推导了其中的公式和理论。
通过实例分析和验证,说明这些方法在计算桩基结构物波浪力上的有效性和可行性。
仅供学习与交流 收集于网络,如有侵权请联系管理员删除 整理后: 波浪荷载的计算理论
波浪是发生在海洋表面的一种波动现象,其波动性质因受浅水区域海底地形影响和水深的变浅,发生波浪破碎现象,成为影响海岸侵蚀和变形以及海岸带污染物迁移与扩散的最主要的水动力环境之一。破浪破碎与冲击现象对海上工程设施的安全也十分重要。由于波浪破碎及冲击作用的机理极其复杂,至今仍然是海岸工程领域没有解决的困难课题之一。因此,开展近海波浪破碎与冲击过程数值模型的研究,就有着重要的理论意义和工程意义。 波浪荷载,也称波浪力,是波浪对港口码头和海洋平台等结构所产生的作用。目前按绕射理论进行分析。波浪对结构物的作用由四部分组成:水流粘性所引起的摩阻力(与水质点速度平方成正比);不恒定水流的惯性或结构物在水流中作变速运动所产生的附加质量力(与波浪中水质点加速度成正比);结构物的存在对入射波浪流动场的辐射作用所产生的压力和结构物运动对入射波浪流动场的辐射作用所引起的压力。包括上述全部作用影响的波浪力理论称为绕射理论。在目前实际工作中,常用只考虑了结构受到波浪摩阻力和质量力影响的半经验半理论的莫里森(Mrison)方程分析波浪力。波浪荷载是由波浪水质点与结构间的相对运动所引起的。波浪是一随机性运动,很难在数学上精确描述。当结构构件(部件)的直径小于波长的20%时,波浪荷载的计算通常用半经验半理论的美国莫里森方程;大于波长的20%时,应考虑结构对入射波场的影响,考虑入射波的绕射,计算时用绕射理论求解。影响波浪荷载大小的因素很多,如波高、波浪周期、水深、结构尺寸和形状、群桩的相互干扰和遮蔽作用以及海生物附着等。 波浪荷载常用特征波法和谱分析法确定。对一些特殊形状或特别重要的海洋仅供学习与交流 收集于网络,如有侵权请联系管理员删除 工程结构,除了用上述的方法进行计算分析外,还应进行物理模型试验,以确定波浪力。 ① 特征波法。 选用某一特征波作为单一的规则波,并以它的参数(有效波高、波浪周期、水深)和结构的有关尺寸代入莫里森方程或绕射理论的公式,求出作用在结构上的波浪力。此法简便易行,在海洋工程设计广泛应用。 ② 谱分析法。利用海浪谱进行波浪荷载计算、结构疲劳和动力响应分析的一种方法。把波浪作为随机性的、由许多不同波高和波周期的规则波线性迭加而成的不规则波,用概率论和数理统计的方法收集、分析处理波浪观测数据,由于它能较精确地反映波浪的能量分布规律,所以是一种比较理想的方法。海洋工程结构设计中常用的有P-M和联合(JONSWAP)谱。波力谱确定后,可求出波浪力分布函数中的统计特征值,进而得到某一累积概率的波浪力。 由于波浪具有明显的随机性,难用确定的函数表达,故在波浪的研究中常采用多个或无限个振幅、频率、方向、位相不同的简单波的叠加,并规定组成波的振幅或相位是随机量,从而叠加的结果为随机函数,以反映波浪的随机性。实践证明这种方法是可行的,它以成为研究波浪要素的统计特性的分布来描述它,另一是用波浪要素的“谱”来表征其内部的频率结构。当然,波浪外观上表现出来的性质和它的内部结构是有联系的。 水库波浪在风里直接作用下产生的运动,表面十分复杂,在统计过程中是把波浪当作准稳定的随即过程来处理,每次测量时间为10-5小时。如果观测是段短、波数少时,为了提高精度,可父子俩偏差大的缺点,也可将各组中每种波的出现概率进行加权统计。左图是根据1966、1967年密云水库和还有那个水库仅供学习与交流 收集于网络,如有侵权请联系管理员删除 的原形观测资料绘出的波高小于H的概率曲线,它与三元海浪概率分布的克雷洛夫共识甚为符合(即图上所示公式)。 波浪荷载作用下土体的动力特性:在波浪荷载作用下,海床中的土单元也受到一系列循环荷载作用. 在某一时刻,当波峰作用在所研究的土单元正上方,则会产生正的竖向压力;当波谷作用在其上时,则产生负的竖向压力. 这样,在一个波长距离的波作用下,产生的应力是由三轴应力作用的圆形轨迹. 在波高为零的瞬时,波作用在土单元上,产生水平剪应力并引起单剪模式的应变,这一水平剪应力分量也随着波的传播而改变其方向,引起剪应力的另一类型的循环交替. 值得注意的是,上述两种循环剪应力是交替作用而不是同时作用的. 三轴试验的剪切模式所产生的循环应力与单剪模式的水平剪应力相位差为90°. 因此,由波浪荷载产生的作用在海床土体的循环应力是沿主应力方向连续旋转的,其应力交替的性状可由图2 (b) 中的τvh与(σv - σh) / 2 之间的圆形关系来表示.
实例分析:直立浮式截圆柱柱群的绕射问题 假设流体为不可压、无粘性、均匀的理想流体,流场中运动处处无旋。对静止于水深为d的水域中的N个相同吃水h、半径a的柱体,坐标系统如图1,单个柱体的圆心Oj坐标为(xoj,yoj,z)(j=1,…,N),建立局部的柱坐标系(γj,θj,z)。这样第k个柱体中心Ok相对于j柱局部坐标系有(Rjk,θjk,z)极坐标,(j,k=1,2,…,N)。入射波采用线性微幅波理论。 仅供学习与交流 收集于网络,如有侵权请联系管理员删除 1 坐标系统 为了将每个单元柱体的不同散射波成分迭加并计入柱间水动力干扰,引入大间距假设,即认为柱间距Rjk,j,k=1,2,……,N与入射波波长相比足够大,k0Rjk1。这样由柱群中任一圆柱在入射波作用下产生的绕射波对其它圆柱的作用可近似为非平面修正的等效平面波,即改进平面波法。
对每一个柱体而言,其速度势中的未知系数与其编号无关,即决定未知系数的方程对每一个柱体都是相同的。因此,柱群情况下只需考虑第j柱附近的速度势即可。
对于第j柱,传播方向与x轴正向夹角为β的线性规则波速度势Φj2I
可记为:
(1) 式中,A为入射波波幅(m),ω为入射波频率(s-1);Jm(x)为第一类m仅供学习与交流 收集于网络,如有侵权请联系管理员删除 阶Bessel函数,εm为Neumann常数,且ε0=1,εm=2(m≥1);k0为波数,应满足色散关系:ω2=gk0thk0d。
PHj=exp{i(k0xjcos β+k0yjsin β)}为相位项。对应第j柱的内、外域速度势应有:
(2) (3) 由入射波速度势Φj2I引起的第j柱的绕射速度势Φj2s为:
(4) 式中,
考虑另一个柱体k,半径亦为a,到j柱的距离为Rjk。由第j柱入射波引起的第k柱绕射势为: 仅供学习与交流 收集于网络,如有侵权请联系管理员删除 (5) 式中:
代表了等效平面波幅:
(6) 为非平面波修正项,其中:
这样对N(N>2)个柱体所组成的群柱中,外部入射波在第j柱的入射势仍如(1)式。与上述二柱情形类似可得,由其他N-1个柱的绕射波在j柱产生的等效平面入射波势Φj2I1:
(7) 仅供学习与交流
收集于网络,如有侵权请联系管理员删除 对于j柱,等效平面入射波的一阶非平面修正项包含两部分:对其它N-1个柱体外部入射波的绕射波的修正;其它柱体的绕射波在j柱的反射后的等效平面波修正。
(8) 由于等效平面波幅Cjk包含两部分:k柱对外部入射波引起的绕射;由其它柱绕射波引起在k柱的二次绕射,这样得:
(9) 式中,j,k=1,2,…,N,j≠k。由(9)式可确定未知的等效平面波幅Cjk。 确定了流场速度势Φi(i=1,2),可由伯努利方程确定流场中任一点压力:
(10) 这样沿湿表面上积分可得波浪对直立浮式柱群的q模态线性干扰力或力矩: 仅供学习与交流
收集于网络,如有侵权请联系管理员删除 (11) 其中:q=1,…,6,分别对应纵荡、横荡、垂荡、横摇、纵摇和首摇等运动模态。
3 数值计算结果分析 本文应用上述理论和方法计算了不同波长、波频情况下两根直立浮式圆柱群的波浪荷载,并与现有的文献结果进行了比较,取得了良好的一致。图中圆柱横截面半径a=10m,柱吃水h=5m,水深d=100m,波幅A=1m,ρ为海水密度,g为重力加速度,k0为波数,ω(s-1)为入射波频率,两柱间距用R表示。图中箭头(→)表示入射波的方向,①表示前柱,②表示后柱。图中的点号(。)和叉号(×)分别表示相应状态下由A N Williams & Z Demirbilek计算所得的双柱的波浪力[6]。图2为单柱及双柱迎浪状态下前柱(柱1)和后柱(柱2)所受x轴方向波浪荷载的幅频变化曲线,此时入射波向角β=0°,h/a=0.5,d/a=10,R=3a。图3与图2的情况相同,只是R=5a。图4为单柱及双柱前、后柱所受y轴方向波浪荷载的幅频变化曲线,此时β=0°,h/a=0.5,d/a=10,R=3a。图5与图4的情况相同,只是R=5a。图6和图7分别R=3a和R=5a时,单柱及双柱迎浪状态下前柱和后柱所受波浪力矩荷载的幅频变化曲线,此时β=0°,h/a=0.5,d/a=10。 仅供学习与交流
收集于网络,如有侵权请联系管理员删除 图2 双柱迎浪间距3a时x轴方向受力幅频曲线 图3 双柱迎浪间距5a时x轴方向受力幅频曲线 图4 双柱迎浪间距3a时z轴方向受力幅频曲线 Fig.4 Nondimensional amplitude-frequency curves of load in z