切线理论与应用
- 格式:pdf
- 大小:709.56 KB
- 文档页数:40

切线理论的主要内容有哪些?有什么需要注意的金融市场中有一个顺应潮流的说法,也就是“顺势而为,不逆势而动”这一道理已成为了投资者的共识,切线理论也就是在这一背景下迅速的发展壮大起来了。
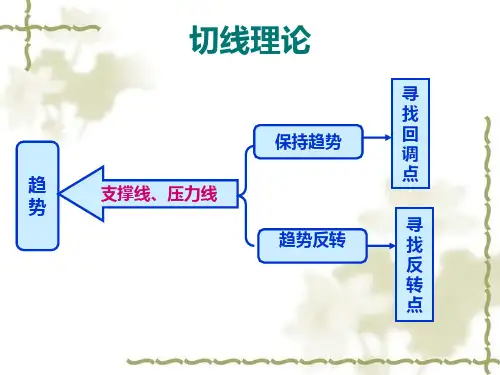
总得来说,切线理论就是帮助投资者识别市场大势变动方向和局势分析的理论方法。
一、切线理论概述切线理论诞生于20世纪70年代左右,是由约翰.墨菲、威尔斯.王德和乔治.恩等人共同提出来的。
切线理论继承了道氏理论的三个基本信条,即市场行为包含一切信息、市场价格以趋势的方式进行演变、历史必然会重演。
切线理论主要为趋势分析、支撑线和压力线、趋势线和轨道线、黄金分割线和百分比线等内容。
图片来源于网络二、切线理论的基本内容(一) 趋势分析趋势就是指商品市场的波动方向,如果确定了一段上升或下降的趋势,那么商品的价格必然朝着这个方向运动下去。
在上升或下降的行情中,虽然中间会出现短暂的下降或上升,但不影响大方向。
趋势的方向主要有以下几种:上升方向:在商品价格的波动图中,如果每个后面的峰和谷都高于前面的峰和谷,则该趋势就是上升趋势。
下降趋势:在商品价格的波动图中,如果每个后面的峰和谷都低于前面的峰和谷,则该趋势就是下降趋势。
水平方向:在商品价格的波动图中,如果后面的峰和谷与前面的峰和谷相比,没有明显的高低之分,几乎呈水平状态,则该趋势就是水平趋势。
(二) 支撑线和压力线支撑线又称抵抗线,是指当商品价格下跌到某个价位时,会出现买方增加、卖方减少的状况,从而使商品的价格停止下跌,甚至有可能回升。
支撑线的作用就是阻止商品价格的进一步下跌。
阻止商品价格下跌的价格就是支撑线所在的位置。
图片来源于网络1、压力线又称阻力线,是指当商品价格上涨到某个价位时,会出现卖方增加、买方减少的状况,从而使商品的价格停止上涨,甚至出现回落。
压力线就是起阻止商品价格继续上升的作用。
阻止商品价格上升的价格就是压力线所在的位置。
2、支撑线和压力线的作用就是阻止或暂时阻止原油价格朝同一个方向继续运动。



切线理论【教学目的和要求】通过本章的学习要求学生在明确趋势含义的基础上,认识趋势分析在证券投资分析中的重要性、掌握趋势分析基本内容。
【本章教学重点】明确趋势含义的掌握趋势的类型趋势线和轨道线的含义支撑线和压力线的作用,趋势线、黄金分割线的画法【本章教学难点】认识趋势分析在证券投资分析中的重要性掌握趋势分析基本内容;支撑线和压力线的作用,趋势线、黄金分割线的画法。
【本章学习目标】●知识点:支撑线和压力线的含义及确认轨道线和趋势线含义及关系黄金分割线和百分比线的画法及应用●技能点:各种切线的绘制各种切线的的应用【本章教学方法】讲述为主,学生结合历史资料绘图,结合实际分析。
【本章教学内容】第一节趋势分析一、趋势的定义简单地说,趋势就是价格的波动方向,或者说是证券市场运动的方向。
若确定了一段上升(或下降)的趋势,则价格的波动必然朝着这个方向运动。
在上升的行情里,虽然也时有下降,但不影响上升的大方向,不断出现新的高价会使偶尔出现的小幅度下降黯然失色。
下降里情况相反,不断出现的新低会使投资者悲观失望,人心涣散。
技术分析的三大假设的第二条明确的说明价格的变化是有趋势的,没有特别的理由,价格将沿着这个趋势继续运动。
这一点就说明趋势这个概念在技术分析中占有很重要的地位,是我们应该注意的核心问题。
一般来说,市场变动不是朝一个方向直来直去,中间肯定要出现曲折,从图形上看就是一条曲折蜿蜒的折线,每个折点处就形成一个峰或谷。
这些峰和谷的相对高度,我们可以看出趋势的方向。
二、趋势的方向趋势的方向有三个:⒈上升方向;⒉下降方向;⒊水平方向,也就是无趋势方向。
如果图形中每个后面的峰和谷都高于前面的峰和谷,则趋势就是上升方向。
这就是常说的一底比一底高,或底部抬高。
如果图形中每个后面的峰和谷都低于前面的峰和谷,则趋势就是下降方向。
这就是常说的一顶比一顶低或顶部降低。
如果价格图形中后面的峰和谷与前面的峰和谷相比,没有明显的高低之分,几乎成水平延伸,这是的趋势就是水平方向。



切线法在函数元不等式中的一个应用切线法(Tangent Line Method)是数学中一种常见的方法,主要用于对函数的增减性、最值等问题进行研究。
而在函数元不等式中,切线法也有着很广泛的应用。
本文将从切线法的基本思想和步骤开始介绍,然后通过具体的例子来展示切线法在函数元不等式中的应用。
切线法的基本思想:切线法的基本思想是通过使用函数的切线来逼近函数的实际取值。
对于函数f(x),如果在其中一点x=a处切线与函数曲线f(x)的拐点相切,那么切线代表了经过点(a,f(a))且与函数曲线f(x)非常接近的线性函数。
通过研究这个切线,我们可以对函数的性质和取值范围进行一些推导。
切线法的步骤:1.找到函数f(x)的切线点:首先需要找到切线点,即函数f(x)的其中一点x=a处。
这个点可以通过对函数f(x)进行求导然后令导数等于一些给定的值来确定。
2.求得切线方程:通过已知切线点和切线的斜率,可以求得切线方程。
切线方程一般形式为y=f'(a)(x-a)+f(a)。
3.利用切线方程求得相应的函数取值:通过已知的切线方程,可以求得相应的函数在切线点处的取值。
在函数元不等式中,我们经常需要研究函数的最值或者函数的增减性。
而切线法正好可以帮助我们对函数的最值或者增减性进行研究。
首先,我们以一个求函数最小值的例子来介绍切线法在函数元不等式中的应用。
示例1:求函数f(x)=x^2的最小值。
解:首先,我们需要找到函数f(x)=x^2的切线点。
由于f(x)=x^2是一个二次函数,其导数f'(x)=2x。
令f'(x)=0,解得x=0。
所以切线点为(0,f(0))=(0,0)。
接下来,我们求得切线方程。
由于切线点为(0,0),切线的斜率可以通过求导得到。
即f'(0)=2(0)=0。
所以切线方程为y=0(x-0)+0=0。
然后,我们求得函数在切线点处的取值。
由于切线点为(0,0),所以函数在切线点处的取值为f(0)=0。