立体几何(知识点总结,解题方法总结)

一、空间点、线、面的位置关系1.1 点与点•点的定义：空间中的任意一点。

•点的坐标表示：a⃗=(a x,a y,a z)。

1.2 直线与直线•直线的定义：无限延伸的平面内的所有点。

•直线的方程表示：r⃗=(x,y,z)，其中Ax+By+Cz+D=0。

1.3 直线与平面•直线的平面方程表示：r⃗=(x,y,z)，其中Ax+By+Cz+D=0。

•直线与平面的交点表示：设直线上的点为P(x0,y0,z0)，则有Ax0+ By0+Cz0+D=0。

1.4 平面与平面•平面的定义：无限延伸的平面内的所有点。

•平面的方程表示：r⃗=(x,y,z)，其中Ax+By+Cz+D=0。

1.5 平面与空间体•平面与空间体的交线表示：设空间体上的点为P(x0,y0,z0)，则有Ax0+By0+Cz0+D=0。

二、空间几何体2.1 柱体•柱体的定义：底面为圆形或矩形，顶面与底面平行的空间几何体。

•柱体的体积公式：V=底面积×高。

2.2 锥体•锥体的定义：底面为圆形或三角形，顶点在底面内的空间几何体。

•锥体的体积公式：V=1底面积×高。

32.3 球体•球体的定义：所有点与球心等距的空间几何体。

•球体的体积公式：V=4πR3。

32.4 空间四边形•空间四边形的定义：四个顶点在空间中的四边形。

•空间四边形的面积公式：S=12|a⃗×b⃗⃗|，其中a⃗和b⃗⃗为四边形的两条对角线。

三、空间角的计算3.1 线线角•线线角的定义：两条直线之间的夹角。

•线线角的计算公式：θ=arccos(|a⃗⃗⋅b⃗⃗||a⃗⃗||b⃗⃗|)，其中a⃗和b⃗⃗为两条直线的方向向量。

3.2 线面角•线面角的定义：直线与平面之间的夹角。

•线面角的计算公式：θ=arccos(|n⃗⃗⋅a⃗⃗||n⃗⃗||a⃗⃗|)，其中n⃗⃗为平面的法向量，a⃗为直线的方向向量。

3.3 面面角•面面角的定义：两个平面之间的夹角。

•面面角的计算公式：θ=arccos(|n⃗⃗1⋅n⃗⃗2||n⃗⃗1||n⃗⃗2|)，其中n⃗⃗1和n⃗⃗2为两个平面的法向量。

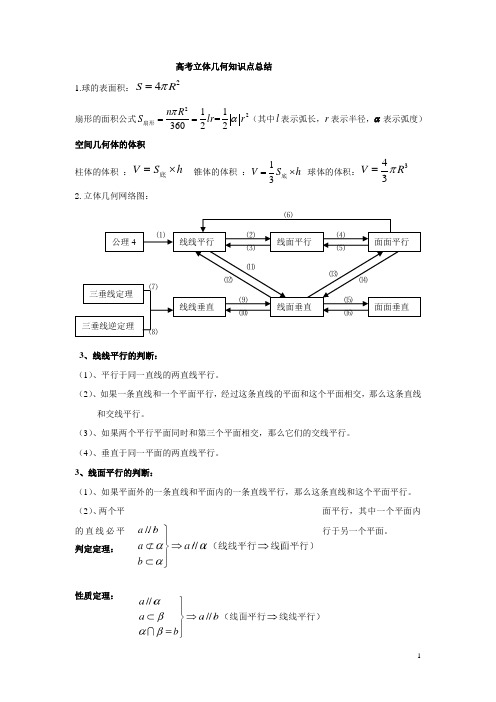
高考立体几何知识点总结 1.球的表面积：24SR π=扇形的面积公式2211=36022n R S lr r πα==扇形（其中l 表示弧长，r 表示半径，α表示弧度） 空间几何体的体积 柱体的体积 ：VS h =⨯底 锥体的体积 ：13V S h =⨯底 球体的体积：343V R π=2.立体几何网络图：3、线线平行的判断：（1）、平行于同一直线的两直线平行。

（2）、如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行。

（3）、如果两个平行平面同时和第三个平面相交，那么它们的交线平行。

（4）、垂直于同一平面的两直线平行。

3、线面平行的判断：（1）、如果平面外的一条直线和平面内的一条直线平行，那么这条直线和这个平面平行。

（2）、两个平面平行，其中一个平面内的直线必平行于另一个平面。

判定定理：性质定理：4、线面垂直的判断：1.如果一直线和平面内的两相交直线垂直，这条直线就垂直于这个平面。

2.如果两条平行线中的一条垂直于一个平面，那么另一条也垂直于这个平面。

3.一直线垂直于两个平行平面中的一个平面，它也垂直于另一个平面。

4.如果两个平面垂直,那么在—个平面内垂直于交线的直线必垂直于另—个平面。

判定定理：性质定理：（1）若直线垂直于平面，则它垂直于平面内任意一条直线。

即：5、面面平行的判断：⑷一个平面内的两条相交直线分别平行于另一个平面，这两个平面平行。

⒀垂直于同一条直线的两个平面平行。

6、面面垂直的判断：⒂一个平面经过另一个平面的垂线，这两个平面互相垂直。

判定定理： 性质定理：⑴ 若两面垂直，则这两个平面的二面角的平面角为90°； （2）四、空间角的求法：（所有角的问题最后都要转化为解三角形的问题，尤其是直角三角形）（1）异面直线所成的角：通过直线的平移，把异面直线所成的角转化为平面内相交直线所成oo 900≤<α（2）线面所成的角：①线面平行或直线在平面内：线面所成的角为o0； ②线面垂直：线面所成的角为o90；oo图2-10 面面垂直性质2图2-11 面面垂直性质3o o2）。

立体几何知识点一.基本概念和原理：1.公理1：如果一条直线上的两点在一个平面内，那么这条直线上的所有的点都在这个平面内。

公理2：如果两个平面有一个公共点，那么它们有且只有一条通过这个点的公共直线。

公理3：过不在同一条直线上的三个点，有且只有一个平面。

推论1: 经过一条直线和这条直线外一点，有且只有一个平面。

推论2：经过两条相交直线，有且只有一个平面。

推论3：经过两条平行直线，有且只有一个平面。

公理4 ：平行于同一条直线的两条直线互相平行。

如果一个角的两边和另一个角的两边分别平行并且方向相同，那么这两个角相等。

异面直线判定定理：用平面内一点与平面外一点的直线，与平面内不经过该点的直线是异面直线。

两异面直线所成的角：范围为( 0°，90° ) esp.空间向量法两异面直线间距离: 公垂线段(有且只有一条) esp.空间向量法2平面的一条斜线和它在这个平面内的射影所成的锐角。

esp.空间向量法(找平面的法向量)（规定：a、直线与平面垂直时，所成的角为直角，b、直线与平面平行或在平面内，所成的角为0°角由此得直线和平面所成角的取值范围为[0°，90°]）斜线与平面所成的角是斜线与该平面内任一条直线所成角中的最小角如果平面内的一条直线,与这个平面的一条斜线的射影垂直，那么它也与这条斜线垂直。

a和一个平面内的任意一条直线都垂直，就说直线a和平面互相垂直.直线a叫平面的垂线，平面叫做直线a的垂面。

直，那么这条直线垂直于这个平面。

如果两条直线同垂直于一个平面，那么这两条直线平行。

如果一条直线和一个平面没有公共点，那么我们就说这条直线和这个平面平行。

行，那么这条直线和这个平面平行。

如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行。

面，那么这两个平面平行。

如果两个平行平面同时和第三个平面相交，则交线平行。

8.（1）二面角：从一条直线出发的两个半平面所组成的图形叫做二面角。

第八章立体几何初步8．1基本立体图形第1课时棱柱、棱锥、棱台的结构特征1．空间几何体的定义及分类(1)定义：如果只考虑物体的形状和大小，而不考虑其他因素，那么由这些物体抽象出来的空间图形就叫做空间几何体．(2)分类：常见的空间几何体有多面体与旋转体两类．2．空间几何体记作棱柱ABCDEF­A′B′C′D′E′F′记作棱锥S­ABCD按底面多边形的边数分为三棱锥、记作棱台ABCD­A′B′C′D′得的棱台分别为三棱台、四棱台、(1)棱柱、棱锥、棱台的关系在运动变化的观点下，棱柱、棱锥、棱台之间的关系可以用下图表示出来(以三棱柱、三棱锥、三棱台为例)．(2)各种棱柱之间的关系①棱柱的分类棱柱⎩⎨⎧直棱柱⎩⎨⎧正棱柱（底面为正多边形）一般的直棱柱斜棱柱②常见的几种四棱柱之间的转化关系典型应用1棱柱的结构特征下列关于棱柱的说法：①所有的面都是平行四边形；②每一个面都不会是三角形；③两底面平行，并且各侧棱也平行；④被平面截成的两部分可以都是棱柱．其中正确说法的序号是__________．【解析】①错误，棱柱的底面不一定是平行四边形；②错误，棱柱的底面可以是三角形；③正确，由棱柱的定义易知；④正确，棱柱可以被平行于底面的平面截成两个棱柱，所以正确说法的序号是③④.【答案】③④棱柱结构特征的辨析技巧(1)扣定义：判定一个几何体是否是棱柱的关键是棱柱的定义．①看“面”，即观察这个多面体是否有两个互相平行的面，其余各面都是四边形；②看“线”，即观察每相邻两个四边形的公共边是否平行．(2)举反例：通过举反例，如与常见几何体或实物模型、图片等不吻合，给予排除．典型应用2棱锥、棱台的结构特征下列关于棱锥、棱台的说法：①用一个平面去截棱锥，底面和截面之间的部分组成的几何体叫棱台；②棱台的侧面一定不会是平行四边形；③棱锥的侧面只能是三角形；④由四个面围成的封闭图形只能是三棱锥；⑤棱锥被平面截成的两部分不可能都是棱锥．其中正确说法的序号是________．【解析】①错误，若平面不与棱锥底面平行，用这个平面去截棱锥，棱锥底面和截面之间的部分不是棱台．②正确，棱台的侧面一定是梯形，而不是平行四边形．③正确，由棱锥的定义知棱锥的侧面只能是三角形．④正确，由四个面围成的封闭图形只能是三棱锥．⑤错误，如图所示四棱锥被平面截成的两部分都是棱锥．所以正确说法的序号为②③④.【答案】②③④判断棱锥、棱台形状的两种方法(1)举反例法结合棱锥、棱台的定义举反例直接判断关于棱锥、棱台结构特征的某些说法不正确．(2)直接法棱锥棱台定底面只有一个面是多边形，此面即为底面两个互相平行的面，即为底面看侧棱相交于一点延长后相交于一点空间几何体的平面展开图(1)水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示，如图是一个正方体的平面展开图(图中数字写在正方体的外表面上)，若图中的“2”在正方体的上面，则这个正方体的下面是()A．1 B．9C．快D．乐(2)如图是三个几何体的侧面展开图，请问各是什么几何体？【解】(1)选B.由题意，将正方体的展开图还原成正方体，“1”与“乐”相对，“2”与“9”相对，“0”与“快”相对，所以下面是“9”．(2)题图①中，有5个平行四边形，而且还有两个全等的五边形，符合棱柱的特点；题图②中，有5个三角形，且具有共同的顶点，还有一个五边形，符合棱锥的特点；题图③中，有3个梯形，且其腰的延长线交于一点，还有两个相似的三角形，符合棱台的特点，把侧面展开图还原为原几何体，如图所示：所以①为五棱柱，②为五棱锥，③为三棱台．多面体展开图问题的解题策略(1)绘制展开图：绘制多面体的平面展开图要结合多面体的几何特征，发挥空间想象能力或者是亲手制作多面体模型．在解题过程中，常常给多面体的顶点标上字母，先把多面体的底面画出来，然后依次画出各侧面，便可得到其平面展开图．(2)由展开图复原几何体：若是给出多面体的平面展开图，来判断是由哪一个多面体展开的，则可把上述过程逆推，同一个几何体的平面展开图可能是不一样的，也就是说，一个多面体可有多个平面展开图．圆柱、圆锥、圆台、球、简单组合体的结构特征1．圆柱、圆锥、圆台和球的结构特征(1)圆柱的结构特征(1)圆柱有无数条母线，它们平行且相等．(2)平行于底面的截面是与底面大小相同的圆，如图1所示．(3)过轴的截面(轴截面)都是全等的矩形，如图2所示．(4)过任意两条母线的截面是矩形，如图3所示．(2)圆锥的结构特征(1)圆锥有无数条母线，它们有公共点即圆锥的顶点，且长度相等．(2)平行于底面的截面都是圆，如图1所示．(3)过轴的截面是全等的等腰三角形，如图2所示．(4)过任意两条母线的截面是等腰三角形，如图3所示．(3)圆台的结构特征(1)圆台有无数条母线，且长度相等，延长后相交于一点．(2)平行于底面的截面是圆，如图1所示．(3)过轴的截面是全等的等腰梯形，如图2所示．(4)过任意两条母线的截面是等腰梯形，如图3所示．(4)球的结构特征(1)球心和截面圆心的连线垂直于截面．(2)球心到截面的距离d与球的半径R及截面圆的半径r有如下关系：r＝R2－d2.2．简单组合体(1)概念由简单几何体组合而成的几何体叫做简单组合体．(2)两种构成形式①由简单几何体拼接而成；②由简单几何体截去或挖去一部分而成．典型应用1圆柱、圆锥、圆台、球的概念(1)给出下列说法：①圆柱的底面是圆面；②经过圆柱任意两条母线的截面是一个矩形面；③圆台的任意两条母线的延长线可能相交，也可能不相交；④夹在圆柱的两个截面间的几何体还是一个旋转体．其中说法正确的是________．(2)给出以下说法：①球的半径是球面上任意一点与球心所连线段的长；②球的直径是球面上任意两点间所连线段的长；③用一个平面截一个球，得到的截面可以是一个正方形；④过圆柱轴的平面截圆柱所得截面形状是矩形．其中正确说法的序号是________．【解析】(1)①正确，圆柱的底面是圆面；②正确，如图所示，经过圆柱任意两条母线的截面是一个矩形面；③不正确，圆台的母线延长相交于一点；④不正确，圆柱夹在两个平行于底面的截面间的几何体才是旋转体．(2)根据球的定义知，①正确；②不正确，因为球的直径必过球心；③不正确，因为球的任何截面都是圆面；④正确．【答案】(1)①②(2)①④(1)判断简单旋转体结构特征的方法①明确由哪个平面图形旋转而成；②明确旋转轴是哪条直线．(2)简单旋转体的轴截面及其应用①简单旋转体的轴截面中有底面半径、母线、高等体现简单旋转体结构特征的关键量；②在轴截面中解决简单旋转体问题体现了化空间图形为平面图形的转化思想．典型应用2简单组合体的结构特征如图所示的几何体是由下面哪一个平面图形旋转而形成的()【解析】该几何体自上而下由圆锥、圆台、圆台、圆柱组合而成，故应选A.【答案】A[变条件、变问法]若将本例选项B中的平面图形旋转一周，试说出它形成的几何体的结构特征．解：①是直角三角形，旋转后形成圆锥；②是直角梯形，旋转后形成圆台；③是矩形，旋转后形成圆柱，所以旋转后形成的几何体如图所示．通过观察可知，该几何体是由一个圆锥、一个圆台和一个圆柱自上而下拼接而成的．不规则平面图形旋转形成几何体的结构特征的分析策略(1)分割：首先要对原平面图形适当分割，一般分割成矩形、梯形、三角形或圆(半圆或四分之一圆)等基本图形．(2)定形：然后结合圆柱、圆锥、圆台、球的形成过程进行分析．典型应用3旋转体中的计算问题如图所示，用一个平行于圆锥SO底面的平面截这个圆锥，截得圆台上、下底面的面积之比为1∶16，截去的圆锥的母线长是3 cm，求圆台O′O的母线长．【解】设圆台的母线长为l cm，由截得的圆台上、下底面面积之比为1∶16，可设截得的圆台的上、下底面的半径分别为r cm，4r cm.过轴SO作截面，如图所示，则△SO′A′∽△SOA，SA′＝3 cm.所以SA′SA＝O′A′OA，所以33＋l＝r4r＝14.解得l＝9，即圆台O′O的母线长为9 cm.解决旋转体中计算问题的方法用平行于底面的平面去截柱、锥、台等几何体，注意抓住截面的性质(与底面全等或相似)，同时结合旋转体中的轴截面(经过旋转轴的截面)的几何性质，利用相似三角形中的相似比，列出相关几何变量的方程(组)而解得．[注意]在研究与截面有关的问题时，要注意截面与物体的相对位置的变化．由于相对位置的改变，截面的形状也会随之发生变化．8．2立体图形的直观图1．用斜二测画法画水平放置的平面图形的直观图的步骤(1)建系：在已知图形中取互相垂直的x轴和y轴，两轴相交于点O.画直观图时，把它们画成对应的x′轴与y′轴，两轴交于点O′，且使∠x′O′y′＝45°(或135°)，它们确定的平面表示水平面．(2)平行不变：已知图形中平行于x轴或y轴的线段，在直观图中分别画成平行于x′轴或y′轴的线段．(3)长度规则：已知图形中平行于x轴的线段，在直观图中保持原长度不变，平行于y轴的线段，长度为原来的一半．2．空间几何体直观图的画法(1)与平面图形的直观图画法相比多了一个z轴，直观图中与之对应的是z′轴．(2)直观图中平面x′O′y′表示水平平面，平面y′O′z′和x′O′z′表示竖直平面．(3)已知图形中平行于z轴(或在z轴上)的线段，在其直观图中平行性和长度都不变．(4)成图后，去掉辅助线，将被遮挡的部分改为虚线.■名师点拨(1)画水平放置的平面图形的直观图，关键是确定多边形顶点的位置，借助于平面直角坐标系确定顶点后，只需把这些顶点顺次连接即可．(2)用斜二测画法画直观图要掌握水平长不变，垂线长减半，直角画45°(或135°)．典型应用1画水平放置的平面图形的直观图画水平放置的直角梯形的直观图，如图所示．【解】(1)在已知的直角梯形OBCD中，以底边OB所在直线为x轴，垂直于OB的腰OD所在直线为y轴建立平面直角坐标系．如图①所示．(2)画相应的x′轴和y′轴，使∠x′O′y′＝45°，在x′轴上截取O′B′＝OB，在y′轴上截取O′D′＝12OD，过点D′作x′轴的平行线l，在l上沿x′轴正方向取点C′使得D′C′＝DC.连接B′C′，如图②.(3)所得四边形O′B′C′D′就是直角梯形OBCD的直观图．如图③.画水平放置的平面图形的直观图的关键及注意事项(1)在画水平放置的平面图形的直观图时，选取适当的直角坐标系是关键，一般要使平面多边形尽可能多的顶点在坐标轴上或边与坐标轴平行，以便于画图．(2)画图时要注意原图和直观图中线段的长度的关系是否发生变化．典型应用2画简单几何体的直观图已知一个正四棱台的上底面边长为2，下底面边长为6，高为4，用斜二测画法画出此正四棱台的直观图．【解】(1)画轴．如图①，画x轴、y轴、z轴，三轴相交于点O，使∠xOy ＝45°，∠xOz＝90°.(2)画下底面．以O为中点，在x轴上取线段EF，使得EF＝6，在y轴上取线段GH，使得GH＝3，再过G，H分别作AB綊EF，CD綊EF，且使得AB的中点为G，CD的中点为H，连接AD，BC，这样就得到了正四棱台的下底面ABCD 的直观图．(3)画上底面．在z轴上截取线段OO1＝4，过O1作O1x′∥Ox，O1y′∥Oy，使∠x′O1y′＝45°，建立坐标系x′O1y′，在x′O1y′中仿照(2)的步骤画出上底面A1B1C1D1的直观图．(4)连接AA1、BB1、CC1、DD1，擦去辅助线，得到的图形就是所求的正四棱台的直观图(如图②)．画空间图形的直观图的原则(1)用斜二测画法画空间图形的直观图时，图形中平行于x 轴、y 轴、z 轴的线段在直观图中应分别画成平行于x ′轴、y ′轴、z ′轴的线段．(2)平行于x 轴、z 轴的线段在直观图中长度保持不变，平行于y 轴的线段长度变为原来的12.典型应用3直观图的还原与计算如图所示，梯形A 1B 1C 1D 1是一平面图形ABCD 的直观图．若A 1D 1∥O ′y ′，A 1B 1∥C 1D 1，A 1B 1＝23C 1D 1＝2，A 1D 1＝O ′D 1＝1.试画出原四边形，并求原图形的面积．【解】 如图，建立直角坐标系xOy ，在x 轴上截取OD ＝O ′D 1＝1，OC ＝O ′C 1＝2.在过点D 与y 轴平行的直线上截取DA ＝2D 1A 1＝2.在过点A 与x 轴平行的直线上截取AB ＝A 1B 1＝2.连接BC ，便得到了原图形(如图)．由作法可知，原四边形ABCD 是直角梯形，上、下底长度分别为AB ＝2，CD ＝3，直角腰长度为AD ＝2.所以面积为S ＝2＋32×2＝5.(1)直观图的还原技巧由直观图还原为平面图的关键是找与x ′轴、y ′轴平行的直线或线段，且平行于x ′轴的线段还原时长度不变，平行于y ′轴的线段还原时放大为直观图中相应线段长的2倍，由此确定图形的各个顶点，顺次连接即可．(2)直观图与原图面积之间的关系若一个平面多边形的面积为S ，其直观图的面积为S ′，则有S ′＝24S 或S ＝22S ′.利用这一公式可由原图形面积求其直观图面积或由直观图面积求原图形面积．柱、锥、台的表面积和体积1．棱柱、棱锥、棱台的表面积多面体的表面积就是围成多面体各个面的面积的和．棱柱、棱锥、棱台的表面积就是围成它们的各个面的面积的和．2．棱柱、棱锥、棱台的体积(1)V棱柱＝Sh；(2)V棱锥＝13Sh；V棱台3S′，S分别是棱台的上、下底面面积，h为棱台的高．3．圆柱、圆锥、圆台的表面积和体积1．柱体、锥体、台体的体积(1)柱体：柱体的底面面积为S ，高为h ，则V ＝Sh . (2)锥体：锥体的底面面积为S ，高为h ，则V ＝13Sh .(3)台体：台体的上、下底面面积分别为S ′、S ，高为h ，则V ＝13()S ′＋SS ′＋S h .2．圆柱、圆锥、圆台的侧面积公式之间的关系 S 圆柱侧＝2πrl ――→r ′＝r S 圆台侧＝π(r ′＋r )l ――→r ′＝0S 圆锥侧＝πrl . 3．柱体、锥体、台体的体积公式之间的关系V 柱体＝Sh ――→S ′＝S V 台体＝13(S ′＋S ′S ＋S )h ――→S ′＝0V 锥体＝13Sh . 典型应用1柱、锥、台的表面积(1)若圆锥的正视图是正三角形，则它的侧面积是底面积的( ) A.2倍 B ．3 倍 C ．2 倍D ．5 倍(2)已知正方体的 8 个顶点中，有 4 个为侧面是等边三角形的三棱锥的顶点，则这个三棱锥与正方体的表面积之比为( )A ．1∶ 2B ．1∶3C ．2∶ 2D ．3∶6(3)已知某圆台的一个底面周长是另一个底面周长的 3 倍，母线长为 3 ，圆台的侧面积为 84π，则该圆台较小底面的半径为( )A ．7B ．6C ．5D ．3【解析】 (1)设圆锥的底面半径为 r ，母线长为 l ，则由题意可知，l ＝2r ，于是 S 侧＝πr ·2r ＝2πr 2，S 底＝πr 2，可知选 C.(2)棱锥 B ′­ACD ′为适合条件的棱锥，四个面为全等的等边三角形，设正方体的棱长为 1，则 B ′C ＝2，S △B ′AC ＝32.三棱锥的表面积 S 锥＝4×32＝23，又正方体的表面积S正＝6.因此S锥∶S正＝23∶6＝1∶ 3.(3)设圆台较小底面的半径为r，则另一底面的半径为3r.由S侧＝3π(r＋3r)＝84π，解得r＝7.【答案】(1)C (2)B (3)A空间几何体表面积的求法技巧(1)多面体的表面积是各个面的面积之和．(2)组合体的表面积应注意重合部分的处理．(3)圆柱、圆锥、圆台的侧面是曲面，计算侧面积时需要将这个曲面展开为平面图形计算，而表面积是侧面积与底面圆的面积之和．典型应用2柱、锥、台的体积如图所示，正方体ABCD­A1B1C1D1的棱长为a，过顶点B，D，A1截下一个三棱锥．(1)求剩余部分的体积；(2)求三棱锥A­A1BD的体积及高．【解】(1)V三棱锥A1­ABD＝13S△ABD·A1A＝13×12·AB·AD·A1A＝16a3.故剩余部分的体积V＝V正方体－V三棱锥A1­ABD＝a3－16a3＝56a3.(2)V三棱锥A­A1BD＝V三棱锥A1­ABD＝1 6a 3.设三棱锥A­A1BD的高为h，则V三棱锥A­A1BD＝13·S△A1BD·h＝13×12×32(2a)2h＝36a2h，故36a2h＝16a3，解得h＝3 3a.求几何体体积的常用方法(1)公式法：直接代入公式求解．(2)等积法：例如四面体的任何一个面都可以作为底面，只需选用底面积和高都易求的形式即可．(3)补体法：将几何体补成易求解的几何体，如棱锥补成棱柱，棱台补成棱锥等．(4)分割法：将几何体分割成易求解的几部分，分别求体积．[提醒]求几何体的体积时，要注意利用好几何体的轴截面(尤其为圆柱、圆锥时)，准确求出几何体的高和底面积．典型应用3组合体的表面积和体积如图在底面半径为2，母线长为 4 的圆锥中内接一个高为3的圆柱，求圆柱的表面积．【解】设圆锥的底面半径为R，圆柱的底面半径为r，表面积为S.则R＝OC＝2，AC＝4，AO＝42－22＝2 3.如图所示，易知△AEB∽△AOC，所以AEAO＝EBOC，即323＝r2，所以r＝1，S 底＝2πr 2＝2π，S 侧＝2πr ·h ＝23π. 所以 S ＝S 底＋S 侧＝2π＋23π ＝(2＋23)π.1．[变问法]本例中的条件不变，求圆柱的体积与圆锥的体积之比． 解：由例题解析可知：圆柱的底面半径为 r ＝1，高 h ＝3，所以圆柱的体积 V 1＝πr 2h ＝π×12×3＝3π.圆锥的体积 V 2＝13π×22×23＝833π. 所以圆柱与圆锥的体积比为 3∶8.2．[变问法]本例中的条件不变，求图中圆台的表面积与体积．解：由例题解析可知：圆台的上底面半径 r ＝1，下底面半径 R ＝2，高 h ＝3，母线 l ＝2，所以圆台的表面积 S ＝π(r 2＋R 2＋r ·l ＋Rl )＝π(12＋22＋1×2＋2×2)＝11π.圆台的体积 V ＝13π(r 2＋rR ＋R 2)h ＝13π(12＋2＋22)×3＝733π.3．[变条件、变问法]本例中的“高为3”改为“高为 h ”，试求圆柱侧面积的最大值．解：设圆锥的底面半径为 R ，圆柱的底面半径为 r ， 则 R ＝OC ＝2，AC ＝4， AO ＝42－22＝2 3.如图所示易知△AEB ∽△AOC ， 所以AE AO ＝EB OC ， 即23－h 23＝r2， 所以 h ＝23－3r ，S 圆柱侧＝2πrh ＝2πr (23－3r ) ＝－23πr 2＋43πr ，所以当 r ＝1，h ＝3时，圆柱的侧面积最大，其最大值为 23π.求组合体的表面积与体积的步骤(1)分析结构特征：弄清组合体的组成形式，找准有关简单几何体的关键量．(2)设计计算方法：根据组成形式，设计计算方法，特别要注意“拼接面”面积的处理，利用“切割”“补形”的方法求体积．(3)计算求值：根据设计的计算方法求值．球的体积和表面积1．球的表面积设球的半径为R，则球的表面积S＝4πR2．2．球的体积设球的半径为R，则球的体积V＝43πR3．■名师点拨对球的体积和表面积的几点认识(1)从公式看，球的表面积和体积的大小，只与球的半径相关，给定R都有唯一确定的S和V与之对应，故表面积和体积是关于R的函数．(2)由于球的表面不能展开成平面，所以，球的表面积公式的推导与前面所学的多面体与旋转体的表面积公式的推导方法是不一样的．(3)球的表面积恰好是球的大圆(过球心的平面截球面所得的圆)面积的4倍．典型应用1球的表面积与体积(1)已知球的体积是32π3，则此球的表面积是()A．12πB．16πC.16π3 D.64π3(2)如图，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径，若该几何体的体积是28π3，则它的表面积是()A．17πB．18πC．20πD．28π【解析】(1)设球的半径为R，则由已知得V＝43πR3＝32π3，解得R＝2.所以球的表面积S＝4πR2＝16π.(2)由三视图可得此几何体为一个球切割掉18后剩下的几何体，设球的半径为r，故78×43πr3＝283π，所以r＝2，表面积S＝78×4πr2＋34πr2＝17π，选A.【答案】(1)B(2)A球的体积与表面积的求法及注意事项(1)要求球的体积或表面积，必须知道半径R或者通过条件能求出半径R，然后代入体积或表面积公式求解．(2)半径和球心是球的最关键要素，把握住了这两点，计算球的表面积或体积的相关题目也就易如反掌了．典型应用2球的截面问题如图，有一个水平放置的透明无盖的正方体容器，容器高8 cm，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6 cm，如果不计容器厚度，则球的体积为()A.500π3cm3 B.866π3cm3C.1 372π3cm 3D.2 048π3cm 3【解析】 如图，作出球的一个截面，则MC ＝8－6＝2(cm)， BM ＝12AB ＝12×8＝4(cm)． 设球的半径为R cm ，则 R 2＝OM 2＋MB 2 ＝(R －2)2＋42， 所以R ＝5，所以V 球＝43π×53＝5003π (cm 3)． 【答案】 A球的截面问题的解题技巧(1)有关球的截面问题，常画出过球心的截面圆，将问题转化为平面中圆的问题．(2)解题时要注意借助球半径R ，截面圆半径r ，球心到截面的距离d 构成的直角三角形，即R 2＝d 2＋r 2.典型应用3与球有关的切、接问题 角度一 球的外切正方体问题将棱长为 2 的正方体木块削成一个体积最大的球，则该球的体积为( )A.4π3B.2π3C.3π2D.π6【解析】 由题意知，此球是正方体的内切球，根据其几何特征知，此球的直径与正方体的棱长是相等的，故可得球的直径为 2，故半径为 1，其体积是43×π×13＝4π3.【答案】 A角度二球的内接长方体问题一个长方体的各个顶点均在同一球的球面上，且一个顶点上的三条棱的长分别为1，2，3，则此球的表面积为________．【解析】长方体外接球直径长等于长方体体对角线长，即2R＝12＋22＋32＝14，所以球的表面积S＝4πR2＝14π.【答案】14π角度三球的内接正四面体问题若棱长为a的正四面体的各个顶点都在半径为R的球面上，求球的表面积．【解】把正四面体放在正方体中，设正方体棱长为x，则a＝2x，由题意2R＝3x＝3×2a2＝62a，所以S球＝4πR2＝32πa2.角度四球的内接圆锥问题球的一个内接圆锥满足：球心到该圆锥底面的距离是球半径的一半，则该圆锥的体积和此球体积的比值为________．【解析】①当圆锥顶点与底面在球心两侧时，如图所示，设球半径为r，则球心到该圆锥底面的距离是r2，于是圆锥的底面半径为r2－⎝⎛⎭⎪⎫r22＝3r2，高为3r 2.该圆锥的体积为13×π×⎝⎛⎭⎪⎫3r22×3r2＝38πr3，球体积为43πr3，所以该圆锥的体积和此球体积的比值为38πr343πr3＝932.②同理，当圆锥顶点与底面在球心同侧时，该圆锥的体积和此球体积的比值为332.【答案】 932或332角度五 球的内接直棱柱问题设三棱柱的侧棱垂直于底面，所有棱的长都为 a ，顶点都在一个球面上，则该球的表面积为( )A ．πa 2 B.73πa 2 C.113πa 2D ．5πa 2【解析】 由题意知，该三棱柱为正三棱柱，且侧棱与底面边长相等，均为 a ．如图，P 为三棱柱上底面的中心，O 为球心，易知 AP ＝23×32a ＝33a ，OP ＝12a ，所以球的半径 R ＝ OA 满足R 2＝⎝ ⎛⎭⎪⎫33a 2＋⎝ ⎛⎭⎪⎫12a 2＝712a 2，故 S 球＝4πR 2＝73πa 2.【答案】 B(1)正方体的内切球球与正方体的六个面都相切，称球为正方体的内切球，此时球的半径为 r 1＝a2，过在一个平面上的四个切点作截面如图(1)．(2)长方体的外接球长方体的八个顶点都在球面上，称球为长方体的外接球，根据球的定义可知，长方体的体对角线是球的直径，若长方体过同一顶点的三条棱长为 a ，b ，c ，过球心作长方体的对角线，则球的半径为 r 2＝12a 2＋b 2＋c 2，如图(2)．(3)正四面体的外接球正四面体的棱长a与外接球半径R的关系为：2R＝6 2a.8．4.1平面1．平面(1)平面的概念几何里所说的“平面”，是从课桌面、黑板面、海面这样的一些物体中抽象出来的．平面是向四周无限延展的．(2)平面的画法我们常用矩形的直观图，即平行四边形表示平面．当水平放置时，常把平行四边形的一边画成横向；当平面竖直放置时，常把平行四边形的一边画成竖向．(3)平面的表示方法我们常用希腊字母α，β，γ等表示平面，如平面α、平面β、平面γ等，并将它写在代表平面的平行四边形的一个角内；也可以用代表平面的平行四边形的四个顶点，或者相对的两个顶点的大写英文字母作为这个平面的名称．如图中的平面α，也可以表示为平面ABCD、平面AC或者平面BD．■名师点拨(1)平面和点、直线一样，是只描述而不加定义的原始概念，不能进行度量．(2)平面无厚薄、无大小，是无限延展的．2．点、线、面之间的关系及符号表示A是点，l，m是直线，α，β是平面．从集合的角度理解点、线、面之间的关系(1)直线可以看成无数个点组成的集合，故点与直线的关系是元素与集合的关系，用“∈”或“∉”表示．(2)平面也可以看成点集，故点与平面的关系也是元素与集合的关系，用“∈”或“∉”表示．(3)直线与平面都是点集，它们之间的关系可看成集合与集合的关系，故用“⊂”或“⊄”表示．3．平面的性质在画两个相交平面时，如果其中一个平面的一部分被另一个平面挡住，通常把被挡住的部分画成虚线或不画，这样可使画出的图形立体感更强一些．如下图①，图②所示：4．平面性质的三个推论推论1经过一条直线和这条直线外一点，有且只有一个平面．如图(1)．推论2经过两条相交直线，有且只有一个平面．如图(2)．推论3经过两条平行直线，有且只有一个平面．如图(3)．典型应用1图形、文字、符号语言的相互转化(1)用符号语言表示下面的语句，并画出图形．平面ABD与平面BDC交于BD，平面ABC与平面ADC交于AC.(2)将下面用符号语言表示的关系用文字语言予以叙述，并用图形语言予以表示．α∩β＝l，A∈l，AB⊂α，AC⊂β.【解】(1)符号语言表示：平面ABD∩平面BDC＝BD，平面ABC∩平面ADC＝AC.用图形表示如图①所示．(2)文字语言叙述为：点A在平面α与平面β的交线l上，直线AB，AC分别在平面α，β内，图形语言表示如图②所示．。

立体几何知识点一.根本概念和原理：1.公理1：如果一条直线上的两点在一个平面内，那么这条直线上的所有的点都在这个平面内。

公理2：如果两个平面有一个公共点，那么它们有且只有一条通过这个点的公共直线。

公理3：过不在同一条直线上的三个点，有且只有一个平面。

推论1: 经过一条直线和这条直线外一点，有且只有一个平面。

推论2：经过两条相交直线，有且只有一个平面。

推论3：经过两条平行直线，有且只有一个平面。

公理4 ：平行于同一条直线的两条直线互相平行。

如果一个角的两边和另一个角的两边分别平行并且方向相同，那么这两个角相等。

异面直线判定定理：用平面内一点与平面外一点的直线，与平面内不经过该点的直线是异面直线。

两异面直线所成的角：范围为( 0°，90° ) esp.空间向量法两异面直线间距离: 公垂线段(有且只有一条) esp.空间向量法2平面的一条斜线和它在这个平面内的射影所成的锐角。

esp.空间向量法(找平面的法向量)〔规定：a、直线与平面垂直时，所成的角为直角，b、直线与平面平行或在平面内，所成的角为0°角由此得直线和平面所成角的取值范围为[0°，90°]〕斜线与平面所成的角是斜线与该平面内任一条直线所成角中的最小角如果平面内的一条直线,与这个平面的一条斜线的射影垂直，那么它也与这条斜线垂直。

a和一个平面内的任意一条直线都垂直，就说直线a和平面互相垂直.直线a叫平面的垂线，平面叫做直线a的垂面。

直，那么这条直线垂直于这个平面。

如果两条直线同垂直于一个平面，那么这两条直线平行。

如果一条直线和一个平面没有公共点，那么我们就说这条直线和这个平面平行。

行，那么这条直线和这个平面平行。

如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行。

面，那么这两个平面平行。

行。

8.〔1〕二面角：从一条直线出发的两个半平面所组成的图形叫做二面角。

二面角的取值范围为[0°，180°]〔2〕二面角的平面角：以二面角的棱上任意一点为端点，在两个面内分别作垂直于棱的两条射线，这两条射线所成的角叫做二面角的平面角。

高中立体几何知识点总结学好立几并不难，空间想象是关键。

点线面体是一家，共筑立几百花园。

点在线面用属于，线在面内用包含。

四个公理是基础，推证演算巧周旋。

下面是为大家整理的关于高中立体几何知识点总结，希望对您有所帮助。

欢迎大家阅读参考学习!高中立体几何知识点总结1点在线面用属于，线在面内用包含。

四个公理是基础，推证演算巧周旋。

空间之中两条线，平行相交和异面。

线线平行同方向，等角定理进空间。

判定线和面平行，面中找条平行线。

已知线与面平行，过线作面找交线。

要证面和面平行，面中找出两交线，线面平行若成立，面面平行不用看。

已知面与面平行，线面平行是必然;若与三面都相交，则得两条平行线。

判定线和面垂直，线垂面中两交线。

两线垂直同一面，相互平行共伸展。

两面垂直同一线，一面平行另一面。

要让面与面垂直，面过另面一垂线。

面面垂直成直角，线面垂直记心间。

一面四线定射影，找出斜射一垂线，线线垂直得巧证，三垂定理风采显。

空间距离和夹角，平行转化在平面，一找二证三构造，三角形中求答案。

引进向量新工具，计算证明开新篇。

空间建系求坐标，向量运算更简便。

知识创新无止境，学问思辨勇攀登。

多面体和旋转体，上述内容的延续。

扮演载体新角色，位置关系全在里。

算面积来求体积，基本公式是依据。

规则形体用公式，非规形体靠化归。

展开分割好办法，化难为易新天地。

高中立体几何知识点总结2三角函数。

注意归一公式、诱导公式的正确性数列题。

1.证明一个数列是等差(等比)数列时，最后下结论时要写上以谁为首项，谁为公差(公比)的等差(等比)数列;2.最后一问证明不等式成立时，如果一端是常数，另一端是含有n的式子时，一般考虑用放缩法;如果两端都是含n的式子，一般考虑数学归纳法(用数学归纳法时，当n=k+1时，一定利用上n=k时的假设，否则不正确。

利用上假设后，如何把当前的式子转化到目标式子，一般进行适当的放缩，这一点是有难度的。

简洁的方法是，用当前的式子减去目标式子，看符号，得到目标式子，下结论时一定写上综上：由①②得证;3.证明不等式时，有时构造函数，利用函数单调性很简单立体几何题1.证明线面位置关系，一般不需要去建系，更简单;2.求异面直线所成的角、线面角、二面角、存在性问题、几何体的高、表面积、体积等问题时，要建系;3.注意向量所成的角的余弦值(范围)与所求角的余弦值(范围)的关系。

高中数学知识点总结立体几何基础高中数学知识点总结：立体几何基础在高中数学中，立体几何是一个非常重要的内容，它研究的是空间中的物体、形状和位置关系。

掌握立体几何的基础知识对于解题和应用数学都有着重要的作用。

本文将对高中数学中的立体几何基础知识点进行总结。

一、点、线、面和空间1. 点：点是最基本的几何图形，它没有长度、宽度和高度，只有位置。

2. 线：线由无数个点连成，具有长度和方向。

3. 面：面由线围成，具有长度和宽度，两个面之间由边界线分隔。

4. 空间：空间就是由无限个点、线和面组成的。

二、立体的分类1. 多面体：多面体是由多个平面围成的空间图形，它有很多面、边和顶点。

常见的多面体有正方体、长方体、正六面体等。

2. 圆锥体：圆锥体是由一个圆和一个顶点连成的线段，再将这个线段旋转一周形成的。

3. 圆柱体：圆柱体是由两个平行的圆底面和连接两个底面的矩形侧面组成的。

4. 球体：球体由一个圆绕着直径旋转一周形成的。

三、体积和表面积1. 体积：体积用来表示立体图形的容量大小，它的单位是立方厘米（cm³）或立方米（m³）。

不同形状的立体图形计算体积的公式也不同，例如长方体的体积公式为长×宽×高。

2. 表面积：表面积是表示立体图形外部各个面积的总和，它的单位是平方厘米（cm²）或平方米（m²）。

各种立体图形的表面积计算公式不同，例如正方体的表面积公式为6×边长×边长。

四、立体图形的投影1. 正交投影：正交投影是指从不同的方向将物体的投影投射到一个平面上，保持形状和大小不变。

常见的正交投影有俯视图、正视图和侧视图。

2. 斜投影：斜投影是指将物体的投影投射到一个斜面上，通过变换物体的位置和大小来表示形状。

五、相似立体和全等立体1. 相似立体：相似立体是指两个立体图形的形状相似，但大小可以不同。

在相似立体中，对应的边长比例相等，对应的面积比例相等，对应的体积比例相等。

高中立体几何最佳解题方法总结一、线线平行的证明方法1、利用平行四边形；2、利用三角形或梯形的中位线；3、如果一条直线和一个平面平行，经过这条直线的平面与这个相交，那么这条直线和交线平行。

（线面平行的性质定理）4、如果两个平行平面同时和第三个平面相交，那么它们的交线平行。

（面面平行的性质定理）5、如果两条直线垂直于同一个平面，那么这两条直线平行。

（线面垂直的性质定理）6、平行于同一条直线的两个直线平行。

7、夹在两个平行平面之间的平行线段相等。

二、线面平行的证明方法1、定义法：直线和平面没有公共点。

2、如果平面外的一条直线和这个平面内的一条直线平行，那么这条直线就和这个平面平行。

（线面平行的判定定理）3、两个平面平行，其中一个平面内的任意一条直线必平行于另一个平面。

4、反证法。

三、面面平行的证明方法1、定义法：两个平面没有公共点。

2、如果一个平面内的两条相交直线都平行于另一个平面，那么这两个平面平行。

（面面平行的判定定理）3、平行于同一个平面的两个平面平行。

4、经过平面外一点，有且只有一个平面与已知平面平行。

5、垂直于同一条直线的两个平面平行。

四、线线垂直的证明方法1、勾股定理；2、等腰三角形；3、菱形对角线;4、圆所对的圆周角是直角；5、点在线上的射影；6、如果一条直线和这个平面垂直，那么这条直线和这个平面内的任意直线都垂直。

7、在平面内的一条直线，如果和这个平面一条斜线垂直，那么它也和这条斜线的射影垂直。

（三垂线定理）8、在平面内的一条直线，如果和这个平面一条斜线的射影垂直，那么它也和这条斜线垂直。

9、如果两条平行线中的一条垂直于一条直线，那么另一条也垂直于这条直线。

五、线面垂直的证明方法：1、定义法：直线与平面内的任意直线都垂直；2、点在面内的射影；3、如果一条直线和一个平面内的两条相交直线垂直，那么这条直线就和这个平面垂直。

（线面垂直的判定定理）4、如果两个平面互相垂直，那么在一个平面内垂直于它们交线的直线必垂直于另一个平面。

高三立体几何知识点总结立体几何是数学中的一个重要分支，它研究的是在三维空间中的图形和其性质。

在高中阶段，立体几何作为数学课程的一部分，对学生的综合能力以及解决实际问题的能力有着重要的提升作用。

本文将对高三立体几何的知识点进行总结，以帮助同学们更好地掌握这一内容。

一、直线与平面的关系1. 平面与平面的关系：（1）相交：两个平面相交于一条直线。

（2）垂直：两个平面相交的直线与第三个平面垂直。

（3）平行：两个平面相交的直线与第三个平面平行。

2. 直线与直线的关系：（1）相交：两条不平行直线相交于一点。

（2）平行：两条直线在平面上不相交。

（3）异面直线：两条直线在空间中不相交。

二、立体图形的性质1. 三棱柱：具有5个面、9条边和6个顶点的立体。

2. 四棱锥：具有5个面、8条边和5个顶点的立体。

3. 三棱锥：具有四个面、6条边和4个顶点的立体。

4. 正方体：具有六个面、12条边和8个顶点的立体，其中每个面都是正方形。

5. 正六面体：具有六个面、12条边和8个顶点的立体，其中每个面都是正六边形。

6. 正八面体：具有八个面、12条边和6个顶点的立体，其中每个面都是正八边形。

7. 正十二面体：具有十二个面、30条边和20个顶点的立体，其中每个面都是正五边形。

三、立体图形的体积与表面积计算1. 三棱柱的体积公式：体积 = 底面积 ×高2. 四棱锥的体积公式：体积 = （底面积 ×高）/ 33. 球的体积公式：体积 = （4/3）πr³，其中r为球的半径。

4. 直角三棱锥的体积公式：体积 = （1/3）×面积 ×高，其中面积为底面积。

5. 立方体的体积公式：体积 = 边长³，其中边长为立方体的边长。

6. 平行四边形棱台的体积公式：体积 = 底面积 ×高四、立体图形的投影1. 平行投影：图形在平行于某个平面的投影面上的投影。

2. 斜向投影：图形在斜向的投影面上的投影。