人教版2018-2019学年七年级数学竞赛试卷A(含答案)

七年级数学竞赛（时间40分钟，满分100分）姓名_______班级________分数_________1、（10）已知关于x 的一元一次方程a x 20223x 20211+=+的解为x=1，那么关于y 的一元一次方程a 6y 202236y 20211++=++）（）（的解为：________________. 2、（10）定义一种对正整数n 的“F ”运算：①当n 为奇数时，F (n )＝3n＋1；②当n 为偶数时，F (n )＝n 2k [其中k 是使F (n )为奇数的正整数]，两种运算交替重复进行．例如，取n ＝24，则：若n ＝13，则第2021次“F ”运算的结果是________________．3、（10）已知多项式－a 12＋a 11b －a 10b 2＋…＋ab 11－b 12.(1)请你按照上述规律写出多项式的第五项，并指出它的系数和次数；(2)这个多项式是几次几项式？4、（10）请你将如图所示的两个正方形和两个长方形拼成一个较大的正方形，并列式计算所拼图形的面积．5、（15）材料阅读题阅读材料：求1＋2＋22＋23＋24＋…＋2100的值．解：设S＝1＋2＋22＋23＋24＋…＋299＋2100.①将等式①两边同时乘2，得2S＝2＋22＋23＋24＋25＋…＋2100＋2101.②②－①，得2S－S＝2101－1，即S＝2101－1.所以1＋2＋22＋23＋24＋…＋2100＝2101－1.请你仿照此法计算：(1)1＋3＋32＋33＋34＋…＋32019＋32020.(2)已知数列：－1，9，－92，93，－94，…. (Ⅰ)它的第100个数是多少？(Ⅰ)求这列数中前100个数的和．6、（15）数学家苏步青先生有一次在德国与另一位数学家同乘一辆电车，这位数学家出了一道题请苏先生解答．甲、乙两人同时从相距10 km的A，B两地出发，相向而行，甲每小时走6 km，乙每小时走4 km，甲带着一只狗和他同时出发，狗以每小时10 km 的速度向乙奔去，遇到乙后立即回头向甲奔去，遇到甲后又回头向乙奔去，直到甲、乙两人相遇时狗才停住．则这只狗共跑了多少千米？7、（15）已知(2x－1)5＝a5x5＋a4x4＋…＋a1x＋a0，求下列各式的值：(1)a1＋a2＋a3＋a4＋a5；(2)a1－a2＋a3－a4＋a5；(3)a1＋a3＋a5.8、（15）如图，数轴上两个动点A，B开始时所对应的数分别为－8，4，A，B两点各自以一定的速度在数轴上运动，且点A的运动速度为2个单位长度/秒．(1)A，B两点同时出发相向而行，在原点处相遇，求点B的运动速度；(2)A，B两点按上面的速度同时出发，向数轴正方向运动，几秒时两点相距6个单位长度？(3)A，B两点按上面的速度同时出发，向数轴负方向运动，与此同时，点C从原点出发向同方向运动，且在运动过程中，始终有CB∶CA＝1∶2，若干秒后，点C表示的数为－10，求此时点B表示的数．参考答案：1、-52、43、[解析] 观察所给条件，a 的指数逐次减1，b 的指数逐次加1，每一项的次数都为12.各项系数分别为－1，1，－1，1，…，“－1”与“1”间隔出现，奇数项系数为－1，偶数项系数为1.解：(1)第五项为－a 8b 4，它的系数为－1，次数为12.(2) 十二次十三项式．4、[解析] 根据题意拼出正方形ABCD ，将两个正方形和两个长方形的面积相加即可求出答案．解：如图所示，正方形ABCD 即为所拼图形．正方形ABCD 的面积是a 2＋ab ＋ab ＋b 2或(a ＋b)2.5、解：(1)设S ＝1＋3＋32＋33＋34＋…＋32019＋32020.①将等式①两边同时乘3，得3S ＝3＋32＋33＋34＋…＋32020＋32021.②②－①，得3S －S ＝32021－1，即S ＝12(32021－1)． 所以1＋3＋32＋33＋34＋…＋32019＋32020＝12(32021－1)． (2)(Ⅰ)第100个数是999.(Ⅰ)设S ＝－1＋9－92＋93－94＋…－998＋999.③将等式③两边同时乘9，得9S ＝－9＋92－93＋94－95＋…－999＋9100.④③＋④，得10S ＝9100－1，即S ＝110(9100－1)． 所以这列数中前100个数的和是110(9100－1)． 6、[解析] 本题已知狗的奔跑速度是每小时10 km ，求狗奔跑的路程，它的奔跑时间是解决本题的关键，狗从甲、乙两人出发到甲、乙两人相遇时，一直在两人之间不断地奔跑，因此狗奔跑的时间即甲、乙两人从出发到相遇的时间．解：根据题意，得x 10＝106＋4.7、解：因为(2x －1)5＝a 5x 5＋a 4x 4＋…＋a 1x ＋a 0，所以令x ＝0，得(－1)5＝a 0，即a 0＝－1.①令x ＝－1，得(－3)5＝－a 5＋a 4－a 3＋a 2－a 1＋a 0，即－a 5＋a 4－a 3＋a 2－a 1＋a 0＝－243.②令x ＝1，得15＝a 5＋a 4＋a 3＋a 2＋a 1＋a 0，即a 5＋a 4＋a 3＋a 2＋a 1＋a 0＝1.③(1)③－①，得a 1＋a 2＋a 3＋a 4＋a 5＝1－(－1)＝2.(2)①－②，得a 1－a 2＋a 3－a 4＋a 5＝(－1)－(－243)＝242.(3)(③－②)÷2，得a 1＋a 3＋a 5＝(1＋243)÷2＝122.8、解：(1)设点B 的运动速度为x 个单位长度/秒，列方程为82x ＝4，解得x ＝1. 答：点B 的运动速度为1个单位长度/秒．(2)设两点运动t 秒时相距6个单位长度．①若点A 在点B 的左侧，则2t －t ＝(4＋8)－6，解得t ＝6；②若点A 在点B 的右侧，则2t －t ＝(4＋8)＋6，解得t ＝18.答：当A ，B 两点运动6秒或18秒时相距6个单位长度．(3)设点C 的运动速度为y 个单位长度/秒．由始终有CB ∶CA ＝1∶2，列方程，得2－y ＝2(y －1)，解得y ＝43. 当点C 表示的数为－10时，所用的时间为1043＝152(秒)，此时点B 所表示的数为4－152×1＝－72. 答：此时点B 表示的数为－72.。

七年级上学期数学竞赛试题七年级上学期数学竞赛试题一、填空题（每小题4分，共40分）分）1. 甲、乙、丙、丁四个数之和等于－90，甲数减－4，乙数加－4，丙数乘－4，丁数除－4彼比相等，则四个数中的最大的一个数比最小的一个数大＿＿2.2.（（-2124 +7113 ÷24113 －38 ）÷）÷11512= =＿＿＿。

＿＿＿。

＿＿＿。

3. 3. 已知已知与是同类项，则＝＿＿。

＝＿＿。

4. 4. 有理数有理数在数轴上的位置如图1所示，化简5．某班学生去参加义务劳动，其中一组到一果园去摘梨子，第一个进园的学生摘了1个梨子，第二个学生摘了2个，第三个学生摘了3个，……以此类推，后来的学生都比前面的学生多摘1个梨子，这样恰好平均每个学生摘了6个梨子，请问这组学生的人数为＿＿＿＿. 6. 6. 小明骑车自甲地经乙地，先上坡后下坡，到达乙地后立即返回甲地，共用小明骑车自甲地经乙地，先上坡后下坡，到达乙地后立即返回甲地，共用34分钟，已知上坡速度是400米／分，下坡速度是450米／分，则甲地到乙地米／分，则甲地到乙地的路程是＿＿米。

的路程是＿＿米。

7. 学校开运动会，班长想分批买汽水给全班50名师生喝，喝完的空瓶根据商店规定每5个空瓶又可换一瓶汽水，则至少要买 瓶汽水，才能保证每人喝上一瓶汽水. 8. 8. 有这样一个衡量体重是否正常的简单算法。

一个男生的标准体重（以公斤为有这样一个衡量体重是否正常的简单算法。

一个男生的标准体重（以公斤为单位）是其身高（以厘米为单位）减去110110。

正常体重在标准体重减。

正常体重在标准体重减。

正常体重在标准体重减 标准体重的1010％和加标准体重的％和加标准体重的10之间。

已知甲同学身高161厘米，体重为W ，如果他的体重正常，则W 的公斤数的取值范围是的公斤数的取值范围是_____. _____.9. m 9. m、、n 、l 都是385385，则，则m+n+l 的最大值是＿＿。

绝密★启用前世界少年奥林匹克数学竞赛（中国区）选拔赛地方海选赛试题:七年级试题（Ａ卷）选手须知:1、本卷共三部分,第一部分:填空题,共计50分；第二部分:计算题,共计12分；第三部分:解答题,共计58分.2、答题前请将自己的姓名、学校、赛场、参赛证号码写在规定的位置.3、比赛时不能使用计算工具.4、比赛完毕时试卷和草稿纸将被收回.七年级试题（Ａ卷）（本试卷满分120分 ,考试时间90分钟 ）一、填空题.（每题5分,共计50分）1、甲数和乙数的比7:3,乙数和丙数的比是6:5,甲数和丙数的比是 .2、购买3斤苹果,2斤橘子需6.90元；购买8斤苹果,9斤橘子需22.80元.那么苹果、橘子各买1斤需 元.3、有盐的质量分数为16％的盐水800克,要得到盐的质量分数为20％的盐水,应蒸发水 克.4、将5,6,7,8,9,0这6个数字填入下面算式中,使乘积最大□□□×□□□5、一个正方形,把它的边长增加4厘米,那么它的面积就增加96平方厘米,则原来正方形的面积是 .6、单独完成某工程,甲队需要10天,乙队需要15天,丙队需要20天,开始三个队一起干,因工作需要甲队中途撤走了,结果一共用了6天完成这一工程,问甲队实际工作了 天.7、在平面上有10条直线,任何两条都不平行,并且任何三条都不交于同一点,这些直线能把平面分成 部分.8、大客车有48个座位,小客车有30个座位,现在306名旅客,要使每个旅客都有座位而且车上无空位,需要大客车 辆,小客车 辆.9、在16点16分这个时刻,钟表盘面上时针和分针的夹角是 度.10、若│a+2014│与│b-2015│互为相反数,则a+b 的值是_________.二、计算题.（每题6分,共计12分）11、6513.3838525.4415÷+÷⎥⎦⎤⎢⎣⎡⨯⎪⎭⎫ ⎝⎛-12、201520141...541431321211⨯++⨯+⨯+⨯+⨯三、解答题.（第13题6分,第14题8分,第15题10分,第16题10分,第17题12分,第18题12分,共计58分）13、某检修队从A 地出发,在东西方向的公路上检修线路.如果规定向东行驶为正,向西行驶为负,这个检修队一天行驶的距离记录如下（单位:千米）-4,+7,-9,+8,+6,-5,-3.若检修队所乘汽车每千米耗油0.07升,问从出发到收工共耗油多少密 封 线 内 不 要 答 题升？14、互不相等的四个整数的积等于4,求这四个数的绝对值的和是多少？15、1只猴子摘了一堆桃子,第一天吃了这堆桃子的71,第二天吃了余下桃子的61,第三天吃了余下桃子的51,第四天吃了余下桃子的41,第五天吃了余下桃子的31,第六天吃了余下桃子的21,这时还剩下桃子12个,那么第一天和第二天所吃桃子的总数是多少？16、有理数a,b,c 在数轴上的位置如图所示若m=│a+b │-│b-1│-│a-c │-│1-c │,求1000m 的值.17、张老师有一套住房价值40万,由于急需现金,他以九折优惠卖给老季,过了一段时间后,房价上涨10％,张老师又想从老季处把房子买回来.想一想,如果张老师买回房子,总共损失多少万元？18、已知数轴上有A,B,C 三点分别代表-24,-10,10,两只电子蚂蚁甲乙分别从A,C 两点,同时相向而行,甲的速度为4个单位/秒.（1）问多少秒后甲到A,B,C 的距离和为40个单位？（2）若乙的速度为6个单位/秒,两只电子蚂蚁甲乙分别从A,C 两地同时相向而行,问甲乙在数轴上的那个点相遇？（3）在（1）（2）的条件下,当甲到A,B,C 的距离和为40个单位时,甲调头返回,问甲乙还能在数轴上相遇吗？若能,求出相遇点；若不能,请说明理由.∕∕∕∕∕∕∕〇∕∕∕∕∕∕ 密 〇 封 〇 装 〇 订 〇 线 ∕∕∕∕∕∕〇∕∕∕∕∕∕〇∕∕∕∕∕∕〇∕∕∕∕∕∕〇∕∕∕∕∕∕七年级A 一、填空题:（每题5分,共计50分）1.14:52.2.7元3.160克4.960*8755.100c ㎡6.3天7.568.2；79.32 10.1二、计算题（每题6分,共计12分）11.157358351163.3351163.383851=+=⨯+=÷+÷⨯ .........................................6分12.201520142015112015120141...41313121211=-=-++-+-+-.............................6分三、解答题（第13,14,15,每题8分,第16题10分,第17题12分,第18题12分,共计58分） 四、13.42×0.07=2.94升 ................................................8分14.(-2)4)1(2=-⨯⨯ .........................................4分 61122=+-++-.........................................4分 15.76711=-.................................................1分 716176=⨯ .................................................1分 7151)71711(=⨯-- ...........................................1分7141)7171711(=⨯---........................................1分7131)717171711(=⨯---- ....................................1分7121)71717171711(=⨯----- .................................1分716711=⨯-............................................................1分12个）(247271=⨯÷............................................1分16.解:由题意知......................................2 分m=-(a+b)+(b-1)+(a-c)-(1-c).....................2分=-a-b+b-1+a-c-1+c............................2分=-2...........................................2分∴1000m=-2×1000=-2000..........................2分17.万元）(369.040=⨯...........................................4分万元）(44)1.01(40=+⨯ (4)44-36=8（万元）..............................4分18.（1）x=2秒或5秒 .........................................1分提示:设x秒后甲道A,B,C的距离和为40,.......................1分分类讨论①甲在B,A间 ,x=2...................................1分②甲在B,C间,x=5..........................................1分(2)在-10.4处相遇提示:假设x秒后相遇,...............................1 分（4+6）x=10-（-24）,.....................1分x=3.4,.........................1分-24+3.4⨯4=-10.4........................1分（3）甲乙能在-44所表示的点处相遇.提示:①设甲向C走2秒后掉头返回x秒与乙相遇,x=7, 求得在-44处相遇...........................................................2分②设甲向C走5秒后掉头返回y秒后相遇,y=-8,不合题意,舍去. ...........................................................2分。

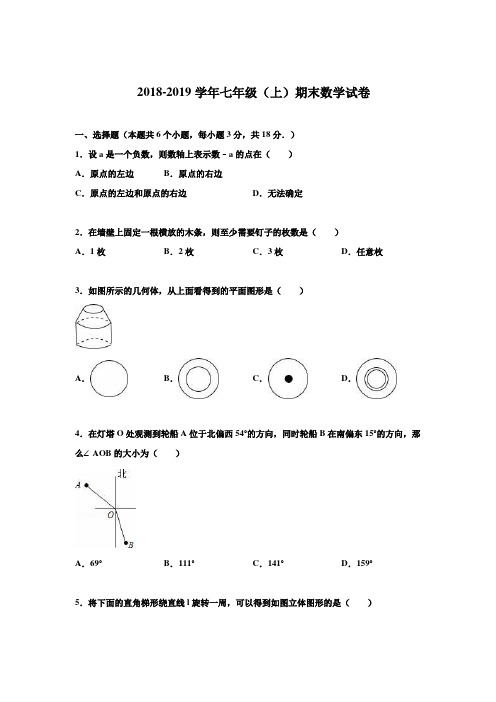
2018-2019学年七年级（上）期末数学试卷一、选择题（本题共6个小题，每小题3分，共18分．）1．设a是一个负数，则数轴上表示数﹣a的点在（）A．原点的左边B．原点的右边C．原点的左边和原点的右边D．无法确定2．在墙壁上固定一根横放的木条，则至少需要钉子的枚数是（）A．1枚B．2枚C．3枚D．任意枚3．如图所示的几何体，从上面看得到的平面图形是（）A．B．C．D．4．在灯塔O处观测到轮船A位于北偏西54°的方向，同时轮船B在南偏东15°的方向，那么∠AOB的大小为（）A．69°B．111°C．141°D．159°5．将下面的直角梯形绕直线l旋转一周，可以得到如图立体图形的是（）A．B．C．D．6．某商店把一种洗涤用品按标价的九折出售，仍可获利20%，若该洗涤用品的进价为21元，则标价为（）元．A．26 B．27 C．28 D．29二、填空题（本大题共8个小题；每小题3分，共24分．把答案写在题中横线上）7．﹣5的相反数是，﹣的倒数是．8．若a3﹣2n b2与5a3n﹣2b2是同类项，则n=．9．青藏高原是世界上海拔最高的高原，它的面积约为2 500 000平方千米．将它的面积用科学记数法表示应为平方千米．10．计算：15°37′+42°51′=．11．根据图提供的信息，可知一个杯子的价格是元．12．用6根火柴最多组成个一样大的三角形，所得几何体的名称是．13．点A、B、C是同一直线上的三个点，若AB=8cm，BC=3cm，则AC=cm．14．填在下面各正方形中的四个数之间都有相同的规律，根据这种规律，m的值是．三、解答题（本大题共10个小题；共78分）15．计算（1）（﹣76）+（+26）+（﹣31）+（+17）（2）2（2b﹣3a）﹣3（2a﹣3b）．16．解下列方程：（1）x﹣7=10﹣4（x+0.5）；（2）﹣=1．17．如图所示，直线l是一条平直的公路，A，B是两个车站，若要在公路l上修建一个加油站，如何使它到车站A，B的距离之和最小，请在公路上表示出点P的位置，并说明理由．（保留作图痕迹，并用你所学的数学知识说明理由）．18．（6分）（2015秋太和县期末）一个角的余角比这个角的少30°，请你计算出这个角的大小．19．先化简再求值：﹣2y3+（2x3﹣xyz）﹣2（x3﹣y3+xyz），其中x=1，y=2，z=﹣3．20．如图，∠AOB=110°，∠COD=70°，OA平分∠EOC，OB平分∠DOF，求∠EOF的大小．21．如图，点C在线段AB上，点M、N分别是AC、BC的中点．（1）若AC=8cm，CB=6cm，求线段MN的长；（2）若C为线段AB上任一点，满足AC+CB=a，其它条件不变，你能猜想MN的长度吗？写出你的结论并说明理由；（3）若C为直线AB上线段AB之外的任一点，且AC=m，CB=n，则线段MN的长为．22．一只小虫从某点P出发，在一条直线上来回爬行，假定把向右爬行的路程记为正数，向左爬行的路程记为负数，则爬行各段路程（单位：厘米）依次为：+5，﹣3，+10，﹣8，﹣6，+12，﹣10．（1）通过计算说明小虫是否回到起点P．（2）如果小虫爬行的速度为0.5厘米/秒，那么小虫共爬行了多长时间．23．如图（1）所示，∠AOB、∠COD都是直角．（1）试猜想∠AOD与∠COB在数量上是相等，互余，还是互补的关系．请你用推理的方法说明你的猜想是合理的．（2）当∠COD绕着点O旋转到图（2）所示位置时，你在（1）中的猜想还成立吗？请你证明你的结论．24．某天，一蔬菜经营户用60元钱从蔬菜批发市场批了西红柿和豆角共40㎏到菜市场去卖，西红柿和豆角这天的批发价与零售价如下表所示：问：他当天卖完这些西红柿和豆角能赚多少钱？品名西红柿豆角批发价（单位：元/kg） 1.2 1.6零售价（单位：元/kg） 1.8 2.52018-2019学年七年级（上）期末数学试卷参考答案与试题解析一、选择题（本题共6个小题，每小题3分，共18分．）1．设a是一个负数，则数轴上表示数﹣a的点在（）A．原点的左边B．原点的右边C．原点的左边和原点的右边D．无法确定【考点】数轴．【分析】根据数轴的相关概念解题．【解答】解：因为a是一个负数，则﹣a是一个正数，二者互为相反数，﹣a在原点的右边．故选B．【点评】解答此题要用到以下概念：数轴的定义：规定了原点、正方向和单位长度的直线叫做数轴；（1）从原点出发朝正方向的射线上的点对应正数，相反方向的射线上的点对应负数，原点对应零．（2）在数轴上表示的两个数，正方向的数大于负方向的数．（3）正数都大于0，负数都小于0，正数大于一切负数．（4）若从点A向右移动|a|个单位，得到B，则B点坐标为A的坐标加|a|，反之B点坐标为A的坐标减|a|．2．在墙壁上固定一根横放的木条，则至少需要钉子的枚数是（）A．1枚B．2枚C．3枚D．任意枚【考点】直线的性质：两点确定一条直线．【分析】根据直线的性质，两点确定一条直线解答．【解答】解：∵两点确定一条直线，∴至少需要2枚钉子．故选B．【点评】本题考查了直线的性质，熟记两点确定一条直线是解题的关键．3．如图所示的几何体，从上面看得到的平面图形是（）A．B．C．D．【考点】简单组合体的三视图．【分析】根据所看位置，找出此几何体的三视图即可．【解答】解：从上面看得到的平面图形是两个同心圆，故选：B．【点评】此题主要考查了简单几何体的三视图，关键是要把所看到的棱都表示到图中．4．在灯塔O处观测到轮船A位于北偏西54°的方向，同时轮船B在南偏东15°的方向，那么∠AOB的大小为（）A．69°B．111°C．141°D．159°【考点】方向角．【分析】首先计算出∠3的度数，再计算∠AOB的度数即可．【解答】解：由题意得：∠1=54°，∠2=15°，∠3=90°﹣54°=36°，∠AOB=36°+90°+15°=141°，故选：C．【点评】此题主要考查了方向角，关键是根据题意找出图中角的度数．5．将下面的直角梯形绕直线l旋转一周，可以得到如图立体图形的是（）A．B．C．D．【考点】点、线、面、体．【专题】常规题型．【分析】面动成体．由题目中的图示可知：此圆台是直角梯形转成圆台的条件是：绕垂直于底的腰旋转．【解答】解：A、是直角梯形绕底边旋转形成的圆台，故A错误；B、是直角梯形绕垂直于底的腰旋转形成的圆台，故B正确；C、是梯形底边在上形成的圆台，故C错误；D、是梯形绕斜边形成的圆台，故D错误．故选：B．【点评】本题考查直角梯形转成圆台的条件：应绕垂直于底的腰旋转．6．某商店把一种洗涤用品按标价的九折出售，仍可获利20%，若该洗涤用品的进价为21元，则标价为（）元．A．26 B．27 C．28 D．29【考点】一元一次方程的应用．【分析】设该商品的标价为x，则商品的售价为0.9x元，根据售价﹣进价=利润为等量关系建立方程求出其解即可．【解答】解：设该商品的标价为x，则商品的售价为0.9x元，由题意，得0.9x﹣21=21×20%，解得：x=28故选C．【点评】本题考查了销售问题的数量关系在生活实际问题的中的运用，一元一次方程的解法的运用，解答时运用售价﹣进价=进价×利润率建立方程是关键．二、填空题（本大题共8个小题；每小题3分，共24分．把答案写在题中横线上）7．﹣5的相反数是5，﹣的倒数是﹣2．【考点】倒数；相反数．【分析】根据只有符号不同的两个数互为相反数，可得一个数的相反数，根据乘积是1的两个数互为倒数，可得一个数的倒数．【解答】解：﹣5的相反数是5，﹣的倒数是﹣2，故答案为：5，﹣2．【点评】本题考查了倒数，分子分母交换位置是求一个数的倒数的关键．8．若a3﹣2n b2与5a3n﹣2b2是同类项，则n=1．【考点】同类项．【分析】根据同类项是字母相同，且相同的字母的指数也相同，可得答案．【解答】解：a3﹣2n b2与5a3n﹣2b2是同类项，3﹣2n=3n﹣2，n=1，故答案为：1．【点评】本题考查了同类项，相同的字母的指数也相同是解题关键．9．青藏高原是世界上海拔最高的高原，它的面积约为2 500 000平方千米．将它的面积用科学记数法表示应为 2.5×106平方千米．【考点】科学记数法—表示较大的数．【专题】应用题．【分析】把一个大于10的数写成科学记数法a×10n的形式时，将小数点放到左边第一个不为0的数位后作为a，把整数位数减1作为n，从而确定它的科学记数法形式．【解答】解：2 500 000=2.5×106平方千米．【点评】将一个绝对值较大的数写成科学记数法a×10n的形式时，其中1≤|a|＜10，n为比整数位数少1的数．10．计算：15°37′+42°51′=58°28′．【考点】度分秒的换算．【分析】把分相加，超过60的部分进为1度即可得解．【解答】解：∵37+51=88，∴15°37′+42°51′=58°28′．故答案为：58°28′．【点评】本题考查了度分秒的换算，比较简单，要注意度分秒是60进制．11．根据图提供的信息，可知一个杯子的价格是8元．【考点】二元一次方程组的应用．【分析】仔细观察图形，可知本题存在两个等量关系，即一个水壶的价格+一个杯子的价格=43，两个水壶的价格+三个杯子的价格=94．根据这两个等量关系可列出方程组．【解答】解：设水壶单价为x元，杯子单价为y元，则有，解得．答：一个杯子的价格是8元．故答案为：8．【点评】解题关键是弄清题意，找到合适的等量关系，列出方程组．12．用6根火柴最多组成4个一样大的三角形，所得几何体的名称是三棱锥或四面体．【考点】认识立体图形．【分析】用6根火柴，要使搭的个数最多，就要搭成立体图形，即三棱锥．【解答】解：要使搭的个数最多，就要搭成三棱锥，这时最多可以搭4个一样的三角形．图形如下：故答案为：4，三棱锥或四面体．【点评】此题主要考查了认识立体图形，本题要打破思维定势，不要只从平面去考虑，要考虑到立体图形的拼组．13．点A、B、C是同一直线上的三个点，若AB=8cm，BC=3cm，则AC=11或5cm．【考点】比较线段的长短．【专题】分类讨论．【分析】分点B在点A、C之间和点C在点A、B之间两种情况讨论．【解答】解：（1）点B在点A、C之间时，AC=AB+BC=8+3=11cm；（2）点C在点A、B之间时，AC=AB﹣BC=8﹣3﹣5cm．∴AC的长度为11cm或5cm．【点评】分两种情况讨论是解本题的难点，也是解本题的关键．14．填在下面各正方形中的四个数之间都有相同的规律，根据这种规律，m的值是158．【考点】规律型：数字的变化类．【专题】压轴题；规律型．【分析】分析前三个正方形可知，规律为右上和左下两个数的积减左上的数等于右下的数，且左上，左下，右上三个数是相邻的偶数．因此，图中阴影部分的两个数分别是左下是12，右上是14．【解答】解：分析可得图中阴影部分的两个数分别是左下是12，右上是14，则m=12×14﹣10=158．故答案为：158．【点评】本题是一道找规律的题目，要求学生通过观察，分析、归纳发现其中的规律，并应用发现的规律解决问题．解决本题的难点在于找出阴影部分的数．三、解答题（本大题共10个小题；共78分）15．计算（1）（﹣76）+（+26）+（﹣31）+（+17）（2）2（2b﹣3a）﹣3（2a﹣3b）．【考点】有理数的加法；整式的加减．【分析】（1）根据有理数的加法法则，即可解答．（2）先去括号，再合并同类项，即可解答．【解答】解：（1）（﹣76）+（+26）+（﹣31）+（+17）=﹣76﹣31+26+17=﹣107+43=﹣64．（2）2（2b﹣3a）﹣3（2a﹣3b）=4b﹣6a﹣6a+9b=13b﹣12a．【点评】本题考查了有理数的加法法则，解决本题的关键是熟记有理数的加法法则．16．解下列方程：（1）x﹣7=10﹣4（x+0.5）；（2）﹣=1．【考点】解一元一次方程．【专题】计算题．【分析】（1）方程去括号，移项合并，把x系数化为1，即可求出解；（2）方程去分母，去括号，移项合并，把x系数化为1，即可求出解．【解答】解：（1）去括号得：x﹣7=10﹣4x﹣2，移项合并得：5x=15，解得：x=3；（2）去分母得：3x﹣3﹣6﹣4x=6，移项合并得：x=﹣15．【点评】此题考查了解一元一次方程，其步骤为：去分母，去括号，移项合并，把x系数化为1，求出解．17．如图所示，直线l是一条平直的公路，A，B是两个车站，若要在公路l上修建一个加油站，如何使它到车站A，B的距离之和最小，请在公路上表示出点P的位置，并说明理由．（保留作图痕迹，并用你所学的数学知识说明理由）．【考点】作图—应用与设计作图．【分析】连接AB，与l的交点就是P点．【解答】解：如图所示：点P即为所求．【点评】此题主要考查了作图与应用作图，关键是掌握两点之间线段最短．18．（6分）（2015秋太和县期末）一个角的余角比这个角的少30°，请你计算出这个角的大小．【考点】余角和补角．【分析】设这个角的度数为x，根据互余的两角的和等于90°表示出它的余角，然后列出方程求解即可．【解答】解：设这个角的度数为x，则它的余角为（90°﹣x），由题意得：x﹣（90°﹣x）=30°，解得：x=80°．答：这个角的度数是80°．【点评】本题考查了余角的定义，熟记概念并列出方程是解题的关键．19．先化简再求值：﹣2y3+（2x3﹣xyz）﹣2（x3﹣y3+xyz），其中x=1，y=2，z=﹣3．【考点】整式的加减—化简求值；合并同类项；去括号与添括号．【专题】计算题．【分析】本题先将括号去掉，进行同类项合并，然后化简后，将值代入，即可求得结果．【解答】解：﹣2y3+（2x3﹣xyz）﹣2（x3﹣y3+xyz），其中x=1，y=2，z=﹣3．当x=1，y=2，z=﹣3时，原式=﹣3×1×2×（﹣3）=18．…（10分）【点评】本题考查整式的加减及化简求值，将式子进行同类项合并后，然后化简后即可求得结果．20．如图，∠AOB=110°，∠COD=70°，OA平分∠EOC，OB平分∠DOF，求∠EOF的大小．【考点】角平分线的定义．【专题】计算题．【分析】由∠AOB=110°，∠COD=70°，易得∠AOC+∠BOD=40°，由角平分线定义可得∠AOE+∠BOF=40°，那么∠EOF=∠AOB+∠AOE+BOF．【解答】解：∵∠AOB=110°，∠COD=70°∴∠AOC+∠BOD=∠AOB﹣∠COD=40°∵OA平分∠EOC，OB平分∠DOF∴∠AOE=∠AOC，∠BOF=∠BOD∴∠AOE+∠BOF=40°∴∠EOF=∠AOB+∠AOE+∠BOF=150°．故答案为：150°．【点评】解决本题的关键利用角平分线定义得到所求角的两边的角的度数．21．如图，点C在线段AB上，点M、N分别是AC、BC的中点．（1）若AC=8cm，CB=6cm，求线段MN的长；（2）若C为线段AB上任一点，满足AC+CB=a，其它条件不变，你能猜想MN的长度吗？写出你的结论并说明理由；（3）若C为直线AB上线段AB之外的任一点，且AC=m，CB=n，则线段MN的长为|m﹣n|．【考点】比较线段的长短．【专题】计算题．【分析】（1）点M是线段AC中点，则MC=AC，点N的线段BC中点，所以CN=CB，AC+BC=AB，AB已知，从而可求出MN长度．（2）根据以上分析可得MN=AB，线段MN的长度是线段AB的一半．（3）当点C在线段AB的延长线上时，MN等于MC减去BC=n，而MC=AC=m，从而可求出MN长度；当点C在线段BA的延长线上时，MN等于NC减去MC，NC=BC=n，MC=AC=m，从而可求出MN的长度．【解答】解：（1）MN=MC+CN=AC CB=7cm；（2）MN=MC+CN=AC=；（3）当点C在线段AB的延长线上时，MN=（m﹣n）；当点C在线段BA的延长线上时，MN=（n﹣m）；综合以上情况得：MN=．【点评】本题前两问主要根据题中图形得到各线段之间的关系，求出MN的长度，而第三问要分情况讨论，M在AB不同侧时有不同的情况，分析各情况得到MN的表达式．22．一只小虫从某点P出发，在一条直线上来回爬行，假定把向右爬行的路程记为正数，向左爬行的路程记为负数，则爬行各段路程（单位：厘米）依次为：+5，﹣3，+10，﹣8，﹣6，+12，﹣10．（1）通过计算说明小虫是否回到起点P．（2）如果小虫爬行的速度为0.5厘米/秒，那么小虫共爬行了多长时间．【考点】有理数的加减混合运算；正数和负数．【专题】应用题．【分析】（1）把记录到得所有的数字相加，看结果是否为0即可；（2）记录到得所有的数字的绝对值的和，除以0.5即可．【解答】解：（1）∵（+5）+（﹣3）+（+10）+（﹣8）+（﹣6）+（+12）+（﹣10），=5﹣3+10﹣8﹣6+12﹣10，=0，∴小虫能回到起点P；（2）（5+3+10+8+6+12+10）÷0.5，=54÷0.5，=108（秒）．答：小虫共爬行了108秒．【点评】此题主要考查正负数在实际生活中的应用，所以学生在学这一部分时一定要联系实际，不能死学．23．如图（1）所示，∠AOB、∠COD都是直角．（1）试猜想∠AOD与∠COB在数量上是相等，互余，还是互补的关系．请你用推理的方法说明你的猜想是合理的．（2）当∠COD绕着点O旋转到图（2）所示位置时，你在（1）中的猜想还成立吗？请你证明你的结论．【考点】余角和补角．【分析】（1）根据直角的定义可得∠AOB=∠COD=90°，然后用∠AOD和∠COB表示出∠BOD，列出方程整理即可得解；（2）根据周角等于360°列式整理即可得解．【解答】解：（1）∠AOD与∠COB互补．理由如下：∵∠AOB、∠COD都是直角，∴∠AOB=∠COD=90°，∴∠BOD=∠AOD﹣∠AOB=∠AOD﹣90°，∠BOD=∠COD﹣∠COB=90°﹣∠COB，∴∠AOD﹣90°=90°﹣∠COB，∴∠AOD+∠COB=180°，∴∠AOD与∠COB互补；（2）成立．理由如下：∵∠AOB、∠COD都是直角，∴∠AOB=∠COD=90°，∵∠AOB+∠BOC+∠COD+∠AOD=360°，∴∠AOD+∠COB=180°，∴∠AOD与∠COB互补．【点评】本题考查了余角和补角的定义，比较简单，用两种方法表示出∠BOD是解题的关键．24．某天，一蔬菜经营户用60元钱从蔬菜批发市场批了西红柿和豆角共40㎏到菜市场去卖，西红柿和豆角这天的批发价与零售价如下表所示：问：他当天卖完这些西红柿和豆角能赚多少钱？品名西红柿豆角批发价（单位：元/kg） 1.2 1.6零售价（单位：元/kg） 1.8 2.5【考点】二元一次方程组的应用．【专题】图表型．【分析】通过理解题意可知本题的两个等量关系，西红柿的重量+豆角的重量=40，1.2×西红柿的重量+1.6×豆角的重量=60，根据这两个等量关系可列出方程组．【解答】解：设西红柿的重量是xkg，豆角的重量是ykg，依题意有解得10×（1.8﹣1.2）+30×（2.5﹣1.6）=33（元）答：他当天卖完这些西红柿和豆角能赚33元．【点评】注意要先求出西红柿和豆角的重量，再计算利润．。

第三届IMC 国际数学竞赛初一年级组数学竞赛试卷A考试时间：90分钟,卷面总分：120分国籍___________ 姓名_________ 成绩________一.选择题40分 1.若200720080a b +=,则ab 是A 、正数B 、非正数C 、负数D 、非负数 2.若n 为正整数,有理数a 、b 满足01=+ba ,则必有 A 、0)1(2=+n nb a B 、0)1(122=++n nb aC 、0)1(32=+n n b aD 、0)1(1212=+++n n ba3.若22540x xy k ++是一个完全平方式,则k 是A 、162y B 、2y C 、42y D 、82y4.若0>-+c b a ,0>+-c b a ,0>++-c b a ,则200620062006⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫⎝⎛c c b b a a 的值A 、－1B 、0C 、1D 、－1或1 5.若20062007a =-,20072008b =-,20082009c =-,则 A 、a b c >> B 、a b c << C 、a c b << D 、c a b << 6.水池有一注水管,单独开放5小时,可注满水池,另有一出水管,单独开放18小时可把满水池的水放完,若两管齐放,注满水池所用的时间是 小时; A 、2390 B 、9023 C 、1390 D 、90137.甲、乙二人去商店购物,他们所带钱数的比是7:6,甲用掉50元,乙用掉60元,二人余下的钱数之比为3:2,则余下的钱数分别为A 、140元、120元B 、60元、40元C 、90元60元D 、80元、80元8. 已知一个三角形中,两个角的度数比为4:5,第三个角的度数比前两角的度数和的13少12︒,则此三角形的三个内角分别为 ;A 、︒9070︒20︒B 、80︒64︒36︒C 、70︒48︒62︒D 、78︒64︒38︒9. Mary spends % of her income and saves $240 a month. Tom saves $330, which is 15% of his monthly income. Then earns more and by how much.A 、Mary earns $1920 more than TomB 、Tom earns $280 more than MaryC 、Tom earns $2200 more than MaryD 、Mary earns $280 more than Tom10. 首位数字是2,且其数字中恰有两个相同的四位数如2556；2677等共有 个;A 、426 B 、432 C 、216 D 、213二、填空题50分 11. The sequence of number: 81, 891, 8991, (109)89991个.Then sum of them is _______12.设1,322,83=-=-=c b a ; 则{}222253(2)a b ab c b c abc b ⎡⎤-+---++⎣⎦=_________ 13.某仓库有一批粮食入库,称粮时记录的重量单位：千克如下：81,76,82,80,83,82,77,79,77,84,则这批粮食共有_________千克; 14. 在自然数中,两个四位自然数之差与2007的和的最小值是_______15.The sum of n different positive integers is less than 2007. The greatest positive value of n is ________ 16. 以A 、B 、C 、D 、E 、F 、G 、H 为端点的线段有_______条;17.在桌上摆有一些大小相同的正方体木块,俯视图、左视图如下,要摆出这样的图形最少要___________块正方体木块 18.已知圆A 和圆B 半径都是r,且圆B 过圆A 的圆心,则阴影部分的面积为______;用r 和π表示19.一张矩形毯子卷成一个6层空心圆柱形状,已知毯子长10米,宽1.5米,厚0.01米,则空心圆柱卷的体积是___________; 20.使得连乘积975×972×965×n 的末四位数字都是零的最小的正整数n 的值是________;三、解答题30分 21. 若已知12=++c b a ,568222=+-+c c b a ,求ca bc ab --的值.22.甲、乙两个粮库要向A 、B 运送粮食,A 地需要70吨,B 地需要110吨;现决定从甲库调出100吨,从乙库调出80吨,甲、乙粮库到A 、B 两地的路程和运费如下表：问：当甲、乙两库各运往A 、B 两地多少吨时,总运费最省最省的总运费是多少元 23.轮船以相等的速度在A 、B 、C 三个港口之间循环航行;B 、C 间所用的时间等于C 、A 间与A 、B 间所需时间之和的四分之三；A 、B 间与B 、C 间所需时间之和等于A 、C 间所需时间的三倍;若轮船的速度每小时增加1海里,则A 、C 间与A 、B 间所需时间之差为1小时20分钟,且三个港口循环航行一周所需时间将缩短1小时20分钟,求三个港口间的距离和轮船的速度; 答案： 1. B 2. D 3. A 4. C 5. A 6. D 7. C 8. B 9. B 10. B 11. 9999009个12. 87713. 801 14. 2007 15. 62 16. 22 17. 818.22332r r -π19. 立方米 20. 20 21. 200822. 甲—A 地70吨,甲—B 地30吨；乙—B80－吨,总运费最省,此时费用为37100元; 23. 船速：14海里；BC 间距：120海里； CA 间距：70海里；AB 间距：90海里第三届IMC 国际数学竞赛 初一级组数学竞赛试卷B考试时间：90分钟,卷面总分：120分国籍___________ 姓名_________ 成绩________一、选择题40分 1.若a 为实数,则代数式1a -的最小值为 ;A 、－2B 、－1C 、0D 、1 2.一个多项式除以21x -所得到的商式是21x +,余式是5x ,则被除式是 ; A 、32321x x x -+- B 、32271x x x -+- C 、322931x x x +-- D 、32771x x x -+- 3.使等式312310x x ++-+=成立的实数x ;A 、不存在B 、只有一个C 、只有2个D 、有无数个 4.若22540x xy k ++是一个完全平方式,则k 是A 、162y B 、2y C 、 42y D 、 82y5.若0>-+c b a ,0>+-c b a ,0>++-c b a ,则200820082008a b c a b c ⎛⎫⎛⎫⎛⎫-+ ⎪ ⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭的值A 、－1B 、0C 、1D 、－1或1 6.如图,已知五角星的顶点为A 、B 、C 、D 、E,则∠A+∠B+∠C+∠D+∠E= A 、︒90 B 、180︒ C 、270︒ D 、360︒ 7.马戏团的“小猴骑车”是由5只猴子用5辆自行车表演的;每只猴子至少骑一次车,但一只猴子不能重复骑同一辆车,表演结束后,5只猴子分别骑了2、2、3、5、x 次,5 辆车分别被骑了1、1、2、4、y 次,则x+y =A 、5B 、6C 、7D 、8 8.把数字和字母组成的列进行轮换,每次轮换把首位的数字和首位的字母分别移放在数字组和字母组的末位;第一次；00708082 MOCMOYNBSI 第二次：07080820 OCMOYNBSIM依次进行下去,当全列还原成原来的顺序时,所需要的次数最少是 次; A 、20 B 、40 C 、60 D 、80 9.Mary and Lily made 240 paper stars in 4 days .For each day, they made 12 more than the day before. Then the number of the paper stars made on the 1st day are________. A 、12 B 、38 C 、42 D 、60 10.设a,b,c 是三个整数,且a,b,c =60,a,b =4,b,c =3．注：a,b,c 表示a,b,c 的最小公倍数,a,b 表示a,b 的最大公约数,则a+b+c 的最小值是A 、30．B 、31．C 、32．D 、33 二、填空题50分 11. 在代数式32x y 中,x 与y 的值各增加10％,则该代数式的值增加了________%12. 222(21)-＋222)23(-＋222)34(-＋222)45(-＋222)56(-=____________13. 若3+-y x 与2007x y +-互为相反数,则=--+22)()2(y x y x 14. 在自然数中,两个四位自然数之差与2007的和的最小值是_______15.如图,∠AOC 是直角,∠COD=20︒,且OB 、OD 分别为∠AOC 、∠BOE 的平分线,则∠AOE=______16. The missing number in the following arrangement is __________.17. 使得连乘积975×972×965×n 的末四位数字都是零的最小的正整数n 的值是________; 18. 设c 为正整数,且a+b=c ,b+c=d, d+a=b, 则a+bb+cc+dd+a 的最小值是__________; 19.已知圆A 和圆B 半径都是r,且圆B 过圆A 的圆心,则阴影部分的面积为______;用r 和π表示20.有一串如下排列的球黑球为实心球,白球为空心球共有2007个,则空心球数为_______;三、解答题30分 21. 设7:4:3::=z y x ,且182=+-z y x ,求z y x -+2的值;22.将分别写有1、2、3、4、5、6、7、8、9的九张正方形卡片排成一排,发现恰为一个能被11整除的最大的九位数,请写出这九张卡片的排列顺序,并简述推理过程; 23.轮船以相等的速度在A 、B 、C 三个港口之间循环航行;B 、C 间所用的时间等于C 、A 间与A 、B 间所需时间之和的四分之三；A 、B 间与B 、C 间所需时间之和等于A 、C 间所需时间的三倍;若轮船的速度每小时增加1海里,则A 、C 间与A 、B 间所需时间之差为1小时20分钟,且三个港口循环航行一周所需时间将缩短1小时20分钟,求三个港口间的距离和轮船的速度; 答案： 1. B 2. B 3. A 4. A 5. C 6. B 7. B 8. B 9. C 10. B 11. 12. 285 13. 9072135 14. 2007 15. 175度 16. 41 17. 20 18. 2419.22332r r -π 20. 61 21. 8 22.23. 船速：14海里；BC 间距：120海里； CA 间距：70海里；AB 间距：90海里初中一年级组决赛试题考试时间：90分钟,卷面总分：120分一、选择每题5分,共50分 1.命题；1对顶角相等；2相等的角是对顶角；3垂直与一条直线的两条直线平行；4平行于一条直线的两条直线垂直;其中命题正确的个数为 A. 1 B. 2 C. 3 D. 42.在a 、b 、c 三个数中,有如下三个结论：甲：至少有两个互为相反数,则a+b+c=0; 乙：至少有两个互为相反数,则a+b+c=0,222()()()0a b b c c a +++++=,丙：至少有两个互为相反数,则()()()0a b b c c a +++=其中正确的结论个数是 A. 0 B. 1 C. 2 D. 3 3.已知4=-y x ,7=+y x ,则y x += A. 23± B. 211± C. 7± D. 11± 4.Given equation 282008x x x ++++=, then the number of its solution is A. 4 B. 3 C. 2 D. 15. △ABC 的三条外角平分线相交成一个△LMN,则△LMN 一定为 A.直角三角形 B.钝角三角形 C.锐角三角形 D.不是锐角三角形6.)1009911()29911()19911(⨯+++⨯++⨯+最接近的整数是 A. 101 B. 149 C. 150 D. 151 7.┄,问第505个位置的数字是B. 1C. 6 8.甲用1000元人民币购买了一手股票,随即他将这手股票转卖给乙,获利10%,而后乙又将这手股票反卖给甲,但乙损失了10%. 最后甲按乙卖给甲的价格的九折将这手股票卖给了乙,在上述股票交易中 ;A ．甲刚好亏盈平衡B ．甲盈利1元C ．甲亏109元D ．甲亏本元 9.如图⑴,小强拿一张正方形的纸,沿虚线对折一次得图⑵,再对折一次得图⑶,然后用剪刀沿图⑶中的虚线剪去一个角,再打开后的形状是 ;A. B. C. D10.将自然数1～2008按以下格式排列：1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 … … … … … … …请你用3×43行,4列的长方形框出12个数,使它们的和是2010; 那么这12个数中最大的数是 ;A ．173B ．174C ．175D ．176 二、填空题每题5分,共50分 11.In the figure given. ABCD and AEFD are all the rectangles, the area of the rectangle ABCD is 12cm . Then the area of the shaded part is ______2cm . 12. Given equation2007122320072008x xx+++=⨯⨯⨯,then x =_______;.13.Alphabetic are puzzles created by replacing numerical digits in arithmetic problems with letters. Each letter represents a digit and no digit represents two different letters ;How many different seven －digit numbers ABCDEFG can be made upAnswer ：________14.2008年8月8日是星期五,问在此以后的第882008天是星期_____15.Let 5x is a two －digit and yz 4 is a three －digit . If x, y, z satisfy the equation 5415120x yz ⋅=, then x +y+z=________; Answer: _________16.已知 x,y 为整数,且y 2= x 2―2008. 则代数式yx y xy x +-+222的值为______;17. 若n x mx x +++111323能被56132+-x x 整除,则整数m 值是_______;18.2008个数排成一行,除了两头的两个数以外,每个数的3倍恰好等于它两边两个数的和,这一行数最左边的几个数是这样的0,1,3,8,21,┄,则这一行数最右边的一个数被3除的余数是______19. Tom earns a fixed amount of money every month. He uses 13of his salary for contributions, taxes and insurance premium. He saves19of the remainder. He has RMB2320 yuan left for other expenses. How much does Tom earn a month Answer :_______ 20.甲、乙、丙三人做游戏;第一盘甲输了,甲要付给乙、丙硬币,分别等于乙和丙原有的硬币数；第二盘乙输了,乙付给甲和丙硬币,分别等于甲和丙现有的硬币数;第三盘丙输了,丙要付给甲和乙硬币,分别等于甲和乙现有的硬币数;结果,三人身上的硬币数都为160个;则乙原有的硬币数是________个;三、解答下列各题;要求写出解答过程,每题10分,共20分 21.一个长方形把平面分成两部分,则10个长方形最多可把平面分成多少部分若n 个长方形能把平面最多分成多少份写出与n 的关系式 . 22.甲、乙两个钟都不准,某天正午,甲、乙两个钟对照无线电报时对钟;第二天白天甲钟12点时,乙钟是11点48分;之后不久,乙钟对照无线电正午的报时对钟,甲还照原样走;第三天白天乙钟12点时,甲钟是12点18分;甲、乙两钟一天走多少分多少秒或一天慢多少又;第四天白天甲钟12点时,乙钟表示的是什么时间 答案：一、选择题每题5分二、填空题每题5分三、解答题每题10分21. 10个长方形最多把平面分成362份;n 个长方形最多能把平面分成2+4n －1份; 22. 解：设甲、乙两钟一天各快x 分、y 分,则甲钟的一小时,在正确的钟上是602424x +小时;因而甲钟的24小时,在正确的钟上是60242424x +⨯小时;所以在这之前甲快2460242424xx ⨯+⨯分,乙钟快2460242424y x ⨯+⨯,甲比乙快126024)(24=+-⨯x y x ;1同样,乙钟的24小时,在正确钟上是60242424y +⨯,所以得6024)(24y y x x +-+=18 2由1和2得≈=119702x 5分秒y=20123-分=—6分9秒;因而第四天甲钟在12点时,乙钟是12是—3×12分＋20123分=11时30分9秒法2：设甲、乙钟和正确的钟的速度为u 、v 、w ,则v u 60482324=,uv w 6018482424=+,从这两式,求满足vy u x w 6024602424+=+=的x 、y。

七年级数学竞赛试题(含答案)一、耐心填一填（每题5分,共50分）1、某天,5名同学去打羽毛球,从上午8:45一直到上午11:05,若这段时间内,他们一直玩双打（即须4人同时上场）,则平均一个人的上场时间为________分2、已知：一条射线OA,若从点O再引两条射线OB、OC,使∠AOB=600,∠BOC=200,则∠AOC=___________度3、()()_______________1541957.0154329417.0=-⨯+⨯+-⨯+⨯。

4、定义a*b=ab+a+b,若3*x=27,则x的值是________。

5、有一个正方体,在它的各个面上分别标上字母A、B、C、D、E、F,甲、乙、丙三位同学从不同方向去观察其正方体,观察结果如图所示。

问：F的对面是_______。

FA DBCAED C6 A、B、C、D、E、F六足球队进行单循环比赛,当比赛到某一天时,统计出A、B、C、D、E、五队已分别比赛了5、4、3、2、1场球,则还没与B队比赛的球队是________。

7、正方体每一面不同的颜色对应着不同的数字,将四个这样的正方体如图拼成一个水平放置的长方体,那么长方体的下底面数字和为________。

8、小李同学参加了学校组织的名为“互帮互助向未来”活动,为此小李自己在家制作了四份小礼物,准备送给他的新同学,四份小礼物分别装在形状完全一样的小长方体的盒子里,每个小长方体的长、宽、高分别是3、1、1,然后把这四个小长方体盒子用漂亮的丝带捆绑成一个大长方体,那么这个大长方体的表面积可能有________ 中不同的值,其中最小值为________。

9、当a ______时,方程组223196922x y a ax y a a⎧+=+-⎪⎨-=-+⎪⎩的解是正数。

10、如图1,棱长分别为1厘米,2厘米,3厘米,5厘米的四个正方体紧贴在一起,则所得到的多面体的表面积是________平方厘米。

二、细心选一选（每题5分,共30分）1、如果有2015名学生排成一列,按1、2、3、4、3、2、1、2、3、4、3、2、1……的规律报数,那么第2015名学生所报的数是（）A、1B、2C、3D、42、俗话说“商场如战场”,“买的永远没有卖的精”。

九仓中学--七年级数学竞赛试题（卷）(时间：120分钟 总分：120分)班级： 姓名 总分________一、选择题（本大题共6小题，每小题5分，共30分）以下每题的四个选项中，仅有一个是正确的）1. 文具店的老板均以60元的价格卖了两个计算器，其中一个赚了20﹪，另一个亏了20﹪，则该老板（ ）A. 赚了5元B. 亏了25元C. 赚了25元D. 亏了5元 2．观察这一列数：34-，57, 910-, 1713,3316-，依此规律下一个数是（ ） A.4521 B.4519 C. 6519 D. 65213.在一个停车场内有24辆车，其中汽车有4个轮子，摩托车有3 个轮子，且停车场上只有汽车和摩托车，这些车共有86个轮子，那么摩托车应为( )A . 14辆B . 10辆C . 16辆D . 12辆 4. 如图是一个4×4的正方形网格，图中所标示的7个角的角度之和等于（ ）A. 585°B. 540°C. 270°D. 0315 5．若14+x 表示一个整数，则整数x 可取值共有( ). A.3个 B.4个 C.5个 D.6个 6.方程13153520052007x x x x +++=⨯的解是 x ＝（ ） A.20072006 B.20062007 C. 10032007 D.10032007二、填空题（本大题共6小题，每小题5分，共30分）．7．若|x-y+3|+()21999-+y x =0，则yx yx -+2= . 8. 等腰三角形的一个外角等于0140, 则这个等腰三角形的顶角为___ ____. 9.有一个正方体，在它的各个面上分别标上字母A 、B 、C 、D 、E 、F ，甲、乙、丙三位同学从不同方向去观察其正方体，观察结果如图所示.问：F 的对面是 .10. 用三种边长相等的正多边形铺地面，已选了正方形和正五边形两种，还应选正___边形.11.北京到兰州的铁路之间有25个站台（含北京和兰州），设制 种票才能满足票务需求. 12.设c b a ,,为有理数，则由abcabcc c b b a a +++ 构成的各种数值是 . 三、解答题（本大题共4小题，每小题15分，共60分） 要求：写出推算过程． 13.岳飞是我国古代宋朝的民族英雄，曾任通泰镇抚史、兼泰州知州.据说在泰州抗击金兵期间，有一次曾向将领们讲了如下一个布阵图，如图4是一座城池，在城池的四周设了八个哨所，一共由24个卫士把守，按直线算，每边都有11个人，后来由于军情发生变化，连续四次给哨所增添兵力，每次增加4人，但要求在增加人员后，仍然保持每边11个人把守.请问，兵力应如何调整？14. 对于有理数x ，y ，定义新运算：x*y=2ax +bx+c ，其中a 、b 、c 是常数，等式右边是通常的加法与乘法运算．已知1*2=9，（-3）*3=6，0*1=2，求2*（-7）的值．5 1 5151 5 115．小明和哥哥在环形跑道上练习长跑。

七年级数学竞赛试题一、选择题：1、已知152004+-=a ，则a 是（ ）A 、合数B 、质数C 、偶数D 、负数 2若7a+9|b|=0，则a b 2一定是（ ）A 、正数B 、负数C 、非负数D 、非正数3、a 与b 之和的倒数的2003次方等于1，a 的相反数与b 之和的2005次方也等于1，则a 2003+b 2004=（ ）A 、22005B 、2C 、1D 、04、如图1，三角形ABC 的底边BC 长3厘米，BC 边上的高是2厘米，将三角形以每秒3厘米的速度沿高的方向向上移动2秒，这时，三角形扫过的面积是（ ）平方厘米。

A 、21B 、19C 、17D 、155、小明的妈妈春节前去市场买了3公斤葡萄和2公斤苹果，花了8元钱，春节后，再去市场买这两种水果，由于葡萄每公斤提价5角钱，苹果每公斤降3角钱，买7公斤葡萄和5公斤苹果共花了21元，则春节后购物时，（葡萄、苹果）每公斤的价格分别是（ ）元。

A 、（2.5，0.7） B 、（2，1） C 、（2，1.3） D 、（2.5，1）6、当1-=x 时，代数式8322+-bx ax 的值为18，这时，代数式269+-a b =（ ） A 、28 B 、—28 C 、32 D 、—327、The sum or n different postitive integers is less than 50.The greatest possible value of n is （ ）A 、10B 、9C 、8D 、7 （英汉小词典positive integer ：正整数） 8、已知∠A 与∠B 之和的补角等于∠A 与∠B 之差的余角，则∠B=（ ）A 、75°B 、60°C 、45°D 、30°9、如图2，一个正方体的六个面上分别标有数字1，2，3，4，5，6。

根据图中三种状态所显示的数字，“？”表示的数字是（ ） A 、1 B 、2 C 、4 D 、6 二、填空题：10、若正整数x ，y 满足2004x=15y ，则x+y 的最小值是___________；11、数列1，1，2，3，5，8，13，21，34，55，…的排列规律：前两个数是1，从第3个数开始，每一个数都是它前两个数的和，这个数列叫做斐波契数列，在斐波契数列前2004个数中共有___________个偶数。

数学试题 第1页（共4页） 数学试题 第2页（共4页）………………○………………内………………○………………装………………○………………订………………○………………线………………○………………………………○………………外………………○………………装………………○………………订………………○………………线………………○………………… 学校：______________姓名：_____________班级：_______________考号：______________________绝密★启用前|豫2018-2019学年下学期期中原创卷A 卷七年级数学（考试时间：100分钟 试卷满分：120分）注意事项：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答第Ⅰ卷时，选出每小题答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

写在本试卷上无效。

3．回答第Ⅱ卷时，将答案写在答题卡上。

写在本试卷上无效。

4．考试结束后，将本试卷和答题卡一并交回。

5．考试范围：人教版七下第5—7章。

第Ⅰ卷一、选择题（本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一个选项是符合题目要求的）1．在下列四个汽车标志图案中，能用平移变换来分析其形成过程的图案是 A ．B ．C ．D ．2．下列四个数中，是无理数的是 A ．|-2|B ．38C ．1.732D ．2-3．16的算术平方根是 A ．2B ．4C ．±2D ．±44．如图，与∠B 是同旁内角的角有A ．1个B ．2个C ．3个D ．4个5．如图，在数轴上表示7的点在哪两个字母之间A ．B 与C B ．A 与B C ．A 与CD ．C 与D6．如图，l 1与l 3交于点P ，l 2与l 3交于点Q ，∠1=104°，∠2=87°，要使得l 1∥l 2，下列操作正确的是A ．将l 1绕点P 逆时针旋转14°B ．将l 1绕点P 逆时针旋转17°C ．将l 2绕点Q 顺时针旋转11°D ．将l 2绕点Q 顺时针旋转14°7．已知点P （m +3，2m +4）在x 轴上，那么点P 的坐标为 A ．（-1，0）B ．（1，0）C ．（-2，0）D ．（2，0）8．如图，点E 在BC 的延长线上，下列条件中不能判定AB ∥CD 的是A ．34∠=∠B ．12∠=∠C ．B DCE ∠=∠D ．180B DAB ∠+∠=︒9．已知点P （a ，b ）到x 轴的距离是2，到y 轴的距离是5，且||a b a b -=-，则P 点的坐标是 A ．（5，2）B ．（2，−5）C ．（5，2）或（5，−2）D ．（2，−5）或（5，2）10．如图，在平面直角坐标系中，从点P 1（-1，0），P 2（-1，-1），P 3（1，-1），P 4（1，1），P 5（-2，1），P 6（-2，-2），……，依次扩展下去，则P 2018的坐标为A ．（-503，503）B ．（504，504）C ．（-506，-506）D ．（-505，-505）第Ⅱ卷二、填空题（本大题共5小题，每小题3分，共15分）1113a ，小数部分是b ，则a -b =__________．数学试题 第3页（共4页） 数学试题 第4页（共4页）………………○………………内………………○………………装………………○………………订………………○………………线………………○………………此卷只装订不密封………………○………………外………………○………………装………………○………………订………………○………………线………………○………………12．如图，DE ∥BC ，EF ∥AB ，图中与∠BFE 互补的角有__________．13．已知一个正数的两个平方根分别是4a +1和a -11，则这个正数是__________． 14．如图，在正方形网格中，若A （1，1），B （2，0），则C 点的坐标为__________．15．已知点A （0，1），B （0，2），点C 在x 轴上，且2ABC S =△，则点C 的坐标__________． 三、解答题（本大题共8小题，共75分．解答应写出文字说明、证明过程或演算步骤）16．（本小题满分8分）计算：（1）23(2)|21|27-+--；（2）310.048|32|34+-++-+．17．（本小题满分9分）求下列代数式的值：（1）如果a 2=4，b 的算术平方根为3，求a +b 的值；（2）已知x 是25的平方根，y 是16的算术平方根，且x <y ，求x -y 的值．18．（本小题满分9分）如图，12180AGF ABC ∠=∠∠+∠=︒，． （1）试判断BF 与DE 的位置关系，并说明理由； （2）若2150BF AC ⊥∠=︒，，求AFG ∠的度数．19．（本小题满分9分）（1）已知：2a +1的算术平方根是3，3a -b -1的立方根是2，求320b a +的值．（2）已知a 是10的整数部分，b 是它的小数部分，求a 2+（b +3）2的值．20．（本小题满分9分）如图，直线AB 与CD 相交于点O ，OF ，OD 分别是∠AOE ，∠BOE 的平分线．（1）写出∠DOE 的补角；（2）若∠BOE =62°，求∠AOD 和∠EOF 的度数；（3）射线OD 与OF 之间的夹角是多少？21．（本小题满分10分）如图，∠BAP +∠APD =180°，∠AOE =∠1，∠FOP =∠2．（1）若∠1=55°，求∠2的度数； （2）求证：AE ∥FP ．22．（本小题满分10分）如图所示，把三角形ABC 向上平移3个单位长度，再向右平移2个单位长度，得到三角形A 1B 1C 1．（1）在图中画出三角形A 1B 1C 1； （2）写出点A 1，B 1的坐标；（3）在y 轴上是否存在一点P ，使得三角形BCP 与三角形ABC 面积相等？若存在，请直接写出点P 的坐标；若不存在，说明理由．23．（本小题满分11分）已知下面四个图形中，AB ∥CD ，探究四个图形中，∠APC 与∠PAB ，∠PCD 的数量关系．（1）图①中，∠APC 与∠PAB ，∠PCD 的关系是__________；（2）图②中，∠APC 与∠PAB ，∠PCD 的关系是__________；（3）请你在图③和图④中任选一个，说明∠APC 与∠PAB ，∠PCD 的关系，并加以证明．。

数学竞赛试卷七年级【含答案】专业课原理概述部分一、选择题（每题1分，共5分）1. 如果一个数的平方根是9，那么这个数是：A. 81B. 9C. 3D. -92. 下列哪个数是有理数？A. √2B. √3C. √5D. √93. 下列哪个数是整数？A. 3.14B. 2.5C. 5.0D. -3.54. 下列哪个数是负数？A. -1B. 0C. 1D. 25. 下列哪个数是偶数？A. 21B. 23C. 25D. 27二、判断题（每题1分，共5分）1. 两个负数相乘的结果是正数。

（）2. 两个正数相乘的结果是负数。

（）3. 两个负数相除的结果是正数。

（）4. 两个正数相除的结果是负数。

（）5. 0乘以任何数都等于0。

（）三、填空题（每题1分，共5分）1. 如果一个数的平方是16，那么这个数是______。

2. 如果一个数的平方根是4，那么这个数是______。

3. 两个负数相乘的结果是______。

4. 两个正数相乘的结果是______。

5. 0乘以任何数都等于______。

四、简答题（每题2分，共10分）1. 请解释有理数的概念。

2. 请解释整数的概念。

3. 请解释负数的概念。

4. 请解释偶数的概念。

5. 请解释奇数的概念。

五、应用题（每题2分，共10分）1. 计算下列各式的值：a) -3 + 7b) 5 (-2)c) -4 × 6d) -9 ÷ 3e) 14 ÷ (-2)2. 判断下列各式的符号：a) -(-5)b) -(+8)c) -(-12)d) -(+15)e) -(-20)3. 计算下列各式的值：a) √16c) √36d) √49e) √644. 判断下列各数是否为整数，并解释原因：a) 3.14b) 2.5c) 5.0d) -3.5e) 8.95. 判断下列各数是否为负数，并解释原因：a) -1b) 0c) 1d) 2e) -3六、分析题（每题5分，共10分）1. 请分析并解释为什么两个负数相乘的结果是正数。