2021-2022年高三数学期末模拟试卷及试卷分析-旧人教

高三模考数学试卷分析与反思
一、试卷概况
高三模考数学试卷一共包括选择题和解答题两部分。

整份试卷共有5道选择题和3道解答题, 总分为150分。

试卷内容涵盖了高三教学的重点难点知识，并以综合能力测试为主。

二、选择题分析
选择题部分的设计主要考查了学生对基础知识的掌握和运用能力。

其中，有一部分题目侧重于考察学生对概念理解的深度，另一部分则注重检验学生解题的技巧和逻辑思维能力。

整体而言，选择题难度适中，符合高三学生的知识水平。

三、解答题分析
解答题部分主要考查了学生对知识点的深度理解和综合运用能力。

其中，第一题要求学生运用导数计算函数在某点的切线斜率，考验了学生的微积分知识掌握情况；第二题涉及到概率统计，考查了学生的数据分析能力；第三题是一道较为综合性的题目，要求学生结合几何知识进行证明，考验了学生的逻辑推理和证明能力。

整体来看，解答题难度适中，但对学生的综合能力提出了更高的要求。

四、试卷反思
通过对这份高三模考数学试卷的分析，我们发现试卷内容较为全面，既涵盖了基础知识的考查，也注重了综合能力的培养。

但同时，也有一些可以改进的地方。

例如，在选择题设计上，可以增加一定的拓展性题目，来引导学生进行更深层次的思考；在解答题部分，可以适当增加一些实际问题，帮助学生将数学知识与生活实际联系起来，提高学生的综合运用能力。

综合而言，高三模考数学试卷是一份比较全面的试卷，既考查了学生的基础知识掌握情况，也注重了学生的综合能力培养。

希望通过此次试卷分析与反思，可以为今后试卷的设计提供一定的参考，帮助学生更好地提升数学学科的学习兴趣和能力。

一、选择题1．如图所示，已知圆1C 和2C 的半径都为2，且1223C C =，若在圆1C 或2C 中任取一点，则该点取自阴影部分的概率为（ ）A 33533π+B 33533π+C 331033π+D 331033π+2．若即时起10分钟内,甲乙两同学等可能到达某咖啡厅,则这两同学到达咖啡厅的时间间隔不超过3分钟的概率为( ) A ．0.3 B ．0.36C ．0.49D ．0.513．某研究机构在对具有线性相关的两个变量x 和y 进行统计分析时，得到如下数据：x 4 6 8 10 12 y12356由表中数据求得y 关于的回归方程为落在回归直线下方的概率为（ ） A ．25B ．35C ．34D ．124．设向量()()1,,a x y x y R =-∈，若1a ≤，则y x ≥的概率为（ ） A ．14B ．1142π- C ．114π-D ．3142π+ 5．计算11111212312310++++⨯⨯⨯⨯⨯⨯⨯，执行如图所示的程序根图，若输入的10N =，则图中①②应分别填入（ ）A ．1T k=，k N > B ．1T k=，k N ≥ C ．TT k=，k N > D ．TT k=，k N ≥ 6．运行如图所示的程序框图，若输出S 的值为129，则判断框内可填入的条件是（ ）A ．4?k <B ．5?k <C ．6?k <D ．7?k <7．执行如图的程序框图，若输出的6n =，则输入整数p 的最大值是( )A ．15B ．16C ．31D ．328．执行如下图的程序框图，如果输入的N 的值是7，那么输出的p 的值是（ ）A ．3B ．15C ．105D ．9459．为了了解某同学的数学学习情况，对他的6次数学测试成绩进行统计，作出的茎叶图如图所示，则下列关于该同学数学成绩的说法正确的是( )A ．中位数为83B ．众数为85C ．平均数为85D ．方差为1910．某班统计一次数学测验的平均分与方差，计算完毕才发现有位同学的分数还未录入，只好重算一次.已知原平均分和原方差分别为x ，2s ，新平均分和新方差分别为1x ，21s ，若此同学的得分恰好为x ，则（ ）A ．1x x =，221s s = B ．1x x =，221s s < C ．1x x =，221s s >D ．1x x <，221s s =11．采用系统抽样方法从960人中抽取32人做问卷调查，为此将他们随机编号1，2，⋯，960，分组后在第一组采用简单随机抽样的方法抽到的号码为29，则抽到的32人中，编号落入区间[]200,480的人数为 A ．7B ．9C ．10D ．1212．高二某班共有学生60名，座位号分别为01, 02, 03，···, 60.现根据座位号，用系统抽样的方法，抽取一个容量为4的样本.已知03号、18号、48号同学在样本中，则样本中还有一个同学的座位号是（ ）A．31号B．32号C．33号D．34号二、填空题13．某同学同时掷两颗骰子，得到点数分别为a，b，则双曲线2222x y1a b-=的离心率e5>的概率是______．14．若从甲、乙、丙、丁4位同学中选出2名代表参加学校会议，则甲、乙两人至少有一人被选中的概率为____.15．甲、乙二人约定某日早上在某处会面，甲在7:00~7:20内某一时刻随机到达，乙在7:05~7:20内某一时刻随机到达，则甲至少需等待乙5分钟的概率是________. 16．若下面程序中输入的n值为2017，则输出的值为__________.17．已知某程序框图如图所示，则执行该程序后输出的结果是_____18．已知下列程序INPUTtIFt≤3THENC=0.2ELSEC=0.2+0.1*(t-3)ENDIFPRINTCEND当输入t=5时，输出结果是____.19．水痘是一种传染性很强的病毒性疾病，容易在春天爆发，武汉疾控中心为了调查某高校高一年级学生注射水痘疫苗的人数，在高一年级随机抽取了5个班级，每个班级的人数互不相同，若把每个班抽取的人数作为样本数据，已知样本平均数为5，样本方差为4，则样本数据中最大值为__________．20．抽样统计甲、乙两位同学5次数学成绩绘制成如下图所示的茎叶图,则成绩较稳定的那位同学成绩的方差为__________．三、解答题21．口袋里装有编号为1，2，3，4的四个小球，有放回．．．的抽取两次，记录两次取到小球的编号分别为x，y.奖励规则如下：xy≤，则奖励玩具一个；①若3xy≥，则奖励水杯一个；②若8③其余情况奖励饮料一瓶. 小亮准备参加此项活动. （Ⅰ）求小亮获得玩具的概率；（Ⅱ）请比较小亮获得水杯与获得饮料的概率的大小，并说明理由.22．某商场有奖销售中，购满100元商品得1张奖券，多购多得，100张奖券为一个开奖单位，每个开奖单位设特等奖1个，一等奖10个，二等奖50个，设一张奖券中特等奖、一等奖、二等奖的事件分别为A ，B ，C ，可知其概率平分别为1(),1000P A =101(),1000100P B ==501()100020P C ==． （1）求1张奖券中奖的概率；（2）求1张奖券不中特等奖且不中一等奖的概率． 23．给出某班45名同学的数学测试成绩，60分及以上为及格，要求统计及格人数，及格同学的平均分，全班同学的平均分，画出程序框图，并写出程序语句.24．设计程序求π的近似值可以用公式:2222π1116123=+++…+21n ,用此公式求2π6,即逐项进行累加,直到21n <0.000 01为止(该项不累加),然后求出π的近似值. 25．某企业投资两个新型项目，投资新型项目A 的投资额m （单位：十万元）与纯利润n（单位：万元）的关系式为 1.70.5n m =-，投资新型项目B 的投资额x （单位：十万元）与纯利润y （单位：万元）的散点图如图所示.（1）求y 关于x 的线性回归方程；（2）根据（1）中的回归方程，若A ，B 两个项目都投资60万元，试预测哪个项目的收益更好.附：回归直线y bx a =+的斜率和截距的最小二乘估计分别为1221ni ii nii x y nx yb xnx==-=-∑∑，a y bx =-.26．我国北方广大农村地区、一些城镇以及部分大中城市的周边区域，还在大量采用分散燃煤和散烧煤取暖，既影响了居民基本生活的改善,也加重了北方地区冬季的雾霾天气.推进北方地区冬季清洁取暖，是重大民生工程、民心工程，关系北方地区广大群众温暖过冬，关系雾霾天能不能减少，是能源生产和消费革命、农村生活方式革命的重要内容.2017年9月国家发改委制定了煤改气、煤改电价格扶植新政策，从而使得煤改气、煤改电用户大幅度增加，下面条形图反映了某省2018年1～7月份煤改气、煤改电的用户数量.（1）在给定坐标系中作出煤改气、煤改电用户数量y随月份t变化的散点图，并用散点图和相关系数说明y与t之间具有线性相关性；（2）建立y关于t的回归方程（系数精确到0.01），预测11月份该省煤改气、煤改电的用户数量.参考数据：7772111y9.24,t7 2.646i i ii i iiy=====⋅≈≈∑∑∑（y-y）.参考公式：相关系数()()()()111niinn ni i i i i i i i t t y y r t ty y t y t y ===⋅--=⋅--=-∑∑∑∑.回归方程ˆy a bt=+中斜率和截距的最小二乘估计公式分别为：()()()121ˆˆˆ,nii i nii tty y bay bt tt==⋅--==-⋅-∑∑.【参考答案】***试卷处理标记，请不要删除一、选择题 1．D 解析：D 【分析】设两圆交于点,A B ，连接11,AC BC ,12,AB C C ，设12,AB C C 交于点D ，由已知的数据可得1AC B △为等边三角形，从而可求出阴影部分的面积，进而求出总面积，即可求出概率. 【详解】设两圆交于点,A B ，连接11,AC BC ,12,AB C C ，设12,AB CC 交于点D ， 则11212C D C C ==190ADC ∠=︒， 所以111cos 2C D AC D AC ∠==，所以130AC D ∠=︒，则160AC B ∠=︒, 所以1ACB △为等边三角形，所以60442(4)36043S ππ⨯=-⨯=-阴，图形的总面积42024(33S πππ=⨯--=+总所以求概率为43203ππ-=+，故选：D【点睛】此题考查几何概型概率的求法，关键是求阴影部分的面积，属于中档题.2．D解析：D 【分析】由几何概型中的面积型得：1277210.511010S P S ⨯⨯⨯==-=⨯阴正，即可得解.【详解】设甲、乙两同学等可能到达某咖啡厅的时间为(),x y ，则010x <≤，010y <≤，其基本事件可用正方形区域表示，如图，则甲、乙两同学等可能到达某咖啡厅的时间间隔不超过3分钟的事件为A ， 则事件A 为：3x y -≤，其基本事件可用阴影部分区域表示，由几何概型中的面积型可得：1277210.511010S P S ⨯⨯⨯==-=⨯阴正.故选：D. 【点睛】本题考查了几何概型中的面积型，属于基础题.3．A解析：A 【分析】求出样本点的中心，求出ˆa的值，得到回归方程得到5个点中落在回归直线下方的有(6,2)，(8,3)，共2个，求出概率即可．【详解】8x=， 3.4y=，故3.40.658ˆa=⨯+，解得： 1.8a=-，则0.65.8ˆ1y x=-，故5个点中落在回归直线下方的有(6,2)，(8,3)，共2个，故所求概率是25p=，故选：A．【点睛】本题考查回归方程概念、概率的计算以及样本点的中心，考查数据处理能力，是一道基础题．4．B解析：B【分析】利用复数模的公式可得点(),x y在以()1,0为圆心，以1为半径的圆上及圆的内部，结合y x≥表示的是图中直线上方且在圆内的弓形，求出圆的面积与弓形的面积利用几何概型可得结果.【详解】因为()()1,,a x y x y R=-∈，且1a≤，所以()2211x y-+≤，∴点(),x y在以()1,0为圆心，以1为半径的圆上及圆的内部，y x≥表示的是图中直线上方且在圆内的弓形，而圆的面积为Sπ=，11=42Sπ-弓，y x∴≥的概率为111142=42SPSπππ-==-弓，故选：B. 【点睛】本题主要考查几何概型中的面积类型，基本方法是：分别求得构成事件A 的区域面积和试验的全部结果所构成的区域面积，两者求比值，即为概率．5．C解析：C 【分析】根据题意计算结果直接判断即可解题. 【详解】 当①②分别是TT k=，k N >时， 首先初始化数据；10N =，1k =，0S =，1T =． 第一次循环，1TT k==，1S S T =+=，12k k =+=，此时不满足k N >； 第二次循环，112T T k ==⨯，1112S S T =+=+⨯，13k k =+=，此时不满足k N >； 第三次循环，1123T T k ==⨯⨯，11112123S S T =+=++⨯⨯⨯，14k k =+=，此时不满足k N >；一直循环下去，第十次循环，112310T T k ==⨯⨯⨯⨯，11111212312310S S T =+=++++⨯⨯⨯⨯⨯⨯⨯，111k k =+=，此时满足k N >，跳出循环． 故输出的11111212312310S =++++⨯⨯⨯⨯⨯⨯⨯．故选：C. 【点睛】本题考查根据计算补全程序框图，是基础题.6．C解析：C 【分析】最常用的方法是列举法，即依次执行循环体中的每一步，直到循环终止，但在执行循环体时要明确循环终止的条件是什么，什么时候要终止执行循环体． 【详解】0S =，1k =；110121S -=+⨯=，2k =；211225S -=+⨯=， 3k =；3153217S -=+⨯=，4k =；41174249S -=+⨯=，5k =；514952129S -=+⨯=，6k =，此时输出S ，即判断框内可填入的条件是“6?k <”. 故选：C ． 【点睛】本题考查循环结构程序框图. 解决程序框图填充问题的思路(1)要明确程序框图的顺序结构、条件结构和循环结构． (2)要识别、执行程序框图，理解框图所解决的实际问题． (3)按照题目的要求完成解答并验证． 7．C解析：C 【分析】根据程序框图的循环结构,依次运行,算出输出值为6n =时S 的值,使得S p <不成立时p 的值即可. 【详解】根据程序框图可知,1,0n S == 则11021,2S n -=+==21123,3S n -=+== 31327,4S n -=+== 417215,5S n -=+== 5115231,6S n -=+==此时应输出6n =,需31p <不成立.因而整数p 的最大值为31 故选:C 【点睛】本题考查了程序框图的简单应用,根据输出结果确定判读框,属于中档题.8．C解析：C 【分析】由已知中的程序框图，得到该程序的功能是利用循环结构计算并输出变量p 的值，模拟程序的运行过程，分析循环中各变量的变化情况，可得答案． 【详解】模拟程序的运行，可得：7,1,1N k p ===， 满足条件7k <，执行循环体，3,3k p ==； 满足条件7k <，执行循环体，5,15k p ==； 满足条件7k <，执行循环体，7,105k p ==； 此时，不满足条件7k <，推出循环，输出p 的值为105，故选C ． 【点睛】本题主要考查了程序框图的应用问题，解答中应模拟程序框图的运行过程，逐次计算是解答的关键，着重考查了推理与运算能力，属于基础题．9．C解析：C 【解析】试题分析：A 选项，中位数是84；B 选项，众数是出现最多的数，故是83；C 选项，平均数是85，正确；D 选项，方差是，错误．考点：•茎叶图的识别 相关量的定义10．C解析：C 【分析】根据平均数和方差公式计算比较即可. 【详解】设这个班有n 个同学，分数分别是123,,,,n a a a a ⋅⋅⋅，假设第i 个同学的成绩没录入，这一次计算时，总分是()1n x -，方差为()()()()()222222121111i i n s a x a x a x a x a x n -+⎡⎤=-+-+⋅⋅⋅+-+-+⋅⋅⋅+-⎣⎦-； 第二次计算时，()11n nxx x -+=x =，方差为()()()()()()222222221121111++i i i n n s a x a x a x a x a x a x s n n-+-⎡⎤=-+-⋅⋅⋅-+-+-+⋅⋅⋅+-=⎣⎦故有1x x =，221s s >.故选:C 【点睛】本题主要考查样本的平均数和方差公式;属于中档题.11．C解析：C 【分析】根据系统抽样的定义，可知抽到的号码数可组成一个以301=-n a n 为通项公式的等差数列，令*200301480,≤-≤∈n n N ，解不等式可得结果． 【详解】每组人数=9603230÷=人，即抽到号码数的间隔为30，因为第一组抽到的号码为29，根据系统抽样的定义，抽到的号码数可组成一个等差数列，且*2930(1)301,=+-=-∈n n n n N a ，令200301480≤-≤n ，得2014813030≤≤n ，可得n 的取值可以从7取到16，共10个，故选C ． 【点睛】本题主要考查系统抽样的定义及应用，转化为等差数列是解决本题的关键．12．C解析：C 【解析】 【分析】根据系统抽样知，组距为604=15÷，即可根据第一组所求编号，求出各组所抽编号. 【详解】学生60名，用系统抽样的方法，抽取一个容量为4的样本,所以组距为604=15÷， 已知03号，18号被抽取，所以应该抽取181533+=号， 故选C. 【点睛】本题主要考查了抽样，系统抽样，属于中档题.二、填空题13．【分析】基本事件总数由双曲线的离心率得利用列举法求出双曲线的离心率包含的基本事件有6个由此能求出双曲线的离心率的概率【详解】某同学同时掷两颗骰子得到点数分别为ab 基本事件总数双曲线的离心率解得双曲线解析：16【分析】基本事件总数n 6636=⨯=，由双曲线2222x y 1a b -=的离心率e >，得b 2a >，利用列举法求出双曲线2222x y 1a b -=的离心率e >()a,b 有6个，由此能求出双曲线2222x y 1a b -=的离心率e >【详解】某同学同时掷两颗骰子，得到点数分别为a ，b ， 基本事件总数n 6636=⨯=，双曲线2222x y 1a b-=的离心率e >ca ∴=>，解得b 2a >，∴双曲线2222x y 1a b-=的离心率e >()a,b 有：()1,3，()1,4，()1,5，()2,5，(1，6)，()2,6，共6个，则双曲线2222x y 1a b-=的离心率e >61p 366==． 故答案为16． 【点睛】本题考查概率的求法，考查古典概型、列举法、双曲线性质等基础知识，考查运算求解能力，是基础题．对于古典概型，要求事件总数是可数的，满足条件的事件个数可数，使得满足条件的事件个数除以总的事件个数即可.14．【分析】由题意从甲乙丙丁4位同学中选出2名代表参加学校的会议求得基本事件的总数再由甲乙两人至少有一人被选中的对立事件是甲乙两人都没有选中求得其包含的基本事件的个数即可求解【详解】由题意从甲乙丙丁4位解析：56【分析】由题意，从甲乙丙丁4位同学中选出2名代表参加学校的会议，求得基本事件的总数，再由甲乙两人至少有一人被选中的对立事件是甲乙两人都没有选中，求得其包含的基本事件的个数，即可求解． 【详解】由题意，从甲乙丙丁4位同学中选出2名代表参加学校的会议，则基本事件的总数为246n C ==，又由甲乙两人至少有一人被选中的对立事件是甲乙两人都没有选中，其包含的基本事件的个数为221m C ==，所以甲乙两人至少有一人被选中的概率为151166m p n =-=-=． 故答案为56． 【点睛】本题主要考查了古典概型及其概率的计算公式，以及对立事件的应用，其中解答中认真审题，合理选择方法，分别求得基本事件的总数和事件所包含的基本事件的个数是解答的关键，着重考查了推理与计算能力，属于基础题．15．【分析】由题意知本题是一个几何概型试验包含的所有事件是Ω＝{（xy ）|0≤x≤205≤y≤20}作出事件对应的集合表示的面积写出满足条件的事件是A ＝{（xy ）|0≤x≤205≤y≤20y ﹣x≥5}算解析：38【分析】由题意知本题是一个几何概型，试验包含的所有事件是Ω＝{（x，y）|0≤x≤20，5≤y≤20}，作出事件对应的集合表示的面积，写出满足条件的事件是A＝{（x，y）|0≤x≤20，5≤y≤20，y﹣x≥5 }，算出事件对应的集合表示的面积，根据几何概型概率公式得答案．【详解】由题意知本题是一个几何概型，设甲和乙到达的分别为7时x分、7时y分，则10≤x≤20，5≤y≤20，甲至少需等待乙5分钟，即y﹣x≥5，则试验包含的所有区域是Ω＝{（x，y）|0≤x≤20，5≤y≤20}，甲至少需等待乙5分钟所表示的区域为A＝{（x，y）|0≤x≤20，5≤y≤20，y﹣x≥5}，如图：正方形的面积为20×15＝300，阴影部分的面积为12⨯15×152252=，∴甲至少需等待乙5分钟的概率是225323008=，故答案为3 8【点睛】本题主要考查“面积型”的几何概型，属于中档题. 解决几何概型问题常见类型有：长度型、角度型、面积型、体积型，求与面积有关的几何概型问题关鍵是计算问题的总面积以及事件的面积；几何概型问题还有以下几点容易造成失分，在备考时要高度关注：（1）不能正确判断事件是古典概型还是几何概型导致错误；（2）基本事件对应的区域测度把握不准导致错误；（3）利用几何概型的概率公式时 , 忽视验证事件是否等可能性导致错误. 16．【分析】根据程序框图的算法功能可知该程序是计算的值再根据裂项相消法即可求出【详解】根据程序框图的算法功能可知该程序是计算的值所以故答案为：【点睛】本题主要考查程序框图的算法功能的理解以及数列求和属于解析：2017 2018【分析】根据程序框图的算法功能可知，该程序是计算111112233420172018++++⨯⨯⨯⨯的值，再根据裂项相消法即可求出． 【详解】根据程序框图的算法功能可知，该程序是计算111112233420172018++++⨯⨯⨯⨯的值． 所以111112233420172018++++⨯⨯⨯⨯111111112017122334201720182018⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-++-=⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭． 故答案为：20172018． 【点睛】本题主要考查程序框图的算法功能的理解以及数列求和，属于基础题．常见的数列求和方法有：公式法，裂项相消法，分组求和法，倒序相加求和法，并项求和法，错位相减法等，根据数列的特征选择对应的方法是解题的关键．17．-1【分析】计算的值找出周期根据余数得到答案【详解】依次计算得：…周期为32019除以3余数为0故答案为-1【点睛】本题考查了程序框图的相关知识计算数据找到周期规律是解题的关键解析：-1 【分析】计算a 的值，找出周期，根据余数得到答案. 【详解】 依次计算得：2,1a i ==1,22a i ==1,3a i =-= 2,4a i == ….周期为32019除以3余数为0，1a =- 故答案为-1 【点睛】本题考查了程序框图的相关知识，计算数据找到周期规律是解题的关键.18．4【分析】由已知中的程序语句可知该程序的功能是计算分段函数 的值将t=5代入即可得到答案【详解】由已知中程序语句可知该程序的功能是： 计算分段函数 的值 故答案为04【点睛】算法是新课标高考的一大解析：4 【分析】由已知中的程序语句可知该程序的功能是计算分段函数 0.2,30.20.1(3),3t C t t ≤⎧=⎨+->⎩ 的值，将t =5代入即可得到答案． 【详解】由已知中程序语句可知该程序的功能是： 计算分段函数 0.2,30.20.1(3),3t C t t ≤⎧=⎨+->⎩的值50.20.1(53)0.4t C =∴=+-=，故答案为0.4. 【点睛】算法是新课标高考的一大热点，其中算法的交汇性问题已成为高考的一大亮，这类问题常常与函数、数列、不等式等交汇自然，很好地考查考生的信息处理能力及综合运用知识解决问題的能力，解决算法的交汇性问题的方：（1）读懂程序框图、明确交汇知识，(2）根据给出问题与程序框图处理问题即可.19．8【分析】先设五个班的人数分别为样本平均数为5又因样本方差为4则代入大于且不相等的整数可得的值依次为24568即可得最大值【详解】解:设五个班的人数分别为则则所以的值依次为24568即有最大值为8故解析：8 【分析】先设五个班的人数分别为1a ,2a ,3a ,4a ,5a ,样本平均数为5,1234525a a a a a ++++=,又因样本方差为4,则()()()()()22222123455555520a a a a a -+-+-+-+-=,代入大于0且不相等的整数,可得1a ,2a ,3a ,4a ,5a 的值依次为2,4,5,6,8,即可得最大值. 【详解】解:设五个班的人数分别为1a ,2a ,3a ,4a ,5a , 则()12345155a a a a a ++++=, 15()()()()()2222212345555554a a a a a ⎡⎤-+-+-+-+-=⎣⎦, 则1234525a a a a a ++++=,()()()()()22222123455555520a a a a a -+-+-+-+-=,所以1a ,2a ,3a ,4a ,5a 的值依次为2,4,5,6,8, 即有最大值为8.故答案为: 8 【点睛】本题考查利用平均数公式和方差公式求样本数据中的最大值,是基础题.合理应用公式是关键.20．2【解析】分析：由茎叶图的分布可知乙同学的成绩会比较稳定先求出乙同学的平均成绩利用求方差的公式即可求得方差值详解：由茎叶图中成绩的分布情况可知乙同学的最低成绩比甲高乙同学的最高成绩比甲低所以成绩分布解析：2 【解析】分析：由茎叶图的分布可知，乙同学的成绩会比较稳定．先求出乙同学的平均成绩，利用求方差的公式即可求得方差值．详解：由茎叶图中成绩的分布情况可知，乙同学的最低成绩比甲高，乙同学的最高成绩比甲低，所以成绩分布相对较为集中，所以乙同学成绩的方差小，成绩较稳定． 设乙同学的平均成绩为x ，则8889909192905x ++++==所以乙同学成绩的方差()()()()()2222221889089909090919092905s ⎡⎤=-+-+-+-+-⎣⎦()14101425=++++= 所以乙同学成绩的方差为2点睛：方差体现了数据的离散程度，茎叶图中都保留了原始数据，因此可以从茎叶图中直接观察来比较方差的大小．要熟练掌握方差的计算公式．本题主要考查了简单的概念和计算，属于简单题．三、解答题21．（Ⅰ）516；（Ⅱ）获得饮料的概率大于获得水杯的概率，理由见解析． 【分析】有放回抽取，每次抽取都有4种可能．可计算出总可能数，（Ⅰ）用列举法列出事件“小亮获得玩具”的所有基本事件后可计算概率； （Ⅱ）同理计算出小亮获得水杯的概率以及获得饮料的概率，两者比较即得． 【详解】有放回抽取，每次抽取都有4种可能，因此总的基本事件数为4416⨯=， （Ⅰ）事件“小亮获得玩具”包含基本事件为：11，12，13，21，31共5种，概率为1516P =； （Ⅱ）事件“小亮获得水杯”包含基本事件为：24，34，44，42，43共5种，概率为2516P =．所以获得饮料的概率为325561161616P P =--=>∴获得饮料的概率大于获得水杯的概率． 【点睛】本题考查古典概型，解题关键是求出基本事件数．本题是用列举法求解． 22．（1）611000（2）9891000【分析】（1）1张奖券中奖包括中特等奖、一等奖、二等奖,且A 、B 、C 两两互斥,利用互斥事件的概率加法公式求解即可；（2）“1张奖券不中特等奖且不中一等奖”的对立事件为“1张奖券中特等奖或中一等奖”,则利用互斥事件的概率公式求解即可 【详解】（1）1张奖券中奖包括中特等奖、一等奖、二等奖, 设“1张奖券中奖”为事件M ,则M A B C =∪∪,因为A 、B 、C 两两互斥,所以()()()()611000P M P A P B P C =++= 故1张奖券中奖的概率为611000（2）设“1张奖券不中特等奖且不中一等奖”为事件N ,则事件N 与“1张奖券中特等奖或中一等奖”为对立事件,所以()()()()()989111000P N P A B P A P B =-⋃=-+=, 故1张奖券不中特等奖且不中一等奖的概率为9891000【点睛】本题考查互斥事件的概率加法公式的应用,考查古典概型,考查利用对立事件求概率 23．程序图见解析. 【解析】 【分析】因为只统计及格人数，所以设计一个条件语句，对于求和设计一个计数变量，一个累加变量，根据结束条件设置成直到型或当型. 最后对应改成基本语句. 【详解】用M 表示及格人数，S 表示及格同学的总分。

一、选择题1．七巧板是我们祖先的一项创造，被誉为“东方魔板”，它是由五块等腰直角三角形（两块全等的小三角形、一块中三角形和两块全等的大三角形）、一块正方形和一块平行四边形组成的．如图是一个用七巧板拼成的正方形，现从该正方形中任取一点，则此点取自黑色部分的概率是A ．316B ．38C ．14D ．182．如图是一边长为8的正方形苗圃图案，中间黑色大圆与正方形的内切圆共圆心，圆与圆之间是相切的，且中间黑色大圆的半径是黑色小圆半径的2倍.若在正方形图案上随机取一点，则该点取自黑色区域的概率为（ ）A ．8π B ．16π C ．18π-D ．116π-3．袋中有白球2个，红球3个，从中任取两个，则互斥且不对立的两个事件是（ ） A ．至少有一个白球；都是白球 B ．两个白球；至少有一个红球 C ．红球、白球各一个；都是白球D ．红球、白球各一个；至少有一个白球4．2019年5月22日具有“国家战略”意义的“长三角一体化”会议在芜潮举行，长三角城市群包括，上海市以及江苏省､浙江省､安徽省三省部分城市，简称“三省一市".现有4名高三学生准备高考后到上海市､江苏省､浙江省､安徽省四个地方旅游，假设每名同学均从这四个地方中任意选取一个去旅游则恰有一个地方未被选中的概率为（ ） A ．2764B ．916C ．81256D ．7165．给出一个算法的程序框图如图所示，该程序框图的功能是（ ）A ．求出,,a b c 三数中的最小数B ．求出,,a b c 三数中的最大数C ．将,,a b c 从小到大排列D ．将,,a b c 从大到小排列6．执行如图的程序框图，若输入1t =-，则输出t 的值等于( )A ．3B ．5C ．7D ．157．如图，“大衍数列”：0，2，4，8，12….来源于《乾坤谱》中对《易传》“大衍之数五十”的推论，主要用于解释中国传统文化中的太极衍生过程中曾经经历过的两仪数量总和.下图是求大衍数列前n 项和的程序框图.执行该程序框图，输入10m =，则输出的S =（ ）A ．100B ．140C ．190D ．2508．对任意非零实数a 、b ，若a b ⊗的运算原理如图所示，则121log 43-⎛⎫⊗ ⎪⎝⎭的值为（ ）A ．13B ．1C ．43D ．29．工人月工资y （元）与劳动生产率x （千元）变化的回归直线方程为=50+80x ，下列判断不正确的是（ ）A ．劳动生产率为1000元时，工资约为130元B ．工人月工资与劳动者生产率具有正相关关系C ．劳动生产率提高1000元时，则工资约提高130元D ．当月工资为210元时，劳动生产率约为2000元10．学校为了解新课程标准提升阅读要求对学生阅读兴趣的影响情况，随机抽取了100名学生进行调查.根据调查结果绘制学生周末阅读时间的频率分布直方图如图所示：将阅读时间不低于30分钟的观众称为“阅读霸”，则下列命题正确的是（ ） A ．抽样表明，该校有一半学生为阅读霸 B ．该校只有50名学生不喜欢阅读 C ．该校只有50名学生喜欢阅读 D ．抽样表明，该校有50名学生为阅读霸 11．①45化为二进制数为(2)101101；②一个总体含有1000个个体（编号为0000，0001，…，0999），采用系统抽样从中抽取一个容量为50的样本，若第一个抽取的编号为0008，则第六个编号为0128； ③已知a ，b ，c 为ABC ∆三个内角A ，B ，C 的对边，其中3a =，4c =,6A π=，则这样的三角形有两个解.以上说法正确的个数是（ ） A ．0B ．1C ．2D ．312．为了解儿子身高与其父亲身高的关系，随机抽取5对父子的身高数据如下： 父亲身高x （cm ）174176176176178儿子身高y （cm ）175175176177177则y 对x 的线性回归方程为 A ．y = x-1B ．y = x+1C ．y =88+12x D ．y = 176二、填空题13．连续抛掷同一颗骰子3次，则3次掷得的点数之和为9的概率是____． 14．在区间[2,4]-上随机地取一个实数x ，若实数x 满足||x m ≤的概率为23，则m=_______.15．北京市某银行营业点在银行大厅悬挂着不同营业时间段服务窗口个数的提示牌，如图所示. 设某人到达银行的时间是随机的，记其到达银行时服务窗口的个数为X，则E X=______________．()16．执行如图的程序框图，则输出的S=__________．17．执行右面的程序框图，若输入的x的值为0，则输出的y的值是________.18．执行如图所示的程序框图,输出的T=______．19．已知一组数据126,,,x x x ⋅⋅⋅的方差是2，并且()()()22212611118x x x -+-+⋅⋅⋅+-=，0x ≠，则x =______.20．某超市统计了一个月内每天光顾的顾客人数，得到如图所示的频率分布直方图，根据该图估计该组数据的中位数为__________．三、解答题21．考试结束以后，学校对甲、乙两个班的数学考试成绩进行分析，规定：大于或等于80分为优秀，80分以下为非优秀．统计成绩后，得到如下的22⨯列联表，且已知在甲、乙两个班全部110人中随机抽取1人为优秀的概率为311. （1）若按99.9%的可靠性要求，能否认为“成绩与班级有关系”；（2）若按下面的方法从甲班优秀的学生中抽取一人：把甲班优秀的10名学生从2到11进行编号，先后两次抛掷一枚均匀的骰子，出现的点数之和为被抽取人的序号．试求抽到9号或10号的概率．参考公式与临界值表：22()()()()()n ad bc K a b c d a c b d -=++++．优秀非优秀合计甲班10乙班30合计11022．手机运动计步已经成为一种新时尚.某单位统计了职工一天行走步数（单位：百步），绘制出如下频率分布直方图：（1）求直方图中a的值，并由频率分布直方图估计该单位职工一天步行数的中位数；（2）若该单位有职工200人，试估计职工一天行走步数不大于13000的人数；（3）在（2）的条件下，该单位从行走步数大于15000的3组职工中用分层抽样的方法选取6人参加远足拉练活动，再从6人中选取2人担任领队，求这两人均来自区间(170]的概率.150,23．相传古代印度国王在奖赏他聪明能干的宰相达依尔(国际象棋发明者)时,问他需要什么,达依尔说:“国王只要在国际象棋棋盘的第一格子上放一粒麦子,第二格子上放二粒,第三格子上放四粒,以后按比例每一格加一倍,一直放到第64格(国际象棋棋盘格数是8×8=64),我就感恩不尽,其他什么也不要了.”国王想:“这才有多少,还不容易!”于是让人扛来一袋小麦,但不到一会儿就用完了,再来一袋很快又没有了,结果全印度的粮食用完还不够,国王很奇怪,怎么也算不清这笔账.请你设计一个程序框图表示其算法,来帮国王计算一下需要多少粒小麦. 24．画出求方程lg x+x-3=0在区间(2,3)内的近似解(精确到0.01)的程序框图.25．为了解某市家庭用电量的情况，该市统计局调查了100户居民去年一年的月均用电量，发现他们的用电量都在50kW·h至350kW·h之间，进行适当分组后，画出频率分布直方图如图所示．（I）求a的值；（Ⅱ）求被调查用户中，用电量大于250kW·h的户数；（III）为了既满足居民的基本用电需求，又提高能源的利用效率，市政府计划采用阶梯定价，希望使80%的居民缴费在第一档（费用最低），请给出第一档用电标准（单位：kW·h）的建议，并简要说明理由．26．如表为某中学近5年被卓越大学联盟录取的学生人数．记2015年的年份序号为1，2016年的年份序号为2，…，2019年的年份序号为5．年份序号x12345录取人数y100130170200250（1）求y关于x的线性回归方程，并估计2020年该中学被卓越大学联盟录取的学生人数．（2）若在2015年和2019年被卓越大学联盟录取的学生中分层抽样7人，再从这7人中任选2人，求这2人恰好来自同一年份的概率．参考数据：521iix=∑＝55，51i iix y=∑＝2920．参考公式：b＝1221ni iiniix y nx yx nx==--∑∑，a y bx=-【参考答案】***试卷处理标记，请不要删除一、选择题1．A【解析】设2AB =，则1BC CD DE EF ====.∴112224BCI S ∆=⨯⨯=，112242BCI EFGHS S ∆==⨯=平行四边形 ∴所求的概率为113422216P +==⨯ 故选A. 2．C解析：C 【分析】设黑色小圆的半径为r ，则黑色大圆的半径为2r ，由题意求得r ，进一步求出黑色区域的面积，由测度比是面积比得答案． 【详解】解：设黑色小圆的半径为r ，则黑色大圆的半径为2r ， 由题意可知，88r =，即1r =．∴图中黑色区域的面积为222884412648ππππ⨯-⨯+⨯⨯+⨯=-，又正方形的面积为64．∴在正方形图案上随机取一点，则该点取自黑色区域的概率为6481648ππ-=-． 故选：C ． 【点睛】本题考查几何概型的概率的求法，考查数形结合的解题思想方法，属于中档题．3．C解析：C 【分析】从装有3个红球和2个白球的红袋内任取两个球，所有的情况有3种：“2个白球”、“一个白球和一个红球”、“2个红球”．由于对立事件一定是互斥事件，且它们之中必然有一个发生而另一个不发生，结合所给的选项，逐一进行判断，从而得出结论． 【详解】从装有3个红球和2个白球的红袋内任取两个球，所有的情况有3种：“2个白球”、“一个白球和一个红球”、“2个红球”．由于对立事件一定是互斥事件，且它们之中必然有一个发生而另一个不发生， 对于A ，至少有1个白球；都是白球，不是互斥事件．故不符合．对于B 两个白球；至少有一个红球，是互斥事件，但也是对立事件，故不符合． 对于C 红球、白球各一个；都是白球是互斥事件，但不是对立事件，故符合． 对于D 红球、白球各一个；至少有一个白，不是互斥事件．故不符合． 故选：C ．本题主要考查互斥事件与对立事件的定义，意在考查学生对这些知识的理解掌握水平．4．B解析：B 【分析】求出4名同学去旅游的所有情况种数，再求出恰有一个地方未被选中的种数，由概率公式计算出概率． 【详解】4名同学去旅游的所有情况有：44256=种恰有一个地方未被选中共有2113424322144C C C A A ⋅⋅=种情况； 所以恰有一个地方未被选中的概率：144925616p ==； 故选：B. 【点睛】本题考查古典概型，解题关键是求出基本事件的个数，本题属于中档题．5．A解析：A 【分析】对a 、b 、c 赋三个不等的值，并根据程序框图写出输出的结果，可得知该程序的功能． 【详解】令2a =，3b =，1c =，则23>不成立，21>成立，则1a =，输出的a 的值为1， 因此，该程序的功能是求出a 、b 、c 三数中的最小数，故选A ． 【点睛】本题考查程序框图的功能，解题的关键就是根据题意将每个步骤表示出来，考查分析问题的能力，属于中等题．6．C解析：C 【分析】直接根据程序框图依次计算得到答案. 【详解】模拟执行程序，可得1t =-，不满足条件0t >，0t =，满足条件()()250t t +-<， 不满足条件0t >，1t =，满足条件()()250t t +-<， 满足条件0t >，3t =，满足条件()()250t t +-<，满足条件0t >，7t =，不满足条件()()250t t +-<，退出循环，输出t 的值为7.故选：C.【点睛】本题考查了程序框图，意在考查学生的计算能力和理解能力.7．C解析：C【分析】根据程序框图进行运算,直到满足判断框中的条件,就停止运行,输出结果.【详解】第一次运行,211,0,0002n n a S -====+=,不符合n m ≥,继续运行; 第二次运行,22,22n n a ===,022S =+=,不符合n m ≥,继续运行, 第三次运行,213,42n n a -===,426S =+=,不符合n m ≥,继续运行, 第四次运行,24,82n n a ===,8614S =+=,不符合n m ≥,继续运行, 第五次运行,5n =,21122n a -==,121426S =+=, 不符合n m ≥,继续运行, 第六次运行,6n =,2182n a ==,182644S =+=, 不符合n m ≥,继续运行, 第七次运行,217,242n n a -===,244468S =+=, 不符合n m ≥,继续运行, 第八次运行,28,322n n a ===,3268100S =+=, 不符合n m ≥,继续运行, 第九次运行,219,40,401001402n n a S -====+=, 不符合n m ≥,继续运行, 第十次运行,210,50,501401902n n a S ====+=,符合n m ≥,退出运行,,输出190S =. 故选:C【点睛】本题考查了程序框图中循环结构,正确理解程序框图是解题关键,属于基础题.8．B解析：B【解析】 模拟执行程序框图可得程序的功能是计算并输出分段函数1,2,b a b a a b a a b b-⎧⎪⎪⊗=⎨+⎪>⎪⎩的值，∵121log 4233-⎛⎫=<= ⎪⎝⎭.∴12131log 4132--⎛⎫⊗== ⎪⎝⎭. 本题选择B 选项. 9．C解析：C【解析】试题分析：根据线性回归方程=50+80x 的意义，对选项中的命题进行分析、判断即可． 解：根据线性回归方程为=50+80x ，得；劳动生产率为1000元时，工资约为50+80×1=130元，A 正确；∵=80＞0，∴工人月工资与劳动者生产率具有正相关关系，B 正确；劳动生产率提高1000元时，工资约提高=80元，C 错误； 当月工资为210元时，210=50+80x ，解得x=2，此时劳动生产率约为2000元，D 正确．故选C ．考点：线性回归方程．10．A解析：A【分析】根据频率分布直方图得到各个时间段的人数，进而得到结果.【详解】根据频率分布直方图可列下表： 阅读时间（分）[0,10) [10,20) [20,30) [30,40) [40,50) [50,60] 抽样人数（名） 10 18 22 25 20 5 故选A.【点睛】这个题目考查了频率分布直方图的实际应用，以及样本体现整体的特征的应用，属于基础题.11．C解析：C【解析】分析：①根据进位制的互化可得结果；②根据系统抽样的性质可得结论；③由正弦定理可得结论.详解：①45222...1÷=，22211...0÷=，112 5...1÷=，52 2...1÷=，22 1...0÷=，120...1÷=，故()()10245101101=，①正确;②因为1000个个题抽取50个样本，∴每个样本编号间隔为20，第六个编号为8205108+⨯=，即编号为0108，故②错误；③由正弦定理可得342,1sin 32sinC C ==，,c a C >∴∠可能是锐角，也可能是钝角，三角形有两个解，③正确,故选C.点睛：本题主要考查进位制、正弦定理的应用，分层抽样的应用，意在考查综合运用所学知识解决问题的能力，属于中档题.12．C解析：C【详解】 试题分析：由已知可得176,176x y ==∴中心点为()176,176，代入回归方程验证可知，只有方程y =88+12x 成立，故选C 二、填空题13．；【分析】利用分步计数原理连续拋掷同一颗骰子3次则总共有：6×6×6=216种情况再列出满足条件的所有基本事件利用古典概型的计算公式计算可得概率【详解】每一次拋掷骰子都有123456六种情况由分步计 解析：25216； 【分析】 利用分步计数原理，连续拋掷同一颗骰子3次，则总共有：6×6×6=216种情况，再列出满足条件的所有基本事件，利用古典概型的计算公式计算可得概率.【详解】每一次拋掷骰子都有1，2，3，4，5，6，六种情况，由分步计数原理：连续抛掷同一颗骰子3次，则总共有：6×6×6=216种情况，则3次掷得的点数之和为9的基本事件为25种情况即：(1,2,6)，(1,3,5)，(1,4,4)，(1,5,3)，(1,6,2)，(2,1,6)，(2,2,5)，(2,3,4)，(2,4,3)，(2,5,2)，(2,6,1)，(3,1,5)，(3,2,4)，(3,3,3)，(3,4,2)，(3,5,1)，(4,1,4)，(4,2,3)，(4,3,2)，(4,4,1)，(5,1,3)，(5,2,2)，(5,3,1)，(6,1,2)，(6,2,1)，共25个基本事件，所以25216P =. 【点睛】本题考查分步计数原理和古典概型概率计算，计数过程中如果前两个数固定，则第三个数也相应固定.14．2【分析】画出数轴利用满足的概率可以求出的值即可【详解】如图所示区间的长度是6在区间上随机地取一个数若满足的概率为则有解得故答案是：2【点睛】该题考查的是有关长度型几何概型的问题涉及到的知识点有长度解析：2【分析】画出数轴，利用x 满足||x m ≤的概率，可以求出m 的值即可.【详解】如图所示，区间[2,4]-的长度是6，在区间[2,4]-上随机地取一个数x ，若x 满足||x m ≤的概率为23， 则有2263m =，解得2m =， 故答案是：2.【点睛】该题考查的是有关长度型几何概型的问题，涉及到的知识点有长度型几何概型的概率公式，属于简单题目.15．【解析】【分析】列出随机变量的分布列求解【详解】由题意知某人到达银行的概率为几何概型所以：其到达银行时服务窗口的个数为的分布列为：5 4 3 4 2 则【点睛】本题考查几何概型及随解析：3.5625【解析】【分析】列出随机变量的分布列求解.【详解】由题意知某人到达银行的概率为几何概型，所以：其到达银行时服务窗口的个数为的分布列为： X5 4 3 4 2 P 18 316 516 14 18则()1351154342 3.56258161648E X =⨯+⨯+⨯+⨯+⨯=. 【点睛】 本题考查几何概型及随机变量的分布列.16．88【解析】运行该程序即答案为88解析：88【解析】运行该程序，2,2;3,7;4,18;5,41;6,88;k S k S k S k S k S ==========即答案为88.17．13【解析】点睛：算法与流程图的考查侧重于对流程图循环结构的考查先明晰算法及流程图的相关概念包括选择结构循环结构伪代码其次要重视循环起点条件循环次数循环终止条件更要通过循环规律明确流程图研究的数学问解析：13【解析】2012,32113x x x y =⇒=⇒==⨯+=点睛：算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项.18．16【解析】第一次运行：；第二次运行：；第三次运行：此时程序结束所以输出的解析：16【解析】第一次运行：1,145,123,134T S S n T ===+==+==+=；第二次运行：45,549,325,459T S S n T =<==+==+==+=；第三次运行：9,9413,527,9716T S S n T ===+==+==+=．此时1613T S =>=，程序结束，所以输出的16T =19．2【解析】【分析】由题意结合方差的定义整理计算即可求得最终结果【详解】由题意结合方差的定义有：①而②①-②有：③注意到将其代入③式整理可得：又故故答案为2【点睛】本题主要考查方差的计算公式整体的数学解析：2【解析】【分析】由题意结合方差的定义整理计算即可求得最终结果.【详解】由题意结合方差的定义有：()()()22212612x x x x x x -+-++-= ①，而()()()22212611118x x x -+-+⋅⋅⋅+-=， ②，①-②有：()()212612666226x x x x x x x x --+++++++=-， ③， 注意到1266x x x x +++=，将其代入③式整理可得：26120x x -+=， 又0x ≠，故2x =.故答案为2．【点睛】 本题主要考查方差的计算公式，整体的数学思想等知识，意在考查学生的转化能力和计算求解能力.20．75【解析】分析：由频率分布直方图算出各频率然后计算中位数详解：由图可知的频率为的频率为的频率为的频率为的频率为前两组频率前三组频率中位数在第三组设中位数为则解得故该组数据的中位数为点睛：本题考查了解析：75.【解析】分析：由频率分布直方图算出各频率，然后计算中位数详解：由图可知，10~20的频率为0.1420~30的频率为0.2430~40的频率为0.3240~50的频率为0.250~60的频率为0.1前两组频率0.140.240.380.5=+=<前三组频率0.140.240.320.70.5=++=>∴中位数在第三组设中位数为x ，则()300.380.320.510x -+⨯= 解得33.75x =故该组数据的中位数为33.75点睛：本题考查了在频率分布直方图中求中位数，此类题目需要先确定中位数所在的组，然后根据公式计算求得结果，较为基础． 三、解答题21．（1）不能；（2）736． 【分析】（1）根据已知条件求得优秀人数，填写22⨯列联表，计算出2K 的值，由此作出判断.（2）根据古典概型概率计算方法，计算出所求概率.【详解】（1）依题意，在甲、乙两个班全部110人中随机抽取1人为优秀的概率为311，所以总的优秀人数为31103011⨯=人.由于甲班优秀10人，故乙班优秀20人，由此填写22⨯列联表如下：根据列联表中的数据，得到()22110103020507.48610.82830805060K ⨯⨯-⨯=≈<⨯⨯⨯， 因此按99.9%的可靠性要求，不能认为“成绩与班级有关系”.（2）设“抽到9或10号”为事件A ，先后两次抛掷一枚均匀的骰子，出现的点数为（x ，y ）．所有的基本事件有：（1，1）、（1，2）、（1，3）、…、（6，6）共36个．事件A 包含的基本事件有：（3，6）、（4，5）、（5，4）、（6，3）、（5，5）、（4，6）（6，4）共7个．所以P (A )=736，即抽到9号或10号的概率为736． 【点睛】本小题主要考查22⨯列联表独立性检验，考查古典概型概率计算，属于中档题.22．（1）0.012a =，125；（2）112人；（3）25 【分析】（1）根据频率分布直方图中矩形的面积和为1求出0.012a =，再求中位数得解；（2）直接利用频率分布直方图估计职工一天行走步数不大于13000的人数；（3）先求出在区间(]150,170中有32人，在区间(]170,190中有8人，在区间(]190,210中有8人，再利用古典概型的概率公式求出这两人均来自区间150,(170]的概率.【详解】（1）由题意得0.002200.006200.00820200.010200.008200.002200.002201a ⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯=解得0.012a = .设中位数为110x +，则0.002200.006200.008200.0120.5x ⨯+⨯+⨯+=解得15x = .∴中位数是125.（2）由()2000.002200.006200.008200.01220112⨯⨯+⨯+⨯+⨯=∴估计职工一天步行数不大于13000步的人数为112人（3）在区间(]150,170中有2000.0082032⨯⨯=人在区间(]170,190中有2000.002208⨯⨯=人在区间(]190,210中有2000.002208⨯⨯=人按分层抽样抽取6人，则从(]150,170抽取4人，(]170,190抽取1人，(]190,210抽取1人设从(]150,170抽取职工为1A ，2A ，3A ，4A ，从(]170,190抽取职工为B ，从(]190,210抽取职工为C ，则从6人中抽取2人的情况有12A A ，13A A ，41A A ，1A B ，1A C ，23A A ，24A A ，2A B ，2A C ，34A A ，3A B ，3A C ，4A B ，4A C ，BC 共15种情况，它们是等可能的，其中满足两人均来自区间(]150,170的有12A A ，13A A ，41A A ，23A A ，24A A ，34A A 共有6种情况， ∴62155P == ∴两人均来自区间(]150,170的概率为25. 【点睛】 本题主要考查频率分布直方图的应用，考查频率分布直方图中中位数的计算，考查古典概型的概率的计算，意在考查学生对这些知识的理解掌握水平和分析推理能力》23．见解析.【解析】试题分析：依题目可知，问题是求1＋2＋22 ＋…＋263 的和的问题，我们引入一个累加变量S ，一个计数变量i ，累加64次就能求其和试题点睛：本题考查的是算法与流程图，对算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项.24．见解析【解析】试题分析：根据据二分法求方程近似解的步骤设计程序框图，注意循环变量.试题程序框图如下图所示.25．（I ）0.006；（Ⅱ）18；（III ）245.5 kW·h.【分析】（1）根据频率和为1计算出a 的值；（2）根据频率分布直方图计算出“用电量大于250kW·h”的频率，再将该频率乘以对应的总户数即可得到结果；（3）根据频率分布直方图计算出频率刚好为0.8时对应的月用电量，由此可得到第一档用电标准.【详解】（1）因为()0.00240.00360.00440.00240.0012501a +++++⨯=，所以0.006a =； （2）根据频率分布直方图可知：“用电量大于250kW·h”的频率为()0.00240.0012500.18+⨯=，所以用电量大于250kW·h 的户数为：1000.1818⨯=， 故用电量大于250kW·h 有18户； （3）因为前三组的频率和为：()0.00240.00360.006500.60.8++⨯=<，前四组的频率之和为()0.00240.00360.0060.0044500.820.8+++⨯=>，所以频率为0.8时对应的数据在第四组，所以第一档用电标准为：0.80.620050245.50.22-+⨯≈kW·h. 故第一档用电标准为245.5 kW·h. 【点睛】本题考查频率分布直方图的综合应用，主要考查利用频率分布直方图进行相关计算，对学生读取图表信息和计算能力有一定要求，难度一般.26．（1）3759y x =+；281；（2）1121． 【分析】（1）由题意计算平均数，代入公式求出回归系数，写出线性回归方程，再利用线性回归方程计算6x =时的值即可；（2）由分层抽样求出抽取的人数，再利用概率公式求出对应的概率即可．【详解】（1）由表格可求()11234+5=35x =+++，()1100130170200+250=1705y =+++， 且521i i x=∑＝55，51i i i x y =∑＝2920， 所以12221292053170375553n i ii n i i x y nx y xnx b ==--⨯⨯==-⨯-=∑∑，17037359a y bx =-=-⨯=， 所以y 关于x 的线性回归方程为3759y x =+，当6x =时，37659281y =⨯+=，所以2020年该中学被卓越大学联盟录取的学生人数约为281；（2）由分层抽样可知7人中有10072100250⨯=+ 人来自2015年，有25075100250⨯=+人来自2019年,从中随机抽取两人共有21种结果，抽取的两人恰好来自同一年的有11种，所以所求概率为1121P =． 【点睛】本题主要考查线性回归方程和古典概型求概率，属于中档题．。

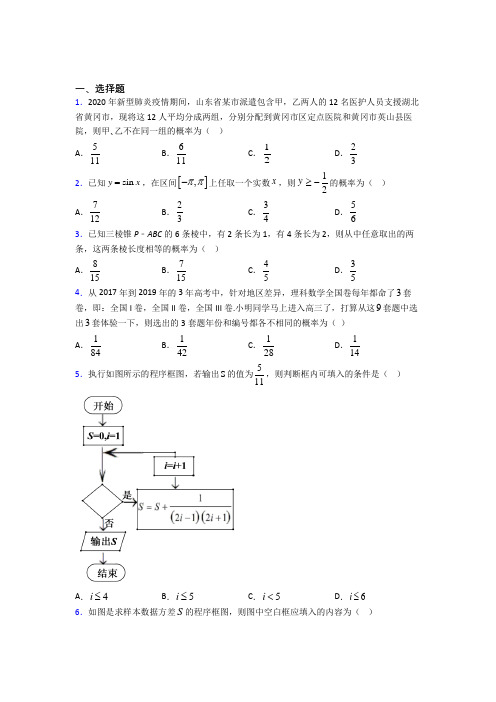
一、选择题1．2020年新型肺炎疫情期间，山东省某市派遣包含甲，乙两人的12名医护人员支援湖北省黄冈市，现将这12人平均分成两组，分别分配到黄冈市区定点医院和黄冈市英山县医院，则甲､乙不在同一组的概率为（ ） A ．511B ．611C ．12D ．232．已知sin y x =，在区间[],ππ-上任取一个实数x ，则y ≥12-的概率为（ ） A ．712B ．23C ．34 D ．563．已知三棱锥P ﹣ABC 的6条棱中，有2条长为1，有4条长为2，则从中任意取出的两条，这两条棱长度相等的概率为（ ） A ．815B ．715C ．45D ．354．从2017年到2019年的3年高考中，针对地区差异，理科数学全国卷每年都命了3套卷，即：全国I 卷，全国II 卷，全国III 卷.小明同学马上进入高三了，打算从这9套题中选出3套体验一下，则选出的3套题年份和编号都各不相同的概率为（ ） A ．184B ．142C ．128D ．1145．执行如图所示的程序框图，若输出S 的值为511，则判断框内可填入的条件是（ ）A ．4i ≤B ．5i ≤C ．5i <D ．6i ≤6．如图是求样本数据方差S 的程序框图，则图中空白框应填入的内容为（ ）A．()28iS x xS+-=B．()2(1)8ii S x xS-+-=C．()2iS x xSi+-=D．()2(1)ii S x xSi-+-=7．如图是一个程序框图，则输出k的值为（）A．6 B．7 C．8 D．9 8．执行如图所示的程序框图，则输出的n值是（）A ．5B ．7C ．9D ．119．工人月工资y （元）与劳动生产率x （千元）变化的回归直线方程为=50+80x ，下列判断不正确的是（ ）A ．劳动生产率为1000元时，工资约为130元B ．工人月工资与劳动者生产率具有正相关关系C ．劳动生产率提高1000元时，则工资约提高130元D ．当月工资为210元时，劳动生产率约为2000元10．已知某8个数的平均数为3，方差为2，现加入一个新数据3，此时这9个数的平均数为x ，方差为2s ，则（ ） A ．3x =，22s < B ．3x =，22s > C ．3x >，22s <D ．3x >，22s >11．某校高一年级有学生1800人，高二年级有学生1500人，高三年级有1200人，为了调查学生的视力状况，采用分层抽样的方法抽取学生，若在抽取的样本中，高一年级的学生有60人，则该样本中高三年级的学生人数为( ) A ．60B ．50C ．40D ．3012．从存放号码分别为1，2，⋯，10的卡片的盒子中，有放回地取100次，每次取一张卡片并记下号码，统计结果如下：则取到号码为奇数的频率是（ ） A ．0.53B ．0.5C ．0.47D ．0.37二、填空题13．甲、乙两人玩猜数字游戏，先由甲心中任想一个数字，记为a ，再由乙猜甲刚才想的数字，把乙猜的数字记为b ，且,{0,1,2,,9}a b ∈.若||1a b -，则称甲乙“心有灵犀”.现任意找两人玩这个游戏，则这两人“心有灵犀”的概率为______.14．如图，在半径为1的圆上随机地取两点,B E，连成一条弦BE，则弦长超过圆内接正 边长的概率是__________．BCD15．从甲、乙、丙、丁四人中选3人当代表，则甲被选上的概率为______．16．运行如图所示的程序框图，则输出的所有y值之和为___________．17．执行如图所示的程序框图，输出的值为__________．18．如图所示的程序框图输出的值是 .19．如图是某地区2018年12个月的空气质量指数以及相比去年同期变化幅度的数据统计图表，根据图表，下面叙述正确的是______.①2月相比去年同期变化幅度最小，3月的空气质量指数最高；②第一季度的空气质量指数的平均值最大，第三季度的空气质量指数的平均值最小； ③第三季度空气质量指数相比去年同期变化幅度的方差最小； ④空气质量指数涨幅从高到低居于前三位的月份为6､8､4月. 20．已知一组数据126,,,x x x ⋅⋅⋅的方差是2，并且()()()22212611118x x x -+-+⋅⋅⋅+-=，0x ≠，则x =______.三、解答题21．在流行病学调查中，潜伏期指自病原体侵入机体至最早临床症状出现之间的一段时间.某地区一研究团队从该地区500名A 病毒患者中，按照年龄是否超过60岁进行分层抽样，抽取50人的相关数据，得到如下表格：潜伏期（单位：天）[]0,2 (]2,4 (]4,6 (]6,8 (]8,10 (]10,12 (]12,14人 数60岁及以上 258752160岁以下0 2 2 4 9 2 1（2）以各组的区间中点值为代表，计算50名患者的平均潜伏期（精确到0.1）； （3）从样本潜伏期超过10天的患者中随机抽取两人，求这两人中恰好一人潜伏期超过12天的概率.22．已知集合{(,)|[0,2],[1,1]}M x y x y =∈∈-. （1）若,x y Z ∈，求0x y +≥的概率； （2）若,x y R ∈，求0x y +≥的概率. 23．已知数列{}n a 的递推公式111n n n a a a --=+，且11a =，请画出求其前10项的流程图. 24．已知直线1:240l x y +-=，阅读如图所示的程序框图，若输入的x 的值为61+，输出的()f x 的值恰为直线2l 在x 轴上的截距，且12l l ⊥.（1）求直线1l 与2l 的交点坐标；（2）若直线3l 过直线1l 与2l 的交点，且在y 轴上的截距是在x 轴上的截距的2倍，求3l 的方程.25．某大学生利用寒假参加社会实践，对机械销售公司7月份至12月份销售某种机械配件的销售量及销售单价进行了调查，销售单价x 和销售量y 之间的一组数据如表所示：（2）若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过2件，则认为所得到的回归直线方程是理想的，试问（1）中所得到的回归直线方程是否理想？（3）预计在今后的销售中，销售量与销售单价仍然服从（1）中的关系，若该种机器配件的成本是2.5元/件，那么该配件的销售单价应定为多元才能获得最大利润？（注：利润=销售收入-成本）． 参考数据：51392i ii x y==∑，521502.5i i x ==∑．参考公式：回归直线方程ˆˆˆybx a =+，其中1221ˆni ii nii x y nx yb xnx ==-=-∑∑，ˆˆay bx =-． 26．某玻璃工艺品加工厂有2条生产线用于生产其款产品，每条生产线一天能生产200件该产品，该产品市场评级规定：评分在10分及以上的为A 等品，低于10分的为B 等品.厂家将A 等品售价定为2000元/件，B 等品售价定为1200元/件. 下面是检验员在现有生产线上随机抽取的16件产品的评分：经计算得16119.9716i i x x ===∑，()1616222211110.0451616i i i i s x x x x ===-=-=∑∑，其中i x 为抽取的第i 件产品的评分，1,2,,16i =⋅⋅⋅.该厂计划通过增加生产工序来改进生产工艺，已知对一条生产线增加生产工序每年需花费1500万元，改进后该条生产线产能不变，但生产出的每件产品评分均提高0.05.已知该厂现有一笔1500万元的资金.（1）若厂家用这1500万元改进一条生产线，根据随机抽取的16件产品的评分. （i ）估计改进后该生产线生产的产品中A 等品所占的比例； （ii ）估计改进后该厂生产的所有产品评分的平均数和方差.（2）某金融机构向该厂推销一款年收益率为8.2%的理财产品，请你利用所学知识分析，将这1500万元用于购买该款理财产品所获得的收益，与通过改进一条生产线使产品评分提高所增加的收益相对比，一年后哪种方案的收益更大？ （一年按365天计算）【参考答案】***试卷处理标记，请不要删除一、选择题 1．B 解析：B 【分析】设“甲､乙不在同一组”为事件M ，12名医护人员平均分配到两所医院的基本事件总数为n 612C ==924，甲､乙在同一组包含的基本事件个数m 4102C ==420，由此能求出甲､乙不在同一组的概率. 【详解】解：设“甲､乙不在同一组”为事件M ，12名医护人员平均分配到两所医院的基本事件总数为n 612C ==924， 甲､乙在同一组包含的基本事件个数m 4102C ==420，∴甲､乙不在同一组的概率P =14206192411m n -=-=. 故选：B 【点睛】本题考查古典概型的应用问题，重点考查分组分配题型，属于基础题型，本题的关键善于用所求事件的对立事件求概率.2．B解析：B 【分析】 求出满足12y ≥-的角x 的范围，由长度比，即可得到该几何概型的概率. 【详解】1sin ,[,]2y x x ππ=≥-∈-，5[,][,]66x ππππ∴∈--⋃-， 则满足12y ≥-的概率为： 5()()266()3P ππππππ---+--==--.故选：B. 【点睛】本题考查了三角不等式的求解，几何概型的计算，属于中档题.3．B解析：B 【分析】从中任意取出的两条，基本事件总数2615n C ==，这两条棱长度相等包含的基本事件个数22247m C C =+=，由此能求出这两条棱长度相等的概率． 【详解】解：三棱锥P ABC -的6条棱中，有2条长为1，有4条长为2，从中任意取出的两条，基本事件总数2615n C ==，这两条棱长度相等包含的基本事件个数22247m C C =+=， ∴这两条棱长度相等的概率715m p n ==． 故选：B ． 【点睛】本题考查概率的求法，考查古典概型、排列组合等基础知识，考查运算求解能力，是基础题．4．D解析：D 【分析】先计算出9套题中选出3套试卷的可能，再计算3套题年份和编号都各不相同的可能，通过古典概型公式可得答案. 【详解】通过题意，可知从这9套题中选出3套试卷共有39=84C 种可能，而3套题年份和编号都各不相同共有336A =种可能，于是所求概率为61=8414.选D. 【点睛】本题主要考查古典概型，意在考查学生的分析能力，计算能力，难度不大.5．B解析：B 【分析】模拟运行程序1i =，满足条件，1013S =+⨯，2i =，满足条件，进入循环体，反复操作，直到输出511S =，核对满足的条件即可. 【详解】1i =，满足条件，1013S =+⨯；2i =，满足条件，111335S =+⨯⨯； 3i =，满足条件，111133557S =++⨯⨯⨯； 4i =，满足条件，111113355779S =+++⨯⨯⨯⨯； 5i =，满足条件，11111115(1)1335577991121111S =++++=-=⨯⨯⨯⨯⨯； 6i =，不满足条件，输出511S =. 故选：B. 【点睛】本题考查了对程序框图的理解与应用，由程序运行结果，补充条件，数列求和的裂项相消法，属于中档题.6．D解析：D 【分析】由题意知该程序的作用是求样本128,,,x x x 的方差，由方差公式可得. 【详解】由题意知该程序的作用是求样本128,,,x x x 的方差，所用方法是求得每个数与x 的差的平方，再求这8个数的平均值，则图中空白框应填入的内容为：()2(1)i i S x x S i-+-=故选：D 【点睛】本题考查了程序框图功能的理解以及样本方差的计算公式，属于一般题.7．B解析：B 【分析】根据程序框图，模拟计算过程即可求解. 【详解】程序框图的执行过程如下：1S =，10k =；1011S =，9k =；911S =，8k ；811S =，7k =， 循环结束. 故选B. 【点睛】 本题主要考查了程序框图，算法结构，属于中档题. 8．C解析：C【分析】根据程序框图列出算法循环的每一步，结合判断条件得出输出的n 的值.【详解】执行如图所示的程序框图如下： 409S =≥不成立，11S 133==⨯，123n =+=； 1439S =≥不成立，1123355S =+=⨯，325n =+=； 2459S =≥不成立，2135577S =+=⨯，527n =+=； 3479S =≥不成立，3147799S =+=⨯，729n =+=. 4499S =≥成立，跳出循环体，输出n 的值为9，故选C. 【点睛】本题考查利用程序框图计算输出结果，对于这类问题，通常利用框图列出算法的每一步，考查计算能力，属于中等题.9．C解析：C【解析】试题分析：根据线性回归方程=50+80x 的意义，对选项中的命题进行分析、判断即可． 解：根据线性回归方程为=50+80x ，得；劳动生产率为1000元时，工资约为50+80×1=130元，A 正确；∵=80＞0，∴工人月工资与劳动者生产率具有正相关关系，B 正确；劳动生产率提高1000元时，工资约提高=80元，C 错误； 当月工资为210元时，210=50+80x ，解得x=2，此时劳动生产率约为2000元，D 正确．故选C ．考点：线性回归方程．10．A解析：A【分析】由题意计算出加入新数据后的平均数，然后比较方差【详解】()18138x x +⋯+=, ()181339x x +⋯++=, 3x ∴=，由方差的定义可知加入新数据3，样本数据会变得更加稳定故22s <故选A【点睛】本题主要考查了加入数据后平均数和方差的变化，代入公式计算出结果，较为基础 11．C解析：C【分析】设该样本中高三年级的学生人数为x ，则1800601200x=，解之即可 【详解】设该样本中高三年级的学生人数为x ， 则1800601200x=，解得40x =， 故选C ．【点睛】 本题考查了分层抽样方法的应用问题，属基础题．12．A解析：A【解析】分析：由题意结合统计表确定频数，然后确定频率即可.详解：由题意可知，取到卡片为奇数的频数为：1356181153++++=，取卡片的次数为100次，则取到号码为奇数的频率是530.53100=. 本题选择A 选项.点睛：本题主要考查频率的定义及其应用等知识，意在考查学生的转化能力和计算求解能力. 二、填空题13．【分析】由题意知本题是一个古典概型从0~9中任意取两个数（可重复）共有100种取法列出满足所有可能情况代入公式得到结果【详解】从0~9中任意取两个数（可重复）共有100种取法则的情况有：共有28种所 解析：725 【分析】 由题意知本题是一个古典概型，从0~9中任意取两个数（可重复）共有100种取法，列出满足||1a b -所有可能情况，代入公式得到结果。

一、选择题1．从单词“book ”的四个字母中任取2个，则取到的2个字母不相同的概率为（ ）A ．13B ．12C ．23D ．342．据《孙子算经》中记载，中国古代诸侯的等级从低到高分为：男、子、伯、侯、公，共五级，若给获得巨大贡献的7人进行封爵，要求每个等级至少有一人，至多有两人，则伯爵恰有两人的概率为（ ） A ．310B ．25C ．825D ．353．勒洛三角形是具有类似圆的“定宽性”的面积最小的曲线，它由德国机械工程专家，机构运动学家勒洛首先发现，其作法是：以等边三角形每个顶点为圆心，以边长为半径，在另两个顶点间作一段弧，三段弧围成的曲边三角形就是勒洛三角形，现在勒洛三角形中随机取一点，则此点取自正三角形外的概率为（ ）A ()23323ππ-- B ()323π- C ()323π+ D ()3323π+4．某人午觉醒来，发现表停了，他打开收音机，想听电台整点报时，则他等待的时间不多于15分钟的概率为（ ） A ．13B ．14C ．15D ．165．阅读如图所示的程序框图，当输入5n =时，输出的S =（ ）A．6 B．4615C．7 D．47156．执行如图所示的程序框图，则输出S的值为（）A．-1010 B．-1009 C．1009 D．1010 7．如图，执行程序框图后，输出的结果是（）A ．140B ．204C ．245D ．3008．某程序框图如图所示，若运行该程序后输出S =（ ）A ．53B ．74C ．95D ．1169．演讲比赛共有9位评委分别给出某选手的原始评分，评定该选手的成绩时，从9个原始评分中去掉1个最高分、1个最低分，得到7个有效评分.7个有效评分与9个原始评分相比，不变的数字特征是 A ．中位数 B ．平均数 C ．方差D ．极差10．已知变量,x y 之间的线性回归方程为0.47.6=-+y x ，且变量,x y 之间的一组相关数据如表所示，则下列说法错误的是（ ）A ．变量,x y 之间呈现负相关关系B ．m 的值等于5C ．变量,x y 之间的相关系数0.4=-rD ．由表格数据知，该回归直线必过点()9,411．某产品的广告费用x 与销售额y 的统计数据如下表： 广告费用（万元）4235销售额（万元）49263954根据上表可得回归方程ˆˆˆybx a =+中的ˆb 为9.4，据此模型预报广告费用为6万元时销售额为A ．63.6万元B ．65.5万元C ．67.7万元D ．72.0万元12．采用系统抽样方法从960人中抽取32人做问卷调查，为此将他们随机编号为1，2，...，960，分组后某组抽到的号码为41．抽到的32人中，编号落入区间[]401,755 的人数为（ ） A ．10B ．11C ．12D ．13二、填空题13．某学校高三年级有A 、B 两个自习教室，甲、乙、丙3名学生各自随机选择其中一个教室自习，则甲、乙两人不在同一教室上自习的概率为________.14．连续抛掷同一颗骰子3次，则3次掷得的点数之和为9的概率是____．15．在未来3天中，某气象台预报天气的准确率为0.8，则在未来3天中，至少连续2天预报准确的概率是______．16．如图是一个算法流程图，若输入x 的值为2，则输出y 的值为_______. .17．执行如图所示的程序框图，若输入的,a k 分别是89，2，则输出的数为__________．18．执行如图所示的程序框图，输出S的值为___________.19．某社会爱心组织面向全市征召义务宣传志愿者．现从符合条件的志愿者中随机抽取100名按年龄分组：第1组[20,25)，第2组[25,30)，第3组[30,35)，第4组[35,40)，第5组[40,45)，得到的频率分布直方图如图所示．若从第3，4，5组中用分层抽样的方法抽取6名志愿者参与广场的宣传活动，应从第3组抽取__________名志愿者．20．一个项目由15个专家评委投票表决，剔除一个最高分96，一个最低分58后所得到的平均分为92，方差为16，那么原始得分的方差为______________．三、解答题21．党的十九大报告指出，要以创新理念提升农业发展新动力，引领经济发展走向更高形态.为进一步推进农村经济结构调整，某村举办水果观光采摘节，并推出配套乡村游项目现统计了4月份200名游客购买水果的情况，得到如图所示的频率分布直方图：（1）若将购买金额不低于80元的游客称为“水果达人”，现用分层抽样的方法从样本的“水果达人”中抽取5人，求这5人中消费金额不低于100元的人数；（2）从（1）中的5人中抽取2人作为幸运客户免费参加山村旅游项目，请列出所有的基本事件，并求2人中至少有1人购买金额不低于100元的概率；（3）为吸引顾客，该村特推出两种促销方案，方案一：每满80元可立减8元；方案二：金额超过50元但又不超过80元的部分打9折，金额超过80元但又不超过100元的部分打8折，金额超过100元的部分打7折.若水果的价格为11元/千克，某游客要购买10千克，应该选择哪种方案更优惠.22．为降低汽车尾气的排放量，某厂生产甲乙两种不同型号的节排器，分别从甲乙两种节排器中各自抽取100件进行性能质量评估检测，综合得分情况的频率分布直方图如图所示.节排器等级及利润如表格表示，其中11107a <＜ 综合得分k 的范围节排器等级 节排器利润率85k ≥ 一级品 a 7585k ≤< 二级品 25a7075k ≤<三级品2a（1）若从这100件甲型号节排器按节排器等级分层抽样的方法抽取10件，再从这10件节排器中随机抽取3件，求至少有2件一级品的概率； （2）视频率分布直方图中的频率为概率，用样本估计总体，则①若从乙型号节排器中随机抽取3件，求二级品数ξ的分布列及数学期望()E ξ； ②从长期来看，骰子哪种型号的节排器平均利润较大？23．设计算法流程图，要求输入自变量x 的值，输出函数()5,020,0,3,02x x f x x x x ππ⎧->⎪⎪==⎨⎪⎪+<⎩的值，并用复合if 语句描述算法．24．已知函数y=21,0,1,0,x xx x ⎧>⎪⎪⎨⎪<⎪⎩设计一个算法的程序框图,计算输入x 的值,输出y 的值.25．“湖广熟，天下足”，鱼米之乡的湖北是全国重要的农产品生产地.而受疫情影响，像莲藕、小龙虾等湖北很多优质农副产品近期都面临销售难题.为了让淜北尽快恢复正常，央视主持人朱广权化身直播带货官，和网红们一起为湖北产品做公益直播.在为湖北某地区的小龙虾进行带货时，需大致了解该地区小龙虾的产量，通过调查发现湖北某地区近几年的小龙虾产量统计如下表：（1）根据表中数据，建立关于t 的线性回归方程y bt a =+； （2）请你根据线性回归方程预测今年（2020年）该地区小龙虾的年产量.附：对于一组数据()11,t y ，()22,t y ，…，(),n n t y ，其回归直线y bt a =+的斜率和截距的最小二乘估计分别为：()()()121ˆniii ni i t t y y bt t ==--=-∑∑，a y bt =-.（参考数据：()()616.3ii i tty y =--=∑）26．班主任为了对本班学生的考试成绩进行分析，决定从本班24名女同学，18名男同学中随机抽取一个容量为7的样本进行分析.（1）如果按照性别比例分层抽样，可以得到多少个不同的样本？（写出算式即可，不必计算出结果）（2）如果随机抽取的7名同学的数学，物理成绩（单位：分）对应如下表：①若规定85分以上（包括85分）为优秀，从这7名同学中抽取3名同学，记3名同学中数学和物理成绩均为优秀的人数为ξ，求ξ的分布列和数学期望；②根据上表数据，求物理成绩y 关于数学成绩x 的线性回归方程（系数精确到0.01）；若班上某位同学的数学成绩为96分，预测该同学的物理成绩为多少分？ 附：线性回归方程y bx a =+，其中121()()()niii nii x x y y b x x ==--=-∑∑，a y bx =-.【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D【分析】从四个字母中取2个，列举出所有的基本事件，即得所求的概率.【详解】从四个字母中取2个，所有的基本事件为：,,,bo bk oo ok，共有4个；其中“取到的2个字母不相同”含有,,bo bk ok3个，故所求概率为3 4 .故选：D.【点睛】本题考查古典概型，属于基础题.2．B解析：B【分析】根据部分平均分组分配的方法可求得分法总数和伯爵恰有两人的分法数，根据古典概型概率公式可求得结果.【详解】7人进行封爵，每个等级至少一人，至多两人，则共有2211225575327555322322C C C C C C AAA A A⋅=种分法；其中伯爵恰有两人的分法有2211142247532247543232C C C CC A C C AA A⋅=种分法，∴伯爵恰有两人的概率2247542257552225C C ApC C AA==.故选：B.【点睛】本题考查数学史与古典概型概率问题的求解，关键是能够利用排列组合中不平均分组分配的方法确定分法总数和符合题意的分法数.3．A解析：A 【分析】设2BC =，将圆心角为3π的扇形面积减去等边三角形的面积可得出弓形的面积，由此计算出图中“勒洛三角形”的面积，然后利用几何概型的概率公式可计算出所求事件的概率. 【详解】如下图所示，设2BC =，则以点B 为圆心的扇形面积为2122=233ππ⨯⨯， 等边ABC ∆的面积为212sin 323π⨯⨯=，其中一个弓形的面积为233π-， 所以，勒洛三角形的面积可视为一个扇形面积加上两个弓形的面积，即222322333πππ⎛⎫+⨯-=- ⎪⎝⎭， ∴在勒洛三角形中随机取一点，此点取自正三角形外部的概率()()323312323πππ--=--，故选A.【点睛】本题考查几何概型概率的计算，解题的关键就是要求出图形相应区域的面积，解题时要熟悉一些常见平面图形的面积计算方法，考查计算能力，属于中等题.4．B解析：B 【分析】由电台整点报时的时刻是任意的知这是一个几何概型，电台整点报时知事件总数包含的时间长度是60，而他等待的时间不多于15分钟的事件包含的时间长度是15，利用时间的长度比即可求出所求. 【详解】解：由题意知这是一个几何概型， ∵电台整点报时，∴事件总数包含的时间长度是60，∵满足他等待的时间不多于15分钟的事件包含的时间长度是15，由几何概型公式得到151604P ==, 故选B ． 【点睛】本题主要考查了几何概型，本题先要判断该概率模型，对于几何概型，它的结果要通过长度、面积或体积之比来得到，属于中档题.5．D解析：D 【分析】根据程序框图，依次运行程序即可得出输出值. 【详解】输入5n =时，1,1,1,5S i a i ===≤，2,3,2a S i ===，5i ≤222,5,32a S i =⨯===，5i ≤ 2442,5,4333a S i =⨯==+=，5i ≤ 42242,5,534333a S i =⨯==++=，5i ≤224424,5,635153315a S i =⨯==+++=，输出424457331515S =+++= 故选：D 【点睛】此题考查程序框图，关键在于读懂框图，根据结构依次运算，求出输出值，尤其注意判断框中的条件.6．D解析：D 【分析】根据程序框图,先计算出N 和T 的含义,再根据S N T =-即可求得输出值.或利用等差数列的求和公式求解. 【详解】依题意：得1352019N =+++⋯+,02462018T =++++⋯+. 解法一：(10)(32)(54)(20192018)1010S N T =-=-+-+-++-=,故选:D.解法二：(12019)1010101010102N +⨯==⨯,(02018)1010100910102T +⨯==⨯,所以10101010101010091010(10101009)1010S N T =-=⨯-⨯=⨯-=,【点睛】本题考查了程序框图的简单应用,数列求和公式的应用,属于中档题.7．B解析：B 【分析】根据程序框图列举出算法的每一步，可得出输出结果. 【详解】18n =>不成立，执行第一次循环，211b ==，011s =+=，112n =+=；28n =>不成立，执行第二次循环，224b ==，145s =+=，213n =+=； 38n =>不成立，执行第三次循环，239b ==，5914s =+=，314n =+=； 48n =>不成立，执行第四次循环，2416b ==，141630s =+=，415n =+=； 58n =>不成立，执行第五次循环，2525b ==，302555s =+=，516n =+=； 68n =>不成立，执行第六次循环，2636b ==，553691s =+=，617n =+=； 78n =>不成立，执行第七次循环，2749b ==，9149140s =+=，718=+=n ； 88n =>不成立，执行第八次循环，2864b ==，14064204s =+=，819n =+=； 98n =>成立，跳出循环体，输出s 的值为204，故选B. 【点睛】本题考查程序框图运行结果的计算，一般利用算法程序框图将算法的每一步列举出来，考查计算能力，属于中等题.8．D解析：D 【分析】通过分析可知程序框图的功能为计算211n S n +=+，根据最终输出时n 的值，可知最终赋值S 时5n =，代入可求得结果. 【详解】根据程序框图可知其功能为计算：()111111111211111112231223111n S n n n n n n +=+++⋅⋅⋅+=+-+-+⋅⋅⋅+-=+-=⨯⨯++++初始值为1n =，当6n =时，输出S 可知最终赋值S 时5n = 25111516S ⨯+∴==+ 本题正确选项：D 【点睛】本题考查根据程序框图的功能计算输出结果，关键是能够明确判断出最终赋值时n 的取值.9．A【分析】可不用动笔，直接得到答案，亦可采用特殊数据，特值法筛选答案． 【详解】设9位评委评分按从小到大排列为123489x x x x x x ≤≤≤≤≤．则①原始中位数为5x ，去掉最低分1x ，最高分9x ，后剩余2348x x x x ≤≤≤，中位数仍为5x ，∴A 正确． ②原始平均数1234891()9x x x x x x x =+++++，后来平均数234817x x x x x '=+++（）平均数受极端值影响较大，∴x 与x '不一定相同，B 不正确 ③()()()222219119S x x x x x x ⎡⎤=-+-++-⎣⎦()()()222223817s x x x x x x ⎡⎤'=-'+-'++-'⎢⎥⎣⎦由②易知，C 不正确．④原极差91=x -x ，后来极差82=x -x 可能相等可能变小，D 不正确． 【点睛】本题旨在考查学生对中位数、平均数、方差、极差本质的理解.10．C解析：C 【解析】分析：根据线性回归方程的性质依次判断各选项即可．详解：对于A ：根据b 的正负即可判断正负相关关系．线性回归方程为0.47.6y x =-+，b=﹣0.7＜0，负相关．对于B ：根据表中数据：x =9．可得y =4．即()16+3244m ++=，解得：m=5． 对于C ：相关系数和斜率不是一回事，只有当样本点都落在直线上是才满足两者相等，这个题目显然不满足，故不正确.对于D ：由线性回归方程一定过（x ，y ），即（9，4）． 故选：C ．点睛：本题考查了线性回归方程的求法及应用，属于基础题，对于回归方程，一定要注意隐含条件，样本中心满足回归方程，再者计算精准，正确理解题意，应用回归方程对总体进行估计.11．B解析：B 【详解】试题分析：4235492639543.5,4244x y ++++++====， ∵数据的样本中心点在线性回归直线上，回归方程ˆˆˆybx a =+中的ˆb 为9.4， ∴42=9．4×3．5+a ， ∴ˆa =9．1，∴线性回归方程是y=9．4x+9．1，∴广告费用为6万元时销售额为9．4×6+9．1=65．5 考点：线性回归方程12．C解析：C 【分析】由题意可得抽到的号码构成以11为首项、以30为公差的等差数列，求得此等差数列的通项公式为a n ＝30n ﹣19，由401≤30n ﹣21≤755，求得正整数n 的个数，即可得出结论． 【详解】∵960÷32＝30，∴每组30人，∴由题意可得抽到的号码构成以30为公差的等差数列， 又某组抽到的号码为41，可知第一组抽到的号码为11，∴由题意可得抽到的号码构成以11为首项、以30为公差的等差数列， ∴等差数列的通项公式为a n ＝11+（n ﹣1）30＝30n ﹣19， 由401≤30n ﹣19≤755，n 为正整数可得14≤n ≤25， ∴做问卷C 的人数为25﹣14+1＝12， 故选C ． 【点睛】本题主要考查等差数列的通项公式，系统抽样的定义和方法，根据系统抽样的定义转化为等差数列是解决本题的关键，比较基础．二、填空题13．【分析】利用乘法计数原理可计算出甲乙丙名学生各自随机选择其中一个教室自习共有种利用分步乘法计数原理计算出甲乙两人不在同一教室上自习的排法种数然后利用古典概型的概率公式可计算出所求事件的概率【详解】由 解析：12【分析】利用乘法计数原理可计算出甲、乙、丙3名学生各自随机选择其中一个教室自习共有32种，利用分步乘法计数原理计算出甲、乙两人不在同一教室上自习的排法种数，然后利用古典概型的概率公式可计算出所求事件的概率. 【详解】由题意可知，甲、乙、丙3名学生各自随机选择其中一个教室自习共有32种，甲、乙两人不在同一教室上自习，可先考虑甲在A、B两个自习教室选一间教室自习，然后乙在另一间教室自习，则丙可在A、B两个自习教室随便选一间自习教室自习，由分步计数原理可知，有224⨯=种选择.因此，甲、乙两人不在同一教室上自习的概率为41 82 =.故答案为：1 2 .【点睛】本题考查利用古典概型的概率公式计算事件的概率，同时也考查了分步计数原理的应用，考查计算能力，属于中等题.14．；【分析】利用分步计数原理连续拋掷同一颗骰子3次则总共有：6×6×6=216种情况再列出满足条件的所有基本事件利用古典概型的计算公式计算可得概率【详解】每一次拋掷骰子都有123456六种情况由分步计解析：25 216；【分析】利用分步计数原理，连续拋掷同一颗骰子3次，则总共有：6×6×6=216种情况，再列出满足条件的所有基本事件，利用古典概型的计算公式计算可得概率.【详解】每一次拋掷骰子都有1，2，3，4，5，6，六种情况，由分步计数原理：连续抛掷同一颗骰子3次，则总共有：6×6×6=216种情况，则3次掷得的点数之和为9的基本事件为25种情况即：(1,2,6)，(1,3,5)，(1,4,4)，(1,5,3)，(1,6,2)，(2,1,6)，(2,2,5)，(2,3,4)，(2,4,3)，(2,5,2)，(2,6,1)，(3,1,5)，(3,2,4)，(3,3,3)，(3,4,2)，(3,5,1)，(4,1,4)，(4,2,3)，(4,3,2)，(4,4,1)，(5,1,3)，(5,2,2)，(5,3,1)，(6,1,2)，(6,2,1)，共25个基本事件，所以25216 P=.【点睛】本题考查分步计数原理和古典概型概率计算，计数过程中如果前两个数固定，则第三个数也相应固定.15．768【分析】至少连续2天预报准确包含3种情况：①三天都预报准确；②第一二天预报准确第三天预报不准确；③第一天预报不准确第二三天预报准确分别求解后根据互斥事件的概率加法公式求解即可【详解】至少连续2解析：768【分析】至少连续2天预报准确包含3种情况：①三天都预报准确；②第一二天预报准确，第三天预报不准确；③第一天预报不准确，第二三天预报准确．分别求解后根据互斥事件的概率加法公式求解即可． 【详解】至少连续2天预报准确包含3种情况： ①三天都预报准确，其概率为30.80.512=；②第一二天预报准确，第三天预报不准确，其概率为20.80.20.128⨯=； ③第一天预报不准确，第二三天预报准确，其概率为20.20.80.128⨯=． ∴在未来3天中，至少连续2天预报准确的概率是0.5120.1280.1280.768P =++=． 即所求概率为0.768． 【点睛】本题考查独立事件同时发生的概率的求法和互斥事件的概率，解答类似问题时首先要分清概率的类型，然后在选择相应的公式求解．某些事件若含有较多的互斥事件，可考虑其对立事件的概率，这样可减少运算量，提高准确率．要注意“至多”“至少”等题型的转化．16．5【分析】直接模拟程序即可得结论【详解】输入的值为2不满足所以故答案是：5【点睛】该题考查的是有关程序框图的问题涉及到的知识点有程序框图的输出结果的求解属于简单题目解析：5 【分析】直接模拟程序即可得结论. 【详解】输入x 的值为2，不满足1x ≤，所以3325y x =+=+=， 故答案是：5. 【点睛】该题考查的是有关程序框图的问题，涉及到的知识点有程序框图的输出结果的求解，属于简单题目.17．1011001【解析】模拟程序框图的运行过程如下；输入a=89k=2q=89÷2=44…1；a=44k=2q=44÷2=22…0；a=22k=2q=22÷2=11…0；a=11k=2a=11÷2=5解析：1011001 【解析】模拟程序框图的运行过程，如下； 输入a=89，k=2，q=89÷2=44…1； a=44，k=2，q=44÷2=22…0； a=22，k=2，q=22÷2=11…0； a=11，k=2，a=11÷2=5…1； a=5，k=2，q=5÷2=2…1； a=2，k=2，q=2÷2=1…0； a=1，k=2，q=1÷20…1；则输出的数为1011001． 故答案为：1011001．18．48【解析】第1次运行成立第2次运行成立第3次运行成立第3次运行不成立故输出的值为48解析：48 【解析】第1次运行，1,2,122,4i S S i ===⨯=<成立 第2次运行，2,2,224,4i S S i ===⨯=<成立 第3次运行，3,4,3412,4i S S i ===⨯=<成立 第3次运行，4,12,41248,4i S S i ===⨯=<不成立， 故输出S 的值为4819．【分析】先分别求出这3组的人数再利用分层抽样的方法即可得出答案【详解】第3组的人数为第4组的人数为第5组的人数为所以这三组共有60名志愿者所以利用分层抽样的方法在60名志愿者中抽取6名志愿者第三组应 解析：3【分析】先分别求出这3组的人数，再利用分层抽样的方法即可得出答案. 【详解】第3组的人数为10050.0630⨯⨯=， 第4组的人数为10050.0420⨯⨯=， 第5组的人数为1000.02510⨯⨯=， 所以这三组共有60名志愿者，所以利用分层抽样的方法在60名志愿者中抽取6名志愿者，第三组应抽取306360⨯=名， 故答案为：3. 【点睛】关键点点睛：该题考查的是有关频率分布直方图的识别以及分层抽样某层抽取个数的问题，正确解题的关键是掌握在抽取过程中每个个题被抽到的机会均等.20．【解析】分析：根据方差与均值的关系求解即可详解：剔除最高分和最低分后的则原始平均分 原始原始方差即原始方差为88点睛：本题考查方差与均值的关系属基础题 解析：88【解析】分析：根据方差与均值的关系()()()22D xE x E x ⎡⎤=-⎣⎦求解即可.详解：剔除最高分和最低分后的222()()()92168480,E x E x D x =+=+=22()8480(152)110240,x E x n ∑=⨯=⨯-=则原始平均分()921?3? 96? 589015E x ；⨯++==原始 22229658()8188,15x E x ∑++==原始方差 222()?()?()81889088.D x E X E X =-=-=原始原始 即原始方差为 88 .点睛：本题考查方差与均值的关系，属基础题.三、解答题21．（1）2；（2）710；（3）应该选择方案二更优惠. 【分析】（1）由题意可求出金额在[)80,100“水果达人”的人数30人和消费金额在[]100,120“水果达人”的人数20人，然后利用分层抽样的比求出5人中消费金额不低于100元的人数为20523020⨯=+人；（2）由（1）可知抽取的5人中消费金额在[)80,100的有3人，分别记为A ，B ，C ，消费金额在[]100,120的有2人，记为a ，b ，即可列出所有的基本事件共有10种，其中满足条件的有7种，从而可求出概率；（3）由题意可得该游客要购买110元水果，分别计算两种方案所需支付金额，即可得解. 【详解】解：（1）由图可知，消费金额在[)80,100“水果达人”的人数为：200200.007530⨯⨯=人， 消费金额在[]100,120“水果达人”的人数为：200200.00520⨯⨯=人，分层抽样的方法从样本的“水果达人”中抽取5人，这5人中消费金额不低于100元的人数为：20523020⨯=+人；（2）由（1）得，消费金额在[)80,100的3个“水果达人”记为A ，B ，C ， 消费金额在[]100,120的2个“水果达人”记为a ，b ， 所有基本事件有：(),A B ，(),A C ，(),B C ，(),A a ，(),A b ，(),B a ，(),B b ，(),C a ，(),C b ，(),a b 共10N =种，2人中至少有1人购买金额不低于100元的有7n =种，所求概率为710n N ==. （3）依题可知该游客要购买110元的水果， 若选择方案一，则需支付()80830102-+=元，若选择方案二，则需支付50300.9200.8100.7100+⨯+⨯+⨯=元， 所以应该选择方案二更优惠. 【点睛】此题考查了频率分布直方图，古典概型，函数等基础知识，考查了数据分析能力，运算求解能力，考查了化归与转化思想，属于中档题. 22．（1）23 ；（2）①分布列见解析，34；②投资乙型号节排器的平均利润率较大. 【分析】（1）由已知及频率分布直方图中的信息知，甲型号节排器中的一级品的概率为0.6，根据分层抽样，计算10件节排器中一级品的个数，再利用互斥事件概率加法公式能求出至少 2件一级品的概率；（2）①由已知及频率分布直方图中的信息知，乙型号节排器中的一级品的概率为710，二级品的概率14，三级品的概率为120，若从乙型号节排器随机抽取3件，则二级品数ξ所有可能的取值为0,1,2,3，且1(3,)4B ξ，由此能求出ξ的分布列和数学期望.②由题意分别求出甲型号节排器的利润的平均值和乙型号节排器的利润的平均值，由此求出投资乙型号节排器的平均利润率较大. 【详解】（1）由已知及频率分布直方图中的信息知，甲型号节排器中的一级品的概率为0.6， 分层抽样的方法抽取10件，则抽取一级品为100.66⨯=（件） 则至少有2件一级品的概率，21364631023C C C P C +== （2）①由已知及频率分布直方图中的信息知，乙型号节排器中的一级品的概率为710，二级品的概率14，三级品的概率为120，若从乙型号节排器随机抽取3件，则二级品数ξ所有可能的取值为0,1,2,3，且1(3,)4B ξ，所以3033127(0)4464P C ξ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭，21133127(1)4464P C ξ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭1223319(2)4464P C ξ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭，0333311(3)4464P C ξ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭， 所以，ξ的分布列为ξ0 1 2 3P2764 2764 964 1642727913()0123646464644E ξ=⨯+⨯+⨯+⨯= ②由题意知，甲型号节排器的利润的平均值221323=52555E a a a a +⨯=+乙型号节排器的利润的平均值 2222711137=5104201010E a a a a a +⨯+=+ 2127171=1010107E E a a a a ⎛⎫--=- ⎪⎝⎭，又11107a << 所以投资乙型号节排器的平均利润率较大. 【点睛】本题考查（1）概率加法公式（2）离散型随机变量的分布列和数学期望，考查计算能力，属于中等题型 23．见解析 【详解】 试题分析：结合题意，将分段函数利用流程图设计为条件结构即可，然后结合流程图即可写出具体的算法语句，注意if 与else 的灵活准确应用. 试题输入x ；if x < 0，then f (x )= π/2∙x +3；else if x = 0，then f (x )=0；else f (x )= π/2∙x -5.输出f (x ).24．答案见解析【解析】【试题分析】主要结构是有一个选择结构,当0x >时为1x ,当0x <时为21x ,当0x =时直接退出程序.【试题解析】根据题意,其自然语言算法如下.第一步,输入x.第二步,判断x>0是否成立.若成立,则输出y=1x,结束算法; 若不成立,则判断x<0是否成立.若成立,则输出y=21x ,结束算法;若不成立,也结束算法. 程序框图如右:【点睛】画程序框图的规则如下：（1）一个完整的程序框图必须有起止框，用来表示程序的开始和结束.（2）使用标准的图形符号表示操作，带箭头的流程线表示算法步骤的先后顺序，框图一般按从上到下、从左到右的方向画（3）算法中间要处理数据或计算，可分别写在不同的处理框中.（4）如果一个流程由于纸面等原因需要分开画.要在断开处画上连结点，并标出连结的号码.如图一.实际 上它们是同一点，只是化不才分开画.用连结点可避免流程线的交叉或过长，使流程图清晰.（5）注释框不是流程图必需的部分，只是为了提示用户 一部分框图的作用以及对某些框图的操作结果进行说明.它帮助阅读流程图的用户更好的理解流程图的来龙去脉.（6）在图形符号内用于描述的语言要非常简练清楚25．（1）0.36 6.24y x =+；（2）8.76万吨.【分析】（1）由题意求得知 3.5t =，7.5=y ，()62117.5i i t t =-=∑，运用公式求得b ，代入可求得y 关于t 的线性回归方程. （2）由（1）得的线性回归方程，代入年份代码7t =计算，可预测2020年该地区小龙虾的年产量.【详解】（1）由题知 3.5t =，7.5=y ，()62117.5i i t t =-=∑，()()()61621 6.30.3617.5ˆi ii i i t t y y b t t ==--===-∑∑， 又 6.24=-=a y bt .所以，y 关于t 的线性回归方程为0.36 6.24y x =+.（2）由（1）得，当年份为2020年时，年份代码7t =，此时0.367 6.248.76=⨯+=y .所以，可预测，2020年该地区小龙虾的年产量为8.76万吨.【点睛】本题考查线性回归方程的求解，利用线性回归方程对总体进行估计，属于中档题. 26．（1）不同的样本的个数为432418C C .（2）①分布列见解析，()E ξ97=. ②线性回归方程为0.6533.60y x =+.可预测该同学的物理成绩为96分.【分析】（1）按比例抽取即可，再用乘法原理计算不同的样本数.（2）7名学生中物理和数学都优秀的有3名学生，任取3名学生，都优秀的学生人数ξ服从超几何分布，故可得其概率分布列及其数学期望.而线性回归方程的计算可用给出的公式计算，并利用得到的回归方程预测该同学的物理成绩.【详解】（1）依据分层抽样的方法，24名女同学中应抽取的人数为724442⨯=名， 18名男同学中应抽取的人数为718342⨯=名， 故不同的样本的个数为432419C C .（2）①∵7名同学中数学和物理成绩均为优秀的人数为3名，∴ξ的取值为0，1，2，3.∴()34374035C P C ξ===，()21433711835C C C P ξ===，。

一、选择题1．如图，在圆心角为2π，半径为1的扇形中，在弦AB 上任取一点，则38AOC π∠≤的概率为（ ）A ．14B ．222C ．34D ．222．已知三棱锥P ﹣ABC 的6条棱中，有2条长为1，有4条长为2，则从中任意取出的两条，这两条棱长度相等的概率为（ ） A ．815B ．715C ．45D ．353．某比赛为甲、乙两名运动员制订下列发球规则：规则一：投掷一枚硬币，出现正面向上，甲发球，否则乙发球；规则二：从装有2个红球与2个黑球的布袋中随机地取出2个球，如果同色，甲发球，否则乙发球；规则三：从装有3个红球与1个黑球的布袋中随机地取出2个球，如果同色，甲发球，否则乙发球. 其中对甲、乙公平的规则是（ ） A ．规则一和规则二B ．规则一和规则三C ．规则二和规则三D ．规则二4．某人午觉醒来，发现表停了，他打开收音机，想听电台整点报时，则他等待的时间不多于15分钟的概率为（ ） A ．13B ．14C ．15D ．165．执行如图所示的程序框图输出的结果是（ ）A ．8B ．6C ．5D ．36．执行如图所示的程序框图，则输出的n 值是（ ）A ．5B ．7C ．9D ．117．我国古代名著《庄子·天下篇》中有一句名言“一尺之棰，日取其半，万世不竭”，其意思为：一尺的木棍，每天截取一半，永远都截不完.现将该木棍依此规律截取，如图所示的程序框图的功能就是计算截取20天后所剩木棍的长度（单位：尺），则①②③处可分别填入的是（ ）A ．20i <，1S S i=-，2i i = B ．20i ≤，1S S i=-，2i i = C ．20i <，2SS =，1i i =+ D ．20i ≤，2SS =，1i i =+ 8．执行如图所示的程序框图，若输出的结果为5，则输入的实数a 的范围是( )A ．[)6,24B ．[)24,120C ．(),6-∞D ．()5,249．某产品的广告费用与销售额的统计数据如下表：（ ） 广告费用（万元） 销售客（万元）根据上表中的数据可以求得线性回归方程中的为，据此模型预报广告费用为万元时销售额为（ ） A ．万元B ．万元C ．万元D ．万元10．一组数据中的每一个数据都乘2，再减去80，得到一组新数据，若求得新数据的平均数是1.2，方差是4.4，则原来数据的平均数和方差分别是 A ．81.2，4.4 B ．40.6，1.1 C ．48.8，4.4D ．78.8，1.111．在学校组织的考试中，45名学生的数学成绩的茎叶图如图所示，则该45名学生的数学成绩的中位数为（ ）A ．127B ．128C ．128.5D ．12912．有一个同学家开了一个小卖部，他为了研究气温对热饮销售的影响，经统计，得到一个卖出的热饮杯数与当天气温的对比表： 温度℃ -5 0 4 7 12 15 19 23 27 31 36 热饮杯数15615013212813011610489937654根据上表数据确定的线性回归方程应该是（ ）A ．ˆ 2.352147.767y x =-+B ．ˆ 2.352127.765yx =-+C ．ˆ 2.35275.501yx =+D ．ˆ 2.35263.674yx =+ 二、填空题13．已知函数2()22f x x =-的定义域为M ，(())y f f x =的定义域为P ，在M 上随机取一个数x ，则x P ∈的概率是____________．14．西周初数学家商高在公元前1000年发现勾股定理的一个特例：勾三，股四，弦五.此发现早于毕达哥拉斯定理五百到六百年.我们把可以构成一个直角三角形三边的一组正整数称为勾股数.现从3,4,5,6,7,8,9,10,11,12,13这11个数中随机抽取3个数，则这3个数能构成勾股数的概率为__________．15．农历戊戌年即将结束，为了迎接新年，小康、小梁、小谭、小刘、小林每人写了一张心愿卡，设计了一个与此心愿卡对应的漂流瓶.现每人随机的选择一个漂流瓶将心愿卡放入，则事件“至少有两张心愿卡放入对应的漂流瓶”的概率为___ 16．如果执行如图所示的程序框图，那么输出的值为__________．17．根据如图所示的算法流程图，可知输出的结果S 为______．18．已知多项式函数5432()254367f x x x x x x =--+-+，当5x =时由秦九韶算法知012,2555,v v ==⨯-=则3v ＝_________．19．下列说法正确的是__________（填序号）（1）已知相关变量(),x y 满足回归方程ˆ24yx =-，若变量x 增加一个单位，则y 平均增加4个单位（2）若,p q 为两个命题，则“p q ∨”为假命题是“p q ∧”为假命题的充分不必要条件（3）若命题0:p x R ∃∈，20010x x -+<，则:p x R ⌝∀∉，210x x -+≥（4）已知随机变量()22X N σ~，，若()0.32P X a <=，则()40.68P X a >-=20．已知数据(1,2,3,4,5)i x i =的平均值为a ，数列2{()}i x a -为等差数列，且3||0.1x a -=，则该组数据的方差为________. 三、解答题21．某中学利用周末组织教职员工进行了一次秋季登山健身的活动，有Ⅳ人参加，现将所有参加者按年龄情况分为[20,25)，[25,30)，[30,35)，[35,40)，[40,45)，[45,50)，[50,55)等七组，其频率分布直方图如图所示，已知[25,30)这组的参加者是6人．（1）已知[35,40)和[40,45)这两组各有2名数学教师，现从这两个组中各选取2人担任接待工作，设两组的选择互不影响，求两组选出的人中恰有1名数学老师的概率； （2）组织者从[45,55)这组的参加者（其中共有4名女教师，其余全为男教师）中随机选取3名担任后勤保障工作，其中女教师的人数为X ，求X 的分布列和均值．22．追求人类与生存环境的和谐发展是中国特色社会主义生态文明的价值取向.为了改善空气质量，某城市环保局随机抽取了一年内100天的空气质量指数（AQI ）的检测数据，结果统计如下：AQI [0,50] (50,100] (100,150] (150,200] (200,250] (250,300]空气质量 优 良 轻度污染 中度污染 重度污染 严重污染 天数61418272510（1）从空气质量指数属于[0,50]，(50,100]的天数中任取3天，求这3天中空气质量至少有2天为优的概率.（2）已知某企业每天因空气质量造成的经济损失y （单位：元）与空气质量指数x 的关系式为0,0100,220,100250,1480,250300.xy xx⎧⎪=<⎨⎪<⎩假设该企业所在地7月与8月每天空气质量为优、良、轻度污染、中度污染、重度污染、严重污染的概率分别为16，13，16，112，112,16,9月每天的空气质量对应的概率以表中100天的空气质量的频率代替.（i）记该企业9月每天因空气质量造成的经济损失为X元，求X的分布列；（ii）试问该企业7月、8月、9月这三个月因空气质量造成的经济损失总额的数学期望是否会超过2.88万元？说明你的理由.23．根据下面的要求，求满足123500n+++⋅⋅⋅+>的最小的自然数n，并画出执行该问题的程序框图.24．某批发部出售袜子,当购买少于300双时,每双批发价为2.5元;不少于300双时,每双批发价为2.2元.试分别画出程序框图和用程序语言编写计算批发金额.25．某学校进行体验，现得到所有男生的身高数据，从中随机抽取50人进行统计（已知这50个身高介于155cm到195cm之间），现将抽取结果按如下方式分成八组：第一组[155,160)，第二组[160,165)，...，第八组[190,195]，并按此分组绘制如图所示的频率分布直方图，其中第六组[180,185)和第七组[185,190)还没有绘制完成，已知第一组与第八组人数相同，第六组和第七组人数的比为5:2．（1）补全频率分布直方图；（2）根据频率分布直方图估计这50位男生身高的中位数；（3）用分层抽样的方法在身高为[170,180]内抽取一个容量为5的样本，从样本中任意抽取2位男生，求这两位男生身高都在[175,180]内的概率．26．某同学在生物研究性学习中，对春季昼夜温差大小与黄豆种子发芽多少之间的关系进行研究，于是他在4月份的30天中随机挑选了5天进行研究，且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数，得到如下资料：日期4月1日4月7日4月15日4月21日4月30日温差x C ︒ 10 11 13 128 发芽数y 颗2325302616（1）从这5天中任选2天，若选取的是4月1日与4月30日的两组数据，请根据这5天中的另三天的数据，求出y 关于x 的线性回归方程y bx a =+；（2）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗，则认为得到的线性回归方程是可靠的，试问（1）中所得的线性回归方程是否可靠？ 附：回归直线的斜率和截距的最小二乘估计公式分别为：()()()1122211nniii ii i nniii i x x y y x y nx yb x x xnx====---==--∑∑∑∑，a y bx =-.【参考答案】***试卷处理标记，请不要删除一、选择题 1．D 解析：D 【分析】由题意可知，38AOCπ∠的概率为AC AB，由题意结合平面几何知识求得1AC =，2AB =，则答案可求．【详解】 如图，4OAB π∠=，若38AOC π∠=，则33488ACO ππππ∠=--=， OAC ∴∆为等腰三角形，即1AC OA ==．在Rt AOB ∆中， 1OA OB ==， 2AB ∴=．由测度比为长度比可得38AOC π∠的概率为2AC AB ==． 故选：D ． 【点睛】本题考查几何概型，考查灵活变形能力，是中档题．2．B解析：B 【分析】从中任意取出的两条，基本事件总数2615n C ==，这两条棱长度相等包含的基本事件个数22247m C C =+=，由此能求出这两条棱长度相等的概率． 【详解】解：三棱锥P ABC -的6条棱中，有2条长为1，有4条长为2，从中任意取出的两条，基本事件总数2615n C ==，这两条棱长度相等包含的基本事件个数22247m C C =+=， ∴这两条棱长度相等的概率715m p n ==． 故选：B ． 【点睛】本题考查概率的求法，考查古典概型、排列组合等基础知识，考查运算求解能力，是基础题．3．B解析：B 【分析】计算出三种规则下甲发球和乙发球的概率，当两人发球的概率均为12时，该规则对甲、乙公平，由此可得出正确选项. 【详解】对于规则一，每人发球的机率都是12，是公平的； 对于规则二，记2个红球分别为红1，红2，2个黑球分别为黑1、黑2，则随机取出2个球的所有可能的情况有（红1，红2），（红1，黑1），（红1，黑2），（红2，黑1），（红2，黑2），（黑1，黑2），共6种，其中同色的情况有2种， 所以甲发球的可能性为13，不公平； 对于规则三，记3个红球分别为红1、红2、红3，则随机取出2个球所有可能的情况有（红1，红2），（红1，红3），（红1，黑），（红2，红3），（红2，黑），（红3，黑），共6种，其中同色的情况有3种，所以两人发球的可能性均为12，是公平的.因此，对甲、乙公平的规则是规则一和规则三. 故选B. 【点睛】本题考查利用规则的公平性问题，同时也考查了利用古典概型的概率公式计算事件的概率，正确理解题意是解题的关键，考查计算能力，属于中等题.4．B解析：B 【分析】由电台整点报时的时刻是任意的知这是一个几何概型，电台整点报时知事件总数包含的时间长度是60，而他等待的时间不多于15分钟的事件包含的时间长度是15，利用时间的长度比即可求出所求. 【详解】解：由题意知这是一个几何概型， ∵电台整点报时，∴事件总数包含的时间长度是60，∵满足他等待的时间不多于15分钟的事件包含的时间长度是15， 由几何概型公式得到151604P ==, 故选B ． 【点睛】本题主要考查了几何概型，本题先要判断该概率模型，对于几何概型，它的结果要通过长度、面积或体积之比来得到，属于中档题.5．A解析：A 【分析】根据程序框图循环结构运算，依次代入求解即可． 【详解】根据程序框图和循环结构算法原理，计算过程如下：1,1,x y z x y ===+第一次循环2,1,2z x y === 第二次循环3,2,3z x y === 第三次循环5,3,5z x y ===第四次循环8z =，退出循环输一次8z =. 所以选A 【点睛】本题考查了程序框图的基本结构和运算，主要是掌握循环结构在何时退出循环结构，属于基础题．6．C解析：C 【分析】根据程序框图列出算法循环的每一步，结合判断条件得出输出的n 的值. 【详解】执行如图所示的程序框图如下：409S =≥不成立，11S 133==⨯，123n =+=； 1439S =≥不成立，1123355S =+=⨯，325n =+=； 2459S =≥不成立，2135577S =+=⨯，527n =+=； 3479S =≥不成立，3147799S =+=⨯，729n =+=. 4499S =≥成立，跳出循环体，输出n 的值为9，故选C. 【点睛】本题考查利用程序框图计算输出结果，对于这类问题，通常利用框图列出算法的每一步，考查计算能力，属于中等题.7．D解析：D 【分析】先由第一天剩余的情况确定循环体，再由结束条件确定循环条件即可. 【详解】根据题意可知，第一天12S =，所以满足2S S =，不满足1S S i=-，故排除AB ，由框图可知，计算第二十天的剩余时，有2SS =，且21i =，所以循环条件应该是20i ≤. 故选D. 【点睛】本题考查了程序框图的实际应用问题，把握好循环体与循环条件是解决此题的关键，属于中档题.8．A解析：A 【解析】 【分析】模拟程序的运行，依次写出每次循环得到的x ，n 的值，由题意判断退出循环的条件即可得解． 【详解】模拟程序的运行，可得n ＝1，x ＝1不满足条件x ＞a ，执行循环体，x ＝1，n ＝2 不满足条件x ＞a ，执行循环体，x ＝2，n ＝3 不满足条件x ＞a ，执行循环体，x ＝6，n ＝4 不满足条件x ＞a ，执行循环体，x ＝24，n ＝5此时，由题意应该满足条件x ＞a ，退出循环，输出n 的值为5． 可得：6≤a ＜24． 故选：A ． 【点睛】本题考查的知识点是循环结构的程序框图的应用，当循环的次数不多，或有规律时，常采用模拟循环的方法解答，属于基础题．9．B解析：B 【解析】 【分析】 先求出，由样本点的中心在回归直线上，可求出，从而求出回归方程，然后令，可求出答案.【详解】 由题意，，则样本中心点在回归方程上，则，故线性回归方程为，则广告费用为万元时销售额为万元，故选B.【点睛】本题考查了线性回归方程的求法，考查了学生的计算能力，属于基础题.10．B解析：B 【分析】先设出原来的数据，然后设出现在的数据，找到两组数据的联系，即可． 【详解】设原来的数据为12,,....,n x x x ，每一个数据都乘以2，再减去80，得到新数据为 12280,280,...,280n x x x --- 已知()122...80 1.2n x x x nn+++-=，则81.240.62X == 方差为：224 4.4, 1.1σσ==，故选B ． 【点睛】本道题目考查的是平均数和方差之间的关系，列出等式，探寻两组数据的联系，即可．11．D解析：D 【解析】分析：由茎叶图得出45名学生的数学成绩，从而求出中位数． 详解：根据茎叶图得出45名学生的数学成绩，可知中位数为129. 故选D.点睛：本题考查了茎叶图的应用问题，解题时应根据茎叶图中的数据，进行解答，属基础题.．12．A解析：A 【解析】分析：先观察表中数据的规律，确定回归系数b 的符号，再计算x 和y ，代入选项确定正确答案.详解：由表中数据规律发现：热饮杯数y 随当天气温x 升高而减少，则0b <，排除C 、D. 计算1169=(504712151923273136)1111x -++++++++++= 11228=(15615013212813011610489937654)111.641111y ++++++++++=≈ 将x 代入选项A ，得1692.352147.767111.6311ˆy=-⨯+= 将x 代入选项B ，得1692.352127.76591.6311ˆy=-⨯+= 所以选项A 正确. 故选A.点睛：本题考查线性回归方程的求法与应用，一次项系数b 符号的判断和回归直线过样本中心点(,)x y 是解题关键.二、填空题13．【分析】根据函数解析式可求得定义域和的定义域即可由几何概型概率求解【详解】函数的定义域为则的定义域为即解得即根据几何概型的概率计算公式得故答案为：【点睛】本题考查了函数定义域的求法复合函数定义域的求解析：22- 【分析】根据函数解析式，可求得()f x 定义域M 和(())y f f x =的定义域P ，即可由几何概型概率求解. 【详解】函数()f x=M，则[1,1]M=-，(())y f f x=的定义域为P[]1,1-，解得1,22x⎡⎤∈--⋃⎢⎥⎣⎦⎣⎦，即1,22P⎡⎤=--⋃⎢⎢⎥⎣⎦⎣⎦．根据几何概型的概率计算公式得212222⎛⎫⨯-⎪⎝⎭=．.【点睛】本题考查了函数定义域的求法，复合函数定义域的求法，几何概型概率求法，属于中档题. 14．【分析】由组合数结合古典概型求解即可【详解】从11个数中随机抽取3个数有种不同的方法其中能构成勾股数的有共三种所以所求概率为故答案为【点睛】本题考查古典概型与数学文化考查组合问题数据处理能力和应用意识解析：155【分析】由组合数结合古典概型求解即可【详解】从11个数中随机抽取3个数有311C种不同的方法，其中能构成勾股数的有共()()()3,4,5,6,8,10,5,12,13三种，所以，所求概率为3113155PC==.故答案为155【点睛】本题考查古典概型与数学文化，考查组合问题，数据处理能力和应用意识.15．【解析】【分析】基本事件总数事件至少有两张心愿卡放入对应的漂流瓶包含的基本事件个数由此能求出事件至少有两张心愿卡放入对应的漂流瓶的概率【详解】为了迎接新年小康小梁小谭小刘小林每人写了一张心愿卡设计了解析：31120【解析】【分析】基本事件总数55n A=，事件“至少有两张心愿卡放入对应的漂流瓶”包含的基本事件个数21335255m C C C C=++，由此能求出事件“至少有两张心愿卡放入对应的漂流瓶”的概率．【详解】为了迎接新年，小康、小梁、小谭、小刘、小林每人写了一张心愿卡， 设计了一个与此心愿卡对应的漂流瓶．现每人随机的选择一个漂流瓶将心愿卡放入，基本事件总数55120n A ==，事件“至少有两张心愿卡放入对应的漂流瓶”包含的基本事件个数2133525531m C C C C =++=，∴事件“至少有两张心愿卡放入对应的漂流瓶”的概率为31120m p n ==， 故答案为31120． 【点睛】本题考查概率的求法，考查古典概型等基础知识，考查运算求解能力，是基础题．16．0【解析】第一次循环：满足条件；第二次循环：满足条件；第三次循环：满足条件；第四次循环：满足条件；第五次循环：满足条件；第六次循环：满足条件；第七次循环：满足条件；可得的值以为周期进行循环所以最后输解析：0 【解析】第一次循环：1cos32n S S π=+=，满足条件2018,12n n n <=+=；第二次循环：cos 03n S S π=+=，满足条件2018,13n n n <=+=；第三次循环：cos 13n S S π=+=-，满足条件2018,14n n n <=+=；第四次循环：3cos 32n S S π=+=-，满足条件2018,15n n n <=+=；第五次循环：cos13n S S π=+=-，满足条件2018,16n n n <=+=；第六次循环：cos 03n S S π=+=，满足条件2018,17n n n <=+=；第七次循环：1cos32n S S π=+=，满足条件2018,18n n n <=+=；...，可得S 的值以6为周期进行循环，所以最后输出的S 的值为0，故答案为0.17．【解析】执行循环为点睛：算法与流程图的考查侧重于对流程图循环结构的考查先明晰算法及流程图的相关概念包括选择结构循环结构伪代码其次要重视循环起点条件循环次数循环终止条件更要通过循环规律明确流程图研究的解析：34【解析】执行循环为1111111131122334223344S =++=-+-+-=⨯⨯⨯ 点睛：算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项.18．【解析】试题分析：当时考点：秦九韶算法 解析：【解析】 试题分析：，当时，，考点：秦九韶算法19．【分析】（1）由回归方程知相关变量与成负相关（2）为假命题则同时为假命题为假命题则中至少有一假命题（3）全称命题与特称命题转换条件不变结论变相反（4）由正态曲线的对称性可解【详解】（1）由回归方程知 解析：(2)【分析】（1）由回归方程ˆ24yx =-知相关变量y 与x 成负相关，（2） “p q ∨”为假命题则,p q 同时为假命题，“p q ∧”为假命题则,p q 中至少有一假命题（3）全称命题与特称命题转换条件不变，结论变相反 （4）由正态曲线的对称性可解. 【详解】（1）由回归方程ˆ24yx =-知相关变量y 与x 成负相关，若变量x 增加一个单位，则y 平均增加4-个单位，故（1）错误（2） “p q ∨”为假命题则,p q 同时为假命题，“p q ∧”为假命题则,p q 中至少有一假命题，所以“p q ∨”为假命题是“p q ∧”为假命题的充分不必要条件是正确的.故（2）正确 （3）全称命题与特称命题转换条件不变，结论变相反，故（3）错误 （4）由正态曲线的对称性知，随机变量()22X N σ~，，若()0.32P X a <=，对称轴是2x = ，则()40.32P X a >-=，故（4）错误. 故答案为; (2) 【点睛】利用正态曲线的对称性求概率是常见的正态分布应用问题．解题的关键是利用对称轴=x μ确定所求概率对应的随机变量的区间与已知概率对应的随机变量的区间的关系，必要时可借助图形判断．对于正态分布2()N μσ，，由=x μ是正态曲线的对称轴知：(1)对任意的a ，有()()P X a P X a μμ<->+＝； (2)()001;()P X x P X x -≥=<;(3)()()=()P a X b P X b P X a <<<≤-．20．1【分析】先根据数列为等差数列求出再根据方差公式可得【详解】因为数列为等差数列且所以所以该组数据的方差为故填01【点睛】考查方差的计算基础题解析：1 【分析】先根据数列2{()}i x a -为等差数列求出()521i i x a =-∑，再根据方差公式可得．【详解】因为数列2{()}i x a -为等差数列,且3x a -=()()52231550.1=ii x a x a =-=-=⨯∑ 0.5，所以该组数据的方差为()52110.15i i x a =-=∑.故填0.1. 【点睛】考查方差的计算，基础题．三、解答题21．（1）1635；（2）见解析. 【分析】（1）根据频率分布直方图，先得到年龄在[25,30)之间的概率，再由[25,30)这组的参加者是6人，求得参加的总人数.然后分别求得年龄在[35,40)和[40,45)之间的人数，然后利用古典概型的概率求解.（2）先得到年龄在[45,55)的人数，根据有4名女教师，则X 的可能取值为：1，2，3，然后求得相应的概率，列出分布列再求期望. 【详解】（1）因为年龄在[25,30)之间的概率为0.035=0.15⨯， 又[25,30)这组的参加者是6人， 所以参加的总人数为6=400.15， 所以年龄在[35,40)之间的人数为0.04540=8⨯⨯， 年龄在[40,45)之间的人数为0.03540=6⨯⨯，所以两组选出的人中恰有1名数学老师的概率112211264624228616=35C C C C C C p C C +=. （2）年龄在[45,55)的人数为：()0.010.02540=6+⨯⨯，从中随机选取3名担任后勤保障工作，其中女教师的人数为X ，X 的可能取值为：1，2，3()124236115C C p X C === ()214236325C C p X C === ()304236135C C p X C === 分布列为：均值()1232555E X =⨯+⨯+⨯= . 【点睛】本题主要考查频率分布直方图，古典概型的概率以及分布列及期望，还考查了运算求解的能力，属于中档题.22．（1）23114（2）（i ）分布列见解析（ii ）这3个月经济损失总额的数学期望会超过2.88万元，理由见详解. 【分析】（1）根据古典概型的概率计算公式即可容易求得；（2）（i ）求得X 的取值，再根据题意，求得对应取值的概率，则分布列得解；（ii ）根据（i ）中所求，结合题意，求得3个月因空气质量造成经济损失的总额，即可容易判断. 【详解】（1）设ξ为选取的3天中空气质量为优的天数，则213061461433202023(2)(2)(3)114C C C C P P P C C ξξξ==+==+=. （2）（ⅰ）X 的可能取值为0，220，1480，201(0)(0100)1005P X P x ====， 707(220)(100250)10010P X P x ==<==，101(1480)(250300)10010P X P x ==<==， 则X 的分布列为P 15710110（ii）由（i）知171022********51010EX=⨯+⨯+⨯=（元），故该企业9月的经济损失的数学期望为309060EX=（元）.设该企业7月与8月每天因空气质量造成的经济损失为Y元，则111(0)632P Y==+=，1111(220)612123P Y==++=，1(1480)6 P Y==，所以111022********236EY=⨯+⨯+⨯=（元），所以7月与8月因空气质量造成经济损失的总额为320(3131)19840⨯+=（元）.因为19840906028900 2.88+=>万，所以这3个月经济损失总额的数学期望会超过2.88万元.【点睛】本题考查古典概型的概率求解，涉及离散型随机变量分布列的求解，涉及数学期望的计算，属综合中档题.23．详见解析【分析】用当型或直到型循环结构写程序框图，当型循环结构是当满足条件时，进入循环体，否时退出循环，判断框填入500S≤，直到型循环结构是当满足条件时退出循环体，否时进入循环，判断框填入500S>.【详解】或者【点睛】本题考查当型或直到型循环结构，需熟悉循环结构特征，分清两种循环结构，并且注意判断框的写法，24．见解析【解析】试题分析：在两个不同的条件下批发金额公式不同，只需编写一个条件语句即可实现.试题程序框图如下图所示.程序如下:i=input(“批发双数i=”);if i<300T=2.5* i;elseT=2.2* i;endprint(%io(2),T);25．（1）见解析；（2）174.5cm；（3）0.3.【详解】试题分析：（1）先分别算出第六组和第七组的人数，进而算出其频率与组距的比，补全直方图；（2）利用中位数两边频率相等，求出中位数的值；（3）先借助分层抽样的特征求出第四、第五组的人数，再运用列举法列举出所有可能数及满足题设的条件的数，运用古典概型的计算公式求解：解：（1）第六组与第七组频率的和为：∵第六组和第七组人数的比为5：2.∴第六组的频率为0.1，纵坐标为0.02；第七组频率为0.04，纵坐标为0.008.（2）设身高的中位数为，则∴估计这50位男生身高的中位数为174.5（3）由于第4，5组频率之比为2：3，按照分层抽样，故第4组中应抽取2人记为1，2，第5组应抽取3人记为3，4，5则所有可能的情况有：{1，2}，{1，3}，{1，4}，{1，5}，{2，3}，{2，4}，{2，5}， {3，4}，{3，5}，{4，5}共10种满足两位男生身高都在[175，180]内的情况有{3，4}，{3，5}，{4，5}共3种， 因此所求事件的概率为．26．（1）532y x =-；（2）线性回归方程是可靠的. 【分析】（1）根据最小二乘法公式，分别将数据代入计算，即可得答案；（2）选取的是4月1日与4月30日的两组数据，即10x =和8x =代入判断即可； 【详解】解：（1）由数据得12x =，27y =，3972x y =，23432x =； 又31977i i i x y ==∑，321434i i x ==∑；97797254344322b -==-，5271232a =-⨯=-；所以y 关于x 的线性回归方程为：532y x =-. （2）当10x =时，5103222y =⨯-=，22232-<； 当8x =时，583222y =⨯-=，17162-<， 所得到的线性回归方程是可靠的. 【点睛】本题考查最小二乘法求回归直线方程及利用回归方程进行判断拟合效果，考查数据处理能力，求解时注意回归直线必过样本点中心的应用.。

2021-2022年高三上学期期末考试数学（文）试题解析一、选择题：本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.设集合，，则集合（）（A）（B）（C）（D）2.已知命题：“，”，那么是（）（A），，（B），（C），（D），3.在平面直角坐标系中，点，，若向量，则实数（）（A）（B）（C）（D）【答案】A【解析】试题分析：=1,3(3OA AB =-（），，k-3)，因为，故，即，解得. 考点：1、向量的坐标运算；2、向量垂直.4.若坐标原点在圆的内部，则实数m 的取值范围是（ ）（A ） （B ）（C ） （D ）【答案】C【解析】试题分析：∵在的内部，则有，解得，选C.考点：1、点和圆的位置关系；2、二次不等式的解法.5.执行如图所示的程序框图，输出的S 值为（ ）（A ） （B ） （C ） （D ）6.若曲线为焦点在轴上的椭圆，则实数,满足（ ）（A）（B）（C）（D）7.定义域为R的函数满足，且当时，，则当时，的最小值为（）（A）（B）（C）（D）8.在平面直角坐标系中，记不等式组0,0,2x yx yy+⎧⎪-⎨⎪⎩≥≤≤所表示的平面区域为. 在映射的作用下，区域内的点对应的象为点，则由点所形成的平面区域的面积为（）（A）（B）（C）（D）第Ⅱ卷（共110分）二、填空题（每题5分，满分30分，将答案填在答题纸上）9.已知复数z满足，那么______．10.在等差数列中，，，则公差______；前17项的和______．11.已知一个正三棱柱的所有棱长均相等，其侧（左）视图如图所示，那么此三棱柱正（主）视图的面积为______．12.在△ABC中，角A，B，C所对的边分别为a，b，c. 若，，，则______；______．【答案】；【解析】试题分析：∵，∴，则，由余弦定理得，，考点：1、诱导公式；2、余弦定理.13.设函数则______；若函数存在两个零点，则实数的取值范围是______．14.．设为平面直角坐标系内的点集，若对于任意，存在，使得，则称点集满足性质. 给出下列三个点集：○1{(,)|cos0}R x y x y=-=；○2；○3.其中所有满足性质的点集的序号是______．【答案】①③三、解答题（本大题共6小题，共80分.解答应写出文字说明、证明过程或演算步骤.）15.（本小题满分13分）已知函数，π()sin()(0)3g x xωω=->，且的最小正周期为.（Ⅰ）若，，求的值；（Ⅱ）求函数的单调增区间.所以函数的单调增区间为.考点：1、三角方程；2、两角和与差的三角函数；3、三角函数的单调性.16.（本小题满分13分）以下茎叶图记录了甲、乙两组各三名同学在期末考试中的数学成绩．乙组记录中有一个数字模糊，无法确认，假设这个数字具有随机性，并在图中以表示．（Ⅰ）若甲、乙两个小组的数学平均成绩相同，求的值；（Ⅱ）求乙组平均成绩超过甲组平均成绩的概率；（Ⅲ）当时，分别从甲、乙两组同学中各随机选取一名同学，求这两名同学的数学成绩之差的绝对值不超过2分的概率．甲组乙组 8 90 1 a8 22们是：，，，，，，，，，所以事件的结果有7种，它们是：，，，，，，. 因此这两名同学的数学成绩之差的绝对值不超过2分的概率.考点：1、平均数；2、古典概型；3、茎叶图.17.（本小题满分14分）如图，在多面体ABCDEF中，底面ABCD是边长为2的正方形，四边形BDEF是矩形，平面BDEF ⊥平面ABCD，BF=3，G和H分别是CE和CF的中点.（Ⅰ）求证：AC⊥平面BDEF；（Ⅱ）求证：平面BDGH//平面AEF；（Ⅲ）求多面体ABCDEF的体积.（Ⅱ）证明：在中，因为分别是的中点，所以，又因为平面，平面，所以平面. 设，连接，在中，因为，，所以，又因为平面，平面，所以平面.又因为，平面，所以平面平面.（Ⅲ）解：由（Ⅰ），得平面，，四边形的面积，所以四棱锥的体积114 3BDEFV AO S=⨯⨯=. 同理，四棱锥的体积.所以多面体的体积考点：1、直线和平面垂直的判定；2、面面平行的判定；3、几何体的体积.18.（本小题满分13分）已知函数，其中是自然对数的底数，.（Ⅰ）求函数的单调区间；（Ⅱ）当时，求函数的最小值.19.（本小题满分14分）已知是抛物线上的两个点，点的坐标为，直线的斜率为.设抛物线的焦点在直线的下方.（Ⅰ）求k的取值范围；（Ⅱ）设C为W上一点，且，过两点分别作W的切线，记两切线的交点为. 判断四边形是否为梯形，并说明理由.试题解析：（Ⅰ）解：抛物线的焦点为. 由题意，得直线的方程为，令，得，即直线与y轴相交于点. 因为抛物线的焦点在直线的下方，所以，解得，因为，所以.20.（本小题满分13分）设无穷等比数列的公比为q，且，表示不超过实数的最大整数（如）,记，数列的前项和为，数列的前项和为.（Ⅰ）若，求；（Ⅱ）证明：（）的充分必要条件为；（Ⅲ）若对于任意不超过的正整数n，都有，证明：.（Ⅲ）证明：因为 ，所以 ， 120142(2)n n n b T T n -=-=≤≤. Ot20528 5030 倰h 28481 6F41 潁20890 519A 冚D\+32861 805D 聝22761 58E9 壩22314 572A 圪。

一、选择题1．古希腊数学家欧多克索斯在深入研究比例理论时，提出了分线段的“中末比”问题：将一线段MN分为两线段MG，GN，使得其中较长的一段MG是全长MN与另一段GN GN的比例中项，即满足512MG NGMN MG-==，后人把这个数称为“黄金分割”数，把点G称为线段MN的“黄金分割”点.在矩形ABCD中，E，F是线段AB的两个“黄金分割”点.在矩形ABCD内任取一点M，则该点落在DEF内的概率为（）A．52-B．51-C．52-D．51-2．从单词“book”的四个字母中任取2个，则取到的2个字母不相同的概率为（）A．13B．12C．23D．343．民间有一种五巧板拼图游戏.这种五巧板（图1）可以说是七巧板的变形，它是由一个正方形分割而成（图2），若在图2所示的正方形中任取一点，则该点取自标号为③和④的巧板的概率为（）A．518B．13C．718D．494．七巧板是古代中国劳动人民的发明，到了明代基本定型．清陆以湉在《冷庐杂识》中写道：近又有七巧图，其式五，其数七，其变化之式多至千余．如图，在七巧板拼成的正方形内任取一点，则该点取自图中阴影部分的概率是（）A．116B．18C．38D．3165．执行如图所示的程序框图，结果是（）A．11 B．12 C．13 D．14 6．执行下面的程序框图，如果输入的a=4，b=6，那么输出的n=（）A．3 B．4 C．5 D．6 7．某程序框图如图所示，该程序运行后输出S的值是（）A．910B．1011C．1112D．1118．阅读如图所示的程序框图，当输入5n=时，输出的S=（）A．6 B．4615C．7 D．47159．为了了解某同学的数学学习情况，对他的6次数学测试成绩进行统计，作出的茎叶图如图所示，则下列关于该同学数学成绩的说法正确的是( )A ．中位数为83B ．众数为85C ．平均数为85D ．方差为1910．为了了解高三学生的数学成绩，抽取了某班60名学生，将所得数据整理后，画出其频率分布直方图（如下图），已知从左到右各长方形高的比为2:3:5:6:3:1，则该班学生数学成绩在(80,100)之间的学生人数是（ ）A ．32B ．27C ．24D ．3311．我校高中生共有2700人,其中高一年级900人,高二年级1200人,高三年级600人,现采取分层抽样法抽取容量为135的样本,那么高一、高二、高三各年级抽取的人数分别为 ( ) A ．45,75,15B ．45,45,45C ．45,60,30D ．30,90,1512．统计某校n 名学生的某次数学同步练习成绩，根据成绩分数依次分成六组：[)[)[)[)[)[]90,100,100,110,110,120,120,130,130,140,140,150，得到频率分布直方图如图所示，若不低于140分的人数为110.①0.031m =；②800n =；③100分以下的人数为60；④分数在区间[)120,140的人数占大半．则说法正确的是（ ）A ．①②B ．①③C ．②③D ．②④二、填空题13．辛普森悖论(Simpson’sParadox)有人译为辛普森诡论，在统计学中亦有人称为“逆论”，甚至有人视之为“魔术”.辛普森悖论为英国统计学家E .H .辛普森(E.H.Simpson)于1951年提出的，辛普森悖论的内容大意是“在某个条件下的两组数据，分别讨论时都会满足某种性质，可是一旦合并考虑，却可能导致相反的结论.”下面这个案例可以让我们感受到这个悖论：关于某高校法学院和商学院新学期已完成的招生情况，现有如下数据： 某高校申请人数性别录取率法学院200人男50% 女 70% 商学院300人男60% 女90%①法学院的录取率小于商学院的录取率；②这两个学院所有男生的录取率小于这两个学院所有女生的录取率；③这两个学院所有男生的录取率不一定小于这两个学院所有女生的录取率； ④法学院的录取率不一定小于这两个学院所有学生的录取率. 其中，所有正确结论的序号是___________.14．某部队在训练之余，由同一场地训练的甲､乙､丙三队各出三人，组成33⨯小方阵开展游戏，则来自同一队的战士既不在同一行，也不在同一列的概率为______.15．设{}{}1,3,5,7,2,4,6a b ∈∈，则函数()log a bf x x =是增函数的概率为__________．16．执行如图所示的程序框图，若输入n 的值为8，则输出的s 的值为_____．17．执行如图所示的流程图，则输出的的值为___________.18．运行如图所示的程序框图，若输入4n ，则输出S的值为_____.19．福利彩票“双色球”中红色球由编号为01，02，…，33的33个个体组成，某彩民利用下面的随机数表（下表是随机数表的第一行和第二行）选取6个红色球，选取方法是从随机数表中第1行的第6列和第7列数字开始，由左到右依次选取两个数字，则选出来的第3个红色球的编号为______.49 54 43 54 82 17 37 93 23 28 87 35 20 56 43 84 26 34 91 6457 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 7620．某校高三年级共有800名学生，现采用系统抽样的方法，抽取25名学生做问卷调查，将这800名学生按1，2，．．．，800随机编号，按编号顺序平均分组．若从第5组抽取的编号为136，则从第2组中抽取的编号为__________．三、解答题21．互联网正在改变着人们的生活方式，在日常消费中手机支付正逐渐取代现金支付成为人们首选的支付方式. 某学生在暑期社会活动中针对人们生活中的支付方式进行了调查研究. 采用调查问卷的方式对100名18岁以上的成年人进行了研究，发现共有60人以手机支付作为自己的首选支付方式，在这60人中，45岁以下的占23，在仍以现金作为首选支付方式的人中，45岁及以上的有30人.（1）从以现金作为首选支付方式的40人中，任意选取3人，求这3人至少有1人的年龄低于45岁的概率；（2）某商家为了鼓励人们使用手机支付，做出以下促销活动：凡是用手机支付的消费者，商品一律打八折. 已知某商品原价50元，以上述调查的支付方式的频率作为消费者购买该商品的支付方式的概率，设销售每件商品的消费者的支付方式都是相互独立的，求销售10件该商品的销售额的数学期望.22．2020年寒假，因为“新冠”疫情全体学生只能在家进行网上学习，为了研究学生网上学习的情况，某学校随机抽取100名学生对线上教学进行调查，其中男生与女生的人数之比为9:11，抽取的学生中男生有30人对线上教学满意，女生中有10名表示对线上教学不满意.（1）完成22⨯列联表，并回答能否有90%的把握认为“对线上教学是否满意与性别有关”；（2）从被调查的对线上教学满意的学生中，利用分层抽样抽取5名学生，再在这5名学生中抽取2名学生，作线上学习的经验介绍，求其中抽取一名男生与一名女生的概率.附：()()()()()22n ad bc K a b c d a c b d ⋅=++++.23．已知直线1:240l x y +-=，阅读如图所示的程序框图，若输入的x 的值为612+，输出的()f x 的值恰为直线2l 在x 轴上的截距，且12l l ⊥.（1）求直线1l与2l的交点坐标；（2）若直线3l过直线1l与2l的交点，且在y轴上的截距是在x轴上的截距的2倍，求3l的方程.24．乘坐火车时，可以托运货物.从甲地到乙地，规定每张火车票托运费用计算方法是：当行李质量不超过50kg时按0.25元/kg；超过50kg而不超过100kg时，其超过部分按0.35元/kg；超过100kg时，其超过部分按0.45元/kg.请设计一个输入行李质量()0ωω≥，计算出托运的费用x元的算法，画出算法框图并用基本语句描述该算法.kg25．某学校进行体验，现得到所有男生的身高数据，从中随机抽取50人进行统计（已知这50个身高介于155cm到195cm之间），现将抽取结果按如下方式分成八组：第一组[155,160)，第二组[160,165)，...，第八组[190,195]，并按此分组绘制如图所示的频率分布直方图，其中第六组[180,185)和第七组[185,190)还没有绘制完成，已知第一组与第八组人数相同，第六组和第七组人数的比为5:2．（1）补全频率分布直方图；（2）根据频率分布直方图估计这50位男生身高的中位数；（3）用分层抽样的方法在身高为[170,180]内抽取一个容量为5的样本，从样本中任意抽取2位男生，求这两位男生身高都在[175,180]内的概率．26．全世界越来越关注环境保护问题，某监测站点于2016年8月某日起连续n天监测空气质量指数(AQI)，数据统计如下：空气质量指数(3/g mμ)0-5051-100101-150151-200201-250空气质量等级空气优空气良轻度污染中度污染重度污染天数2040m105(1)根据所给统计表和频率分布直方图中的信息求出,n m的值，并完成频率分布直方图；(2)在空气质量指数分别为51-100和151-200的监测数据中，用分层抽样的方法抽取5天，从中任意选取2天，求事件A“两天空气都为良”发生的概率.【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】分别求出对应的面积，进而求得结论．【详解】解：设正方形ABCD的边长为1，则51AF BE-==，∴2152EF AF=-=，∴所求的概率为21522DEFABCDEF ADSPS AD⨯⨯-===正方形故选：C．【点睛】本题主要考查几何概型，几何概型的概率估算公式中的“几何度量”，可以为线段长度、面积、体积等，而且这个“几何度量”只与“大小”有关，而与形状和位置无关．解决的步骤均为：求出满足条件A 的基本事件对应的“几何度量” ()N A ，再求出总的基本事件对应的“几何度量” N ，最后根据()N A PN求解，属于中档题． 2．D解析：D 【分析】从四个字母中取2个，列举出所有的基本事件，即得所求的概率. 【详解】从四个字母中取2个，所有的基本事件为：,,,bo bk oo ok ，共有4个； 其中“取到的2个字母不相同”含有,,bo bk ok 3个， 故所求概率为34. 故选：D. 【点睛】本题考查古典概型，属于基础题.3．C解析：C 【分析】分别求出③和④的巧板的面积，根据几何概型的概率关系转化为面积比. 【详解】设巧板①的边长为1，则结合图2可知大正方形的边长为3， 其面积239S ==.其中巧板③是底边长为2的等腰直角三角形，其面积为112112S =⨯⨯=，巧板④的正方形 与腰长为1的等腰直角三角形的组合图形，其面积为22151122S ⨯⨯+==， 故所求的概率12718S S P S +==. 故选:C . 【点睛】本题考查几何概型的概率求法，转化为面积比，属于中档题 .4．B解析：B 【分析】设阴影部分正方形的边长为a ，计算出七巧板所在正方形的边长，并计算出两个正方形的面积，利用几何概型概率公式可计算出所求事件的概率.【详解】如图所示，设阴影部分正方形的边长为a，则七巧板所在正方形的边长为，由几何概型的概率公式可知，在七巧板拼成的正方形内任取一点，则该点取自图中阴影部分的概率()2218a =，故选：B.【点睛】本题考查几何概型概率公式计算事件的概率，解题的关键在于弄清楚两个正方形边长之间的等量关系，考查分析问题和计算能力，属于中等题.5．B解析：B【分析】根据已知的程序语句可得，该程序的功能是利用循环结构计算并输出k 的值，模拟程序的运行过程，可得答案.【详解】根据题意，模拟程序框图的运行过程，如下：17,0n k ==17不是偶数，3171=52n =⨯+，011k =+=，521≠；52是偶数，52262n ==，112k =+=，261≠； 26是偶数，26132n ==，213k =+=，131≠； 13不是偶数，3131=40n =⨯+，314k =+=，401≠；40是偶数，40202n ==，415k =+=，201≠； 20是偶数，20102n ==，516k =+=，101≠； 10是偶数，1052n ==，617k =+=，51≠； 5不是偶数，351=16n =⨯+，718k =+=，161≠； 16是偶数，1682n ==，819k =+=，81≠； 8是偶数，842n ==，9110k =+=，41≠； 4是偶数，422n ==，10111k =+=，21≠；2是偶数，212n ==，11112k =+=，11=； 故选：B【点睛】关键点睛： 解题的关键是要读懂程序框图，模拟程序框图的运行过程，即突破难点.6．B解析：B【解析】试题分析：模拟执行程序, 可得4,6,0,0a b n s ====,执行循环体,2,4,6,6,1a b a s n =====,不满足条件16s >,执行循环体,2,6,4,10,2a b a s n =-====, 不满足条件16s >,执行循环体,2,4,6,16,3a b a s n =====, 不满足条件16s >,执行循环体,2,6,4,20,4a b a s n =-====,不满足条件16s >,退出循环, 输出n 的值为4,故选B. 考点：1、程序框图；2、循环结构.7．B解析：B【分析】模拟程序运行后,可得到输出结果,利用裂项相消法即可求出答案.【详解】模拟程序运行过程如下:0)1,0k S ,判断为否,进入循环结构, 1)110,2122S k =+==⨯,判断为否,进入循环结构, 2)11,3223S k =+=⨯,判断为否,进入循环结构, 3)111,422334S k =++=⨯⨯,判断为否,进入循环结构, …… 9)111,10223910S k =+++=⨯⨯,判断为否,进入循环结构, 10)1111,112239101011S k =++++=⨯⨯⨯,判断为是, 故输出1112231011S =+++⨯⨯111111101122310111111=-+-++-=-=, 故选:B.【点睛】 本题主要考查程序框图,考查裂项相消法,难度不大.一般遇见程序框图求输出结果时,常模拟程序运行以得到结论.8．D解析：D【分析】根据程序框图，依次运行程序即可得出输出值.【详解】输入5n =时，1,1,1,5S i a i ===≤，2,3,2a S i ===，5i ≤ 222,5,32a S i =⨯===，5i ≤ 2442,5,4333a S i =⨯==+=，5i ≤ 42242,5,534333a S i =⨯==++=，5i ≤ 224424,5,635153315a S i =⨯==+++=， 输出424457331515S =+++= 故选：D【点睛】此题考查程序框图，关键在于读懂框图，根据结构依次运算，求出输出值，尤其注意判断框中的条件. 9．C解析：C【解析】试题分析：A 选项，中位数是84；B 选项，众数是出现最多的数，故是83；C 选项，平均数是85，正确；D 选项，方差是，错误．考点：•茎叶图的识别 相关量的定义10．D解析：D【详解】高的比就是频率的比，所以各区间上的频率可依次设为2x,3x,5x,6x,3x,x,，同它们的和为1235631,20x x x x x x x +++++=∴=,所以该班学生数学成绩在［80，100)之间的学生人数是1(56)6011603320x +⨯⨯=⨯⨯=,故选D 11．C解析：C【解析】因为共有学生2700，抽取135，所以抽样比为1352700，故各年级分别应抽取135900452700⨯=，1351200602700⨯=，135600302700⨯=，故选C. 12．B解析：B【分析】根据频率分布直方图的性质和频率分布直方图中样本估计总体，准确运算，即可求解.【详解】由题意，根据频率分布直方图的性质得10(0.0200.0160.0160.0110.006)1m +++++=，解得0.031m =.故①正确；因为不低于140分的频率为0.011100.11⨯=，所以11010000.11n ==，故②错误； 由100分以下的频率为0.00610=0.06⨯，所以100分以下的人数为10000.06=60⨯， 故③正确；分数在区间[120,140)的人数占0.031100.016100.47⨯+⨯=，占小半.故④错误. 所以说法正确的是①③.故选B.【点睛】本题主要考查了频率分布直方图的应用，其中解答熟记频率分布直方图的性质，以及在频率分布直方图中，各小长方形的面积表示相应各组的频率，所有小长方形的面积的和等于1，着重考查了分析问题和解答问题的能力，属于基础题.二、填空题13．②④【分析】根据题意结合古典概型的概率计算公式逐项进行判定即可求解【详解】设申请法学院的男生人数为女生人数为则法学院的录取率为设申请商学院的男生人数为女生人数为则商学院的录取率为由该值的正负不确定所 解析：②④【分析】根据题意，结合古典概型的概率计算公式，逐项进行判定，即可求解.【详解】设申请法学院的男生人数为x ，女生人数为y ，则200x y +=， 法学院的录取率为0.50.70.50.7(200)0.70.001200200x y x x x ++⨯-==-， 设申请商学院的男生人数为m ，女生人数为n ，则300m n +=，商学院的录取率为0.60.90.60.9(300)0.90.001200200m n m m m ++⨯-==-， 由()()0.90.0010.70.0010.20.001()0.001(200)m x m x m x ---=--=-+， 该值的正负不确定，所以①错误，④正确； 这两个学院所有男生的录取率为0.50.6x m x m ++， 这两个学院所有女生的录取率为0.70.9y n y n++， 因为0.50.60.70.90.20.40.10.30()()x m y n xy xn my nm x m y n x m y n +++++-=<++++， 所以②正确；③错误.故答案为：②④.【点睛】本题主要考查了古典概型的概率公式的应用，其中解答中正确理解题意，结合古典概型的概率计算公式求得相应的概率是解答的关键，着重考查数学阅读能力，属于基础题. 14．【分析】分两步进行：首先先排第一行再排第二行最后排第三行；其次对每一行选人；最后利用计算出概率即可【详解】首先第一行队伍的排法有种；第二行队伍的排法有2种；第三行队伍的排法有1种；然后第一行的每个位 解析：1140【分析】分两步进行：首先，先排第一行，再排第二行，最后排第三行；其次，对每一行选人；最后，利用计算出概率即可.【详解】首先，第一行队伍的排法有33A 种；第二行队伍的排法有2种；第三行队伍的排法有1种；然后，第一行的每个位置的人员安排有111333C C C 种；第二行的每个位置的人员安排有111222C C C 种；第三行的每个位置的人员安排有111⨯⨯种.所以来自同一队的战士既不在同一行，也不在同一列的概率311111133332229921140A C C C C C C P A ⋅⋅⋅==. 故答案为：1140. 【点睛】 本题考查了分步计数原理，排列与组合知识，考查了转化能力，属于中档题.15．【解析】【分析】列举出所有的结果选出的所有的结果根据古典概型概率公式可求出函数是增函数的概率【详解】所有取值有：共12个值当时为增函数有共有6个所以函数是增函数的概率为故答案为【点睛】本题主要考查古解析：12【解析】【分析】 列举出a b 所有的结果，选出1a b >的所有的结果，根据古典概型概率公式可求出函数()log a b f x x =是增函数的概率.【详解】a b 所有取值有：135713571157,,,,,,,,,,,222244446266共12个值， 当1a b >时，()f x 为增函数，有357577,,,,,222446共有6个， 所以函数()log a b f x x =是增函数的概率为61122=，故答案为12. 【点睛】本题主要考查古典概型概率公式的应用以及对数函数的性质，属于中档题. 在求解有关古典概型概率的问题时，首先求出样本空间中基本事件的总数n ，其次求出概率事件中含有多少个基本事件m ，然后根据公式m P n=求得概率. 16．8【分析】根据程序框图知该程序的功能是计算并输出变量的值模拟程序的运行过程即可求解【详解】当时满足循环条件当时满足循环条件当时满足循环条件；当时不满足循环条件跳出循环输出故填【点睛】本题主要考查了程 解析：8【分析】根据程序框图知，该程序的功能是计算并输出变量s 的值，模拟程序的运行过程即可求解.【详解】当2i =时，满足循环条件，2,4,2s i k ===，当4i =时，满足循环条件，4,6,3s i k === ，当6i =时，满足循环条件，8,8,4s i k ===；当8i =时，不满足循环条件，跳出循环，输出8s =.故填8.【点睛】本题主要考查了程序框图，循环结构，属于中档题.17．【解析】试题分析：由程序框图第一次循环时第二次循环时第三次循环时第四次循环时退出循环输出考点：程序框图解析：4【解析】试题分析：由程序框图，第一次循环时，1,1k S ==，第二次循环时，22,112k S ==+=，第三次循环时，23,226k S ==+=，第四次循环时，24,63156k S ==+=>，退出循环，输出4k =．考点：程序框图．18．11【解析】试题分析：根据程序框图可知该程序执行的是所以输出的值为11考点：本题考查程序框图容易题点评：程序框图的题目离不开循环结构和条件结构要仔细辨别循环条件弄清楚循环次数避免多执行或少执行一次 解析：11【解析】试题分析：根据程序框图可知该程序执行的是1123411S =++++=，所以输出的值为11.考点：本题考查程序框图，容易题.点评：程序框图的题目离不开循环结构和条件结构，要仔细辨别循环条件，弄清楚循环次数，避免多执行或少执行一次.19．05【分析】根据给定的随机数表的读取规则从第一行第67列开始两个数字一组从左向右读取重复的或超出编号范围的跳过即可【详解】根据随机数表排除超过33及重复的编号第一个编号为21第二个编号为32第三个编解析：05【分析】根据给定的随机数表的读取规则，从第一行第6、7列开始，两个数字一组，从左向右读取，重复的或超出编号范围的跳过，即可.【详解】根据随机数表，排除超过33及重复的编号，第一个编号为21，第二个编号为32，第三个编号05，故选出来的第3个红色球的编号为05.【点睛】本题主要考查了简单随机抽样中的随机数表法，属于容易题.20．8【解析】由题意得从名学生中采用系统抽样的方法抽取名学生需要把名学生平均分成组每组人设第一组抽取的号码为则第组抽取的号码为解得点睛：本题考查了抽样方法中的系统抽样问题对于系统抽样的抽法是先对总体编号 解析：8【解析】由题意得，从800名学生中采用系统抽样的方法抽取25名学生，需要把800名学生平均分成25组，每组8003225=人， 设第一组抽取的号码为x ，则第5组抽取的号码为432136x +⨯=，解得8x =. 点睛：本题考查了抽样方法中的系统抽样问题，对于系统抽样的抽法是先对总体编号，根据样本平均分组，确定组距，再在第一组中抽取一个编号，依次等距抽取，其中把握系统抽样的原则是解答此类问题的关键.三、解答题21．（1）291494；（2）440 【分析】（1）先计算出选取的3人中，全都是高于45岁的概率，然后用1减去这个概率，求得至少有1人的年龄低于45岁的概率.（2）首先确定“销售的10件商品中以手机支付为首选支付的商品件数”满足二项分布，求得销售额的表达式，然后利用期望计算公式，计算出销售额的期望.【详解】（1）设事件A 表示至少有1人的年龄低于45岁，则()3303402911494C P A C =-=. （2）由题意知，以手机支付作为首选支付方式的概率为6031005=. 设X 表示销售的10件商品中以手机支付为首选支付的商品件数，则3~10,5X B ⎛⎫ ⎪⎝⎭，设Y 表示销售额，则()40501050010Y X X X =+-=-，所以销售额Y 的数学期望35001050010104405EY EX =-=-⨯⨯=（元）. 【点睛】本小题主要考查利用对立事件来计算古典概型概率问题，考查二项分布的识别和期望的计算，考查随机变量线性运算后的数学期望的计算.22．（1）填表见解析；有90%的把握认为“对线上教学是否满意与性别有关”；（2）35. 【分析】（1）根据题目所给出的数据填写22⨯列联表，计算K 的观测值，对照题目中的表格，得出统计结论.（2）由题可知，从被调查中对线上教学满意的学生中，利用分层抽样抽取5名学生，其中男生2名，女生3人，分别标号，列出所有的基本事件，再利用古典概型的概率公式即可得出结果.【详解】解：（1）22⨯列联表如下：又()210030104515 3.03 2.70675254555K ⨯-⨯=≈>⨯⨯⨯， 这说明有90%的把握认为“对线上教学是否满意与性别有关”.（2）方法一：由题可知，从被调查中对线上教学满意的学生中，利用分层抽样抽取5名学生，其中男生2名，设为A 、B ；女生3人设为,,a b c ，则从这5名学生中抽取2名学生的基本事件有：(),A B ，(),A a ，(),A b ，(),A c ，(),B a ，(),B b ，(),B c ，(),a b ，(),a c ，(),b c ，共10个基本事件，其中抽取一名男生与一名女生的事件有(),A a ，(),A b ，(),A c ，(),B a ，(),B b ，(),B c ，共6个基本事件，根据古典概型，从这5名学生中抽取一名男生与一名女生的概率为63105=. 方法二：由题可知，从被调查中对线上教学满意的学生中，利用分层抽样抽取5名学生， 其中男生2名，设为；女生3人，根据古典概型，从这5名学生中抽取一名男生与一名女生的概率为11222563105C C C == 【点睛】本题考查了独立性检验的应用问题，考查了古典概型的概率公式，也考查了计算能力的应用问题，是基础题.23．（1）(2,1)；（2）20x y -=或250x y +-=【分析】（1）根据程序框图，可得输出的函数()f x ，由输入x 的值为1+可得直线2l 在x 轴上的截距.由12l l ⊥，可得直线2l 的斜率.根据点斜式可得直线2l 的方程，联立两直线方程，即可求得交点坐标.（2）讨论截距是否为0：当截距为0时，易得直线方程；当截距不为0时，根据在y 轴上的截距是在x 轴上的截距的2倍，设出直线方程，代入所过的点，即可求解.【详解】（1）由程序框图，若输入x 的值为1+，由10+> 所以输出()221f x x x =-+代入可得21112232122f ⎛⎫⎛⎛⎫=-⨯+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭+++ 所以2l 在x 轴上的截距为32， ∵12l l ⊥，∴121l l k k =-⋅所以22l k =∴直线2l 的方程为3022y x ⎛⎫-=- ⎪⎝⎭，即23y x =-. 联立240230x y x y +-=⎧⎨--=⎩，解得21x y =⎧⎨=⎩. ∴直线1l 和2l 的交点坐标为(2,1).（2）当直线3l 经过原点时，可得方程为12y x =. 当直线3l 不经过原点时，设在x 轴上截距为0a ≠，则在y 轴上的截距为2a ， 其方程为12x y a a +=，将交点坐标(2,1)代入可得2112a a +=，解得52a =， ∴方程为25x y +=. 综上可得直线3l 方程为20x y -=或250x y +-=.【点睛】本题考查了程序框图的简单应用，垂直直线的斜率关系，直线交点的求法，截距式方程的用法，注意讨论截距是否为0，属于中档题.24．见解析【解析】试题分析：分三类列出托运的费用关于行李质量的函数关系，设行李质量为kg ω，应付运费为x 元，，则得到其运费公式，要计算托运的费用必须对行李质量分类讨论，因此要用条件语句来实现.试题设行李重量为kg ω，应付托运费为x 元，则()()0.25,500.25500.3550,501000.25500.35500.45100,100x ωωωωωω⎧≤⎪=⨯+-<≤⎨⎪⨯+⨯+->⎩则0.25,500.355,501000.4515,100x ωωωωωω≤⎧⎪=-<≤⎨⎪->⎩程序框图如图所示：程序如下：25．（1）见解析；（2）174.5cm；（3）0.3.【详解】试题分析：（1）先分别算出第六组和第七组的人数，进而算出其频率与组距的比，补全直方图；（2）利用中位数两边频率相等，求出中位数的值；（3）先借助分层抽样的特征求出第四、第五组的人数，再运用列举法列举出所有可能数及满足题设的条件的数，运用古典概型的计算公式求解：解：（1）第六组与第七组频率的和为：∵第六组和第七组人数的比为5：2.∴第六组的频率为0.1，纵坐标为0.02；第七组频率为0.04，纵坐标为0.008.（2）设身高的中位数为，则∴估计这50位男生身高的中位数为174.5（3）由于第4，5组频率之比为2：3，按照分层抽样，故第4组中应抽取2人记为1，2，第5组应抽取3人记为3，4，5则所有可能的情况有：{1，2}，{1，3}，{1，4}，{1，5}，{2，3}，{2，4}，{2，5}， {3，4}，{3，5}，{4，5}共10种满足两位男生身高都在[175，180]内的情况有{3，4}，{3，5}，{4，5}共3种， 因此所求事件的概率为． 26．(1)答案见解析；(2)35. 【解析】【试题分析】（1）借助题设中提供的频率分布直方图，算出0-50的频率为0.004500.2⨯=，进而求出样本容量200.2100n =÷=，从而求出25m =，最后完成频率分布直方图；（2）先运用分层抽样的方法求出空气质量指数为51-100和151200-的监测天数中分别抽取4天和1天，即将空气质量指数为51-100的4天分别记为,,,a b c d ；将空气质量指数为151-200的1天记为e ，算出从中任取2天的基本事件数为10种和其中事件A “两天空气都为良”包含的基本事件数为6种，进而算得事件A “两天都为良”发生的概率是()63105P A ==： (1)由频率分布直方图可知0-50的频率为0.004500.2⨯=，所以200.2100n =÷=，从而25m =，频率分布直方图补充如下图所示.。

一、选择题1．在OMN 中，1OM =，3ON =，2MN =，在OMN 内任取一点，该点到点M 的距离大于1的概率为（ ）A ．39π B ．319π-C ．318π D ．3118π-2．如图，一个边长为2的正方形里有一个月牙形的图案，为了估算这个月牙形图案的面积，向这个正方形里随机投入500粒芝麻，经过统计，落在月牙形图案内的芝麻有150粒，则这个月牙图案的面积约为（ ）A ．35B ．45C ．1D ．653．民间有一种五巧板拼图游戏.这种五巧板（图1）可以说是七巧板的变形，它是由一个正方形分割而成（图2），若在图2所示的正方形中任取一点，则该点取自标号为③和④的巧板的概率为（ ）A ．518B ．13C ．718D ．494．勒洛三角形是具有类似圆的“定宽性”的面积最小的曲线，它由德国机械工程专家，机构运动学家勒洛首先发现，其作法是：以等边三角形每个顶点为圆心，以边长为半径，在另两个顶点间作一段弧，三段弧围成的曲边三角形就是勒洛三角形，现在勒洛三角形中随机取一点，则此点取自正三角形外的概率为（ ）A ．()23323ππ-- B ．()323π-C ．()323π+ D ．()23323ππ-+5．执行如图所示的程序框图，则输出s 的值为（ ）A ．34B ．56C ．1324D ．771206．如图的程序框图，当输出15y =后，程序结束，则判断框内应该填（ ）A ．1x ≤B ．2x ≤C ．3x ≤D ．4x ≤7．执行如图所示的程序框图，输出的S 值为（ ）A ．1B ．-1C ．0D ．-28．执行如图所示的程序框图，若输出的结果为5，则输入的实数a 的范围是( )A ．[)6,24B ．[)24,120C ．(),6-∞D ．()5,249．某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量之间的关系，随机抽查52名中学生，得到统计数据如表1至表4，这与性别有关联的可能性最大的变量是（ ）A．成绩B．视力C．智商D．阅读量a a>得到一组新10．一组数据的平均数为x，方差为2s，将这组数据的每个数都乘以()0数据，则下列说法正确的是（）A．这组新数据的平均数为x B．这组新数据的平均数为a x+C．这组新数据的方差为2as D．这组新数据的标准差为2a s11．如果在一次试验中，测得(x，y)的四组数值分别是A(1,3)，B(2,3.8)，C(3,5.2)，D(4,6)，则y与x之间的回归直线方程是 ()A．y＝x＋1.9 B．y＝1.04x＋1.9C．y＝1.9x＋1.04 D．y＝1.05x－0.912．为了了解某社区居民是否准备收看电视台直播的“龙舟大赛”，某记者分别从社区60～70岁，40～50岁，20～30岁的三个年龄段中的128，192，x人中，采用分层抽样的方法共抽出了30人进行调查，若60～70岁这个年龄段中抽查了8人，那么x为（）A．64 B．96 C．144 D．160二、填空题13．住在同一城市的甲、乙两位合伙人,约定在当天下午4.00-5：00间在某个咖啡馆相见商谈合作事宜，他们约好当其中一人先到后最多等对方10分钟,若等不到则可以离去,则这两人能相见的概率为__________．14．西周初数学家商高在公元前1000年发现勾股定理的一个特例：勾三，股四，弦五.此发现早于毕达哥拉斯定理五百到六百年.我们把可以构成一个直角三角形三边的一组正整数称为勾股数.现从3,4,5,6,7,8,9,10,11,12,13这11个数中随机抽取3个数，则这3个数能构成勾股数的概率为__________．15．如图，M是半径为R的圆周上一个定点，在圆周上等可能的任取一点N，连接MN，则弦MN的长度不超过3R的概率是__________．16．使用如图所示算法对下面一组数据进行统计处理，则输出的结果为__________．数据：19.3a=，29.6a=，39.3a=49.4a=，59.4a=，69.3a=79.3a=，89.7a=，99.2a=109.5a=，119.3a=，129.6a=17．根据如图所示的伪代码可知,输出的结果为______.18．某程序框图如图所示，该程序运行后输出的S 为____________.19．为了了解2100名学生早晨到校时间，计划采用系统抽样的方法从全体学生中抽取容量为100栋样本，则分段间隔为__________．20．能够说明“若甲班人数为m ，平均分为a ；乙班人数为n n m ≠（），平均分为b ，则甲乙两班的数学平均分为2a b+”是假命题的一组正整数a ,b 的值依次为_____． 三、解答题21．已知函数()f x ax b =+，分别在下列条件下，求函数图象经过第二、三、四象限的概率.（1）设,{2,1,1,2}a b ∈--且a b ；（2）实数,a b 满足条件11,1 1.a b -⎧⎨-⎩22．一工厂对某条生产线加工零件所花费时间进行统计，得到如下表的数据： 零件数x （个）1020304050加工时间y （分钟）6268 75 82 88（1）从加工时间的五组数据中随机选择两组数据，求该两组数据中至少有一组数据小于加工时间的均值的概率；（2）若加工时间y 与零件数x 具有相关关系，求y 关于x 的回归直线方程；若需加工80个零件，根据回归直线预测其需要多长时间.(121()()()ˆniii ni i x x y y bx x ==--=-∑∑，^^a yb x =-)23．写出一个求解任意二次函数()20y ax bx c a =++≠的最值的算法.24．已知某算法的程序框图如图所示,若将输出的(x ,y )值依次记为(x 1,y 1),(x 2,y 2),…,(x n ,y n ),… (1)若程序运行中输出的一个数组是(9,t ),求t 的值. (2)程序结束时,共输出(x ,y )的组数为多少? (3)写出程序框图的程序语句.25．为培养学生在高中阶段的数学能力，某校将举行数学建模竞赛.已知该竞赛共有60名学生参加，他们成绩的频率分布直方图如图所示.（1）估计这60名参赛学生成绩的中位数；（2）为了对数据进行分析，将60分以下的成绩定为不合格.60分以上（含60分）的成绩定为合格，某评估专家决定利用分层抽样的方法从这60名学生中选取10人，然后从这10人中抽取4人参加座谈会，记ξ为抽取的4人中，成绩不合格的人数，求ξ的分布列与数学期望；（3）已知这60名学生的数学建模竞赛成绩Z 服从正态分布()2,N μσ，其中μ可用样本平均数近似代替，2σ可用样本方差近似代替（同一组数据用该区间的中点值作代表），若成绩在46分以上的学生均能得到奖励，本次数学建模竞赛满分为100分，估计此次竞赛受到奖励的人数（结果根据四舍五人保留整数）.参考数据：()0.6827P Z μσμσ-<≤+≈，()220.9545P Z μσμσ-<≤+≈，()330.9973P Z μσμσ-<≤+≈.26．某地区不同身高的未成年男性的体重平均值如下表： 身高/cm6070 80 90 100 110 120 130 140 150 160 170 体重/kg 6.137.909.9012.1515.0217.5020.9226.8631.1138.8547.2555.05（1）根据散点图判断，y a bx =+与x y a b =⋅哪一个能比较近似地反映这个地区未成年男性体重kg y 与身高cm x 的回归方程类型？（给出判断即可，不必说明理由） （2）根据（1）的判断结果及下表中数据，建立y 关于x 的回归方程（表中ln i i u y =，0.66 1.93e ≈，0.22 1.02e ≈）.xyu()1221ii x x =-∑()()121iii x x y y =--∑ ()()121iii x x u u =--∑11524.0532.9614200 6143.3 284参考公式：()()()1122211n niii ii i nniii i x x y y x y nx yb x x xnx====---⋅==--∑∑∑∑，a y b x =-⋅.【参考答案】***试卷处理标记，请不要删除一、选择题 1．B 解析：B 【分析】在OMN ∆内任取一点，该点到点M 的距离大于1的区域是OMN ∆中去掉扇形MOC 的剩余部分，由几何概型能求出该点到点M 的距离大于1的概率． 【详解】解：以M 为原点，以1为半径作圆，交MN 于点C ， 在OMN ∆中，1OM =，3ON =，2MN =，MO NO∴⊥，60OMC ∠=︒，21166OMC S ππ∴=⨯⨯=扇形，13132MON S ∆=⨯⨯=．在OMN ∆内任取一点，该点到点M 的距离大于1的区域是OMN ∆中去掉扇形MOC 的剩余部分，∴由几何概型得该点到点M 的距离大于1的概率为：332613MON OMCMONS S P S ππ∆∆--===-扇形．故选：B ．【点睛】本题考查概率的求法，考查几何概型等基础知识，考查运算求解能力，是基础题．2．D解析：D 【分析】利用与面积有关的几何概型概率计算公式求解即可. 【详解】由题可知,正方形的面积为=22=4S ⨯正,设这个月牙图案的面积为S , 由与面积有关的几何概型概率计算公式可得,向这个正方形里随机投入芝麻,落在月牙形图案内的概率为150=4500S S P S ==正,解得65S =. 故选:D 【点睛】本题考查与面积有关的几何概型概率计算公式;属于基础题、常考题型.3．C解析：C 【分析】分别求出③和④的巧板的面积，根据几何概型的概率关系转化为面积比. 【详解】设巧板①的边长为1，则结合图2可知大正方形的边长为3， 其面积239S ==.其中巧板③是底边长为2的等腰直角三角形，其面积为112112S =⨯⨯=，巧板④ 与腰长为1的等腰直角三角形的组合图形，其面积为22151122S ⨯⨯+==， 故所求的概率12718S S P S +==. 故选:C . 【点睛】本题考查几何概型的概率求法，转化为面积比，属于中档题 .4．A解析：A 【分析】设2BC =，将圆心角为3π的扇形面积减去等边三角形的面积可得出弓形的面积，由此计算出图中“勒洛三角形”的面积，然后利用几何概型的概率公式可计算出所求事件的概率. 【详解】如下图所示，设2BC =，则以点B 为圆心的扇形面积为2122=233ππ⨯⨯，等边ABC ∆的面积为212sin 23π⨯⨯=23π- 所以，勒洛三角形的面积可视为一个扇形面积加上两个弓形的面积，即222233πππ⎛+⨯=- ⎝ ∴在勒洛三角形中随机取一点，此点取自正三角形外部的概率()()323312323πππ--=--，故选A.【点睛】本题考查几何概型概率的计算，解题的关键就是要求出图形相应区域的面积，解题时要熟悉一些常见平面图形的面积计算方法，考查计算能力，属于中等题.5．D解析：D 【分析】模拟执行程序框图，只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可得到输出的ｓ的值． 【详解】由0s =，1k =满足条件， 则3k =，14s =，满足条件； 5k =，1154612s =+=，满足条件； 7k =，511312824s =+=，满足条件； 9k =，131772410120s =+=，不满足条件， 此时输出77120s =. 故选：D. 【点睛】本题主要考查程序框图的循环结构流程图，属于中档题. 解决程序框图问题时一定注意以下几点：(1) 不要混淆处理框和输入框；(2) 注意区分程序框图是条件分支结构还是循环结构；(3) 注意区分当型循环结构和直到型循环结构；(4) 处理循环结构的问题时一定要正确控制循环次数；(5) 要注意各个框的顺序,（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.6．C解析：C 【分析】计算出输出15y =时，3x =；继续运行程序可知继续赋值得：4x =，此时不满足判断框条件，结束程序，从而可得判断框条件.【详解】解析 当x ＝－3时，y ＝3；当x ＝－2时，y ＝0； 当x ＝－1时，y ＝－1；当x ＝0时，y ＝0； 当x ＝1时，y ＝3；当x ＝2时，y ＝8； 当x ＝3时，y ＝15，x ＝4，结束． 所以y 的最大值为15，可知x ≤3符合题意． 判断框应填：3x ≤ 故选C 【点睛】本题主要考查程序框图的循环结构流程图，属于中档题. 解决程序框图问题时一定注意以下几点：(1) 不要混淆处理框和输入框；(2) 注意区分程序框图是条件分支结构还是循环结构；(3) 注意区分当型循环结构和直到型循环结构；(4) 处理循环结构的问题时一定要正确控制循环次数；(5) 要注意各个框的顺序,（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.7．B解析：B 【分析】由题意结合流程图运行程序，考查5i >是否成立来决定输出的数值即可. 【详解】结合流程图可知程序运行过程如下： 首先初始化数据：1,2i S ==， 此时不满足5i >，执行循环：111,122S i i S =-==+=； 此时不满足5i >，执行循环：111,13S i i S=-=-=+=； 此时不满足5i >，执行循环：112,14S i i S=-==+=； 此时不满足5i >，执行循环：111,152S i i S =-==+=； 此时不满足5i >，执行循环：111,16S i i S=-=-=+=； 此时满足5i >，输出1S =-. 本题选择B 选项. 【点睛】本题主要考查循环结构流程图的识别与运行过程，属于中等题.8．A解析：A 【解析】 【分析】模拟程序的运行，依次写出每次循环得到的x ，n 的值，由题意判断退出循环的条件即可得解． 【详解】模拟程序的运行，可得 n ＝1，x ＝1不满足条件x ＞a ，执行循环体，x ＝1，n ＝2 不满足条件x ＞a ，执行循环体，x ＝2，n ＝3 不满足条件x ＞a ，执行循环体，x ＝6，n ＝4 不满足条件x ＞a ，执行循环体，x ＝24，n ＝5此时，由题意应该满足条件x ＞a ，退出循环，输出n 的值为5． 可得：6≤a ＜24． 故选：A ． 【点睛】本题考查的知识点是循环结构的程序框图的应用，当循环的次数不多，或有规律时，常采用模拟循环的方法解答，属于基础题．9．D解析：D 【解析】试题分析：由表中数据可得 表1:()25262210140.00916362032K ⨯⨯-⨯=≈⨯⨯⨯；表2: ()2524201216 1.76916362032K ⨯⨯-⨯=≈⨯⨯⨯；表3: ()252824128 1.316362032K ⨯⨯-⨯=≈⨯⨯⨯；表4: ()25214302623.4816362032K ⨯⨯-⨯=≈⨯⨯⨯．其中23.48最大,所以阅读量与性别有关联的可能性最大．故D 正确． 考点：独立性检验．10．D解析：D 【分析】根据平均数及方差的定义可知，一组数据的每个数都乘以a 得到一组新数据，平均值变为原来a 倍，方差变为原来2a 倍. 【详解】设一组数据1234,,,,,n x x x x x ⋯的平均数为x ，方差为2s , 则平均值为()12341n ax ax ax ax ax ax n++++⋯+=， ()()()()()22222212341n s x x x xx xx xx x n ⎡⎤=-+-+-+-+⋯+-⎢⎥⎣⎦，()()()()()222222212341n ax axax axax axax axax ax a s n ⎡⎤∴-+-+-+-+⋯+-=⋅⎢⎥⎣⎦故选：D. 【点睛】本题主要考查了方差，平均数的概念，灵活运用公式计算是解题关键，属于中档题.11．B解析：B 【解析】分析：根据所给的这组数据，取出这组数据的样本中心点，把样本中心点代入所给的四个选项中验证，若能够成立的只有一个，这一个就是回归直线方程. 详解：123+4=2.54x ++=， 3 3.8 5.264.5,4y +++==∴这组数据的样本中心点是（2.5,4.5）把样本中心点代入四个选项中，只有y ＝1.04x ＋1.9成立，故选B.点睛：这是一道关于考查回归直线方程的题目，关键掌握回归直线必过样本中心点的特点，首先分析题目，由四组数据可得,x y ，进而得到样本中心点的坐标，接下来根据回归直线必过样本中心点，即可解答此题.12．D解析：D 【解析】 【分析】根据60～70岁这个年龄段中128人中抽查了8人，可知分层抽样的抽样比为81=12816，因为共抽出30人，所以总人数为3016=480⨯人，即可求出20～30岁年龄段的人数. 【详解】根据60～70岁这个年龄段中128人中抽查了8人，可知分层抽样的抽样比为81=12816, 因为共抽出30人，所以总人数为3016=480⨯人,所以，20～30岁龄段的人有480128192160--=，故选D. 【点睛】本题主要考查了分层抽样，抽样，样本容量，属于中档题二、填空题13．【分析】将甲乙到达时间设为（以为0时刻单位为分钟）则相见需要满足：画出图像根据几何概型公式得到答案【详解】根据题意：将甲乙到达时间设为（以为0时刻单位为分钟）则相见需要满足：画出图像：根据几何概型公解析：11 36【分析】将甲、乙到达时间设为,x y（以4:00为0时刻，单位为分钟）.则相见需要满足：10y x-≤画出图像，根据几何概型公式得到答案.【详解】根据题意：将甲、乙到达时间设为,x y（以4:00为0时刻，单位为分钟）则相见需要满足：10y x-≤画出图像：根据几何概型公式：2500111360036P=-=【点睛】本题考查了几何概型的应用，意在考查学生解决问题的能力.14．【分析】由组合数结合古典概型求解即可【详解】从11个数中随机抽取3个数有种不同的方法其中能构成勾股数的有共三种所以所求概率为故答案为【点睛】本题考查古典概型与数学文化考查组合问题数据处理能力和应用意识解析：155【分析】由组合数结合古典概型求解即可【详解】从11个数中随机抽取3个数有311C种不同的方法，其中能构成勾股数的有共()()()3,4,5,6,8,10,5,12,13三种，所以，所求概率为3113155PC==.故答案为155【点睛】本题考查古典概型与数学文化，考查组合问题，数据处理能力和应用意识.15．【分析】先根据题意先找出弦的长度不超过对应的点其构成的区域是点M 两侧各圆周既而求得概率【详解】根据题意满足条件弦的长度不超过对应的点其构成的区域是点M 两侧各圆周所以弦MN 的长度不超过的概率是故答案为解析：23【分析】先根据题意，先找出弦MN 对应的点，其构成的区域是点M 两侧各13圆周，既而求得概率. 【详解】根据题意，满足条件“弦MN ”对应的点，其构成的区域是点M 两侧各13圆周，所以弦MN 的概率是23P 故答案为23【点睛】本题主要考查了几何概型的意义，关键是找出满足条件弦MN 的图形测度，再带入公式求解.16．【分析】分析程序框图的功能在于寻找和输出一组数据的最大值观察该题所给的数据可知其最大值为M 的值即为取最大时对应的脚码从而求得结果【详解】仔细分析程序框图的作用和功能所解决的问题是找出一组数据的最大值 解析：9.7,8【分析】分析程序框图的功能，在于寻找和输出一组数据的最大值，观察该题所给的数据，可知其最大值为9.7，M 的值即为取最大时对应的脚码，从而求得结果. 【详解】仔细分析程序框图的作用和功能， 所解决的问题是找出一组数据的最大值，并指明其为第几个数，观察数据得到第八个数是最大的，且为9.7， 所以答案是9.7,8. 【点睛】该题考查的是有关程序框图的问题，涉及到的知识点有框图的作用和功能，观察所给的数据，从而得到结果，所以要读取框图的作用非常关键.17．72【分析】模拟程序的运行依次写出每次循环得到的的值可得当时不满足条件退出循环输出的值为72【详解】模拟程序的运行可得满足条件执行循环体满足条件执行循环体；满足条件执行循环体;满足条件执行循环体；不解析：72 【分析】模拟程序的运行，依次写出每次循环得到的S i ，的值，可得当9i = 时不满足条件8i ＜，退出循环，输出S 的值为72. 【详解】模拟程序的运行，可得10,i S ==， 满足条件8i ＜，执行循环体，39;i S ==，满足条件8i ＜，执行循环体，524i S ==， ； 满足条件8i ＜，执行循环体，745i S ==， ; 满足条件8i ＜，执行循环体，9i =，72S =； 不满足条件8i ＜，退出循环，输出S 的值为72, 故答案为72 【点睛】本题考查循环结构的程序框图的应用，当循环的次数不多或有规律时，常采用模拟执行程序的方法解决，属于基础题．18．【分析】列出前几次循环找出该算法循环的周期性然后利用周期性求出输出结果的值【详解】成立执行第一次循环；成立执行第二次循环；成立执行第三次循环；成立执行第四次循环；成立执行第五次循环由上可知该算法循环解析：13. 【分析】列出前几次循环，找出该算法循环的周期性，然后利用周期性求出输出结果S 的值. 【详解】12011i =≤成立，执行第一次循环，12312S +==--，112i =+=； 22011i =≤成立，执行第二次循环，()()131132S +-==---，213i =+=； 32011i =≤成立，执行第三次循环，11121312S ⎛⎫+- ⎪⎝⎭==⎛⎫-- ⎪⎝⎭，314i =+=；42011i =≤成立，执行第四次循环，1132113S +==-，415i =+=； 52011i =≤成立，执行第五次循环，12312S +==--，516i =+=.由上可知，该算法循环是以4次为一个循环周期，执行完最后一次循环，2012i =，201255024=⨯+，因此，输出的结果S 的值为13，故答案为13.【点睛】本题考查算法的周期性，解题时要结合算法程序框图得出算法循环的周期性，考查推理能力与计算能力，属于中等题.19．【解析】【分析】根据系统抽样的特征求出分段间隔即可【详解】根据系统抽样的特征得：从2100名学生中抽取100个学生分段间隔为故答案是21【点睛】该题所考查的是有关系统抽样的组距问题应用总体除以样本容 解析：21【解析】 【分析】根据系统抽样的特征，求出分段间隔即可. 【详解】根据系统抽样的特征，得：从2100名学生中抽取100个学生，分段间隔为210021100=， 故答案是21. 【点睛】该题所考查的是有关系统抽样的组距问题，应用总体除以样本容量等于组距，得到结果，属于简单题目.20．是不相等的正整数即可【解析】∵甲班人数为平均分为乙班人数为平均分为∴甲乙两班的数学平均分为∵∴当时∴该命题是假命题时应满足是不相等的正整数故答案为：是不相等的正整数解析：,a b 是不相等的正整数即可 【解析】∵甲班人数为m ,平均分为a ，乙班人数为()n n m ≠,平均分为b ∴甲、乙两班的数学平均分为ma nbm n++ ∵m n ≠ ∴当a b =时，2ma nb a bm n ++=+ ∴该命题是假命题时，应满足,a b 是不相等的正整数 故答案为：,a b 是不相等的正整数三、解答题21．（1）16；（2）14【分析】（1）分别求出从{2,1,1,2}--中任取两个不同的数所构成的直线条数及满足图象经过第二、三、四象限的直线条数，由古典概型概率公式求解； （2）由题意画出图形，再由测度比是面积比得答案． 【详解】（1）从{2,1,1,2}--中任取两个不同的数，所构成直线()f x ax b =+的条数为2412A =条，满足图象经过第二、三、四象限的直线有21y x =--与2y x =--两条，∴所求概率21126P ==； （2）满足约束条件1111a b -⎧⎨-⎩的区域的面积为224⨯=，若函数()f x ax b =+的图象经过第二、三、四象限，则1010a b -<⎧⎨-<⎩，所占区域面积为111⨯=．∴所求概率为14P =．【点睛】本题考查古典概型与几何概型的概率计算，考查数形结合思想和数据处理能力． 22．（1）710（2）108分钟. 【分析】（1）利用列举法和古典概型的概率公式计算可得；（2）根据公式计算可得回归方程，根据回归公式计算可得答案. 【详解】 解：（1）6268758288755y ++++==记：“两组数据中至少有一组数据小于加工时间的均值” 为事件A ，基本事件：（62，68），（62，75），（62，82），（62，88），（68，75），（68，82），（68，88），（75，82），（75，88），（82，88）共10种，其中事件A ：（62，68），（62，75），（62，82），（62，88），（68，75），（68，82），（68，88）共7个，所以7()10P A =. （2）由题，1020304050305x ++++==,()5214001001004001000i i x x =-=+++=∑()()5126070070260660iii x x y y =--=++++=∑()()()121ˆ0.66,niii nii x x y y bx x ==--==∴-∑∑ˆˆ55.2a y bx=-= 所以回归方程为ˆ0.6655.2yx =+. 80x =时，ˆ0.668055.2108yx =⨯+=，即预测其加工80个零件需要108分钟. 【点睛】本题考查了利用列举法和古典概型概率公式计算概率，考查了求线性回归方程，考查了运算求解能力，属于中档题. 23．见解析 【分析】由二次函数的性质知,当0a >时,二次函数()20y ax bx c a =++≠开口方向向上，函数有最小值为244ac b a -；当0a <时, 二次函数()20y ax bx c a =++≠开口方向向下,函数有最大值为244ac b a-. 【详解】第一步，输入a ，b ，c第二步，计算244ac b m a-=；第三步，若0a >，min y m =，否则， max y m =. 【点睛】本题考查算法步骤的书写和一元二次函数的最值问题;同时让学生体会算法在解决数学问题中的作用;求解本题的关键是对一元二次函数最值情况必须熟悉;属于中档题. 24．(1)-4；(2)1009；(3)答案见解析. 【解析】 试题分析：(1)利用所给的程序框图运行程序可得当x=9时,y=-4,则t 的值为-4. (2)结合程序的算法和循环结构的特点可知共输出(x ,y )的组数为1009；(3)将所给的程序框图翻译为算法语句，利用循环语句设计相应的程序即可，注意循环语句应设计为DO 语句的形式.试题(1)由程序框图知,当x=1时,y=0;当x=3时,y=-2;当x=9时,y=-4,所以t=-4.(2)当n=1时,输出一对,当n=3时,又输出一对,…,当n=2 017时,输出最后一对,共输出(x ,y )的组数为20182=1 009. (3)程序框图的程序语句如下:x =1y =0n =1DOPRINT (x ,y )n =n +2x =3*xy =y -2LOOP UNTIL n >2 017END点睛：程序框图的条件结构和循环结构分别对应算法语句的条件语句和循环语句，两种语句的阅读理解是复习重点．输入、输出和赋值语句是任何一个算法必不可少的语句，一个语句可以输出多个表达式．在赋值语句中，一定要注意其格式的要求，如“＝”的右侧必须是表达式，左侧必须是变量；一个语句只能给一个变量赋值；变量的值始终等于最近一次赋给它的值，先前的值将被替换.25．（1）中位数为65；（2）分布列见解析；期望为5635；（3）50. 【分析】（1）由图中的数据可判断中位数在60分到80分之间，若设中位数为x ，则()0.005200.01520600.020.5x ⨯+⨯+-⨯=，从而可求得中位数；（2）结合频率分布直方图和分层抽样的方法可知，抽取的10人中合格的人数为6人，不合格的人数为4人，则ξ的可能取值为0，1，2，3，4，求出各自的概率，从而可得ξ的分布列与数学期望；（3）由已知求出=64=18μσ，，从而可得()()6418641846820.6827P Z P Z -<≤+=<≤≈，再利用正态分布的对称性可求得结果【详解】（1）设中位数为x ，则()0.005200.01520600.020.5x ⨯+⨯+-⨯=，解得65x =，所以这60名参赛学生成绩的中位数为65.（2）结合频率分布直方图和分层抽样的方法可知，抽取的10人中合格的人数为()0.010.0220106+⨯⨯=，不合格的人数为1064-=.由题意可知ξ的可能取值为0，1，2，3，4.则()464101014C P C ξ===，()134********C C P C ξ===，()2246410327C C P C ξ===，()31464103435C C C P ξ===，()4441014210C P C ξ===. 所以ξ的分布列为所以ξ的数学期望01234142173521035E ξ=⨯+⨯+⨯+⨯+⨯=. （3）由题意可得，()300.005500.015700.02900.012064μ=⨯+⨯+⨯+⨯⨯=，()()()222230640.150640.370640.4σ=-⨯+-⨯+-⨯()290640.2324+-⨯=，则18σ=，由Z 服从正态分布()2,N μσ，得()()6418641846820.6827P Z P Z -<≤+=<≤≈，则()()18210.68270.158652P Z >≈-=，()460.68270.158650.84135P Z >≈+=，所以此次竞赛受到奖励的人数为600.8413550⨯≈.【点睛】此题考查频率分布直方图、分层抽样、离散型随机变量的分布列、正态分布等知识，考查分析问题的能力和计算能力，属于中档题26．（1）x y a b =⋅；（2） 1.93 1.02x y =⨯.【分析】（1）根据散点图的趋势可以判断回归方程类型.（2）令ln u y =，由x y a b =⋅，得()1212ln ,ln u c x c c b c a =+==，由公式计算可得回归方程.【详解】（1）根据散点图判断，x y a b =⋅能比较近似地反映这个地区未成年男性体重kg y 与身高cm x 的回归方程类型.（2）令ln u y =，由x y a b =⋅，得()1212ln ,ln u c x c c b c a =+==，()()()121112212840.0214200i ii ii x x u u c x x ====--=-∑∑， 而 2.96u =，所以21 2.960.021150.66c u c x =-⋅=-⨯=， 0.020.66u x =+，所以0.020.660.660.02 1.93 1.02x x x y e e e +==⨯=⨯， y 关于x 的回归方程为 1.93 1.02x y =⨯.【点睛】本题考查由散点图辨别回归方程的类型，求回归方程，属于中档题.。