齿轮的数控加工原理及误差分析
- 格式:doc
- 大小:82.50 KB
- 文档页数:5


齿轮传动轴的传动误差与回转间隙分析引言齿轮传动是常见的一种机械传动形式,广泛应用于工业机械领域。
在齿轮传动中,传动误差和回转间隙是重要的性能指标,对传动系统的精度和运行稳定性有着重要影响。
本文将针对齿轮传动轴的传动误差与回转间隙进行详细分析,探讨它们的原因以及对传动系统性能的影响。
一、传动误差的定义与分类传动误差是指齿轮传动轴在工作过程中由于齿轮的制造、装配等因素,导致输出轴承载方向的误差。
在齿轮传动中,常见的传动误差主要包括齿形误差、齿隙误差和轴向移位误差。
1. 齿形误差:齿形误差是指齿轮齿廓形状与理想齿廓的差异。
齿形误差可以通过齿轮的制造工艺、加工精度以及齿形检测仪器的性能等因素引起。
齿形误差会导致传动系统的噪声和振动增加,降低传动系统的工作效率。
2. 齿隙误差:齿隙误差是指齿轮齿槽之间的间隙大小不一致。
齿隙误差可以由齿轮的制造工艺、装配过程中的间隙控制等因素引起。
齿隙误差会导致传动系统的动态特性变差,降低传动系统的响应速度和稳定性。
3. 轴向移位误差:轴向移位误差是指齿轮轴在工作过程中由于装配不精确或轴向载荷造成的轴向偏移。
轴向移位误差会导致传动系统的运行不平稳,产生冲击和振动,严重时会导致传动轴的断裂。
二、传动误差的影响因素传动误差的产生与多个因素相关,主要包括齿轮的加工工艺、装配精度、使用环境、负载情况等。
1. 加工工艺:齿轮的加工工艺是影响传动误差的重要因素之一。
制造齿轮时,加工精度越高产生的传动误差就越小。
高精度的加工设备和工艺可以减少齿形误差和齿隙误差的产生。
2. 装配精度:齿轮装配过程中的精度控制也会对传动误差产生重要影响。
装配精度越高,齿轮的传动误差就越小。
装配精度主要包括齿轮齿轮间隙的控制、轴向偏移的控制等。
3. 使用环境:齿轮传动系统的使用环境对传动误差有着重要影响。
高温、高湿、高腐蚀等环境会导致齿轮表面的磨损加剧,进而影响传动误差。
4. 负载情况:齿轮传动系统的负载情况也会对传动误差产生影响。

影响齿轮工作平稳性的加工误差分析影响齿轮传动工作平稳性的主要因素是齿轮的齿形误差△ff和基节偏差△fpb。
齿形误差会引起每对齿轮啮合过程中传动比的瞬时变化;基节偏差会引起一对齿过渡到另一对齿啮合时传动比的突变。
齿轮传动由于传动比瞬时变化和突变而产生噪声和振动,从而影响工作平稳性精度。
滚齿时,产生齿轮的基节偏差较小,而齿形误差通常较大。
下面分别进行讨论。
(1)齿形误差齿形误差主要是由于齿轮滚刀的制造刃磨误差及滚刀的安装误差等原因造成的,因此在滚刀的每一转中都会反映到齿面上。
常见的齿形误差有如图9-6所示的各种形式。
图a为齿面出棱、图b为齿形不对称、图c为齿形角误差、图d为齿面上的周期性误差、图e为齿轮根切。
由于齿轮的齿面偏离了正确的渐开线,使齿轮传动中瞬时传动比不稳定,影响齿轮的工作平稳性。
(2)基节极限偏差滚齿时,齿轮的基节极限偏差主要受滚刀基节偏差的影响。
滚刀基节的计算式为:pb0=pn0cosα0=pt0cosλ0cosα0≈pt0cosα0式中:pb0――滚刀基节;pn0――滚刀法向齿距;pt0――滚刀轴向齿距;α0――滚刀法向齿形角;λ0――滚刀分度圆螺旋升角,一般很小,因此cosλ0≈1。
由上式可见,为减少基节偏差,滚刀制造时应严格控制轴向齿距及齿形角误差,同时对影响齿形角误差和轴向齿距误差的刀齿前刀面的非径向性误差也要加以控制。
影响齿轮接触精度的加工误差分析齿轮齿面的接触状况直接影响齿轮传动中载荷分布的均匀性。
滚齿时,影响齿高方向的接触精度的主要原因是齿形公差△ff和基节极限偏差△fpb。
影响齿宽方向的接触精度的主要原因是齿向公差△Fβ。
产生齿向公差的主要原因:(1)滚齿机刀架导轨相对于工作台回转轴线存在平行度误差。
(2)齿坯装夹歪斜由于心轴、齿坯基准端面跳动及垫圈两端面不平行等引起的齿坯安装歪斜,会产生齿向误差。
(3)滚切斜齿轮时,除上述影响因素外,机床差动挂轮计算的误差,也会影响齿轮的齿向误差。
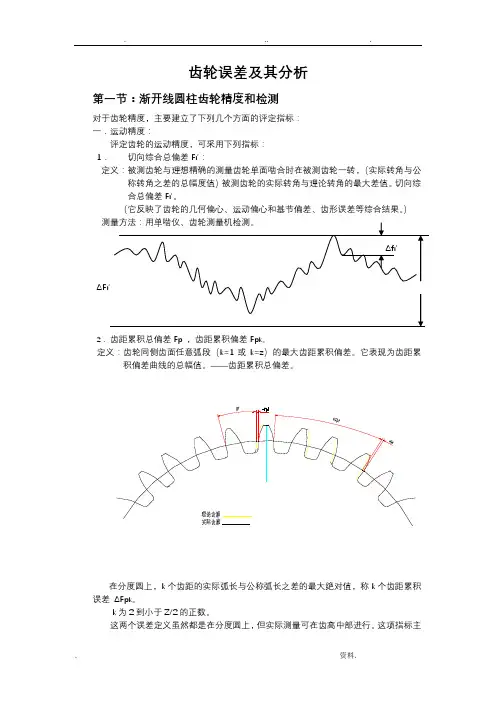
齿轮误差及其分析第一节:渐开线圆柱齿轮精度和检测对于齿轮精度,主要建立了下列几个方面的评定指标:一.运动精度:评定齿轮的运动精度,可采用下列指标:1.切向综合总偏差F i′:定义:被测齿轮与理想精确的测量齿轮单面啮合时在被测齿轮一转,(实际转角与公称转角之差的总幅度值)被测齿轮的实际转角与理论转角的最大差值。
切向综合总偏差F i′。
(它反映了齿轮的几何偏心、运动偏心和基节偏差、齿形误差等综合结果。
)ΔF i2.齿距累积总偏差F p,齿距累积偏差F pk。
定义:齿轮同侧齿面任意弧段(k=1或k=z)的最大齿距累积偏差。
它表现为齿距累积偏差曲线的总幅值。
——齿距累积总偏差。
在分度圆上,k个齿距的实际弧长与公称弧长之差的最大绝对值,称k个齿距累积误差ΔF pk。
k为2到小于Z/2的正数。
这两个误差定义虽然都是在分度圆上,但实际测量可在齿高中部进行。
这项指标主要反映齿轮的几何偏心、运动偏心。
用ΔF p 评定不如ΔF i′全面。
因为ΔF i是在连续切向综合误差曲线上取得的,而ΔF p不是连续的,它是折线。
ΔF i′= ΔF p+ Δf f测量方法:一般用相对法,在齿轮测量机上测量。
3.齿圈径向跳动ΔF r与公法线长度变动ΔF w:ΔF r定义:在齿轮一转围,测头在齿槽,于齿高中部双面接触,测头相对于齿轮轴线的最大变动量。
它只反映齿轮的几何偏心,不能反映其运动偏心。
(用径跳仪测量检测。
)由于齿圈径跳ΔF r 只反映齿轮的几何偏心,不能反映其运动偏心。
因此要增加另一项指标。
公法线长度变动ΔF w。
ΔF w定义:在齿轮一周围,实际公法线长度最大值与最小值之差。
ΔF w=W max-W min测量公法线长度实际是测量基圆弧长,它反映齿轮的运动偏心。
测量方法:用公法线千分尺测量。
4.径向综合误差ΔF i″和公法线长度变动ΔF w:齿轮的几何偏心还可以用径向综合误差这一指标来评定。
ΔF i″定义:被测齿轮与理想精确的测量齿轮双面啮合时,在被测齿轮一转,双啮中心距的最大变动量。

阐述渐开线齿轮齿形误差的分析方法1.前言渐开线齿轮是机器中常用的一种零件,它的用途是传递动力或运动。
齿轮之间的传动,是依靠主动轮的牙齿依次推动被动轮的牙齿来实现的。
牙齿两侧面的形状(齿面形状,即齿形)对于齿轮的传动和工作平稳性都有重要影响。
因此,必须了解渐开线齿轮齿形误差产生的原因及分析方法。
2.渐开线齿轮齿形特点所谓渐开线,是一根切线在基圆(作为描绘渐开线基础的一个圆)上纯滚动(即没有滑动的转滚运动)时,画出该切线滚动边缘上任意一点的运动轨迹。
如图1所示:图中的aa1和bb1就是切线纯滚动时a1和b1两点所画出来的渐开线。
显然,因为是同一个基圆,所以这两条渐开线是完全一样的,仅仅是它们的起点不同。
渐开线齿轮传动时,具有在任何瞬时的转速比都不改变,并且在相互啮合的齿轮的齿轮副中心距发生变化时传动比仍保持不变的特点。
在加工时,可以用模数、压力角相同的齿轮刀具加工模数、压力角相同而齿数不同的齿轮,因此,在机械制造行业中渐开线齿形齿轮应用得最为普遍。
3.渐开线齿轮齿形误差的分类及产生原因齿形误差是指在齿轮工作部分容纳实际齿形的两理论齿形间的法向距离,其△f只允许偏向齿体内。
在渐开线齿轮加工过程中,容易产生以下几种齿形误差:a.齿形角误差:即不是标准压力角的齿形,而是压力角大于或小于标准值的齿形,产生这种情况是由于磨齿时砂轮磨削角调整偏大或偏小,以至使所磨齿轮的基圆半径发生了变化。
b.齿形不对称:即齿歪现象,一面齿形的压力角大于标准值,而另一面齿形的压力角小于标准值。
齿形不对称的原因往往是由于采用锥面砂轮时,砂轮两边锥面磨削角修整得大小不同所致。
c.齿形曲率改变:即实际齿形曲率大于或小于理论齿形曲率,曲率的改变是由齿轮加工时的安装误差引起的。
d.齿形根切:即齿根部的渐开线齿形被切去,它的形成多数是由于所磨齿轮齿数较少,而磨削角又太小以及砂轮外圆无圆角引起的。
e.齿根圆角和齿顶特粗误差:即齿根过渡曲线部分的圆角太大,或接近齿顶的一部分齿形特别粗大。

关于数控加工的误差分析及应对措施xx年xx月xx日•数控加工误差概述•数控加工误差分析•数控加工误差应对措施目录•数控加工误差控制案例分析•总结与展望01数控加工误差概述数控加工误差是指工件在数控加工过程中产生的尺寸、形状、表面质量等参数与理想状态下的工件参数之间的偏差。
数控加工误差包括机床、刀具、夹具、工件、切削液等多个因素的影响,这些因素相互作用,导致加工误差的产生。
由于工件或刀具的位置不准确,导致加工出的工件与理想状态下的工件参数之间的偏差。
定位误差由于机床、刀具、夹具等设备的制造、安装、调整不当,导致加工出的工件与理想状态下的工件参数之间的偏差。
几何误差由于切削过程中切削力的大小、方向、作用点等因素发生变化,导致加工出的工件与理想状态下的工件参数之间的偏差。
切削力误差由于机床、工件、刀具等在切削过程中产生的热量变化,导致加工出的工件与理想状态下的工件参数之间的偏差。
热误差1 2 3数控加工误差会导致工件的尺寸、形状、表面质量等参数与理想状态下的工件参数存在偏差,从而影响加工精度。
加工精度下降由于数控加工误差的存在,可能导致工件在装配、使用过程中出现故障,影响产品的整体性能和寿命。
产品质量下降为了控制数控加工误差,需要进行反复的调试和修正,增加了生产周期和成本。
生产效率降低02数控加工误差分析编程误差数控编程过程中,由于计算方法或近似处理等原因,导致加工路径与实际路径存在偏差,从而产生误差。
工件误差工件本身存在形状、尺寸等方面的误差,也会对加工精度产生影响。
机床误差机床本身精度不高或长期使用导致磨损,也会对加工精度产生影响。
刀具误差刀具在加工过程中会受到磨损、变形等因素影响,导致加工精度降低。
误差产生的原因分析03尺寸误差加工过程中,由于刀具磨损、温度变化等因素影响,导致加工出的工件尺寸与设计要求存在偏差。
误差对加工精度的影响01位置误差加工过程中,刀具与工件之间的相对位置不准确,导致加工出的工件形状、尺寸与设计要求存在偏差。

滚齿机:主要用滚刀按展成法加工圆柱齿轮,蜗轮,链轮等齿面的齿轮加工机床。
滚齿机校正机构常见种类:行星式,复式偏心式,凸轮摆杆式,附加回转工作台式等。
决于齿轮机床的精度、刚度、刀具和齿轮毛坯的质量及其安装精度。
所以针对滚齿机工作台误差的滚齿机主要用滚刀按展成法加工圆柱齿轮、蜗轮、链轮等齿面的齿轮加工技术,在机械加工中占有重要地位。
因为在齿轮加工中出现了分度蜗轮的周节累计误差和周期误差,而齿轮加工精度取来源这一问题,本文使用滚齿机行星摆杆机构对其进行校正,用以减少分度蜗轮的周节累计误差和周期误差,使加工出来的齿轮达到满足加工精度的要求。
国内采用的滚齿机校正构,在机床制造行业中, 一开始制造精密机床, 由于各厂的设备条件差, 在滚齿机上不能加工精度较高的蜗轮, 分度精度满足不了产品的要求。
因而, 各厂先后在各型滚齿机上采用了各种类型的校正机构, 大都取得了不同程度的效果, 制出了精密分度蜗轮。
当时, 着重引进国外现成为结构, 近几年来, 无论在结构型式上, 或在简化结构, 或校正效果等方面均有较快的发展。
我国共采用了行星式、复式偏心式、凸轮摆杆式、和附加回转工作台式等多种类型的校正机构。
RS2 型滚齿机校正机构,只能能校正分度蜗轮副的周期误差。
但结构不够紧凑,校正机构在机床的外边,需要另置地基,并将机床的罩壳也换掉。
5355M型滚齿机校正机构也属于行星式,但没有周期误差校正凸轮, 机构是封闭的。
其结构复杂, 构件将近85 种, 使用不方便, 需将机床的双蜗杆传动改成单蜗杆传动, 此时, 必需拆除一根蜗杆。
由于校正机构安装位置不够妥当,使得一部分齿轮外露。
这种结构不太适用于大型滚齿机。
FO-10滚齿机行星式校正机构,该机构有一定的简化, 它省去了四根摆杆和一根长套筒, 结构就比较紧凑一些。
它装在机床分度挂轮箱处, 不需另置地基, 但其构件的种数仍然较多, 达45种, 放大比为0.182毫米每秒。
这种机构的轮廓尺寸较大。

机械加工误差产生的原因及措施汇报人:2024-01-01•机械加工误差产生的原因•减小机械加工误差的措施•机械加工误差的补偿措施目录•提高机械加工精度的途径01机械加工误差产生的原因原理误差总结词原理误差是由于加工原理的不完善而导致的误差。
详细描述原理误差主要表现在机床或刀具的转动和移动过程中,由于设计原理或机构原理的限制,导致加工出的零件与理论值存在偏差。
例如,齿轮加工中,由于齿轮的齿廓理论是完美的,但在实际加工中,由于机床和刀具的精度限制,无法完全复制理想的齿廓形状,从而产生原理误差。
工具、夹具与机床的制造误差总结词工具、夹具与机床的制造误差是由于这些设备的制造精度不足而导致的误差。
详细描述工具、夹具和机床是机械加工中的重要组成部分,它们的制造精度直接影响着零件的加工精度。
例如,刀具的制造误差会导致加工表面的粗糙度不均匀,夹具的定位精度不高会导致零件的位置精度偏差,机床的主轴回转误差则会影响零件的圆度等。
调整误差是由于加工过程中的调整不准确而导致的误差。
详细描述在机械加工过程中,需要对工具、夹具和机床进行多次调整,如刀具的更换、夹具的定位、机床的校准等。
由于调整过程中的人为操作和设备本身的特性,往往会产生一定的调整误差。
例如,刀具的安装角度偏差会影响切削深度和表面粗糙度,夹具的调整不当会导致零件的定位不准确。
总结词VS总结词测量误差是由于测量设备的精度限制和测量方法的不完善而导致的误差。
要点一要点二详细描述测量是机械加工中不可或缺的一环,但由于测量设备的精度限制和测量方法的不完善,往往会产生测量误差。
例如,使用卡尺测量时,由于卡尺的刻度精度有限,会导致测量结果存在误差;同时,测量方法的不正确也会导致误差的产生。
如测量时没有保证工件与卡尺之间的平行度或垂直度,就会产生测量误差。
02减小机械加工误差的措施直接减小或消除误差法直接减小或消除误差法是通过直接减少或消除原始误差来降低加工误差的方法。
例如,通过提高机床的几何精度、减小刀具和夹具的制造误差、提高工件的定位精度等措施,可以有效地减小加工误差。

齿轮误差测量技术齿轮误差测量技术是一种用于评估齿轮传动精度的重要手段,它能够帮助我们了解齿轮系统的性能特征和运行稳定性。
本文将介绍齿轮误差测量技术的原理、方法和应用。
一、齿轮误差的定义齿轮误差是指齿轮齿面形状与标准理论齿面形状之间的偏差。
齿轮误差包括齿距误差、齿厚误差、齿形误差和齿向误差等。
这些误差会直接影响齿轮的传动性能和运行精度。
二、齿轮误差测量的原理齿轮误差测量的原理基于齿轮传动中齿轮的相对运动。
通过比较实际齿轮的齿面形状与理论标准齿面形状之间的差异,可以得到齿轮的误差信息。
三、齿轮误差测量的方法1. 压痕法:利用齿轮传动中的轻微滑动,通过测量齿面的压痕形状和尺寸来推测齿轮的误差。
2. 测量仪法:使用齿轮测量仪器,如齿轮测量机、齿轮检测仪等,通过测量齿轮齿距、齿厚、齿形等参数来评估齿轮的误差。
3. 光学法:利用光学原理,通过测量齿轮齿面的反射光线,可以得到齿轮的误差信息。
4. 数学建模法:采用计算机模拟和数学建模的方法,通过建立齿轮传动的数学模型,可以计算出齿轮的误差。
四、齿轮误差测量的应用1. 齿轮制造和质量控制:齿轮误差测量技术可以用于齿轮的制造过程中,帮助制造商控制齿轮的质量,提高齿轮的精度和可靠性。
2. 齿轮故障诊断:通过测量齿轮的误差,可以判断齿轮是否存在故障或磨损,及时进行维修和更换,避免齿轮故障对机械设备的影响。
3. 齿轮优化设计:通过分析齿轮的误差信息,可以优化齿轮的设计和制造工艺,提高齿轮的传动效率和性能。
4. 齿轮研究和发展:齿轮误差测量技术可以用于齿轮的研究和发展,帮助研究人员了解齿轮的性能特点,推动齿轮技术的进步和创新。
总结起来,齿轮误差测量技术可以帮助我们评估齿轮的传动精度和运行稳定性。
通过测量齿轮的误差,可以指导齿轮的制造、质量控制和故障诊断,同时也促进了齿轮技术的研究和发展。
在实际应用中,我们可以根据具体情况选择合适的测量方法和仪器,以获得准确可靠的齿轮误差信息。


成形磨齿机的机床误差分析与校正成形磨齿机是一种常用于齿轮加工的机床。
在齿轮加工过程中,精确的齿轮尺寸和质量是非常重要的。
然而,在成形磨齿机的使用过程中,机床误差可能会对齿轮加工产生一定的影响。
因此,对于成形磨齿机的机床误差进行分析与校正是必不可少的。
首先,我们需要了解成形磨齿机的机床误差的来源。
机床误差主要包括几何误差、运动误差和热误差等。
几何误差是由于工艺、装配和加工等原因导致的机床结构偏差引起的,如机床导轨的平面度、垂直度等。
运动误差是由于机床主轴、丝杠传动、滚动轴承等运动部件的加工精度和装配精度不足引起的。
热误差是由于机床在工作过程中因为温升产生的机械结构变形引起的。
然后,针对不同的机床误差,我们需要采取相应的分析与校正措施。
首先是几何误差。
几何误差可以通过使用精密测量仪器进行测量,比如激光干涉仪、三坐标测量仪等。
通过测量,我们可以得到机床导轨的偏差值,然后采取适当的调整措施,如刮平、调整螺栓等,来消除导轨的偏差。
另外,通过改进机床的加工工艺和装配工艺,也可以减小几何误差的产生。
其次是运动误差。
运动误差的分析与校正一般包括两个方面:主轴误差和丝杠误差。
主轴误差是由于主轴加工和安装不精确引起的。
我们可以通过使用高精度的主轴、精密的轴承以及适当的装配方法来减小主轴误差。
丝杠误差是由于丝杠传动装置的制造和安装精度不足引起的。
我们可以通过使用高精度的丝杠,调整丝杠螺距,采取适当的润滑措施等来减小丝杠误差。
最后是热误差。
热误差主要是由于机床在工作过程中发热引起的机械结构变形。
为了降低热误差,我们可以改进机床的结构设计,增加散热设备,采取降温措施等。
此外,我们还可以使用温度传感器进行实时监测,及时调整机床的工作状态,以避免热误差的产生。
总而言之,成形磨齿机的机床误差分析与校正是提高齿轮加工质量和效率的关键。
通过对几何误差、运动误差和热误差的分析,并采取相应的校正措施,可以使机床误差控制在合理范围内,确保齿轮加工的精度和质量。
数控加工中的误差及补偿方法分析摘要:数控机床现在应用十分普遍,相比普通机床,无论是生产效率还是加工精度均有了明显提升,可保证产品质量满足市场要求。
以提高数控加工精度为目的,分析各种误差产生的原因,以及寻求高精度误差补偿方法,保障数控机床可以稳定运行,维持高精度加工状态。
文章就数控加工误差类型以及补偿方法进行了简单的分析。
关键词:数控加工;高精度;误差补偿数控加工存在着精度高且柔性自动化等特点,对于复杂零件的加工优势突出,被越发广泛的应用于制造业,且取得了显著成果。
为了进一步做到高精度加工,不断减小误差,就需要在生产加工中总结各类误差的表现形式,并分析其产生的原因,寻求更有效的误差补偿方法,例如通过控制温度与振动从根源上来减少甚至消除误差,或者是应用软件工程来进行纠错等,更大程度上实现高精度数控加工。
一、数控加工误差分析1.加工误差分类数据加工生产过程中受多种因素影响而产生加工误差,一类是根据误差条件可分为静态误差、准静态误差和动态误差。
其中,静态误差即数控加工过程中准确度和误差不会因为时间影响而发生变化。
准静态误差是在给定工作环境中会缓慢的发生变化,但是该条件下会始终保持不变,例如特定工作条件下产生的准静态误差本质并不会发生变化或者是变化速度非常缓慢[1]。
另一类则是根据误差来源可分为位置误差与非位置误差。
位置误差即数控加工生产过程中,随着零部件的运动,产生的运动轨迹以及位置与理想条件有着一定偏差,同时期望运动轨迹以及位置与指令相差较大,如几何误差。
数控机床不同零件与零件在生产运动过程中因外界条件的干扰,零部件的实际运行轨迹以及位置与理想条件偏差较大,包括力误差、热误差以及刀具磨损误差等。
2.误差产生原因数控加工生产中因各因素的影响不可避免的会有误差形成,促使切削工艺中工件与刀具的位置发生变化,影响零部件加工精度。
一般数控加工误差产生原因可从加工方法误差与调安误差两个方面分析,只有当误差总和低于允许差值时,才能够做到高精度数控加工。
传递运动准确性要求传递运动准确可靠,保证传动比恒定,限制转角误差传动平稳性要求传递运动要稳。
冲击,噪音和震动要小,限制瞬时速比载荷分布均匀性要求受力均匀,避免接触应力过大合理的齿轮副侧隙要求非工作面应有间隙以补偿安装,制造的误差,热变形、弹性变形等。
一、主要误差来源:机—刀—工件系统的周期性的误差。
1、安装偏心e {齿坯;机床心轴}结果:齿圈有径跳。
周节,齿厚也有误差。
2、ek {f分度蜗轮;工作台}结果:周节,公法线由长变短。
有误差。
这两种误差是以齿坯转一转为一个周期,叫长周期误差(低频)。
3、ew{分度蜗杆;轴的穿动}n次结果:周节和齿形误差。
4、ed{滚刀,轴线倾斜;轴向举动}结果:径向和轴向误差。
5、滚刀本身的基节,齿形误差结果:基节和齿形误差。
后三项是在3坯一转中多次重复出现的,叫短周期误差(交频)。
二、影响运动准确性的误差及测量——主要是长周期误差,即以齿坯转一转为一个周期的误差,第Ⅰ公差组。
1、切向综合误差ΔFi ·(控制运动的不均匀)3测齿轮与理想精确齿轮单面啮合时,被测齿轮在一转内的最大转角误差(其量值以分度圆的弧长计)2、齿距累积误差误差ΔFp(齿跳不均匀)它是指在分度圆任意两个同侧齿面的实际弧长与公称弧长之差的最大绝对值。
ΔFp=ΔFpmax-ΔFpminΔFp3e,ek的综合误差,必要时,亦可控制局部的累积误差ΔFpk,k from 2 to z/2的整数。
测量主要是相对测量。
用齿轮仪测3、齿圈径向跳动ΔFr(径向误差)在齿轮一转中,测头相对于齿轮轴线的最大变动量。
ΔFr=Rmax-Rmin主要齿轮偏心造成的齿轮径向长周期误差。
测量:用偏摆仪。
最大读数差{小圆棒;百分表}标准齿轮:d球=d棒=1.68m(m:模数)4、径向综合误差ΔFi″(径向误差)ΔFi″被测与理想齿轮双面啮合时,x被测齿轮一转内没,双啮中心距的最大变动。
ΔFi″主要反映齿坯偏心造成齿轮的径向综合误差。
基于UG的正交直齿面齿轮插齿仿真加工及误差分析摘要随着航空及航天事业的飞速发展,航天飞机等装置逐渐向轻盈化、大功率化等方面发展,这些装置的减速设备需要符合大传动比、结构简单等要求。
基于此,面齿轮传动以其传动稳定、重合度大、噪声小、占用空间体积小、圆周速度大等优点从众多传动方式中脱颖而出。
由于面齿轮应用领域的独特性,需要对面齿轮传动进行系统地研究,在确保安全稳定的前提下,应尽量减小面齿轮的制造误差。
因此,对面齿轮的加工制造和误差分析的研究具有重要的意义。
本文以正交直齿面齿轮为研究对象,借助MATLAB和UG NX8.0等软件分析其数学精确建模和插齿仿真加工的具体过程,并对比研究了这两种模型。
主要的研究内容如下:1. 首先,根据微分几何与齿轮啮合原理,建立正交直齿面齿轮空间坐标系,并得到各个坐标系之间的转化关系;其次,依据齿面成形原理,再结合圆柱齿轮刀具方程以及刀具和面齿轮啮合点的相对速度,求解出正交直齿面齿轮的齿面方程和过渡齿面方程;最后,依据齿宽的限制条件,确定面齿轮齿顶变尖的最大外半径方程和防止齿根根切的最小内半径方程。
2. 基于一组正交直齿面齿轮传动的实例,在给定部分参数的情况下,借助MATLAB对上述方程进行计算,得到轮齿的内、外半径具体数值,从而确定面齿轮的齿宽。
采用Z向截面放样法求解面齿轮齿面方程和过渡齿面方程的求解,通过MATLAB软件实现齿面离散点和齿面轮廓的可视化。
3. 将齿面离散点存入文本,借助UG NX8.0将点汇集成线,再由齿面线形成齿面,最终完成面齿轮数学方程的精确建模。
同时,在UG中完成刀具齿轮和圆柱齿轮的渐开线建模,并进行面齿轮传动的装配。
4. 依据之前所求参数,建立面齿轮圆环毛坯模型。
根据齿轮插齿加工原理,建立刀具齿轮和圆环毛坯加工运动模型,通过布尔运算来模拟插齿加工,从而完成面齿轮插齿仿真加工。
采用提取齿面的新型建模方法,完成面齿轮精确建模,验证插齿仿真加工的正确性和提取齿面建模方法的可行性。
数控加工产生误差的根源及解决方案本文从数控机床加工过程中误差产生的根源入手,分析了各类误差产生的原因并找出了减少误差的解决方案。
数控机床是机电一体化的高科技产品,用数控加工程序控制数控机床自动加工零件,不必使用复杂、特制的工装夹具,就能够较好地解决中、小批量,多品种复杂曲面零件的自动化加工问题。
但在零件加工过程中,由于种种原因,会造成零件不合格,甚至于产生废品。
本文从加工中误差产生的原因入手,分析并找出减少误差的解决办法。
零件在数控机床上加工过程中,误差主要四个方面:一、误差是制造工艺不合理造成的;二、误差是程序编制不科学造成的;三、是工装使用不当造成的;四、是机床系统自身误差产生的。
制造工艺不合理造成的加工误差在现实生产中,由于工艺设计不合理而造成的误差一般有以下几种形式。
2.1.加工路线不合理而产生的误差由于孔的位置精度要求较高,因此安排镗孔路线问题就显得比较重要,安排不当就有可能把坐标轴的反向间隙带入,直接影响孔的位置精度。
2.2.刀具切入切出安排不当产生的误差铣削整圆时,要安排刀具从切向进入圆周进行铣削加工,当整圆加工完毕之后,不要在切点处取消刀补或退刀,要安排一段沿切线方向继续运动的距离,这样可以避免在取消刀补时,刀具与工件相撞而造成工件和刀具报废。
当铣切内圆时也应该遵循此种切入切出的方法,最好安排从圆弧过渡到圆弧的加工路线,切出时也应多安排一段过渡圆弧再退刀,这样可以降低接刀处的接痕,从而可以降低孔加工的粗糙度和提高孔加工的精度。
2.3.工艺分析不足而造成的误差普遍性的零件结构工艺性并不完全适用于数控加工中,但以下几点的特别注意:2.3.1.采用统一的定位基准,数控加工中若没有统一的定位基准,会因零件的重新___而引起加工后两个面上的轮廓位置及尺寸不协调,造成较大的误差。
2.3.2.避免造成欠切削或过切削现象,在数控车床上加工圆弧与直线或圆弧与圆弧连接的内外轮廓时,应充分考虑其过渡圆弧半径的大小,因为刀具刀尖半径的大小可能会造成欠切削或过切削现象。
进口数控成型磨齿机加工齿形角度误差分析作者:虞俊来源:《科技视界》2017年第30期【摘要】数控成型磨齿机是利用成形法把砂轮修整成和工件轮廓相吻合的形状,进而加工出齿形。
在磨齿加工过程中,引起齿形倾斜角度误差的因素有很多,机床精度误差、砂轮误差,温度误差等都会引起齿形角度误差,南京高速齿轮制造有限公司自2001年引进德国的HOFLER、NILES及GLEASON-PFAUTER等数控成型磨齿机用于生产,它们目前在国内外使用也是最为广泛的,因此本文就进口数控成型磨在实际应用过程中出现的一些常见齿形角度误差作一些原因分析,从规律中找出相应减小齿形角度误差的解决方案。
【关键词】数控成型磨齿机;齿形角度误差;砂轮误差;机床精度误差;温度误差1 齿形误差的定义想知道齿形角度误差产生的原因首先需要了解什么是齿形误差。
齿形误差又称为齿廓偏差,它是指实际齿廓偏离设计齿廓的量,该量在端平面内且垂直于渐开线齿廓的方向记值。
齿形误差包括齿形总误差Fa、齿形形状误差ffa、齿形倾斜误差fHa,具体定义如下:1.1 齿形总误差Fa在齿形评价记值范围内,包容实际齿形线的两条设计齿形线间的距离,见图1中①所示。
1.2 齿形形状误差ffa在齿形评价记值范围内,包容实际齿形线的两条与平均齿形线完全相同的曲线间的距离,且两条曲线与平均齿形线的距离为常数,见图1中②所示。
1.3 齿形倾斜角度误差fHa在齿形评价记值范围内,两端与平均齿形线相交的两条设计齿形线间的距离,见图1中③所示。
设计齿形线:符合设计要求的齿形线。
平均齿形线:实际齿形线偏离平均齿形线偏差的平方和最小,平均齿形线的位置和倾斜角度可以用“最小二乘法”确定,图一中BB线表示。
B’B’ B”B”表示在齿形评价记值范围内,包容实际齿形线的两条与平均齿形线完全相同的曲线;C’C’ C”C”表示在齿形评价记值范围内,两端与平均齿形线相交的两条设计齿形线;AA A’A’表示在齿形评价记值范围内,包容实际齿形线的两条设计齿形线。
齿轮误差及其分析第一节:渐开线圆柱齿轮精度和检测对于齿轮精度,主要建立了下列几个方面的评定指标:一.运动精度:评定齿轮的运动精度,可采用下列指标:1.切向综合总偏差F i′:定义:被测齿轮与理想精确的测量齿轮单面啮合时在被测齿轮一转,(实际转角与公称转角之差的总幅度值)被测齿轮的实际转角与理论转角的最大差值。
切向综合总偏差F i′。
(它反映了齿轮的几何偏心、运动偏心和基节偏差、齿形误差等综合结果。
)Δ2.齿距累积总偏差F p,齿距累积偏差F pk。
定义:齿轮同侧齿面任意弧段(k=1或k=z)的最大齿距累积偏差。
它表现为齿距累积偏差曲线的总幅值。
——齿距累积总偏差。
在分度圆上,k个齿距的实际弧长与公称弧长之差的最大绝对值,称k个齿距累积误差ΔF pk。
k为2到小于Z/2的正数。
这两个误差定义虽然都是在分度圆上,但实际测量可在齿高中部进行。
这项指标主要反映齿轮的几何偏心、运动偏心。
用ΔF p 评定不如ΔF i′全面。
因为ΔF i是在连续切向综合误差曲线上取得的,而ΔF p不是连续的,它是折线。
ΔF i′= ΔF p + Δf f测量方法:一般用相对法,在齿轮测量机上测量。
3.齿圈径向跳动ΔF r与公法线长度变动ΔF w:ΔF r定义:在齿轮一转围,测头在齿槽,于齿高中部双面接触,测头相对于齿轮轴线的最大变动量。
它只反映齿轮的几何偏心,不能反映其运动偏心。
(用径跳仪测量检测。
)由于齿圈径跳ΔF r 只反映齿轮的几何偏心,不能反映其运动偏心。
因此要增加另一项指标。
公法线长度变动ΔF w。
ΔF w定义:在齿轮一周围,实际公法线长度最大值与最小值之差。
ΔF w=W max-W min测量公法线长度实际是测量基圆弧长,它反映齿轮的运动偏心。
测量方法:用公法线千分尺测量。
4.径向综合误差ΔF i″和公法线长度变动ΔF w:齿轮的几何偏心还可以用径向综合误差这一指标来评定。
ΔF i″定义:被测齿轮与理想精确的测量齿轮双面啮合时,在被测齿轮一转,双啮中心距的最大变动量。
齿轮的数控加工原理及误差分析
1 引言
随着生产的发展, 数控机床特别是加工中心已得到广泛的应用。
在数控机床上, 加工齿轮是复合加工要解决的问题, 目前大多数数控机床已具备了齿轮加工的潜在能力。
为了在数控机床上加工齿轮并保证齿轮的加工精度, 应了解齿轮加工过程中可能产生的各种误差, 以便针对各种误差找出原因, 寻求相应的解决办法。
本文提出数控机床加工齿轮的方法, 并分析、比较在数控机床上由不同的加工方式加工齿轮所产生的误差。
2 滚齿加工原理
用齿轮滚刀加工齿轮, 其传动原理与一对螺旋齿轮的啮合原理相同, 而滚刀可以看成是一个齿数无穷多(头数可以为1) 的螺旋齿轮。
切削运动是滚刀的转动; 分齿运动是随着滚刀的转动, 齿坯也要相应的转动, 要求滚刀转速n刀与齿坯转速n工之间严格保持着相当于齿条与这个被加工齿轮啮合的关系。
也就是滚刀转动中刀齿在轴向移动一个齿距, 齿坯也相应地转过相应的齿距, 这个运动是滚齿加工最重要的运动。
垂直进给运动即滚刀沿齿坯齿宽方向的垂直进给(走刀) S。
加工过程如图1所示。
图1 滚齿加工示意图
3 对数控机床的要求
为了实现齿轮的加工, 需控制2 个伺服进给轴和2个伺服旋转轴。
以卧式加工中心为例,齿轮加工需要的运动有: 切削运动, 由机床主轴驱动滚刀回转; 展成运动, 即回转工作台按啮合关系回转; 齿宽方向的进给运动, 即滚刀的走刀运动, 由Y轴提供; 齿径方向的进给运动, 由X轴提供; 除有上述4 个基本运动外, 主轴相对“工作台”还应有可调的α角度(图2) 。
主轴的旋转运动实现滚刀在加工中的主体运动,滚刀的旋转运动和工件的旋转运动形成范成运动。
如图2所示为滚齿加工的示意图。
图2 齿轮加工运动示意图
4 误差分析
数控系统精度。
由图2可看出, 保证各轴的位置精度和运动精度是保证齿轮加工精度的重要条件。
对于配有设计完善的位置伺服系统的加工中心, 其定位精度和加工精度主要取决于位置检测元器件的精度和2个旋转轴静态和动态的同步精度。
一般来说,高精度的数控系统完全可以满足上述精度要求。
如果是一般的数控系统, 则要计算刀具旋转轴的分度误差, 按展成关系折算到旋转工作台上是否能满足所加工齿轮的精度要求。
例如, 滚齿时所要求达到7级精度, 加工一个齿数为100, 模数为3 的齿轮, 折算到刀具主轴的分度精度应大于01035°。
加工误差。
主要是由于工作台和刀具转速不均匀, 使刀具相对工
作台的瞬时传动比发生变化, 从而使被加工齿轮引起误差, 该误差是由回转工作台分度蜗轮本身的制造误差(采用电子齿轮分度可不考虑此项误差) 和滚刀轴的跳动所造成的。
在数控机床上加工齿轮, 由于刀具主轴是悬臂梁, 刀具所受到的力矩对刀具主轴有影响。
一般滚齿机的刀具主轴是简支梁, 在同样的受力情况下, 悬臂梁产生翘曲变形, 对加工误差影响很大。
铣齿与滚齿有所不同。
在普通机床上是采用具有渐开线齿形的“模数铣刀”逐齿铣出齿轮的齿廓,这种方法的加工精度受齿数的影响。
基于数控加工的特点, 可以采用柱状或片状铣刀用展成法加工齿轮。
柱状铣刀加工原理如图3所示: 垂直进给运动S走出齿深; 铣刀沿齿坯齿宽方向进给(走刀) 一次, 展成回转一个φ角度, 如图4所示, 再次沿齿宽方向进给一次, 直至展成整个齿面; 分齿后加工下一个齿面。
由图3可以看出, 柱状铣刀用展成法对齿轮进行断续展成切削加工, 其理论上的渐开线是由单一参数的基圆渐开螺旋线的有限切平面族来近似的, 而理论渐开螺旋面是这个单一参数的无限个平面的包络面,由它引起的齿形误差在齿形和齿面上都可以反映出来, 误差形成原理如图4所示。
图3 铣齿加工示意图图4齿形棱度形成示意图
式中: φ—工件齿形上相邻切削点在工件上的相邻角度; ρx —齿面某点的曲率半径; ρ—切削刃处的曲率半径。
又因为
假设: ρH —展成长度; N ′—展成的次数; rj—基圆半径; α—分度圆上的齿形压力角。
上式表明展成时的回转角度φ越大, 展成的次数就越少; 基圆直径越小, 引起的齿形误差就越大。
展成的最小回转角度取决于刀具主轴上的分度精度。
在展成过程中, 刀具的径向跳动量ΔEr 和刀具轴向窜动量ΔEx , 对被切齿轮齿形的影响有如下关系:
滚齿时的误差公式为
Δf =ΔEr sinα+ΔEx cosα( 6)
铣齿时的误差公式为
Δf =ΔEr cosα+ΔEx sinα( 7)
刀具径向跳动量的大小将直接反映在齿形上。
因此, 采取有效措施保证刀具主轴的精度是稳定齿轮加工精度的主要措施之一。
5 结论
(1) 在数控机床上加工齿轮, 需要机床具有至少两个联动旋转轴, 否则不能实现齿轮加工需要的基本运动, 通常采用机床主轴并附加一个数控旋转工作
台。
(2) 在数控机床上采用滚齿方式加工齿轮时,主轴的径向跳动和运动平稳性是保证齿轮精度的关键因素。
主轴的误差直接影响齿轮的齿形误差, 同时对
齿面波形高度影响也很大。
(3) 使用数控机床加工齿轮, 对刀具展成时回转角度的分辨率有严格的要求, 即对编码器能达到的最大分辨率有要求。
(4) 使用滚齿方式加工齿轮, 较铣齿展成方式更为方便和具有较高的效率, 齿面的波形高度也较低。