第12讲 周长的计算

人教版三年级上册数学《周长》一. 教材分析《周长》是人教版三年级上册数学的一章内容。

本章主要让学生理解周长的概念，学会用不同的方法计算物体的周长，并能解决一些简单的实际问题。

本章内容包括周长的定义、计算周长的方法、周长的应用等。

二. 学情分析三年级的学生已经掌握了基本的数学运算能力和初步的逻辑思维能力。

但是对于周长的概念和计算方法可能还比较陌生，需要通过实际操作和练习来理解和掌握。

同时，学生对于实际问题的解决能力还需要进一步提高。

三. 说教学目标1.知识与技能目标：学生能够理解周长的概念，学会用不同的方法计算物体的周长。

2.过程与方法目标：学生通过实际操作和练习，提高解决问题的能力。

3.情感态度与价值观目标：学生培养对数学的兴趣和自信心，培养合作和探究的精神。

四. 说教学重难点1.教学重点：学生能够理解周长的概念，学会用不同的方法计算物体的周长。

2.教学难点：学生能够解决一些实际的周长问题，并能够灵活运用所学的知识。

五. 说教学方法与手段本节课采用讲授法、实践法、讨论法等多种教学方法。

同时，利用实物、图片、动画等教学手段，帮助学生直观地理解和掌握周长的概念和计算方法。

六. 说教学过程1.导入：通过展示一些物体，如圆形、正方形等，引导学生观察和思考它们的边界，引出周长的概念。

2.讲解：讲解周长的定义和计算方法，用实物和图片进行演示，让学生直观地理解周长的概念。

3.实践：学生分组进行实际操作，测量和计算物体的周长，培养学生的动手能力和解决问题的能力。

4.讨论：学生分组讨论实际问题，并合作解决问题，培养学生的合作和探究精神。

5.总结：总结本节课的学习内容，强调周长的概念和计算方法。

七. 说板书设计板书设计要简洁明了，突出重点。

可以设计一个简单的，列出物体的名称和对应的周长，让学生直观地看到不同物体的周长计算结果。

八. 说教学评价教学评价可以通过学生的课堂表现、作业完成情况和解决问题的能力来进行。

可以设置一些选择题和填空题来检测学生对周长概念的理解，设置一些实际问题来检测学生解决问题的能力。

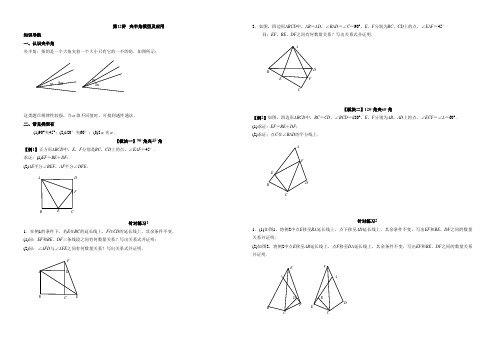
第12讲 夹半角模型及应用知识导航 一、认识夹半角夹半角：指的是一个大角夹着一个大小只有它的一半的角．如图所示：这类题目规律性较强，当α取不同值时，可找到通性通法． 二、常见类型有(1)90°夹45°；(2)120°夹60°；(3)2α夹α．【板块一】90°角夹45°角【例1】正方形ABCD 中，E ，F 分别是BC ，CD 上的点，∠EAF ＝45°． 求证：(1)EF ＝BE ＋DF ：(2)AE 平分∠BEF ，AF 平分∠DFE ．FEDCBA针对练习11．在例1的条件下，若E 在BC 的延长线上，F 在CD 的延长线上，其余条件不变． (1)问：EF 和BE ，DF 三条线段之间有何数量关系？写出关系式井证明； (2)问：∠AFD 与∠AFE 之间有何数量关系？写出关系式并证明．FEDCBA2．如图，四边形ABCD 中，AB ＝AD ，∠BAD ＝∠C ＝90°，E ，F 分别为BC ，CD 上的点，∠EAF ＝45°问：EF ，BE ，DF 之间有何数量关系？写出关系式并证明．FEDCBA【板块二】120°角夹60°角【例2】如图，四边形ABCD 中，BC ＝CD ，∠BCD ＝120°，E ，F 分别为AB ，AD 上的点，∠ECF ＝∠A ＝60°． (1)求证：EF ＝BE ＋DF ；(2)求证；点C 在∠BAD 的平分线上．FEDCBA针对练习21．(1)如图1，将例2中点E 移至BA 延长线上，点下移至AD 延长线上，其余条件不变，写出EF 和BE ，DF 之间的数量关系并证明；(2)如图2，将例2中点E 移至AB 延长线上，点F 移至DA 延长线上，其余条件不变，写出EF 和BE ，DF 之间的数量关系并证明．FED CBAFEDCBA【板块三】2a 度角夹a 度角从特珠到一般，揭示夹半角横型本质：条件：如图1，四边形ABCD 中，点E 为AB 上一点，点F 为AD 上一点，具备以下三个条件：①CB ＝CD ；②∠BCD ＝2∠EC ；③∠B ＋∠D ＝180°(或∠A ＋∠BCD ＝180°)．结论：①EF ＝BE ＋DF ：②CE 平分∠BEF ，CF 平分∠DFE ．当点E ，F 分别移到AB ，AD 延长线或反向延长线上时，EF ＝BE -DF 或EF ＝DF -BE ．21FEDC BAGABC DEF123FEDCBAG证法： 方法技巧第一步；延长AD 至G (若是E ，F 在延长线上一般在长线段上截取)，使DG ＝BE ，连接CG ．第二步：证明△BCE ≌△DCG (SAS )，全等条件：∠B ＋∠ADC ＝180°得∠CDG ＝∠B ，CB ＝CD ，DG ＝BE ；得到：CG ＝CE ，∠3＝∠1；第三步：证明△ECF ≌△GCF (SAS )．由∠3＝∠1得∠ECG ＝∠BCD ＝2∠ECF ，得∠ECF ＝∠GCF ，又CE ＝CG ，CF 公共，∴△ECF ≌△GCF (SAS )，得EF ＝FG ＝DG ＋DF ＝BE ＋DF ．由△ECF ≌△GCF 得∠CFE ＝∠CFD ，得CF 平分∠DFE ；∠BEC ＝∠G ＝∠CEF 得CE 平分∠BEF ． 本质：(1)等腰三角形腰的旋转； (2)通过旋转对剩余半角进行拼凑； (3)产生一组旋转全等和一组对称全等； (4)旋转全等的旋转角度为2 ；(5)对角互补使夹半角模型产生一组“截长补短”的相应结论针对练习31．已知如图，五边形ABCDE 中，AB ＝AE ，BC ＋DE ＝CD ，∠ABC ＋∠AED ＝180°．求证： (1)AD 平分∠CDE ； (2)∠BAE ＝2∠CAD ．DE CBA2．如图，平面直角坐标系中，A (15，0)，B (0，15)，取点D (0，10)并连接AD ，将△AOD 沿直线AD 折叠得到△ADE ，过点B 作y 轴的垂线BF 交DE 的延长线于F 点，连接AF ，DF ＝13．求BF 的长．3．如图，B (4，4)，BC ⊥y 轴于C ，BA ⊥x 轴于A ，E 为BC 上一动点(不与B ，C 重合)，F 为AB 上一动点，且满足∠OEF ＝∠AOE ，在运动过程中，△BEF 的周长变吗？若不变求其值；若变化求其变化范围．4．如图，平面直角坐标系中，点A (1，4)，B (3，0)，N (1，0)，R (4，3)，点P 为线段AN 上的一动点，连接PR ，以PR 为一边作∠PRM ＝45°，交轴于点M ，连PM ，请问点P 在运动的过程中，线段PM ，PA ，BM 之间有怎样的数量关系？证明你的结论．6．如图，正方形ABOC ，点M ，N 分别在 AB ，AC 上．（1）若∠NMO =∠MOC ，问△AMN 的周长是否变化，若不变，求出其值；（2）若点M 在AB 延长线上，点N 在CA 的延长线上，其它条件不变，问：CN ，MN ，BM 三者存在怎样的关系？试证明．5．在等边△ABC 的两边AB ，AC 所在直线上分别有两点M ，N ，点D 为△ABC 外一点，且∠MDN =60°，∠BDC =120°，BD =DC ．探究：当M ，N 分别在直线AB ，AC 上移动时，BM ，NC ，MN 之间的数量关系及△AMN 的周长Q 与等边△ABC 的周长L 的关系．（1）如图1，当M ，N 分别在边AB ，AC 上，且DM =DN 时，BM ，NC ，MN 之间的数量关系是 ；此时_______QL； （2）如图2，当点M ，N 分别在边AB ，AC 上，且DM DN 时，猜想（1）问的两个结论还成立吗？写出你的猜想并加以证明；（3）如图3，当点M ，N 分别在边AB ，CA 的延长线上时，若AN x ，则Q = （用x ，L 表示）NCD M BA图3图2图1ABM D CN N CD M BA。

第十二讲 圆的方程1、圆的定义：平面内到定点的距离等于定长的点的轨迹叫圆，定点为圆心，定长为圆的半径。

2、圆的方程（1点00(,)M x y 与圆222()()x a y b r -+-=的位置关系：①当2200()()x a y b -+-____2r ，点在圆外；②当2200()()x a y b -+-_____2r ，点在圆上 ；③当2200()()x a y b -+-_____2r ，点在圆内； （2①当时，方程表示圆，此时圆心为___________，半径为②当时，表示一个点；③ 当时，方程不表示任何图形。

3、圆系方程1、以(,)a b 为圆心的同心圆系方程：222()()(0)x a y b λλ-+-=>与圆22y x +＋Dx ＋Ey ＋Ｆ＝０同心的圆系方程为：22y x +＋Dx ＋Ey ＋λ＝０ 04>-+F E D F E D r 42122-+=0422=-+F E D 0422<-+F E D2、过直线Ax ＋By ＋Ｃ＝０与圆22y x +＋Dx ＋Ey ＋Ｆ＝０交点的圆系方程为：22y x +＋Dx ＋Ey ＋Ｆ＋λ（Ax ＋By ＋Ｃ）＝０（λ∈Ｒ）3、过两圆1C :22y x +＋111F y E x D ++＝0，2C :22y x +＋222F y E x D ++＝０交点的圆系方程为：22y x +＋111F y E x D ++＋λ（22y x +＋222F y E x D ++）＝0（λ≠-１，此圆系不含2C :22y x +＋222F y E x D ++＝０）特别地，当λ＝－１时，上述方程为根轴方程．两圆相交时，表示公共弦方程；两圆相切时，表示公切线方程．注：为了避免利用上述圆系方程时讨论圆2C ，可等价转化为过圆1C 和两圆公共弦所在直线交点的圆系方程:22111121212[()()()]0x y D x E y F D D x E E y F F λ+++++-+-+-=例1、圆心为()1,1且过原点的圆的方程是（ ）A ．()()22111x y -+-=B ．()()22111x y +++=C ．()()22112x y +++=D ．()()22112x y -+-=解析：由圆心可以设出圆的标准方程，设出半径r ，又知圆过原点带入求出半径继而求出圆的方程。

正十二边形周长公式在我们的数学世界里，正十二边形可是个有趣的家伙！咱们今天就来好好聊聊正十二边形周长的公式。

先来说说正十二边形是啥。

想象一下，有一个图形，它有十二条边，而且这十二条边长度都一模一样，像十二个兄弟姐妹整整齐齐地站成一圈，这就是正十二边形啦。

那正十二边形的周长公式是啥呢？其实很简单，就是“周长 = 边长×12”。

这就好比你有 12 个一模一样的小积木，每个积木的长度就是边长，把它们一个接一个排起来的总长度就是正十二边形的周长。

记得有一次，我带着一群小朋友在操场上做数学游戏。

我在地上用粉笔画了一个大大的正十二边形，然后问小朋友们怎么才能算出这个图形的周长。

小朋友们都瞪着大眼睛，一脸的迷茫。

我就引导他们说：“咱们先看看这十二条边是不是一样长呀？”小朋友们纷纷点头。

我接着说：“那好呀，如果我们知道其中一条边的长度，是不是就能算出整个图形的周长啦？”有个聪明的小朋友马上就说：“老师，是不是用一条边的长度乘以 12 就行啦？”我高兴地给他竖起了大拇指。

从那以后，每次讲到正十二边形周长公式，我都会想起那些可爱的小朋友们，他们充满好奇和探索的眼神，让我觉得教数学真是一件特别有意思的事儿。

在实际生活中，正十二边形的周长公式也有不少用处呢。

比如说，你要做一个正十二边形的相框，知道了每条边的长度，就能很快算出需要多长的边框材料。

又或者，在建筑设计中，设计师们可能会用到正十二边形的元素，这时候周长公式就能帮他们准确计算所需的材料和尺寸。

咱们再回到公式上来，“周长 = 边长×12”这个公式看起来简单，但是要真正理解和运用好可不容易。

比如说，给你一个正十二边形，告诉你它的周长是 120 厘米，让你求边长，这时候就得反过来用公式，边长 = 周长÷12，也就是 120÷12 = 10 厘米。

总之，正十二边形周长公式虽然简单，但却非常实用。

只要我们认真去学，用心去体会，就能在数学的海洋里畅游，发现更多有趣的奥秘！希望大家以后看到正十二边形，就能马上想到它的周长公式，轻松解决各种相关的数学问题。

五年级春季知识点总结吴超超第十二讲立体图形与空间想象对于小学几何而言，立体图形多考察的表面积和体积计算。

而公式计算既可以具体考查学生在公式应用中处理相关数据的能力，又可以很好地培养学生的空间想象能力，空间想象能力，所以，所以，所以，继寒假学完正方体和长方体的基本计算公式后，今天我们继寒假学完正方体和长方体的基本计算公式后，今天我们将一起学习立体图形的空间想象。

一．正方体展开图1.正方体展开图共有：11种：①“①“141141141”型：——”型：——”型：——66种②“②“333333”型：——”型：——”型：——11种③“③“231231231”型：——”型：——”型：——33种④“④“222222222”型：——”型：——”型：——11种注意：正方体展开图中一定没有以下形状：“田”字格，“凹”字形，大“L ”型。

2.初步判断正方体展开图的基本方法：找对面①同一排：隔一个面的两个面为对面①同一排：隔一个面的两个面为对面①同一排：隔一个面的两个面为对面②没有三个面一排的时候：隔一排的两个面是对面②没有三个面一排的时候：隔一排的两个面是对面②没有三个面一排的时候：隔一排的两个面是对面3.每个展开图都有 6 个面；周长为 14 条棱长；要把一个正方体展开，需要剪 7 刀。

4.找对应的立体图形或展开图的方法：①基本方法：①基本方法：①基本方法：标顶点字母标顶点字母②其他常用方法：利用表面图形的位置关系，例如立体图形与展开图中，表②其他常用方法：利用表面图形的位置关系，例如立体图形与展开图中，表面标记的顺时针（或逆时针）关系一致。

面标记的顺时针（或逆时针）关系一致。

二．由三视图推出立体图形1.基本方法：——标数法在俯视图上，根据正视图和侧视图的信息标数在俯视图上，根据正视图和侧视图的信息标数 2.最值问题：求“最少”时，要注意“中空”的情况三．最短路径问题从长方体的一个顶点到对角顶点的最短路径：⑴任意走：体对角线为最短路径⑴任意走：体对角线为最短路径⑴任意走：体对角线为最短路径⑵只能走表面：一定要过两个相邻的面，最多有以下三种情况作比较：⑵只能走表面：一定要过两个相邻的面，最多有以下三种情况作比较：①l 2=长2+(宽+高)20 ②l 2=宽2+(长+高)2③l 2=高2+(长+宽)2其中，最小的l 2对应的l 即为最短路径。

【易错题精析】第12讲圆的面积和扇形小学数学六年级上册易错专项练（人教版，含答案）第12讲圆的面积和扇形（讲义）小学数学六年级上册易错专项练（知识梳理+易错汇总+易错精讲+易错专练）1.圆的面积。

圆所占平面的大小叫圆的面积，一般用字母S表示。

圆的面积的大小与半径的长短有关。

2.圆的面积计算公式。

如果用S表示圆的面积，那么S = π r2或S = π( d÷2）2。

3.圆环。

两个半径不等的同心圆之间的部分叫作圆环，也叫作环形。

4.圆环的面积计算公式。

外圆的半径是R，内圆的半径是r，圆环的面积＝外圆面积－内圆面积，用字母表示为S=π R2-π r2或S=π （R2- r2）。

5.“外方内圆”和“外圆内方”的问题。

（1）在正方形内画一个最大的圆，这个圆的直径等于正方形的边长。

如果圆的半径是r，那么正方形和圆之间部分的面积为0.86r2。

（2）在圆内画一个最大的正方形，这个正方形的对角线等于圆的直径。

如果圆的半径是r，那么正方形和圆之间部分的面积为1.14r2。

6.扇形。

弧：圆上任意两点（如下图A、B）之间的部分叫作弧，读作弧AB。

圆心角：由两条半径组成，顶点在圆心的角叫圆心角。

如下图∠AOB。

扇形：一条弧和经过这条弧两端的两条半径所围成的图形叫作扇形。

如下图中涂色部分就是扇形。

在同一个圆中，扇形的大小与这个扇形的圆心角的大小有关。

1.在计算圆的面积时，r2是r×r，不是r×2。

2.圆环必须是两个同心圆形成。

3.求圆环的面积时，要先算出的是“平方差”，不是“差的平方”。

4.在正方形内画一个最大的圆，这个圆的直径等于正方形的边长，在长方形内画一个最大的圆，这个圆的直径等于长方形的宽。

5.在圆内画一个最大的正方形，这个正方形的对角线等于圆的直径。

6.圆心角必须具备两个条件：一是顶点在圆心上；二是角的两边是圆的半径。

7.在同一个圆中，扇形越大，这个扇形所对的圆心角就越大。

【易错一】长方形、正方形和圆的周长相等时，面积最大的是（）。

一．等底等高三角形三角形的面积等于底乘以高除以2，于是我们就可以得到：等底等高的两个三角形面积相等．也就是说两个三角形的形状可以不同，但只要底与高分别相等，它们的面积就相等．但注意这个问题不能反过来说成是“面积相等的两个三角形底与高一定分别相等”． 二．常见两类情况1．两个三角形有一个公共顶点，而这个公共顶点所对的边在一条直线上且相等．如图，三角形ABC 与ACD ，它们有公共顶点A ，边BC ，CD 在同一直线上且BC CD =，那么就有三角形ABC 与三角形ACD 的面积相等．2．两个三角形有一条公共的底边，而这条底边上的高相等，即这条底边所对的顶点在一条与底边平行的直线上．如图中的三角形1A BC 与2A BC 、3A BC 的面积都相等．三．梯形翅膀相等如图，梯形ABCD 为任意梯形，则有ABO CDO S S ∆∆=． 重难点：会找与所求三角形面积相等的三角形． 熟练应用梯形翅膀相等来解题． 题模一：快乐三角仔例1.1.1图中的两个三角形都是等边三角形，面积分别是20平方厘米和30平方厘米．B 点和C点都是三角形边上的中点．求阴影部分的面积．几何第12讲_等底等高模型B AC DBC例1.1.2如图，两个正方形放在一起，大正方形半场为10厘米，求阴影部分的面积．例1.1.3已知右图中两个正六边形的面积分别是20和4，则阴影部分的面积是__________．例1.1.4如右图，ABC 是直角三角形，DE 与AC 平行，已知18BD =，10CF =，那么BEF 的面积是_______．例1.1.5正方形ABCD 、ECGF 、HGJI 并排放在一起，其中E 是CD 的中点，H 是GF 的中点，E 在线段AH 上．如果正方形HGJI 的对角线HJ 长8厘米，那么三角形AHJ 的面积是_______平方厘米．C ABDE F例1.1.6如图，有两个小正方形和一个大正方形，大正方形的边长是小正方形边长的2倍，阴影部分三角形面积为240，请问三个正方形的面积和是_________．例1.1.7如图，正六边形边长2.4，以六边形的一组对边为边长向外作正方形，那么阴影三角形的面积是___________．例1.1.8如图，四边形EFCD 是平行四边形．如果梯形ABCD 的面积是320，四边形ABGH 的面积是80，那么三角形OCD 的面积是__________．题模二：梯形蝴蝶翅膀相等例1.2.1如图，长方形被一些直线分成了若干个小块，已知三角形ADG 的面积是13平方厘米，三角形BCH 的面积是25平方厘米，四边形EGFH 的面积是多少平方厘米？CGD E F BAGH CDFEABO例1.2.2如图，在长方形中有几部分的面积已经标出，那么四边形ABCD 的面积=_______．例 1.2.3如图，四边形ABCD 与四边形CNMP 都是平行四边形．若三角形DFP 与三角形AEF 的面积分别是21和43，则三角形BNE 的面积为多少？例1.2.4在梯形ABCD 中，OE ∥AD ，如果△AOB 的面积是7平方厘米．则△DCE 的面积是_________平方厘米．例1.2.5如图所示，梯形ABCD 的面积为117平方厘米，AD ∥BC ，EF =13厘米，MN =4厘米，又已知MN ⊥EF 与O 点，那么阴影部分的总面积为________平方厘米．随练1.1如图，已知正方形ABCD 边长是8厘米，正方形DEFG 边长是5厘米．则三角形ACFABCDF EGHDCBA 463110A ODCBEONMED CBA的面积是____________平方厘米．随练1.2如图，甲、乙两图形都是正方形，它们的边长分别是5厘米和6厘米．则阴影部分的面积是________平方厘米．随练 1.3如图，梯形ABCD 的AD 平行于BC ，对角线AC 、BD 交于点E ，已知三角形ADE 的面积是64平方厘米，三角形BEC 的面积是25平方厘米，三角形ABC 的面积是65平方厘米，那么梯形ABCD 的面积是多少平方厘米？随练1.4如图，在长方形ABCD 中，三角形ADP 的面积为20平方厘米，三角形CBQ 的面积为35平方厘米．那么阴影四边形的面积是________平方厘米．作业1三个正方形ABCD ，BEFG ，HKPF 如图所示放置在一起，图中正方形BEFG 的周长等于24厘米．求图中阴影部分的面积．DABCE作业2如图，大小三个正方形，其中AB =8，BE =6；求阴影部分面积．作业3面积为8的长方形AEFG 和面积为20的长方形ABCD 如图放置（A 、E 、D 三点在一条直线上），BF 交AD 于P ，连接PC 、EC ，求图中阴影部分面积．作业4如图，两个正方形放在一起，4AB ，求阴影部分的面积．作业5正方形ABCD 的面积为9平方厘米，正方形EFGH 的面积为64平方厘米．如图所示，边BC 落在EH 上．已知三角形ACG 的面积为 6.75平方厘米，则三角形ABE 的面积为___________平方厘米．KHPFGD C EB A FG PEDC BAD BAHF作业6如图，在钝角三角形ABC 中，M 为AB 边的中点，MD 、EC 都垂直于BC 边．若BDE ∆的面积是3平方厘米，则三角形ABC 的面积是多少？作业7梯形ABCD 中，8AB cm =，6BC cm =，4AF cm =，求AEF S △．作业8图中的长方形被分成若干小块，其中四块的面积已经标出，那么阴影部分的面积是多少？作业9如图在梯形ABCD 中，对角线AC 、BD 相交于O 点，OE 平行于AB 交腰BC 于E 点，如果三角形OBC 的面积是115平方厘米，则三角形ADE 的面积为__________平方厘米．HGF E DCB AA BCDEM作业10如图，梯形ABCD 的对角线相互垂直．三角形AOB 的面积是12，OD 的长是4，则OC 的长为______．A ．5B ．6C ．7D ．8O D ECBA ABCDO。

第12讲环形行程问题【知识要点】<要点1> 同地背向情景设置：两人从同一个地点相背出发①环形1次相遇，相遇时间=路程和÷速度和，路程和=整个环形长度，这里使用1份时间；②环形2次相遇，这里使用2份时间；③环形3次相遇，这里使用3份时间；……环形跑道问题同一地点出发，如果是相背出发，则每合走一圈相遇一次<要点2> 同地相向情景设置：两人从同一个地点同向出发①环形1次相遇，相遇时间=路程差÷速度差，路程差=整个环形长度，这里使用1份时间；②环形2次相遇，这里使用2份时间；③环形3次相遇，这里使用3份时间；……环形跑道问题同一地点出发，如果是同向出发，则每追上一圈相遇一次【精讲精练】<例题1>一个圆形操场跑道的周长是500米，两个学生同时同地背向而行．黄莺每分钟走66米，麻雀每分钟走59米．经过几分钟第一次相遇？再过多少分钟第二次相遇？<练习1>甲、乙两人骑自行车从环形公路上同一地点同时出发，背向而行。

这条公路长2400米，甲骑一圈需要10分钟。

如果第一次相遇时甲骑了1440米。

请问：乙骑一圈需要多少分钟？再过多久他们第二次相遇？<例题2>甲、乙两人在300米长的环形跑道上跑步，他俩同时同地同向出发，甲的速度是每秒5米，乙的速度是每秒3米，那么过多少时间后甲第一次追上乙？再过多少时间甲第三次追上乙？<练习2>一条环形跑道长400米，甲骑自行车每分钟骑450米，乙跑步每分钟250米，两人同时从同地同向出发，经过多少分钟两人相遇？再过多少分钟第4次相遇？上海小学有一长300米长的环形跑道，小亚和小胖同时从起跑线起跑，小亚每秒钟跑6米，小胖每秒钟跑4米，(1)小亚第一次追上小胖时两人各跑了多少米？(2)小亚第二次追上小胖两人各跑了多少圈？<练习3>幸福村小学有一条200米长的环形跑道，冬冬和晶晶同时从起跑线起跑，冬冬每秒钟跑6米，晶晶每秒钟跑4米，问冬冬第一次追上晶晶时两人各跑了多少米，第2次追上晶晶时两人各跑了多少圈？<例题4>在300米的环形跑道上，田奇和王强同学同时同地起跑，如果同向而跑2分30秒相遇，如果背向而跑则半分钟相遇，求两人的速度各是多少？<练习4>在环形跑道上，两人在一处背靠背站好，然后开始跑，每隔4分钟相遇一次；如果两人从同处同向同时跑，每隔20分钟相遇一次，已知环形跑道的长度是1600米，那么两人的速度分别是多少？甲和乙两人分别从圆形场地的直径两端点同时开始以匀速按相反的方向绕此圆形路线运动，当乙走了100米以后，他们第一次相遇，在甲走完一周前60米处又第二次相遇。

一：周长与面积公式知识精讲在同一平面内，到定点的距离等于定长的点的集合叫做圆．点O就称为该圆的圆心；圆心与圆周上任意一点的连线（例如线段OA）叫做半径；通过圆心，并且两端都在圆上的线段叫做直径．直径长恰好是半径长的两倍．圆心确定了圆所在的位置，半径长度确定了圆的大小．一个圆只要确定了“圆心”和“半径”，就能完全确定下来．圆周长与直径的比值是一个固定不变的数，我们称之为圆周率，用希腊字母表示．圆周率是一个无限不循环小数，无法写成分数的形式．在实际问题的计算中，常常取近似值．一．圆的周长与面积公式1．直径长度通常用字母d表示，半径长度通常用r表示，圆周长通常用C 表示，圆面积通常用字母S表示．2．圆周长公式：蜜蜂飞行：无论小圆有多少个，大小是否相等，只要所有小圆的直径之和等于大圆的直径，那么它们的周长之和也等于大圆的周长．3．圆面积公式：二．扇形的周长与面积公式扇形是指圆上被两条半径和半径之间的弧所包围的部分．其中，圆的半径也称为扇形的半径，而两条半径所成的夹角称为扇形的圆心角．扇形是圆的一部分．要想知道扇形的弧长与面积，只要知道它是所在圆的几分之几就可以了．它是圆的几分之几，它的弧长就是圆周长的几分之几，它的面积也同样就是圆面积的几分之几．1．扇形弧长公式：2．扇形面积公式：3．温馨提示：扇形的弧长不是它的周长，扇形的周长还必须加上两条半径．三点剖析重难点：扇形周长公式，需要加上两条半径题模精讲题模一圆的周长与面积公式例、已知一个圆的直径为2厘米，那么这个圆的周长为_________厘米，面积为_________平方厘米．答案：；解析：周长为厘米，面积为平方厘米．例、已知一个圆的周长为厘米，那么这个圆的直径为_________厘米．答案：16解析：直径为厘米．例、有一个圆形花坛，直径为20米，一只小蜜蜂沿着花坛外周飞了一圈，请问它飞了多少米如果小蜜蜂沿着图中的虚线，飞一个“8”字，路线构成过花坛圆心的两个小圆，那么这次它飞了多少米（取）答案：（1）米（2）米解析：小圆半径是5米，飞行路线为两个小圆周长，所以是米．无论小圆有多少个，大小是否相等，只要所有小圆的直径之和等于大圆，那么它们的周长之和也等于大圆．例、如图，已知长方形的面积是12，则图中阴影部分的面积是多少（取）答案：解析：长方形可以分成两个面积相等的正方形，面积都是6．方中圆，方和圆的面积比为，可求出小圆的面积是，那么阴影部分的面积是．例、如图，在一块面积为平方厘米的圆形铝板中，裁出了7个同样大小的圆铝板．问：余下的边角料的总面积是多少平方厘米（取）答案：平方厘米解析：，大圆半径是3厘米．小圆半径是1厘米，所以边角料面积为平方厘米．例、已知大圆的直径为10厘米，有四个大小不等的圆，圆心都在大圆的一条直径上，并且它们的直径之和与大圆相等．那么4个小圆的周长之和是________厘米．（取）答案：解析：假设中间4个小圆的直径分别为a、b、c、d，则有，4个小圆的周长之和为厘米．例、如图，直角三角形的面积是40平方厘米，圆的面积是________平方厘米（π取3）．答案：240解析：直角三角形的直角边即为圆的半径，所以，，圆的面积是平方厘米．题模二扇形的周长与面积公式例、如图3，圆P的直径OA是圆O的半径，，，则阴影部分的面积是__________．（π取3）答案：75解析：阴影部分的面积等于大圆面积的一半减去小圆的面积，即．例、一个扇形的半径为6平方厘米，圆心角为60°，这个扇形的周长是__________厘米．（取）答案：解析：这个扇形是它所在圆的，所以这个扇形的弧长是cm，扇形的周长是厘米．例、一个扇形的面积为平方厘米，圆心角为45°，这个扇形的周长是_______厘米．（取）解析：这个扇形是它所在圆的，所以这个圆的半径的平方是，所以这个圆的半径是4厘米，所以扇形的半径是4厘米，扇形的周长是厘米．例、在荷兰的小镇卡茨赫弗尔，2013年6月建成了一个由三个半圆组成的城市雕塑，三个半圆的直径分别为，，．这个雕塑的原始图形来自于阿基米德《引理集》中的鞋匠刀形（Arbelos），即下图中阴影部分所示的图形．那么，该城市雕塑中的鞋匠刀形的周长为__________（圆周率用π表示）答案：πm解析：鞋匠刀形的周长是由3条半圆形弧线组成，所以周长为m．例、如图，等边三角形ABC的边长是1，依次以A、C、B为圆心，以BA、CD、BE为半径画扇形，那么三个扇形的面积和是多少（结果保留π）答案：解析：各扇形圆心角均为，半径分别为1、2、3，因此三个扇形的面积和是．例、一个半径为3分米的扇形，面积为平方分米，那么它的圆心角是__________，它的弧长又是__________分米．答案：80°，根据题意得，，所以，所以圆心角是度．弧长为．例、如图，边长为3cm与5cm的两个正方形并排放在一起，在大正方形中画一个以它的顶点B为圆心，边长为半径的圆弧，则阴影部分的面积是________（结果保留π）．答案：解析：连结AC、FB．易知，故，．例、如图，有三个同心半圆，它们的直径分别为2，6，10，用线段分割成9块，如果每块字母代表这一块的面积并且相同的字母代表相同的面积，那么(A＋B)：C ＝_______答案：55：48解析：设A的半径为，B的半径为，C的半径为A的面积：B的面积：3B=，．C的面积：5C=，．．题模三捆圆的周长和面积已知下图中的每个小圆的半径均为1，这个图形的面积是__________．（取）答案：解析：如图，对图形进行分割后可知这个图形的面积相当于8个边长为2的正方形和一个半径为1的圆的面积的和．面积为．例、如图，有8个半径为1的小圆，用它们圆周的一部分连成一个花瓣图形，图中的黑点是这些圆的圆心．那么花瓣图形的周长和面积分别是多少答案：周长，面积解析：如图，做辅助线后可以看出周长为4个的圆弧加上4个半圆弧，所以周长为；而面积为正方形减去4个半圆加上4个圆，即．例、如图，每个圆的面积都为，求该图形的外周长．答案：解析：圆半径为2．图形外周长可以分为三段长为4的线段和三段120°角的圆弧，则外周长为．如图，有七根直径为5厘米的塑料管，用一根橡皮筋把它们扎成一捆，此时橡皮筋的长度是多少厘米答案：解析：如图，作辅助线后可以发现外周长是由6段长度为5的线段和6个60°角的圆弧组成，所以皮筋长度为．随堂练习随练、已知一个圆的直径是12厘米，那么这个圆的面积为__________平方厘米（取）答案：解析：直径为12厘米，那么半径为6厘米，面积是平方厘米．随练、已知一个圆的面积为314平方厘米，那么这个圆的直径为_______厘米（取）答案：20解析：这个圆的半径为平方是，所以这个圆的半径是10厘米，直径是20厘米．随练、半径分别为1、2、3、4厘米的四个圆的周长之和是多少厘米（取）答案：厘米解析：圆的周长公式为，周长之和为厘米．随练、如图，在一块面积为平方厘米的纸板中，裁出了2个同样大小的圆纸板．问：余下的纸板的总面积是多少平方厘米（取）答案：平方厘米解析：大圆的面积是平方厘米，可求出大圆的半径是2厘米，那么小圆的半径是1厘米，面积是平方厘米．阴影部分的面积是平方厘米．随练、已知三个小圆的圆心在大圆同一直径上，周长分别为3、1、2厘米，则大圆周长为多少厘米（π取近似值）答案：6解析：大圆的直径等于三个小圆的直径之和，周长也恰为3个小圆周长之和．随练、如图，边长为3cm与5cm的两个正方形并排放在一起，在大正方形中画一个以它的顶点B为圆心，边长为半径的圆弧，则阴影部分的面积是__________（结果保留π）．答案：解析：阴影部分面积为梯形ABFE与扇形ABC的面积之和减去三角形FEC的面积，易得为．随练、已知一个扇形的半径是10厘米，圆心角是，那么：（1）这个扇形所在圆的周长是_________厘米，扇形的圆心角占圆周角的_________，它的弧长占圆周长的_________，这个扇形的弧长是_________厘米，周长是_________厘米．（2）这个扇形面积占它所在圆的面积的_________，是_________平方厘米．答案：（1）；；；；（2）；解析：（1）这个扇形所在圆的周长是厘米，扇形的圆心角占圆周角的，它的弧长占圆周长的，这个扇形的弧长是厘米，周长是．（2）这个扇形面积占它所在圆的面积的，面积是平方厘米．随练、半径为10、20、30的三个扇形如下图放置，是的__________倍．答案：5解析：为，为，所以是的5倍．随练、根据图中所给的数值，求这个图形的面积．（π取近似值）答案：解析：平方厘米．4个直角扇形的面积之和是4，因此整个圆角矩形的面积就是．随练、如图，有七根直径为4厘米的塑料管，用一根橡皮筋把它们扎成一捆，此时橡皮筋的长度是多少厘米（π取近似值）答案：解析：把圆角六边形的周长分为12个部分，由6条直线段和6段圆弧组成．6条直线段中，每段的长度都是5厘米，它们的长度和是厘米6段圆弧中，每段所对应的圆心角都是60°，每段的弧长都是圆周长的，6段圆弧恰好能拼成一个完整的圆周．它们的弧长之和就是圆周长，即厘米．圆角六边形的周长就是这两部分长度之和，即厘米．课后作业作业1、已知圆的直径为20米，那这个圆的周长为多少米（π取近似值）答案：解析：圆周长的计算公式为：C圆=π×D．作业2、把两根横截面半径都是10厘米的钢管用铁丝紧紧捆在一起，如果捆绑处不计，至少要用铁丝____________厘米．答案：解析：厘米．作业3、一辆压路机的前轮是圆柱形，轮宽米，直径是米．前轮转动一周，压路的面积是______平方米．答案：平方米解析：轮子压一周，周长为米，即压在路面上的长是米，压路的面积=长×宽平方米．作业4、已知圆的面积是314平方米，那圆的周长是多少米（π取近似值）答案：解析：由圆的面积可以求出半径的平方，算出半径后可由公式计算圆的周长，为．作业5、已知三个小圆的圆心在大圆同一直径上，周长分别为1、2、3厘米，则大圆周长为多少厘米（π取近似值）答案：6解析：大圆的直径等于三个小圆的直径之和，周长也恰为3个小圆周长之和．作业6、如图，在一块面积为36平方厘米的圆形铝板中，裁出了7个同样大小的圆铝板．问：余下的边角料的总面积是多少平方厘米答案：8平方厘米解析：小圆的半径是整个大圆半径的，因此小圆的面积是大圆面积的，为平方厘米；大圆去掉7个小圆后剩下的面积是平方厘米．作业7、已知一个扇形的圆心角为120°，半径为2，这个扇形的面积是________，周长是________（π取）．答案：面积，周长解析：扇形的面积；周长．作业8、如图，求各图中阴影部分的面积．（取）答案：解析：阴影部分面积为半径为4的半圆面积减去对角线为8的等腰直角三角形面积．阴影部分面积为．作业9、已知扇形的半径为3米，面积为米，那扇形的圆心角为多少度（π取近似值）答案：180解析：扇形所在圆的面积≈×32=平方米，由此可知该扇形是它所在圆的．那么圆心角应该是360°的二分之一．作业10、已知一个扇形的半径为5厘米，弧长为厘米，这个扇形的面积是多少答案：解析：因为扇形的弧长为厘米，所以，可得．扇形面积为平方厘米．作业11、根据图中所给的数值，求这个图形的面积．（π取近似值）答案：解析：平方厘米．4个直角扇形的面积之和是，因此整个圆角矩形的面积就是．作业12、如图，三个圆的半径都是4，那整个图形的外周长是多少（π取近似值）答案：解析：整个外周长可以分为3段直线和3段弧形．作业13、如图，有七根直径为10厘米的塑料管，用一根橡皮筋把它们扎成一捆，此时橡皮筋的长度是多少厘米（π取近似值）答案：解析：把圆角六边形的周长分为12个部分，由6条直线段和6段圆弧组成．6条直线段中，每段的长度都是5厘米，它们的长度和是厘米6段圆弧中，每段所对应的圆心角都是60°，每段的弧长都是圆周长的，6段圆弧恰好能拼成一个完整的圆周．它们的弧长之和就是圆周长，即厘米．圆角六边形的周长就是这两部分长度之和，即厘米．。

长方形的周长教案10篇长方形的周长教案篇1教材分析：本课时的教学是在学生已认识了长、正方形，并了解和掌握了长、正方形的特点，学会了测量长度，了解一些测量单位，对周长有了初步认识的基础上进行的。

本课时的教学又为学生今后学习计算其它图形的周长和面积奠定了基础。

教材的设计是从联系学生的实际出发，重视创设情境，让学生通过自己动手，探索新知。

通过小组讨论、交流的合作学习的方式，让他们从不同的角度，提出方法，从中总结归纳出长方形周长的计算方法，进而让学生独立思考，进行推理，归纳出正方形周长的计算方法。

一、教学目标：1、在学生认识平面图形的周长的基础上，引导、组织学生通过探索活动总结出长正方形周长的计算公式，并能准确地进行计算。

2、通过解决生活中的简单问题，增强学生应用数学的意识。

3、培养学生的探索意识和推理能力，学会合作学习。

二、教学重、难点：长方形周长计算公式的推导过程。

三、教学具准备：投影仪、每小组木棒4支（长、宽各一对）四、教学过程：（一）动手操作揭示课题。

1、教师出示长方形、正方形、三角形、梯形等平面图形，让学生指出各个图形的周长。

意图：联系学生已有的“周长”概念为探索“周长的计算”的活动予做准备。

2、让学生分小组摆出一个长方形。

3、教师提出探索活动的目的、要求，并板书课题。

师：你能求出所摆出的长方形的周长吗？这是我们师生今天要研究的课题。

（师：板书：长方形的周长）（二）分级探究，发现规律。

1、教师提出要求：先量出长方形的长与宽，再通过不同的方法算出它的周长，请小组的记录员做好记录。

意图：提出明确的要求，使学生明确思维方向。

2、学生分组进行探索活动。

学生可能会出现以下三种意见：（1）长+宽+长+宽（2）长某2+宽某2（3）（长+宽）某2意图：通过全体学生参与学习过程，培养他们的探究意识，学会合作学习，让学生从不同的方法得出探索结果培养他们的发散思维能力。

（三）汇报交流，总结规律。

1、让学生代表到讲台前，通过投影仪，说自己小组探索结果（教师边板书上来）2、师生共同总结规律。