当前位置：文档之家 › 伸缩变换 ppt课件

伸缩变换 ppt课件

  • 格式：ppt
  • 大小：392.00 KB
  • 文档页数：19

下载文档原格式

  / 19

合集下载

1.5正弦型函数图象的平移和伸缩变换

1.5正弦型函数图象的平移和伸缩变换

向右平移 个单位
y sin x
3
y
sin(x
3
)
纵坐标不变 横坐ห้องสมุดไป่ตู้变为原来的1
倍
y sin(2x )
3
2
横坐标不变 总坐标变为原来的3倍
y 3sin(2x ) 向上平移1个单位
3
y 3sin(2x ) 1
3
法二：先伸缩（ 变换）后平移（ 变换）：
纵坐标不变
y sin x 横坐标变为原来的1 倍 y sin 2x 2
函数y Asin(x ) b的图象
A是振幅：A变换也叫振幅变换；
T为周期：T 2 ，变换也叫周期变换；
f是频率：f 1 ; T
x 是相位：变换也叫相位变换； 是初相：x 0时的相位.
要得到y 3sin(2x ) 1的图象,需将y sin x的图象作怎样的变换？
3
法一：先平移（ 变换）后伸缩（ 变换）：
向右平移 个单位 6
y sin(2x )
3
横坐标不变 总坐标变为原来的3倍
y 3sin(2x ) 向上平移1个单位
3
y 3sin(2x ) 1
3
总结：1.箭头图：起始→终止；
2. 四个数据，四个变换：先：， 后：A，b

函数的图像----图像的伸缩变换

函数的图像----图像的伸缩变换
y
o
x
2.作函数y sin 2x, y sin 1 x
简图.
2
解时:的函图数象y=.sin2x的周期T
列x 表:
0
4
2x
0
2
sin2x 0 1
的
,因x此先[0,作 ]
2
3 4
3 2
2
0 -1 0
解:函数 y sin 1 x 时的图象. 2
T 的4周 期
x [0, 4,]因此先作
列x
可得到（ ）
的图像上所有点向左 6
平移个单位，
A.y sin(2x ) 6
C.y sin(2x ) 3
B.y sin(2x ) 6
D.y sin(2x ) 3
2.要得到函数
y
2
cos(2x
3
)
，只需将函y数 2sin 2x
的
图像（ ）
A.向左平移 个单位 12
C.向右平移 个单位
的纵坐标伸长(A>1)或缩短(A<1)为原来的A倍，横坐标不变
得到。值域为[-A，A]
y=sinx
相位 y=Asin(x+) 周期
变换
变换
y=Asinx
周期 变换
y=Asinωx
y=Asin(ωx+)
相位 变换
★阅读P49– P52，完成“基础感知”； ★巩固固化，完成“深入学习”.
★对议，小组内两人讨论，完成“基础感知”； ★组议，小组讨论运用公式，完成“深入学习”
0
表:
1 2
x
0
sin 12x 0
2 3 4
2
3 2
2
1 0 -1 0

--坐标系ppt(共38张PPT)

--坐标系ppt(共38张PPT)
角.
高考总复习·数学理科（RJ）
第十四章 系列4选讲
（2）极坐标与直角坐标的互化
设 M 为平面内的一点，它的直角坐标为（x，y），极坐标为
（ρ，θ）.由图可知下面关系式成立：
x＝ρcos
y＝ρsin
θ， ρ2＝x2＋y2，
θ
或 tan
θ＝yx（x≠0）.
高考总复习·数学理科（RJ）
第十四章 系列4选讲 这就是极坐标与直角坐标的互化公式.
即 ρ＝4sin
3
θ－2cos
θ.
高考总复习·数学理科（RJ）
第十四章 系列4选讲
【思维升华】 求曲线的极坐标方程的步骤：（1）建立适
当的极坐标系，设P（ρ， θ ）是曲线上任意一点；（2）由曲线
上的点所适合的条件，列出曲线上任意一点的极径 ρ 和极角 θ
之间的关系式；（3）将列出的关系式进行整理、化简，得出曲 线的极坐标方程.
高考总复习·数学理科（RJ）
第十四章 系列4选讲
【解析】 （1）设（x1，y1）为圆上的点，在已知变换下变 为曲线 C 上的点（x，y），依题意，得xy＝＝x21y，1.
由 x21＋y21＝1 得 x2＋2y2＝1， 即曲线 C 的方程为 x2＋y42＝1.
高考总复习·数学理科（RJ）
第十四章 系列4选讲
第十四章 系列4选讲
高考总复习·数学理科（RJ）
第十四章 系列4选讲
坐标系与参数方程 第1课时 坐标系
1.平面直角坐标系
设点 P（x，y）是平面直角坐标系中的任意一点，在变换 φ：
x′＝λ·x y′＝μ·y
（λ>0）， （μ>0） 的作用下，点 P（x，y）对应到点 P（ ′ x′，

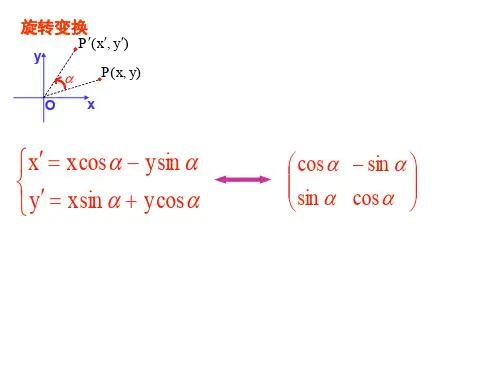
位似变换和伸缩变换

位似变换和伸缩变换

P(x, y) l
y
P(x, y)

O
x

T=
B2 A2
A2 B2

2 AB
A2 B2

2 AB

A2 B2
A2 B2

A2 B2
位似变换与伸缩变换
求一个变换的矩阵可从两种途径得到
（一）用公式， （二）直接从坐标关系式得到。
怎样由正弦曲线 y=sinx 得到曲线 y=sin2x?
2
-5 -2Leabharlann 510-4
y=sinx
-6
y=3sinx
坐标对应关系为：
x’= x y’=3y

x y
' '
＝
1 0
0 x
3

y
问题分析：
(3)怎样由正弦曲线y sin x得到曲线 y 3sin 2x?
纵坐标y不变，将横坐标x缩为原来的 1， 2
横坐标不变，纵坐标伸长为原来的3倍，

0
3


3
0


0
3


0
1

x' kx

y
'

ky

x y
' '
＝
k 0
0 x
k

y

位似变换对应矩阵为：k 0
0
k

当为 1 时它是什么变换
例 1.已知圆 x2 y2 1，变换 T 为： 横坐
标不变,纵坐标缩短到 1 倍。求圆在 T 变换作 5

平面直角坐标系及伸缩变换

平面直角坐标系及伸缩变换

＝4.动圆 M 与圆 O1 内切，又与圆 O2 外切，建立适当的坐标系，
求动圆圆心 M 的轨迹方程，并说明轨迹是何种曲线．
解: 如图所示，以 O1O2 的中点 O 为原点，O1O2 所在直线为
x 轴建立平面直角坐标系．
y
由由|O|O1O1O2|＝2|＝4，4,得得OO11((－ -22, ,00)),、OO2(22(,20,0))．．
A1（- a，0），A2（a，0）
ec (e1) a
y b x a
A1（0，-a），A2（0，a）
ec (e1) a
y a x b
图形 ly
OF x
标准方程
y2=2px (p>0)
焦点坐标 准线方程
( p ,0 ) x p
2
2
二 抛
物
yl
FO
y2=-2px x (p>0)
( p ,0) 2
lll和和和lll的的的距距距离离离的的的最最最小小小值值值为为为|1|122||1±5±52441|±5.2|.45|.4 | .
O
x
∴∴∴点点点QQQ与与与ll的l的的最最最小小小值值值为为为88558555..5.
题 型 三 定义法求轨迹方程
【例 3】已知两个定圆 O1和 O2，它们的半径分别是 1 和 2，且|O1O2|
所以有 x02
4
把①代入②,
y02
得
4
1.
(2x)2
②
(2y)2 1,
4
整理, 得 x24y21.
MP
O
x
所以点M的轨迹方程是 x24y21.
课堂小结
平面直角坐标系建系时，根据几何特点选 择适当的直角坐标系。

高中数学：131《三角函数图像的变换》课件必修

高中数学：131《三角函数图像的变换》课件必修
这些操作包括平移、伸缩、翻折和旋转等，可以单独或组合使用。
变换的目的是为了更好地理解三角函数的性质，解决实际问题，以及进行图像处理 等。
变换的种类和特点
01
02
03
04
平移变换
将图像沿x轴或y轴方向移动 ，保持图像形状不变。
伸缩变换
通过改变x轴和y轴的比例来 改变图像的大小，可以横向或
纵向伸缩。
翻折变换
利用伸缩变换的性质求解函数的极值
例如，利用正弦函数的伸缩性质，可以求解y=sin(3x)在x=π/9处的极小值为1。
利用对称变换的性质求解函数的对称轴或对称中心
例如，利用正弦函数的对称性质，可以求解y=sin(x)的对称轴为x=kπ+π/2，k∈Z。
变换在实际问题中的应用
物理学中的应用
三角函数图像的综合变换在物理学中有广泛的应用，如振 动和波动现象、交流电等。通过变换可以更好地理解物理 现象和解决实际问题。
x轴缩短为原来的1/2，则图像的 周期变为原来的2倍。
01
03
02 04
总结词：影响相位
详细描述：沿x轴伸缩不仅改变 了图像的周期，还会影响函数的 相位。例如，将x轴缩短为原来 的1/2，相当于将相位滞后了π。
沿y轴伸缩
总结词：改变振幅
详细描述：沿y轴伸缩是 指保持x轴不变，通过改 变y轴的长度来改变整个 图像的振幅。例如，将y 轴放大为原来的2倍，则 图像的振幅变为原来的2 倍。
翻折变换
旋转变换
$y = -f(-x)$ 或 $y = f(x)$，前者表示沿x 轴翻折，后者表示沿y轴翻折。
$x = xcostheta - ysintheta$ 和 $y = xsintheta + ycostheta$，其中$theta$为 旋转角度。

人教版高中数学必修四课件：1.5 三角函数图像平移伸缩变换(共22张PPT)

人教版高中数学必修四课件：1.5 三角函数图像平移伸缩变换(共22张PPT)

x
sin x 2sin x 1 sin x 2
y
2
1
o
-1 -2
0

2

3
2
2
0
1
0
-1 0
0
2
0
-2 0
0
1
2
0
1 2
0
y=2sinx y=sinx
y= 12sinx


2
3
2
2
x
小结1 函数 y Asin x, x R 的图象
（其中A 0且 A 1）
可以看作把正弦曲线上所有点的
纵坐标伸长（当A>1时）或缩短（当
0<A<1时）到原来的A倍（横坐标不变）
而得到． A的作用
引起值域 改变
纵向伸缩
函数 y Asin x, x R 的值域是 A, A
问题2
在同一坐标系中作出函数y=sin2x 及图y象=间sin的12关x的系简。图，并指出它们y=sinx
x
0


4
• 再把所有点的纵坐标伸长（当A>1时）或缩短（当
0<A<1时）到原来的A倍（横坐标不变）, 得到
y=Asin( x+ )。
变换2:
函数y=Asin(x+ )(其中A>0, >0)的
图象，可看作由下面方法得到：
• 把y=sinx图象上所有点的横坐标缩短(当
>1时)或伸长(当0< <1时)到原来的 1 倍
函数y Asin(x )的图像
复习：
2．用五点法作函数 y sin x, x 0,2

函数图象的变换PPT

函数图象的变换PPT
总结词
水平平移是指函数图像在水平方向上移动一定的距离。
详细描述
水平平移不改变函数的值，只是改变了图像的位置。对于函数y=f(x)，若图像向 右平移a个单位，则新的函数为y=f(x-a)；若图像向左平移a个单位，则新的函 数为y=f(x+a)。
垂直平移
总结词
垂直平移是指函数图像在垂直方向上移动一定的距离。
函数图象的变换
• 函数图象变换概述 • 平移变换 • 伸缩变换 • 翻折变换 • 旋转变换 • 应用实例
01
函数图象变换概述
函数图象变换的定义
01
函数图象变换是指通过平移、伸 缩、翻转等几何变换操作，改变 函数图象的位置、形状和大小。
02
这些变换操作可以通过代数表达 式或矩阵变换来实现，使得函数 图象在坐标系中按照特定的规则 进行移动、旋转和缩放。
详细描述
当函数图像在y轴方向上伸缩时，其形状和大小会发生变化，但x轴上的比例保持不变。例如，将函数y=f(x)的图 像在y轴方向上放大2倍，得到新的函数y=2f(x)。
斜向伸缩
要点一
总结词
斜向伸缩是指同时沿x轴和y轴方向对函数图像进行放大或 缩小。
要点二
详细描述
当函数图像在x轴和y轴方向上同时伸缩时，其形状和大小 会发生变化，x轴和y轴上的比例都会改变。例如，将函数 y=f(x)的图像在x轴方向上放大2倍，在y轴方向上放大3倍 ，得到新的函数y=3f(2x)。
逆时针旋转
总结词
当函数图像按照逆时针方向旋转时，其形状和大小也不会发生变化，同样只是位置发生 了移动。
详细描述
与顺时针旋转相反，当函数图像按照逆时针方向旋转一定的角度时，每个点的坐标同样 会发生变化，但方向是远离原点。同样地，这种变化也可以用三角函数的性质来描述。

函数图像的变换课件

函数图像的变换课件

向右平移
总结词
图像沿x轴正方向移动
数学表达式
y=f(x-a)
详细描述
对于函数y=f(x)，若图像向右平移a个单位，则新的函数 解析式为y=f(x-a)。
举例
函数y=cos(x)的图像向右平移π/2个单位后，得到新的函 数y=cos(x-π/2)，其图像与原图像相比沿x轴正方向移动 了π/2个单位。
双向伸缩
总结词
同时改变x轴和y轴的长度。
详细描述
当函数图像在x轴和y轴方向上都发生伸缩时，x轴和y轴的长度都会发生变化。这 种变换可以通过将函数中的x和y都替换为其倍数来实现，例如将f(2x)/3替换为 f(x)会使x轴压缩为原来的一半，同时y轴拉伸为原来的三倍。
04
函数图像的旋转变换
逆时针旋转
关于y轴对称
总结词
函数图像关于y轴对称时，图像在y轴两侧对称分布，x值 不变，y值相反。
详细描述
当一个函数图像关于y轴对称时，图像在y轴两侧呈现出 对称分布的特点。这意味着对于任意一个点$(x, y)$在图 像上，关于y轴对称的点$(x, -y)$也在图像上。这种对称 变换不会改变x值，只是将y值取反。例如，函数$f(x) = x^3$的图像关于y轴对称，因为$f(-y) = (-y)^3 = -y^3 = -f(y)$。
任意角度旋转
总结词
任意角度旋转是指将函数图像按照任意角度进行旋转。
详细描述
任意角度旋转函数图像是指将图像上的每个点都按照任意指定的角度进行旋转。这种旋转可以通过参数方程或极 坐标系来实现，其中参数方程为$x = x cos theta - y sin theta$，$y = x sin theta + y cos theta$，极坐标系 下的表示为$x = r cos theta$，$y = r sin theta$。

直角坐标系中的伸缩变换课件PPT

直角坐标系中的伸缩变换课件PPT

03 伸缩变换的矩阵表示
二维伸缩变换的矩阵表示
总结词
描述二维平面上的点通过伸缩变换后的坐标变化。
详细描述
在二维直角坐标系中，伸缩变换可以通过一个矩阵来表示。假设原点为 $(x, y)$， 经过伸缩变换后变为 $(x', y')$，则变换矩阵可以表示为
二维伸缩变换的矩阵表示
• $\begin{pmatrix}
02
在直角坐标系中，设原点为 $O(0,0)$，点$P(x,y)$经过伸缩变 换后变为点$P'(x',y')$，则变换公 式为：$x' = kx, y' = ky$，其中 $k$为伸缩系数。
伸缩变换的性质
伸缩变换保持点之间 的距离不变，即 $|OP| = |OP'|$。
伸缩变换可以同时对 x和y进行放大或缩小， 但比例系数必须相同。
伸缩变换的理论研究
01
02
03
理论框架
深入探讨伸缩变换的基本 原理、数学表达和推导过 程，建立完善的理论框架。
性质研究
研究伸缩变换的性质，如 线性、可逆性、连续性和 可微性等，并探讨其在不 同坐标系下的表现。
几何意义
从几何角度解释伸缩变换， 探究其在图形、曲线和曲 面等几何对象上的应用和 表现。
伸缩变换的应用研究
02 伸缩变换在直角坐标系中 的应用
横向伸缩变换
总结词
在直角坐标系中，横向伸缩变换 是指沿x轴方向的伸长或缩短。
详细描述
横向伸缩变换通过乘以一个大于1 的系数来增加x轴上的长度，或者 乘以一个小于1的系数来减小x轴 上的长度。这种变换不会改变点 在y轴上的坐标。
纵向伸缩变换
总结词
纵向伸缩变换是指沿y轴方向的伸长或缩短。

伸缩变换

伸缩变换

因此，这两个旋转变换的坐标变换公式及对应的二阶矩阵 是分别相同的 ，这时我们称这两个旋转变换相等

引例伸缩 变换
y
y=2 sin 2x
y=sin x
伸缩变换
y= 2sin 2x
O y=sin x
x
在平面直角坐标系中，过任意一点P作某一直线的垂线
垂足为P’，则称P’为点P在该直线上的投影。如果将每一 点变为它在该直线上的投影这个变换为关于这条直线的
投影变换。
求关于x轴的投影变换的坐标 变换公式及其对应的二阶矩阵
称这类变换为平行于x轴的切变变换。
y 平行于x轴的切变变换的坐标变换公式 及其对应的二阶矩阵； (x ,y)P O tan θ y =ky
P’ (x’ ,y’)
θ
y
x
将每一点P(x, y)沿着与Y轴平行的方向平移
k X个单位变成点P’（x’，P(x ,y)
x
回顾

线性变换
二阶矩阵
2. 两种特殊的线性变换
旋转转变换
P’（x’ ,y’）
a P（x ,y）
P’(x’ ,y’) y a
l
P(x ,y) x
O
反射变换
伸缩变换
y y=2 sin 2x
O
y=sin x
x
关于x轴
关于y轴
切变变换
平行于x 轴 平行于y 轴
变换、矩阵相等


对应的矩阵
P (x ,y)
P’ (x’ ,y’)
关于x轴的投影变换的坐标
y
P (x ,y)
x O
变换公式及其对应的二阶矩阵；
P’ (x’ ,y’)
关于y轴的投影变换的坐标

2024届新高考一轮总复习人教版 第二章 第7节 函数的图象 课件(45张)

2024届新高考一轮总复习人教版 第二章 第7节 函数的图象 课件(45张)

f(x)－k
f(x)－h
(2)伸缩变换 ①y＝f(x)―a0―><1a―，<1―横，―坐横―标坐―缩标―短伸为―长原为―来原―的来―1a的―倍a1―，倍―纵，―坐纵―标坐不―标变不―变→ y＝__f(_a_x_)__． ②y＝f(x)―0―<a>a―<1，1―，纵―纵坐―坐标―标伸―缩长―短为为―原原―来来―的的―a倍a―倍，―，横―横坐―坐标―标不不―变变→ y＝__a_f(_x_)__．
(2) (2022·全国乙卷)如图是下列四个函数中的某个函数在区间[－3，3]的大致图象， 则该函数是( )
x2－2x－1，x≥0， (3)y＝x2＋2x－1，x<0， 其图象如图③所示．
【思维升华】 作函数图象的两种常用方法 (1)直接法：当函数表达式(或变形后的表达式)是熟悉的基本初等函数时，就可根据 这些函数的特征直接作出； (2)图象变换法：若函数图象可由某个基本初等函数的图象经过平移、翻折、对称得 到，可利用图象变换作出，但要注意变换顺序．
(4)函数 y＝f(x)与 y＝2b－f(2a－x)的图象关于点(a，b)对称．
【小题热身】 1．思考辨析(在括号内打“√”或“×”) (1)函数 y＝f(1－x)的图象可由 y＝f(－x)的图象向左平移 1 个单位长度得到．( ) (2)当 x∈(0，＋∞)时，函数 y＝|f(x)|与 y＝f(|x|)的图象相同．( ) (3)函数 y＝f(x)与 y＝－f(－x)的图象关于原点对称．( ) (4)若函数 y＝f(x)满足 f(1＋x)＝f(1－x)，则函数 f(x)的图象关于直线 x＝1 对称．( ) 答案：(1)× (2)× (3)√ (4)√
2．将函数 y＝log2(2x＋2)的图象向下平移 1 个单位长度，再向右平移 1 个单位长度，
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
写出其坐标变换。
在正弦曲线y=sinx上任取一点P(x,y)，保持纵坐标不变，将横 坐 就标得到x缩正为弦原曲来线的y=123s，in在2x.此基础上，将纵坐标变为原来的3倍，
即：设点P（x , y）经变换得到点为P′ (x
y′=3y
3
通常把 3 叫做平面直角坐P标PT课件系中的一个坐标伸缩变换10 。
2 3 3 2
x y
B
x
'
y
'
3 2 2 3
x y
x ' y x' x 1
C
y'
x
D
y'
y
1
PPT课件
17
4 曲线 x2y22x0变成曲线
的伸缩变换是
.
x'21y6'24x'0
5 在伸缩变换
x' y'
2x y
与伸缩变换
x' 2x
y'
2
y
的作用下，
单位圆 x2 y2 1分别变成什么图形？
在正弦曲线上任取一点P（x , y），保持横坐标x不变， 将纵坐标伸长为原来的3倍，就得到曲线y=3sinx。 即：设点P（x , y）经变换得到点为P′ (x′, y′)
x′=x 2
y′=3y
通常把 2 叫做平面直角坐标系中的一个坐标伸长变换。
PPT课件
9
问题分析：
（3）怎样由正弦曲线y=sinx得到曲线y=3sin2x?
一点，保持纵坐标不变，将横坐标x缩 为原来 1 ，得到点 P′(x′, y′).坐标对应关
y=sin2x
系为： 2
2
x’=
1 2
x
1
y’=y
O
x
y=sinx
通常把 1 叫做平面直角坐标系中的一个压缩变换。
PPT课件
8
问题分析：
（2）怎样由正弦曲线 y=sinx得到曲线 y=3sinx? 写出其坐标变换。
坐标系下进行伸缩变换。
PPT课件
11
例1.在直角坐标系中，求下列方程所对应
的图形经过伸缩变换
x’=2x
y’=3y
后的图形。
（1）2x+3y=0; (2)x2+y2=1
(1)x’+y’=0
因此，在该伸缩变换下，直线仍然变成直线，而圆可以变为
椭圆。
PPT课件
12
例2：在同一坐标系中，如何将直线 x-2y=2 变成直线 2x’-y’=4,写出其坐标变换。
PPT课件
18
7 在同一直角坐标系下，求满足下列图形的伸缩变 换：曲线 4x2+9y2=36 变为曲线 x’2+y’2=1
8 在同一直角坐标系下，经过伸缩变换
x 3x
y
y
后,曲线C变为x’2－9y’2 =1,求曲线C的方程,并画出图形。
PPT课件
19
PPT课件
13
例3.在同一直角坐标系下，求满足下列图形 的伸缩变换：曲线4x2+9y2=36变为曲线 x’2+y’2=1
PPT课件
14
例4.在同一直角坐标系下，经过伸缩变
x’=3x
换 y’=y 后，曲线C变为x’2－9y’2 =1， 求曲线C的方程并画出图形。
PPT课件
15
思考：在伸缩 变换
:
伸缩变换的定义：设P(x,y)是平面直角坐标系中 任意一点，在变换
:
x y
' '
x y
( 0) ( 0)
4
的作用下，点P(x,y)对应P’(x’,y’).称 为平面直角
坐标系中的伸缩变换。
注：（1）0,0
（2）把图形看成点的运动轨迹，平面图形的伸缩变换可 以用坐标伸缩变换得到；
（3）在伸缩变换下，平面直角坐标系不变，在同一直角
PPT课件
2
精品资料
• 你怎么称呼老师？ • 如果老师最后没有总结一节课的重点的难点，你
是否会认为老师的教学方法需要改进？ • 你所经历的课堂，是讲座式还是讨论式？ • 教师的教鞭 • “不怕太阳晒，也不怕那风雨狂，只怕先生骂我
笨，没有学问无颜见爹娘 ……” • “太阳当空照，花儿对我笑，小鸟说早早早……”
选修4-4 1.1伸缩变换
PPT课件
1
1.对称变换
在直角坐标系中，已知点M(a,b)，则
（1）点M关于原点O对称的点为_____________； （2）点M关于x轴对称的点为_____________； （3）点M关于y轴对称的点为_____________； （4）点M关于直线y=x对称的点为_____________； （5）点M关于直线y=-x对称的点为_____________； （6）点M关于直线y=x+t对称的点为_____________；
PPT课件
16
补充练习：
1 求下列点经过伸缩变换
x' 2x
y'
3
y
①（1，2）； ②（-2，-1）.
后的点的坐标：
2 曲线C经过伸缩变换 则曲线C的方程是
x
'
y
'
1 3 1 2
x y
后的曲线方程是 .
4x'29y'236
3 将点（2，3）变成点（3，2）的伸缩变换是（ ）
A
x' y'
PPT课件
5
练习：填空题
PPT课件
6
3.平面直角坐标系中的伸缩变换
• 思考： • （1）怎样由正弦曲线y=sinx得到曲线y=sin2x?
y
y=sin2x
2
O
x
PPT课件 y=sinx
7
在正弦曲线y=sinx上任取一点P(x , y)，保持纵坐标不变，将横 坐标x缩为原来的 1 ，就得到正弦曲线y=sin2x. 即：设P(x , y)是平2面直角坐标系中任意
x y
' '
x y
( 0) ( 0)
下，椭圆是否可以变成圆？抛物线，双曲线变
成什么曲线？
对于双曲线和抛物线的方程,不管进行什么样的伸缩变换之后,方程特点 仍然没有变,抛物线方程的二次项和一次项都没有变,双曲线的两个二次 项仍然是二次项,这两个二次项之间的减号也没有变; 从另外一个角度来说,把它们的图象进行压缩时,图象特点是没有变的, 压缩后的图象仍然是抛物线型和双曲线型的,所以它们的图象是没有变 化的,仍然是双曲线和抛物线.