云南省陆良县第八中学2019_2020学年高二数学11月月考试题(无答案)

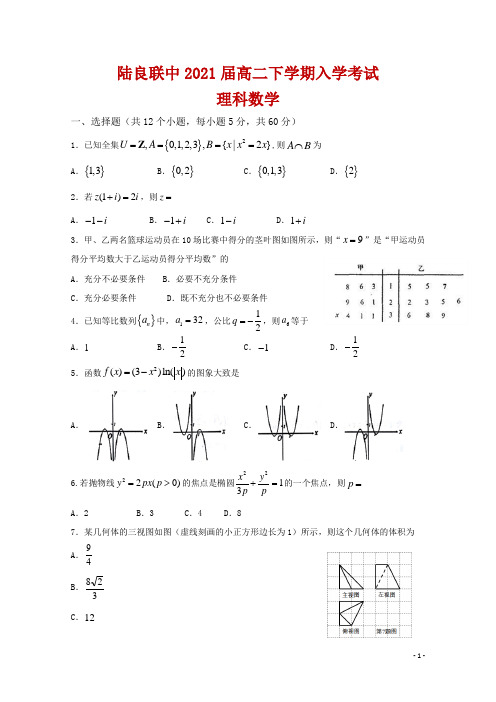
陆良联中2021届高二下学期入学考试理科数学一、选择题（共12个小题，每小题5分，共60分）1．已知全集{}2,0,1,2,3,{|2}U A B x x x ====Z ,则A B ⋂为A ．{}1,3B ．{}0,2C ．{}0,1,3D ．{}22．若(1)2z i i +=，则z = A ．1i --B ．1i -+C ．1i -D ．1i +3．甲、乙两名篮球运动员在10场比赛中得分的茎叶图如图所示，则“9x =”是“甲运动员得分平均数大于乙运动员得分平均数”的 A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．既不充分也不必要条件 4．已知等比数列{}n a 中，132a =，公比12q =-，则6a 等于 A ．1B ．12-C ．1-D ．12-5．函数2()(3)ln()f x x x =-的图象大致是A ．B ．C ．D ．6.若抛物线22(0)y px p =>的焦点是椭圆2213x y p p+=的一个焦点，则p = A ．2 B ．3 C ．4 D ．87．某几何体的三视图如图（虚线刻画的小正方形边长为1）所示，则这个几何体的体积为 A ．49B ．328 C ．12D ．38 8．在ABC ∆中，AB AC AB AC +=-u u u r u u u r u u u r u u u r ，4AB =，3AC =，则BC u u u r 在CA u u u r方向上的投影是 A ．4B ．3C ．-4D ．-39．直线20x y ++=分别与x 轴，y 轴交于A ，B 两点，点P 在圆()2222x y -+=上，则ABP △面积的取值范围是 A ．[]26，B ．[]48，C． D．⎡⎣ 10. 设0.2log 0.3a =，2log 0.3b =，则A ．0a b ab +<<B ．0ab a b <+<C ．0a b ab +<<D ．0ab a b <<+11．设A ，B ，C ，D 是同一个半径为4的球的球面上四点，△ABC为等边三角形且面积为则三棱锥D ﹣ABC 体积的最大值为A． B． C．D．12．已知双曲线22221(0,0)x y a b a b-=>>的左、右两个焦点分别为12F F 、，A B 、为其左右顶点,以线段12F F 、为直径的圆与双曲线的渐近线在第一象限的交点为M ，且30MAB ∠=o ,则双曲线的离心率为 AB．3CD二、填空题（共4个小题，每小题5分，共20分）13． ABC △的内角,,A B C 的对边分别为,,a b c .若π6,2,3b ac B ===，则ABC △的面积为__________.14．若,x y 满足约束条件25023050x y x y x +-≥⎧⎪-+≥⎨⎪-≤⎩，，， 则z x y =+的最大值为__________．15．已知sin cos 1αβ+=，cos sin 0αβ+=，则sin()αβ+=__________．16．已知函数()f x 是定义在R 上的偶函数，若对于0x ≥，都有()()2f x f x +=-且当[)0,2x ∈时，()e 1x f x x =-，则()()20172018f f -+=__________．三、解答题（共6题，共70分）17（12分）、为了纪念“一带一路”倡议提出五周年,某城市举办了一场知识竞赛,为了了解市民对“一带一路”知识的掌握情况,从回收的有效答卷中按青年组和老年组各随机抽取了40份答卷,发现成绩都在[]50,100内,现将成绩按区间[)50,60,[)60,70,[)70,80,[)80,90，[]90,100进行分组,绘制成如下的频率分布直方图．青年组 老年组(1)利用直方图估计青年组的中位数和老年组的平均数；(2)从青年组[)80,90,[]90,100的分数段中,按分层抽样的方法随机抽取5份答卷,再从中选出3份答卷对应的市民参加政府组织的座谈会,求选出的3位市民中有2位来自[]90,100分数段的概率．18（12分）、在ABC ∆中，a ，b ，c 分别为角A ，B ，C 所对边的长.cos 2cos b A a B =，3cos 3B =. （1）求角A 的值； （2）若22c =+，求ABC ∆的面积.19（12分）、已知数列{}n a 是各项都为正数的等比数列，且345122,1a a a a a +=+=. （1）求{}n a 的通项公式；（2）若22log 3log n n b a =+，求数列122n n b b ++⎧⎫⎨⎬⎩⎭的前n 项和n S .20（12分）、已知四棱锥P ABCD -，12BC CD DA ==，//BC AD，90ADC ∠=o ，点P 在底面ABCD 上的射影是BD 的中点O ，PC =（1）求证：直线BD ⊥平面POC ；（2）若1BC =，M 、N 分别为PO 、CD 的中点，求直线MN 与平面PCD 所成角的正弦值；（3）当四棱锥P ABCD -的体积最大时，求二面角B PC D --的大小．21（12分）、已知椭圆C: 22221(0)x y a b a b+=>>的左,右焦点分别为12,F F 且椭圆C 上的点P (1,2到12,F F 两点的距离之和为4 (1)求椭圆C 的方程;(2)若直线y kx m =+与椭圆C 交于,M N 两点,O 为坐标原点直线,OM ON 的斜率之积等于14-，试探求△OMN 的面积是否为定值，并说明理由 22（10分）、 在直角坐标系xOy 中，圆C 的参数方程为1cos sin x y αα=+⎧⎨=⎩，其中a 为参数，以坐标原点O 为极点，x 轴正半轴为极轴建立极坐标系． (1)求圆C 的极坐标方程；(2)B 为圆C 上一点，且B 点的极坐标为()000,,,26ππρθθ⎛⎫∈- ⎪⎝⎭，射线OB 绕O 点逆时针旋转3π，得射线OA ，其中A 也在圆C 上，求OA OB +的最大值．陆良联中2021届高二下入学考试理科数学一、选择题（共12个小题，每小题5分，共60分）1． B 2．D 3．A4．C5．A6.D 7．D 8．D9．A10．B11．B 12．B二、填空题（共4个小题，每小题5分，共20分）13.14．9 15．12-16．e三、解答题（共6题，共70分）17（12分）、 (1)中位数为80，平均数为73.5(2)310(1)由青年组的频率分布直方图可知,前3个小矩形的面积和为0.5,后2个小矩形的面积和为0.5,所以中位数为80．中老年组成绩的平均数为()550.01650.03750.03850.025950.0051073.5⨯+⨯+⨯+⨯+⨯⨯=．(2)青年组[)80,90,[]90,100的分数段中答卷分别为12份,8份, 抽取比例为511284=+,所以两段中分别抽取的答卷分别为3份,2份． 记[)80,90中的3位市民为a ,b ,c ,[]90,100中的2位市民为x ,y , 则从中选出3位市民，共有不同选法种数10种：(),,a b c ,(),,a b x ,(),,a b y ,(),,a c x ,,(),,a x y ,(),,b c x ,(),,b c y ,(),,b x y ,(),,c x y ．其中,有(),,a c y 2位来自[]90,100的有3种：(),,a x y ,(),,b x y ,(),,c x y ． 所以所求概率310P =．18（12分）、（1）4π；（2）2+.（1）在ABC ∆中,因为cos B =,0B π<<所以sin 3B ==因为cos cos b A B =由正弦定理,得sin cos cos B A A B =,即cos 33A A =⋅所以cos sin A A =若cos 0A =,则sin 0A =,与22sin cos 1A A +=矛盾,故cos 0A ≠ 于是tan 1A = 又因为0A π<< 所以4A π=（2）因为2c =+4A π=,cos 3B =,sin 3B =所以sin sin()sin cos cos sin 23236C A B Ac B A B =+=+=+=由正弦定理sin sin b cB C=,得(2sin sin c B b C +⋅===所以ABC ∆的面积为11sin (22222S bc A ==⨯+⨯=+19（12分）、（1）设数列{}n a 的公比为q ，则3452a a a +=，可变形为2341112a q a q a q +=，化简为220q q --= 解得2q =或1q =-（舍去）因为121a a +=，所以1121a a +=，解得113a =所以数列{}n a的通项公式为1 112233nnna--=⨯=（2）因为()12222log3log log3log21nn n nb a a n-=+===-所以1222112(1)1n nb b n n n n++⎛⎫==-⎪++⎝⎭所以1111122122311nnSn n n⎛⎫=-+-+⋯+-=⎪++⎝⎭20（12分）、（1）证明见解析（2）10535（3）23π（1）连接OC，因为PO⊥平面ABCD，BD⊂平面ABCD，所以PO BD⊥，又因为BC CD=，且O为BD的中点，故OC BD⊥．又PO OC O=I，所以BD⊥平面POC；（2）以C为原点，CD、CB所在直线分别为x、y轴建立直角坐标系如图所示，则()0,0,0C，()0,1,0B，()1,0,0D，11,,22P m⎛⎫⎪⎝⎭，于是211244PC m =++=，解得6=m ．即116,,222P⎛⎫ ⎪ ⎪⎝⎭． 所以1,0,02N ⎛⎫⎪⎝⎭，116,,224M ⎛⎫ ⎪ ⎪⎝⎭，160,,24NM ⎛⎫= ⎪ ⎪⎝⎭u u u u r 设平面PCD 的法向量为(),,n x y z =r ，()1,0,0CD =u u u r，116,,222CP ⎛⎫= ⎪ ⎪⎝⎭u u u r ，则0011660222n CD x x y z n CP x y z ⎧⋅===⎧⎪⎪⇒⎨⎨=-⎪⋅=++=⎩⎪⎩u u u v v u u u v v ，令1z =-，得()0,6,1n =-r ， 所以66024105sin cos ,351661416n NM n NM n NMθ+-⋅=<>===⋅+⋅+r u u u u rr u u u u r r u u u u r ．故直线MN 与平面PCD 所成角的正弦值为105； （3）设2BC a =，则2OC a =，222PO a =-，所以()24212422222232P ABCDa a V a a a a -+=⨯⨯⨯-=-32222246239a a a ⎛⎫++-≤= ⎪⎝⎭，当且仅当2222a a =-即263a ==26BC CD ==，43BD =， 以C 为原点，CD 、CB 所在直线分别为x 、y 轴建立空间直角坐标系如图所示，则()0,0,0C ，26D ⎫⎪⎪⎝⎭，26B ⎛⎫ ⎪ ⎪⎝⎭，666P ⎝⎭． 设平面PBC 的法向量为()1111,,n x y z =u r，26CB ⎛⎫= ⎪ ⎪⎝⎭u u u r ，666CP =⎝⎭u u u r ，则)111111112600360n CB y y x z n CP x y z ⎧⋅==⎪=⎧⎪⇒⎨⎨=-⎩⎪⋅=++=⎪⎩u v u u uv u u u v v ，令11z =-，得()11,0,1n =-u r ，同理，可得平面PCD 的一个法向量为的()20,1,1n =-u u r，所以1212121cos ,2⋅<>==⋅u u r u u ru u r u u r uu r u u r n n n n n n ， 又因为二面角B PC D --为钝二面角，所以二面角B PC D --的大小为23π．21（12分）、（1）2214x y +=；（2）定值1 【详解】（1）由已知24a =，即2a =，又点3P 在椭圆上， 所以2231214b+=（），所以21b =，故椭圆方程为2214x y +=. （2）设1122(,),(,)M x y N x y ，由2214y kx m x y =+⎧⎪⎨+=⎪⎩，得2214)84(1)0k mkx m +++-=（， 则22226416(14)(1)0m k k m ∆=-+->，即22140k m +->，且212122284(1),1414mk m x x x x k k-+=-=++， 因为直线,OM ON 的斜率之积等于14-， 2212121212121212()()()14y y kx m kx m km x x k x x m x x x x x x +++++===-， 所以22222222(8)4(1)(14)414(1)4(1)4km km k m m k m k m m -+-++-==---，即22241m k =+， 又O 到直线MN的距离为d =MN ==所以112OMN S MN d ∆=⋅==.22（12分）、（1）1cos sin x y αα=+⎧⎨=⎩2222(1)120x y x y x ⇒-+=⇒+-=，由222,cos ,x y x ρρα=+=可得圆C 的极坐标方程2cos ρθ=．（2）由题意可知：10(,)6A πρθ+,所以0002cos 2cos 36OA OB ππθθθ⎛⎫⎛⎫+=++=+ ⎪ ⎪⎝⎭⎝⎭0,26ππθ⎛⎫∈- ⎪⎝⎭，所以0()(,)633πππθ+∈-01cos()(,1]62πθ⇒+∈，从而OA OB +最大值为- 11 -。

陆良县高中2018-2019学年高二上学期第二次月考试卷数学 班级__________ 姓名__________ 分数__________一、选择题1． 如图是某几何体的三视图，则该几何体任意两个顶点间的距离的最大值为（ ）A ．4B ．5C ．32D ．332． 已知点P （1，﹣），则它的极坐标是（ ）A ．B ．C ．D ．3． 如图，网格纸上小正方形的边长为1，粗线画出的是一正方体被截去一部分后所得几何体的三视图，则该几何体的表面积为（ ）A ．54B ．162C ．54+18D ．162+184． 已知2a =3b =m ，ab ≠0且a ，ab ，b 成等差数列，则m=（ ）A ．B ．C ．D ．65． 已知,A B 是球O 的球面上两点，60AOB ∠=︒，C 为该球面上的动点，若三棱锥O ABC -体积的最大值为3O 的体积为（ ）A ．81πB ．128πC ．144πD ．288π【命题意图】本题考查棱锥、球的体积、球的性质，意在考查空间想象能力、逻辑推理能力、方程思想、运算求解能力．6．若，则等于（）A．B．C．D．7．如图，长方形ABCD中，AB=2，BC=1，半圆的直径为AB．在长方形ABCD内随机取一点，则该点取自阴影部分的概率是（）A．B．1﹣C．D．1﹣8．函数f（x）是以2为周期的偶函数，且当x∈（0，1）时，f（x）=x+1，则函数f（x）在（1，2）上的解析式为（）A．f（x）=3﹣x B．f（x）=x﹣3 C．f（x）=1﹣x D．f（x）=x+19．已知点F1，F2为椭圆的左右焦点，若椭圆上存在点P使得，则此椭圆的离心率的取值范围是（）A．（0，）B．（0，] C．（，] D．[，1）10．某几何体的三视图如图所示（其中侧视图中的圆弧是半圆），则该几何体的表面积为（）A．20+2πB．20+3πC．24+3πD．24+3π11．若命题p：∃x∈R，x﹣2＞0，命题q：∀x∈R，＜x，则下列说法正确的是（）A．命题p∨q是假命题B．命题p∧（￢q）是真命题C．命题p∧q是真命题 D．命题p∨（￢q）是假命题12．已知f （x ）是R 上的偶函数，且在（﹣∞，0）上是增函数，设，b=f （log 43），c=f （0.4﹣1.2）则a ，b ，c 的大小关系为（ ）A ．a ＜c ＜bB ．b ＜a ＜cC ．c ＜a ＜bD ．c ＜b ＜a二、填空题13．已知椭圆+=1（a ＞b ＞0）上一点A 关于原点的对称点为B ，F 为其左焦点，若AF ⊥BF ，设∠ABF=θ，且θ∈[，]，则该椭圆离心率e 的取值范围为 ．14．自圆C ：22(3)(4)4x y -++=外一点(,)P x y 引该圆的一条切线，切点为Q ，切线的长度等于点P 到原点O 的长，则PQ 的最小值为（ ） A ．1310 B ．3 C ．4 D ．2110【命题意图】本题考查直线与圆的位置关系、点到直线的距离，意在考查逻辑思维能力、转化能力、运算求解能力、数形结合的思想．15．设x R ∈，记不超过x 的最大整数为[]x ，令{}[]x x x =-.现有下列四个命题: ①对任意的x ，都有1[]x x x -<≤恒成立； ②若(1,3)x ∈，则方程{}22sincos []1x x +=的实数解为6π-；③若3n n a ⎡⎤=⎢⎥⎣⎦（n N *∈），则数列{}n a 的前3n 项之和为23122n n -；④当0100x ≤≤时，函数{}22()sin []sin1f x x x =+-的零点个数为m ，函数{}()[]13xg x x x =⋅--的 零点个数为n ，则100m n +=.其中的真命题有_____________.（写出所有真命题的编号）【命题意图】本题涉及函数、函数的零点、数列的推导与归纳，同时又是新定义题，应熟悉理解新定义，将问题转化为已知去解决，属于中档题。

云南省陆良县第八中学2019-2020学年高二物理11月月考试题一、单项选择题(本大题共10小题,每小题3分,共30分。

在每小题给出的四个选项中只有一个选项符合题目要求)1.关于点电荷，下列说法正确的是（ ）A ．点电荷一定带正电B ．点电荷是实际带电体的理想化模型C ．点电荷一定带负电D ．只有带电量很小的带电体才能看作点电荷2.真空中相距为r 的两个点电荷，电荷量分别为4Q 和3Q ，相互作用的静电力大小为F 。

如果它们的电荷量变为2Q 和6Q ，其余条件不变。

则相互作用的静电力大小为（ ）A ． 3FB ．FC ．2FD ．4F3.下列说法是某同学对电学中相关概念及公式的理解，其中正确的是( )A ．电场强度公式E ＝U d 适用于一切电场B ．根据电容的定义式C ＝Q U,电容器极板上的电荷量每增加1 C ，电压就增加1 VC ．根据电场力做功的计算式W ＝qU ，一个电子在1 V 的电压下加速，电场力做功为1 eVD ．电场线就是正电荷只在电场力的作用下运动的轨迹4、如图所示，平行板电容器与电动势为E 的直流电源（内阻不计）连接，下极板接地．一带电油滴位于电容器中的P 点且恰好处于平衡状态．现将平行板电容器的上极板竖直向上移动一小段距离，则下列说法正确的是:( )A ．带电油滴将沿竖直方向向上运动B ．P 点的电势将降低C ．带电油滴的电势能不变D ．电容器的电容减小，极板带电量将增大5.在示波管中，电子枪2 s 内发射了6×1013个电子，则示波管中电流的大小为（ ）A.3×10-13 AB.4.8×10-6 AC.9.6×10-6 AD.3×10-6 A6．如图所示是研究串联电路中电流、电压特点的实物连接图．当开关闭合时，灯L 1亮，灯L 2不亮，电流表和电压表均有读数．则故障原因可能是( )A ．L 1断路B ．L 1短路C ．L 2断路D ．L 2短路7.有A 、B 两个电阻，它们的I -U 图线如图所示，从图线可以判断（ ）A. 电阻A 的电阻率大于电阻B 的电阻率B. 电阻A 的阻值小于电阻B 的阻值C. 两电阻并联时,流过电阻A 的电流强度较小D. 两电阻串联时,电阻A 消耗的功率较大8.如图所示是某款理发用的电吹风的电路图，它主要由电动机M 和电热丝R 构成．当闭合开关S 1、S 2后，电动机驱动风叶旋转，将空气从进风口吸入，经电热丝加热，形成热风后从出风口吹出．已知电吹风的额定电压为220 V ，吹冷风时的功率为120 W ，吹热风时的功率为1 000 W ．关于该电吹风，下列说法正确的是( )A ．电热丝的电阻为55 ΩB ．电动机的电阻为1 2103 ΩC ．当电吹风吹冷风时，电热丝每秒钟消耗的电能为120 JD ．当电吹风吹热风时，电动机每秒钟消耗的电能为880 J 9.如图是有两个量程的电压表，当使用a 、b 两个端点时，量程为0～10V ，当使用a 、c 两个端点时，量程为0～100 V ．已知电流表的内阻R g 为500 Ω，满偏电流I g 为1 mA ，则电阻R 1、R 2的值( )A ．90 000 Ω 9 500 ΩB ．9 500 Ω 90 000C ．9 500 Ω 9 000 ΩD ．9 000 Ω 9 500 Ω10.在如图所示的图象中，直线Ⅰ为某一电源的路端电压与电流的关系图象，直线Ⅱ为某一电阻R 的伏安特性曲线用该电源与电阻R 组成闭合电路由图象判断错误的是( )A.电源的电动势为3 V ，B.电阻R 的阻值为C.电源的内阻为D.电源的输出功率为6W二、多项选择题(本大题共4小题,每小题4分,共16分。

云南省陆良联中—下学期高二期中考试试题数学（理科） 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。共150分，考试时间1。 第Ⅰ卷（选择题 共60分）

一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中， 只有一项是符合题目要求的。

1．设P=｛x︱x<4｝,Q=｛x︱<4｝，则（ B） A. QP B. PQ C. QCPR D. PCQR 2．若命题p: 0是偶数，命题q: 2是3的约数. 则下列命题中为真的是 A.p且q 非p且非q C.非p p或q

3．设的（ B ） A．充要条件 B．充分不必要条件 C．必要不充分条件 D．既不充分也不必要条件

4．椭圆2211625xy的焦点坐标为 ( A ) （A）)3,0( （B）)0,3( （C）)5,0( （D）)0,4(

5．抛物线2yax的准线方程为2y，则a的值为 （ Ｂ ） Ａ．18 Ｂ．18 Ｃ．8 Ｄ．8 6．若椭圆两准线间的距离等于焦距的4倍，则这个椭圆的离心率为 （ D ）

A．41 B．22 C．42 D． 21 7．已知向量)5,3,2(a与向量)215,,3(b平行，则等于 （ C. ） A. 23 B. 92 C. 92 D. 23 8．已知x，y满足223100xyxyxy，则z = 2 x + y有（ B ） A：最大值1 B：最小值1 C：最大值4 D ：最小值4 9． .双曲线22221xyab的两条渐近线互相垂直，那么该双曲线的离心率是 （ C ） （A）2 （B）3 （C）2 （D）23 10．在△ABC 中，若a、b、c成等比数列，且c = 2a，则cos B等于（ B ）

A．41 B．43 C．42 D．32 11．已知点（3，1）和（－4，6）在直线3x－2y+a=0的两侧，则a的取值范围是（ C ） A．a<－7或a>24 B．a=7或a=24 C．－7

2019-2020学年高二数学上学期第二次月考试题(11)一、选择题：本大题共12个小题,每小题5分,共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．等差数列{}n a 中，14739a a a ++=，36927a a a ++=，则前9项和9S 的值为（ ） A ．66 B ．99 C ．144 D ．297 2．在ABC ∆中，若3a =，1cos 2A =-，则ABC ∆的外接圆半径是（ ）A ．12 B C ．3．不等式()()120x x --≥的解集为（ ）A ．{}12x x ≤≤ B ．{1x x ≤或}2x ≥ C ．{}12x x << D ．{1x x <或}2x >4．设数列{}n a 的前n 项和21n S n =+，1315a a a +++=L （ ） A ．124 B ．120 C ．128 D ．1215．在ABC ∆中，若2cos sin sin B A C =，则ABC ∆的形状一定是（ ）A ．等腰直角三角形B ．直角三角形C ．等腰三角形D ．等边三角形 6．设,a b 是非零实数，若a b >，则一定有（ ） A ．11a b < B ．2a ab > C ．2211ab a b > D ．11a b a b->-7．在ABC ∆中，2a =，b =4A π=，则角B =（ ）A ．6π B ．6π或56π C ．3π D ．56π8．设数列{}n a 满足()21*1232222n n n a a a a n -++++=∈N L ，通项公式是（ ）A ．12n a n =B ．112n n a -=C ．12n n a =D ．112n n a +=9．若221xy+=，则x y +的取值范围是（ ）A ．[]0,2B ．[]2,0-C ．[)2,-+∞D ．(],2-∞- 10．在ABC ∆中，角A B C 、、所对的边分别为a b c 、、，若3A π=，()1cos cos b C c A -=，2b =，则ABC ∆的面积为（ ）A ．．3D 11．ABC ∆的内角,,A B C 的所对的边,,a b c 成等比数列，且公比为q ，则sin sin Cq A+的取值范围为（ ）A ．()0,+∞B ．(1,2+C ．()1,+∞D ．)112．数列{}n a 的通项公式为123n a n =-，12n n n n b a a a ++=⋅⋅，n S 是数列{}n b 的前n 项和，则n S 的最大值为（ ）A ．280B ．308C ．310D ．320第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13．在ABC ∆中，三边a b c 、、所对的角分别为A B C 、、，若2220a b c +-=，则角C 的大小为 ．14．在数列{}n a 中，其前n 项和32n n S k =⋅+，若数列{}n a 是等比数列，则常数k 的值为 ． 15．已知0x >，0y >，141x y+=，不等式280m m x y ---<恒成立，则m 的取值范围是 ．（答案写成集合或区间格式）16．已知数列{}n a 的通项公式为3n n a =，记数列{}n a 的前n 项和为n T ，若对任意的*n ∈N ，3362n T k n ⎛⎫+≥- ⎪⎝⎭恒成立，则实数k 的取值范围 ．（答案写成集合或区间格式） 三、解答题 （本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．） 17．已知()211f x x a x a ⎛⎫=-++ ⎪⎝⎭. （1）当12a =时，解不等式()0f x ≤； （2）若0a >，解关于x 的不等式()0f x ≤.18．设ABC ∆的内角,,A B C 所对的边分别为,,a b c 且1cos 2a C cb +=. （1）求角A 的大小；（2）若1a =，求ABC ∆的周长L 的取值范围.19．某房地产开发公司计划在一楼区内建造一个长方形公园ABCD ，公园由长方形的休闲区1111A B C D （阴影部分）和环公园人行道组成.已知休闲区1111A B C D 的面积为4000平方米，人行道的宽分别为4米和10米.（1）若设休闲区的长11A B x =米，求公园ABCD 所占面积S 关于x 的函数()S x 的解析式； （2）要使公园所占面积最小，休闲区1111A B C D 的长和宽该如何设计？20．已知数列{}n a 中，12a =，11322n nn n a a ++=+. （1）求数列{}n a 的通项公式； （2）求数列{}n a 的前n 项和.21．（1）在锐角ABC ∆中，1BC =，2B A =，求cos ACA的值及AC 的取值范围； （2）在ABC ∆中，已知2221cos cos cos A B C +=+，试判断ABC ∆的形状.22．设正项数列{}n a 的前n 项和n S ，且满足22n n n S a a =+.（1）求数列{}n a 的通项公式； （2）若数列1221n n n n n a a b a a ++++=+，数列{}n b 的前n 项和为n T ，求证：122n T n <+.南阳一中2017秋高二第二次月考数学答案一、选择题1-5:BDADC 6-10:CACDD 11、12：BC 二、填空题 13．34π（或135°） 14．3- 15．()1,9- 16．2,27⎡⎫+∞⎪⎢⎣⎭三、解答题 17．解：（1）当12a =时，有不等式()25102f x x x =-+≤， ∴()1202x x ⎛⎫--≤ ⎪⎝⎭，∴不等式的解集为122x x ⎧⎫≤≤⎨⎬⎩⎭（2）∵不等式()()10f x x x a a ⎛⎫=--≤ ⎪⎝⎭当1a a >时，有01a <<，∴不等式的解集为1x a x a ⎧⎫≤≤⎨⎬⎩⎭； 当1a a <时，有1a >，∴不等式的解集为1x x a a ⎧⎫≤≤⎨⎬⎩⎭； 当1a a=时，有1a =，∴不等式的解集为{}1. 18．解:（1）∵1cos 2a C cb +=，由正弦定理得12sin cos 2sin 2sin 2R A C R C R B +=，即1sin cos sin sin 2A C CB +=，又∵()sin sin sin cos cos sin B A C A C A C =+=+， ∴1sin cos sin 2C A C =， ∵sin 0C ≠， ∴1cos 2A =， 又∵0A π<<， ∴3A π=.（2）由正弦定理得：sinsin a B b A ==c =∴1a b c =++)1sin sinB C =+ ())1sin sinB A B =++112cos 2B B ⎫=++⎪⎪⎝⎭12sin 6B π⎛⎫=++ ⎪⎝⎭∵3A π=，∴20,3B π⎛⎫∈ ⎪⎝⎭，∴5,666B πππ⎛⎫+∈ ⎪⎝⎭， ∴1sin ,162B π⎛⎫⎛⎤+∈ ⎪ ⎥⎝⎭⎝⎦. 故ABC ∆的周长L 的取值范围为(]2,3. 19．解：（1）由11A B x =，知114000B C x=()4000208S x x ⎛⎫=++ ⎪⎝⎭()8000416080x x x=++>（2）8000041608S x x =++≥41605760+= 当且仅当800008x x=即100x =时取等号 ∴要使公园所占面积最小，休闲区1111A B C D 的长为100米，宽为40米. 20．解：（1）2n n n a b =，则1112n n n a b +++=，由题13n n b b +=+ 则13n n b b +-= ∴2n n a ⎧⎫⎨⎬⎩⎭是公差为3，首项为1的等差数列， ∴()131322nn a n n =+-=- ∴()322n n a n =-⋅ （2）设23124272n S =⋅+⋅+⋅++L ()()1352322n n n n --⋅+-⋅则2342124272n S =⋅+⋅+⋅++L ()()1352322n n n n +-⋅+-⋅相减得()()23123222322n n n S n +-=++++--⋅L()()2112212332221n n n -+-=+⋅--⋅-()()112324322n n n ++=+---⋅()110532n n +=-+-⋅∴()110352n n S n +=+-⋅.21．解：（1）设2A B θθ∠=⇒=，由正弦定理得sin 2sin AC BCθθ=，∴122cos cos AC ACθθ=⇒=.由锐角ABC ∆得0290045θθ<<⇒<<︒ooo，又01803903060θθ︒<︒-<︒⇒︒<<︒，故3045cos θθ︒<<︒⇒<<∴2cos AC θ=∈.（2）由题，2222sin 2sin sin A B C -=--，∴222sin sin sin A B C =+ 由正弦定理得222a b c =+，∴ABC ∆为直角三角形.22．解：（1）由题意可得22n n n S a a =+，21112n n n S a a ---=+，两式相减得， 22112n n n n n a a a a a --=-++，所以22110n n n n a a a a -----=，即()()1110n n n n a a a a --+--=，又因为数列{}n a 为正项数列，所以11n n a a -+=，即数列{}n a 为等差数列，又1n =时，2112a a a =+，所以11a =，11n a a n n =+-=.（2）由（1）知1221n n n b n n ++=+++，又因为12121n n n b n n ++=+=-++1111122112n n n n ++=+-++++，所以()12222n n T b b b =+++=+++L L 111111233412n n ⎡⎤⎛⎫⎛⎫⎛⎫+-+-++-⎪ ⎪ ⎪⎢⎥++⎝⎭⎝⎭⎝⎭⎣⎦L所以12n n T b b b =+++=L 11122222n n n +-<++.。

2020年云南省昆明市是第八中学高二数学理测试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 抛物线y2=4x，直线l过焦点且与抛物线交于A（x1，y1），B（x2，y2）两点，x1+x2=3，则AB中点到y轴的距离为（）A．3 B．C．D．4参考答案：B【考点】抛物线的简单性质；直线与抛物线的位置关系．【分析】利用已知条件求出A、B的中点的横坐标即可．【解答】解：直线l过抛物线的焦点且与抛物线y2=4x交于A（x1，y1），B（x2，y2）两点，x1+x2=3，AB中点的横坐标为：，则AB中点到y轴的距离为：．故选：B．2. 已知i是虚数单位，则对应的点在复平面的（）A．第一象限B．第二象限C．第三象限D．第四象限参考答案：D【考点】A5：复数代数形式的乘除运算．【分析】利用复数代数形式的乘除运算化简，求出对应的点在复平面的坐标得答案．【解答】解：∵ =，∴对应的点在复平面的坐标为（1，﹣1），在第四象限．故选：D．3. 某产品的广告费用与销售额的统计数据如下表：广告费用（万元）销售额（万元）根据以上表可得回归方程中的为据此模型预报广告费用为万元时销售额为（）A.63.6万元B. 65.5万元C.67.7万元D.72.0万元参考答案：B4. PA，PB，PC是从P引出的三条射线，每两条的夹角都是60o，则直线PC与平面PAB所成的角的余弦值为（）A． B. C. D.参考答案：C略5. 抛物线y2= 2x的准线方程是( )A．y=B．y=－C．x=D．x=－参考答案：D略6. 已知，若，则的值是（）A． B．或 C．，或 D．参考答案：C7. 数列的一个通项公式为（）A．B．C．D．参考答案：B略8. 已知等差数列{an}的前n项和为Sn，a5＝5，S5＝15，则数列的前100项和为( )．A. B. C. D.参考答案：A略9. 在正方体ABCD-A1B1C1D1中,E是棱CC1的中点, F是侧面BCC1B1内的动点, 且A1F//平面D1AE,则A1F与平面BCC1B1所成角的正切值构成的集合是 ( )参考答案：D10. 从4双不同的鞋中任意摸出4只，事件“4只全部成对”的对立事件是()A．至多有2只不成对B．恰有2只不成对C．4只全部不成对D．至少有2只不成对参考答案：D略二、填空题:本大题共7小题,每小题4分,共28分11. 设O为坐标原点，抛物线y2=4x的焦点为F，P为抛物线上一点．若|PF|=3，则△OPF的面积为．参考答案：【考点】抛物线的简单性质．【分析】根据抛物线方程求得抛物线的准线方程与焦点坐标，利用|PF|=3求得P点的横坐标，代入抛物线方程求得纵坐标，代入三角形面积公式计算．【解答】解：由抛物线方程得：抛物线的准线方程为：x=﹣1，焦点F（1，0），又P为C上一点，|PF|=3，∴x P=2，代入抛物线方程得：|y P|=2，∴S△POF=×|OF|×2=．故答案为：．【点评】本题考查了抛物线的定义及几何性质，熟练掌握抛物线上的点所迷住的条件是解题的关键．12. 在△ABC中，已知a=17，则b·CosC＋c·CosB=_________________。