《曲线与方程》精品课件 公开课课件

(3)由(x－2)2＋ y2－4＝0，得
x－2＝0， y2－4＝0，
∴yx＝＝22，
或xy＝ ＝2－，2.
因此，原方程表示两个点(2,2)和(2，－2).
1.判断方程表示什么曲线，就要把方程进行同解变形，常用的方法有：配 方法、因式分解或化为我们熟悉的曲线方程的形式，然后根据方程、等式的性 质作出准确判定.
在 Rt△ABC 中，斜边长是定长 2a(a＞0)，求直角顶点 C 的轨迹方 程.
【精彩点拨】 (1)如何建立坐标系？(2)根据题意列出怎样的等量关系？(3) 化简出的方程是否为所求轨迹方程？
【自主解答】 取AB边所在的直线为x轴，AB的中点O为坐标原点， 过O与AB垂直的直线为y轴，建立如图所示的直角坐标系， 则A(－a,0)，B(a,0)，设动点C为(x，y). 由于|AC|2＋|BC|2＝|AB|2， 所以( x＋a2＋y2)2＋( x－a2＋y2)2＝4a2，整理得x2＋y2＝a2. 由于当x＝±a时，点C与A或B重合，故x≠±a. 所以所求的点C的轨迹方程为x2＋y2＝a2(x≠±a).
1.求曲线方程的一般步骤 (1)建系设点； (2)写几何点集； (3)翻译列式； (4)化简方程； (5)查漏排杂：即证明以化简后方程的解为坐标的点都是曲线上的点.
2.一般情况下，化简前后方程的解集是相同的，步骤(5)可以省略不写，如 有特殊情况，可适当予以说明，另外，根据情况，也可以省略步骤(2)，直接列 出曲线方程.
(2)到两坐标轴的距离的积等于5的点的坐标不一定满足方程xy＝5，但以方 程xy＝5的解为坐标的点与两坐标轴的距离之积一定等于5.因此到两坐标轴的距 离的积等于5的点的轨迹方程不是xy＝5.
(3)第二、四象限角平分线上的点的坐标都满足x＋y＝0，反之，以方程x＋ y＝0的解为坐标的点都在第二、四象限角平分线上.因此第二、四象限角平分线 上的点的轨迹方程是x＋y＝0.

• P(x0, y0)
点 P 到 原 点 的 距 离 为 5
x02y0225
(x 0 ,y 0 )是 方 程 x2y22 5 的 解 。
x2y2 25
( 2 ) 设 （ x 0 , y 0 ) 是 方 程 x 2 y 2 2 5 的 解 。
x02y0225 x02y02 5
M (x 0 ,y 0 ) 求 的 方 程 为 ： x4y120
例 3 ： 两 个 定 点 的 距 离 为 6 ， 点 M 到 两 个 定 点 的 距 离 的 平 方 和 为 2 6 ，
求 点 M 的 轨 迹 方 程 ？
解 ： 建 立 如 图 所 示 的 坐 标 系 ， 设 A （ - 3 ， 0 ） ， B （ 3 ， 0 ） ,
( 2 ) 设 点 M 的 坐 标 （ x , y ) 是 方 程 ： x 4 y 1 2 0 的 解
x4y12 M A (x 1 )2 (y 1 )217y2102y170
MAMB M B(x 1 )2 (y 7 )2 17y2102y170
x 4 y 1 2 0 的 解 为 坐 标 都 在 线 段 A B 的 垂 直 平 分 线 上
小结：曲线和方程的关系
点M
按 某 中 规 律 运 动 曲线C
几何意义
x,y的 制 约 条 件
坐标(x,y)
方 程 f(x,y)0
代数意义
“数形结合” 数学思想的基础
例 2 ： 设 A ， B 两 点 的 坐 标 为 （ 1 ， - 1 ） ， （ - 1 ， 7 ） ， 求 线 段 A B 的 垂 直 平 分 线 的 方 程 ？
y x2
• A(x1, y1)
A(x1, y1)
y1 x12

第二步，设(x0,y0)是f(x,y)=0的解，证明 点M (x0,y0)在曲线C上.
第9页/共16页
课堂练习1:下列各题中，下图各曲线的曲线方程是所
列出的方程吗？为什么？
(1)曲线C为过点A(1，1)，B(-1，1)的
折线(如图(1))其方程为(x-y)(x+y)=0; 不是
(2)曲线C是顶点在原点的抛物线其方
⑵若 (x0 , y0 ) 是方程 y kx b 的解,则 M (x0 , y0 ) 是经过点 P (0, b) 和斜率为 k 的直线 l 上的一点.
继续
第12页/共16页
课外练习3：
设圆M的方程为
, 直线
l 的方程为x+y-3=0, 点P的坐标为(2,1)，那
么（C
）
A.点P在直线上，但不在圆上 B.点P在圆上，但不在直线上； C.点P既在圆上，也在直线上 D.点P既不在圆上，也不在直线上
两边开方取算术根，得：
即点M (x0,y0)到坐标原点的距离等于5，点M (x0,y0)是这 个圆上的一点.
第7页/共16页
由(1)、(2)可知， x2 +y2 = 25,是以坐标原点为圆 心，半径等于5的圆的方程.
第8页/共16页
归纳: 证明已知曲线的方程的方法和步骤
第一步，设M (x0,y0)是曲线C上任一点， 证明(x0,y0)是f(x,y)=0的解；
y
f(x,y)=0
这条曲线C叫做这个方程f(x,y)=0
0
x
的曲线.
说明:1.曲线的方程——反映的是图形所满足的数量关系; 方程的曲线——反映的是数量关系所表示的图形.
第2页/共16页
2.方程的曲线与曲线的方程的关系:

第二章 圆锥曲线与方程
2．1 曲线与方程
2．1．1 曲线与方程 2．1．2 求曲线的方程
第二章 圆锥曲线与方程
1．了解曲线与方程的概念． 2．理解曲线上的点与 方程的解之间的一一对应关系，领会“曲线的方程”与“方 程的曲线”的含义． 3．掌握求轨迹方程建立坐标系的一般 方法，熟悉求曲线方程的五个步骤．
选 B．
栏目 导引
第二章 圆锥曲线与方程
(2)由方程(x＋y－1) x－1＝0， 可得xx－＋1y－≥10＝，0 或xx－－11≥＝00，， 即 x＋y－1＝0(x≥1)或 x＝1． 故方程表示一条射线 x＋y－1＝0(x≥1)和一条直线 x＝1．
栏目 导引
第二章 圆锥曲线与方程
栏目 导引
第二章 圆锥曲线与方程
探究点 1 曲线与方程的概念
(1)已知 0≤α＜2π，点 P(cos α，sin α)在曲线(x－2)2
＋y2＝3 上，则 α 的值为( )
A．π3
B．53π
C．π3或53π
D．π3或π6
栏目 导引
第二章 圆锥曲线与方程
(2)“曲线 C 上的点的坐标都是方程 f(x，y)＝0 的解”是“曲 线 C 的方程是 f(x，y)＝0”的( ) A．充要条件 B．充分不必要条件 C．必要不充分条件 D．既不充分又不必要条件
[变条件]若把本例(2)中的方程变为“(x2＋y2－1)· x－1＝ 0”，判断方程表示的曲线是什么． 解：由方程(x2＋y2－1) x－1＝0 得xx2－＋1y≥2－0 1＝0， 或xx－－11＝≥00，， 即点(1，0)或 x＝1， 故方程表示直线 x＝1 或点(1，0)．
栏目 导引
第二章 圆锥曲线与方程
探究点 2 由方程判断曲线

[解] (1)过点A(2,0)平行于y轴的直线上的点的坐标都是方
程|x|＝2的解；但以方程|x|＝2的解为坐标的点不一定都在过点 A(2,0)且平行于y轴的直线上．因此，|x|＝2不是过点A(2,0)平行 于y轴的直线的方程．
(2)与两坐标轴的距离的积等于5的点的坐标不一定满足方程 xy＝5；但以方程xy＝5的解为坐标的点与两坐标轴的距离之积 一定等于5.因此，与两坐标轴的距离的积等于5的点的轨迹方程 不是xy＝5.
()
A．π
B．4π
C．8π
D．9π
解析：设 P(x，y)，由|PA|＝2|PB|，得 x＋22＋y2＝2 x－12＋y2， 整理得 x2－4x＋y2＝0，即(x－2)2＋y2＝4.所以点 P 的轨迹是以(2,0) 为圆心，2 为半径的圆，则其面积是 22·π＝4π. 答案：B
3．若点 P(2，－3)在曲线 x2－ky2＝1 上，则实数 k＝________. 解析：将点 P(2，－3)代入曲线方程得 4－9k＝1，∴k＝13. 答案：13
曲线与方程
曲线与方程
[提出问题] 在平面直角坐标系中： 问题 1：直线 x＝5 上的点到 y 轴的距离都等于 5，对吗？
提示：对．
问题 2：到 y 轴的距离都等于 5 的点都在直线 x＝5 上，对吗？
提示：不对，还可能在直线 x＝－5 上． 问题 3：到 y 轴的距离都等于 5 的点的轨迹是什么？
曲线的方程与方程的曲线的概念
[例 1] 分析下列曲线上的点与相应方程的关系： (1)过点 A(2,0)平行于 y 轴的直线与方程|x|＝2 之间的关系； (2)与两坐标轴的距离的积等于 5 的点与方程 xy＝5 之间的关系； (3)第二、四象限两坐标轴夹角平分线上的点与方程 x＋y＝0 之间 的关系．

2.指出方程(2x+3y-5)( x 3 -1)=0表示的曲线是什么？
【解析】1.选A.选项A是表示直线l的方程，而B，C，D都不是 表示直线l的方程.选项B中，直线l上的点的坐标不全是方程的 解，如(－1，－1)等，即不符合“直线上的点的坐标都是方程 的解”这一结论.选项C中，虽然“直线l上的点的坐标都是方程 的解”，但以方程x2－y2=0的解为坐标的点不全在直线l上， 如点(2，－2)等，即不符合“以方程的解为坐标的点都在直线 上”这一结论.选项D中，依照选项B，C的分析方式得出不符 合“直线上的点的坐标都是方程的解”这一结论，比如点(－1， -1).故选A.
当Δ＝0，即－4a2－16a+48=0时，得a=－6或a=2，此时方
程组有一解；
当Δ>0，即－4a2－16a+48>0时，得－6<a<2，此时方程组
有两解；
当Δ<0，即－4a2－16a+48<0时，得a<－6或a>2，此时方 程组无实数解. 综上所述，当a=－6或a=2时有一个交点； 当－6<a<2时有两个交点； 当a<－6或a>2时无交点.
曲线与方程
曲线的方程与方程的曲线的定义 一般地，在直角坐标系中，如果某曲线C上的点与一个二元方 程f(x,y)=0的实数解建立了如下的关系： (1)曲线上点的坐标都是_这__个__方__程__的__解__； (2)以这个方程的解为坐标的点都是_曲__线__上__的__点__. 那么，这个方程就叫做曲线的方程；这条曲线就叫做方程的曲 线.
(2)判断点是否在曲线上，其实质就是判断点的坐标是否适合 曲线的方程. (3)判定方程是否是曲线的方程或判定曲线是否是方程的曲线， 只要一一检验定义中的“两条性质”是否都满足，并作出相应 的回答即可.这是解决“曲线”与“方程”问题的关键.

x 2 y 2 1上的动点B，求线段 AB的中点P的轨迹方程。
例题中用到的求轨迹方程的方法通常叫做“代入法”
这类求轨迹方程的问题的特点是: 问题中一般含有两个（或两个以上）的相关联的 动点, 其中一个动点在已知曲线上运动, 所以 “代入法”又叫做相关点法.
例题讲解
例4：已知两点A 2，0和B(2,0),动点M与点
A及点B的连线的斜率之积等于1 ，求点M 3
的轨迹方程。
复习引入
• 曲线的方程和方程的曲线的定义 • 一般地，在直角坐标系中，如果某曲线
C（看作适合某种条件下的点的集合或轨迹） 上的点与一个方程f(x,y)=0有以下的关系: • （1）曲线上的点的坐标都是这个方程的解； • （2）以这个方程的解为坐标的点都在曲线 上。那么，这个方程叫曲线的方程，这条 曲线叫做方程的曲线（图形）。
总结
求曲线的方程一般步骤 1.建立适当的坐标系（如果已给出, 本步骤省 2.设曲线上任意一点的坐标为(x.y)
3.根据曲线上所适合的条件, 写成等式 4.用坐标x.y表示这个等式（方程）, 并化简 5.证明以化简后的方程的解为坐标的点都是 曲线上的点（在本教材中, 这一步不做要求）
例题讲解
例3：已知定点A（4，0）和曲线
新课讲授
平面解析几何研究的两个基本问题:
1.根据条件, 求出表示题讲解
例1：已知两定点A(1,0）和B(3,0) 求到点A和B的距离的平方和是16 的点的轨迹方程。
例题讲解
例2：动点M与距离为4的两个定点
A、B满足MA• MB 5,建立适当的 坐标系，求动点M的轨迹方程。

由曲线和方程的这一对应关系,既可以通过方程研究曲线的性 质,又可以通过曲线求出曲线的方程.
类型 一 曲线的方程与方程的曲线的概念 【典型例题】 1.设方程f(x,y)=0的解集非空,如果命题“坐标满足方程 f(x,y)=0的点都在曲线C上”是不正确的,则下面命题中正确 的是( ) A.坐标满足f(x,y)=0的点都不在曲线C上 B.曲线C上的点的坐标不满足f(x,y)=0 C.坐标满足f(x,y)=0的点有些在曲线C上,有些不在曲线C上 D.一定有不在曲线C上的点,其坐标满足f(x,y)=0
x x
y 或1 者0, 30
-1=x0,也3 就是x+y-1=0(x≥3)或x=4.
故方程表示一条射线和一条直线.
【拓展提升】
1.曲线与方程的判定技巧 (1)若方程f(x,y)=0无实数解,则与之对应的曲线是不存在的. 反之曲线不存在,则方程f(x,y)=0无实数解. (2)判断点是否在曲线上,其实质就是判断点的坐标是否适合曲 线的方程. (3)判定方程是否是曲线的方程或判定曲线是否是方程的曲线, 只要一一检验定义中的“两条性质”是否都满足,并作出相应 的回答即可.这是解决“曲线”与“方程”问题的关键.
曲线与方程
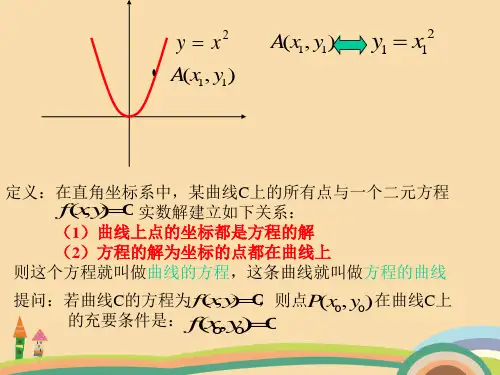
曲线的方程和方程的曲线的定义
一般地,在直角坐标系中,如果某曲线C(看作点的集 前提 合或适合某种条件的点的轨迹)上的点与一个二元
方程f(x,y)=0的实数解建立了如下的关系: 条件 ①曲线上点的坐标都是_这__个__方__程__的__解__;
②以这个方程的解为坐标的点都是_曲__线__上__的__点__ 这个方程就叫做曲线的方程;这条曲线就叫做方程 结论 的曲线
判断:(正确的打“√”,错误的打“×”) (1)以方程f(x,y)=0的解为坐标的点都在曲线上,那么方程 f(x,y)=0就是曲线的方程.( ) (2)如果f(x,y)=0是某曲线C的方程,则曲线上的点的坐标都适 合方程.( ) (3)x2+y2=1(x>0)表示的曲线是单位圆.( )

A.3x62 ＋2y72 ＝1(y≠0)
B.49x2＋y2＝1(y≠0)
C.94x2＋3y2＝1(y≠0)
D.x2＋43y2＝1(y≠0)
15
知识衍化体验
考点聚集突破
解析 依题意知 F1(－1，0)，F2(1，0)，设 P(x0，y0)(y0≠0)，G(x，y)，则由三角形 重心坐标公式可得xy＝ ＝xy300， －31＋1，即xy00＝ ＝33xy， ，代入椭圆 C：x42＋y32＝1， 得重心 G 的轨迹方程为94x2＋3y2＝1(y≠0). 答案 C
考点聚集突破
6.(2019·汉中模拟)在平面直角坐标系中，O 为坐标原点，A(1，0)，B(2，2)，若点 C 满足 O→C＝O→A＋t(O→B－O→A)，其中 t∈R，则点 C 的轨迹方程是________. 解析 设 C(x，y)，则由O→C＝O→A＋t(O→B－O→A)得O→C－O→A＝t(O→B－O→A)，所以A→C＝tA→B， 即(x－1，y)＝t(1，2)，故xy－ ＝12＝ t t，消去 t 得 y＝2(x－1)，即 2x－y－2＝0.
12
知识衍化体验
考点聚集突破
规律方法 利用直接法求轨迹方程 (1)利用直接法求解轨迹方程的关键是根据条件准确列出方程，然后进行化简. (2)运用直接法应注意的问题：①在用直接法求轨迹方程时，在化简的过程中，有 时破坏了方程的同解性，此时就要补上遗漏的点或删除多余的点，这是不能忽视的； ②若方程的化简过程是恒等变形，则最后的验证可以省略.
∴|PM|＝ |MA|2＋|PA|2＝ 2，
即|PM|2＝2，∴(x－1)2＋y2＝2. 答案 D
14
知识衍化体验
考点聚集突破
考点二 相关点(代入)法求轨迹方程 【例 2】 (1)(2019·宜春调研)已知 F1，F2 分别为椭圆 C：x42＋y32＝1 的左、右焦点，点 P