初中几何辅助线课件的ppt

线段的中点是几何图形中的一个特殊点，与中点有关的线段主要有中线和中位线，其中中线在三角形中经常遇到，而中位线一般出现在三角形和四边形中.这两种线段都是在作与中点有关的辅助线时的重要依据.下面结合具体例题，谈谈关于中点辅助线的几种作法.类型一：一个中点的辅助线作法方法1：倍长中线若图中出现中线或与中点有关的线段时，可以延长中线，使所延长部分与中线相等，再连接相应的顶点，则对应角、对应边都对应相等，其目的是构造全等三角形或平行四边形解题.例1如图1，在∆ABC中,AD交BC于点D,点E是BC的中点，EF∥AD交CA的延长线于点F，交AB于点G，若AD为∆ABC的角平分线，求证：BG=CF.图1图2证明：如图2，延长FE到点H，使HE=FE，连接BH.因为CE=BE，∠CEF=∠BEH，FE=HE，所以∆CEF≌∆BEH，所以∠F=∠H，CF=BH.因为EF∥AD，所以∠BGH=∠BAD，∠CAD=∠F.又∠BAD=∠CAD，所以∠H=∠BGH，所以BG=BH，所以BG=CF.方法2：构造“三线合一”在等腰三角形中，顶角的角平分线、底边的中线和高线，三条线互相重合，就简称为三线合一.因此，若题目条件中出现等腰三角形底边上的中点时，则连接底边中线，构造三线合一，运用等腰三角形“三线合一”的性质可以证明角相等、线段相等或垂直，进而减少证明三角形全等的次数，简化解题过程.例2如图3，点P是等腰RtΔABC底边BC上一点，过点P作BA，AC的垂线，垂足分别为点E，F，设点D为BC的中点.求证：△DEF 是等腰直角三角形.图3初中数学：与线段中点相关的辅助线做法图4证明：如图4，连接ME ，MD .因为BD 是∆ABC 的高，所以∠BDC =90°.在Rt∆BCD 中，BM =MC ，所以MD =12BC ，同理ME =12BC ，所以ME =MD .又因为PE =PD ，所以PM ⊥DE .类型二：两个及以上中点的辅助线作法当图中有多个中点时，除了上述利用中点的性质作辅助线外，同时还要考虑作中位线.若已知三角形的两边有中点，可以连接两点构造中位线；若已知三角形的一边中点，可以在另一边上取中点，连接两点构造中位线；若已知三角形的一边中点，过中点作平行线可构造相似三角形.例4如图5，在△ABC 中，分别以AB ，AC 为斜边作等腰直角三角形ABM 和CAN ，P 为BC 的中点，求证：PM =PN.图5证明：如图5，分别取AB ，AC 的中点D ，Q ，连接DM ，DP ，QN ，QP .因为点P 为BC 的中点，所以DP ∥AC ，DP =12AC ，同理可得PQ ∥AB ，PQ =12AB .所以∠BDP =∠PQC =∠BAC ，因为△ABM ，△ACN 均为等腰直角三角形，且D ，Q 均为AB ，AC 的中点，所以MD =12AB ，NQ =12AC ，∠MDB =∠NQC =90°，所以MD =PQ ，PD =NQ ，∠MDP =∠PQN =90°-∠BAC ，所以△MDP ≌△PQN ，所以PM =PN .从上述几例含有中点条件的问题可以看出，在三角形中，如果已知一点或两点是三角形某边上的中点，或题目的已知条件中出现了中点与其它条件的组合，则要由中点联想到作三角形的中线、中位线或加倍延长线段等方法，添加辅助线，然后依据相关性质，即可迅速找到解题的思路．解析：如图3，连接AD . 由题意知，∠B =∠C =45°.因为D 为中点，所以AD =BD =DC ，且∠BAD =∠CAD =45°. 因为∠PEA =∠EAF =∠AFP =90°， 所以四边形AEPF 是矩形，所以PE =AF . 由∠PEA =90°，∠B =45°，所以∠B =∠BPE =45°，所以BE =PE =AF . 因为BD =AD ，∠B =∠DAF ，BE =AF ， 所以∆DBE ≌∆DAF ， 所以DE =DF ，∠BDE =∠ADF ， 所以∠BDA =∠EDF =90°， 所以△DEF 是等腰直角三角形. 方法3：连接斜边中线若题目条件中出现直角三角形斜边上的中点时，经常会作斜边上的中线，利用直角三 角形斜边上的中线等于斜边的一半，得到三 条相等的线段和两对相等的角，还可以得到 两个等腰三角形，从而为解题创造条件.例3如图 4，∆ABC 中，BD 和 CE 是高，M 为 BC 的中点，P 为 DE 的中点.求证:PM ⊥DE .。

初中几何辅助线做法辅助线,如何添把握定理和概念;还要刻苦加钻研,找出规律凭经验;三角形图中有角平分线,可向两边作垂线;也可将图对折看,对称以后关系现;角平分线平行线,等腰三角形来添;角平分线加垂线,三线合一试试看;线段垂直平分线,常向两端把线连;要证线段倍与半,延长缩短可试验;三角形中两中点,连接则成中位线;三角形中有中线,延长中线等中线;四边形平行四边形出现,对称中心等分点;梯形里面作高线,平移一腰试试看;平行移动对角线,补成三角形常见;证相似,比线段,添线平行成习惯;等积式子比例换,寻找线段很关键;直接证明有困难,等量代换少麻烦;斜边上面作高线,比例中项一大片;圆半径与弦长计算,弦心距来中间站;圆上若有一切线,切点圆心半径连;切线长度的计算,勾股定理最方便;要想证明是切线,半径垂线仔细辨;是直径,成半圆,想成直角径连弦;弧有中点圆心连,垂径定理要记全;圆周角边两条弦,直径和弦端点连;弦切角边切线弦,同弧对角等找完;要想作个外接圆,各边作出中垂线;还要作个内接圆,内角平分线梦圆;如果遇到相交圆,不要忘作公共弦;内外相切的两圆,经过切点公切线;若是添上连心线,切点肯定在上面;要作等角添个圆,证明题目少困难;辅助线,是虚线,画图注意勿改变; 假如图形较分散,对称旋转去实验;基本作图很关键,平时掌握要熟练; 解题还要多心眼,经常总结方法显;切勿盲目乱添线,方法灵活应多变; 分析综合方法选,困难再多也会减;一、见中点引中位线,见中线延长一倍在几何题中,如果给出中点或中线,可以考虑过中点作中位线或把中线延长一倍来解决相关问题;二、在比例线段证明中,常作平行线;作平行线时往往是保留结论中的一个比,然后通过一个中间比与结论中的另一个比联系起来;三、对于梯形问题,常用的添加辅助线的方法有1、过上底的两端点向下底作垂线2、过上底的一个端点作一腰的平行线3、过上底的一个端点作一对角线的平行线4、过一腰的中点作另一腰的平行线5、过上底一端点和一腰中点的直线与下底的延长线相交6、作梯形的中位线7、延长两腰使之相交四、在解决圆的问题中1、两圆相交连公共弦;2、两圆相切,过切点引公切线;3、见直径想直角4、遇切线问题,连结过切点的半径是常用辅助线5、解决有关弦的问题时,常常作弦心距;。

常用辅助线做法➢考点考向1. 与角平分线有关的辅助线2. 与线段长度相关的辅助线3. 与等腰、等边三角形相关的辅助线4. 与中点相关的辅助线5. 构造一线三垂直（等角）6. 等面积法常见辅助线的作法总结1)遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题，思维模式是全等变换中的“对折”．2)遇到三角形的中线，倍长中线，使延长线段与原中线长相等，构造全等三角形，利用的思维模式是全等变换中的“旋转”．3)遇到角平分线，可以自角平分线上的某一点向角的两边作垂线，利用的思维模式是三角形全等变换中的“对折”，所考知识点常常是角平分线的性质定理或逆定理．4)过图形上某一点作特定的平分线，构造全等三角形，利用的思维模式是全等变换中的“平移”或“翻转折叠”。

5)截长法与补短法，具体做法是在某条线段上截取一条线段与特定线段相等，或是将某条线段延长，是之与特定线段相等，再利用三角形全等的有关性质加以说明．这种作法，适合于证明线段的和、差、倍、分等类的题目．6)构造等腰三角形或作等腰三角形的高利用“三线合一”性质。

7)作三角形的中位线。

8)引平行线构造全等三角形。

9）特殊方法：在求有关三角形的定值一类的问题时，常把某点到原三角形各顶点的线段连接起来，利用三角形面积的知识解答．（等面积法）10）构造三垂直模型。

✧考点一：与角平分线有关的辅助线（1）可向两边作垂线。

（2）可构造等腰三角形（3）在角的两边截取相等的线段，构造全等三角形【例1】已知：∠AOB＝90°，OM是∠AOB的平分线，将三角板的直角顶点P在射线OM上滑动，两直角边分别与OA、OB交于C、D，PC和PD有怎样的数量关系，请说明理由．✧考点二：与线段长度有关的辅助线（1）截长：证明某两条线段的和或差等于第三条线段时，经常在较长的线段上截取一段，使得它和其中的一条相等，再利用全等证明余下的等于另一条线段即可（2）补短：证明某两条线段的和或差等于第三条线段时，也可以在较短的线段上延长一段，使得延长的部分等于另外一条较短的线段，再利用全等证明延长后的线段等于那一条长线段即可（3）倍长中线：题目中如果出现了三角形的中线，方法是将中线延长一倍，再将端点连结，便可得到全等三角形。

几何专题——辅助线平面几何是初中教学的重要组成部分，它的基础知识在生产实践和科学研究中有着广泛的应用，又是继续学习数学和其他学科的基础，但许多初中生对几何证实题感到困难，尤其是对需要添加辅助线的证实题，往往束手无策。

一、辅助线的定义：为了证实的需要，在原来图形上添画的线叫做辅助线。

二、几种常用的辅助线：连结、作平行线、作垂线、延长等注意：1）添加辅助线是手段，而不是目的，它是沟通已知和未知的桥梁，不能见到题目，就无目的地添加辅助线。

一则没用、二则辅助线越多，图形越乱，反而妨碍思考问题。

2）添加辅助线时，一条辅助线只能提供一个条件三、正确添加辅助线歌人说几何很困难，难点就在辅助线。

辅助线，如何添？把握定理和概念。

还要刻苦加钻研，找出规律凭经验。

图中有角平分线，可向两边作垂线。

也可将图对折看，对称以后关系现。

角平分线平行线，等腰三角形来添。

角平分线加垂线，三线合一试试看。

线段垂直平分线，常向两端把线连。

要证线段倍与半，延长缩短可试验。

三角形中两中点，连接则成中位线。

三角形中有中线，延长中线等中线。

平行四边形出现，对称中心等分点。

梯形里面作高线，平移一腰试试看。

平行移动对角线，补成三角形常见。

证相似，比线段，添线平行成习惯。

等积式子比例换，寻找线段很关键。

直接证实有困难，等量代换少麻烦。

斜边上面作高线，比例中项一大片。

半径与弦长计算，弦心距来中间站。

圆上若有一切线，切点圆心半径连。

切线长度的计算，勾股定理最方便。

要想证实是切线，半径垂线仔细辨。

是直径，成半圆，想成直角径连弦。

弧有中点圆心连，垂径定理要记全。

圆周角边两条弦，直径和弦端点连。

弦切角边切线弦，同弧对角等找完。

要想作个外接圆，各边作出中垂线。

还要作个内接圆，内角平分线梦圆假如碰到相交圆，不要忘作公共弦。

内外相切的两圆，经过切点公切线。

若是添上连心线，切点肯定在上面。

要作等角添个圆，证实题目少困难。

辅助线，是虚线，画图注重勿改变。

假如图形较分散，对称旋转去实验。

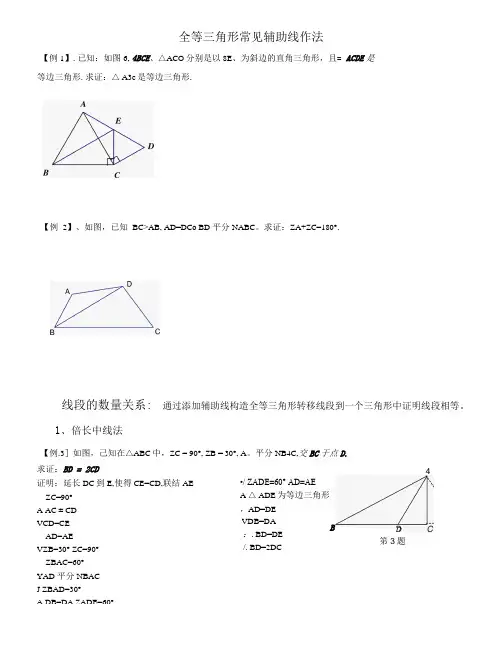
全等三角形常见辅助线作法【例1】.已知：如图6, 4BCE、△ACO分别是以8E、为斜边的直角三角形，且= ACDE是等边三角形.求证：△ A3c是等边三角形.【例2】、如图，已知BC>AB, AD=DCo BD 平分NABC。

求证：ZA+ZC=180°.线段的数量关系: 通过添加辅助线构造全等三角形转移线段到一个三角形中证明线段相等。

1、倍长中线法【例.3］如图，己知在△ABC中，ZC = 90°, ZB = 30°, A。

平分NB4C,交BC于点D.求证：BD = 2CD证明：延长DC到E,使得CE=CD,联结AEZC=90°A AC ± CDVCD=CEAD=AEVZB=30° ZC=90°ZBAC=60°YAD 平分NBACJ ZBAD=30°A DB=DA ZADE=60°VDB=DA：.BD=DE/. BD=2DC4B D笫3题•/ ZADE=60° AD=AEA △ ADE为等边三角形，AD=DE【例4.】如图，。

是AABC的边上的点，且CD = AB, ZADB = ZBAD, AE是AARD的中线。

求证：AC = 2AEo 证明：延长AE至IJ点F,使得EF=AE联结DF在4ABE和4FDE中BE=DEZAEB=ZFEDAE=FE/.△ABE 也AFDE (SAS) A AB=FD ZABE=ZFDE VAB=DCJ FD = DCZADC=ZABD+ZBAD ZADB = ZBAD，ZADC=ZABD+ZBDA VZABE=ZFDE・・・NADONADB+NFDE即ZADC= ZADF ffiAADF 和AADC 中AD=AD< ZADF= ZADC、DF =DC・•・△ ADF也ADC(SAS) AAF=ACAC=2AE【变式练习】、如图，AABC中，BD二DOAC, E是DC的中点，求证：AD平分NBAE.【小结】熟悉法一、法三“倍长中线”的辅助线包含的基本图形“八字型”和“倍长中线”两种基本操作方法, 倍长中线，或者倍长过中点的一条线段以后的对于解决含有过中点线段有很好的效果。

初中几何常见辅助线作法歌诀人说几何很困难，难点就在辅助线。

辅助线，如何添？把握定理和概念。

还要刻苦加钻研，找出规律凭经验。

三角形图中若有角分线，可向两边作垂线。

也可将图对折看，对称以后关系现。

角平分线平行线，等腰三角形来添。

角平分线加垂线，三线合一试试看。

线段垂直平分线，常向两端把线连。

要证线段倍与半，延长缩短可试验。

三角形中两中点，连接则成中位线。

三角形中有中线，延长中线等中线。

四边形平行四边形出现，对称中心等分点。

梯形里面作高线，平移一腰试试看。

平行移动对角线，补成三角形常见。

证相似，比线段，添线平行成习惯。

等积式子比例换，寻找线段很关键。

直接证明有困难，等量代换少麻烦。

斜边上面作高线，比例中项一大片。

圆半径与弦长计算，弦心距来中间站。

圆上若有一切线，切点圆心半径连。

切线长度的计算，勾股定理最方便。

要想证明是切线，半径垂线仔细辨。

是直径，成半圆，想成直角径连弦。

弧有中点圆心连，垂径定理要记全。

圆周角边两条弦，直径和弦端点连。

弦切角边切线弦，同弧对角等找完。

要想作个外接圆，各边作出中垂线。

还要作个内接圆，内角平分线梦圆。

如果遇到相交圆，不要忘作公共弦。

内外相切的两圆，经过切点公切线。

若是添上连心线，切点肯定在上面。

要作等角添个圆，证明题目少困难。

辅助线，是虚线，画图注意勿改变。

假如图形较分散，对称旋转去实验。

基本作图很关键，平时掌握要熟练。

解题还要多心眼，经常总结方法显。

切勿盲目乱添线，方法灵活应多变。

分析综合方法选，困难再多也会减。

虚心勤学加苦练，成绩上升成直线。

初中几何辅助线口诀三角形图中有角平分线，可向两边作垂线。

也可将图对折看，对称以后关系现。

角平分线平行线，等腰三角形来添。

角平分线加垂线，三线合一试试看。

线段垂直平分线，常向两端把线连。

要证线段倍与半，延长缩短可试验。

三角形中两中点，连接则成中位线。

三角形中有中线，延长中线等中线。

四边形平行四边形出现，对称中心等分点。

梯形里面作高线，平移一腰试试看。

平行移动对角线，补成三角形常见。

证相似，比线段，添线平行成习惯。

等积式子比例换，寻找线段很关键。

直接证明有困难，等量代换少麻烦。

斜边上面作高线，比例中项一大片。

圆半径与弦长计算，弦心距来中间站。

圆上若有一切线，切点圆心半径连。

切线长度的计算，勾股定理最方便。

要想证明是切线，半径垂线仔细辨。

是直径，成半圆，想成直角径连弦。

弧有中点圆心连，垂径定理要记全。

圆周角边两条弦，直径和弦端点连。

弦切角边切线弦，同弧对角等找完。

要想作个外接圆，各边作出中垂线。

还要作个内接圆，内角平分线梦圆如果遇到相交圆，不要忘作公共弦。

内外相切的两圆，经过切点公切线。

若是添上连心线，切点肯定在上面。

要作等角添个圆，证明题目少困难。

辅助线，是虚线，画图注意勿改变。

假如图形较分散，对称旋转去实验。

基本作图很关键，平时掌握要熟练。

解题还要多心眼，经常总结方法显。

切勿盲目乱添线，方法灵活应多变。

分析综合方法选，困难再多也会减。

虚心勤学加苦练，成绩上升成直线作辅助线的方法一、中点、中位线，延线，平行线。

如遇条件中有中点，中线、中位线等，那么过中点，延长中线或中位线作辅助线，使延长的某一段等于中线或中位线；另一种辅助线是过中点作已知边或线段的平行线，以达到应用某个定理或造成全等的目的。

二、垂线、分角线，翻转全等连。

如遇条件中，有垂线或角的平分线，可以把图形按轴对称的方法，并借助其他条件，而旋转180度，得到全等形，，这时辅助线的做法就会应运而生。

其对称轴往往是垂线或角的平分线。

三、边边若相等，旋转做实验。

初中几何辅助线专题——等腰三角形中最重要的辅助线是“三
线合一”
初中几何辅助线专题——等腰三角形中最重要的辅助线是“三线合一”
初中几何辅助线专题课程
初中几何辅助线专题——见等腰三角形底边中点，必三线合一
初中几何辅助线专题——见中点，延长线段，可造全等
初中几何辅助线专题——“有中点，再造中点”与“见中点，倍长线段”
初中几何辅助线专题——有中点，再造中点，连成中位线
初中几何辅助线专题——有斜边的一半，必作斜边上的中线（2）初中几何辅助线专题——有斜边的一半，必作斜边上的中线（1）初中几何辅助线专题——直角三角形斜边上的中线等于斜边的一半
初中几何辅助线专题——见中点倍长线段与勾股定理
初中几何辅助线专题——角分垂等腰归与中位线
初中几何辅助线专题——有中点，再造中点（2）
初中几何辅助线专题——有中点，再造中点（1）
初中几何辅助线专题——连中点，得中位线（2）
初中几何辅助线专题——连中点，得中位线（1）
初中几何辅助线专题——见中点，倍长线段（3）
初中几何辅助线专题——见中点，倍长线段（2）
初中几何辅助线专题——见中点，倍长线段（1）
初中几何辅助线专题——角分垂，等腰归（3）
初中几何辅助线专题——角分垂，等腰归（2）
初中几何辅助线专题——角分垂，等腰归（1）
初中几何辅助线专题——点分线，垂两边（2）
初中几何辅助线专题——点分线，垂两边（1）
初中几何辅助线专题——角边等，造全等（3）
初中几何辅助线专题——角边等，造全等（2）初中几何辅助线专题——角边等，造全等（1）。