三种经典网格细分算法的研究与分析

典型三角网格细分算法
江焯林;黎绍发;贾西平;祝红丽
【期刊名称】《计算机工程》
【年(卷),期】2009(35)6
【摘要】介绍7种典型的三角网格细分算法,对各种细分算法在连续性、具备优点及应用状况等几个方面进行比较和归类.为提高三角网格细分效果的可视化程度,将基于功能类机制的状态机模型作为软件运行模式,利用MFC和OpenGL实现交互式显示控制,并在此基础上对最具典型意义的Loop算法进行原型实现,给出优化方法.
【总页数】4页(P7-10)
【作者】江焯林;黎绍发;贾西平;祝红丽
【作者单位】华南理工大学计算机科学与工程学院,广州,510640;华南理工大学计算机科学与工程学院,广州,510640;华南理工大学计算机科学与工程学院,广
州,510640;华南理工大学资源科学与造纸工程学院,广州,510640
【正文语种】中文
【中图分类】TP301.6
【相关文献】
1.基于型面曲率的三角网格快速自适应细分算法 [J], 孙殿柱;朱昌志;李延瑞
2.基于三角形细分的三角网格模型表面体素化算法 [J], 赵芳垒;敬石开;李向前;邢昊;刘晨燕;宋国华
3.三角网格顶点重要度的自适应Loop细分算法 [J], 王艳艳;惠丽峰;罗晓锋;张荣国
4.基于二次误差的三角网格自适应细分算法研究 [J], 孙翰英;乔秀春;范强
5.面向移动终端的三角网格逆细分压缩算法 [J], 马建平;罗笑南;陈渤;李峥
因版权原因，仅展示原文概要，查看原文内容请购买。

网格细化方案概述网格细化是指在数值计算中将初始网格进行进一步细分，以提高数值模拟的准确性和精度的一种方法。

通过合理地细化网格，可以更好地捕捉复杂的几何形状和物理过程。

本文将介绍几种常见的网格细化方案，并探讨它们的优缺点和适用场景。

1. 均匀网格细化均匀网格细化是最简单的网格细化策略之一。

它按照固定的步长将初始网格划分为更小的网格单元。

这种方法的优点是简单易实现，且计算效率较高。

然而，它存在的问题是无法适应复杂的几何形状和物理过程，对于一些细节变化较大的区域，无法提供足够的分辨率。

因此，均匀网格细化主要适用于处理简单的几何形状和物理过程。

2. 自适应网格细化自适应网格细化是一种根据问题需要动态调整网格的方法。

它根据初始网格上的解的特点，通过一定的误差估计准则来判断是否需要进行网格细化。

这种方法的优点是可以根据问题的要求精确地捕捉局部细节，提高计算的准确性。

然而，自适应网格细化也存在一些问题，如在复杂的区域和物理过程中，调整网格的复杂度较高，计算时间较长。

因此，自适应网格细化主要适用于需要高精度解或处理复杂几何形状和物理过程的问题。

3. 多重网格细化多重网格细化是一种层次结构的网格细化方法。

它将问题划分为多个层次的网格，通过在不同层次的网格上进行迭代计算来逐渐提高解的精度。

多重网格细化的优点是可以在保持计算效率的同时提高解的精度。

然而，多重网格细化的实现较为复杂，需要进行网格层次间的数据交换和差值操作。

因此，多重网格细化主要适用于需要高精度解且计算时间要求较高的问题。

4. 网格细化方案的选择选择合适的网格细化方案取决于具体问题的特点和要求。

在实际应用中，需要根据问题的复杂程度、几何形状的复杂度、精度要求和计算效率等因素综合考虑。

对于简单的几何形状和物理过程，均匀网格细化是一种简单而有效的选择。

对于需要高精度解或处理复杂几何形状和物理过程的问题，自适应网格细化和多重网格细化是更合适的选择。

结论网格细化是提高数值模拟准确性和精度的重要方法之一。

表面细分算法
表面细分算法是一种用于生成高精度、高质量几何模型的方法。

它可
以将简单的三角形网络逐步细分为更复杂的几何形状，提高模型的准确性
和细节。

常见的表面细分算法包括：
1. Catmull-Clark细分算法：该算法是一种基于网格的方法，通过
对三角面片进行逐层细分，生成平滑的模型表面。

该算法适用于几何体、
动画和游戏等领域。

2. Loop细分算法：该算法是一种适用于细分高精度模型表面的方法，能够生成更细腻、更真实的表面细节。

该算法通过连接顶点和面片，生成
具有更高阶曲率的曲面。

3. Doo-Sabin细分算法：该算法可以将四边形及其子孙面细分为另
外四个四边形，从而生成更复杂的几何形状。

该算法可以产生类似于细胞、泡沫等复杂几何形状。

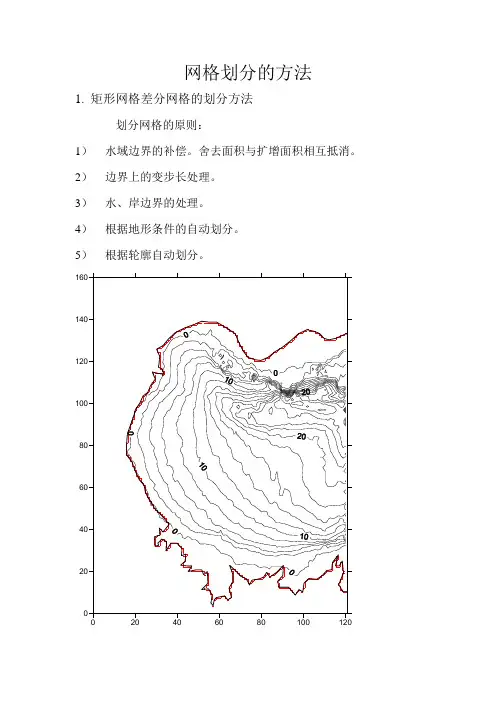
网格划分的方法1.矩形网格差分网格的划分方法划分网格的原则：1）水域边界的补偿。

舍去面积与扩增面积相互抵消。

2）边界上的变步长处理。

3）水、岸边界的处理。

4）根据地形条件的自动划分。

5）根据轮廓自动划分。

2.有限元三角网格的划分方法1）最近点和稳定结构原则。

2）均布结点的网格自动划分。

3）逐渐加密方法。

353025201510505101520253035距离(m)距离(m)3. 有限体积网格的划分方法1） 突变原则。

2） 主要通道边界。

3） 区域逐步加密。

距离(100m)离距(100m)距离(100m)离距(100m )4. 边界拟合网格的划分方法1） 变换函数：在区域内渐变，满足拉普拉斯方程的边值问题。

),(ηξξξP yy xx =+),(ηξηηQ yy xx =+2） 导数变化原则。

⎪⎪⎪⎪⎭⎫⎝⎛∂∂∂∂=⎪⎪⎪⎪⎭⎫ ⎝⎛∂∂∂∂-ηξ1J y x ，⎪⎪⎭⎫ ⎝⎛=ηηξξy x y x J 为雅可比矩阵，⎪⎪⎭⎫ ⎝⎛--=-ηηξξy x y x J J 11， ξηηξy x y x J -=)22(1222233ηηξηξηηξηξξηηηηηξξηηξξξηξy y x y y y x y y x x y y x y y x y J xx +-+-+-= 同理可得yy ξ，xx η，yy η。

变换方程为020222=+++-=+++-）（）（ηξηηξηξξηξηηξηξξγβαγβαQy Py J y y y Qx Px J x x x 其中2222,,ξξηξξηηηγβαy x y y x x y x +=+=+=。

几种经典网格细分算法的比较
王金生;韩臻;施寅;尹直诺
【期刊名称】《计算机应用研究》
【年(卷),期】2004(21)6
【摘要】曲面造型方法由于其局部性好、计算量小、算法简单、响应速度高等优点,已经广泛应用于计算机图形学、CAGD、计算机动画以及虚拟现实等领域.网格细分是一种离散造型方法,可以从数字化仪等设备直接获得数据.介绍了近年来提出的一些细分算法,对其中几种比较经典的算法进行了简单的分类和比较,并论述了各自的适用范围.
【总页数】3页(P139-141)
【作者】王金生;韩臻;施寅;尹直诺
【作者单位】北京交通大学,计算机与信息技术学院,北京,100044;北京交通大学,计算机与信息技术学院,北京,100044;北京交通大学,计算机与信息技术学院,北
京,100044;青岛市城阳区国家税务局,山东,青岛,266109
【正文语种】中文
【中图分类】TP391
【相关文献】
1.几种经典插值算法的放大结果比较 [J], 马书红
2.几种经典快速块匹配运动估计算法的比较研究 [J], 肖敏连
3.三种经典网格细分算法的研究与分析 [J], 王世江
4.约瑟夫环经典问题的几种算法比较 [J], 王永红
5.几种经典的最短路径算法比较分析 [J], 赵卫绩;巩占宇;王雯;樊守芳
因版权原因，仅展示原文概要，查看原文内容请购买。

基于三角网格的任意尺度细分方法模板细分方法是现代最重要的曲线曲面生成技术之一,现已被广泛应用于曲线曲面设计、造型等工程领域.细分方法按一定的细分规则多尺度地逼近一个光滑曲面,在进行局部特征调控的同时,能够保证曲面整体的光滑性,能够处理任意拓扑的控制网格,是联系连续模型和离散表示的桥梁.与其它造型方法相比,细分方法具有明显的优势,其算法简单,容易实现,具有广泛的应用前景和很强的生命力.目前,大多细分方法都是二尺度细分或三尺度细分,对于任意尺度细分研究还不是十分深入和完善.本文给出了基于三角形网格空间S42(△)的任意尺度细分掩模的一般表达式.在此基础上,得出了求规则点的任意尺度细分模板的具体方法,对于细分方法的理论研究和实际应用具有重要意义.同主题文章[1].李燕琴. 一种生态旅游者的识别与细分方法——以北京市百花山自然保护区为例' [J]. 北京大学学报(自然科学版). 2005.(06)[2].冯兵,罗新星,周永生. 非契约型客户关系演变模型及其运用研究' [J]. 预测. 2006.(06)[3].张智丰,张亚荣. 细分曲线参数化与累加弦长参数化的数值比较' [J]. 湘潭师范学院学报(自然科学版). 2009.(04)[4].蒋玉明. 均匀B样条曲线(段)曲面(片)的非均匀细分算法' [J]. 四川大学学报(工程科学版). 1991.(05)[5].王建卫,张泽银,黄达人. 四边形网格的削角细分' [J]. 浙江大学学报(理学版). 2004.(02)[6].崔柳,张书练. 双频氦氖激光回馈位移测量系统的实验与应用研究' [J]. 应用光学. 2007.(03)[7].楚兴春,吕海宝,杜列波,周卫红. 任意相位差条纹信号细分方法的研究' [J]. 光学学报. 2005.(04)[8].郭俊鹏,刘西林. 基于ID3算法的进一步客户细分方法' [J]. 工业工程. 2006.(02)[9].Said ,M.Easa,余又生. 地块细分的直接计算法' [J]. 测绘科学. 1990.(Z1)[10].刘晓芬,潘日晶. 基于Loop细分方法的曲线插值' [J]. 福建师范大学学报(自然科学版). 2006.(01)【关键词相关文档搜索】：计算数学; Box样条; 细分模板; Loop细分; 细分曲面【作者相关信息搜索】：吉林大学;计算数学;李强;战扬;。

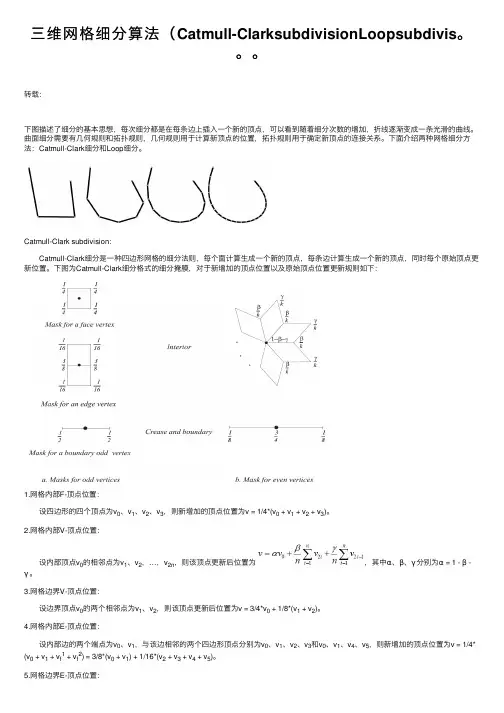
三维⽹格细分算法（Catmull-ClarksubdivisionLoopsubdivis。

转载：下图描述了细分的基本思想，每次细分都是在每条边上插⼊⼀个新的顶点，可以看到随着细分次数的增加，折线逐渐变成⼀条光滑的曲线。

曲⾯细分需要有⼏何规则和拓扑规则，⼏何规则⽤于计算新顶点的位置，拓扑规则⽤于确定新顶点的连接关系。

下⾯介绍两种⽹格细分⽅法：Catmull-Clark细分和Loop细分。

Catmull-Clark subdivision： Catmull-Clark细分是⼀种四边形⽹格的细分法则，每个⾯计算⽣成⼀个新的顶点，每条边计算⽣成⼀个新的顶点，同时每个原始顶点更新位置。

下图为Catmull-Clark细分格式的细分掩膜，对于新增加的顶点位置以及原始顶点位置更新规则如下：1.⽹格内部F-顶点位置： 设四边形的四个顶点为v0、v1、v2、v3，则新增加的顶点位置为v = 1/4*(v0 + v1 + v2 + v3)。

2.⽹格内部V-顶点位置： 设内部顶点v0的相邻点为v1、v2，…，v2n，则该顶点更新后位置为，其中α、β、γ分别为α = 1 - β -γ。

3.⽹格边界V-顶点位置： 设边界顶点v0的两个相邻点为v1、v2，则该顶点更新后位置为v = 3/4*v0 + 1/8*(v1 + v2)。

4.⽹格内部E-顶点位置： 设内部边的两个端点为v0、v1，与该边相邻的两个四边形顶点分别为v0、v1、v2、v3和v0、v1、v4、v5，则新增加的顶点位置为v = 1/4* (v0 + v1 + v f1 + v f2) = 3/8*(v0 + v1) + 1/16*(v2 + v3 + v4 + v5)。

5.⽹格边界E-顶点位置： 设边界边的两个端点为v0、v1，则新增加的顶点位置为v = 1/2*(v0 + v1)。

效果：function [VV, FF, S] = CC_subdivision(V, F, iter)% Catmull_Clark subdivisionif ~exist('iter','var')iter = 1;endVV = V;FF = F;for i = 1:iternv = size(VV,1);nf = size(FF,1);O = outline(FF);original = 1:nv;boundary = O(:,1)';interior = original(~ismember(original, boundary));no = length(original);nb = length(boundary);ni = length(interior);%% SvEtmp = sort([FF(:,1) FF(:,2);FF(:,2) FF(:,3);FF(:,3) FF(:,4);FF(:,4) FF(:,1)],2);[E, ~, idx] = unique(Etmp, 'rows');Aeven = sparse([E(:,1) E(:,2)], [E(:,2) E(:,1)], 1, no, no);Aodd = sparse([FF(:,1) FF(:,2)], [FF(:,3) FF(:,4)], 1, no, no);Aodd = Aodd + Aodd';val_even = sum(Aeven,2);beta = 3./(2*val_even);val_odd = sum(Aodd,2);gamma = 1./(4*val_odd);alpha = 1 - beta - gamma;Sv = sparse(no,no);Sv(interior,:) = ...sparse(1:ni, interior, alpha(interior), ni, no) + ...bsxfun(@times, Aeven(interior,:), beta(interior)./val_even(interior)) + ...bsxfun(@times, Aodd(interior,:), gamma(interior)./val_odd(interior));Sboundary = ...sparse([O(:,1);O(:,2)],[O(:,2);O(:,1)],1/8,no,no) + ...sparse([O(:,1);O(:,2)],[O(:,1);O(:,2)],3/8,no,no);Sv(boundary,:) = Sboundary(boundary,:);%% SfSf = 1/4 .* sparse(repmat((1:nf)',1 ,4), FF, 1);i0 = no + (1:nf)';%% Seflaps = sparse([idx;idx], ...[FF(:,3) FF(:,4);FF(:,4) FF(:,1);FF(:,1) FF(:,2);FF(:,2) FF(:,3)], ...1);onboundary = (sum(flaps,2) == 2);flaps(onboundary,:) = 0;ne = size(E,1);Se = sparse( ...[1:ne 1:ne]', ...[E(:,1); E(:,2)], ...[onboundary;onboundary].*1/2 + ~[onboundary;onboundary].*3/8, ...ne, ...no) + ...flaps*1/16;%% new faces & new verticesi1 = no + nf + (1:nf)';i2 = no + 2*nf + (1:nf)';i3 = no + 3*nf + (1:nf)';i4 = no + 4*nf + (1:nf)';FFtmp = [i0 i4 FF(:,1) i1; ...i0 i1 FF(:,2) i2; ...i0 i2 FF(:,3) i3; ...i0 i3 FF(:,4) i4];reidx = [(1:no)'; no+(1:nf)'; no+nf+idx];FF = reidx(FFtmp);S = [Sv; Sf; Se];VV = S*VV;endendLoop subdivision： Loop细分是⼀种三⾓形⽹格的细分法则，它按照1-4三⾓形分裂，每条边计算⽣成⼀个新的顶点，同时每个原始顶点更新位置。

在中国CAE论坛上看到这个，挺不错的壳体单元网格划分时，如果能了解一些网格划分的技巧和策略，将会事半功倍。

壳体网格划分可以从3个方面入手：几何模型、划分方法和解决策略。

1 几何模型可以从以下几个方面了解和处理几何模型问题（1）了解部件的形状，主要集中在尺寸小的部分。

（2）什么样的特征可以被忽略，例如小的倒角和圆孔。

（3）何种特征对分析是关键的特征，这些特征对确保好的单元质量是需要的。

2 划分方法(自动＋手工）可以采用如下方法（1）将部件分割为不同的区域。

（2）每个区域必须有可能只使用一种三维网格模式。

（3）寻找下述特点区域：大量生成区域、对称性区域、产生困难的区域。

（4）寻找大量不同区域和方法。

（5）注意什么样的二维网格模式被要求。

（6）观察周围区域：什么功能可以在那里使用。

（7）二维网格模式是否可以延伸到相邻区域中。

（8）寻找对网格模式不能处理位置进行网格划分的方法：如果这样做了，寻找网格可以触及的曲面；注意周围网格将与此模式相融合。

（9）小特征融入大特征中；大特征划分网格时必须考虑到小特征。

（10）注意网格模式。

3 解决策略壳体网格划分的主要策略如下（1）内部特征衔接外部特征：l 不能变成被限制的。

l 网格模式需要一个面流入以便它们可以停止l 从内到外划分网格可以避免此问题。

（2）小特征融入到大特征中：注意模式、大特征划分网格时必须考虑到小特征。

（3）硬特征应当先处理，否则它们会变得难于处理。

（4）通常情况下首先进行大量的生成，后面的编辑是比较容易的。

某些区域比较重要的网格划分的质量要求高些，如力的作用区域，边界条件所在的区域。

一些设计区域和离设计区域比较远的地方可以适当放宽要求，但是最好是一些网格性能指标要满足。

三角形网格生成算法的研究与应用一、引言三角网格是计算机图形学领域中最常见的图形表示方式之一。

三角形网格生成算法的出现为图形学在各个领域的应用提供了强有力的支持，如计算机辅助设计、数字娱乐、医学图像处理等等。

然而目前三角形网格的生成算法依然存在许多难点，本文将针对这些难点进行研究和分析，探讨三角形网格生成算法的研究与应用。

二、先进的三角形网格生成算法三角形网格生成算法主要分为离散型和连续型两种。

离散型算法主要是针对离散数据点进行分析和处理，是传统算法的核心。

而连续型算法则主要考虑通过合理的数值方法对连续函数进行求解得到三角形网格。

2.1 离散型算法离散型算法主要方法包括 Delaunay 三角剖分、Voronoi 图、alpha 参数、最小生成树等等。

Delaunay 三角剖分是三角形网格分割中最常见的算法之一。

该算法的核心思想是保持尽量少的单纯形边长相交。

Voronoi 图是一种基于点的分割方法，可以将平面分割成一系列多边形。

Alpha 参数是控制 Delaunay 三角剖分质量的措施之一，通过调整 alpha 参数，可以在不同场景下获得合适的 Delaunay 三角剖分。

最小生成树算法则是对点集进行聚类的一种方法，通常用于优化 Delaunay三角剖分的质量。

2.2 连续型算法连续型算法主要包括渐近线、等值线、样条曲面拟合、卷积核方法等等。

渐近线的求解方法主要是对三角形网格表面进行采样后，通过函数空间中的拟合逼近来求解渐近线。

等值线方法则是在网格表面中寻找等值线，从而实现扫描三角形网格的目的。

样条曲面拟合是利用拟合优化方法，对离散的三角形网格点进行拟合，得到连续的三角形网格。

卷积核方法则通过对三角形表面求导以及在线性空间中构建卷积核，从而求得三角形网格表面的连续性信息。

三、三角形网格生成算法在计算机图形学领域的应用三角形网格生成算法在计算机图形学领域的应用十分广泛，主要包括三维重构、曲面拟合、形状建模、虚拟现实等等。

第3章网格划分技术及技巧-图文创建几何模型后，必须生成有限元模型才能分析计算，生成有限元模型的方法就是对几何模型进行网格划分，网格划分主要过程包括三个步骤：⑴定义单元属性单元属性包括单元类型、实常数、材料特性、单元坐标系和截面号等。

⑵定义网格控制选项★对几何图素边界划分网格的大小和数目进行设置；★没有固定的网格密度可供参考；★可通过评估结果来评价网格的密度是否合理。

⑶生成网格★执行网格划分，生成有限元模型；★可清除已经生成的网格并重新划分；★局部进行细化。

3.1定义单元属性3.1.1单元类型1.定义单元类型命令：ET,ITYPE,Ename,KOP1,KOP2,KOP3,KOP4,KOP5,KOP6,INOPRITYPE---用户定义的单元类型的参考号。

KOP1~KOP6---单元描述选项，此值在单元库中有明确的定义，可参考单元手册。

也可通过命令KEYOPT进行设置。

INOPR---如果此值为1则不输出该类单元的所有结果。

例如：et,1,link8!定义LINK8单元，其参考号为1；也可用ET,1,8定义et,3,beam4!定义BEAM4单元，其参考号为3；也可用ET,3,4定义2.单元类型的KEYOPT命令：KEYOPT,ITYPE,KNUM,VALUEITYPE---由ET命令定义的单元类型参考号。

KNUM---要定义的KEYOPT顺序号。

VALUE---KEYOPT值。

该命令可在定义单元类型后，分别设置各类单元的KEYOPT参数。

例如：et,1,beam4!定义BEAM4单元的参考号为1et,3,beam189!定义BEAM189单元的参考号为3keyopt,1,2,1!BEAM4单元考虑应力刚度时关闭一致切线刚度矩阵keyopt,3,1,1!考虑BEAM189的第7个自由度，即翘曲自由度!当然这些参数也可在ET命令中一并定义，如上述四条命令与下列两条命令等效：et,1,beam4,,1et,3,beam189,13.自由度集命令：DOF,Lab1,Lab2,Lab3,Lab4,Lab5,Lab6,Lab7,Lab8,Lab9,Lab104.改变单元类型命令：ETCHG,Cnv5.单元类型的删除与列表删除命令：ETDELE,ITYP1,ITYP2,INC列表命令：ETLIST,ITYP1,ITYP2,INC3.1.2实常数1.定义实常数命令：R,NSET,R1,R2,R3,R4,R5,R6续：RMORE,R7,R8,R9,R10,R11,R12NSET---实常数组号（任意），如果与既有组号相同，则覆盖既有组号定义的实常数。