2017年高考真题分类汇编(理数)导数

专题04 导数及其应用（解答题）1．【2019年高考全国Ⅰ卷文数】已知函数f （）=2sin -cos -，f ′（）为f （）的导数． （1）证明：f ′（）在区间（0，π）存在唯一零点；（2）若∈[0，π]时，f （）≥a ，求a 的取值范围．2．【2019年高考全国Ⅱ卷文数】已知函数()(1)ln 1f x x x x =---．证明：（1）()f x 存在唯一的极值点；（2）()=0f x 有且仅有两个实根，且两个实根互为倒数．3．【2019年高考天津文数】设函数()ln (1)e x f x x a x =--，其中a ∈R .（Ⅰ）若a ≤0，讨论()f x 的单调性； （Ⅱ）若10ea <<， （i ）证明()f x 恰有两个零点；（ii ）设0x 为()f x 的极值点，1x 为()f x 的零点，且10x x >，证明0132x x ->.4．【2019年高考全国Ⅲ卷文数】已知函数32()22f x x ax =-+．（1）讨论()f x 的单调性；（2）当0<a <3时，记()f x 在区间[0，1]的最大值为M ，最小值为m ，求M m -的取值范围．5．【2019年高考北京文数】已知函数321()4f x x x x =-+． （Ⅰ）求曲线()y f x =的斜率为1的切线方程；（Ⅱ）当[2,4]x ∈-时，求证：6()x f x x -≤≤；（Ⅲ）设()|()()|()F x f x x a a =-+∈R ，记()F x 在区间[2,4]-上的最大值为M （a ），当M （a ）最小时，求a 的值．6．【2019年高考浙江】已知实数0a ≠，设函数()=ln 0.f x a x x +> （1）当34a =-时，求函数()f x 的单调区间；（2）对任意21[,)e x ∈+∞均有()2f x a ≤ 求a 的取值范围． 注：e=2.71828…为自然对数的底数．7．【2019年高考江苏】设函数()()()(),,,f x x a x b x c a b c =---∈R 、()f 'x 为f （）的导函数．（1）若a =b =c ，f （4）=8，求a 的值；（2）若a ≠b ，b =c ，且f （）和()f 'x 的零点均在集合{3,1,3}-中，求f （）的极小值；（3）若0,01,1a b c =<=…，且f （）的极大值为M ，求证M ≤427．8．【2018年高考全国Ⅲ卷文数】已知函数21()ex ax x f x +-=． （1）求曲线()y f x =在点(0,1)-处的切线方程；（2）证明：当1a ≥时，()e 0f x +≥．9．【2018年高考全国Ⅰ卷文数】已知函数()e ln 1xf x a x =--． （1）设2x =是()f x 的极值点，求a ，并求()f x 的单调区间；（2）证明：当1e a ≥时，()0f x ≥．10．【2018年高考全国Ⅱ卷文数】已知函数()()32113f x x a x x =-++．（1）若3a =，求()f x 的单调区间；（2）证明：()f x 只有一个零点．11．【2018年高考北京文数】设函数2()[(31)32]e x f x ax a x a =-+++.（Ⅰ）若曲线()y f x =在点(2,(2))f 处的切线斜率为0，求a ；（Ⅰ）若()f x 在1x =处取得极小值，求a 的取值范围.12．【2018年高考天津文数】设函数123()=()()()f x x t x t x t ---，其中123,,t t t ∈R ,且123,,t t t 是公差为d 的等差数列．（I ）若20,1,t d ==求曲线()y f x =在点(0,(0))f 处的切线方程；（II ）若3d =，求()f x 的极值；（III ）若曲线()y f x =与直线2()y x t =---d 的取值范围．13．【2018年高考浙江】已知函数f．（Ⅰ）若f()在=1，2(1≠2)处导数相等，证明：f(1)+f(2)>8−8ln2；（Ⅱ）若a≤3−4ln2，证明：对于任意>0，直线y=+a与曲线y=f()有唯一公共点．14．【2018年高考江苏】某农场有一块农田，如图所示，它的边界由圆O的一段圆弧MPN（P为此圆弧的中点）和线段MN构成．已知圆O的半径为40米，点P到MN的距离为50米．现规划在此农田上修建两个温室大棚，大棚Ⅰ内的地块形状为矩形ABCD，大棚Ⅱ内的地块形状为CDP△，要求,A B均在线段MN上，,C D均在圆弧上．设OC与MN所成的角为θ．（1）用θ分别表示矩形ABCD和CDP△的面积，并确定sinθ的取值范围；（2）若大棚Ⅰ内种植甲种蔬菜，大棚Ⅱ内种植乙种蔬菜，且甲、乙两种蔬菜的单位面积年产值之比为4:3．求当θ为何值时，能使甲、乙两种蔬菜的年总产值最大．15．【2018年高考江苏】记(),()f x g x ''分别为函数(),()f x g x 的导函数．若存在0x ∈R ，满足00()()f xg x =且00()()f x g x ''=，则称0x 为函数()f x 与()g x 的一个“S 点”．（1）证明：函数()f x x =与2()22g x x x =+-不存在“S 点”；（2）若函数2()1f x ax =-与()ln g x x =存在“S 点”，求实数a 的值； （3）已知函数2()f x x a =-+，e ()xb g x x =．对任意0a >，判断是否存在0b >，使函数()f x 与()g x 在区间(0,)+∞内存在“S 点”，并说明理由．16．【2017年高考全国Ⅰ卷文数】已知函数()f x =e(e−a )−a 2．（1）讨论()f x 的单调性；（2）若()0f x ≥，求a 的取值范围．17．【2017年高考全国Ⅱ卷文数】设函数2()(1)e x f x x =-.（1）讨论()f x 的单调性；（2）当0x ≥时，()1f x ax ≤+，求a 的取值范围.18．【2017年高考全国Ⅲ卷文数】已知函数()2(1)ln 2x ax a x f x =+++． （1）讨论()f x 的单调性；（2）当a ﹤0时，证明3()24f x a≤--．19．【2017年高考浙江】已知函数f ()=（e x -（12x ≥）． （1）求f ()的导函数；（2）求f ()在区间1[+)2∞，上的取值范围．20．【2017年高考北京文数】已知函数()e cos x f x x x =-．（Ⅰ）求曲线()y f x =在点(0,(0))f 处的切线方程； （Ⅱ）求函数()f x 在区间π[0,]2上的最大值和最小值．21．【2017年高考天津文数】设,a b ∈R ，||1a ≤．已知函数32()63(4)f x x x a a x b =---+，()e ()x g x f x =．（Ⅰ）求()f x 的单调区间；（Ⅱ）已知函数()y g x =和e x y =的图象在公共点（0，y 0）处有相同的切线，（i ）求证：()f x 在0x x =处的导数等于0；（ii ）若关于的不等式()e x g x ≤在区间00[1,1]x x -+上恒成立，求b 的取值范围．22．【2017年高考山东文数】已知函数()3211,32f x x ax a =-∈R . （Ⅰ）当a =2时,求曲线()y f x =在点()()3,3f 处的切线方程；（Ⅱ）设函数()()()cos sin g x f x x a x x =+--,讨论()g x 的单调性并判断有无极值,有极值时求出极值.23．【2017年高考江苏】已知函数32()1(0,)f x x ax bx a b =+++>∈R 有极值，且导函数()'f x 的极值点是()f x 的零点．（极值点是指函数取极值时对应的自变量的值）（1）求b 关于a 的函数关系式，并写出定义域；（2）证明：23>b a ；（3）若()f x ，()'f x 这两个函数的所有极值之和不小于72-，求a 的取值范围．。

1. 【2016高考山东理数】若函数()y f x =的图象上存在两点，使得函数的图象在这两点处的切线互相垂直，则称()y f x =具有T 性质.下列函数中具有T 性质的是（ ）（A ）sin y x = （B ）ln y x =（C ）e x y =（D ）3y x =【答案】A 【解析】试题分析：由函数的图象在两点处的切线互相垂直可知，存在两点处的切线斜率的积，即导函数值的乘积为负一.当sin y x =时，cos y x '=，有cos0cos 1π⋅=-，所以在函数sin y x =图象存在两点0,x x π==使条件成立，故A 正确；函数3ln ,,x y x y e y x ===的导数值均非负，不符合题意，故选A考点：1.导数的计算；2.导数的几何意义.2. 【2016年高考四川理数】设直线l 1，l 2分别是函数f (x )= ln ,01,ln ,1,x x x x -<<⎧⎨>⎩图象上点P 1，P 2处的切线，l 1与l 2垂直相交于点P ，且l 1，l 2分别与y 轴相交于点A ，B ，则△P AB 的面积的取值范围是( )（A ）(0,1) （B ）(0,2) （C ）(0,+∞) （D ）(1,+∞) 【答案】A 【解析】试题分析：设()()111222,ln ,,ln P x x P x x -（不妨设121,01x x ><<），则由导数的几何意义易得切线12,l l 的斜率分别为121211,.k k x x ==-由已知得12122111,1,.k k x x x x =-∴=∴=∴切线1l 的方程分别为()1111ln y x x x x -=-，切线2l 的方程为()2221ln y x x x x +=--，即1111ln y x x x x ⎛⎫-=-- ⎪⎝⎭.分别令0x =得()()110,1ln ,0,1ln .A x B x -++又1l 与2l 的交点为2111221121,ln 11x x P x x x ⎛⎫-+ ⎪++⎝⎭，11x >，21122112111211PABA B P x x S y y x x x ∆+∴=-⋅=<=++，01PAB S ∆∴<<．故选A ． 考点：1.导数的几何意义；2.两直线垂直关系；3.直线方程的应用；4.三角形面积取值范围.3.【2016高考新课标3理数】已知()f x 为偶函数，当0x <时，()ln()3f x x x =-+，则曲线()yf x =在点(1,3)-处的切线方程是_______________． 【答案】21y x =-- 【解析】试题分析：当0x >时，0x -<，则()ln 3f x x x -=-．又因为()f x 为偶函数，所以()()ln 3f x f x x x =-=-，所以1()3f x x'=-，则切线斜率为(1)2f '=-，所以切线方程为32(1)y x +=--，即21y x =--．考点：1、函数的奇偶性与解析式；2、导数的几何意义．【知识拓展】本题题型可归纳为“已知当0x >时，函数()y f x =，则当0x <时，求函数的解析式”．有如下结论：若函数()f x 为偶函数，则当0x <时，函数的解析式为()y f x =-；若()f x 为奇函数，则函数的解析式为()y f x =--．4.【2014广东理10】曲线25+=-x e y在点()0,3处的切线方程为 .【答案】53y x =-+或530x y +-=. 【解析】55x y e -'=-，所求切线的斜率为55y e =-=-，故所求切线的方程为35y x -=-，即53y x =-+或530x y +-=. 【考点定位】本题考查利用导数求函数图象的切线问题，属于容易题.【名师点晴】本题主要考查的是导数的几何意义和直线的方程，属于容易题．解题时一定要抓住重要字眼“在点()0,3处”，否则很容易出现错误．解导数的几何意义问题时一定要抓住切点的三重作用：①切点在曲线上；②切点在切线上；③切点处的导数值等于切线的斜率．5.【2014江苏理11】在平面直角坐标系xoy 中，若曲线2by ax x=+（,a b 为常数）过点(2,5)P -，且该曲线在点P 处的切线与直线7230x y ++=平行，则a b += .【答案】3-【解析】曲线2b y ax x =+过点(2,5)P -，则452b a +=-①，又2'2by ax x=-，所以7442b a -=-②，由①②解得1,2,a b =-⎧⎨=-⎩所以3a b +=-． 【考点定位】导数与切线斜率．6.【2017山东，理20】已知函数，，其中是自然对数的底数.（Ⅰ）求曲线在点()(),f ππ处的切线方程；（Ⅱ）令，讨论的单调性并判断有无极值，有极值时求出极值.【答案】（Ⅰ）.（Ⅱ）综上所述：当时，在上单调递减，在上单调递增，函数有极小值，极小值是；当时，函数在和和上单调递增，在上单调递减，函数有极大值，也有极小值，极大值是极小值是；当时，函数在上单调递增，无极值；当时，函数在和上单调递增，在上单调递减，函数有极大值，也有极小值，极大值是；极小值是.【解析】试题分析：（Ⅰ）求导数得斜率，由点斜式写出直线方程.试题解析：（Ⅰ）由题意又，所以，因此 曲线在点处的切线方程为，即 .（Ⅱ）由题意得 2()(cos sin 22)(2cos )x h x e x x x a x x =-+--+，因为，令则所以在上单调递增.因为(0)0,m =所以 当时，()0,m x >当0x <时，(1)当时，当时，，单调递减，当时，，单调递增，所以 当时取得极小值，极小值是 ；(2)当时，由 得 ，①当时，，当时，，单调递增；当时，，单调递减；当时，，单调递增.所以当时取得极大值.③当时，所以当时，，单调递增；当时，，单调递减；当时，，单调递增；所以当时取得极大值，极大值是；当时取得极小值.极小值是.综上所述：当时，在上单调递减，在上单调递增，当时，函数在上单调递增，无极值；当时，函数在和上单调递增，在上单调递减，函数有极大值，也有极小值，极大值是；极小值是.【考点】1.导数的几何意义.2.应用导数研究函数的单调性、极值.3.分类讨论思想.力、基本计算能力、分类讨论思想等。

2017年高考数学理试题分类汇编：三角函数二填空选择题【答案】【答案】【解析】1. (2017年天津卷文)设函数f(X )2sin( x ),x R ，其中o’ 丨兀若 f(5n )2，f0,且f(x)的 最小正周期大2 n ,则2 3 1 3n12 11 n 24(B ) (D)2 3 1 311 n 72 7n 24【解析】由题意得58 11 82匕k2，其中k i ,k 2所以3(k 22kJ -，又 T —23，所以1，所以2k 1，由|也，故选A .2. (2017年天津卷理 )设函数f(x) 2si n(R ，其中)0，且f (x)的最小正周期大于2 ，则(A )12 (B )12 24(D)24【解析】由题意81182k 1 k2所以 2k 11 12 ，3.( 2017年全国川卷文22，其中 k 1,k 2 Z,所以故选A.ABC 内角 3(k2A, B,C 的对边分别为a,b,c ，已知2kJ ，又T 0■,所以015根据正弦定理有:sin 600sin B2 n已知曲线 C 1： y =cos x ，C 2： y =sin (2x +)，则下面结论正确的是3冗A •把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线C 2450 A7504.(2017年新课标I ) 9.A.4B.2C.D.B .把C 1上各点的横坐标伸长到原来的 2 倍,纵坐标不变，再把得到的曲线向左平移n 个单位长度，得到曲线12 C 2C . 把C 1上各点的横坐标缩短到原来的1倍, 2纵坐标不变, 再把得到的曲线向右平移n个单位长度，得到曲线6C 2D . 把C 上各点的横坐标缩短到原来的1倍, 2纵坐标不变, 再把得到的曲线向左平移n个单位长度，得到曲线12C2【答案】D6.（2017年浙江卷）14 .已知△ABC , AB = AC =4 , BC =2.点D 为AB 延长线上一点，BD=2，连结CD ,贝U △BDC 的面积是 _____ cos Z BDC = _____ ,8.（ 2017年新课标n 文）16.△ ABC 的内角 A,B,C 的对边分别为 a,b,c 若2b cosB= a cosC+c cosA,则B=— 39. （ 2017年新课标n 文）3.函数f x = sin （ 2x+—）的最小正周期为 （C ）3【解析】f x 1 cos 2 x , 3cosx3 cos 2x \ 3 cosx -44cosx乜21, x 0,：那么cosx 0,1，当 cosx3时函数取得最大值222【答案】11.【解析】取 BC 中点E , DC 中点F , 由题意：AE BC,BF CD , .15 △ ABE 中，BE 1DBC1DBC 1cos ABCcos一 ,siL 1—AB 44:164SA BCD5. （ 2017年新课标n 卷理）14•函数f x .2sin x 3 cosx 0,2的最大值是-BD BC sin DBC .2 22又 cos DBC 1 2s in DBF1, sin DBF 410 4cos BDC sin DBF综上可得，△ BCD 面积为cos BDC-10 47.（2017年新课标n 文）.13函数f x =2cosxsinx 的最大值为10.(2017年浙江卷)11.我国古代数学家刘徽创立的“割圆术”可以估算圆周率 n,理论上能把n 的值计算到任意精度.【解析】本题选择D 选项.4]! tan( -)ta^ 1 丄 4 4 614.(2017年江苏卷 5. tan()若15. (2017年新课标I 文)11 . △ABC 的内角A 、B 、C 的对边分别为 a 、b 、c 。

2017年高考真题分类汇编（理数）：专题1 集合与函数一、单选题（共15题；共30分）1、（2017•新课标Ⅰ卷）已知集合A={x|x＜1}，B={x|3x＜1}，则（）A、A∩B={x|x＜0}B、A∪B=RC、A∪B={x|x＞1}D、A∩B=∅2、（2017•新课标Ⅱ）设集合A={1，2，4}，B={x|x2﹣4x+m=0}．若A∩B={1}，则B=（）A、{1，﹣3}B、{1，0}C、{1，3}D、{1，5}3、（2017•新课标Ⅲ）已知集合A={（x，y）|x2+y2=1}，B={（x，y）|y=x}，则A∩B中元素的个数为（）A、3B、2C、1D、04、（2017•山东）已知命题p：∀x＞0，ln（x+1）＞0；命题q：若a＞b，则a2＞b2，下列命题为真命题的是（）A、p∧qB、p∧￢qC、￢p∧qD、￢p∧￢q5、（2017•山东）设函数y= 的定义域为A，函数y=ln（1﹣x）的定义域为B，则A∩B=（）A、（1，2）B、（1，2]C、（﹣2，1）D、[﹣2，1）6、（2017·天津）设集合A={1，2，6}，B={2，4}，C={x∈R|﹣1≤x≤5}，则（A∪B）∩C=（）A、{2}B、{1，2，4}C、{1，2，4，5}D、{x∈R|﹣1≤x≤5}7、（2017•浙江）已知集合P={x|﹣1＜x＜1}，Q={x|0＜x＜2}，那么P∪Q=（）A、（﹣1，2）B、（0，1）C、（﹣1，0）D、（1，2）8、（2017•北京卷）若集合A={x|﹣2＜x＜1}，B={x|x＜﹣1或x＞3}，则A∩B=（）A、{x|﹣2＜x＜﹣1}B、{x|﹣2＜x＜3}C、{x|﹣1＜x＜1}D、{x|1＜x＜3}9、（2017·天津）已知奇函数f（x）在R上是增函数，g（x）=xf（x）．若a=g（﹣log25.1），b=g（20.8），c=g（3），则a，b，c的大小关系为（）A、a＜b＜cB、c＜b＜aC、b＜a＜cD、b＜c＜a10、（2017·天津）设θ∈R，则“|θ﹣|＜”是“sinθ＜”的（）A、充分而不必要条件B、必要而不充分条件C、充要条件D、既不充分也不必要条件11、（2017•北京卷）根据有关资料，围棋状态空间复杂度的上限M约为3361，而可观测宇宙中普通物质的原子总数N约为1080，则下列各数中与最接近的是（）（参考数据：lg3≈0.48）A、1033B、1053C、1073D、109312、（2017•北京卷）已知函数f（x）=3x﹣（）x，则f（x）（）A、是奇函数，且在R上是增函数B、是偶函数，且在R上是增函数C、是奇函数，且在R上是减函数D、是偶函数，且在R上是减函数13、（2017•新课标Ⅰ卷）函数f（x）在（﹣∞，+∞）单调递减，且为奇函数．若f（1）=﹣1，则满足﹣1≤f（x﹣2）≤1的x的取值范围是（）A、[﹣2，2]B、[﹣1，1]C、[0，4]D、[1，3]14、（2017•山东）已知当x∈[0，1]时，函数y=（mx﹣1）2的图象与y= +m的图象有且只有一个交点，则正实数m的取值范围是（）A、（0，1]∪[2 ，+∞）B、（0，1]∪[3，+∞）C、（0，）∪[2 ，+∞）D、（0，]∪[3，+∞）15、（2017•新课标Ⅰ卷）设x、y、z为正数，且2x=3y=5z，则（）A、2x＜3y＜5zB、5z＜2x＜3yC、3y＜5z＜2xD、3y＜2x＜5z二、填空题（共7题；共8分）16、（2017•江苏）已知集合A={1，2}，B={a，a2+3}．若A∩B={1}，则实数a的值为________．17、（2017•北京卷）能够说明“设a，b，c是任意实数．若a＞b＞c，则a+b＞c”是假命题的一组整数a，b，c的值依次为________．18、（2017•江苏）已知函数f（x）=x3﹣2x+e x﹣，其中e是自然对数的底数．若f（a﹣1）+f（2a2）≤0．则实数a的取值范围是________．19、（2017•山东）若函数e x f（x）（e≈2.71828…是自然对数的底数）在f（x）的定义域上单调递增，则称函数f（x）具有M性质．下列函数中所有具有M性质的函数的序号为________．①f（x）=2﹣x②f（x）=3﹣x③f（x）=x3④f（x）=x2+2．20、（2017•浙江）已知a∈R，函数f（x）=|x+ ﹣a|+a在区间[1，4]上的最大值是5，则a 的取值范围是________．21、（2017•北京卷）三名工人加工同一种零件，他们在一天中的工作情况如图所示，其中A i的横、纵坐标分别为第i名工人上午的工作时间和加工的零件数，点B i的横、纵坐标分别为第i名工人下午的工作时间和加工的零件数，i=1，2，3．①记Q i为第i名工人在这一天中加工的零件总数，则Q1，Q2，Q3中最大的是________．②记p i为第i名工人在这一天中平均每小时加工的零件数，则p1，p2，p3中最大的是________．22、（2017•江苏）设f（x）是定义在R上且周期为1的函数，在区间[0，1）上，f（x）= ，其中集合D={x|x= ，n∈N*}，则方程f（x）﹣lgx=0的解的个数是________．答案解析部分一、单选题1、【答案】A【考点】并集及其运算，交集及其运算，指数函数的图像与性质【解析】【解答】解：∵集合A={x|x＜1}，B={x|3x＜1}={x|x＜0}，∴A∩B={x|x＜0}，故A正确，D错误；A∪B={x|x＜1}，故B和C都错误．故选：A．【分析】先分别求出集合A和B，再求出A∩B和A∪B，由此能求出结果．2、【答案】C【考点】交集及其运算【解析】【解答】解：集合A={1，2，4}，B={x|x2﹣4x+m=0}．若A∩B={1}，则1∈A且1∈B，可得1﹣4+m=0，解得m=3，即有B={x|x2﹣4x+3=0}={1，3}．故选：C．【分析】由交集的定义可得1∈A且1∈B，代入二次方程，求得m，再解二次方程可得集合B．3、【答案】B【考点】交集及其运算【解析】【解答】解：由，解得：或，∴A∩B的元素的个数是2个，故选：B．【分析】解方程组求出元素的个数即可．4、【答案】B【考点】复合命题的真假，对数函数的单调性与特殊点，不等式比较大小【解析】【解答】解：命题p：∀x＞0，ln（x+1）＞0，则命题p为真命题，则￢p为假命题；取a=﹣1，b=﹣2，a＞b，但a2＜b2，则命题q是假命题，则￢q是真命题．∴p∧q是假命题，p∧￢q是真命题，￢p∧q是假命题，￢p∧￢q是假命题．故选B．【分析】由对数函数的性质可知命题p为真命题，则￢p为假命题，由不等式的性质可知，命题q是假命题，则￢q是真命题．因此p∧￢q为真命题．5、【答案】D【考点】交集及其运算，函数的定义域及其求法，一元二次不等式的解法【解析】【解答】解：由4﹣x2≥0，解得：﹣2≤x≤2，则函数y= 的定义域[﹣2，2]，由对数函数的定义域可知：1﹣x＞0，解得：x＜1，则函数y=ln（1﹣x）的定义域（﹣∞，1），则A∩B=[﹣2，1），故选D．【分析】根据幂函数及对数函数定义域的求法，即可求得A和B，即可求得A∩B．6、【答案】B【考点】交、并、补集的混合运算【解析】【解答】解：∵A={1，2，6}，B={2，4}，∴A∪B={1，2，4，6}，又C={x∈R|﹣1≤x≤5}，∴（A∪B）∩C={1，2，4}．故选：B．【分析】由并集概念求得A∪B，再由交集概念得答案．7、【答案】A【考点】并集及其运算【解析】【解答】解：集合P={x|﹣1＜x＜1}，Q={x|0＜x＜2}，那么P∪Q={x|﹣1＜x＜2}=（﹣1，2）．故选：A.【分析】直接利用并集的运算法则化简求解即可．8、【答案】A【考点】交集及其运算【解析】【解答】解：∵集合A={x|﹣2＜x＜1}，B={x|x＜﹣1或x＞3}，∴A∩B={x|﹣2＜x＜﹣1}故选：A【分析】根据已知中集合A和B，结合集合交集的定义，可得答案．9、【答案】C【考点】函数单调性的判断与证明，函数单调性的性质，函数奇偶性的判断，对数值大小的比较，对数函数的图像与性质【解析】【解答】解：奇函数f（x）在R上是增函数，当x＞0，f（x）＞f（0）=0，且f′（x）＞0，∴g（x）=xf（x），则g′（x）=f（x）+xf′（x）＞0，∴g（x）在（0，+∞）单调递增，且g（x）=xf（x）偶函数，∴a=g（﹣log25.1）=g（log25.1），则2＜﹣log25.1＜3，1＜20.8＜2，由g（x）在（0，+∞）单调递增，则g（20.8）＜g（log25.1）＜g（3），∴b＜a＜c，故选C．【分析】由奇函数f（x）在R上是增函数，则g（x）=xf（x）偶函数，且在（0，+∞）单调递增，则a=g（﹣log25.1）=g（log25.1），则2＜﹣log25.1＜3，1＜20.8＜2，即可求得b＜a＜c 10、【答案】A【考点】必要条件、充分条件与充要条件的判断，正弦函数的图象，正弦函数的单调性，绝对值不等式的解法【解析】【解答】解：|θ﹣|＜⇔﹣＜θ﹣＜⇔0＜θ＜，sinθ＜⇔﹣+2kπ＜θ＜+2kπ，k∈Z，则（0，）⊂[﹣+2kπ，+2kπ]，k∈Z，可得“|θ﹣|＜”是“sinθ＜”的充分不必要条件．故选：A．【分析】运用绝对值不等式的解法和正弦函数的图象和性质，化简两已知不等式，结合充分必要条件的定义，即可得到结论．11、【答案】D【考点】指数式与对数式的互化【解析】【解答】解：由题意：M≈3361，N≈1080，根据对数性质有：3=10lg3≈100.48，∴M≈3361≈（100.48）361≈10173，∴≈ =1093，故本题选：D．【分析】根据对数的性质：T= ，可得：3=10lg3≈100.48，代入M将M也化为10为底的指数形式，进而可得结果．12、【答案】A【考点】函数单调性的性质，函数奇偶性的性质，奇偶性与单调性的综合【解析】【解答】解：显然，函数的定义域为全体实数，f（x）=3x﹣（）x=3x﹣3﹣x，∴f（﹣x）=3﹣x﹣3x=﹣f（x），即函数f（x）为奇函数，又由函数y=3x为增函数，y=（）x为减函数，故函数f（x）=3x﹣（）x为增函数，故选：A．【分析】由已知得f（﹣x）=﹣f（x），即函数f（x）为奇函数，由函数y=3x为增函数，y=（）x为减函数，结合“增”﹣“减”=“增”可得答案．13、【答案】D【考点】函数的单调性及单调区间，函数奇偶性的性质，奇偶性与单调性的综合，抽象函数及其应用【解析】【解答】解：∵函数f（x）为奇函数．若f（1）=﹣1，则f（﹣1）=1，又∵函数f（x）在（﹣∞，+∞）单调递减，﹣1≤f（x﹣2）≤1，∴f（1）≤f（x﹣2）≤f（﹣1），∴﹣1≤x﹣2≤1，解得：x∈[1，3]，故选：D【分析】由已知中函数的单调性及奇偶性，可将不等式﹣1≤f（x﹣2）≤1化为﹣1≤x﹣2≤1，解得答案．14、【答案】B【考点】函数的值域，函数单调性的性质，函数的图象【解析】【解答】解：根据题意，由于m为正数，y=（mx﹣1）2为二次函数，在区间（0，）为减函数，（，+∞）为增函数，函数y= +m为增函数，分2种情况讨论：①、当0＜m≤1时，有≥1，在区间[0，1]上，y=（mx﹣1）2为减函数，且其值域为[（m﹣1）2，1]，函数y= +m为增函数，其值域为[m，1+m]，此时两个函数的图象有1个交点，符合题意；②、当m＞1时，有＜1，y=（mx﹣1）2在区间（0，）为减函数，（，1）为增函数，函数y= +m为增函数，其值域为[m，1+m]，若两个函数的图象有1个交点，则有（m﹣1）2≥1+m，解可得m≤0或m≥3，又由m为正数，则m≥3；综合可得：m的取值范围是（0，1]∪[3，+∞）；故选：B．【分析】根据题意，由二次函数的性质分析可得：y=（mx﹣1）2为二次函数，在区间（0，）为减函数，（，+∞）为增函数，分2种情况讨论：①、当0＜m≤1时，有≥1，②、当m＞1时，有＜1，结合图象分析两个函数的单调性与值域，可得m的取值范围，综合可得答案．15、【答案】D【考点】指数式与对数式的互化，对数的运算性质，对数值大小的比较，不等式比较大小【解析】【解答】解：x、y、z为正数，令2x=3y=5z=k＞1．lgk＞0．则x= ，y= ，z= ．∴3y= ，2x= ，5z= ．∵= = ，＞= ．∴＞lg ＞＞0．∴3y＜2x＜5z．故选：D．【分析】x、y、z为正数，令2x=3y=5z=k＞1．lgk＞0．可得x= ，y= ，z= ．可得3y= ，2x= ，5z= ．根据= = ，＞=．即可得出大小关系．二、填空题16、【答案】1【考点】交集及其运算【解析】【解答】解：∵集合A={1，2}，B={a，a2+3}．A∩B={1}，∴a=1或a2+3=1，解得a=1．故答案为：1．【分析】利用交集定义直接求解．17、【答案】﹣1，﹣2，﹣3【考点】命题的否定，命题的真假判断与应用【解析】【解答】解：设a，b，c是任意实数．若a＞b＞c，则a+b＞c”是假命题，则若a＞b＞c，则a+b≤c”是真命题，可设a，b，c的值依次﹣1，﹣2，﹣3，（答案不唯一），故答案为：﹣1，﹣2，﹣3【分析】设a，b，c是任意实数．若a＞b＞c，则a+b＞c”是假命题，则若a＞b＞c，则a+b≤c”是真命题，举例即可，本题答案不唯一18、【答案】[-1，]【考点】函数奇偶性的性质，利用导数研究函数的单调性，一元二次不等式的解法，基本不等式【解析】【解答】解：函数f（x）=x3﹣2x+e x﹣的导数为：f′（x）=3x2﹣2+e x+ ≥﹣2+2 =0，可得f（x）在R上递增；又f（﹣x）+f（x）=（﹣x）3+2x+e﹣x﹣e x+x3﹣2x+e x﹣=0，可得f（x）为奇函数，则f（a﹣1）+f（2a2）≤0，即有f（2a2）≤﹣f（a﹣1）=f（1﹣a），即有2a2≤1﹣a，解得﹣1≤a≤ ，故答案为：[﹣1，]．【分析】求出f（x）的导数，由基本不等式和二次函数的性质，可得f（x）在R上递增；再由奇偶性的定义，可得f（x）为奇函数，原不等式即为2a2≤1﹣a，运用二次不等式的解法即可得到所求范围．19、【答案】①④【考点】函数单调性的性质，指数函数的图像与性质，利用导数研究函数的单调性【解析】【解答】解：对于①，f（x）=2﹣x，则g（x）=e x f（x）= 为实数集上的增函数；对于②，f（x）=3﹣x，则g（x）=e x f（x）= 为实数集上的减函数；对于③，f（x）=x3，则g（x）=e x f（x）=e x•x3，g′（x）=e x•x3+3e x•x2=e x（x3+3x2）=e x•x2（x+3），当x＜﹣3时，g′（x）＜0，∴g（x）=e x f（x）在定义域R上先减后增；对于④，f（x）=x2+2，则g（x）=e x f（x）=e x（x2+2），g′（x）=e x（x2+2）+2xe x=e x（x2+2x+2）＞0在实数集R上恒成立，∴g（x）=e x f（x）在定义域R上是增函数．∴具有M性质的函数的序号为①④．故答案为：①④．【分析】把①②代入e x f（x），变形为指数函数判断；把③④代入e x f（x），求导数判断．20、【答案】（﹣∞，）【考点】函数的最值及其几何意义，绝对值不等式的解法【解析】【解答】解：由题可知|x+ ﹣a|+a≤5，即|x+ ﹣a|≤5﹣a，所以a≤5，又因为|x+ ﹣a|≤5﹣a，所以a﹣5≤x+ ﹣a≤5﹣a，所以2a﹣5≤x+ ≤5，又因为1≤x≤4，4≤x+ ≤5，所以2a﹣5≤4，解得a≤ ，故答案为：（﹣∞，）．【分析】通过转化可知|x+ ﹣a|+a≤5且a≤5，进而解绝对值不等式可知2a﹣5≤x+ ≤5，进而计算可得结论．21、【答案】Q1；p2【考点】函数的图象与图象变化【解析】【解答】解：①若Q i为第i名工人在这一天中加工的零件总数，Q1=A1的综坐标+B1的综坐标；Q2=A2的综坐标+B2的综坐标，Q3=A3的综坐标+B3的综坐标，由已知中图象可得：Q1，Q2，Q3中最大的是Q1，②若p i为第i名工人在这一天中平均每小时加工的零件数，则p i为A i B i中点与原点连线的斜率，故p1，p2，p3中最大的是p2故答案为：Q1，p2【分析】①若Q i为第i名工人在这一天中加工的零件总数，则Q i=A i的综坐标+B i的综坐标；进而得到答案．②若p i为第i名工人在这一天中平均每小时加工的零件数，则p i为A i B i中点与原点连线的斜率；进而得到答案．22、【答案】8【考点】分段函数的解析式求法及其图象的作法，函数的周期性，对数函数的图像与性质，根的存在性及根的个数判断【解析】【解答】解：∵在区间[0，1）上，f（x）= ，第一段函数上的点的横纵坐标均为有理数，又f（x）是定义在R上且周期为1的函数，∴在区间[1，2）上，f（x）= ，此时f（x）的图象与y=lgx有且只有一个交点；同理：区间[2，3）上，f（x）的图象与y=lgx有且只有一个交点；区间[3，4）上，f（x）的图象与y=lgx有且只有一个交点；区间[4，5）上，f（x）的图象与y=lgx有且只有一个交点；区间[5，6）上，f（x）的图象与y=lgx有且只有一个交点；区间[6，7）上，f（x）的图象与y=lgx有且只有一个交点；区间[7，8）上，f（x）的图象与y=lgx有且只有一个交点；区间[8，9）上，f（x）的图象与y=lgx有且只有一个交点；在区间[9，+∞）上，f（x）的图象与y=lgx无交点；故f（x）的图象与y=lgx有8个交点；即方程f（x）﹣lgx=0的解的个数是8，故答案为：8【分析】由已知中f（x）是定义在R上且周期为1的函数，在区间[0，1）上，f（x）= ，其中集合D={x|x= ，n∈N*}，分析f（x）的图象与y=lgx图象交点的个数，进而可得答案．。

课时2 导数的应用1．函数e x y x =-的单调增区间为 A ．(1,)+∞ B ．(0,)+∞ C ．(0),-∞D ．(1),-∞2．若函数()3f x x ax =-在2x =处取得极小值,则a = A ． B ．12 C ．D ．2-3．函数y =ln xx的最大值为 A ．e −1 B ．e C ．e 2D ．1034．已知对任意实数x ，有()()f x f x -=-，()()g x g x -=，且0x >时，()0f x '>，()0g x '>，则0x <时 A ．()0f x '>，()0g x '> B ．()0f x '>，()0g x '< C ．()0f x '<，()0g x '>D ．()0f x '<，()0g x '<5．若()eln ,0e f x x x a b =-<<<,则下列说法一定正确的是 A ．f (a )<f (b ) B ．f (a )> f (b )C ．f (a )>f (e)D ．f (e) >f (b )6．若函数()f x 在R 上可导,其导函数为()f x ',且函数()1()y x f x '=-的图象如图所示,则下列结论中一定成立的是A ．函数()f x 有极大值(2)f -,无极小值B ．函数()f x 有极小值(1)f ,无极大值C ．函数()f x 有极大值(2)f -和极小值(1)fD ．函数()f x 有极大值(1)f 和极小值(2)f -7．已知某生产厂家的年利润y (单位：万元)与年产量 (单位：万件)的函数关系式为31812343y x x =-+-，则使该生产厂家获取最大年利润的年产量为A ．13万件B ．11万件C ．9万件D ．7万件8．已知函数()f x 的定义域为,(1)2f -=R ,若对任意,()2x f x '∈>R ,则()24x f x >+的解集为 A ．(1,1)-B ．()1,-+∞C ．(),1-∞-D ．(,)-∞+∞9．若关于x 的方程x 3−3x ＋m =0在0,2]上有实根,则实数m 的取值范围是 A ．−2,2] B ．0,2]C ．−2,0]D ．(−∞,−2)∪(2,＋∞)10．设函数()()e xf x F x =是定义在R 上的函数,其中f (x )的导函数f ′(x )满足f ′(x )<f (x )对于x R 恒成立,则A ．f (2)>e 2f (0),f (2016)>e 2016f (0)B ．f (2)<e 2f (0),f (2016)>e 2016f (0)C ．f (2)<e 2f (0),f (2016)<e 2016f (0)D ．f (2)>e 2f (0),f (2016)<e 2016f (0)11．对于函数y =f (x )，x (a ，b )，“()f x '>0”是“函数y =f (x )为增函数”的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件12．函数y =x −sin x ，π[,π]2x ∈的最大值是A ．π−1B ．π12- C ．πD ．π＋113．设a ∈R ，若函数e 3,ax y x x =+∈R 有大于零的极值点，则A ．3a >-B ．3a <-C ．13a >-D ．13a <-14．若函数32()6f x x ax x =--+在()01，上单调递减，则实数a 的取值范围是A ．1a ≥B ．1a =C ．1a ≤D ．01a <<15．如图,将直径为d 的圆木锯成长方体横梁,横截面为矩形,横梁的强度同它的断面高的平方与宽x 的积成正比(强度系数为k ,k >0).要将直径为d 的圆木锯成强度最大的横梁,断面的宽x 应为A ．3dB ．2d C．3d D．2d 16．已知平行于x 轴的直线分别交曲线y =−1x(x <0)与y于A ,B 两点,则|AB|的最小值为 A ．32 B ．12C ．52D ．17．若函数()e 2x f x x a =-+有零点,则实数的取值范围为 .18．若对任意的x 1,x 2∈12,2],都有1a x +x 1ln x 1≥32x −22x −3成立,则实数a 的取值范围是 .19．（2012年高考陕西卷）设函数()e xf x x =，则A ．1x =为()f x 的极大值点B ．1x =为()f x 的极小值点C ．1x =-为()f x 的极大值点D ．1x =-为()f x 的极小值点20．（2013年高考全国Ⅱ卷）已知函数f (x )=x 3＋ax 2＋bx ＋c ，下列结论中错误的是A ． x 0∈R ，f (x 0)＝0B ．函数y ＝f (x )的图象是中心对称图形C ．若x 0是f (x )的极小值点，则f (x )在区间(−∞，x 0)上单调递减D ．若x 0是f (x )的极值点，则f ′(x 0)＝021．（2015年高考全国Ⅱ卷）设函数()f x '是奇函数()()f x x ∈R 的导函数，(1)0f -=，当0x >时，()()0xf x f x '-<，则使得()0f x >成立的的取值范围是A ．(,1)(0,1)-∞-B ．(1,0)(1,)-+∞C ．(,1)(1,0)-∞--D ．(0,1)(1,)+∞22．（2014年高考辽宁卷）当[2,1]x ∈-时，不等式32430ax x x -++≥恒成立，则实数a 的取值范围是A ．[5,3]--B ．9[6,]8-- C ．[6,2]--D ．[4,3]--23．（2015年高考福建卷）若定义在R 上的函数()f x 满足(0)1f =-，其导函数()f x '满足()1f x k '>>，则下列结论中一定错误的是A ．11()f k k <B ．11()1f kk >- C ．11()11f k k <-- D ．1()11k f k k >-- 24．（2015年高考全国Ⅰ卷）设函数()f x =e (21)xx ax a --+,其中a <1，若存在唯一的整数0x ，使得0()f x <0，则的取值范围是 A ．−32e，1) B ．−32e ，34)C ．32e ，34)D ．32e，1) 25．（2015年高考陕西卷）对二次函数2()f x ax bx c =++(为非零整数)，四位同学分别给出下列结论，其中有且只有一个结论是错误的，则错误的结论是 A ．1-是()f x 的零点 B ．1是()f x 的极值点 C ．3是()f x 的极值 D. 点(2,8)在曲线()y f x =上1．C 【解析】由题意可得，1e x y '=-，令1e 0x y '=->，解得x <0，即e x y x =-的单调增区间为(),0-∞.2．B 【解析】()23f x x a '=-，由题意可知()212f a '=-=0，则a =12.3．A 【解析】令y'=()22ln ln 1ln x x x x x xx''-⋅-==0,得x =e,当x >e 时,y'<0;当x <e 时,y' >0,y 极大值=y |x =e =e −1,在定义域内只有一个极值,所以y max =e −1.4．B 【解析】由题意可知y =f (x )是奇函数，y =g (x )是偶函数.∵x >0时，y =f (x )，y =g (x )都是增函数，∴x <0时，y =f (x )是增函数，y =g (x )是减函数，即x <0时，f ′(x )>0，g′(x )<0. 5．C 【解析】()e1f x x'=-,由()0f x '>得x >,由()0f x '<得0<x <,所以，当x=时，f (e)是最小值，因此C 正确.6．A 【解析】由函数的图象可知, ()20,f '-=并且当2x <-时, ()0,2f x x >'-<当<1时, ()0f x '<,所以函数()f x 有极大值()2f -;又当1x >时, ()0f x '<,所以函数()f x 无极小值.故选A ．7．C 【解析】y′=−x 2＋81，令y′=0，得x =9，且经讨论知x =9是函数的极大值点，所以厂家获得最大年利润的年产量是9万件.8．B 【解析】设()()24g x f x x =--,因为()2f x '>,所以()()20g x f x '-'=>,又()12f -=,所以()()11240g f -=-+-=,所以由()0g x >得x >1-, 即()24f x x >+的解集为()1,-+∞．9．A 【解析】依题意，3 3m x x =-+，设3()3,[0,2]f x x x x =-+∈，则()233f x x =-'+，当01x ≤<时，()0f x '>，函数递增，当12x <≤时，()0f x '<，函数递减，故当1x =时函数()f x 有最大值，由()()00,22f f ==-，知函数有最小值2-，则()22f x -≤≤，所以若关于x 的方程x 3−3x ＋m =0在0,2]上有实根,则实数m 的取值范围是−2,2].故本题正确答案为A ． 10．C 【解析】因为f ′(x )<f (x )，所以f ′(x )− f (x )<0，则()()()0e xf x f x F x '-'=<，所以函数()F x 在R 上是减函数，所以(2)(0)F F <，(2016)(0)F F <，即2020160(2)(0)(2016)(0),e e e ef f f f <<,所以f (2)<e 2f (0)，f (2016)<e 2016f (0)，选C. 11．A 【解析】由()0f x '>⇒函数f (x )为增函数，但函数f (x )为增函数()0f x '>¿，所以“()f x '>0”是“函数y =f (x )为增函数”的充分不必要条件，故选A ．12．C 【解析】因为1cos y x =-'，当π[,π]2x ∈时，0y '>，则函数在区间π[,π]2上为增函数，所以y 的最大值为max πsin ππy =-=，故选C. 13．B 【解析】令e 30ax y a '=+=，得3eaxa=-.设0x x =为大于0的极值点，则3e ax a =-，∴0a <，∴00ax <，∴00e 1ax <<，即301a<-<，∴3a <-.14．A 【解析】()f x '=3x 2−2ax −1.∵f (x )在()01，上单调递减，∴不等式3x 2−2ax −10在(0，1)上恒成立.∴()0f '≤0，()1f '≤0，∴a ≥1.故选A ．15．C 【解析】设断面高为h ，则h 2=d 2−x 2.设横梁的强度函数为f (x )，则f(x )=k ·xh 2=k ·x (d 2−x 2)，0<x <d .令f '(x )=k (d 2−3x 2)=0，解得xd (舍去负值).当0<xd 时，f '(x )>0，f (x )单调递<x <d 时,f '(x )<0，f (x )单调递减.所以函数f (x )在定义域(0,d )内只有一个极大值点x=3d .所以x=3d 时，f (x )有最大值，故选C. 16．A 【解析】设平行于x 轴的直线方程为y =a (a >0)，A (x 1，y 1)，B (x 2，y 2)，则a =11x -⇒x 1=1a -,而x 2满足a，x 2>0，x 1<0，那么|AB|=x 2−x 1=x 2+1a =x 2设f (x )=，则f '(x )=1=, 显然当0<x <12时,2−1<0,得f '(x )<0,此时函数f (x )单调递减;当x>12时,2−1>0,得f '(x )>0,此时函数f (x )单调递增.于是当x =12时, f (x )取得最小值f(12)=1232=,即|AB|的最小值为32. 17．(,2ln 22]-∞- 【解析】令函数()2e x g x x =-,则()2e xg x '=-,令()0g x '=,得ln 2x =,令()0g x '>,得ln 2x <,令()0g x '<,得ln 2x >,所以函数()g x 在(,ln 2)-∞上是增函数，在(ln 2,)+∞上是减函数，所以函数()g x 的最大值为(ln 2)2ln 22g =-.因此，的取值范围就是函数()g x 的值域，所以(,2ln 22]a ∈-∞-. 18．1,+∞) 【解析】令f (x )=a x +x ln x ,g (x )=x 3−x 2−3,则问题转化为f (x 1)≥g (x 2)对任意的x 1,x 212,2]恒成立,则f (x )min ≥g (x )max .由g'(x )=3x 2−2x =x (3x−2)>0,得23<x ≤2,由g'(x )<0,得12≤x <23,所以函数g (x )在(23,2]上单调递增,在12,23)上单调递减,且g (12)=258-,g (2)=1,所以g (x )max =g (2)=1,则f (x )min ≥1,即f (x )=a x +x ln x ≥1恒成立,所以a ≥2max ln ()x x x -.令h (x )=x−x 2ln x ,则h'(x )=1−x−2x ln x ,当x 12,1)时,h'(x )>0,h (x )单调递增,当x ∈(1,2]时,h'(x )<0,h (x )单调递减,故h (x )max =h (1)=1,故a ≥1.19．D 【解析】∵()(1+)e x f x x '=，∴当1x <-时，()0f x '<，()f x 单调递减；当1x >-时，()0f x '>，单调递增，又(1)0f '-=，所以1x =-为()f x 的极小值点.20．C 【解析】若x 0是f (x )的极小值点，则y ＝f (x )的大致图象如下图所示，则在(−∞，x 0)上不单调，故C 不正确．21．A 【解析】记函数()()f x g x x =，则2()()()xf x f x g x x'-'=，因为当0x >时，()()0x f x f x '-<，故当0x >时，()0g x '<，所以()g x 在(0,)+∞上单调递减；又因为函数()()f x x ∈R 是奇函数，故函数()g x 是偶函数，所以()g x 在(,0)-∞上单调递增，且(1)(1)0g g -==．当01x <<时，()0g x >，则()0f x >；当1x <-时，()0g x <，则()0f x >，综上所述，使得()0f x >成立的的取值范围是(,1)(0,1)-∞-，故选A ．22．C 【解析】当x (0,1]时，得a ≥−3(1x )3−4(1x )2+1x ，令t=1x，则t 1,+∞)，a ≥−3t 3−4t 2+t ， 令g (t )=−3t 3−4t 2+t ，t 1,+∞)，则g'(t )=−9t 2−8t +1=−(t +1)(9t −1)，显然在1,+∞)上，g'(t )<0，g (t )单调递减，所以g (t )max =g (1)=−6，因此a ≥−6；同理，当x −2,0)时，得a ≤−2.由以上两种情况得−6≤a ≤−2，显然当x =0时也成立.故实数a 的取值范围为−6,−2].23．C 【解析】由已知条件，构造函数()()g x f x kx =-，则()()0g x f x k ''=->，故函数()g x 在R 上单调递增，且101k >-，故1()(0)1g g k >-，所以1()111k f k k ->---，11()11f k k >--，所以结论中一定错误的是C ，选项D 无法确定；构造函数()()h x f x x =-，则()()10h x f x ''=->，所以函数()h x 在R 上单调递增，且10k>，所以1()(0)h h k >，即11()1f k k ->-，11()1f k k>-，选项A,B 无法确定，故选C ．24．D 【解析】由题意可知存在唯一的整数x 0,使得000e (21)xx ax a -<-,设()e (21)x g x x =-,h (x )=ax a -,由()e (21)x g x x '=+可知当12x <-时，()g x '＜0，g (x )在(−∞,−12)上单调递减, 当12x>-时，()g x'＞0，()g x在(−12,+∞)上单调递增,作出g(x)与h(x)的大致图象如图所示,故(0)(0)(1)(1)h gh g>⎧⎨-≤-⎩,即132eaa<⎧⎪⎨-≤-⎪⎩,所以32e≤a<1,故选D. 25．A 【解析】若选项A错误，选项B、C、D正确，()2f x ax b'=+，因为是()f x的极值点，是()f x的极值，所以(1)0(1)3ff'=⎧⎨=⎩，即203a ba b c+=⎧⎨++=⎩，解得23b ac a=-⎧⎨=+⎩，因为点(2,8)在曲线()y f x=上，所以428a b c++=，即()42238a a a+⨯-++=，解得5a=，所以10b=-，8c=，所以2()5108f x x x=-+.此时2(1)5(1)10(1)8230f-=⨯--⨯-+=≠，即1-不是()f x的零点，所以选项A错误，选项B、C、D正确，故选A．。

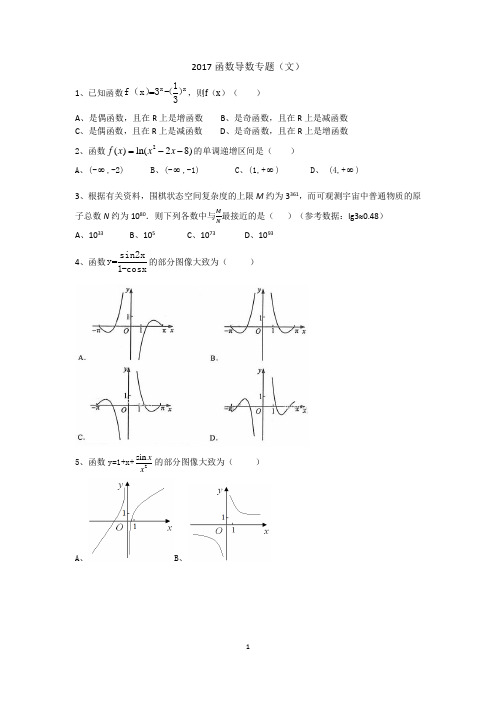
2017函数导数专题（文）1、已知函数xx ）31（-3）x （f =，则f （x ）（ ） A 、是偶函数，且在R 上是增函数 B 、是奇函数，且在R 上是减函数C 、是偶函数，且在R 上是减函数D 、是奇函数，且在R 上是增函数2、函数2()ln(28)f x x x =--的单调递增区间是（ ）A 、(-∞,-2)B 、(-∞,-1)C 、(1,+∞)D 、 (4,+∞)3、根据有关资料，围棋状态空间复杂度的上限M 约为3361，而可观测宇宙中普通物质的原子总数N 约为1080．则下列各数中与M N 最接近的是（ ）（参考数据：lg3≈0.48） A 、1033 B 、105 C 、1073 D 、10934、函数cosx-1sin2x y =的部分图像大致为（ ）A 、B 、C 、D 、 6、已知函数211()2()x x f x x x a ee --+=-++有唯一零点，则a=（ ） 7、已知函数f (x )=lnx +ln⁡（2−x ），则（ ）A 、f (x )在（0,2）单调递增B 、f (x )在（0,2）单调递减C 、y =⁡f (x )的图像关于直线x =1对称D 、y =⁡f (x )的图像关于点（1,0）对称8、设())021＜＜1,1=-≥⎪⎩x f x x x ，若f (a )=f (a +1),则1=⎛⎫ ⎪⎝⎭f a （ ） A 、2 B 、4 C 、6 D 、89、已知奇函数()f x 在R 上是增函数.若0.8221(log ),(log 4.1),(2)5a fb fc f =-==，则,,a b c 的大小关系为（ ）A 、a b c <<B 、b a c <<C 、c b a <<D 、c a b <<10、若函数f (x )=x 2+ ax +b 在区间[0,1]上的最大值是M ，最小值是m ，则M – m （ ）A 、与a 有关，且与b 有关B 、与a 有关，但与b 无关C 、与a 无关，且与b 无关D 、与a 无关，但与b 有关11、若函数()x e fx （e=2.71828……是自然对数的底数）在()f x 的定义域上单调递增，则称函数()f x 具有M 性质，下列函数中具有M 性质的是（） A 、()2-x f x = B 、()2f x =x C 、()3-xf x = D 、()cos f x =x12、已知函数||2,1,()2, 1.x x f x x x x +<⎧⎪=⎨+≥⎪⎩设a ∈R ，若关于x 的不等式()||2x f x a ≥+在R 上恒成立，则a 的取值范围是（ ）A 、[2,2]-B 、[2]-C 、[2,-D 、[-13、已知a ∈R ，设函数()ln f x ax x =-的图象在点（1，(1)f ）处的切线为l ，则l 在y 轴上的截距为 .14、已知f (x )是定义在R 上的偶函数，且f (x +4)=f (x -2).若当[3,0]x ∈-时，()6xf x -=，则f (919)= .1516、曲线在点（1，2）处的切线方程为_________________________.17、已知函数()f x 是定义在R 上的奇函数，当x ()-，0∈∞时，()322=+f x x x ,则()2=f18、已知函数()e cos x f x x x =-． （1）求曲线()y f x =在点(0,(0))f 处的切线方程；（2）求函数f （x ）在区间[0，,π2]上的最大值和最小值。

全国卷13-17高考真题分类汇编：函数、导数及其应用一.选择题1.（2015.Ⅱ理5）设函数211log (2),1,()2,1,x x x f x x -+-<⎧=⎨≥⎩,2(2)(log 12)f f -+=( )A ．3B ．6C ．9D ．122.【2017.Ⅰ理5】函数()f x 在(,)-∞+∞单调递减，且为奇函数．若(11)f =-，则满足21()1x f --≤≤的x 的取值范围是（ ）A ．[2,2]-B ．[1,1]-C ．[0,4]D ．[1,3]3. (2014·Ⅱ理8)设曲线y=ax-ln(x+1)在点(0,0)处的切线方程为y=2x,则a= ( )A.0 B.1 C.2 D.34．（2013·Ⅰ文）已知函数f (x )＝⎩⎪⎨⎪⎧－x 2＋2x ，x ≤0，ln (x ＋1)，x >0.若|f (x )|≥ax ，则a 的取值范围是 ( )A ．(－∞，0]B ．(－∞，1]C ．[－2,1]D ．[－2,0]5．（2013·大纲卷理）已知函数f (x )的定义域为(－1,0)，则函数f (2x ＋1)的定义域为( ) A ．(－1,1) B.⎝⎛⎭⎫－1，－12 C ．(－1,0) D .⎝⎛⎭⎫12，1 6．（2016.III.理6）已知432a =，254b =，1325c =，则（ ）（A ）b a c << （B ）a b c << （C ）b c a << （D ）c a b <<7、（2016.I 理8）若101a b c >><<，，则（ ） A ．c c a b < B ．c cab ba < C ．log log b a a c b c<D ．log log a b c c<8.【2017.Ⅰ理11】设x 、y 、z 为正数，且235x y z==，则（ ）A ．2x <3y <5zB ．5z <2x <3yC ．3y <5z <2xD ．3y <2x <5z9．（2013·大纲理）若函数f (x )＝x 2＋ax ＋1x 在⎝⎛⎭⎫12，＋∞是增函数，则a 的取值范围是 （ ） A ．[－1,0] B ．[－1，＋∞) C ．[0,3] D ．[3，＋∞)6、（2016.I 理8）若101a b c >><<，，则（ ） （A ）c c a b <（B ）c cab ba <（C ）log log b a a c b c <（D ）log log a b c c <10. (2014·Ⅱ文11)若函数f (x )=kx-lnx 在区间(1,+∞)单调递增,则k 的取值范围是( ) A. (,2]-∞- B. (,1]-∞- C. [2,)+∞ D. [1,)+∞(D)(C)(B)(A)xyπ4π23π4π22π3π4π2π4yxxyπ4π23π4π22π3π4π2π4yx11、（2016.I 理7）函数y =2x 2–e |x |在[–2,2]的图像大致为（ ）（A ）（B ）（C ）（D ）12.（2015.Ⅱ理10）如图，长方形ABCD 的边2AB =，1BC =，O 是AB 的中点，点P 沿着边BC ，CD 与DA 运动，记BOP x ∠=．将动P 到A 、B 两点距离之和表示为x 的函数()f x ，则()y f x =的图像大致为（ ）13.（2015.Ⅰ文12）设函数()y f x =的图像与2x ay +=的图像关于直线y x =-对称，且(2)(4)1f f -+-=，则a =( )（A ） 1- （B ）1 （C ）2 （D ）414．（2016.II.理12）已知函数()()f x x ∈R 满足()2()f x f x -=-，若函数1x y x+=与()y f x =图像的交点为1122(,),(,),,(,),m m x y x y x y ⋅⋅⋅则1()miii x y =+=∑（ ）（A ）0 （B ）m （C ）2m （D ）4m15.【2017.II 理11】若2x =-是函数21()(1)x f x x ax e -=+-的极值点，则()f x 的极小值为（ ） A.1- B.32e -- C.35e - D.1 16.（2014二理12）设函数函数f(x)=3sin x mπ.若存在f(x)的极值点x 0满足20x +()20f x ⎡⎤⎣⎦<m 2,则m 的取值范围是( ) A. ()(),66,-∞-+∞ B. (),4-∞-∪()4,+∞B. (),2-∞-∪()2,+∞ D. (),1-∞-∪()4,+∞ 17.【2017.Ⅲ理11】已知函数211()2()x x f x x x a ee --+=-++有唯一零点，则a =（ ）A ．12-B ．13C ．12D ．1DPCB OA x18.（2015.Ⅱ理12）设函数'()f x 是奇函数()()f x x R ∈的导函数，(1)0f -=，当0x >时，'()()0xf x f x -<，则使得()0f x >成立的x 的取值范围是（ ）A ．(,1)(0,1)-∞-B ．(1,0)(1,)-+∞C ．(,1)(1,0)-∞-- D ．(0,1)(1,)+∞19.（2015.Ⅰ理12）设函数()f x =(21)xe x ax a --+,其中a 1，若存在唯一的整数0x ，使得0()f x 0，则a 的取值范围是（ ） (A)[-32e ，1） (B)[-错误！未找到引用源。

2017年普通高等学校招生全国统一考试理科数学一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合A ={x |x <1}，B ={x |31x <}，则( )A ．{|0}AB x x =< B ．A B =RC ．{|1}A B x x =>D ．A B =∅2．如图，正方形ABCD 内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点，则此点取自黑色部分的概率是( ) A ．14B ．π8C ．12D ．π43．设有下面四个命题1p ：若复数z 满足1z∈R ，则z ∈R ；2p ：若复数z 满足2z ∈R ，则z ∈R ； 3p ：若复数12,z z 满足12z z ∈R ，则12z z =； 4p ：若复数z ∈R ，则z ∈R .其中的真命题为( ) A ．13,p pB ．14,p pC ．23,p pD ．24,p p4．记n S 为等差数列{}n a 的前n 项和．若4524a a +=，648S =，则{}n a 的公差为( )A ．1B ．2C ．4D ．85．函数()f x 在(,)-∞+∞单调递减，且为奇函数．若(11)f =-，则满足21()1x f --≤≤的x 的取值范围是( ) A ．[2,2]-B ．[1,1]-C ．[0,4]D ．[1,3]6．621(1)(1)x x++展开式中2x 的系数为( ) A ．15B ．20C ．30D ．357．某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形，这些梯形的面积之和为( ) A ．10B ．12C ．14D ．168．右面程序框图是为了求出满足3n −2n >1000的最小偶数n ，那么在和两个空白框中，可以分别填入( ) A ．A >1 000和n =n +1 B ．A >1 000和n =n +2 C ．A ≤1 000和n =n +1D ．A ≤1 000和n =n +29．已知曲线C 1：y =cos x ，C 2：y =sin (2x +2π3)，则下面结论正确的是( ) A ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2 B ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 2C ．把C 1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2D ．把C 1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 210．已知F 为抛物线C ：y 2=4x 的焦点，过F 作两条互相垂直的直线l 1，l 2，直线l 1与C 交于A 、B 两点，直线l 2与C 交于D 、E 两点，则|AB |+|DE |的最小值为( ) A ．16B ．14C ．12D ．1011．设x ，y ，z 为正数，且235x y z ==，则( )A ．2x <3y <5zB ．5z <2x <3yC ．3y <5z <2xD ．3y <2x <5z12．几位大学生响应国家的创业号召，开发了一款应用软件。