光子材料、微结构与微米共30页文档
- 格式:ppt
- 大小:2.39 MB
- 文档页数:30

一维光子晶体一维光子晶体是一种具有重要应用前景的新型光子学结构,它可以有效地利用晶体衍射机理来把光束指向指定的方向,从而在光子学领域有广泛的应用前景,比如光纤传输和传感系统等。
一维光子晶体是结构调制型光子器件,它包括一个可以传导电磁波的光子媒质,一系列由非常小的金属微粒或者其他材料形成的尺寸在几个微米到几十微米的衍射掩模,以及一组由致密反射器成形的边界条件。
这些衍射掩模组成的结构特性决定了光在光子晶体上衍射的特性。
一维光子晶体具有很高的可塑性,能够对光进行控制和分布,实现空间和光谱上的局域立体图。
它可以利用反射和衍射来改变和分散光,从而实现各种功能的光子学应用。
例如,它可以实现远距离的光纤通信,实现从宽带到单脉冲的高效传输。
此外,一维光子晶体还可以实现高分辨率的光谱分析,将小的变化可视化,从而实现传感技术,用于环境监测、测量和质量控制等应用。
一维光子晶体的基本结构如下,它包括光子媒质、边界条件、衍射掩模等部分。
首先,光子媒质是由晶体栅组成的,它具有电磁波的传导性能,可以有效把光束传导到掩模处。
其次,边界条件是光子晶体的结构和表面特性,它们包括一系列密封的反射层、折射层和透射层,它们由不同类型的材料组成,用于建立理想的光学界面。
最后,衍射掩模是一维光子晶体的核心结构,它由金属微粒或者其他材料形成,在几个微米到几十微米之间。
这些金属微粒会通过不同的衍射角,将光束折射到指定的方向,从而实现聚焦。
当前,一维光子晶体已经在实际的应用中得到广泛的应用,已经发展成为多种应用的重要技术。
它可以实现多种光子学应用,如透射成像、反射成像、光纤传输等,也可以实现传感器应用,用于环境监测、气象监测、测量和质量控制等。
未来,一维光子晶体将在更多的应用中得到广泛的应用,如光学计算和超精细细胞分析等。
总之,一维光子晶体是一种重要的光子学结构,它可以利用反射和衍射来改变和分散光,从而实现多种应用的光子学应用,如光纤通信和传感技术,具有广阔的应用前景。

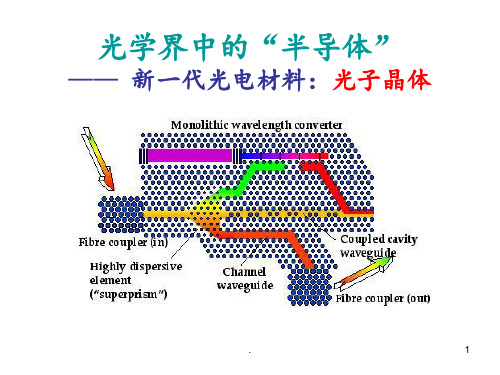

光子带隙结构
光子带隙(photonic Bandgap-PBG)结构,又称为光子晶体(photonic Crystal),它是一种介质材料在另一种介质材料中周期分布所组成的周期结构。
尽管光子带隙最初应用于光学领域,然而由于其禁带特性,近年来在微波和毫米波领域也获得极大关注。
在光子带隙结构中,电磁波经周期性介质散射后,某些波段电磁波强度会因干涉而呈指数衰减,无法在该结构中传播,于是在频谱上形成带隙。
PBG结构的这种特性,在天线领域和微波电路中都有着巨大的应用价值。
时域有限差分(FDTD方法是分析PBG结构一种非常有效的数值计算方法。
然而,由于微波光子晶体结构的精细,网格量必须很大,内存容量就成为计算中的瓶颈。
此外当PBG结构为圆环形时,一般的阶梯近似不足以满足计算精度。
针对以上两个问题,本文采用本课题组带有共形网格建模的MPI并行FDTD程序对圆环形PBG 结构进行了分析。
讨论了单元数目,单元间距,圆孔内径和导带宽度对S参数的影响,最后设计了一种宽禁带圆环形PBG结构。


一位光子晶体的计算引言:光子晶体是一种由孔径大小相近的周期性微结构排列而成的晶体,它可以控制光的传输和分散特性。
光子晶体的设计和计算涉及到电磁理论和半导体物理等多个领域的知识。
本文将利用几种常见的计算方法对一位光子晶体进行计算。
一、光子晶体的周期性结构光子晶体的周期性结构是由孔径大小相近的周期性微结构组成的。
完美的周期性结构可以通过布拉格方程来描述,即:nλ = 2dsin(θ)其中,n为波长λ的波数,d为晶格常数(晶格孔的周期),θ为入射角。
利用布拉格方程,可以计算得到晶格常数d和入射角θ的关系。
二、光子晶体的带隙计算光子晶体具有光子带隙,处于该带隙内的光无法传播。
带隙的存在与晶体的周期性结构有关,可以通过计算得到。
最常用的计算方法是平面波展开法和有限差分时间域法。
1.平面波展开法平面波展开法是计算光子晶体带隙的常见方法之一、该方法利用周期性边界条件和布拉格散射原理,将光场展开成正弦函数的和,然后通过计算能量本征值来确定带隙的存在。
2.有限差分时间域法有限差分时间域法是一种数值模拟方法,用于计算光子晶体的传输和分散特性。
该方法基于麦克斯韦方程组和时域有限差分离散,将光的传输过程分割成空间离散的网格,通过时间步进算法来计算光的传播。
利用该方法可以计算出光子晶体中的模式和带隙。
三、光子晶体的优化设计光子晶体的设计通常涉及到优化问题,即找到最佳的微结构参数来实现所需的光学性能。
常用的优化算法有遗传算法、蚁群算法、粒子群算法等。
1.遗传算法遗传算法是一种模拟生物进化过程的优化算法,通过遗传操作和自然选择来求解最优解。
在光子晶体的优化设计中,可以将晶体的微结构参数看作遗传信息,通过遗传操作和适应度函数的评价,不断迭代最佳的参数组合。
2.蚁群算法蚁群算法是一种模拟蚁群觅食行为的优化算法,通过模拟蚂蚁在空间中的行为来求解最优解。
在光子晶体的优化设计中,可以将蚂蚁在空间中的路径看作微结构参数的路径,通过蚂蚁的和信息素的更新,不断迭代最佳的参数组合。
光子晶体基础知识汇总引言在过去的 50 年中,对半导体技术的深入研究和广泛应用推动了电子工业和信息产业的迅速发展。
目前半导体技术正向着高速度、高集成化方向发展,但这也不可避免地引发了一系列问题:比如电路中能量损耗过大导致集成片发热,此外由于高速处理对信号在器件中的延迟提出了更高的要求。
半导体器件的能力已基本到达了极限,为此科学家们把目光从电子转向了光子。
与电子相比,光子具有如下优势:1、极高的信息容量和效率;2、极快的响应能力;3、极强的互连能力和并行能力;4、极大的存储能力;5、光子间相互作用很弱,可极大地降低能量损耗。
但是与集成电路相比,集成光学器件的尺寸和集成度问题,一直是困扰集成光学发展的重要问题之一。
采用传统的光波导原理设计和制作光学元件,如果要想缩小尺寸是非常困难的。
因而严重限制了可达到的集成度。
目前对光子晶体的研究与开发,不失为解决以上困难的一种有效途径。
§1.1 光子晶体简介光子晶体是八十年代末提出的新概念和新材料,迄今取得异常迅猛的发展。
光子晶体不仅具有理论价值,更具有非常广阔的应用前景,这个领域已经成为国际学术界的研究热点。
1.1.1 光子晶体的概念光子晶体的概念是由Yablonvitch和 John在1987年各自提出的,它是根据传统的晶体概念类比而来的。
他们最初的想法是用一种材料来改变在其中传播的光的性质,就像我们利用半导体材料改变在其中通过的电子的性质一样。
众所周知,在半导体材料中,原子排布的晶格结构产生的周期性电势场影响着在其中运动的电子的性质,电子将形成能带结构。
将介电常数不同的介质材料在空间中周期性排列而形成的结构将改变在其间传播的光的性质。
由于介电常数存在空间上的周期性,所以它对光的折射率同样有周期性分布,在其中传播的光波的色散曲线也会形成带状能带结构,叫做光子能带(Photonic band)。
光子能带之间可能出现带隙,即光子带隙也叫光子禁带(Photonic bandgap简称 PBG)。