基于MATLAB的六自由度工业机器人运动分析和仿真

选择MATLAB2016a版，高版本不能安装。

安装好按照下面的操作做出来，然后截图做成Word文档发给我。

MATLAB2016a版同学们网上下载安装，安装方法网上随便可找到。

机器人工具箱我发给你们。

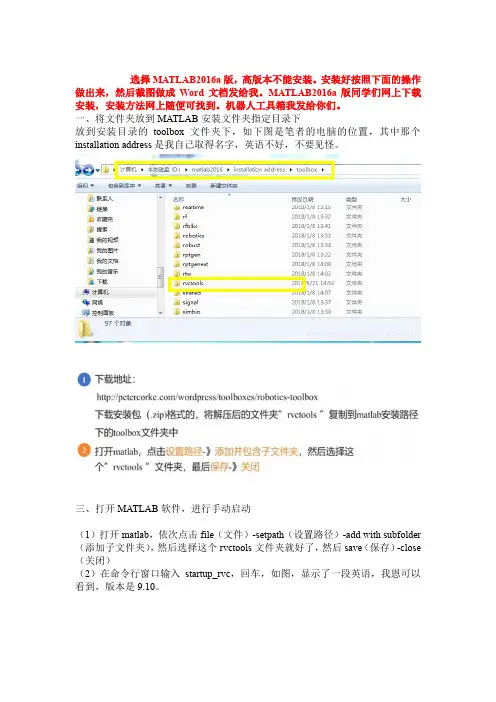
一、将文件夹放到MATLAB安装文件夹指定目录下放到安装目录的toolbox文件夹下，如下图是笔者的电脑的位置，其中那个installation address是我自己取得名字，英语不好，不要见怪。

三、打开MATLAB软件，进行手动启动（1）打开matlab，依次点击file（文件）-setpath（设置路径）-add with subfolder （添加子文件夹），然后选择这个rvctools文件夹就好了，然后save（保存）-close （关闭）（2）在命令行窗口输入startup_rvc，回车，如图，显示了一段英语，我恩可以看到，版本是9.10。

本文主要是给大家一个系统的概念，如何用Matlab实现六轴机器人的建模和实现轨迹规划。

以后将会给大家讲解如何手写正逆解以及轨迹插补的程序。

程序是基于Matlab2016a，工具箱版本为Robotic Toolbox 9.10。

1.D-H建模三个两两相互垂直的XYZ轴构成欧几里得空间，存在六个自由度：沿XYZ 平移的三个自由度，绕XYZ旋转的三个自由度。

在欧几里得空间中任意线性变换都可以通过这六个自由度完成。

Denavit-Hartenberg提出的D-H参数模型能满足机器人学中的最小线性表示约定，用4个参数就能描述坐标变换：绕X轴平移距离a；绕X轴旋转角度alpha；绕Z轴平移距离d；绕Z轴旋转角度theta。

2.标准D-H模型和改进D-H模型对比来看参数并没有改变，标准的D-H 模型是将连杆的坐标系固定在该连杆的输出端（下一关节），也即坐标系i-1与关节i对齐；改进的D-H模型则是将坐标系固定在该连杆的输入端（上一关节），也即坐标系i-1与关节对齐i-1。

六自由度机械臂运动学分析与仿真研究肖俊明;韩伟;王瑷珲;李继朋;梁旺【摘要】运用D-H参数法确定机械臂的参数、坐标系,建立机械臂的运动学方程.在Matlab软件中进行数值计算,通过分析机械臂的工作空间,得到了机械臂工作空间图.在Matlab工作环境下,用机器人工具箱Robotics Toolbox对所建六自由度机械臂运动学模型的正运动学、逆运动学、轨迹规划进行验证与仿真,得到了各关节的角位移、角速度、角加速度与时间的关系曲线.研究表明,该机械臂运动空间设计直观、精确,为机械臂控制系统设计、动力学分析及轨迹规划提供了理论基础和参考依据.【期刊名称】《中原工学院学报》【年(卷),期】2018(029)004【总页数】7页(P77-83)【关键词】机械臂;六自由度;运动学;仿真【作者】肖俊明;韩伟;王瑷珲;李继朋;梁旺【作者单位】中原工学院电子信息学院,河南郑州450007;中原工学院电子信息学院,河南郑州450007;中原工学院电子信息学院,河南郑州450007;中原工学院电子信息学院,河南郑州450007;中原工学院电子信息学院,河南郑州450007【正文语种】中文【中图分类】TP24220世纪60年代初机器人问世以来，机器人技术逐步取得了实质性的进步与成果[1]，目前已被应用于很多行业，在航空航天、汽车工业、海洋探索、医疗手术等行业的高科技领域发挥着重要作用，促进了人们生活的改善。

机械臂是最早应用于实际生产领域的一种机器人[2]。

其中，串联机械臂应用最为广泛，它是由若干通过关节连接在一起的连杆组成的具有多个自由度的开链型连杆机构。

它的一端固定在基座上，另一端为末端执行器，主要进行抓取操作，中间部分是由若干带驱动的转动或移动关节串联而成的机构体。

机械臂运动学研究的是各连杆关节的运动与机械臂各部分(一般为末端执行器)的位置、姿态之间的数学关系。

研究这种关系是设计机械臂运动控制器所必需的。

机械臂运动学的研究主要有正运动学问题和逆运动学问题两类。

基于MATLAB的六⾃由度⼯业机器⼈运动分析和仿真基于MATLAB 的六⾃由度⼯业机器⼈运动分析及仿真摘要：以FANUC ARC mate100⼯业机器⼈为研究对象，对其机构和连杆参数进⾏分析，采⽤D-H 法对机器⼈进⾏正运动学和逆运动学分析，建⽴运动学⽅程。

在MATLAB 环境下，运⽤机器⼈⼯具箱进⾏建模仿真，仿真结果证明了所建⽴的运动学正、逆解模型的合理性和正确性。

关键词:FANUC ARC mate100⼯业机器⼈; 运动学; MATLAB 建模仿真 1引⾔⼯业机器⼈技术是在控制⼯程、⼈⼯智能、计算机科学和机构学等多种学科的基础上发展起来的⼀种综合性技术。

经过多年的发展，该项技术已经取得了实质性的进步[1]。

⼯业机器⼈的发展⽔平随着科技的进步和⼯业⾃动化的需求有了很⼤的提⾼，同时⼯业机器⼈技术也得到了进⼀步的完善。

⼯业机器⼈的运动学分析主要是通过⼯业机器⼈各个连杆和机构参数，以确定末端执⾏器的位姿。

⼯业机器⼈的运动学分析包括正运动学分析和逆运动学分析。

随着对焊接件要求的提⾼，弧焊等机器⼈的需求越来越多。

本⽂就以FANUC ARC mate100机器⼈为研究对象，通过分析机构和连杆参数，运⽤D-H 参数法建⽴坐标系，求出连杆之间的位姿矩阵，建⽴⼯业机器⼈运动学⽅程。

并在MATLAB 环境下，利⽤RoboticsToolbox 进⾏建模仿真。

2 FANUC ARC mate100 D-H 坐标系的建⽴mate100是FANUC 公司⽣产的6⾃由度⼯业机器⼈，包括底座、机⾝、臂、⼿腕和末端执⾏器，每个⾃由度对应⼀个旋转关节，如图1所⽰。

图1FANUC ARC mate 100机器⼈三维模型DENAVIT 和HARTENBERG 于1955年提出了⼀种为关节链中的每⼀个杆件建⽴坐标系的矩阵⽅法，即D-H 参数法，在机器⼈运动学分析得到了⼴泛运⽤。

采⽤这种⽅法建⽴坐标系:(1) Z i 轴沿关节i +1的轴线⽅向。

基于MATLAB的六自由度机械臂运动仿真分析
王春荣;夏尔冬
【期刊名称】《榆林学院学报》
【年(卷),期】2017(027)002
【摘要】以某六自由度机械臂为研究对象,利用PRO/E建立其三维建模.分析了机械臂的D-H坐标参数、运动学以及雅克比矩阵,借助MATLAB软件构建机械臂模型.仿真分析机械臂在直角坐标系与关节坐标系下的轨迹规划.仿真实验表明,机械臂手部末端的运动轨迹平稳且没有跳跃点,并且在插补过程中,每个关节的角位移,角速度和角加速度的变化十分连贯、匀速没有任何跳跃点,该机械臂设计合理.
【总页数】5页(P11-14,25)
【作者】王春荣;夏尔冬
【作者单位】三明学院机电工程学院,福建三明365004;三明学院机电工程学院,福建三明365004
【正文语种】中文
【中图分类】TP242
【相关文献】
1.基于MATLAB和ADAMS的六自由度并联运动机床运动学仿真 [J], 李滨城;杨丹;顾金凤
2.基于 MATLAB／Robotics Toolbox的六自由度机械臂仿真 [J], 王彦璋
3.六自由度机械臂运动学及奇异性仿真分析 [J], 袁媛
4.基于放疗的六自由度医用机械臂动力学仿真分析 [J], 陈继朋;陈惠贤;杨小龙;刘
晓娟;乔宇;马利强
5.六自由度机械臂的运动学分析与Matlab仿真 [J], 夏亚飞;魏国春;吝健全;夏楠因版权原因，仅展示原文概要，查看原文内容请购买。

《六自由度机械臂控制系统设计与运动学仿真》篇一一、引言随着科技的飞速发展，自动化与机器人技术已广泛应用于各种领域，六自由度机械臂是其中一种重要而常见的自动化工具。

它具备灵活的运动能力与复杂操作功能，能够在高精度的环境中完成一系列作业。

本篇论文旨在介绍六自由度机械臂控制系统的设计与运动学仿真，旨在提升机械臂的性能和可靠性。

二、六自由度机械臂控制系统设计1. 硬件设计六自由度机械臂控制系统主要由机械臂主体、驱动器、传感器和控制单元等部分组成。

其中，机械臂主体由多个关节组成，每个关节由一个驱动器驱动。

传感器用于检测机械臂的位置、速度和加速度等信息，控制单元则负责处理这些信息并发出控制指令。

2. 软件设计软件设计部分主要包括控制算法的设计和实现。

我们采用了基于PID（比例-积分-微分）的控制算法，以实现对机械臂的精确控制。

此外，我们还采用了路径规划算法，使机械臂能够按照预定的路径进行运动。

3. 控制系统架构控制系统采用分层架构，分为感知层、决策层和执行层。

感知层通过传感器获取机械臂的状态信息；决策层根据这些信息计算控制指令；执行层则根据控制指令驱动机械臂进行运动。

三、运动学仿真运动学仿真主要用于模拟机械臂的运动过程，验证控制系统的性能。

我们采用了MATLAB/Simulink软件进行仿真。

1. 模型建立首先，我们需要建立机械臂的数学模型。

根据机械臂的结构和运动规律，我们可以建立其运动学方程。

然后，将这些方程导入到MATLAB/Simulink中，建立仿真模型。

2. 仿真过程在仿真过程中，我们设定了不同的工况和任务，如抓取、搬运、装配等。

通过改变控制参数和路径规划算法，观察机械臂的运动过程和性能表现。

我们还对仿真结果进行了分析，以评估控制系统的性能和可靠性。

四、实验结果与分析我们通过实验验证了六自由度机械臂控制系统的性能。

实验结果表明，该系统能够实现对机械臂的精确控制和灵活操作。

在各种工况和任务下，机械臂都能以较高的速度和精度完成任务。

六自由度并联机器人运动学和动力学研究摘要：运动学、动力学以及控制是任何机器人系统开发中要解决的关键问题。

为了验证课题组所设计的六自由度并联机器人的合理性，运用刚体运动学原理，通过分析动平台各铰链点与动平台自身的速度和加速度之间的关系，建立了并联机器人的运动学模型。

然后，综合拉格朗日方程法和凯恩法的优点，建立了并联机器人的动力学模型，该模型不仅全面的表征了并联机器人的动力学特性，而且具有简单的、通用的形式，为并联机器人控制算法的研究开辟了一条捷径。

最后，在给定的工作空间下，采用MATLAB编程和Adams仿真，对并联机器人动平台的运动过程进行了模拟，绘制出动平台做圆周平动时的速度、加速度曲线，通过对比分析，验证了运动学模型的正确性；同时，采用Adams-MATLAB Simulink联合仿真，通过分析Simulink模块绘制出的的驱动力误差曲线以及仿真出的动平台运动轨迹，验证了动力学模型的正确性。

其研究结果不仅为所设计机构后续的优化与控制提供依据，也为其他并联机构的研究提供参考。

关键词：六自由度并联机器人运动学模型动力学模型联合仿真Research on Kinematics and Dynamics of 6-DOF Parallel RobotYANG Junqiang1，2 WAN Xiaojin1，2 LIU Licheng1，2 TANG Ke1，2Abstract：Kinematics，dynamics，and control are key issues to be addressed in the development of any robotic system.To verify the the rationality of the 6-DOF parallel robot designed by the research group，this paper applied the rigid body kinematics principle to analyze the relationship between the velocity and accelerationof the moving platform's hinge points and moving platform itself，and established the kinematics models.Then，based on the advantages of Lagrange equation method and Kane’s method，the dynamic model of parallel robot is established，which not only fully characterizes the dynamics of parallel robot，but also has a simple and universal form to make the research of robot control algorithm easy.Finally，under the given working space，using MATLAB programming and Adams simulation，the motion process of the parallel manipulator is imitated，and the velocity and acceleration curves of the moving platform are plotted.Through comparative analysis，the kinematics models are verified.What’s more， Adams-MATLAB Simulink co-simulation is used to verify the correctness of the dynamic model by analyzing the driving force error curves and the trajectory of the moving platform.The results of this paper notonly provide the basis for the subsequent optimization and control of the mechanism，but also provide the reference for the research of other parallel mechanisms.Key words：6-DOF parallel robot kinematics models dynamic model co-simulation引言Stewart平台[1]的出现始于1965年德国学者Stewart发明的具有六自由度运动能力的并联机构飞行模拟器，因其具有刚度高、精度高、承载能力强、动态特性好等优点，因此近年来被广泛应用于并联机床、精密定位平台和振动隔离平台等方面[2]，而且基于Stewart平台的并联机器人[3，4]设计也相继出现，如图1所示，即为课题组基于Stewart平台设计的六自由度并联机器人。

基于Matlab的六足机器人优化设计仿真王伟伟;陈锋【摘要】The hexapod robots are highly integrated electromechanical bionic systems, whose dynamic performance is determined by the structure system and the control system. In order to improve the overall dynamic performance of the hexapod robots, the integration of optimized design of the hexapod robot is needed. Design variables, constraints and objective functions involved in the optimization process are discussed based on the geometric characteristics; the integrated optimization model of hexapod robot systems is built. With examples, comparative analysis of simulation results is done. Simulation results illustrate that integrated design can get better dynamic performance for the hexapod robot system.%六足机器人是机电高度集成的仿生系统，它的动态性能由其结构系统与控制系统一起决定。

为了提高六足机器人整体的动态性能，对六足机器人进行集成优化设计。

描述六足机器人系统的结构；根据六足机器人机构的几何特征，讨论在优化过程中涉及到的设计变量、约束方程以及目标函数；对六足机器人系统进行集成优化建模。

基于MATLAB的PUMA560机器人运动学仿真作者：董慧颖梁爽来源：《无线互联科技》2014年第05期摘要：随着机器人技术的发展和应用，机器人在现代工业生产中扮演着越来越重要的角色。

机器人诞生是科学技术与社会进步的必然结果，从根本上改变了原来传统的生产体系和生产方式。

本文在MATLAB环境下，对PUMA560机器人进行参数设计，分析PUMA560机器人的运动，讨论机器人的正运动学、逆运动学、轨迹规划及仿真。

关键词：机器人运动学；PUMA560；轨迹规划；计算机仿真对机器人进行图形仿真，可以将机器人仿真的结果以图形的形式表示出来，从而直观地显示出机器人的运动情况，得到从数据曲线或数据本身难以分析出来的许多重要信息，还可以从图形上看到机器人在一定控制条件下的运动规律。

一个新的机器人工作程序编制完成后，先在仿真软件中观察运行结果，分析检验轨迹规划和作业规划的正确性和合理性，为离线编程技术的研究提供有效的验证手段。

本文在MATLAB环境下，对六自由度的PUMA560机器人进行参数设计，然后讨论了正、逆运动学算法，轨迹规划问题，最后在MATLAB环境下，运用机器人工具箱编制简单的程序语句，快速完成了机器人的运动学仿真。

1 PUMA560机器人参数设计1.1 连杆参数和坐标系一般移动关节及转动关节共同作用组成机器人的操作臂，各个关节都具有1个自由度。

着重研究具有6个自由度的工业机器人。

通常规定连杆O表示基座，还规定基座，即连杆O不在探讨的6个连杆之中。

关节1使基座与连杆1相接；关节2使连杆1与连杆2相接；关节3使连杆2与连杆3相接，以此类推。

如图1所示，为PUMA560机器人的关节和连杆坐标系，该机器人通过六个关节及六个连杆组合而成。

机器人的基座，即连杆O保持静止不动，连杆6与手固定相连。

1.2 PUMA560机器人连杆坐标系在每个连杆上固接一个坐标系，用来判断机器人各连杆间的相对运动关系。

规定{0}代表坐标系与基座固接，{i}代表坐标系与连杆i固接。

基于MATLAB和RobotStudio的6-DOF机器人运动学分析与仿真郝建豹;宋春华【摘要】Aiming at the working difficulties of ship cabin,cabinet and other narrow space,a 6 degrees of freedom(6-DOF)robot was developed.First analyzes the mechanical structure of the robot,the robot D-H and robot coordinate form of forward and inverse kinematics equation was established based on the theory of D-H coordinates,followed by the application of MATLAB kinematics of the robot simulation,the results show that the robot kinematics and inverse kinematics equations exactly;finally a virtual prototype is designed,and the movement of the welding case is analyzed by RobotStudio simulation.In order to further verify the performance of the designed robot,it is compared with the general 6-DOF robot.The results show that the feasibility of the new robot,and provides a theoretical basis for the design of industrial robots to adapt to the cabinet and so on narrow space.%针对船体密封舱、箱柜等狭窄空间普遍存在的机器人难以工作问题,提出了一种新型6-DOF(degrees of freedom)机器人.首先分析了该机器人的机械结构,基于D-H坐标理论建立了机器人D-H坐标表格以及机器人正、逆运动学方程,其次应用MATLAB对机器人的运动学进行了仿真,结果表明所得的机器人正、逆运动学方程完全正确;最后设计了虚拟样机,利用RobotStudio 仿真分析了机器人箱体焊接的优点;为进一步验证设计的机器人运动性能,与通用6-DOF机器人做了对比分析.研究结果表明新型机器人运动的可行性,为设计适应箱柜等狭窄空间的工业机器人提供了理论依据.【期刊名称】《机械设计与制造》【年(卷),期】2018(000)002【总页数】4页(P238-241)【关键词】6-DOF机器人;正逆运动学;MATLAB仿真;RobotStudio【作者】郝建豹;宋春华【作者单位】广东交通职业技术学院机电工程系,广东广州510800;广东交通职业技术学院机电工程系,广东广州510800【正文语种】中文【中图分类】TH161 引言随着工业自动化的发展，业界希望工业机器人能够像人类的手臂一样能够高效、灵活、优美自然的运动，6-DOF机器人是工业机器人应用最为广泛的一种类型[1]。

六自由度机械臂matlab运动学逆解六自由度机械臂是一种常见的工业机器人，它由六个旋转关节组成，每个关节都可以在空间中进行运动。

机械臂的运动学逆解是指根据机械臂末端执行器的位置和姿态，求解出每个关节的角度，从而实现机械臂的逆运动学问题。

在机械臂的运动学逆解问题中，我们需要知道机械臂的末端执行器的位置和姿态，以及机械臂的结构参数。

首先，我们可以通过机械臂的正运动学问题来求解末端执行器的位置和姿态。

正运动学问题是指已知机械臂的关节角度，求解出末端执行器的位置和姿态。

通过正运动学问题求解出的末端执行器的位置和姿态，可以作为运动学逆解问题的输入。

运动学逆解问题的目标是求解出机械臂每个关节的角度，使得机械臂的末端执行器达到所需的位置和姿态。

为了求解运动学逆解问题，我们可以使用旋转矩阵或四元数来表示机械臂的姿态，使用向量来表示机械臂的位置。

运动学逆解问题的求解方法有多种，其中一种常用的方法是使用解析方法。

解析方法通过将机械臂的运动学模型转化为一系列的方程，然后求解这些方程，从而得到机械臂的关节角度。

解析解法的优点是求解速度快，计算量小，但是对于复杂的机械臂结构和运动学模型，可能无法得到解析解。

另一种常用的求解方法是数值方法，例如使用迭代法或优化算法。

数值方法通过迭代的方式逼近机械臂的关节角度，使得机械臂的末端执行器的位置和姿态与所需的位置和姿态尽可能接近。

数值方法的优点是适用于复杂的机械臂结构和运动学模型，但是求解速度相对较慢。

在MATLAB中，可以使用机器人工具箱（Robotics Toolbox）来求解六自由度机械臂的运动学逆解问题。

机器人工具箱提供了一系列的函数和工具，用于求解机械臂的正运动学和逆运动学问题。

使用机器人工具箱，我们可以通过输入机械臂的结构参数和末端执行器的位置和姿态，来求解机械臂的逆运动学问题。

除了MATLAB中的机器人工具箱，还有其他的机器人运动学库和软件可以用于求解机械臂的运动学逆解问题，例如ROS（Robot Operating System）和OpenRave等。

六自由度机械臂控制系统设计与运动学仿真摘要：随着机械臂技术的不断发展与应用推广，对于机械臂的控制系统设计与运动学仿真的研究显得尤为重要。

本文基于六自由度机械臂，着重探讨了其控制系统设计与运动学仿真方面的问题。

通过建立数学模型，设计控制器以实现机械臂的运动。

并在MATLAB环境下进行仿真分析，探究了机械臂的各种运动状态与路径规划。

实验结果表明，所设计的控制系统能够实现精确的机械臂运动，并能根据特定任务进行灵活的路径规划。

关键词：六自由度机械臂；控制系统设计；运动学仿真；路径规划1. 引言机械臂是一种具有多自由度并能执行各种精密操作任务的机械装置。

近年来，机械臂在制造业、医疗、物流、无人驾驶等领域得到广泛应用。

机械臂的控制系统设计与运动学仿真是机械臂研究的重要组成部分，对于提高机械臂的精确度和效率具有重要意义。

2. 控制系统设计2.1 机械臂建模与运动学方程六自由度机械臂由臂架、关节和执行器等组成。

首先，根据机械臂结构和参数建立其数学模型。

然后，根据运动学原理，通过矩阵变换和旋转矩阵等方法推导出机械臂的运动学方程。

由运动学方程可以得到机械臂各关节之间的几何关系。

2.2 控制器设计基于机械臂的运动学方程，设计适当的控制器来控制机械臂的运动。

常用的控制方法有PID控制、模糊控制和神经网络控制等。

在此，我们选择PID控制器为例，通过调整PID控制器的参数，实现机械臂的位置和速度控制。

利用反馈控制原理，将机械臂的实际位置和速度与期望位置和速度进行比较，通过对误差信号进行反馈调整，控制机械臂按照预定轨迹运动。

3. 运动学仿真与路径规划在MATLAB环境下，建立机械臂的仿真模型，并进行运动学仿真与路径规划。

通过对仿真模型的参数设定和运动规划，模拟机械臂在不同工作状态下的运动。

比如，模拟机械臂抓取和放置物体的动作，模拟机械臂在空间中的路径规划等。

4. 实验结果与讨论通过运动学仿真与路径规划的实验，验证所设计的控制系统的性能。

基于MATLAB的六自由度工业机器人运动分析及仿真六自由度工业机器人是一种常见的工业自动化设备，通过对其运动进行分析和仿真，可以对其性能进行评估和优化。

MATLAB是一种强大的数学计算软件，在工程领域广泛应用，可以帮助我们进行机器人的运动分析和仿真。

首先，我们可以使用MATLAB对六自由度机器人进行建模。

六自由度机器人具有六个自由度，分别为三个旋转自由度和三个平移自由度。

我们可以使用MATLAB的机器人工具箱来建立机器人的模型，并定义其关节参数和连接方式。

通过模型可以获得机器人的几何结构、动力学参数和运动学方程。

接下来，我们可以使用MATLAB进行机器人的运动分析。

运动分析是指通过对机器人的运动学和动力学进行计算，从而获得机器人的运动和力学特性。

机器人的运动学分析主要是利用机器人的几何结构来推导出末端执行器的位置和姿态。

可以使用MATLAB的运动学工具函数来计算机器人的正运动学和逆运动学。

机器人的动力学分析主要是研究机器人的运动和力学特性之间的关系。

动力学分析可以帮助我们确定机器人的运动特性和关节力矩。

我们可以使用MATLAB的动力学工具箱来建立机器人的动力学模型，并使用动力学工具函数来计算机器人的动力学性能。

最后，我们可以使用MATLAB进行机器人的仿真。

机器人的仿真是通过对机器人的动力学进行数值计算，来模拟机器人的运动和力学特性。

通过仿真可以验证机器人的设计和控制方案，并进行参数优化。

在MATLAB 中，我们可以使用数值计算函数和绘图函数来进行机器人的仿真和可视化。

总结起来，基于MATLAB的六自由度工业机器人运动分析及仿真可以帮助我们对机器人的运动和力学特性进行研究和优化。

通过建立机器人的模型，进行运动分析和动力学分析，以及进行仿真和可视化，可以帮助我们理解和改进机器人的性能，在工业自动化领域发挥更大的作用。

机器人实验报告学院：专业：姓名：学号：教师：日期：实验一一．实验目的：1.对斯坦福6自由度机械手相邻连杆D-H矩阵的构建以及每一个连杆的坐标系的构建进行详细叙述和说明，并对每一对相邻连杆的4个D-H参数进行详细说明；2.对RRRR机械手受力分析的Matlab验证过程进行详细说明，并构建相邻连杆的D-H坐标系，列表说明每一对相邻连杆的D-H参数3.对斯坦福机械手逆向运动分析中seta1的求解进行简化并和教材计算结果进行对比4.阐述齐次变换矩阵变换方法在斯坦福机械手中应用，加上自己的理解进行文字叙述二．对RRRR机械手受力分析的Matlab验证过程进行详细说明，并构建相邻连杆的D-H坐标系，列表说明每一对相邻连杆的D-H参数分析下图RRRR 机械手其正向变换矩阵和转动雅可比矩阵如下(a)求解当各个关节坐标为q = [0, 900,−900, 0] T 的时候，相对于基坐标系的雅可比矩阵 Jo(b) 一个作用在坐标系 {4} 上的力 [0, 6, 0, 7, 0, 8]T . 在 (a)中所描述的位置, 计算用于平衡的关节力矩>> syms theta1 theta2 theta3 theta4 >>F=[(2^0.5)*cos(theta1+theta2)*cos(theta3)-sin(theta1+theta2)*(sin(theta3)-1)+cos(theta1);...(2^0.5)*sin(theta1+theta2)*cos(theta3)+cos(theta1+theta2)*(sin(theta3)-1)+sin(theta1);... sin(theta3)+1]>> V=[theta1;theta2 ;theta3 ;theta4]>> Jv=jacobian(F,V)4(90)(90)(90)(90)(90)(90)(90)(90)(90)(90)(90)(90)((90)1)(90)(90)(90)(90)(90)(90)(90)(90)(90)(90)(90)(90)(90)((90)1)(90)(90)(c c s c s c c s s c s c s s s c c c s s T ---------+------+--+=-90)(90)1001s ⎛⎫⎪⎪ ⎪⎪⎪ ⎪--+⎪⎪ ⎪⎝⎭402220101002201T ⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪⎝⎭>> Jv01=subs(Jv,theta1,0)>> Jv01=subs(Jv01,theta2, 1.5707953) %1.5707953 为90度的弧度表示>> Jv01 =subs(Jv01,theta3,- 1.5707953)>> Jv01 =subs(Jv01,theta4,0)>> Jw=[0 0 (2^0.5)/2 (2^0.5)/2;0 0 0 0;1 1 (2^0.5)/2 (2^0.5)/2]>> Jac=[Jv01;Jw]>> R40=[(2^0.5)/2 0 (2^0.5)/2;0 1 0;-(2^0.5)/2 0 (2^0.5)/2]>> E0=[0 0 0;0 0 0;0 0 0]>> R40ZG=[R40 E0;E0 R40]>> F40=R40ZG*[0;-6;0;-7;0;-8]>> Tao=Jac'*F40Tao =-18.5701-12.5701-15.9863-8.0000三．对斯坦福机械手逆向运动分析中seta1的求解进行简化并和教材计算结果进行对比逆向运动学分析示例：>> syms c1 s1 c2 s2 d3 c4 s4 c5 s5 c6 s6 d2>> T10=[c1 -s1 0 0;s1 c1 0 0;0 0 1 0;0 0 0 1]>> T21=[c2 -s2 0 0;0 0 1 d2;-s2 -c2 0 0;0 0 0 1]>> T32=[1 0 0 0;0 0 -1 -d3;0 1 0 0;0 0 0 1]>> T43=[c4 -s4 0 0;s4 c4 0 0;0 0 1 0;0 0 0 1]>> T54=[c5 -s5 0 0;0 0 1 0; -s5 -c5 0 0;0 0 0 1]>> T65=[c6 -s6 0 0;0 0 -1 0;s6 c6 0 0;0 0 0 1]>> T60=T10*T21*T32*T43*T54*T65>> T10nizhen=inv(T10)>> T21nizhen=inv(T21)>> T32nizhen=inv(T32)>> T43nizhen=inv(T43)>> T54nizhen=inv(T54)>> T65nizhen=inv(T65)>> syms nx ox ax px ny oy ay py nz oz az pz>> T60yizhi=[nx ox ax px;ny oy ay py;nz oz az pz;0 0 0 1]下面计算：1）T10nizhen*T60yizhi=T21*T32*T43*T54*T652）T21nizhen*T10nizhen*T60yizhi = T32*T43*T54*T653）T32nizhen*T21nizhen *T10nizhen* T60yizhi= T43*T54*T654）T43nizhen*T32nizhen *T21nizhen *T10nizhen* T60yizhi= T54*T65 5）T54nizhen*T43nizhen* T32nizhen *T21nizhen *T10nizhen* T60yizhi= T651）对比矩阵两边第二行第四列有-s1/(c1^2+s1^2)*px+c1/(c1^2+s1^2)*py= d2 >> syms st1 st2 st3 st4 st5 st6 d2 d3>> [x]=solve('-sin(st1)*px+cos(st1)*py=d2','st1') Simplify()四．MTLAB 验证斯坦福雅可比矩阵 1．已知计算各级T 矩阵 由公式：1111111111s 0001i i i i i i i i i ii ii i i i i i c a s c c c s s d T s s c s c c d θθθαθαααθαθααα-----------⎡⎤⎢⎥--⎢⎥=⎢⎥⎢⎥⎣⎦以及各连杆坐标系之间的参数表，可得：665544445436546655221132210321220000000010001000000000100001000100011000000000100101000000101---⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦--⎡⎤⎡⎤⎢⎥⎢⎥--⎢⎥⎢⎥===⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦⎣⎦-c s c s c s s c T T T s c s c c s c s d d T T T s c 1100001001⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦s c与斯坦福大学开发课件比较发现其课件中T21计算有错：2．计算出各连杆坐标系到基坐标系0的变换矩阵：11110111212112112121121022221211213212121121321203222000000001010010000000100-⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦----⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥==⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦⎣⎦---+++=-可知可知c s s c T z c c c s s s d s s c s s c c d c T z s c c c s c s c d s s d s c c s s s d s c d T s c c d 1212332010⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦可知c s s s z c124141241412123121241412414121231204242422312414125124145125124141231212414505001()()()----⎡⎤⎢⎥+-++⎢⎥=⎢⎥-⎢⎥⎣⎦--------+-=++c c c s s c c s s c c s c s d s d s c c c s s c s c c s s s s d c d T s c s s c c d c c c s s c s s c c c s s s c s c c c s s c c s d s d s c c c s c s T 12512414512512414123122423124514512512312124514512512312062455223()24525245250011234560⎡⎤⎢⎥-+--+--+++⎢⎥⎢⎥-⎢⎥⎣⎦-+-++++=-s s s c c c s s s s c s c s c c s s d c d s c c c s s c s c c s s c d X X c c c s s s s c s c c s d s d X X s c c s c s s s s c s s d c d T X X s c s c c c d 01⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦与斯坦福开发课程课件比较Matlab 计算过程如下： >> clear>> syms c1 s1 c2 s2 c3 s3 c4 s4 c5 s5 c6 s6 d1 d2 d3 d4 d5 d6 a1 a2 a3a4 a5 a6>> T10=[c1 -s1 0 0;s1 c1 0 0;0 0 1 0;0 0 0 1] >> T21=[c2 -s2 0 0;0 0 1 d2;-s2 -c2 0 0;0 0 0 1] >> T32=[1 0 0 0;0 0 -1 -d3;0 1 0 0;0 0 0 1] >> T43=[c4 -s4 0 0;s4 c4 0 0;0 0 1 0;0 0 0 1] >> T54=[c5 -s5 0 0;0 0 1 0; -s5 -c5 0 0;0 0 0 1] >> T65=[c6 -s6 0 0;0 0 -1 0;s6 c6 0 0;0 0 0 1] >> T20=T10*T21 >> T30=T20*T32 >> T40=T30*T43 >> T50=T40*T54 >> T60=T50*T65可以用simplify 函数简化，如： >> T60=simplify(T60)3．用速度矢量合成的方法计算雅可比矩阵Jv 部分：356124123456102450601626346566612456102162631245600000⎡⎤=⎢⎥⎢⎥⎣⎦⎡⎤⨯⨯⨯⨯⨯=⎢⎥⎣⎦⎡⎤⨯⨯=⎢⎥⎣⎦v v v v v v J J J J J J J J J J J J J z p z p z z p z p z p z z z z z z p z p z z z z z z ωωωωωω（1）.计算1016⨯zp1z 为连杆1坐标系的z 轴单位向量在基坐标系0中的描述；106p为连杆1坐标系原点到连杆6坐标系原点连线矢量16O O，在基坐标系0中的描述，计算过程为：计算矩阵T61，T61的第四列即为16O O，由于坐标系1相对于坐标系0有绕Z 轴的转动，故需要对其进行转换，转换方法为；116O O ⋅ R ，01R为T10中旋转部分注：Matlab 中向量叉积方法：e=cross (a,b)>> T61=T21*T32*T43*T54*T65 %计算出16O O在坐标系1中的描述>> P161=[s2*d3;d2;c2*d3]>> Rot10=[c1 -s1 0;s1 c1 0;0 0 1] %由T10知道旋转部分变换3*3矩阵>> P160= Rot10* P161 % 与P60最后一列比较 >> z1=[0;0;1] >> e=cross(z1,P160)%可得到Jv 第一列：e =[ -s1*s2*d3-c1*d2; c1*s2*d3-s1*d2;0] （2）.计算2026⨯zp2z 为连杆2坐标系的z 轴单位向量在基坐标系0中的描述；206p为连杆2坐标系原点到连杆6坐标系原点连线矢量26O O，在基坐标系0中的描述，计算过程为：计算矩阵P62，P62的第四列即为26O O，由于坐标系2相对于坐标系0有姿态变化，故需要对其进行转换，转换方法为；226O O ⋅R ，02R为T20中旋转部分注：Matlab 中向量叉积方法：e=cross (a,b)>> T62= T32*T43*T54*T65 %计算出26O O在坐标系2中的描述>> P262=[0;-d3;0]>> Rot20=[c1*c2 -c1*s2 -s1;s1*c2 -s1*s2 c1;-s2 -c2 0] %由T20知旋转部分变换3*3矩阵 >> P260= Rot20* P262 >> z2=[-s1;c1;0] >> e=cross(z2, P260)%可得到Jv 第一列：e =[c1*c2*d3; s1*c2*d3; -s1^2*s2*d3-c1^2*s2*d3]（3）.由于连杆3坐标系为移动坐标系，故起对连杆6的速度贡献不能计算为3036⨯zp ，而应该为Z3的单位向量在基坐标系0中的表示；故由T30直接可得Jv 第三列为：1212320⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦c s s s z c（4）.由于坐标系4、5、6和坐标系6的坐标原点重合故对应6066)=⨯=⨯ i i ()q (q i i O i i i v z O O z p 的计算结果均为0 ，于是可得3561241234561212312312121231231223211241412414124514512511241412414124500000000000000⎡⎤=⎢⎥⎢⎥⎣⎦---+-=------+-+-++v v v v v v J J J J J J J J J J J J J c d s s d c c d c s s d c s d s c d s s s d c s c c s s c c c s s c c c c s s s s c s c c s c s c c s c s c c s c c s c ωωωωωω14512524242455210⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥+⎢⎥-+⎢⎥⎣⎦s s s s c s s s s s c s c c 五.试验体会：掌握相关软件，认真分析实验要求，克服试验中的困难，争取做出符合要求的结果。

基于MATLAB的六自由度工业机器人运动分析及仿真摘要：工业机器人是现代制造工业中广泛应用的先进装备之一，其主要功能是进行重复、高精度和高负荷的工作。

机器人的运动分析和仿真是机器人研究中一个重要的方面，可以通过模拟机器人的运动过程来优化机器人的工作效率和准确性。

本文基于MATLAB环境，对六自由度的工业机器人进行运动分析和仿真研究，提供一种快速、准确且可靠的方法。

引言：工业机器人具有广泛的应用领域，包括汽车制造、电子设备组装、医疗设备等。

机器人的运动分析和仿真是机器人研究中的一个重要步骤，可以帮助工程师优化机器人的设计和运动控制算法。

MATLAB是一种强大的科学计算和虚拟实验环境，可以用于机器人的运动分析和仿真。

方法：本文基于MATLAB环境，采用正运动学和逆运动学方法实现了六自由度工业机器人的运动分析和仿真。

正运动学通过已知关节角度计算机器人末端执行器的位置和姿态。

逆运动学则根据给定的末端执行器的位置和姿态确定关节角度。

同时，使用MATLAB中的3D绘图工具箱将机器人的运动过程进行仿真展示。

结果与讨论：通过正运动学和逆运动学计算，可以得到机器人在给定关节角度下的位置和姿态信息。

MATLAB的3D绘图工具箱可以将机器人的运动过程以三维动画的形式展示出来，方便工程师对机器人的运动轨迹和工作空间进行可视化分析。

结论：本文基于MATLAB环境实现了六自由度工业机器人的运动分析和仿真，提供了一种快速、准确且可靠的方法。

通过正运动学和逆运动学计算，可以得到机器人在给定关节角度下的位置和姿态信息。

MATLAB的3D绘图工具箱可以将机器人的运动过程进行可视化展示，帮助工程师对机器人的运动轨迹和工作空间进行分析和优化。

1.邱华根.《现代机器人控制技术》，清华大学出版社，2024年。

2.张骞.《机器人学导论及控制技术》，电子工业出版社，2024年。

六自由度工业机器人的建模与仿真研究共3篇六自由度工业机器人的建模与仿真研究1六自由度工业机器人的建模与仿真研究随着工业自动化的不断发展，工业机器人已经成为工厂中不可或缺的重要设备之一。

其中，六自由度工业机器人因其具有灵活性强、运动范围广等优点而得到广泛应用。

因此，对于六自由度工业机器人的建模和仿真研究具有非常重要的意义。

一、六自由度工业机器人的概述六自由度工业机器人是指具有6个自由度的工业机器人，通常由机身、驱动器和控制器组成。

其中，机身由臂、手和手腕组成，可根据任务需求进行操作或载物。

驱动器是机身各部分的驱动器件，常用的驱动器有电机、气缸等。

控制器是控制机器人的核心部分，可完成运动的规划、控制和反馈等。

二、六自由度工业机器人的建模六自由度工业机器人的建模是建立机器人的数学模型，目的是为了分析机器人的运动规律和控制过程，同时也是设计自动控制器的重要基础。

1. 正向运动学模型正向运动学模型是指将机器人的变量作为输入，根据手臂各段的长度和角度、各关节的偏转角度等信息，计算机器人的末端位置、姿态等信息的模型。

这个模型对机器人的分析非常重要，因为它可以方便地解决机器人的直观显示、位置控制等问题。

在建模时，需要对机器人进行分段处理，每一段均要计算其末端的位置和姿态信息，并将其传递到下一段中。

2. 逆向运动学模型逆向运动学模型是指将机器人所需的输出信息作为输入，根据末端位置、姿态等信息，反推出机器人各关节需要转动的角度等信息的模型。

这个模型对机器人的姿态调节、轨迹规划等问题非常重要。

3. 动力学模型动力学模型是指对机器人的力学特性进行建模，为机器人的运动规划和控制提供必要的参考和依据。

在建模时，需要考虑力、转矩、惯性等因素，并通过控制器控制机器人的动作。

三、六自由度工业机器人的仿真研究仿真是对机器人进行数字化模拟的过程。

通过仿真，可以在事先构建好的环境中，对机器人进行各种测试和优化，进而提高其运动精度、速度和稳定性等。