基于FPGA的m伪随机数产生
- 格式:pdf
- 大小:409.89 KB
- 文档页数:5

基于FPGA的伪随机序列的生成方法及应用
张金宝;李新阳;陈波
【期刊名称】《微计算机信息》
【年(卷),期】2009(025)029
【摘要】通过分析各种伪随机序列生成方法,提出了一种基于M序列的连续抽样方法,可以生成满足自适应光学系统SPGD控制算法要求的多路、相互独立以及服从伯努利分布的伪随机序列.该方法适合于用FPGA等超大规模集成电路实现,且具有占用硬件资源较少,实现方便等优点.用FPGA实现了用于61单元自适应光学系统SPGD控制算法的伪随机序列,并将此方法应用于基于SPGD控制算法的自适应光学系统实验中,实验表明,该方法能够满足自适应光学系统SPGD算法的需求,系统实现成功闭环.
【总页数】3页(P153-155)
【作者】张金宝;李新阳;陈波
【作者单位】610209,成都,中国科学院光电技术研究所;100039,北京,中国科学院研究生院;610209,成都,中国科学院光电技术研究所;610209,成都,中国科学院光电技术研究所;100039,北京,中国科学院研究生院
【正文语种】中文
【中图分类】TP301.6;TP331.1+1
【相关文献】
1.基于余数系统与置换多项式的高速长周期伪随机序列生成方法 [J], 马上;刘剑锋;杨泽国;张艳;胡剑浩
2.基于非规则二值化的伪随机序列生成方法 [J], 陈亚如;张雪锋
3.基于随机序列统计特性的伪随机序列生成方法 [J], 柏森;周龙福;郭辉;闫兵;
4.基于FPGA的Leap-forward型线性反馈移位寄存器在伪随机序列算法中的应用[J], 郝洪伟;
5.基于海绵函数的快速伪随机序列生成方法 [J], 赵磊; 郑东; 任方
因版权原因,仅展示原文概要,查看原文内容请购买。

2.4 m序列产生器的设计原理m序列是最长线性反馈移位寄存器序列,其产生方法比较简单,可以通过移位寄存器的级联实现任意m序列,本文是结合FPGA芯片的结构特点,以Altera 的QuartusⅡ软件为开发平台,设计出了m序列产生器。
通过FPGA平台,我们可以采用硬件描述语言VHDL语言来实现m序列产生器,也可以通过输入原理图来实现m序列产生器,也可以通过两者的结合来实现m序列产生器。
由于m 序列产生器的实现方法已经能够成熟,本文采用输入原理图的方法实现m 序列产生器的仿真设计。
利用n级移位寄存器可以产生长度为2n-1的m序列。
m序列的设计主要解决的问题是寻求系统的特征多项式为本原多项式的过程,部分本原多项式可以通过查表方法很方便的得到。
本文通过设计一个码长为L=31的m序列,来说明任意m序列产生器如何进行仿真设计。
由码长为31可知道所需的移位寄存器的数目为5,特征多项式的系数通过查表可以选择为100101,110111,111101三个反馈系数,可以从中选择100101来构成m序列产生器。
则特征多项式系数取值为C 5=C2=C=1,C4=C3=C1=0.根据特征多项式就可以构造出该m序列,图5就是L=31的m序列产生器的原理图。
图5 L=31的m序列产生器图5利用D触发器级联的方式完成移位寄存器的功能, CLRN是清零信号,低电平有效。
在系统初始时,CLRN置低电平使系统清零,D触发器的输出状态均为低电平,当CLRN置高时新非零值被置入。
CLK为外界时钟脉冲信号,当CLK 上升沿来临时实现移位功能。
通过异或门将反馈接入系统的输入端,反馈系数根据特征多项式的系数来断定是否接入反馈,在模2加后面加入一个非门,避免了m序列产生器输出静止的状态,如不加非门直接接入反馈到输入端,系统无法自动运动起来,造成输出序列进入了全“1”的静止状态,这样就无法产生m序列。
图中的Q1-Q5是五个D触发器的输出,这些点均可得到同宗序列,只序列的初始相位不同而已。


基于FPGA的伪随机码序列发生器实现方案研究
于燕;焦晖
【期刊名称】《电脑与电信》
【年(卷),期】2006(000)006
【摘要】本文重点设计实现了基于FPGA的伪随机码序列发生器,论文首先对FPGA技术进行了分析研究,阐述了伪随机序列理论,在此基础上,本文阐述了伪随机码发生器原理,并提出了基于FPGA的伪随机码序列发生器设计实现方案.
【总页数】4页(P47-49,52)
【作者】于燕;焦晖
【作者单位】郑州轻工业学院民族职业学院,河南,郑州,450011;郑州轻工业学院民族职业学院,河南,郑州,450011
【正文语种】中文
【中图分类】TP3
【相关文献】
1.基于"匹配滤波+序列估计"模式的新型长周期伪随机码快速捕获方案 [J], 郭黎利;王东凯;张昕;张曙
2.基于DSP和FPGA的GPS伪随机码并行快速捕获方案设计 [J], 周应强;冯克明
3.基于FPGA伪随机码发生器的实现 [J], 章潋;秦会斌
4.一种伪随机码发生器的DSP实现方法研究 [J], 刘展威;赵晓博
5.m序列伪随机码发生器的低功耗实现 [J], 沈泊;温涛;孙承绶
因版权原因,仅展示原文概要,查看原文内容请购买。

基于FPGA的伪随机序列发生器设计方案1基本概念与应用1)1FSR:线性反馈移位寄存器(1inear feedbackshiftregister,1FSR)是指给定前一状态的输出,将该输出的线性的薮再用作输入的移位寄存器。
异或运算是最常见的单比特线性函数:对寄存器的某些位进行异或操作后作为输入,再对寄存器中的各比特进行整体移位。
1FSR产生的两种形式为伽罗瓦(Ga1ois)和斐波那契(FibonaCCi)两种形式。
也有成为外部(Ex隹rna1)执行方式和内部(Interna1)执行方式。
(1)伽罗瓦方式(Interna1)X0X4X17! ! TepCount ,-Θ□□EF-Γ>4300000000Θ{3B0-*~*DaiaFtowW>)∙ι.x4.χ“(Ga1oisImp1ementation)Ga1ois方式特征数据的方向从左至右,反馈线路是从右至左。
其中XCo项(本原多项式里面的T'这一项)作为起始项。
按照本原多项式的指示确定异或门(XOR)在移位寄存器电路上的位置。
如上图所示XM。
因此Ga1ois方式也有人称作线内或模类型(M-型)1FSRo(2)斐波那契方式(Externa1)TapCountB*0;E3t3-⅛QEHIH30GHZHHDGIFSHpcivncrTMrig(M)-X14.X,>♦X n»1(Fibonacciimp1ementation)从图中我们可以看到Fibonacci方式的数学流向和反馈形式是恰好跟Ga1ois方式相反的,按照本原多项式,其中XCO这一项作为最后一项,这里需要一个XOR∏,将本原多项式中所给的taps来设定它的异或方式。
因此Fibonacci方式也被叫做线外或者简型(S-型)1FSR。
2)本原多项式本原多项式是近世代数中的一个概念,是唯一分解整环上满足所有系数的最大公因数为1的多项式。
本原多项式不等于零,与本原多项式相伴的多项式仍为本原多项式。

摘要:通过分析各种伪随机序列生成方法,提出了一种基于M 序列的连续抽样方法,可以生成满足自适应光学系统SPGD 控制算法要求的多路、相互独立以及服从伯努利分布的伪随机序列。
该方法适合于用FPGA等超大规模集成电路实现,且具有占用硬件资源较少,实现方便等优点。
用FPGA 实现了用于61 单元自适应光学系统SPGD 控制算法的伪随机序列,并将此方法应用于基于SPGD 控制算法的自适应光学系统实验中,实验表明,该方法能够满足自适应光学系统SPGD 算法的需求,系统实现成功闭环。
1 引言随机序列是一组满足特定统计学规律的数据,在信号理论分析中应用非常普遍。
由于精确的随机序列生成方法较为复杂,产生的随机序列不具有可重复性等特点,在很多应用场合使用伪随机序列。
伪随机序列在扩频通信、信息加密和系统测试等诸多领域中都有着广泛的应用。
在自适应光学SPGD 算法中,伪随机序列亦有相当重要的作用。
Vorontsov 等人在1997 年将SPGD 算法引入到自适应光学领域[2]。
国内在近几年开始了对 SPGD 算法在自适应光学系统应用的研究,并且在计算机上用软件编程实现了算法,进行了自适应光学的系统实验[3]。
自适应光学SPGD 控制算法的研究趋势是使用专用的信号处理硬件电路作为算法的实现平台,以获得更高的迭代速度和更好的收敛效果。
Cauwenberghs等人设计了专用的模拟超大规模集成电路实现SPGD 控制算法,并且在一些应用领域进行了实验[5]。
目前自适应光学系统的规模普遍达到几十上百单元。
针对多单元自适应光学系统SPGD 控制算法的特殊要求,本文提出了一种适合于用FPGA 硬件电路产生满足算法要求的多路伪随机序列的生成方法,完成了FPGA 电路的硬件实现,并将其用于实现61 单元自适应光学SPGD控制算法,同时进行自适应光学的闭环实验。
2 自适应光学 SPGD 控制算法对伪随机序列的要求SPGD(the Stochastic Parallel Gradient Descent algorithm)算法通过对多路的控制参数加入随机并行的扰动,使用性能指标测量值的变化量与控制参数的变化量进行控制参数的梯度估计,以迭代方式在梯度下降方向上进行控制参数的搜索。

0 引言伪随机序列现已广泛应用于密码学、扩频通讯、导航、集成电路的可测性设计、现代战争中的电子对抗技术等许多重要领域。
伪随机序列的伪随机性表现在预先的可确定性、可重复产生与处理。
伪随机序列虽然不是真正的随机序列,但是当伪随机序列周期足够长时,它便具有随机序列的良好统计特性。
在已有的序列中,m序列的应用最为成熟和广泛,为此,本文给出线性m序列和基于m序列的非线性m子序列的FPGA实现方法。
由于FPGA的内部逻辑功能是通过向内部静态存储器单元加载配置数据来实现的,其配置文件决定了逻辑单元的逻辑功能以及模块间或与I/O间的连接,故可最终决定FPGA实现的功能。
FPGA的这种结构允许多次编程,并享有快速有效地对新设计进行优化的灵活性,为此,本文选用了altera 的cvclone系列FPGA芯片EPlC12-240PQFP,该芯片内部有12060个逻辑单元、239616 bit RAM、两个锁相环(PLL)。
本文应用移位寄存器理论来产生序列,其算法的关键是找到线性m序列和非线性m子序列移位寄存器的反馈逻辑式。
1 m序列的实现1.1 基于FPGA的m序列实现利用反馈移位寄存器产生0、1序列时,其n位反馈移位寄存器的逻辑功能如图1所示。
图中,xi蕾表示寄存器所处的状态,通常用0和1来代表两个可能的状态,并且把0和1看成是有限域GF(2)的两个元素。
f(x0,x1,…,xn-1)刻划了移位寄存器反馈逻辑的功能,它可以看成一个定义在GF(2)上并且在GF(2)中取值的n元函数,当f(x0,x1…,xn-1)可以表示成一线性齐次函数时。
即,相应的反馈移位寄存器是线性的,而由线性移位寄存器产生的序列就称为线性移位寄存器序列。
m序列就是线性移位寄存器序列。
对于一个n级m序列移位寄存器来说。
它在每一时刻的内部状态都可以看做有限域GF(2)上的一个n维向量,而反馈函数就是刻划了从每一时刻的状态到下一时刻状态的转移规律,或者说反馈函数定义了n维向量空间上的一个线性变换。

基于FPGA的伪随机序列发生器设计随着通信理论的发展,早在20世纪40年代末,香农(Shannon)就曾指出,在某些情况下,为了实现最有效的通信,应采用具有白噪声的统计特性的信号。
目前广泛应用的伪随机噪声由数字电路产生的周期序列(经滤波等处理后)得到的。
我们将这种周期序列称为伪随机序列。
伪随机序列概述伪随机序列发展及应用随着通信技术的发展,在某些情况下,为了实现最有效的通信应采用具有白噪声统计特性的信号;为了实现高可靠的保密通信,也希望利用随机噪声;另外在测试领域,大量的需要使用随机噪声来作为检测系统性能的测试信号。
然而,利用随机噪声的最大困难是它难以重复再生和处理。
伪随机序列的出现为人们解决了这一难题。
伪随机序列具有类似于随机噪声的一些统计特性,同时又便于重复产生和处理,有预先的可确定性和可重复性。
由于它的这些优点,在通信、雷达、导航以及密码学等重要的技术领域中伪随机序列获得了广泛的应用。
而在近年来的发展中,它的应用范围远远超出了上述的领域,如计算机系统模拟、数字系统中的误码测试、声学和光学测量、数值式跟踪和测距系统等也都有着广阔的使用。
伪随机序列通常由反馈移位寄存器产生,又可分为线性反馈移位寄存器和非线性反馈移位寄存器两类。
由线性反馈移位寄存器产生出的周期最长的二进制数字序列称为最大长度线性反馈移位寄存器,即为通常说的m序列,因其理论成熟,实现简单,应用较为广泛。
伪随机序列的特点决定了它有着重要并且广泛的应用,这里仅举出一些有代表性的用途。
误码率测量。
在数字通信中误码率是一项重要的质量指标,在实际测量数字通信系统的误码率时,一般来说,测量结果与信源发出信号的统计特性有关。
通常认为二进制信号0和1是以等概率随机出现的。
所以测量误码率时最理想的信源应是伪随机序列产生器。
这样测量的结果,我们认为是符合实际运用时的情况。
时延测量。
有时我们需要测量信号经过某一传输路径所收到的时间延迟,例如,需要测量某一延迟线的时间延迟。

1绪论近年来,以FPG为代表的可编程ASIC器件发展极快,从最初的数百个门发展到现今的数百万个门,系列品种增多,功能更强,速度更快,功耗更小,价格更低。
因此,愈来愈受到电子界的青睐,开发基于FPGA勺数字集成系统设计的新技术方法将逐渐成为主流。
FPG技术发展出现几个新动向:一是在FPG中嵌人处理器(包括CPU微处理器、微控制器);二是高速并行I/O 口;三是实现数字信号处理功能。
针对以上动态,本课题通过对FPG技术的研究,对在FPG中实现伪随机序列发生器做了有益的研究与实践,设计中充分运用了自上而下、结构化、模块化设计思想。
伪随机序列具有良好的随机性,它的相关函数接近白噪声的相关函数(函数),即有窄的高峰或宽的功率谱密度,使它易于从其他信号或干扰中分离出来。
伪随机序列的伪随机性表现在:预先的可确定性、可重复性,使它易于实现相关接收和匹配接收,故有良好的抗干扰性能。
伪随机序列(又称伪噪声序列)广泛应用于通信、雷达、导航等重要的技术领域。
近年来,在自动控制、计算机、声学、光学测量、数字式跟踪和测距系统,以及数字网络系统的故障分析检测也得到广泛的应用。
1.1课题背景在现代工程实践中,伪随机信号在移动通信、导航、雷达和保密通信、通信系统性能的测量等领域中有着广泛的应用。
例如,在连续波雷达中可用作测距信号,在遥控系统中可用作遥控信号,在多址通信中可用作地址信号,在扩频通信系统中,抗干扰、抗噪声、抗截获、信息数据隐蔽和保密、抗衰落、多址通信、实现同步与捕获等都与扩频码的设计密切相关。
在数字通信中可用作群同步信号,还可用作噪声源以及在保密通信中的加密作用等。
伪随机发生器在测距、通信等领域的应用日益受到人们重视。
EDA(电子设计自动化)技术就是以计算机为工具,在EDA软件平台上,对以硬件描述语言VHDL为系统逻辑描述手段完成的设计文件,自动的完成逻辑编译、逻辑化简、逻辑综合及优化、逻辑仿真,直至对特定目标芯片的适配编译、逻辑映像和编程下载等工作(本文选用的开发工具为Altera公司的Quartus H)。

基于FPGA的随机小数发生器及其生成方法FPGA(Field Programmable Gate Array)是一种可编程逻辑器件,被广泛应用于数字信号处理和数字电路设计中。
在很多情况下,需要产生一些随机的数字。
在本文中,我们将介绍使用FPGA实现随机数生成器的方法以及其生成方法。
一、FPGA实现随机数生成器的方法在FPGA中实现随机数生成器的主要方法是使用基于硬件随机数生成器的模块。
硬件随机数生成器通常使用基于物理随机现象的原理,例如温度变化,电压噪声等。
这类原理的随机性是天然的,因此可以通过它产生高质量的随机数。
随机数生成器模块实际上是一个包含一些函数和逻辑的电路板。
它通常由三个基本模块组成,分别是输入、控制和输出模块。
输入模块用于确定要生成的随机数类型和长度。
控制模块用于控制随机数生成器的工作,例如初始化和重置随机数生成器,控制采集速率和检查随机数的质量等。
输出模块用于输出生成的随机数序列。
二、FPGA随机数发生器的生成方法随机数生成器可能会生成不同类型的随机数。
有些类型随机数比其他类型随机数更适合特定的应用。
下面列出了一些随机数类型及其生成方法。
1. 真随机数:真随机数是从物理过程中收集的数字。
例如,它可以是根据波动性噪声进行采样生成的。
因为真随机数是天然的,所以非常适合安全应用。
真随机数生成器可以通过使用硬件和噪声发生器来实现。
噪声发生器可用于收集真随机数的物理噪声成分,例如温度、电场和光。
2. 伪随机数:伪随机数是非随机数序列,经过置换、屏蔽等方法处理后,具有随机数的一些属性。
在计算机系统中,伪随机数通常由大量数学操作生成。
在FPGA中实现伪随机数生成有很多方法。
最常见的方法是使用伪随机数生成算法进行实现,例如线性反馈移位寄存器(LFSR)方法。
3. 混沌随机数:混沌随机数是由混沌系统生成的随机数,这些系统通常由非线性常微分方程组成。
混沌随机数生成器通常采用放大迭代和模数操作。
比较常用的混沌随机数生成器有洞簧系统和蛤蟆映射系统。
基于FPGA的多路伪随机序列发生器的设计与实现引言伪随机序列生成器(Pseudorandom Number Generator,PRNG)在许多计算机应用中都是必不可少的工具。
PRNG通过输入一个种子(seed),然后根据一定的算法生成一个看似随机的序列。
然而,由于PRNG本质上是基于算法的,所以生成的序列实际上是可重复的、周期性的。
本文将介绍基于FPGA的多路伪随机序列发生器的设计与实现。
设计目标本设计的目标是实现一个多路的伪随机序列发生器,该发生器具有高速性能和可扩展性。
设计需满足以下要求:1.高速性能:PRNG需要生成大量的伪随机序列,因此需要具备较高的计算速度;2.可扩展性:PRNG需要同时生成多个伪随机序列,因此需要具备可扩展性,方便根据需求扩展生成的路数;3.随机性:生成的伪随机序列需要具备较高的随机性,能够满足实际应用的需求。
设计思路本设计采用LFSR(Linear Feedback Shift Register)算法来实现PRNG。
LFSR算法是一种经典的PRNG实现方式,可以通过移位寄存器和异或门来实现。
LFSR算法的优势在于其计算速度快、硬件实现简单。
具体实现步骤如下:1.设计LFSR模块:LFSR模块是PRNG的核心模块,通过移位寄存器和异或门来实现。
LFSR模块接收一个种子作为输入,并根据一定的生成多路伪随机序列的算法生成对应的伪随机序列。
2.设计控制模块:控制模块用于控制LFSR模块的生成和输出。
控制模块根据输入的控制信号来决定生成的路数和序列长度,并将生成的伪随机序列进行输出。
3.设计顶层模块:顶层模块对上述模块进行组合,实现多路伪随机序列发生器。
顶层模块接收输入的控制信号和种子,并将控制信号传递给控制模块,种子传递给LFSR模块。
最后将生成的伪随机序列输出。
实现与验证本设计实现采用FPGA开发板进行验证。
首先,搭建基本的开发板环境,包括连接FPGA开发板、安装相应的开发软件等。
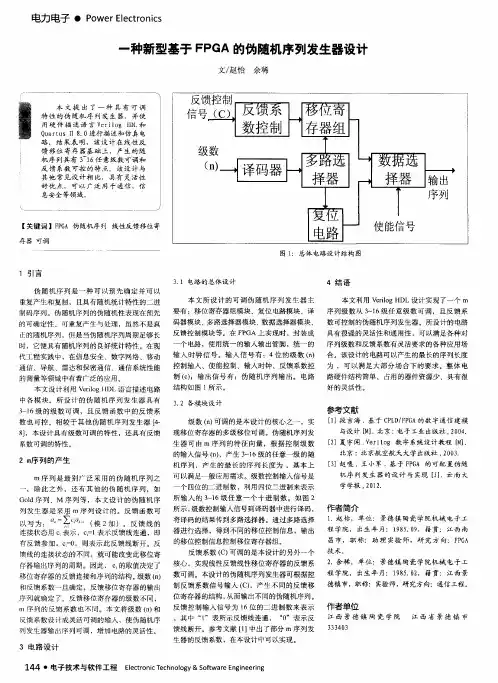
一种新型基于FPGA的伪随机序列发生器设计作者:赵怡余稀来源:《电子技术与软件工程》2013年第18期摘要:本文提出了一种具有可调特性的伪随机序列发生器,并使用硬件描述语言Verilog HDL和QuartusⅡ8.0进行描述和仿真电路。
结果表明,该设计在线性反馈移位寄存器基础上,产生的随机序列具有3~16任意级数可调和反馈系数可控的特点。
该设计与其他常见设计相比,具有灵活性好优点,可以广泛用于通信、信息安全等领域。
【关键词】FPGA 伪随机序列线性反馈移位寄存器可调1 引言伪随机序列是一种可以预先确定并可以重复产生和复制,且具有随机统计特性的二进制码序列。
伪随机序列的伪随机性表现在预先的可确定性、可重复产生与处理,虽然不是真正的随机序列,但是当伪随机序列周期足够长时,它便具有随机序列的良好统计特性。
在现代工程实践中,在信息安全、数字网络、移动通信、导航、雷达和保密通信、通信系统性能的测量等领域中有着广泛的应用。
本文设计利用Verilog HDL语言描述电路中各模块。
所设计的伪随机序列发生器具有3~16级的级数可调,且反馈函数中的反馈系数也可控。
相较于其他伪随机序列发生器[4-8],本设计具有级数可调的特性,还具有反馈系数可调的特性。
2 m序列的产生m序列是最别广泛采用的伪随机序列之一,除此之外,还有其他的伪随机序列,如Gold 序列、M序列等,本文设计的伪随机序列发生器是采用m序列设计的。
反馈函数可以写为:(模2加)。
反馈线的连接状态用ci表示,ci=1表示反馈线连通,即有反馈参加;ci=0,则表示此反馈线断开。
反馈线的连接状态的不同,就可能改变此移位寄存器输出序列的周期。
因此, ci的取值决定了移位寄存器的反馈连接和序列的结构。
级数(n)和反馈系数一旦确定,反馈移位寄存器的输出序列就确定了。
反馈移位寄存器的级数不同,m序列的反馈系数也不同。
本文将级数(n)和反馈系数设计成灵活可调的输入,使伪随机序列发生器输出序列可调,增加电路的灵活性。
基于FPGA的m序列发生器摘要m序列广泛应用于密码学、通信、雷达、导航等多个领域,本文提出了一种基于FPGA的伪随机序列产生方法,应用移位寄存器理论从序列的本原多项式出发,获得产生该序列的移位寄存器反馈逻辑式,结合FPGA芯片结构特点,在序列算法实现中采用元件例化语句。
算法运用VHDL语言编程,以A1tera的QuartusⅡ软件为开发平台,给出了序列的仿真波形。
序列的统计特性分析表明:该方法产生的序列符合m序列的伪随机特性,验证了算法的正确性。
关键词:m序列;移位寄存器理论;VHDL语言1 m序列m序列是伪随机序列的一种 ,结构简单 ,实现方便。
在现代工程实践中 , m 序列在通讯、导航、雷达、通信系统性能的测量等领域中有着广泛的应用。
例如 , 在连续波雷达中可用作测距信号 , 在遥控系统中可用作遥控信号 , 在多址通信中可用作地址信号 , 在数字通信中可用作群同步信号 ,还可用作噪声源及在保密通信中起加密作用等。
伪噪声发生器在测距、通信等领域的应用日益受到人们重视。
目前,m序列产生实现方法主要有3种:(1)门电路实现该方法设计简单,但随移位寄存器级数的增长,电路装调困难,且占用的印制板面积较大。
(2)DSP编程实现该方法专业性过强,不适合一般用户。
(3)VHDL与CPLD实现由于CPLD的高集成度,而且VHDL语言编程较为方便,故可以大大减少电路的装调的困难。
文章提出VHDL语言实现,,l序列电路是周期、初相位可编程变化的,其应用较为灵活,通过微处理器对其进行适当的初始化,即可产生用户所需周期、初相位的m序列输出。
用软件方式构成的特点是采用灵活的数据查询方式可以获得任意级数 n 的本原多项式系数 ,从而实现 m 序列的产生 , 但速度受到单片机工作速度的限制。
而 FPGA 具有硬件电路实现的优点 , 又具有设计上的灵活性 , 并且由于FPGA 便于实现大规模的数字系统。
1.1 理论基础m 序列是最长线性反馈移位寄存器序列的简称,它是由带线性反馈的移位寄存器产生的周期最长的一种序列。
矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。