离散LSI系统的时域分析

实验四离散LTI 系统的时域和z 域分析【实验目的】1. 掌握利用MATLAB 计算离散系统响应的数值方法，包括冲激响应、全响应等。

2. 掌握离散信号z 变换和逆z 变换的MATLAB 实现方法；3. 掌握离散系统的系统函数零极点分布与系统频率特性分析的MATLAB 实现方法。

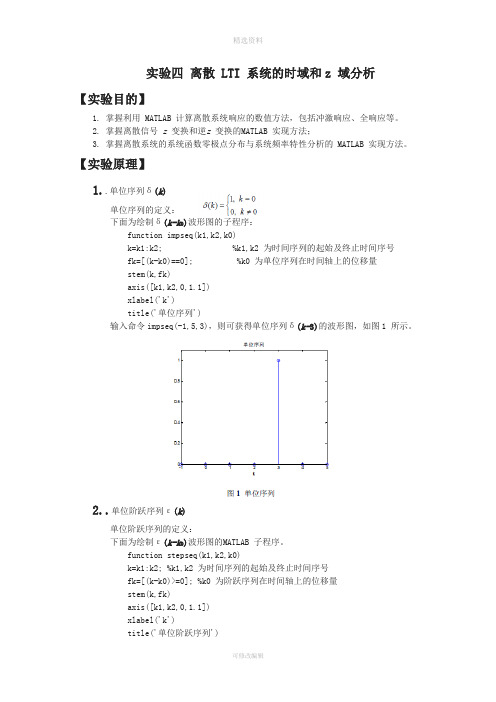
【实验原理】1..单位序列δ(k)单位序列的定义：下面为绘制δ(k-k0)波形图的子程序：function impseq(k1,k2,k0)k=k1:k2; %k1,k2 为时间序列的起始及终止时间序号fk=[(k-k0)==0]; %k0 为单位序列在时间轴上的位移量stem(k,fk)axis([k1,k2,0,1.1])xlabel('k')title('单位序列')输入命令impseq(-1,5,3)，则可获得单位序列δ(k-3)的波形图，如图1 所示。

2..单位阶跃序列ε(k)单位阶跃序列的定义：下面为绘制ε(k-k0)波形图的MATLAB 子程序。

function stepseq(k1,k2,k0)k=k1:k2; %k1,k2 为时间序列的起始及终止时间序号fk=[(k-k0)>=0]; %k0 为阶跃序列在时间轴上的位移量stem(k,fk)axis([k1,k2,0,1.1])xlabel('k')title('单位阶跃序列')运行如命令stepseq(-1,10,3)，则可获得单位阶跃序列ε(k-3)的波形图，如图2 所示。

3..离散系统的时域响应利用MATLAB 分析离散系统时域响应的常用函数是：计算系统单位序列响应的函数：impz(b,a)；计算系统全响应的函数：filter(b,a,x,zi)；其中，a、b 分别为系统差分方程左端和右端各阶差分项的系数；x 为输入；zi 为系统的初始值。

注意，zi 并不是y(-1)，y(-2)，其推导如下。

第三章离散系统的时域分析❖LTI离散系统的响应●差分方程的经典解●零输入响应与零线性响应❖单位序列与单位序列响应●输入为单位序列时的零状态响应❖卷积和●定义法●图解法1§3.1 LTI离散系统的响应注意离散系统与连续系统分析方法上的联系、区别、对比，与连续系统有并行的相似性。

●差分与差分方程●差分方程的经典解●零输入响应和零状态响应1.定义差分（1）一阶前向差分定义：∆f (k) = f (k+1) –f (k)（2）一阶后向差分定义：∇f (k) = f (k) –f (k –1)式中，∆和∇称为差分算子，两者仅移位不同，无原则区别。

本书主要用后向差分，简称为差分。

（3）差分的线性性质：[][][][][])()( )1()()1()( )1()1()()()()(2211222111221122112211k f a k f a k f k f a k f k f a k f a k f a k f a k f a k f a k f a ∇+∇=--+--=-+--+=+∇（4）二阶差分定义：∇2f (k) = ∇[∇f (k)] = ∇[f (k) –f (k-1)] = ∇f (k) –∇f (k-1)32. 差分方程包含未知序列y(k)及其各阶差分的方程式称为差分方程。

将差分展开为移位序列，得一般形式y(k) + an-1y(k-1) +…+ ay(k-n) = bmf(k)+…+ bf(k-m)差分方程本质上是递推的代数方程，若已知初始条件和激励，利用迭代法可求得其数值解。

一般不易得到解析形式的(闭合)解。

差分方程迭代解举例例：若描述某系统的差分方程为y(k)+3y(k–1)+2y(k–2)=f(k)已知初始条件y(0)=0,y(1)=2,激励f(k)=2kε(k),求y(k)。

解：y(k)=–3y(k–1)–2y(k–2)+f(k)k=2y(2)=–3y(1)–2y(0)+f(2)=–2k=3y(3)=–3y(2)–2y(1)+f(3)=10k=4y(4)=–3y(3)–2y(2)+f(4)=–10……二、差分方程的经典解 1.齐次解：与微分方程经典解类似，y (k) = y h (k) + y p (k)y (k) + a n-1y (k-1) +…+ a 0y (k-n) = b m f (k)+…+ b 0f (k-m)齐次方程y (k) + a n-1y (k-1) + … + a 0y (k-n) = 0特征方程1 + a n-1λ–1 + … + a 0λ–n = 0，即λn + a n-1λn –1 + … + a 0= 0其根λi ( i = 1，2，…，n)称为差分方程的特征根。

MATLAB 源程序为： >> H=sym('1/(s^3+6*s^2+11*s+6'; >> h=ilaplace(H 输出结果为： h= exp(-t/2 - exp(-2*t + exp(-3*t/2 即h t = e−t − e−2t + e−3t 2 2 1 1 方法二：部分分式展开法 MATLAB 源程序为： >> A=[1 6 11 6]; >> B=[1]; >>[r,p]=residue(B,A 输出结果为： r= 0.5000 -1.0000 0.5000 p= -3.0000 -2.0000 -1.0000 1 1 2 2 可见，两种方法的输出结果是相同的。

即h t = e−t − e−2t + e−3t 6. 一离散系统的框图如图所示： x（n）10 Σ -0.1 0.12 z-1 z-1 y（n）（1）.列写系统的差分方程；（2）.求系统函数 H （z），并求出 H （z）的零极点图（matlab）；（3）.求当输入为 x（n）=u（n）时的零状态响应 yzs（n）（matlab）；（4 ）．求系统的频域相应（matlab）（5 ）．判断系统的稳定性；解： (1 系统差分方程为y n + 0.1y n − 1 − 0.12y n − 2 = 10x(n (2 H z = 101+0.1z −1 −0.12z −2 = 10z 2 z 2 +0.1z −0.12 求零极点图的 MATLAB 源程序为： >> A=[1 0.1 -0.12]; >> B=[10 0 0]; >> zplane(B,A;grid on >> legend('零点','极点' >> title('零极点分布图' 输出的结果如图 6-1 所示：图 6-1 (3 MATLAB 源程序为： >> A=[1 0.1 -0.12]; >> B=[10]; >> n=0:30; >> x=heaviside(n; >> y=filter(B,A,x; >>stem(n,y,'fill',grid on >> xlabel('n',title(' 系统零状态响应 yzs(n' 程序运行结果如图6-2 所示：图 6-2(4 MATLAB 源程序为： >> A=[1 0.1 -0.12]; >> B=[10]; >> [Hw]=freqz(B,A,400,'whole'; >> Hm=abs(H; >> Hp=angle(H; >> subplot(121 >>plot(w,Hm,grid on >> xlabel('\omega(rad/s',ylabel('幅度' >> title('离散系统幅频特性曲线' >> subplot(122 >> plot(w,Hp,grid on >> xlabel('\omega(rad/s',ylabel('相位' >> title('离散系统相频特性曲线' 程序运行结果如图 6-3 所示：图 6-3 (5由零极点图可得，系统极点全部在单位圆内，则系统稳定。

信号、系统与信号处理实验报告实验一、离散时间系统的时域特性分析姓名:学号:班级：专业：一．实验目的线性时不变（LTI）离散时间系统在时域中可以通过常系数线性差分方程来描述，冲激响应列可以刻画时域特性。

本次实验通过使用MATLAB函数研究离散时间系统的时域特性，以加深对离散时间系统的差分方程、冲激响应和系统的线性和时不变性的理解。

二．基本原理一个离散时间系统是将输入序列变换成输出序列的一种运算。

离散时间系统中最重要、最常用的是“线性时不变系统”。

1.线性系统满足叠加原理的系统称为线性系统，即若某一输入是由N个信号的加权和组成的，则输出就是系统对这几个信号中每一个输入的响应的加权和。

即那么当且仅当系统同时满足和时，系统是线性的。

在证明一个系统是线性系统时，必须证明此系统同时满足可加性和比例性，而且信号以及任何比例系数都可以是复数。

2.时不变系统系统的运算关系在整个运算过程中不随时间（也即序列的先后）而变化，这种系统称为时不变系统（或称移不变系统）。

若输入的输出为，则将输入序列移动任意位后，其输出序列除了跟着位移外，数值应该保持不变，即则满足以上关系的系统称为时不变系统。

3.常系数线性差分方程线性时不变离散系统的输入、输出关系可用以下常系数线性差分方程描述：当输入为单位冲激序列时，输出即为系统的单位冲激响应。

当时，是有限长度的，称系统为有限长单位冲激响应（FIR）系统；反之，则称系统为无限长单位冲激响应（IIR）系统。

三．实验内容及实验结果1.实验内容考虑如下差分方程描述的两个离散时间系统：系统1：系统2：输入：（1）编程求上述两个系统的输出，并画出系统的输入与输出波形。

（2）编程求上述两个系统的冲激响应序列，并画出波形。

（3）若系统的初始状态为零，判断系统2是否为时不变的？是否为线性的？2.实验结果（1）编程求上述两个系统的输出和冲激响应序列，并画出系统的输入、输出与冲激响应波形。

clf;n=0:300;x=cos((20*pi*n)/256)+cos((200*pi*n)/256);num1=[0.5 0.27 0.77];den1=[1];num2=[0.45 0.5 0.45];den2=[1 -0.53 0.46];y1=filter(num1,den1,x);y2=filter(num2,den2,x);subplot(3,1,1);stem(n,x);xlabel('时间信号');ylabel('信号幅度');title('输入信号');subplot(3,1,2);stem(y1);xlabel('时间信号n');ylabel('信号幅度');title('输出信号');subplot(3,1,3);stem(y2);xlabel('时间序号n ');ylabel('信号幅度');title('冲激响应序列');（2）N=40;num1=[0.5 0.27 0.77];den1=[1];num2=[0.45 0.5 0.45];den2=[1 -0.53 0.46];y1=impz(num1,den1,N);y2=impz(num2,den2,N);subplot(2,1,1);stem(y1);xlabel('时间信号n ');ylabel('信号幅度');title('³冲激响应');subplot(2,1,2);stem(y2);xlabel('时间信号n ');ylabel('信号幅度');title('³冲激响应');1.应用叠加原理验证系统2是否为线性系统：clear allclcn = 0 : 1 : 299;x1 = cos(20 * pi * n / 256);x2 = cos(200 * pi * n / 256);x = x1 + x2;num = [0.45 0.5 0.45];den = [1 -0.53 0.46];y1 = filter(num, den, x1);y2 = filter(num, den, x2);y= filter(num, den, x);yt = y1 + y2;figuresubplot(2, 1, 1);stem(n, y, 'g');xlabel('时间信号n');ylabel('信号幅度');axis([0 100 -2 2]);grid;subplot(2, 1, 2);stem(n, yt, 'r');xlabel('时间信号n');ylabel('信号幅度');axis([0 100 -2 2]);grid;2.应用时延差值来判断系统2是否为时不变系统。

学生实验报告开课学院及实验室：2012年月日[1] 抄写函数文件delta[2] 抄写函数文件u5.修改程序Program1_4，并存盘，利用axis()函数，将图形窗口的横坐标范围改为-2≤n≤5，纵坐标范围改为-1.5≤ x ≤1.5。

[1] 修改Program1_4后得到的程序[2] 信号的波形图6.仿照前面的示例程序的编写方法，编写一个MATLAB程序，并存盘，使之能够在同一个图形窗口中的两个子图中分别绘制信号x[n]=0.5|n| 和x(t)=cos(2πt)[u(t)-u(t-3)]。

要求选择的时间窗能够表现出信号的主要部分（或特征）。

[1] 编写的程序[2] 信号x[n]=0.5|n| 的波形图和信号x(t)=cos(2πt)[u(t)-u(t-3)]的波形图7.根据示例程序的编程方法，编写一个MATLAB程序，并存盘，由给定信号 x(t) = e-0.5tu(t)，求信号y(t) = x(1.5t+3)，并绘制出x(t) 和y(t)的图形。

[1] 编写的程序[2] 信号x(t)的波形图和信号y(t) = x(1.5t+3) 的波形图8.给定一个离散时间信号x[n] = u[n] – u[n-8]，仿照示例程序Program1_5，编写程序，产生x[n]的左移序列x1[n] = x[n+6]和右移序列x2[n] = x[n-6]，并在同一个图形窗口的三个子图中分别绘制这三个序列的图形。

[1] 编写的程序[2] 信号波形图9.编写程序，使之能够接受以键盘方式输入的定义在不同时间段的两个不同连续时间信号并完成卷积运算，分别绘制这两个信号及其卷积的结果的图形，图形按照22分割成四个子图。

[1] 编写的程序[2] 信号x (t)、h(t)和x (t)*h(t)的波形图10.给定两个离散时间序列x[n] = 0.5n{u[n]-u[n-8]}h[n] = u[n]-u[n-8]编写程序，计算它们的卷积，并分别绘制x[n]、h[n]和它们的卷积y[n]的图形。

第七章离散时间系统的时域分析§7-1 概述一、离散时间信号与离散时间系统离散时间信号：只在某些离散的时间点上有值的信号。

离散时间系统：处理离散时间信号的系统。

混合时间系统：既处理离散时间信号，又处理连续时间信号的系统。

二、连续信号与离散信号连续信号可以转换成离散信号，从而可以用离散时间系统（或数字信号处理系统）进行处理：三、离散信号的表示方法：1、 时间函数：f(k)<——f(kT)，其中k 为序号，相当于时间。

例如：)1.0sin()(k k f =2、 （有序）数列：将离散信号的数值按顺序排列起来。

例如：f(k)={1,0.5,0.25,0.125,……,}时间函数可以表达任意长（可能是无限长）的离散信号，可以表达单边或双边信号，但是在很多情况下难于得到；数列的方法表示比较简单，直观，但是只能表示有始、有限长度的信号。

四、典型的离散时间信号1、 单位样值函数：⎩⎨⎧==其它001)(k k δ 下图表示了)(n k −δ的波形。

这个函数与连续时间信号中的冲激函数)(t δ相似，也有着与其相似的性质。

例如：)()0()()(k f k k f δδ=，)()()()(000k k k f k k k f −=−δδ。

2、 单位阶跃函数：⎩⎨⎧≥=其它001)(k k ε这个函数与连续时间信号中的阶跃函数)(t ε相似。

用它可以产生（或表示）单边信号（这里称为单边序列）。

3、 单边指数序列：)(k a k ε比较：单边连续指数信号：)()()(t e t e t a at εε=，其底一定大于零，不会出现负数。

(a) 0.9a = (d) 0.9a =−(b) 1a = (e) 1a =−(c) 1.1a = (f) 1.1a =−4、 单边正弦序列：)()cos(0k k A εφω+双边正弦序列：)cos(0φω+k A五、离散信号的运算1、 加法：)()()(21k f k f k f +=<—相同的k 对应的数相加。

实验一 离散时间系统的时域响应及稳定性1.1实验目的1）加深对离散线性移不变（LSI ）系统时域特性的认识；2）掌握MATLAB 求解离散时间系统响应的基本方法；3）了解MATLAB 中求解系统响应的函数及其应用方法；4）分析、观察及检验离散时间系统的稳定性。

1.2实验涉及的MATLAB 函数dlsim功能：求解离散系统的响应。

调用格式：y ＝dlsim(b ，a ，x )；求输入信号为x 时系统的响应。

说明：b 和a 分别表示系统函数H (z )中，由对应的分子项和分母项系数所构成的数组。

1.3实验原理1）离散LSI 系统时域响应的求解方法一个线性移不变离散系统可以用线性常系数差分方程表示，也可以用系统函数表示。

无论是差分方程还是系统函数，一旦式中的系数m b 和k a 的数据确定了，则系统的性质也就确定了。

因此，在程序编写时，往往只要将系数m b 和k a 列写成数组，然后调用相应的处理函数，就可以求出系统的响应。

对于离散LSI 系统的响应，MATLAB 提供了多种求解方法：(1) 用conv 子函数进行卷积积分，求任意输入的系统零状态响应。

(2) 用dlsim 子函数求任意输入的系统零状态响应。

(3) 用filter 和filtic 子函数求任意输入的系统完全响应。

本实验重点介绍(2)、(3)两种方法。

2）用dlsim 子函数求LSI 系统对任意输入的响应对于离散LSI 系统任意输入信号的响应，可以用MATLAB 提供的仿真dlsim 子函数来求解。

例1： 已知一个IIR 数字低通滤波器的系统函数公式为1231230.13210.39630.39630.1321()10.343190.604390.20407z z z H z z z z −−−−−−+++=−+− 输入两个正弦叠加的信号序列：1sin()sin(10)23n x n =+ 求该系统的响应。

MATLAB 程序如下：nx=0: 8*pi;x=sin(nx/2)+sin(10*nx)/3; %产生输入信号序列subplot(3, 1, 1); stem(nx, x);a=[1, -0.34319, 0.60439, -0.20407]; %输入系统函数的系数b=[0.1321, 0.3963, 0.3963, 0.1321];nh=0: 9;h=impz(b, a, nh); %求系统的单位冲激响应subplot(3, 1, 2); stem(nh, h);y=dlsim(b, a, x); %求系统的响应subplot(3, 1, 3); stem(y);从程序执行结果可见，输出响应y(n)中，原输入序列中的高频信号部分通过低通滤波器后已被滤除，仅剩下频率较低的sin(n/2)分量。