代数问题的几何解法几例
- 格式:pdf
- 大小:499.98 KB
- 文档页数:1



代数问题的几何解法例析
张笃芳
【期刊名称】《数学教育研究》
【年(卷),期】2004(000)001
【摘要】解析几何是用代数方法研究几何图形问题的一门学科.具体的说,就是
借助于坐标系,用坐标表示点,用曲线上点的坐标所满足的方程表示曲线,通过研究方程的性质间接的研究曲线的性质,从而把几何上的许多图形和概念给出了其代数表示.反过来,许多代数问题,如果我们能联想到它们对应的图形,借助于图形,转化为几何问题去解决,则显得简捷、明了、形象、直观.本文归纳介绍代数上可转化为几何问题解决的若干方面,供同学们在学习中参考.
【总页数】3页(P45-47)
【作者】张笃芳
【作者单位】山东省淄博四中,255100
【正文语种】中文
【中图分类】G623.503
【相关文献】
1.代数问题图形化和几何问题代数化 [J], 何晓静;
2.几何综合题中函数关系问题的归类思考——一类中考压轴题的解法例析 [J], 吴
龙梅
3.代数与几何齐飞\r——破解高考解析几何中的定值、定点问题 [J], 夏锦
4.代数与几何齐飞——破解高考解析几何中的定值、定点问题 [J], 夏锦
5.几何图形中存在性问题的解法例析 [J], 李胜军
因版权原因,仅展示原文概要,查看原文内容请购买。


等量代换常见题型等量代换,即根据已知条件进行推理,将题目中的量词符号替换成具体的数量,从而解决问题。
在数学中,等量代换是一种常见的解题方法,可以在不改变题目本意的情况下,简化问题的复杂度,使计算更加方便和准确。
下面将通过一系列常见题型来介绍等量代换的应用。
一、代数方程求解例如,求解方程2x-5=7的解。
我们可以对方程进行等量代换,将x的系数和常数项替换成具体的数值,得到等效的方程2a-5=7,其中a代表x的值。
然后解得a=6,再将a的值代回原方程可得x=3。
等量代换简化了求解过程,使得问题变得更加清晰和易于理解。
二、几何题解法例如,一个正方形的面积是16平方厘米,求其边长。
我们可以用等量代换的方法解决这个问题。
设正方形的边长为a,则根据已知条件可得a^2=16,即a=4。
通过等量代换,我们将未知量边长a替换成具体的数值4,从而得到答案。
三、函数求值例如,求函数f(x)=2x^2-3x+1在x=2时的取值。
我们可以用等量代换的方法计算出f(x)在x=2时的值。
将x替换成具体的数值2,得到f(2)=2(2)^2-3(2)+1=9。
等量代换使得函数求值变得更加简单和直观。
四、逻辑推理例如,对于命题“若小明考试及格,则小明有奖品”,我们可以进行等量代换,将命题中的变量替换成具体的事实,从而判断命题的真假。
假设小明考试及格,我们可以代换成小明考试得了80分。
如果小明确实得了80分,并且我们知道考试及格的分数线是60分,则根据已知条件,我们可以得出结论:“小明考试及格,小明有奖品”。
等量代换帮助我们从复杂的命题中抽象出具体的事实,从而进行合理的推理和判断。
综上所述,等量代换是一种常见的解题方法,在各个学科中都有广泛的应用。
通过将未知量替换成具体的数值,等量代换能够简化问题的复杂度,使计算更加简单和准确。
无论是代数方程求解、几何题解法、函数求值还是逻辑推理,等量代换都是解决问题的有力工具。
因此,掌握等量代换的技巧对于提高解题能力和应对各种考试都是非常重要的。
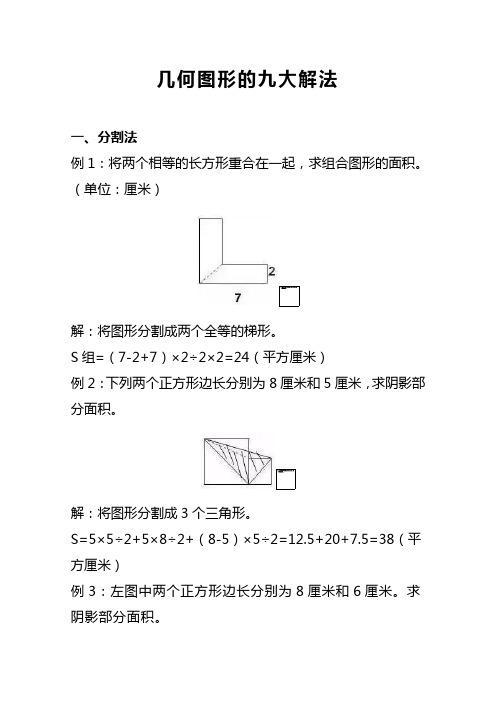
几何图形的九大解法一、分割法例1:将两个相等的长方形重合在一起,求组合图形的面积。
(单位:厘米)解:将图形分割成两个全等的梯形。
S组=(7-2+7)×2÷2×2=24(平方厘米)例2:下列两个正方形边长分别为8厘米和5厘米,求阴影部分面积。
解:将图形分割成3个三角形。
S=5×5÷2+5×8÷2+(8-5)×5÷2=12.5+20+7.5=38(平方厘米)例3:左图中两个正方形边长分别为8厘米和6厘米。
求阴影部分面积。
解:将阴影部分分割成两个三角形。
S阴=8×(8+6)÷2+8×6÷2=56+24=80(平方厘米)二、添辅助线例1:已知正方形边长4厘米,A、B、C、D是正方形边上的中点,P是任意一点。
求阴影部分面积。
解:从P点向4个定点添辅助线,由此看出,阴影部分面积和空白部分面积相等。
S阴=4×4÷2=8(平方厘米)例2:将下图平行四边形分成三角形和梯形两部分,它们面积相差40平方厘米,平行四边形底20.4厘米,高8厘米。
梯形下底是多少厘米?解:因为添一条辅助线平行于三角形一条边,发现40平方厘米是一个平行四边形。
所以梯形下底:40÷8=5(厘米)例3:平行四边形的面积是48平方厘米,BC分别是这个平行四边形相邻两条边的中点,连接A、B、C得到4个三角形。
求阴影部分的面积。
解:如果连接平行四边形各条边上的中点,可以看出空白部分占了整个平行四边形的八分之五,阴影部分占了八分之三。
S阴=48÷8×3=18(平方厘米)三、倍比法例1:已知OC=2AO,SABO=2㎡,求梯形ABCD的面积。
解:因为OC=2AO,所以SBOC=2×2=4(㎡)SDOC=4×2=8(㎡)SABCD=2+4×2+8=18(㎡)例2:已知S阴=8.75㎡,求下图梯形的面积。
代数式方程的解法与应用代数式方程是代数学中的重要概念,它描述了数学中的关系和变量之间的等式。
解代数式方程是数学研究中的一个基本问题,它在各个领域都有广泛的应用。
本文将探讨代数式方程的解法和其在实际问题中的应用。
一、代数式方程的解法1. 一元一次方程的解法一元一次方程是最简单的代数式方程,它的一般形式为ax + b = 0。
解一元一次方程的方法是通过移项和化简,将方程转化为x = c的形式,其中c为常数。
例如,对于方程2x + 3 = 7,我们可以通过将3移到等式右边,得到2x = 7 - 3,进一步化简得到x = 2。
2. 一元二次方程的解法一元二次方程是一种常见的代数式方程,它的一般形式为ax^2 + bx + c = 0。
解一元二次方程的方法有多种,包括因式分解、配方法、求根公式等。
其中,求根公式是最常用的方法,它可以直接求得一元二次方程的解。
求根公式为x = (-b ±√(b^2 - 4ac)) / 2a。
例如,对于方程x^2 - 5x + 6 = 0,我们可以通过代入a = 1,b = -5,c = 6,利用求根公式求得方程的解为x = 2或x = 3。
3. 多元方程组的解法多元方程组是包含多个未知数的方程组,它的解是满足所有方程的共同解。
解多元方程组的方法包括代入法、消元法、矩阵法等。
其中,消元法是一种常用的方法,它通过对方程组进行变换和消元,将方程组化简为最简形式。
例如,对于方程组2x + 3y = 74x - y = 1我们可以通过将第二个方程乘以2,并将其与第一个方程相减,得到新的方程6x = 9。
进一步化简得到x = 3,代入第一个方程可求得y = 1。
二、代数式方程的应用1. 几何问题中的代数式方程代数式方程在几何问题中有广泛的应用。
例如,对于一个矩形,已知其周长为10,我们可以设矩形的长为x,宽为y,根据周长的定义得到方程2x + 2y = 10。
通过解这个方程,我们可以求得矩形的长和宽。
几何问题的代数解法在数学的广袤领域中,几何与代数如同两座巍峨的山峰,各自展现着独特的魅力。
而将几何问题转化为代数解法,就像是在这两座山峰之间架起了一座桥梁,让我们能够以一种全新的视角去探索和解决那些看似复杂的几何难题。
几何问题通常涉及图形的形状、大小、位置关系等,需要我们通过直观的观察和几何定理的运用来求解。
然而,有时候这种直观的方法可能会让我们陷入困境,尤其是当问题变得较为复杂或者涉及多个变量时。
这时,代数解法就展现出了它的强大威力。
代数解法的核心思想是将几何中的元素,如点、线、面、角等,用代数符号和方程来表示。
通过建立这些代数关系,我们可以利用代数运算和方程求解的方法来得出几何问题的答案。
比如说,在平面直角坐标系中,一个点可以用坐标(x, y) 来表示。
这样,一条直线就可以用方程 y = kx + b 来描述,其中 k 是斜率,b 是截距。
通过这样的代数表示,我们可以很方便地研究直线的性质,比如判断两条直线是否平行、相交,或者计算它们的交点坐标。
再来看一个具体的例子,求一个三角形的面积。
如果我们知道三角形三个顶点的坐标,那么可以通过行列式的方法来计算其面积。
设三角形三个顶点的坐标分别为(x₁, y₁),(x₂, y₂),(x₃, y₃),则其面积可以表示为:\S =\frac{1}{2}\left|\begin{array}{ccc}x₁& y₁& 1 \\x₂& y₂& 1 \\x₃& y₃& 1\end{array}\right|\这种方法将几何中的面积问题转化为了代数中的行列式计算,大大简化了求解过程。
另外,在解决几何最值问题时,代数解法也常常能发挥关键作用。
比如,求平面上一点到给定几个点的距离之和的最小值。
我们可以设该点的坐标为(x, y),然后根据距离公式列出目标函数,再通过代数方法,如求导数、配方等,来找到最值。
代数解法不仅在平面几何中有着广泛的应用,在立体几何中同样能大放异彩。
几何图形的十大解法(30例)一、分割法例1:将两个相等的长方形重合在一起,求组合图形的面积。
(单位:厘米)2例2:下列两个正方形边长分别为8厘米和5厘米,求阴影部分面积。
例3:左图中两个正方形的边长分别为8厘米和6厘米。
求阴影部分面积。
二、添辅助线例1:已知正方形边长4厘米,A、B、C、D是正方形边上的中点,P是任意一点。
求阴影部分面积。
CPD BA例2:将下图平行四边形分成三角形和梯形两部分,它们面积相差40平方厘米,平行四边形底20.4厘米,高8厘米。
梯形下底是多少厘米?例3:平行四边形的面积是48平方厘米,BC分别是A 这个平行四边形相邻两条边的中点,连接A、B B、C得到4个三角形。
求阴影部分的面积。
C三、倍比法例1: A B 已知:OC=2AO,S ABO=2㎡,求梯形ABCDO 的面积。
D C例2:7.5 已知:S阴=8.75㎡,求下图梯形的面积。
2.5例3: A 下图AB是AD的3倍,AC是AE的5倍,D E 那么三角形ABC的面积是三角形ADE的多少倍?B C四、割补平移例1: A B 已知:S阴=20㎡, EF为中位线E F 求梯形ABCD的面积。
D C例2:10 求左图面积(单位:厘米)5510例3:把一个长方形的长和宽分别增加2厘米,面积增加24平方厘米。
求原长方形的周长。
2五、等量代换例已知:AB平行于EC,求阴影部分面积。
8E 10 D(单位:m)例2:下图两个正方形边长分别是6分米、4分米。
求阴影部分面积。
例3:已知三角形ABC的面积等于三角形AED的面积(形状大小都相同),它们重叠在一起,比较三角形BDF和三角形CEF的面积大小。
()A A 三角形DBF大B三角形CEF大D C C两个三角形一样大D无法比较B FE六、等腰直角三角形例1:已知长方形周长为22厘米,长7 厘米,求阴影部分面积。
45°例2:已知下列两个等腰直角三角形,直角边分别是10厘米和6厘米。
类型一:标准方程的求解例1 已知椭圆06322=-+m y mx 的一个焦点为(0,2)求m 的值.分析:把椭圆的方程化为标准方程,由2=c ,根据关系222c b a +=可求出m 的值.解:方程变形为12622=+my x .因为焦点在y 轴上,所以62>m ,解得3>m . 又2=c ,所以2262=-m ,5=m 适合.故5=m .例2 已知椭圆的中心在原点,且经过点()03,P ,b a 3=,求椭圆的标准方程.分析:因椭圆的中心在原点,故其标准方程有两种情况.根据题设条件,运用待定系数法,求出参数a 和b (或2a 和2b )的值,即可求得椭圆的标准方程.解:当焦点在x 轴上时,设其方程为()012222>>=+b a by a x .由椭圆过点()03,P ,知10922=+b a .又b a 3=,代入得12=b ,92=a ,故椭圆的方程为1922=+y x .当焦点在y 轴上时,设其方程为()012222>>=+b a bx a y .由椭圆过点()03,P ,知10922=+b a .又b a 3=,联立解得812=a ,92=b ,故椭圆的方程为198122=+x y .例3 已知方程13522-=-+-k y k x 表示椭圆,求k 的取值范围. 解:由⎪⎩⎪⎨⎧-≠-<-<-,35,03,05k k k k 得53<<k ,且4≠k .∴满足条件的k 的取值范围是53<<k ,且4≠k .说明:本题易出现如下错解:由⎩⎨⎧<-<-,03,05k k 得53<<k ,故k 的取值范围是53<<k .出错的原因是没有注意椭圆的标准方程中0>>b a 这个条件,当b a =时,并不表示椭圆.例4 已知1cos sin 22=-ααy x )0(πα≤≤表示焦点在y 轴上的椭圆,求α的取值范围.分析:依据已知条件确定α的三角函数的大小关系.再根据三角函数的单调性,求出α的取值范围.解:方程可化为1cos 1sin 122=+ααy x .因为焦点在y 轴上,所以0sin 1cos 1>>-αα. 因此0sin >α且1tan -<α从而)43,2(ππα∈.说明:(1)由椭圆的标准方程知0sin 1>α,0cos 1>-α,这是容易忽视的地方. (2)由焦点在y 轴上,知αcos 12-=a ,αsin 12=b . (3)求α的取值范围时,应注意题目中的条件πα<≤0.例5 求中心在原点,对称轴为坐标轴,且经过)2,3(-A 和)1,32(-B 两点的椭圆方程.分析:由题设条件焦点在哪个轴上不明确,椭圆标准方程有两种情形,为了计算简便起见,可设其方程为122=+ny mx (0>m ,0>n ),且不必去考虑焦点在哪个坐标轴上,直接可求出方程.解:设所求椭圆方程为122=+ny mx (0>m ,0>n ).由)2,3(-A 和)1,32(-B 两点在椭圆上可得⎪⎩⎪⎨⎧=⋅+-⋅=-⋅+⋅,11)32(,1)2()3(2222n m n m 即⎩⎨⎧=+=+,112,143n m n m 所以151=m ,51=n .故所求的椭圆方程为151522=+y x . 例6 已知P 点在以坐标轴为对称轴的椭圆上,点P 到两焦点的距离分别为354和352,过P 点作焦点所在轴的垂线,它恰好过椭圆的一个焦点,求椭圆方程.解:设两焦点为1F 、2F ,且3541=PF ,3522=PF .从椭圆定义知52221=+=PF PF a .即5=a . 从21PF PF >知2PF 垂直焦点所在的对称轴,所以在12F PFRt ∆中,21sin 1221==∠PF PF F PF , 可求出621π=∠F PF ,3526cos21=⋅=πPF c ,从而310222=-=c a b .∴所求椭圆方程为1103522=+y x 或1510322=+y x .例7 已知动圆P 过定点()03,-A ,且在定圆()64322=+-y x B :的内部与其相内切,求动圆圆心P 的轨迹方程. 分析:关键是根据题意,列出点P 满足的关系式.解:如图所示,设动圆P 和定圆B 内切于点M .动点P 到两定点, 即定点()03,-A 和定圆圆心()03,B 距离之和恰好等于定圆半径,即8==+=+BM PB PM PB PA .∴点P 的轨迹是以A ,B 为两焦点,半长轴为4,半短轴长为73422=-=b 的椭圆的方程:171622=+y x . 说明:本题是先根据椭圆的定义,判定轨迹是椭圆,然后根据椭圆的标准方程,求轨迹的方程.这是求轨迹方程的一种重要思想方法.类型二:直线与椭圆的位置关系(代数法-两根之和-积-判别式)一、公共点问题通过方程判别式来判断直线与椭圆的位置关系,几何的交点问题与代数的方程根问题完美结合于此例8 判断直线03=+-y kx 与椭圆141622=+y x 的位置关系 解:由⎪⎩⎪⎨⎧=++=1416322y x kx y 可得02024)14(22=+++kx x k )516(162-=∆∴k (1)当45450)516(162-<>>-=∆k k k 或即时,直线03=+-y kx 与椭圆141622=+y x 相交 (2)当45450)516(162-===-=∆k k k 或即时,直线03=+-y kx 与椭圆141622=+y x 相切(3)当45450)516(162<<-<-=∆k k 即时,直线03=+-y kx 与椭圆141622=+y x 相离 例9 若直线)(1R k kx y ∈+=与椭圆1522=+my x 恒有公共点,求实数m 的取值范围 解法一:由⎪⎩⎪⎨⎧=++=15122m y x kx y 可得05510)5(22=-+++m kx x m k ,0152≥--=∆∴k m 即1152≥+≥k m 51≠≥∴m m 且解法二:直线恒过一定点)1,0(当5<m 时,椭圆焦点在x 轴上,短半轴长m b =,要使直线与椭圆恒有交点则1≥m 即51<≤m 当5>m 时,椭圆焦点在y 轴上,长半轴长5=a 可保证直线与椭圆恒有交点即5>m综述:51≠≥m m 且 解法三:直线恒过一定点)1,0(要使直线与椭圆恒有交点,即要保证定点)1,0(在椭圆内部115022≤+m 即1≥m 51≠≥∴m m 且[评述]由直线方程与椭圆方程联立的方程组解的情况直接导致两曲线的交点状况,而方程解的情况由判别式来决定,直线与椭圆有相交、相切、相离三种关系,直线方程与椭圆方程联立,消去y 或x 得到关于x 或y 的一元二次方程,则(1)直线与椭圆相交0>∆⇔(2)直线与椭圆相切0=∆⇔(3)直线与椭圆相离0<∆⇔,所以判定直线与椭圆的位置关系,方程及其判别式是最基本的工具。