高等传热学-相变-第4章
- 格式:pdf
- 大小:307.79 KB
- 文档页数:13

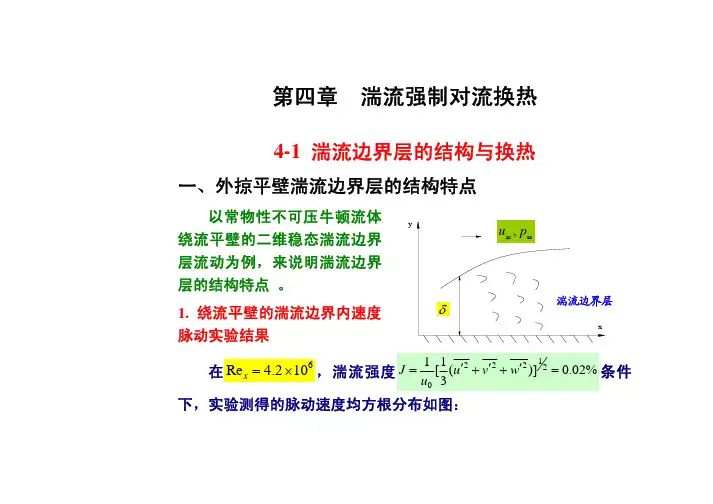
第四章 湍流强制对流换热4-1 湍流边界层的结构与换热一、外掠平壁湍流边界层的结构特点以常物性不可压牛顿流体绕流平壁的二维稳态湍流边界层流动为例,来说明湍流边界层的结构特点 。
1. 绕流平壁的湍流边界内速度脉动实验结果在6Re 4.210x =×下,实验测得的脉动速度均方根分布如图:y湍流边界层内脉动速度的均方根值变化由实验结果发现:a)由于受壁面束缚作用,壁面附近的脉动速度很小,时均速度梯度很大;(分子粘性应力占主导)。
b)随着离开壁面距离的增加,脉动速度增大,达到最大值后又减小,而时均速度分布趋于平坦;(雷诺应力增大又减小)。
c )在沿壁面的法线方向上,湍流边界层可大致分为内层区和外层区两个区域,又称壁区和尾迹区。
d )内层区约占边界层厚度的20%,(0.2y δ≤),内层区的大部分处于湍流状态,时均速度梯度较大。
在靠近壁面处,因受壁面影响,湍流脉动速度减小,雷诺应力大大减弱,粘性应力占主要作用,把壁区内紧靠壁面的这一薄层称为粘性底层;e )在外层区,脉动受壁面影响较弱,湍流应力仍处主要作用,但由于时均速度梯度比内层区小,使外层区的湍流生成项所占比例也减小。
f )外层区与边界层外主流区的界面并不整齐,存在着间歇的湍流脉动,随着接近主流,湍流脉动逐渐减小。
g )实验还表明:在内层区,流线基本上平行于壁面,流动近似具有剪切流的特性,即沿x 方向,u2. 时均守恒方程组及在内层区的简化(4.1.1)采用Boussinesq假设,湍流附加应力为:(a)动量方程可写作:(4.1.2)式中,τ是湍流总应力,等于分子粘性应力与湍流附加应力之和。
(4.1.3)内层区流动的动量方程简化由连续性方程0u v x y ∂∂+=∂∂,对内层区流动,因其剪切流特性,0u x∂=∂,0v y∂⇒=∂,yv v dy y∂=∂∫ ⇒于是,动量方程:()u u u v x y yτρ∂∂∂+=∂∂∂可化简为:. w ττ⇒= (4.1.4)即:在内层区,湍流总应力与离开壁面的距离无关,等于壁面处的切应力w τ。

4-2 管内湍流充分发展流对流换热一、管内湍流充分发展流对常物性、不可压牛顿流体的管内湍流充分发展流,有:0ux∂=∂,0v =,0p r ∂=∂ 于是,其二维稳态的动量方程化简为:(4.2.1)(4.2.2) 积分得到:(4.2.3)上式表明:管内湍流充分发展流的总切应力沿径向是线性分布的。
当w r r =时,w ττ=,于是:(4.2.4)) 定义:y 是沿半径方向离开壁面的距离,则w y r r =−。
于是τ可表示为:y(4.2.4)采用无量纲参数:u u u τ+=, y u y τν+⋅=, u τ=(4.2.5)与平壁湍流边界层的无量纲速度关系式:(内层区)所以,管内湍流充分发展流的近壁区与扰流平壁的湍流边界近壁区都遵循通用速度分布。
△另外,在管内充分发展湍流中,不存在平壁湍流边界层边缘那.种间歇湍流脉动,因而,在近壁区外,速度分布规律偏离壁面规律不像平壁湍流边界层那样显著。
这样,可近似地用通用速度分布来描述整个管截面内的速度场。
正如前面一节提到的,Von Kármán的三层结构通用速度分布也适用于管内湍流,即:(4.2.6)但也存在以下缺点:>时,用上式计算管内湍流对流换热结果不满意,(1)当Pr30原因是完全忽略了粘性底层中的脉动(t ν=0);(2出的结果不为零,这不符合实际。
赖卡特(H.Reichardt ),对此进行了改进,提出了公式:(4.2.7) 由上式可以看出,当50y +≤时,t νν随y +减小而减小,在壁面处,t νν=0(y +=0);在中心线处,w y r =将上式代入动量方程:(1)1t wdu y dy r νν+++++=−得(4.2.8)当0r =时,00r dudr ==。
最终可得无量纲通用速度分布:(4.2.9)工程上更多地直接采用尼古拉兹提出的速度分布。
尼古拉兹对36410Re 3.210×<<×范围内的管内湍流阻力与速度分布进行了广泛的实验研究,认为管内的湍流速度分布可表示为:(4.2.10) 其中,max u 是管中心线处速度,指数n 随Re 的变化(Re m u dν⋅=),如下表:施里希延(Schlichting.H.)推荐下面的速度分布式:(4.2.11)系数()c n 随n 的变化如下表:Re5105510× 61.310× 63.210×n78 9 10 ()c n8.749.7110.611.5普朗特基于通用速度分布,并综合实验数据修正,得出了通用的管内充分发展湍流阻力公式:(4.2.12) 上式称为光滑圆管的普朗特通用阻力公式,适用于6Re 3.410<×。




图4-16 蒸气冷凝方式 (a )、(b )膜状冷凝(c )滴状冷凝 第四节 有相变的对流传热蒸气冷凝和液体沸腾都是伴有相变化的对流传热过程。
这类传热过程的特点是相变流体要放出或吸收大量的潜热,对流传热系数较无相变时更大,例如水的沸腾或水蒸气冷凝。
本节只讨论纯流体的沸腾和冷凝传热。
4-4-1 蒸气冷凝传热一、蒸气冷凝方式当饱和蒸气与低于饱和温度的壁面接触时,蒸气放出潜热,并在壁面上冷凝成液体。
蒸气冷凝有膜状冷凝和滴状冷凝两种方式。
1.膜状冷凝若冷凝液能够润湿壁面,则在壁面上形成一层完整的液膜,称为膜状冷凝,如图4-16(a )和(b )所示。
在壁面上一旦形成液膜后,蒸气的冷凝只能在液膜的表面上进行,即蒸气冷凝时放出的潜热,必须通过液膜后才能传给冷壁面。
由于蒸气冷凝时有相的变化,一般热阻很小,因此这层冷凝液膜往往成为膜状冷凝的主要热阻。
若冷凝液膜在重力作用下沿壁面向下流动,则所形成的液膜愈往下愈厚,故壁面愈高或水平放置的管径愈大,整个壁面的平均对流传热系数也就愈小。
2.滴状冷凝若冷凝液不能润湿壁面,由于表面张力的作用,冷凝液在壁面上形成许多液滴,并沿壁面落下,此种冷凝称为滴状冷凝,如图4-16(c )所示。
在滴状冷凝时,壁面大部分的面积直接暴露在蒸气中,可供蒸气冷凝。
由于没有大面积的液膜阻碍热流,因此滴状冷凝传热系数比膜状冷凝可高几倍甚至十几倍。
工业上遇到的大多是膜状冷凝,因此冷凝器的设计总是按膜状冷凝来处理。
下面仅介绍纯组分的饱和蒸气膜状冷凝传热系数的计算方法。
二、膜状冷凝对流传热系数1.蒸气在垂直管或板外冷凝膜状冷凝对流传热系数理论公式的推导中作以下假定:(1)冷凝液膜呈层流流动,传热方式为通过液膜的热传导(Re <1800)。
(2)蒸气静止不动,对液膜无摩擦阻力。
(3)蒸气冷凝成液体时所释放的热量仅为冷凝潜热,蒸气温度和壁面温度保持不变。
(4)冷凝液的物性可按平均液膜温度取值,且为常数。
根据上述假定,对于蒸气在垂直管外或垂直平板侧的冷凝,可得到如下理论公式:943.0⎪⎪⎭ ⎝=t L ∆μα (4-47)特征尺寸 取垂直管或板的高度。

⾼等传热学相变导热解(移动边界)⾼等传热学导热理论——相变导热(移动边界问题)讨论第五讲:相变导热(移动边界问题):移动边界的导热问题有许多种,本讲只讲固液相变时的导热模型。
5.1 相变换热特点与分类:特点:(1) 相变处存在⼀个界⾯把不同相的物质分成两个区间(实际不是⼀个⾯,⽽是⼀个区)。
(2) 相变⾯随时间移动,移动规律时问题的⼀部分。
(3) 移动⾯可作为边界,决定了相变问题是⾮线性问题。
分类:(1) 半⽆限⼤体单区域问题(Stefan Question ) (2) 半⽆限⼤体双区域问题(Neumman Question ) (3) 有限双区域问题5.2 相变导热的数学描述和解:假定:固液两相内部只有导热,没有对流(适⽤于深空中相变)。
物性为常量。
不考虑密度变化引起的体积变化。
控制⽅程:对固相: 221s s s t t a x τ??=?? 对液相:221l ll t t a x τ??=??初值条件:0:s l t t t τ∞=== 边界条件:0:::s l w l s l s x t ort t x t ort orx t ort t ∞===∞≠∞=?=在相变界⾯,热量守恒,温度连续,Q l 为相变潜热:()():s l sl l l s l p t t d x Q and t t t x x d δτδτλλρτ==+== 5.2.1 半⽆限⼤体单区域问题(Stefan Question )的简化解:以融解过程为例:忽略液相显热,2210l ll t t a xτ??==??,⽅程解为⼀直线,由边界条件得:()/l w p w t t t t x δ=+-对固相,忽略温差:w p t t t ∞==,即固相温度恒等于相变温度等于初始温度。
由相变处得换热条件求δ的变化规律:()()():0()l l ll l p w l l t d d x Q t t Q x dx d λδτδτδτλρρδτδ?==+=-+?==式中:()/l l p w l Ste c t t Q =-叫Stefan ’s Number ,物理意义是相变时液相显热和液固潜热⽐。



第四讲 管内层流换热1. Introdution:1) 假定:除上述条件外, Laminar flow: 管内流Re=u m d e /ν<2200 d e =4A c /Pd e 小,换热面积强度β:β大,β>656m 2/m 3, 紧凑式换热器 β>3000m 2/m 3, 管翅式换热器 β>6000m 2/m 3, 板翅式换热器 β>16000m 2/m 3, 回转式换热器 β>20000m 2/m 3, 人肺2) 平均速度:u m =G/(ρm A)= udr r r udA A rt Am ⎰⎰=002021ρρ 圆管,半径r 0。
3) 平均温度:)(210020x f utdr r r u tdA u uC C A t rm t m A pm p m f ===⎰⎰ρρ, 圆管,半径r 0。
4) 入口段长度L h 、L t : V , VG VFD: Re 05.0=dL hT, TG TFD:.,Pr Re 05.0const t dL w t==.,Pr Re 07.0const q dL w t==Pr<1, L t <L h Pr>1, L t >L h 5) 充分发展段:0=∂∂x u 或 w f v u h C xτ,,,,)(0)(可以是∙=∂∙∂ ,但t,P 除外。
证明如下:v=0, 0)(21222=∂∂∂∂===∂∂===r r fm w mf r r w yx u dx dC u dx d u C yuηρτρητ4/f C f =;TFD: 0,0=∂∂≠∂∂x xt f θfw ww f w t t t t t t t t --=--=θ2. 圆管内充分发展段换热(VFD, TFD ) 1) governing eqs)(1)(0)(1rt r r r a r t v x t u x Pr u r r r r u v x u u r rv r x u ∂∂∂∂=∂∂+∂∂∂∂-∂∂∂∂=∂∂+∂∂=∂∂+∂∂ρν ⇒ )(1)(0,,0)(,0rt r r r a x t u x Pr u r r r v c o n s t rv r rv x u ∂∂∂∂=∂∂∂∂=∂∂∂∂===∂∂=∂∂ρν B.C:wh t t v u r r v ru r L x ======∂∂=>0,0:0,0:0:03) 速度解:))(1(42020r rdx dP r u --=ηdx dP r u m η820-=, dxdPr u u m η4220max -== 200214m f m y w u C u r dydu ρηητ==== Re644,Re16===f f C f C 4) 温度解: 当TFD ,0,0=∂∂≠∂∂xxt f θ,const rr y =∂∂=⇒=0),(θθθconst r t t r t t t t rt h r r f w r r w f w r r x =∂∂=-∂-∂=-∂∂-====0)/()()/(θλλλ当TFD ,const q w =时, const t t h q f w x w =-=)(, 因为const h x =,dx dt dxdt w f =, const dxdt dx dt dx dt dx dt dx dt x t f w w w f ===++-=∂∂θθ )(r t r r r a x t u x t uw ∂∂∂∂=∂∂=∂∂, )()(rtr r r a x t r u w ∂∂∂∂=∂∂,为ODE 。
7-4,常物性流体在两无限大平行平板之间作稳态层流流动,下板静止不动,上板在外力作用下以恒定速度U 运动,试推导连续性方程和动量方程。
解:按照题意0,0=∂∂=∂∂=xv y v v 故连续性方程0=∂∂+∂∂yv x u 可简化为0=∂∂xu因流体是常物性,不可压缩的,N-S 方程为 x 方向:)(12222yu x u v y p F y u v x u u x ∂∂+∂∂+∂∂-=∂∂+∂∂ρρ 可简化为022=∂∂+∂∂-yv x p F x ηy 方向)(12222yv x v v y p F y v v x v u y ∂∂+∂∂+∂∂-=∂∂+∂∂ρρ 可简化为0=∂∂=ypF y8-3,试证明,流体外掠平壁层流边界层换热的局部努赛尔特数为12121Re Prx Nu r =证明:适用于外掠平板的层流边界层的能量方程22t t t u v a x y y∂∂∂+=∂∂∂ 常壁温边界条件为0w y t t y ∞==→∞时,时,t=t引入量纲一的温度wwt t t t ∞-Θ=-则上述能量方程变为22u v a x y y∂Θ∂Θ∂Θ+=∂∂∂引入相似变量12Re ()y yx x ηδ===有11()(()22x x xηηηηη∂Θ∂Θ∂''==Θ-=-Θ∂∂∂()y y ηηη∂Θ∂Θ∂'==∂∂∂;22()U y x ηυ∞∂Θ''=Θ∂ 将上三式和流函数表示的速度代入边界层能量方程,得到1Pr 02f '''Θ+Θ=当Pr1时,速度边界层厚度远小于温度边界层厚度,可近似认为温度边界层内速度为主流速度,即1,f f η'==,则由上式可得Pr ()2d f d η''Θ'=-'Θ,求解可得 11()()Pr 2Pr(0)()erf ηηπΘ='Θ=则12120.564RePrx xNu =8-4,求证,常物性不可压缩流体,对于层流边界层的二维滞止流动,其局部努赛尔特数满足10.4220.57Re Pr x Nu =⋅证明:对于题中所给情况,能量方程可表示为22u v x y yθθθα∂∂∂+=∂∂∂其中,,,()u v y x ψψψθθηθ∂∂==-===∂∂ 故上式可转化为Pr02θζθ'''+⋅⋅= 经两次积分,得到0000Pr [exp()]2()Pr [exp()]2d d d d ημμζηηθμζηη∞-=-⎰⎰⎰⎰ 定义表面传热系数s x s q h T T ∞=-,则(0)q '= 进一步,进行无量纲化处理,引入局部努赛尔特数12(0)Re x x x h x Nu k ⋅'===其中1200Re (0)Pr [exp()]2xd d μθζηη∞'=-⎰⎰ 针对层流边界层的条件,查由埃克特给出的计算表如下:不同Pr 数下,常物性层流边界层,12Re x Nu -⋅的值故可看出,12Re x Nu -⋅=常数,进而,12()=x h xu k υ-∞⋅=1常数C ,由1m u C x ∞=⋅,得11212m C kh xυ-=⋅对于二维滞止流,m=1,则h 也为常数,从x=0到x 处的平均热导率h m 定义为1xm h hdx x =⎰故11112212120121m m x m C k C k h x dx x x m υυ--=⋅=⋅⋅+⎰, 则21m h h m =+,由此可看出, 在m=1时,努赛尔特数的近似解可以很好的表示为10.4220.57Re Pr x Nu =⋅ 同样的,我们也可以得到三维滞止流的近似解10.4220.76Re Pr x Nu =⋅9-1,试证明:圆管内充分发展流动的体积流量可表示为: ()0408p p Lr V i -=μπ9-2,常物性不可压缩流体在两平行平板间作层流流动,下板静止,上板以匀速U 运动,板间距为2b ,试证明充分发展流动的速度分布为⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--=b y b y dx dp b b y U u 2222μ 证:二维流体质量、动量方程0=∂∂+∂∂yvx u ① ⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂-=∂∂+∂∂2222)(y u xu x py u v x u u μρ ②⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂-=∂∂+∂∂2222)(y v xv y py v v x v u μρ ③ 在充分发展区,截面上只有沿流动方向的速度u 在断面上变化,法向速度v 可以忽略,因此可由方程①得:0=v ,0=∂∂xu④ 将式④代入③得到,0=∂∂yp,表明压力P 只是流动方向x 的函数,即流道断面上压力是均匀一致的进一步由式②得,t cons y udx dp tan 22=∂∂=μ ⑤相应的边界条件:Uu b y u y ====,20,0对⑤积分得:11C y dx dpyu +=∂∂μμ21221C y C y dxdp U ++=μ ddp b b u C μ-=21,02=C ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--=⇒b y b y dx dp b b y U u 2222μ1. 强迫流动换热如何受热物性影响?答:强迫对流换热与Re 和Pr 有关;加热与对流的粘性系数发生变化。
第四章 流动沸腾液体在管道或回路中流动时,产生的沸腾现象称为流动沸腾。
这种流动可能是外力强制形成,也可能是回路内的流体的密度差引起的自然循环。
由于流动沸腾中伴随着各种类型的汽液两相流动,所以比池内沸腾更复杂。
目前还无法对流动沸腾过程进行解析求解,研究的途径主要是实验。
§4-1 流型与沸腾工况流动沸腾的特点:1). 由于管道的沿途加热和液体蒸发,汽液两相流的流型会发生一系列的变化。
2). 随着容积流量的增大,流体逐步加速使压力降增大,而引起系统压力的下降,饱和温度也随之降低,这反过来对流型和沸腾产生影响。
因此,对沿加热管的流动沸腾,需分段进行分析计算。
3). 工程上,加热管的配置有竖直和水平两种典型方式(倾斜布置管道处于二者之间)。
在这两种情况下的流动和沸腾特性有明显的差别,一般分开研究。
一、竖直管内流动沸腾的流型和换热工况如图,是典型的竖直管内流动沸腾的流型和换热工况。
当单相流体从下部进入加热管后,①一开始,加热壁上尚不具备成核条件,这时流动为单相流,换热工况为液体的单相对流换热(A区)。
②随着液体被加热,温度升高,逐步使壁面上的某些开始满足成核条件,开始出现小汽泡。
当汽泡长大到一定尺寸后,脱离壁面进入主流,在汽泡刚开始产生的阶段,液体核心区的温度高低于对应的主流压力下的饱和温度,使脱离壁面而后的小汽泡很快在过冷的液体中凝结,加速液体升温,使换热增强。
这时的换热工况为流动过冷沸腾,其流型是泡状流(B区)。
③当液体的主流温度达到饱和温度后,进入主流的汽泡不再凝结,换热进入饱和沸腾工况。
④随着液体中汽泡数量的不断增加,小汽泡之间发生碰撞与合并,开始出现较大的汽团或称弹状大汽泡,其流型由泡状流演变为弹状流动(仍为饱和沸腾)。
⑤随着液体的进一步汽化,含汽量的增加,两相流型转变为环状流,即汽相在管中心区,而液相附着于管壁上。
⑥随着液层的变薄,壁面上的沸腾逐渐被抑制,汽化转变为汽液分界面上的蒸发,换热工况由饱和沸腾逐步变为强制对流蒸发。
这时,若壁面温度很高或壁面热流密度很大,则从环状流可以一直演变为雾环状流和雾状流,或者以泡状流直接过度到反环状流。
环状流与反环状流的区别与成因:a). 环状流发生在两相流干度(质量含汽率x大)较高的条件,(汽多),核心区以蒸汽夹带夜滴为主;b). 反环状流则发生在高热负荷低干度(x小)的条件下,在壁面上形成一层气膜,主流核心区则是液体。
⑦当加热壁面无液膜后,进入雾状流动,蒸汽中夹带小液滴。
对应的换热工况称为干涸后换热或缺液区换热。
⑧当蒸汽中的液体全部蒸发后,进入蒸汽的单相流动和换热工况。
注意:a). 从加热面与液体直接接触演变到与蒸汽直接接触,中间有一段不稳定的过渡区。
b). 过冷沸腾和饱和沸腾通常发生在泡状流区,饱和沸腾也可发生在弹状流、甚至环状流区,过热沸腾通常发生在不稳定流动区。
膜态沸腾则发生于反环状流或雾状流区。
(壁面上形成一层汽膜)。
△ 液体从过冷被加热到饱和状态后,在两相流动区内,一直维持饱和温度不变,干涸点后的蒸汽过热,但蒸汽中的液滴仍然维持饱和温度,直到液体全部蒸发后,气温开始大幅度升高。
△ 壁面温度总是高于液体的温度,在过冷沸腾后。
由于换热系数高于单相区,壁温会有所下降,在干涸点后,由于换热系数突然下降,壁温迅速升高,在雾状流区,由于液滴的蒸发,两相流流速增加,换热系数相应加大。
换热系数相应增大,而使壁温略微下降,进入纯蒸汽区后,壁温和蒸汽温度同时均匀升高。
二、水平管内流动沸腾的流型水平加热管内汽液两相流型的演变过程与竖直管内的流型演变过程大致类似。
但由于加热管水平放置,使蒸汽在管内截面上的分布不均匀(浮升力作用)。
大部分汽泡聚集在管子的上部空间,当蒸汽含量较大时会出现汽液分层流动,流速越低,分层流动的趋势愈大。
随着汽液两相相对速度的增大,两相分界面会出现波动,当这种波动很剧烈时,会引起液体周期性地冲刷管壁上表面,在某些部位出现间断式的干涸状态。
随着蒸汽含量进一步增大,两相流发展为环状流动和雾状流动,最后形成蒸汽的单相对流结构。
三、干度x与截面空隙率ϕ干度x截面上的蒸汽质量流量占截面总质量流量的份额,称为蒸汽干度,或质量含汽率。
空隙率ϕ截面上汽相占整个截面面积的份额,称为空隙率或截面含汽率。
v v v lA A A A A ϕ==+§4-2流动过冷沸腾一、过冷沸腾的起始点起始点:液体从单相对流换热向核态沸腾换热过渡的标志,发生在壁温超过当地液体饱和温度的某些地点。
由壁面上汽化核心活化的判剧,起始点应当满足:汽泡温度曲线和管壁附近过热液体层中温度分布曲线相切的条件,这时的壁面热流密度即是流动沸腾的起始热流密度i q : ()Pr 28L fg v w s i s lh T T q T λρσ−= (4.1) 上式对水和其它液体都适用。
在lg i q 与lg()w s T T −的坐标图上,该式为一条直线。
若将单相液体强制对流换热的公式对应的直线也画在该图上,则两条直线的交点,就是实际流动沸腾的起始点。
这种方法得出的i q 和()w s i T T −与实验值较符合。
临界气泡温度T b过热液体温度T l二、流动过冷沸腾换热实验关联式1. 过冷沸腾曲线如图。
a). “部分过冷沸腾”:过冷沸腾起始时,气泡只在加热面的个别地点产生,气泡未脱离壁面时就被冷凝而消失,或者以小气泡的形式,一直附着再壁面上,这时的沸腾工况称为“部分过冷沸腾”。
部分过冷沸腾时,热量由单相对流和核态沸腾共同传递,即:c n q q q =+ (4.2)式中,q —总热流;c q —单相对流换热热流分量;n q —核态沸腾换热分量。
b). “充分发展过冷沸腾”:随着液体温度的上升,当液体主流温度仍低于主流压力下的饱和温度,而整个加热面都被汽泡所布满时,换热过程完全由核态沸腾控制,这时的沸腾工况称为“充分发展过冷沸腾”。
2. 流动过冷沸腾换热计算流动过冷沸腾换热分成三个区域计算:a). w ONB T T <(ONB T 是沸腾起始点温度)时,为单相强制对流换热:()c l w b q q h T T ==− (4.3)l h 是单相强制对流换热系数.b). ONB w FDB T T T ≤≤(FDB T 是充分发展过冷沸腾点温度)时,为部分过冷沸腾换热:()()1w s n c b l w b T T q q q h T T c−=+=−+ (4.4) 实验发现,在局部过冷沸腾区,过冷度s T ∆和流速w 对换热影响很大。
c). w FDB T T >时,为充分发展过冷沸腾换热:()1w s n b T T q q c−== (4.5) 式中,常数c 和指数n 应根据充分发展过冷流动沸腾的实验数据整理得到。
1972年Moles & Shaw 推荐了一个无量纲综合关系式:.....Pr ()()()04605306707785fg v f l pl s fg v lh h q h c T h w ρρρ=∆ (4.6) 式中,h 是过冷流动沸腾的换热系数。
过冷度10o s s b T T T C ∆=−>,b T 是截面的液体平均温度。
§4-3 流动饱和沸腾当液体的核心区温度达到对应系统压力下的饱和温度时,液体进入饱和沸腾工况。
从原理上讲,流动饱和沸腾的机理与池内沸腾的机理与池内沸腾的机理相同,流速和干度对沸腾不会产生明显的影响。
但实验证明,除质量流速较低或者汽泡布满加热面的高热流密度这两类情况外,采用池内沸腾公式来计算流动饱和沸腾换热是不可靠的,差别很大。
一、流动饱和沸腾的特点一般来说,当流动饱和沸腾液体中的含汽量增加到一定程度时,总会导致致环状流型。
因为,随汽泡流中含汽率的增加,根据伯努利效应,在加速的两相流中,在同样的压力梯度作用下,密度小的一相可获得较高的流速,所以气泡慢慢集中到中心高速区,而形成环状流。
当环状液层的厚度较大时,核态沸腾仍可在液层中发生,随着液体不断蒸发,液层变薄,最后变成附着在加热面上的一层液膜。
这时,汽液界面和蒸汽核心区都处于(当地压力)饱和温度,壁温为:w s L T T T =+∆ (4.6)L T ∆—液膜的温度降,即w L T T ∆=∆(壁面过热度等于液膜的温度降)。
由于液膜厚度δ的变小,壁面过热度及它附近液体的过热度都较小,汽化核心的活化受到抑制,使核态沸腾难以维持。
此时,核心区蒸汽的流速很高,汽液界面波动剧烈,换热机制发生了变化。
热量主要靠导热和对流从加热面通过液膜传递到汽液分界面上,在汽液界面上进行蒸发,换热系数受流动状况的影响很明显。
通常把这种核态沸腾受到抑制的传热状况称为两相强制对流蒸发。
二、两相强制对流蒸发液膜内分层流和湍流两种不同的流态。
1. 层流液膜换热 模型:对管径不太小的竖直园管内的环状液膜,可近似的看成是无限大竖直平面上的二维层流液膜,忽略轴向导热,粘性耗散。
液膜传热过程控制方程为:22pl l z l T T c w z yρλ∂∂=∂∂ (4.7) 可解出,液膜的换热系数为:()2122L i L L w s L q h T T V λτλδµ⋅===−⋅ (4.8) 其中,δ-液膜温度;i τ-界面切应力,22L i L L dw d V dy dyτµµ===常数;V 是单位时间流过液膜单位宽度的液体量。
0z V w dy δ=∫ (4.9) 2. 湍流液膜()l Nu F w += (4.10) 这里,l L Q w ρµ+⋅=是无量纲液膜流量。
3. 液膜换热的经验关联式()1n l tth A h X = (4.11) 其中,h 是强制对流蒸发的换热系数;l h 是管内液体单相对流换热系数;A ,n ,实验常数,对水:.29A =,.066n =。
tt X :是两相流的马蒂内利参数,...0501091v l tt l v x X x ρµρµ⎛⎞⎛⎞−⎛⎞=⎜⎟⎜⎟⎜⎟⎝⎠⎝⎠⎝⎠ (4.12)三、流动饱和沸腾换热计算核态沸腾和强制对流蒸发同时发生,其相互关系随液厚度变化。
工程上广泛采用Chen 氏公式。
陈氏假定核态沸腾与强制对流蒸发的贡献是叠加的,总换热系数为:mac mic h h h =+ (4.13)其中,mac h 是强制对流蒸发的换热系数;mic h 是核态沸腾的换热系数。
.Re ()Re 08TP mac l l lh h F h =⋅=⋅ (4.14) ..()051781tt F X −=+ (4.15) mic n h S h =⋅ (4.16)式中,n h 是池内核态沸腾换热系数;S 是沸腾抑制因子。
(1S ≤)。
则流动饱和沸腾的换热系数为:l n h F h S h =⋅+⋅ (4.17)。