车载捷联惯导系统定位测姿算法研究
- 格式:pdf
- 大小:392.32 KB
- 文档页数:6

捷联惯导系统双矢量定姿方法研究
张剑慧;秦永元;龙瑞
【期刊名称】《计算机测量与控制》
【年(卷),期】2010(018)011
【摘要】利用两相交矢量确定运载体姿态矩阵的方法为双矢量定姿;分别对静基座和动基座情况下的捷联惯导系统双矢量定姿问题进行了研究;静基座条件下利用地球自转角速度和重力加速度信息直接解析实现定姿,动基座条件下利用重力加速度信息,构造中间参考矢量通过矩阵传递的方法实现定姿,并对不同环境下的定姿误差进行了分析;仿真实验结果表明,利用重力加速度和地球自转角速度信息完全能够实现运载体的定姿,且定姿精度能够满足进一步采用线性模型进行精定姿的要求.【总页数】4页(P2634-2637)
【作者】张剑慧;秦永元;龙瑞
【作者单位】西北工业大学,自动化学院,陕西,西安,710129;西北工业大学,自动化学院,陕西,西安,710129;西北工业大学,自动化学院,陕西,西安,710129
【正文语种】中文
【中图分类】U666.1
【相关文献】
1.光纤陀螺捷联惯导系统改进航姿算法应用 [J], 宋桂华;赵伟;刘建业;祝燕华
2.基于矢量定姿的捷联惯导惯性系对准误差分析 [J], 郑振宇;苑志江;郑智林;翟玉婷
3.捷联惯导系统航姿算法的比较及仿真分析 [J], 王小峰;董正芳
4.双矢量定姿算法提高海参捕捞装置捷联惯导系统粗对准精度 [J], 包建华;乔曦;李道亮
5.激光捷联惯导多矢量定姿法晃动基座粗对准 [J], 孙立江;周召发;陈河;刘朋朋;郭琦
因版权原因,仅展示原文概要,查看原文内容请购买。


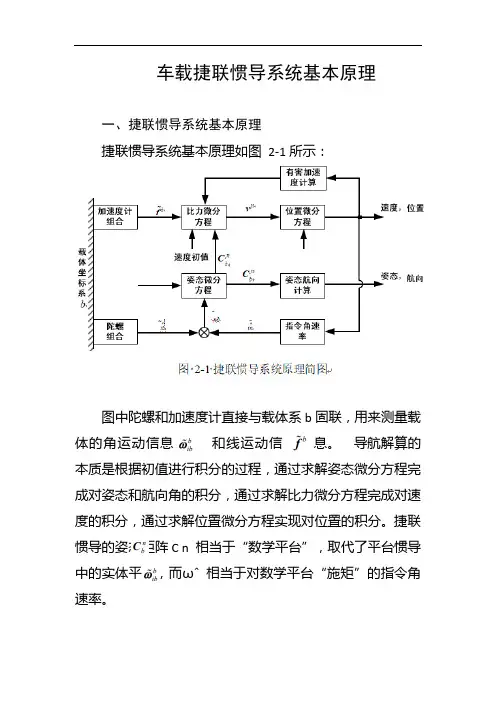
车载捷联惯导系统基本原理一、捷联惯导系统基本原理捷联惯导系统基本原理如图2-1所示:图中陀螺和加速度计直接与载体系b固联,用来测量载体的角运动信息和线运动信息。
导航解算的本质是根据初值进行积分的过程,通过求解姿态微分方程完成对姿态和航向角的积分,通过求解比力微分方程完成对速度的积分,通过求解位置微分方程实现对位置的积分。
捷联惯导的姿态矩阵C n 相当于“数学平台”,取代了平台惯导中的实体平台,而ωˆ相当于对数学平台“施矩”的指令角速率。
二、捷联惯导微分方程(一)姿态微分方程在捷联惯导系统中,导航坐标系n 和载体坐标系b 之间的角位置关系通常用姿态矩阵、四元数和欧拉角表示,相应也存在姿态矩阵微分方程、四元数微分方程和欧拉角微分方程三种形式。
姿态矩阵微分方程的表达式为:在欧拉角微分方程式(2.2-7)中,当俯仰角θ趋于90º时,cosθ趋于0,tanθ趋于无穷,方程存在奇异性,所以这种方法不能在全姿态范围内正常工作;姿态矩阵微分方程式(2.2-1)可全姿态工作,但姿态矩阵更新相当于求解包含9个未知量的线性微分方程组,计算量大;四元数微分方程式(2.2-6)同样可以全姿态工作,且更新算法只需求解4个未知量的线性微分方程组,计算量小,算法简单,是较实用的工程算法。
(二)速度微分方程速度微分方程即比力方程,是惯性导航解算的基本关系式:三、捷联惯性导航算法捷联惯导解算的目的是根据惯性器件输出求解载体姿态、速度和位置等导航信息,实际上就是求解三个微分方程的过程,相应存在姿态更新算法、速度更新算法和位置更新算法。
(一)姿态更新算法求解微分方程式(2.2-6)可得四元数姿态更新算法为:在车辆行驶过程中,一般不存在高频大机动环境,并且车载导航系统往往不工作在纯惯性导航方式,而是利用里程仪或零速条件进行组合导航,所以算法误差的影响有限,常用的5ms采样周期和二子样优化算法即可满足要求。
四、捷联惯导误差模型传感器误差、初值误差和算法误差是SINS的主要误差源,其中器件误差和初值误差又是影响导航结果的主要因素。


捷联惯导与组合导航系统高精度初始对准技术研究捷联惯导与组合导航系统高精度初始对准技术研究引言捷联惯导与组合导航系统是一种集捷联惯导和其他导航传感器(如GPS、气压计、陀螺仪等)的优势于一体的导航系统,具有在惯导滞后情况下实现导航信息快速、准确更新的优势。
为了确保导航精度和可靠性,捷联惯导与组合导航系统的初始对准是不可或缺的关键技术之一。
本文将重点探讨捷联惯导与组合导航系统高精度初始对准技术的研究。
一、捷联惯导与组合导航系统概述捷联惯导与组合导航系统是一种通过融合多种导航传感器测量数据来计算导航解的导航系统。
其中,捷联惯导通过惯性导航算法利用加速度计和陀螺仪提供的姿态、速度和位移信息进行导航计算,而组合导航则通过融合GPS和其它传感器的信息来修正惯导的误差,提供更准确的导航结果。
二、初始对准技术的研究现状初始对准技术在捷联惯导与组合导航系统中起到了决定性的作用,对其精度和可靠性具有重大影响。
目前,针对初始对准技术的研究主要集中在以下几个方面:1. 惯性传感器标定:惯导系统的精度和准确性直接依赖于惯性传感器的性能。
因此,对于惯导系统而言,惯性传感器的标定至关重要。
传感器标定主要涉及惯性传感器的误差估计、参数校准和标定方法等。
2. 导航状态估计算法:捷联惯导与组合导航系统的核心是导航状态估计算法。
目前常用的算法包括扩展卡尔曼滤波(EKF)、无迹卡尔曼滤波(UKF)以及粒子滤波(PF)等。
这些算法通过融合多种传感器的信息,实现对导航状态的准确估计。
3. 高精度传感器融合:为了提高初始对准的精度和可靠性,可以考虑使用更高精度的传感器,如高精度的加速度计和陀螺仪。
此外,对于GPS系统而言,使用双频技术和高精度的差分GPS技术可以进一步提高导航精度。
三、捷联惯导与组合导航系统高精度初始对准技术研究在捷联惯导与组合导航系统高精度初始对准技术的研究中,可以采用以下方法来提高初始对准的精度和可靠性:1. 多目标标定方法:采用多目标标定方法来标定捷联惯导系统中的惯性传感器。

捷联惯导算法与组合导航原理讲义严恭敏,翁浚编著西北工业大学2016-9前言近年来,惯性技术不论在军事上、工业上,还是在民用上,特别是消费电子产品领域,都获得了广泛的应用,大到潜艇、舰船、高铁、客机、导弹和人造卫星,小到医疗器械、电动独轮车、小型四旋翼无人机、空中鼠标和手机,都有惯性技术存在甚至大显身手的身影。
相应地,惯性技术的研究和开发也获得前所未有的蓬勃发展,越来越多的高校学生、爱好者和工程技术人员加入到惯性技术的研发队伍中来。
惯性技术涉及面广,涵盖元器件技术、测试设备和测试方法、系统集成技术和应用开发技术等方面,囿于篇幅和作者知识面限制,本书主要讨论捷联惯导系统算法方面的有关问题,包括姿态算法基本理论、捷联惯导更新算法与误差分析、组合导航卡尔曼滤波原理、捷联惯导系统的初始对准技术、组合导航系统建模以及算法仿真等内容。
希望读者参阅之后能够对捷联惯导算法有个系统而深入的理解,并能快速而有效地将基本算法应用于解决实际问题。
本书在编写和定稿过程中得到以下同行的热心支持,指出了不少错误之处或提出了许多宝贵的修改建议,深表谢意:西北工业大学自动化学院:梅春波、赵彦明、刘洋、沈彦超、肖迅、牟夏、郑江涛、刘士明、金竹、冯理成、赵雪华;航天科工第九总体设计部:王亚军;辽宁工程技术大学:丁伟;北京腾盛科技有限公司:刘兴华;东南大学:童金武;中国农业大学:包建华;南京航空航天大学:赵宣懿;武汉大学:董翠军;网友:Zoro;山东科技大学:王云鹏。
书中缺点和错误在所难免,望读者不吝批评指正.作者2016年9月目录第1章概述 (6)1.1捷联惯导算法简介 (6)1.2 Kalman滤波与组合导航原理简介 (7)第2章捷联惯导姿态解算基础 (10)2。
1反对称阵及其矩阵指数函数 (10)2。
1。
1 反对称阵 (10)2。
1.2 反对称阵的矩阵指数函数 (12)2。
2方向余弦阵与等效旋转矢量 (13)2.2.1 方向余弦阵 (13)2。

捷联惯导算法与组合导航原理讲义严恭敏,翁浚编著西北工业大学2021-9前言近年来,惯性技术不管在军事上、工业上,还是在民用上,特别是消费电子产品领域,都获得了广泛的应用,大到潜艇、舰船、高铁、客机、导弹和人造卫星,小到医疗器械、电动独轮车、小型四旋翼无人机、空中鼠标和手机,都有惯性技术存在甚至大显身手的身影。
相应地,惯性技术的研究和开发也获得前所未有的蓬勃开展,越来越多的高校学生、爱好者和工程技术人员参加到惯性技术的研发队伍中来。
惯性技术涉及面广,涵盖元器件技术、测试设备和测试方法、系统集成技术和应用开发技术等方面,囿于篇幅和作者知识面限制,本书主要讨论捷联惯导系统算法方面的有关问题,包括姿态算法根本理论、捷联惯导更新算法与误差分析、组合导航卡尔曼滤波原理、捷联惯导系统的初始对准技术、组合导航系统建模以及算法仿真等内容。
希望读者参阅之后可以对捷联惯导算法有个系统而深化的理解,并能快速而有效地将根本算法应用于解决实际问题。
本书在编写和定稿过程中得到以下同行的热心支持,指出了不少错误之处或提出了许多珍贵的修改建议,深表谢意:西北工业大学自动化学院:梅春波、赵彦明、刘洋、沈彦超、肖迅、牟夏、郑江涛、刘士明、金竹、冯理成、赵雪华;航天科工第九总体设计部:王亚军;辽宁工程技术大学:丁伟;北京腾盛科技:刘兴华;东南大学:童金武;中国农业大学:包建华;南京航空航天大学:赵宣懿;武汉大学:董翠军;网友:Zoro;山东科技大学:王云鹏。
书中缺点和错误在所难免,望读者不吝批评指正。
作者2021年9月目录第1章概述 (6)捷联惯导算法简介 (6)1.2 Kalman滤波与组合导航原理简介 (7)第2章捷联惯导姿态解算根底 (10)反对称阵及其矩阵指数函数 (10)2.1.1 反对称阵 (10)2.1.2 反对称阵的矩阵指数函数 (12)方向余弦阵与等效旋转矢量 (13)2.2.1 方向余弦阵 (13)2.2.2 等效旋转矢量 (14)方向余弦阵微分方程及其求解 (16)2.3.1 方向余弦阵微分方程 (16)2.3.2 方向余弦阵微分方程的求解 (17)姿态更新的四元数表示 (19)2.4.1 四元数的根本概念 (19)2.4.2 四元数微分方程 (23)2.4.3 四元数微分方程的求解 (24)等效旋转矢量微分方程及其泰勒级数解 (26)2.5.1 等效旋转矢量微分方程 (26)2.5.2 等效旋转矢量微分方程的泰勒级数解 (29)圆锥运动条件下的等效旋转矢量算法 (31)2.6.1 圆锥运动的描绘 (31)2.6.2 圆锥误差补偿算法 (33)第3章地球形状与重力场根底 (40)地球的形状描绘 (40)地球的正常重力场 (46)地球重力场的球谐函数模型 (50)3.3.1 球谐函数的根本概念 (50)3.3.2 地球引力位函数 (58)3.3.3 重力位及重力计算 (63)第4章捷联惯导更新算法及误差分析 (69)4.1捷联惯导数值更新算法 (69)4.1.1 姿态更新算法 (69)4.1.2 速度更新算法 (70)4.1.3 位置更新算法 (76)捷联惯导误差方程 (76)惯性传感器测量误差 (76)姿态误差方程 (78)速度误差方程 (79)位置误差方程 (79)误差方程的整理 (80)静基座误差特性分析 (82)4.3.1 静基座误差方程 (82)4.3.2 高度通道 (83)4.3.3 程度通道 (83)4.3.4 程度通道的简化 (88)4.3.5 程度通道误差方程的仿真 (90)第5章卡尔曼滤波根本理论 (92)递推最小二乘法 (92)5.2 Kalman滤波方程的推导 (94)连续时间随机系统的离散化与连续时间Kalman滤波 (101)噪声相关条件下的Kalman滤波 (107)序贯滤波 (111)信息滤波与信息交融 (113)平方根滤波 (116)遗忘滤波 (123)5.9 Sage-Husa自适应滤波 (125)最优平滑算法 (126)非线性系统的EKF滤波、二阶滤波与迭代滤波 (129)间接滤波与滤波校正 (135)联邦滤波〔待完善〕 (135)滤波的稳定性与可观测度分析 (140)第6章初始对准及组合导航技术 (146)捷联惯导粗对准 (146)矢量定姿原理 (146)解析粗对准方法 (148)间接粗对准方法 (151)捷联惯导精对准 (152)惯性/卫星组合导航 (156)空间杆臂误差 (156)时间不同步误差 (157)状态空间模型 (157)车载惯性/里程仪组合导航 (158)航位推算算法 (158)航位推算误差分析 (160)6.惯性/里程仪组合 (163)低本钱姿态航向参考系统〔AHRS〕 (166)简化的惯导算法及误差方程 (166)6地磁场测量及误差方程 (168)低本钱组合导航系统模型 (169)低本钱惯导的姿态初始化 (170).5捷联式地平仪的工作原理 (172)第7章捷联惯导与组合导航仿真 (175)飞行轨迹和惯性器件信息仿真 (175)飞行轨迹设计 (175)7.1.2 捷联惯导反演算法 (176)7.1.3 仿真 (177)捷联惯导仿真 (179)7.2.1 Matlab子函数 (179)捷联惯导仿真主程序 (184)惯导/卫星组合导航仿真 (184)子函数 (184)组合导航仿真主程序 (186)附录 (188)A一些重要的三维矢量运算关系 (188)B 运载体姿态的欧拉角描绘 (190)C 姿态更新的毕卡算法、龙格—库塔算法及准确数值解法 (197)D 从非直角坐标系到直角坐标系的矩阵变换 (205)E 线性系统根本理论 (209)F 加权最小二乘估计 (214)G 矩阵求逆引理 (215)H 几种矩阵分解方法〔QR、Cholesky与UD〕 (217)I 二阶滤波中的引理证明 (221)J 方差阵上界的证明 (223)K 三阶非奇异方阵的奇异值分解 (224)L Matlab仿真程序 (229)M 练习题 (235)参考文献 (239)第1章概述第1章概述 (6)捷联惯导算法简介 (6)1.2 Kalman滤波与组合导航原理简介 (7)1.1捷联惯导算法简介在捷联惯导系统〔SINS〕中惯性测量器件〔陀螺和加速度计〕直接与运载体固联,通过导航计算机采集惯性器件的输出信息并进展数值积分求解运载体的姿态、速度和位置等导航参数,这三组参数的求解过程即所谓的姿态更新算法、速度更新算法和位置更新算法。

摘要捷联惯性导航系统(Strapdown Inertial Navigation System,SINS)已经在军事、民用等领域得到了广泛应用。
初始对准作为整个捷联惯导系统工作前的关键步骤,其精度决定了整个导航系统的精度。
车载捷联惯导初始对准分为静基座初始对准和动基座初始对准,其技术指标主要包括对准精度和对准时间。
本课题针对车载捷联惯导系统实际工作环境中出现的惯性器件启动漂移、静基座初始对准过程中人为噪声干扰以及动基座初始对准过程中全球定位系统(Global Positioning System,GPS)速度误差和噪声失配等问题,提出相应的解决办法,具体研究内容如下:首先,针对车载捷联惯导系统初始对准情况下光纤陀螺和加速度计出现启动漂移的问题,通过采集分析光纤陀螺和加速度计在不同温度下启动的实测数据,研究了光纤陀螺和加速度计漂移与温度及温度变化率之间的关系,通过对目前光纤陀螺和加速度计漂移补偿模型进行简化,减小了计算量,实测数据验证了简化的模型能够有效补偿惯性器件启动漂移并缩短系统初始对准时间。
其次,针对车载捷联惯导系统静基座初始对准过程中人为噪声干扰的问题,通过采集车载捷联惯导静基座下人员上下车、驻车发动机启动等情况的惯性器件数据输出,分析了其噪声特性,提出了改进的基于小波阈值策略的经验模态分解降噪算法,实测数据验证了该方法的降噪效果以及对提高静基座下初始对准算法稳定性的有效性。
然后,针对动基座初始对准过程中GPS速度误差导致量测矢量误差增大的问题,提出了基于鲁棒反馈策略的惯性系初始对准算法,该方法基于前一个时刻估计的姿态预测当前时刻的量测矢量,并根据当前时刻的量测矢量求得当前时刻的方差,对前一个时刻的方差和当前时刻的方差进行比较并基于鲁棒控制的策略对当前量测矢量进行调整和反馈,仿真和实测数据验证了该方法能够有效提高动基座对准精度。
最后,针对动基座初始对准过程中噪声失配的问题,通过对姿态误差进行分析建立系统状态空间模型,并引入无偏有限冲击响应(Unbiased Finite Impulse Response,UFIR)滤波的思想,提出了基于UFIR的惯性系初始对准算法,UFIR滤波器不需要像卡尔曼滤波器(Kalman Filter,KF)一样设置Q阵和R阵,其利用观测窗长内的有限测量数据进行无偏状态估计,降低了系统噪声和量测噪声特性未知或者改变时对姿态估计的影响,仿真和实测数据验证了该方法的有效性。


捷联惯导系统姿态算法研究
柴卫华;侯芸
【期刊名称】《现代防御技术》
【年(卷),期】2001(029)004
【摘要】姿态算法是捷联惯导系统算法中的一个重要组成部分,研究了一种新的递推补偿方法并在Borland C语言环境下进行了仿真,使其更接近工程实践.
【总页数】4页(P42-45)
【作者】柴卫华;侯芸
【作者单位】中国航天机电集团公司二院二部,;中国航天机电集团公司二院二部,【正文语种】中文
【中图分类】TJ765.2+2
【相关文献】
1.捷联惯导系统姿态测量算法研究 [J], 周亢;闫建国;屈耀红
2.枪炮弹微型惯导系统捷联姿态控制算法研究 [J], 高凤;李正喜
3.捷联惯导系统初始姿态和仪表误差标定迭代算法研究 [J], 杨大烨;谢天怀;胡宝余
4.基于角速度的捷联惯导系统姿态算法研究 [J], 邓洪洁
5.一种微捷联惯导系统姿态角最优估计算法研究 [J], 刘瑞华
因版权原因,仅展示原文概要,查看原文内容请购买。
车载捷联惯性导航系统在线标定方法分析苏忠【摘要】To improve the performance of vehicular strap-down inertial navigation system,the accelerometers and gyroscopes need to be online calibrated.First the system state error model and measurement model are given and an 8-state extended kalman filter (EKF)using loosely coupled integration scheme is employed.Finally three calibration schemes are analyzed through the simulation data.The result shows that the sensors bias can be estimated effectively and ac-curacy of integrated navigation system are improved significantly with the augmented yaw angle aiding as well as varying the vehicle maneuver.%为了提高车载捷联惯导系统的定位精度,需要对加速度计和陀螺仪进行实时在线标定。
首先推导了惯性导航系统状态方程和组合导航系统量测方程,然后构建了8状态松组合扩展卡尔曼滤波模型,最后利用仿真数据验证分析了3种标定方案。
结果表明,增加航向角辅助观测值或改变载体的机动性,可以有效估计惯性传感器误差,明显改善了导航系统的精度。
【期刊名称】《金陵科技学院学报》【年(卷),期】2016(032)003【总页数】6页(P12-17)【关键词】捷联惯性导航系统;扩展卡尔曼滤波;惯性传感器;在线标定【作者】苏忠【作者单位】金陵科技学院信息化建设与管理中心,江苏南京 211169【正文语种】中文【中图分类】U666.1微机电系统(Micro-electro-mechanical system, MEMS)惯性传感器由于成本低、体积小以及灵活性强等优点,使得低成本捷联惯性导航系统(Strap-down inertial navigation system, SINS)成为未来GNSS/SINS组合导航系统的发展方向[1-4]。
第15卷第l期2007年2月中国惯性技术学报JoumalofChineseInertialTcchnologyVbl.15No.1Feb.2007
文章编号:1005-6734(2007)01一0024-04
车载捷联惯导系统定位测姿算法研究陈允芳1,叶泽田2,钟若飞3(1.山东科技大学地球信息科学与工程学院,青岛266510;2.中国测绘科学研究院,北京100039;3.首都师范大学,北京100037)
摘要:GPs/INs组合精确测定平台的位置和姿态是移动测图系统中的重要模块。对陀螺仪和加速度计所测角速度和比力进行两次积分得载体姿态、速度和位置即sINs力学机械编排。目前该过程大多在地理坐标系进行。这里详细推导了地球坐标系中完整的解算过程,以四元数姿态矩阵更新及重力计算为核心,由IMu原始观测值解算出了载体位置、速度和姿态等参数,可快速高效与GPs输出的位置速度信息进行组合滤波处理,可据此编
程进行工程应用数据处理。关键词:捷联惯导系统;姿态矩阵;坐标转换;力学编排;四元数中图分类号:u666.1文献标识码:A
PositioningandorientationcomputationonVehicle-borneSINSanddiscussofcalculationerror
cHENYun.‰91,YEze-tian2,zHONG
Ruo.fei3
(1.Geo·info衄ationScience&EngineeringCollege,ShandongUniverSi哆ofScienceaIldTbchnology,Qingdao
266510,China;2.SurveyingaTldMappingScienceResearchInStituteofChina,Beijing100039,China;3.C印ital
NomlalUniverSi劬Beijing100037,China)
Abstract:GPSandINSintegratedtoaccuratelydeteminingpositionaIldattitudeofnatI‘oofisVitalmoduleinmobile
mappingSystem.Specincforcc行omspeedometer蚰d舭glerate矗om留roareinte铲atedtwicerespectiVelyto
achievean沁de,veloc时aIldpositionn锄elySINSmechaIlization.Currentlythistookplacedingeogr印hic
coordinate,whiIeheredemonstratedindetailmewholemechaJlizationineanll-centclrcdearth-fixedcoordinate,mostlyquatemiona钍itudematrixupdating锄dgravit)rcaIculation.Ultimatelyvehiclenavigation
par锄eterssuchaSattitude,
veIocity锄dpositionwercgahed丘omIMUorigin“0bservations.Mathematicsplatfo眦isfomlcdinSrNSto
carry
outsuⅣeyingaJldcalculatingpreciselythenavigationmoVementpar锄cterS.Theresultsarcprone
tointe黟ate
witll
similarpammeters疔omGPStofilterprocessing.Pro可锄minghercbyc锄pmcessdatainengineeringapplication
Keywords:SINS;attitudematrix;coordinatetransfomation;mechanization;quatemion
随着惯性技术与卫星导航定位技术的发展,由GPS/INs不同程度组合而成的定位定姿传感器已成为移动测图系统中确定载体轨迹和平台姿态的重要工具,其中GPs多用于定位而INS则用于测姿。捷联惯导系统(sINs)是将惯性仪表直接固联在载体上而无须采用机械陀螺稳定平台,通过导航计算机中相应程序建立“数学的”陀螺稳定平台,即计算机处理测量值得到载体位置、速度和运动方向估计值以实现导航平台功能。尽管sINS于20世纪50年代即在美国获得专利,但因受限于惯性设备和计算机技术的发展而一直未能实用。近年来,电子和高速计算机技术的发展使得捷联技术得以实现和充分发展,这是惯性技术在近20年内发展的一个重要的标志。INS的核心部件是惯性测量单元(IMU),按照其陀螺仪和加速计等元件的精度,可将惯导分为不同等级:战略级(<0.000l(o)/}l,l岖)、导航级(0:000l~0.015)(o)/Il,5~100嵋)、低成本((1~10(。冲,(0.1~1)n培)。考虑到惯性设备出口管制政策及需求与成本等问题,民用INs精度范围一般为低成本级别。
收稿日期:2006—06—16;修回日期:2006—12—22基金项目:国家863基金课题(2006AAl22324);教育部三维信息获取与应用重点实验室开放基金作者简介:陈允芳(1977一),女,博士生,讲师,主要从事移动测图与组合导航。
万方数据万方数据25陈允芳等:车载捷联惯导系统定位测姿算法研究第1期1惯性导航初始对准因INs系统属航位推算系统(DR,DeadReckoning),它是依赖于前一时刻导航参数估计值的递推更新运算,故位置、
速度和姿态等初始导航参数等信息是准确进行解算的基础。惯导系统初始化包括给定初始速度和位置、惯导平台初始对准、陀螺仪测漂定标等。重点是确定INs的初始姿态矩阵,水平对准可由加速度计的量测输出获得水平方位,即俯仰角和横滚角来实现,但因低成本IMu的陀螺仪精度不足以感受地球自转角速率,无法获得航向信息,只能引入外部航向信息,如利用GPS所测速度进行匹配对准,或引入其它方位测量方法,如磁航向或双天线GPs定向系统等来获得初始航向信息。为得到较高精度初始姿态数据,本研究中水平对准由倾角仪提供横滚角和俯仰角来完成,方位对准采用vEcTOR航向测量系统实现,其2m基线方位精度可达O.10(RMS),足以满足方位对准的精度要求。由此可获取三个初始姿态角。可利用卡尔曼滤波对平台误差角进行估计出并校正系统,使载体坐标系与导航坐标系对准f51。对低成本INS,一般需要进行动基座对准”1。
2地球坐标系力学编排本研究所用IMu的陀螺仪和加速计分辨率分别为0.0006(。)/s和O.15m毋属低成本精度级别INS。它包括三个FOGs陀螺(测量角速率)和三个iMEMS加速度计(测量比力),将陀螺仪和加速度计输出信息进行捷联姿态解算,即可求得运动载体不断变化的姿态角及速度、位移增量。
2.1导航坐标系及导航方程因陀螺仪敏感的是相对于惯性空间的运动,而要测量的是载体相对于某个参照系的运动,故必须进行坐标变换。此外,加速度计所测加速度输出信号中往往包含重力加速度分量和有害加速度分量,必须对重力加速度分量进行修正,对有害加速度分量进行补偿,然后经过积分运算得到运载体的速度和所在的地理位置。惯性导航的基础是精确定义的一系列右手参考坐标系,较常用的是惯性坐标系(j系)、地球坐标系(e系)、地理坐标系(n系)、载体坐标系(b系)及计算坐标系(k系)等,详细定义参见文献【3】。如图1所示,其中e和n系都三轴定义为东北天方向,b系三轴定义为右前天方向。下面重点考虑k系的合理选取问题。工程应用中,常选取e、n坐标系中的任一系作为k。若选取n系,计算时可直接输出地理坐标(五,仍办)和运行姿态,且重力计算模型简单,但因n系本身随载体运动而旋转,需要附加大量计算工作来补偿由此产生的影响,且须不断进行e系和n系间的坐标转换,即将n系的INS导航结果转换到e系中,或将e系中的GPS定位测速结果转换到n系中,此频繁转换势必影响计算精度;在e系计算时,e系本身不随载体运动变化,计算过程及公式简单,可直接获
三鼓二豫妄孕地理坐标系图l各坐标系示意图F培1CoordinatesSketchMap
得载体在地心直角坐标系(如wGS84)中的三维直角坐标(置y,z),直接用于修正INs,适合与GPs数据进行组合处理,且省去了反复的坐标变换,程序更简洁和模块化,导航计算精度也较n系稍优,但正常重力计算模型和姿态角的提取计算较复杂。考虑到要用GPs,INS进行组合导航,而GPS定位是在e系进行,故本文选e系作为计算坐标系【1】【31。导航方程可从任何坐标系导出,不同坐标系导航方程会有不同形式。选e系后,根据牛顿第二定律和科里奥里定律,载体相对于b系的速度变化可由惯性轴系的速度变化来表示,载体相对于地球的加速度由三部分加速度组成哺1:壬Kl。=茂,t《×y。+g。Ⅲ
,6为加速度计所得比力加速度,∞:×y。为科里奥里加速度,g。是e系表示的正常重力。因GPs观测量、引力常量都是e系的值,由上式可推得e系表示的SINS导航方程“¨”:『,。¨y。]
.Y‘=l矿。}=l群,。一2球y。+窖。II农lⅨ(蹴一球)
其中,,。=《厂6即转化至e系后的比力值。上述方程又称为INS力学(或机械)编排,它描述了待求导航信息与各观测量间的数学关系,其中比力和角速度是动态系统输入的观测值,位置、速度及姿态信息是状态变量。注意,上标(如b)表示向量各分量所对应的坐标系,下标ib则代表b系相对于i系的旋转,
万方数据万方数据