第2章平面力系
- 格式:pdf
- 大小:758.60 KB
- 文档页数:5



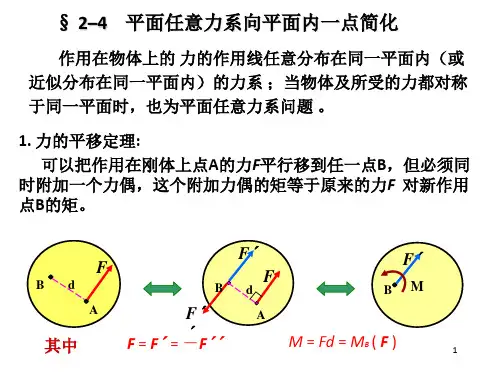

平面力系——各力作用线都在同一平面内的力系。
空间力系——各力作用线不在同一平面内的力系。
汇交力系——作用线交于一点的力系。
平行力系——作用线相互平行的力系。
一般力系——作用线既不完全交于一点又不完全平行的力系。
2.1 平面汇交力系平面汇交力系的工程实例:2.1.1 力的分解按照平行四边形法则,两个共作用点的力,可以合成为一个合力,解是唯一的;但反过来,要将一个已知力分解为两个力,如无足够的条件限制,其解将是不定的。
2.1.2 力在坐标轴上的投影注意:力的投影是代数量,它的正负规定如下:如由a到b的趋向与x轴(或y轴)的正向一致时,则力F的投影Fx(或Fy)取正值;反之,取负值。
2.1.3合力投影定理合力投影定理——合力在某一轴上的投影等于各分力在同一轴上投影的代数和。
2.1.4 平面汇交力系的平衡条件平面汇交力系可以合成为一个合力,即平面汇交力系可用其合力来代替。
显然,如果合力等于零,则物体在平面汇交力系的作用下处于平衡状态。
平面汇交力系平衡的必要和充分条件是该力系的合力F等于零。
即即力系中所有各力在两个坐标轴中每一轴上投影的代数和都等于零。
这是两个独立的方程,可以求解两个未知量。
例2-1 如图所示为一吊环受到三条钢丝绳的拉力作用。
已知F1=2000N,水平向左;F2=5000N,与水平成30度角;F3=3000N,铅直向下,试求合力大小。
(仅是求合力大小)例2-2 图示为一简易起重机装置,重量G=2kN的重物吊在钢丝绳的一端,钢丝绳的另一端跨过定滑轮A,绕在绞车D的鼓轮上,定滑轮用直杆AB和AC支承,定滑轮半径较小,大小可忽略不计,定滑轮、直杆以及钢丝绳的重量不计,各处接触都为光滑。
试求当重物被匀速提升时,杆AB、AC所受的力。
解因为杆AB、AC都与滑轮接触,所以杆AB、AC上所受的力就可以通过其对滑轮的受力分析求出。
因此,取滑轮为研究对象,作出它的受力图并以其中心为原点建立直角坐标系。
由平面汇交力系平衡条件列平衡方程有解静力学平衡问题的一般方法和步骤:1.选择研究对象所选研究对象应与已知力(或已求出的力)、未知力有直接关系,这样才能应用平衡条件由已知条件求未知力;2.画受力图根据研究对象所受外部载荷、约束及其性质,对研究对象进行受力分析并得出它的受力图。





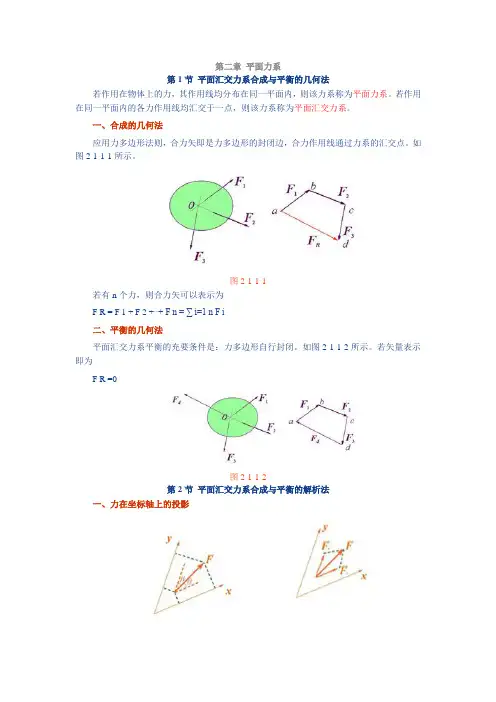
第二章平面力系第1节平面汇交力系合成与平衡的几何法若作用在物体上的力,其作用线均分布在同一平面内,则该力系称为平面力系。
若作用在同一平面内的各力作用线均汇交于一点,则该力系称为平面汇交力系。
一、合成的几何法应用力多边形法则,合力矢即是力多边形的封闭边,合力作用线通过力系的汇交点。
如图2-1-1-1所示。
图2-1-1-1若有n个力,则合力矢可以表示为F R = F 1 + F 2 +⋯+ F n = ∑ i=1 n F i二、平衡的几何法平面汇交力系平衡的充要条件是:力多边形自行封闭。
如图2-1-1-2所示。
若矢量表示即为F R =0图2-1-1-2第2节平面汇交力系合成与平衡的解析法一、力在坐标轴上的投影力在坐标轴上的投影等于力的模乘以力与投影轴正向间夹角的余弦,如图2-2-1-1所示,它是一标量,即F x =Fcosθ; F y =Fcosβ力沿坐标轴的分力是一矢量,其合力与分力之间应满足力的平行四边形法则。
如图2-2-1-2所示。
当坐标轴为直角坐标轴时,力沿坐标轴分解的分力可以表示为F x = F x i; F y = F y i合力投影定理:合力在某轴上的投影等于各分力在同一轴上投影的代数和,即F x = ∑ i=1 n F xi ; F y = ∑ i=1 n F yi当投影轴x与y垂直时,其合力的大小与方向为F R = F x 2 + F y 2 , cos( F R ,i)= F x F R ; cos( F R ,j)= F y F R二、合成的解析法当为直角坐标轴时,可按以下方法来合成F R = F x 2 + F y 2 = ( ∑ F xi ) 2 + ( ∑ F yi ) 2cos( F R ,i)= F x F R = ∑ F xi F R ; cos( F R ,j)= F y F R = ∑ F yi F R三、平衡的解析法力系中各力在两个坐标轴上投影的代数和分别等于零,即∑ F x =0; ∑ F y =0上式称为平面汇交力系的平衡方程。