2010年部分省市中考数学试题分类汇编(共28专题)17.四边形(平行四边形,矩形,菱形,正方形)

10．(2010贵阳市)如图3是小华画的正方形风筝图案，他以图中的对角线AB为对称轴，在对角线的下方再画一个三角形，使得新的风筝图案成为轴对称图形，若下列有一图形为此对称图形，则此图为( )C
（图3）（A）（B）（C）（D）
（2010龙岩市）在平面直角坐标系中，△AOB的位置如图所示．（1）若
△A1OB1是△AOB
关于原点O的中心对称图形，则顶点A1的坐标为( ， )；
（2）在网格上画出△AOB关于y轴对称的图形；
（3）在网格上画出将△AOB三个顶点的横、纵坐标均扩大为原来的2倍后的图形，并求出
变换后图形的周长等于______；若把△AOB顶点的横、纵坐标均扩大为原来的n 倍，试猜想变换后图形的周长等于______．
答案：（1） A1(-3，-4 )
（2）正确画出图形
（3）正确画出图形
（2010福州）下面四个中文艺术字中，不是．．。

2010年部分省市中考数学试题分类汇编操作探究(2010年安徽省B 卷)10．在二行三列的方格棋盘上沿骰子的某条棱翻动骰子（相对面上分别标有1点和6点，2点和5点，3点和4点），在每一种翻动方式中，骰子不能后退．开始时骰子如图（1）那样摆放，朝上的点数是2；最后翻动到如图（2）所示的位置，此时骰子朝上的点数不可能．．．是下列数中的（ ）A ．5【关键词】图形的变换 【答案】D ．23（2010年浙江省东阳县）如图，在一块正方形ABCD 木板上要贴三种不同的墙纸，正方形EFCG 部分贴A 型墙纸，△ABE 部分贴B 型墙纸，其余部分贴C 型墙纸。

A 型、B 型、C 型三种墙纸的单价分别为每平方60元、80元、40元。

探究1：如果木板边长为2米，FC ＝1米，则一块木板用墙纸的费用需 元； 探究2：如果木板边长为1米，求一块木板需用墙纸的最省费用； 探究3：设木板的边长为a （a 为整数），当正方形 EFCG 的边长为多少时？墙纸费用最省；如要用这 样的多块木板贴一堵墙（7×3平方米）进行装饰， 要求每块木板A 型的墙纸不超过1平方米，且尽量 不浪费材料，则需要这样的木板 块。

【关键词】操作探究 【答案】（1）220 （2）y=20x 2—20x+60 当x=21时，y 小=55元。

（3）y=20x 2—20ax+60a 2当x=21a 时，21块23．（2010年山东省青岛市）问题再现现实生活中，镶嵌图案在地面、墙面乃至于服装面料设计中随处可见．在八年级课题学习“平面图形的镶嵌”中，对于单种多边形的镶嵌，主要研究了三角形、四边形、正六边形的镶嵌问题．今天我们把正多边形．．．．的镶嵌作为研究问题的切入点，提出其中几个问题，共同来探究.我们知道，可以单独用正三角形、正方形或正六边形镶嵌平面．如右图中，用正方形镶嵌平面，可以发现在一个顶点O 周围围绕着4个正方形的内角. 试想：如果用正六边形来镶嵌平面，在一个顶点周围应该围绕着 个 正六边形的内角．问题提出如果我们要同时用两种不同的正多边形镶嵌平面，可能设计出几种不同的组合方案？ 问题解决猜想1：是否可以同时用正方形、正八边形两种正多边形组合进行平面镶嵌？分析：我们可以将此问题转化为数学问题来解决．从平面图形的镶嵌中可以发现，解决问题的关键在于分析能同时用于完整镶嵌平面的两种正多边形的内角特点．具体地说，就是在镶嵌平面时，一个顶点周围围绕的各个正多边形的内角恰好拼成一个周角．验证1：在镶嵌平面时，设围绕某一点有x 个正方形和y 个正八边形的内角可以拼成一个周角．根据题意，可得方程：()82180903608x y -⨯+= ，整理得：238x y +=，我们可以找到惟一一组适合方程的正整数解为12x y =⎧⎨=⎩ ．结论1：镶嵌平面时，在一个顶点周围围绕着1个正方形和2个正八边形的内角可以拼成一个周角，所以同时用正方形和正八边形两种正多边形组合可以进行平面镶嵌．猜想2：是否可以同时用正三角形和正六边形两种正多边形组合进行平面镶嵌？若能，请按照上述方法进行验证，并写出所有可能的方案；若不能，请说明理由．验证2：结论2： ． 上面，我们探究了同时用两种不同的正多边形组合镶嵌平面的部分情况，仅仅得到了一部分组合方案，相信同学们用同样的方法，一定会找到其它可能的组合方案．问题拓广O请你仿照上面的研究方式，探索出一个同时用三种不同的正多边形组合进行平面镶嵌的方案，并写出验证过程．猜想3：.验证3：结论3：.【关键词】【答案】解：3个；················ 1分验证2：在镶嵌平面时，设围绕某一点有a个正三角形和b个正六边形的内角可以拼成一个周角．根据题意，可得方程：60120360a b+=．整理得：26a b+=，可以找到两组适合方程的正整数解为22ab=⎧⎨=⎩和41ab=⎧⎨=⎩．························· 3分结论2：镶嵌平面时，在一个顶点周围围绕着2个正三角形和2个正六边形的内角或者围绕着4个正三角形和1个正六边形的内角可以拼成一个周角，所以同时用正三角形和正六边形两种正多边形组合可以进行平面镶嵌．5分猜想3：是否可以同时用正三角形、正方形和正六边形三种正多边形组合进行平面镶嵌？······························ 6分验证3：在镶嵌平面时，设围绕某一点有m个正三角形、n个正方形和c个正六边形的内角可以拼成一个周角. 根据题意，可得方程：6090120360m n c++=，整理得：23412m n c++=，可以找到惟一一组适合方程的正整数解为121mnc=⎧⎪=⎨⎪=⎩. ······························ 8分结论3：镶嵌平面时，在一个顶点周围围绕着1个正三角形、2个正方形和1个正六边形的内角可以拼成一个周角，所以同时用正三角形、正方形和正六边形三种正多边形组合可以进行平面镶嵌. （说明：本题答案不惟一，符合要求即可.）1.（2010年福建省晋江市）如图，将一张正方形纸片剪成四个小正方形，得到4个小正方形，称为第一次操作；然后，将其中的一个正方形再剪成四个小正方形，共得到7个小正方形，称为第二次操作；再将其中的一个正方形再剪成四个小正方形，共得到10个小正方形，称为第三次操作；...，根据以上操作，若要得到2011个小正方形，则需要操作的次数是( ) .A. 669B. 670C.671D. 672【关键词】正方形、实验操作、规律探索答案：B；22．(2010年北京崇文区) 正方形A B C D 的边长为a ，等腰直角三角形F A E 的斜边A E b = （a b 2<），且边A D 和A E 在同一直线上 ．小明发现：当b a =时，如图①，在B A 上选取中点G ，连结F G 和C G ,裁掉F A G ∆和C H D ∆的位置构成正方形F G C H ． （1）类比小明的剪拼方法，请你就图②和图③两种情形分别画出剪拼成一个新正方形的示意图．（2）要使（1）中所剪拼的新图形是正方形，须满足=AEBG ．【关键词】正方形的剪拼、 【答案】（1）（2）21．(2010年浙江省绍兴市)分别按下列要求解答：（1）在图1中,将△ABC 先向左平移5个单位,再作关于直线AB 的轴对称图形,经两次变换后得到△A 1B 1 C 1.画出△A 1B 1C 1； （2）在图2中,△ABC 经变换得到△A 2B 2C 2.描述变换过程.1211 10 9 8 76 5 4 32 AC2B 2 12 11 10 9 8 7 6 5 4 3 2 C【答案】(1) 如图．(2) 将△ABC先关于点A作中心对称图形,再向左平移2个单位,得到△A2B2C2．（变换过程不唯一）2.（2010年宁德市）如图所示，如果将矩形纸沿虚线①对折后，沿虚线②剪开，剪出一个直角三角形，展开后得到一个等腰三角形.则展开后三角形的周长是（）.A．2＋10B．2＋210C．12 D．18【答案】B27．（2010江苏泰州，27，12分）如图，二次函数cxy+-=221的图象经过点D⎪⎭⎫⎝⎛-29,3，与x轴交于A、B两点．⑴求c的值；⑵如图①，设点C为该二次函数的图象在x轴上方的一点，直线AC将四边形ABCD的面积二等分，试证明线段BD被直线AC平分，并求此时直线AC的函数解析式；⑶设点P、Q为该二次函数的图象在x轴上方的两个动点，试猜想：是否存在这样的点P、Q，使△AQP≌△ABP？如果存在，请举例验证你的猜想；如果不存在，请说明理由．（图②供选用）第18题图1 第18题图2第18题图②4【答案】⑴ ∵抛物线经过点D (29,3-)∴29)3(212=+-⨯-c∴c=6.⑵过点D 、B 点分别作AC 的垂线，垂足分别为E 、F ，设AC 与BD 交点为M ， ∵AC 将四边形ABCD 的面积二等分，即：S △ABC =S △ADC ∴DE =BF 又∵∠DME =∠BMF ， ∠DEM =∠BFE ∴△DEM ≌△BFM∴DM =BM 即AC 平分BD ∵c =6. ∵抛物线为6212+-=x y∴A （0,32-）、B （0,32）∵M 是BD 的中点 ∴M （49,23） 设AC 的解析式为y =kx +b ，经过A 、M 点∴⎪⎩⎪⎨⎧=+=+-4923032b k b k 解得⎪⎪⎩⎪⎪⎨⎧==591033b k ∴直线AC 的解析式为591033+=x y.⑶存在．设抛物线顶点为N (0，6)，在Rt △AQN 中，易得AN=，于是以A 点为圆心，AB =为半径作圆与抛物线在x 上方一定有交点Q ，连接AQ ，再作∠QAB 平分线AP 交抛物线于P ，连接BP 、PQ ，此时由“边角边”易得△AQP ≌△ABP ．【关键词】二次函数、一次函数、解直角三角形及其知识的综合运。

G FE DCBAFDBAED CBA 2010年中考数学第一轮复习专题训练 多边形及四边形一、填空题：1．五边形的内角和为 ；2．在平行四边形ABCD 中，∠A ＋∠C ＝200°，则∠A ＝ ； 3．矩形的两边长分别是3cm 和4cm ，则对角线长 cm ； 4．等腰梯形的中位线长为 6，腰长为 5，则周长为 ；5．如果矩形一条较短的边是 5，两条对角线的夹角是 60°，则对角线长是 ； 6．菱形两条对角线的长分别是 12 和 16，则它的边长为 ； 7．如图1，正方形的周长为 8cm ，则矩形EFBG 的周长为 ；图1 图2 图3 8．两条对角线 的四边形是正方形；9．等腰梯形的锐角等于60°，它的两底分别为 15cm ，19cm ，则它的腰长为 ； 10．顺次连续四边形ABCD 各边的中点，组成 形；11．如图2，一张矩形的纸片，要折出一个正方形，只要把一个角沿折痕AF 翻折上去，使AB 和AD 边上的AE 重合，则四边形ABFE 就是一个正方形，判断的根据是 ；12．如图3，请写出等腰梯形ABCD （AB ∥CD ）特有而一般梯形不具有的二个特征： ； 二、选择题：13．下列多边形中，不能铺满地面的是 （ ） A 、正三角形 A 、正方形 C 、正五边形 D 、正六边形14．一个多边形的内角和等于外角和的 2 倍，则它的边数是 （ ） A 、5 B 、6 C 、7 D 、815．四个内角都相等的四边形是 （ ） A 、矩形 B 、菱形 C 、正方形 D 、平行四边形 16．符合下列条件的四边形不一定是菱形的是 （ ）DFD C BA A 、四边都相等B 、两组邻边分别相等C 、对角线互相垂直平分D 、两条对角线分别平分一组对角17．已知：梯形ABCD 中，AD ∥BC ，AB ＝AD ＝CD ，BD ⊥CD ，则∠C ＝ （ ）A 、30° A 、45° C 、60° D 、75°18．如图，延长正方形ABCD 的一边BC 至E ，使CE ＝AC ，连结AE 交CD 于F ，则∠AFC 的度数是 （ ） A 、112.5° B 、120° C 、122.5° D 、135°19．下列说法中，错误的是 （ ） A 、一组对边平行且相等的四边形是平行四边形；B 、四个角都相等的四边形是矩形 C 、两条对角线互相垂直且平分的四边形是菱形；D 、邻边相等菱形是正方形20．E 、F 、G 、H 分别是四边形ABCD 四条边的中点，要使四边形EFGH 为矩形，四边形 ABCD 应具备的条件是 （ ） A 、对角线相等 B 、一组对边平行而另一组对边不平行 C 、对角线互相垂直 D 、对角线互相平分21．小强拿了一张正方形的纸如图（1），沿虚线对折一次得图（2），再对折一次得图（3），然后用剪刀沿图（3）中的虚线（虚线与底边平行）剪去一个角，再打开后的形状应是 （ ）22．不能判定四边形ABCD 为平行四边形的题设是 （ ） A 、AB ∥CD 且AB=CD B 、AB=CD ，AD=BC C 、AB ∥CD 且AB=BC D 、AB//CD ，BC//CD23．一张矩形纸片纸对折（如图），然后沿着图中的虚线剪下，得到①、②两部分，将①展开后得到的平面图形是 （ ） A 、三角形 B 、矩形 C 、菱形 D 、梯形24．过矩形ABCD 的四个顶点作对角线AC 、BD 的平行线，分别相交于E 、F 、G 、H 四点，则四边形EFGH 为 （ ） A 、平行四边形 B 、矩形 C 、菱形 D 、正方形 25．如图，在菱形ABCD 中，∠BAD ＝80°，AB 的垂直平分线交DCBA EFDCBA EDCBA对角线AC 于点F ，E 为垂足，连结DF ，则∠CDF 等于 （ ）A 、80°B 、70°C 、65°D 、60°26．顺次连结等腰梯形四边中点得到一个四边形，再顺次连结所得四边形四边的中点得到的图形是 （ ） A 、等腰梯形 B 、直角梯形 C 、菱形 D 、矩形 三、解答题：27．已知五边形ABCD 中，AE ∥CD ，∠A ＝100°，∠B ＝120°，求∠C 的度数；28．在平行四边形ABCD 中，E 、F 分别是AB 、CD 上的点，且AE ＝CF ，求证：BF ∥DE ；29．已知：梯形ABCD 中，AD ∥BC ，BD 平分∠ABC ，求证：AB ＝AD ；30．菱形ABCD 的对角线交于O 点，DE ∥AC ，CE ∥BD 。

2010中考数学分类汇编 一、选择题1．(2010江苏苏州)如图，在平行四边形ABCD 中，E 是AD 边上的中点．若∠ABE=∠EBC ，AB=2，则平行四边形ABCD 的周长是 ▲ ． 【答案】122．（2010台湾）图(十)为一个平行四边形ABCD ，其中H 、G 两点分别在BC 、 CD 上，AH ?BC ，AG ?CD ，且AH 、AC 、AG 将?BAD 分成 ?1、?2、?3、?4四个角。

若AH =5，AG =6，则下列关系何者 正确？ (A) ?1=?2 (B) ?3=?4 (C) BH =GD (D) HC =CG 。

【答案】A3．（2010重庆綦江县）如图，在ABCD Y中，分别以AB 、AD 为边向外作等边△ABE 、△ADF ，延长CB 交AE 于点G ，点G 在点A 、E 之间，连结CG 、CF ，则以下四个结论一定正确的是（ ）①△CDF ≌△EBC ②∠CDF ＝∠EAF ③△ECF 是等边三角形 ④CG ⊥AE A ．只有①② B ．只有①②③ C ．只有③④ D ．①②③④【答案】B4．（2010山东临沂）如图，在ABCD Y 中，AC 与BD 相交于点O ，点E 是边BC 的中点，4AB =，则OE 的长是（A ）2 （B（C ）1 （D ）12【答案】A5．（2010湖南衡阳）如图，在□ABCD 中，AB=6，AD=9，∠BAD 的平分线交BC 于点E ，EODCBAA BCD G H12 3 4图(十)交DC 的延长线于点F ，BG ⊥AE ，垂足为G ，BG=24，则ΔCEF 的周长为（ ） B.9.5 C.10 【答案】A6．（2010 河北）如图2，在□ABCD 中，AC 平分∠DAB ，AB?=?3，则□ABCD 的周长为A ．6B ．9C ．12D ．15【答案】C7．（2010浙江湖州）如图在ABCD 中，AD ＝3cm ，AB ＝2cm ，则ABCD 的周长等于（ ）A ．10cmB ．6cmC ．5cmD ．4cm【答案】A ．8．（2010 四川成都）已知四边形ABCD ，有以下四个条件：①//AB CD ；②AB CD =；③//BC AD ；④BC AD =．从这四个条件中任选两个，能使四边形ABCD 成为平行四边形的选法种数共有（ ）（A ）6种 （B ）5种 （C ）4种 （D ）3种 【答案】C9．（2010山东泰安）如图，E 是□ABCD 的边AD 的中点，CE 与BA 的延长线交于点F ，若∠FCD=∠D ，则下列结论不成立的是（ ）A 、AD=CFB 、BF=CFC 、AF=CD D 、DE=EF 【答案】C10．（2010 内蒙古包头）已知下列命题： ①若00a b >>，，则0a b +>；②若a b ≠，则22a b ≠；③角的平分线上的点到角的两边的距离相等； ④平行四边形的对角线互相平分．其中原命题与逆命题均为真命题的个数是（ ）AD CB AB CD图2A ．1个B ．2个C ．3个D ．4个【答案】B11．（2010 重庆江津）如图，四边形ABCD 的对角线互相平分，要使它成为矩形， 那么需要添加的条件是（ ） A ．AB CD = B ．AD BC = C ．AB BC = D ．AC BD =【答案】D12．（2010宁夏回族自治区）点A 、B 、C 是平面内不在同一条直线上的三点，点D 是平面内任意一点，若A 、B 、C 、D 四点恰能构成一个平行四边形，则在平面内符合这样条件的点D 有 （ ）A ．1个B ．2个C ．3个D ．4个 【答案】C13．（2010鄂尔多斯）如图，在□ABCD 中，E 是BC 的中点，且∠AEC=∠DCE ，则下列结论不．正确．．的是 △ADF=2S △EBF =21DF C .四边形AECD 是等腰梯形 D . ∠AEC=∠ADC 【答案】A14．（2010广东清远）如图2，在Y ABCD 中，已知∠ODA ＝90°，AC ＝10cm ，BD ＝6cm ，则AD 的长为( ) A ．4cmB ．5cmC ．6cmD ．8cm【答案】A 二、填空题1．（2010福建福州）如图，在Y ABCD 中，对角线AC 、BD 相交于点O ，若AC ＝14，BD ＝8，AB ＝10，则△OAB 的周长为_______． (第14题)【答案】212．（2010福建宁德）如图，在□ABCD 中，AE ＝EB ，AF ＝2，则FC 等于_____．【答案】4第16题图FA E BCD3．（2010 山东滨州）如图,平行四边形ABCD 中, ∠ABC=60°,E 、F 分别在CD 、BC 的延长线上,AE ∥BD,EF ⊥BC,DF=2,则EF 的长为 .【答案】234．（2010山东潍坊）如图，在△ABC 中，AB ＝BC ，AB ＝12cm ，F 是AB 边上的一点，过点F 作FE ∥BC 交CA 于点E ，过点E 作ED ∥AB 交于BC 于点D ，则四边形BDEF 的周长是 ． 【答案】24cm5．（2010湖南常德）如图2，四边形ABCD 中，AB 填一个即可）.【答案】AB CD A C AD =∠=∠或或∥BC 等6．（2010湖南郴州）如图，已知平行四边形ABCD ，E 是AB 延长线上一点，连结DE 交BC 于点F ，在不添加任何辅助线的情况下，请补充一个条件，使CDF BEF △≌△，这个条件是．（只要填一个）【答案】DC EB =或CF BF =或DF EF = 或F 为DE 的中点或F 为BC 的中点或AB BE =或B 为AE 的中点7．（2010湖北荆州）如图，在平行四边形ABCD 中，∠A=130°，在AD 上取DE=DC ， 则∠ECB 的度数是 . 【答案】65°8．（2010湖北恩施自治州）如图，在ABCD 中，已知AB =9㎝，AD =6㎝，BE 平分∠ABC 交DC 边于点E ，则DE 等 于 ㎝. 【答案】39．（2010云南红河哈尼族彝族自治州） 如图4，在图（1）中，A 1、B 1、C 1分别是△ABC的边BC 、CA 、AB 的中点，在图（2）中，A 2、B 2、C 2分别是△A 1B 1C 1的边B 1C 1、C 1 A 1、 A 1B 1的中点，…，按此规律，则第n 个图形中平行四边形的个数共有 个.ABEFDC第13题DBCA图2【答案】3n10．（2010 江苏镇江）如图，在平行四边形ABCD 中，CD=10，F 是AB 边上一点，DF 交AC 于点E ，且的面积的面积则CDE AEF EC AE ∆∆=,52= ，BF= . 【答案】6,254 11．（2010 广西钦州市）如图，□ABCD 的对角线AC 、BD 相交于点O ，点E 是CD 的中点， 若AD ＝4cm ，则OE 的长为 ▲ cm ．【答案】212．（2010青海西宁）如图1，在□ABCD 中，对角线AC 、BD 相交于点O ，如果AC=14，BD=8，AB=x ，那么x 的取值范围是 .图1 【答案】3﹤x ﹤11.13．（2010广西梧州）如图2，在□ABCD 中，E 是对角线BD 上的点，且E F ∥AB ，DE ：EB =2：3，E F =4，则CD =的长为________【答案】1014．（2010广东深圳）如图3，在□ABCD 中，AB=5，AD=8，DE 平分∠ADC ，则BE=【答案】3图2ABCD F ED第5题ECBAO(3)(2)(1)C 3B 3A 3A 2C 1B 11CBAC 2B 2B 2C 2ABC1B 1C 1A 2C 1B 11CBA…图415．（2010辽宁本溪）过□ABCD 对角线交点O 作直线m ，分别交直线AB 于点E ，交直线CD 于点F ，若AB =4，AE =6，则DF 的长是 . 【答案】2或1016．（2010广西河池）如图1，在□ABCD 中，∠A ＝120°，则∠D ＝ °．【答案】60 三、解答题1． （2010浙江嘉兴）如图，在□ABCD 中，已知点E 在AB 上，点F 在CD 上，且CF AE =． （1）求证：BF DE =；（2）连结BD ，并写出图中所有的全等三角形．（不要求证明）【答案】（1）在□ABCD中，AB BFDE =ABCD AD BC CDAB =C A ∠=∠︒=∠+∠180C B ABCD ABCD 已知：在四边形ABCD 中，①AD ∥BC ，③C A ∠=∠.ABCD图1ABDCEF（第19题）ABDCEF （第19题）ABC求证：四边形ABCD 是平行四边形． 证明：∵ AD ∥BC∴︒=∠+∠180B A ，︒=∠+∠180D C ∵C A ∠=∠，∴D B ∠=∠ ∴四边形ABCD 是平行四边形4．（2010江苏宿迁）（本题满分8分）如图，在□ABCD 中，点E 、F 是对角线AC 上两点，且AE =CF ．求证：∠EBF =∠FDE ．【答案】证明：连接BD 交AC 于O 点∵四边形ABCD 是平行四边形 ∴OA=OC ，OB=OD 又∵AE=CF ∴OE=OF∴四边形BEDF 是平行四边形∴∠EBF=∠EDF 5．（2010 浙江衢州）(本题6分)已知：如图，E ，F 分别是Y ABCD 的边AD ，BC 的中点．求证：AF =CE ．【答案】证明：方法1：∵ 四边形ABCD 是平行四边形，且E ，F 分别是AD ，BC 的中点，∴ AE = CF ．又 ∵ 四边形ABCD 是平行四边形，∴ AD ∥BC ，即AE ∥CF ． ∴ 四边形AFCE 是平行四边形． ∴ AF =CE ．方法2：∵ 四边形ABCD 是平行四边形，且E ，F 分别是AD ，BC 的中点， ∴ BF =DE ．又 ∵ 四边形ABCD 是平行四边形， ∴ ∠B =∠D ，AB =CD ． ∴ △ABF ≌△CDE ．ADEFBC ADEF BC(第19题)∴ AF =CE ．6．（2010年贵州毕节）如图，已知：平行四边形 ABCD 中，BCD ∠的平分线CE 交边AD 于E ，ABC ∠的平分线BG 交CE 于F ，交AD 于G ．求证：AE DG =．【答案】证明：∵ 四边形ABCD 是平行四边形（已知），AD BC ∴∥，AB CD =（平行四边形的对边平行，对边相等）GBC BGA∴∠=∠，BCE CED ∠=∠（两直线平行，内错角相等） 又∵ BG 平分ABC ∠，CE 平分BCD ∠（已知） ABG GBC ∴∠=∠，BCE ECD ∠=∠（角平分线定义）ABG GBA ∴∠=∠，ECD CED ∠=∠．AB AG ∴=，CE DE =（在同一个三角形中，等角对等边）AG EG DE EG ∴-=-，即AE DG =．7．（2010 湖南株洲）（本题满分6分）如图，已知平行四边形ABCD ，DE 是ADC ∠的角平分线，交BC 于点E ． （1）求证：CD CE =；（2）若BE CE =，80B ∠=︒，求DAE ∠的度数．【答案】（1）如图，在ABCD Y 中，//AD BC 得，13∠=∠又12∠=∠，∴23∠=∠，∴CD CE = （2）由ABCD Y 得，AB CD = 又CD CE =，BE CE = ∴AB BE = ∴BAE BEA ∠=∠ ∵80B ∠=︒，∴50BAE ∠=︒， 得：180508050DAE ∠=︒-︒-︒=︒．8．（2010广东中山）如图，分别以Rt ΔABC 的直角边AC 及斜边AB 向外作等边ΔACD 、等边ΔABE ．已知∠BAC=030，EF ⊥AB ，垂足为F ，连结DF ． （1）试说明AC=EF ；（2）求证：四边形ADFE 是平行四边形． 【答案】（1）解：在Rt ΔABC ，∠BAC=030， ∴∠ABC=060等边ΔABE 中，∠ABE=060，且AB=BE ∵EF ⊥AB∴∠EFB=090∴Rt ΔABC ≌Rt ΔEBF ∴AC=EFA B CE FG 1 23EDCBA（2）证明：等边ΔACD 中，∠DAC=060，AD=AC 又∵∠BAC=030 ∴∠DAF=090 ∴AD ∥EF 又∵AC=EF ∴AD=EF∴四边形ADFE 是平行四边形．9．（2010湖南郴州）已知：如图，把ABC V 绕边BC 的中点O 旋转180°得到DCB V .求证：四边形ABDC 是平行四边形.【答案】 .证明：因为 DCB V 是由ABC V 旋转180︒所得所以点A 、D ，B 、C 关于点O 中心对称 所以OB =OC OA =OD 所以四边形ABCD 是平行四边形（注：还可以利用旋转变换得到AB =CD ，AC =BD 相等；或证明ABC DCB ≅V V 证ABCD 是平行四边形）10．2010湖南怀化） 如图7，平行四边形ABCD 的对角线相交于点O ，直线EF 经过点O,分别与AB,CD 的延长线交于点E,F. 求证：四边形AECF 是平行四边形.【答案】证明：∵四边形ABCD 是平行四边形，∴OD=OB,OA=OC∴∠DFO=∠BEO, ∠FDO=∠EBO ∴△FDO ≌△EBO ∴OF=OE∴四边形AECF 是平行四边形图7OCBD第23题11．（2010湖北省咸宁）问题背景（1）如图1，△ABC 中，DE ∥BC 分别交AB ，AC 于D ，E 两点， 过点E 作EF ∥AB 交BC 于点F ．请按图示数据填空：四边形DBFE 的面积S = ， △EFC 的面积1S = ，△ADE 的面积2S = ．探究发现（2）在（1）中，若BF a =，FC b =，DE 与BC 间的距离为h ．请证明2124S S S =． 拓展迁移（3）如图2，□DEFG 的四个顶点在△ABC 的三边上，若 △ADG 、△DBE 、△GFC 的面积分别为2、5、3，试利用．．（2．） 中的结论．．．．求△ABC 的面积．【答案】（1）6S =，19S =，21S =．（2）证明：∵DE ∥BC ，EF ∥AB ，∴四边形DBFE 为平行四边形，AED C ∠=∠，A CEF ∠=∠． ∴△ADE ∽△EFC ． ∴22221()S DE a S FC b==． ∵112S bh =， ∴222122a a h S S b b =⨯=．∴2212144()22a hS S bh ah b=⨯⨯=．而S ah =， ∴2124S S S =（3）解：过点G 作GH ∥AB 交BC 于H ，则四边形DBHG 为平行四边形． ∴GHC B ∠=∠，BD HG =，DG BH =．BCDGFE 图2A图1BCDGFE 图2A H∵四边形DEFG 为平行四边形， ∴DG EF =． ∴BH EF =． ∴BE HF =． ∴△DBE ≌△GHF ． ∴△GHC 的面积为538+=．由（2）得，□DBHG 的面积为2288⨯=． ∴△ABC 的面积为28818++=．12．（2010湖北恩施自治州）如图，已知，在ABCD 中，AE=CF ，M 、N 分别是DE 、BF 的中点.求证：四边形MFNE 是平行四边形 .【答案】证明：由平行四边形可知，AB=CD ，∠BAE=∠DFC ，∴BE=DF ，∠AEB=∠CDF 又∵M 、N 分别是BE 、DF 的中点，∴ME=NF 又由AD ∥BC ，得∠ADF=∠DFC ∴∠ADF=∠BEA ∴ME ∥NF∴四边形MFNE 为平行四边形。

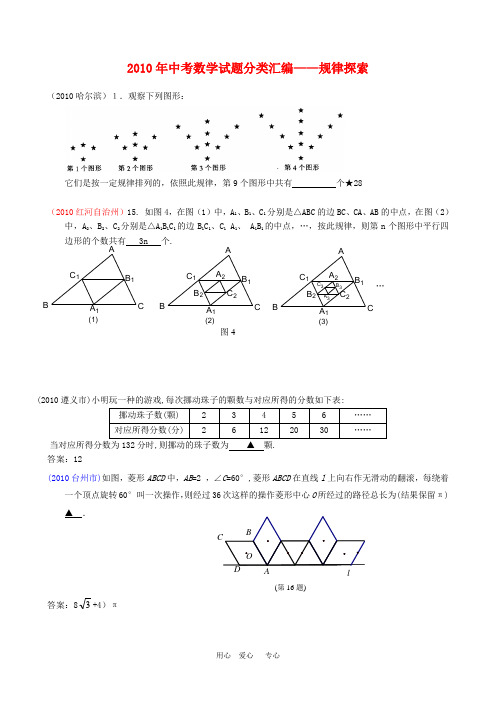
(3)(2)(1)C 3B 3A 3A 2C 1B 1A 1CBAC 2B 2B 2C 2ABC1B 1C 1A 2C 1B 11C B A …图42010年中考数学试题分类汇编——规律探索（2010哈尔滨）１．观察下列图形：它们是按一定规律排列的，依照此规律，第9个图形中共有 个★28（2010红河自治州）15. 如图4，在图（1）中，A 1、B 1、C 1分别是△ABC 的边BC 、CA 、AB 的中点，在图（2）中，A 2、B 2、C 2分别是△A 1B 1C 1的边B 1C 1、C 1 A 1、 A 1B 1的中点，…，按此规律，则第n 个图形中平行四边形的个数共有 3n 个.(2010遵义市)小明玩一种的游戏,每次挪动珠子的颗数与对应所得的分数如下表:当对应所得分数为132分时,则挪动的珠子数为 ▲ 颗.答案：12(2010台州市)如图，菱形ABCD 中，AB =2 ，∠C =60°,菱形ABCD 在直线l 上向右作无滑动的翻滚，每绕着一个顶点旋转60°叫一次操作，则经过36次这样的操作菱形中心O 所经过的路径总长为(结果保留π) ▲ ．答案：83+4）π(第16题)l（玉溪市2010）22. 平面内的两条直线有相交和平行两种位置关系.（1）AB 平行于CD ．如图a ，点P 在AB 、CD 外部时，由AB ∥CD ，有∠B=∠BOD ，又因∠BOD 是△POD 的外角，故∠BOD=∠BPD +∠D ，得∠BPD=∠B-∠D ．如图b ，将点P 移到AB 、CD 内部，以上结论是否成立？，若不成立，则∠BPD 、∠B 、∠D 之间有何数量关系？请证明你的结论；（2）在图b 中，将直线AB 绕点B 逆时针方向旋转一定角度交直线CD 于点Q ， 如图c ，则∠BPD ﹑∠B ﹑∠D ﹑∠BQD 之间有何数量关系？（不需证明）； （3）根据（2）的结论求图d 中∠A+∠B+∠C+∠D+∠E+∠F 的度数．解：（1）不成立，结论是∠BPD=∠B+∠D.延长BP 交CD 于点E,∵AB ∥CD. ∴∠B=∠BED.又∠BPD=∠BED+∠D ，∴∠BPD=∠B+∠D. …………4分 （2）结论： ∠BPD=∠BQD+∠B+∠D. …………7分（3）由（2）的结论得：∠AGB=∠A+∠B+∠E. 又∵∠AGB=∠CGF. ∠CGF+∠C+∠D+∠F=360°∴∠A+∠B+∠C+∠D ∠E+∠F=360°. …………11分（桂林2010）18．如图：已知AB =10，点C 、D 在线段AB 上且AC =DB =2； P 是线段CD 上的动点，分别以AP 、PB 为边在线段AB 的同侧作等边△AEP 和等边△PFB ，连结EF ，设EF 的中点为G ；当点P 从点C运动到点D 时，则点G 移动路径的长是________．3图aO图bO图c图dG第17题 AB CA 1A 2A 3B 1 B 2 B 3（2010年连云港）17．如图，△ABC 的面积为1，分别取AC 、BC 两边的中点A 1、B 1，则四边形A 1ABB 1的面积为34，再分别取A 1C 、B 1C 的中点A 2、B 2，A 2C 、B 2C 的中点A 3、B 3，依次取下去…．利用这一图形，能直观地计算出3 4＋3 42＋3 43＋…＋34n ＝________．(2010济宁市)18．（6分）观察下面的变形规律：211⨯ ＝1－12； 321⨯＝12－31；431⨯＝31－41；…… 解答下面的问题：（1）若n 为正整数，请你猜想)1(1+n n ＝ ；（2）证明你猜想的结论； （3）求和：211⨯＋321⨯＋431⨯＋…＋201020091⨯ . （2010宁波市）25．十八世纪瑞士数学家欧拉证明了简单多面体中顶点数（V）、面数（F ）、棱数（E ）之间存在的一个有趣的关系式，被称为欧拉公式请你观察下列几种简单多面体模型，解答下列问题：（1）根据上面多面体的模型，完成表格中的空格：你发现顶点数（V ）、面数（F ）、棱数（E ）之间存在的关系式是________； （2）一个多面体的面数比顶点数大8，且有30条棱，则这个多面体的面数是；……图③图②图①（3）某个玻璃饰品的外形是简单的多面体，它的外表面是由三角形和八边形两种多边形拼接而成，且有24个顶点，每个顶点处都有3条棱．设该多面体外表面三角形的个数为x 个，八边形的个数为y ，求x ＋y 的值．（2010年成都）24．已知n 是正整数，111222(,),(,),,(,),n n n P x y P x y P x y 是反比例函数ky x=图象上的一列点，其中121,2,,,n x x x n ===．记112A x y =，223A x y =，1n n n A x y +=，，若1A a =（a是非零常数），则12n A A A 的值是________________________（用含a 和n 的代数式表示）． 答案：(2)1na n +（2010年眉山）16．如图，将第一个图（图①）所示的正三角形连结各边中点进行分割，得到第二个图（图②）；再将第二个图中最中间的小正三角形按同样的方式进行分割，得到第三个图（图③）；再将第三个图中最中间的小正三角形按同样的方式进行分割，……，则得到的第五个图中，共有________个正三角形．答案：17北京12. 右图为手的示意图，在各个手指间标记字母A 、B 、C 、D 。

8．（南通市）如图，菱形ABCD中，AB = 5，∠BCD = 120°，则对角线AC的长是A．20 B．15C．10 D．59．（南通市）如图，已知□ABCD的对角线BD=4cm，将□ABCD绕其对称中心O旋转180°，则点D所转过的路径长为A．4π cm B．3π cmC．2π cm D．π cm6．（盐城市）如图所示，在菱形ABCD中，两条对角线AC＝6，BD＝8，则此菱形的边长为A．5 B．6 C．8 D．1016．（南通市）如图，小章利用一张左、右两边已经破损的长方形纸片ABCD做折纸游戏，他将纸片沿EF折叠后，D、C两点分别落在D ′、C ′的位置，并利用量角器量得∠EFB＝65°，则∠AED ′等于▲度．17．（南通市）如图，正方形ABCD的边长为4，点M在边DC上，M、N两点关于对角线AC对称，若DM=1，则tan∠ADN=▲．17．（盐城市）小明尝试着将矩形纸片ABCD（如图①，AD>CD）沿过A点的直线折叠，使得B点落在AD边上的点F处，折痕为AE（如图②）；再沿过D点的直线折叠，使得C点落在DA边上的点N处，E点落在AE 边上的点M处，折痕为DG（如图③）．如果第二次折叠后，M点正好在∠NDG的平分线上，那么矩形ABCD 长与宽的比值为▲．①②D③BACD（第8题）（第9题）AB CDOA（第17题）BDMNC··11. （兰州市）如图所示，菱形ABCD 的周长为20cm ，DE ⊥AB ，垂足为E ，sin A=53，则下列结论正确的个数有①cm DE 3= ②cm BE 1= ③菱形的面积为215cm ④cm BD 102= A ． 1个 B ． 2个 C ． 3个 D ． 4个17. （兰州市）如图，直角梯形ABCD 中，AD ∥BC ，AB ⊥BC ，AD = 2，将腰CD 以D 为中心逆时针旋转90°至DE ，连接AE 、CE ，△ADE 的面积为3，则BC 的长为 ．21. （青岛市）已知：如图，在正方形ABCD 中，点E 、F 分别在BC 和CD 上，AE = AF ．（1）求证：BE = DF ；（2）连接AC 交EF 于点O ，延长OC 至点M ，使OM = OA ，连接EM 、FM ．判断四边形AEMF 是什么特殊四边形？并证明你的结论．21．（本小题满分8分)证明：（1）∵四边形ABCD 是正方形，∴AB ＝AD ,∠B = ∠D = 90°．∵AE = AF ，∴Rt Rt ABE ADF △≌△．∴BE ＝DF ． （2）四边形AEMF 是菱形． ∵四边形ABCD 是正方形，∴∠BCA = ∠DCA = 45°，BC = DC ．∵BE ＝DF ，∴BC －BE = DC －DF . 即CE CF =． ∴OE OF =． ∵OM = OA ，∴四边形AEMF 是平行四边形． ∵AE = AF ，∴平行四边形AEMF 是菱形．A DB E F OC第21题图13．（青岛市）把一张矩形纸片（矩形ABCD ）按如图方式折叠，使顶点B 和点D 重合，折痕为EF ．若AB = 3 cm ，BC = 5 cm ，则重叠部分△DEF 的面积是 cm 2．22.（8分）（济宁市）数学课上，李老师出示了这样一道题目：如图1，正方形ABCD 的边长为12，P 为边BC 延长线上的一点，E 为DP 的中点，DP 的垂直平分线交边DC 于M ，交边AB 的延长线于N .当6CP =时，EM 与EN 的比值是多少？经过思考，小明展示了一种正确的解题思路：过E 作直线平行于BC 交DC ，AB 分别于F ，G ，如图2，则可得：DF DEFC EP=，因为DE EP =，所以DF FC =.可求出EF 和EG 的值，进而可求得EM 与EN 的比值. (1) 请按照小明的思路写出求解过程.(2) 小东又对此题作了进一步探究，得出了DP MN =的结论.你认为小东的这个结论正确吗？如果正确，请给予证明；如果不正确，请说明理由.22．（1）解：过E 作直线平行于BC 交DC ，AB 分别于点F ，G ，则DF DE FC EP=，EM EFEN EG =，12GF BC ==. ∵DE EP =，∴DF FC =. ············································································ 2分∴116322EF CP ==⨯=，12315EG GF EF =+=+=.∴31155EM EF EN EG ===. ·················································································· 4分 （2）证明：作M H ∥BC 交AB 于点H ， ···································································· 5分则MH CB CD ==，90MHN ∠=︒. ∵1809090DCP ∠=︒-︒=︒，HBCDEMNAPABCFE'A 第13题图（'B ）D∴DCP MHN ∠=∠.∵90MNH CMN DME CDP ∠=∠=∠=︒-∠，90DPC CDP ∠=︒-∠， ∴DPC MNH ∠=∠.∴DPC MNH ∆≅∆. ··················································· 7分 ∴DP MN =. ······························································································· 8分22．（盐城市）（本题满分8分）如图，在梯形ABCD 中，AD ∥BC ，AB =CD =AD ，BD ⊥CD ．（1）求sin ∠DBC 的值；（2）若BC 长度为4cm ，求梯形ABCD 的面积．22．解：(1)∵AD =AB ∴∠ADB =∠ABD∵AD ∥CB ∴∠DBC = ∠ADB =∠ABD ……………（1分） ∵在梯形ABCD 中，AB =CD ，∴∠ABD +∠DBC =∠C =2∠DBC ∵BD ⊥CD ∴3∠DBC =90º ∴∠DBC =30º ……（3分） ∴sin ∠DBC =12……………………（4分） （2）过D 作DF ⊥BC 于F …………………………（5分） 在Rt △CDB 中，BD =BC ×c os ∠DBC =2 3 （cm ） …………………（6分） 在Rt △BDF 中，DF =BD ×sin ∠DBC = 3 （cm ） …………………（7分）∴S 梯=12(2+4)·3 =3 3 （cm 2）………………………………………（8分）27. （兰州市）（本题满分10分）已知平行四边形ABCD 中，对角线AC 和BD 相交于点O ，AC=10，BD=8．（1）若AC ⊥BD ，试求四边形ABCD 的面积 ；（2）若AC 与BD 的夹角∠AOD=60，求四边形ABCD 的面积；（3）试讨论：若把题目中“平行四边形ABCD ”改为“四边形ABCD ”，且∠AOD=θAC=a ，BD=b ，试求四边形ABCD 的面积（用含θ，a ，b 的代数式表示）．27. （本题满分10分） 解：（1）∵AC ⊥BD∴四边形ABCD 的面积（2）过点A分别作AE ⊥BD ，垂足为EB AC D B A CD F （第22题图）∵四边形ABCD 为平行四边形521===AC CO AO 421===BD DO BO在Rt ⊿AOE 中，AO AEAOE =∠sin ∴ 23523560sin sin =⨯=⨯=∠∙=o AO AOE AO AE∴3552342121=⨯⨯⨯=∙=∆AE OD S AOD∴四边形ABCD 的面积 3204==∆AO D S S(3）如图所示过点A,C 分别作AE ⊥BD ，CF ⊥BD ，垂足分别为E,F在Rt ⊿AOE 中，AO AE AOE =∠sin ∴θsin sin ⨯=∠∙=AO AOE AO AE同理可得θsin sin ⨯=∠∙=CO COF CO CF∴四边形ABCD 的面积27．（盐城市）（本题满分12分）如图1所示，在直角梯形ABCD 中，AD ∥BC ，AB ⊥BC ，∠DCB =75º，以CD为一边的等边△DCE 的另一顶点E 在腰AB 上． （1）求∠AED 的度数； （2）求证：AB =BC ；（3）如图2所示，若F 为线段CD 上一点，∠FBC =30º．求DFFC 的值．27.解：(1)∵∠BCD =75º，AD ∥BC ∴∠ADC =105º …………………………………（1分） 由等边△DCE 可知：∠CDE =60º，故∠ADE =45ºAB C DE 图1AB CDEF 图2 θθθsin 21sin 21)(sin 212121ab AC BD CO AO BD CF BD AE BD S S S CBD ABD =∙=+=∙+∙=+=∆∆由AB ⊥BC ，AD ∥BC 可得：∠DAB =90º ， ∴∠AED =45º…………………（3分）(2)方法一：由(1)知：∠AED =45º，∴AD =AE ，故点A 在线段DE 的垂直平分线上．由△DCE 是等边三角形得：CD =CE ，故点C 也在线段DE 的垂直平分线上． ∴AC 就是线段DE 的垂直平分线，即AC ⊥DE …………………（5分） 连接AC ，∵∠AED =45º，∴∠BAC =45º，又AB ⊥BC ∴BA =BC ．…………（7分） 方法二：过D 点作DF ⊥BC ，交BC 于点 ………………（4分） 可证得：△DFC ≌△CBE 则DF=BC ……………………（6分） 从而：AB =CB ………………………………………………（7分） （3）∵∠FBC =30º，∴∠ABF =60º连接AF ，BF 、AD 的延长线相交于点G ，∵∠FBC =30º，∠DCB =75º，∴∠BFC =75º，故BC =BF 由(2)知：BA =BC ，故BA =BF ，∵∠ABF =60º，∴AB =BF =F A ，又∵AD ∥BC ，AB ⊥BC ，∴∠F AG =∠G =30º∴FG =F A = FB ……………………………（10分） ∵∠G =∠FBC =30º，∠DFG =∠CFB ，FB =FG ∴△BCF ≌△GDF ………………………（11分） ∴DF =CF ，即点F 是线段CD 的中点． ∴DFFC=1………………………………………（12分）13．（连云港市）一只自由飞行的小鸟，将随意地落在如图所示方格地面上（每个小方格都是边长相等的正方形），则小鸟落在阴影方格地面上的概率为___________．2.（常德市）如图2，四边形ABCD 中，AB ∥CD ，要使四边形ABCD 为平行四边形，则可添加的条件为_____________________.(填一个即可)18．（连云港市）矩形纸片ABCD 中，AB ＝3，AD ＝4，将纸片折叠，使点B 落在边CD 上的B ’处，折痕为AE ．在折痕AE 上存在一点P 到边CD 的距离与到点B 的距离相等，则此相等距离为________．DABC图2 A B CD EF 图1A B CD E F 图2 G5．（淮安市）若一个多边形的内角和小于其外角和,则这个多边形的边数是A．3 B．4 C．5 D．6题17图题18图18．（淮安市）已知菱形ABCD中,对角线AC=8cm，BD=6cm，在菱形内部(包括边界)任取一点P，使△A CP的面积大于6 cm2的概率为．26．（淮安市）(本小题满分10分)(1)观察发现如题26(a)图，若点A，B在直线l同侧，在直线l上找一点P，使AP+BP的值最小．做法如下：作点B关于直线l的对称点B'，连接AB'，与直线l的交点就是所求的点P再如题26(b)图，在等边三角形ABC中，AB=2，点E是AB的中点，AD是高，在AD上找一点P，使BP+PE的值最小．做法如下：作点B关于AD的对称点，恰好与点C重合，连接CE交AD于一点，则这点就是所求的点P，故BP+PE的最小值为．题26(a)图题26(b)图(2)实践运用如题26(c)图，已知⊙O的直径CD为4，AD的度数为60°，点B是 AD的中点，在直径CD上找一点P，使BP+AP的值最小，并求BP+AP的最小值．题26(c)图题26(d)图(3)拓展延伸如题26(d)图，在四边形ABCD的对角线AC上找一点P，使∠APB=∠APD．保留作图痕迹，不必写出作法．A 第24题BCDOE图1 ABCD图2 24．（连云港市）（本题满分10分）如图，正方形网格中的每一个小正方形的边长都是1，四边形ABCD 的四个顶点都在格点上，O 为AD 边的中点，若把四边形ABCD 绕着点O 顺时针旋转，试解决下列问题： （1）画出四边形ABCD 旋转后的图形； （2）求点C 旋转过程事所经过的路径长；（3）设点B 旋转后的对应点为B ’，求tan ∠DAB ’的值．7．（连云港市）如图，四边形ABCD 的对角线AC 、BD 互相垂直，则下列条件能判定四边形ABCD 为菱形的是（ ）A ．BA ＝BCB ．AC 、BD 互相平分 C ．AC ＝BD9.（常德市）四边形的内角和为（ ）A 。

2010年中考数 学 试 卷*考试时间120分钟 试卷满分150分一、选择题（本大题共7小题，每小题4分，共28分）每题所给的四个选项中只有一项是符合题目要求的，请将所选项的代号字母填在答卷的相应位置处． 1） A． BC．-D2．反比例函数23m y x--=的图象位于（ ）A ．第一、三象限B ．第二、四象限C ．第二、三象限D ．第一、二象限3．从2、3、4、5这四个数中，任取两个数()p q p q ≠和，构成函数2y px y x q =-=+和，并使这两个函数图象的交点在直线2x =的右侧，则这样的有序数对()p q ，共有（ ） A ．12对 B ．6对 C ．5对 D ．3对4．把多项式2288x x -+分解因式，结果正确的是（ ） A ．()224x -B ．()224x -C ．()222x -D ．()222x +5．某等腰三角形的两条边长分别为3cm 和6cm ，则它的周长为（ ） A ．9cm B ．12cm C ．15cm D ．12cm 或15cm6．一次函数y kx b =+（k b ，是常数，0k ≠）的图象如图所示，则不等式0kx b +>的解集是A ．2x >-；B ．0x >；C ．2x <-；D ．0x <7．若0a >且2x a =，3y a =，则x ya -的值为（ ）A ．1-B ．1C ．23D ．32二、填空题（本大题共6小题，每小题4分，共24分）把答案直接填在答卷的相应位置处．xb +8．将点(12)，向左平移1个单位，再向下平移2个单位后得到对应点的坐标是 ．9．幼儿园把新购进的一批玩具分给小朋友．若每人3件，那么还剩余59件；若每人5件，那么最后一个小朋友分到玩具，但不足4件，这批玩具共有 件．10．李师傅随机抽查了本单位今年四月份里6天的日用水量（单位：吨）结果如下：7，8，8，7，6，6，根据这些数据，估计四月份本单位用水总量为 吨．11．我们知道利用相似三角形可以计算不能直接测量的物体的高度，阳阳的身高是1.6m ，他在阳光下的影长是 1.2m ，在同一时刻测得某棵树的影长为 3.6m ，则这棵树的高度约为 m ． 12．如图所示的半圆中，AD 是直径，且3AD =，2AC =，则sin B 的值是 ．13．某个圆锥的侧面展开图形是一个半径为6cm ，圆心角为︒120的扇形，则这个圆锥的底面半径为______________cm ．三、解答题（本大题Ⅰ—Ⅴ题，共10小题，共98分）解答时应在答卷的相应位置处写出文字说明、证明过程或演算过程． Ⅰ．（本题满分12分，第14题6分，第15题6分）14．计算：230116(2)(πtan60)3-⎛⎫--÷-+-- ⎪⎝⎭．15．先化简，再求值：221111121x x x x x +-÷+--+，其中1x =． Ⅱ．（本题满分28分，第16题7分，第17题10分，第18题11分）C BD A16．如图，线段AB 与⊙O 相切于点C ，连结OA ，OB ，OB 交⊙O 于点D ，已知6OA OB ==，AB =（1）求⊙O 的半径； （2）求图中阴影部分的面积．17．响应“家电下乡”的惠农政策，某商场决定从厂家购进甲、乙、丙三种不同型号的电冰箱80台，其中甲种电冰箱的台数是乙种电冰箱台数的2倍，购买三种电冰箱的总金额不超．．过．132 000元．已知甲、乙、丙三种电冰箱的出厂价格分别为：1 200元/台、1 600元/台、2 000元/台．(1)至少购进乙种电冰箱多少台？(2)若要求甲种电冰箱的台数不超过丙种电冰箱的台数，则有哪些购买方案？18．甲、乙两名运动员进行长跑训练，两人距终点的路程y （米）与跑步时间x （分）之间C OABD的函数图象如图所示，根据图象所提供的信息解答问题：(1) 他们在进行 米的长跑训练，在0＜x ＜15的时段内，速度较快的人是 ；(2) 求甲距终点的路程y （米）和跑步时间 x （分）之间的函数关系式； (3) 当x =15时，两人相距多少米？在15＜x ＜20的时段内，求两人速度之差．Ⅲ．（本题满分36分，第19题12分，第20题12分，第21题12分）19．把一副扑克牌中的3张黑桃牌（它们的正面牌面数字分别是3、4、5）洗匀后正面朝下放在桌面上．（1）如果从中随机抽取一张牌，那么牌面数字是4的概率是多少？（2）小王和小李玩摸牌游戏，游戏规则如下：先由小王随机抽出一张牌，记下牌面数字后放回，洗匀后正面朝下，再由小李随机抽出一张牌，记下牌面数字．当2张牌面数字相同时，小王赢；当2张牌面数字不相同时，小李赢．现请你利用树状图或列表法分析游戏规则对双方是否公平？并说明理由．20．如图，河流两岸a b ，互相平行，C D ，是河岸a 上间隔50m 的两个电线杆．某人在河分)岸b 上的A 处测得30DAB ∠= ，然后沿河岸走了100m 到达B 处，测得60CBF ∠=，求河流的宽度CF 的值（结果精确到个位）．21．三个生产日光灯管的厂家在广告中宣称，他们生产的日光灯管在正常情况下，灯管的使用寿命为12个月．工商部门为了检查他们宣传的真实性，从三个厂家各抽取11只日光灯管进行检测，灯管的使用寿命（单位：月）如下：试问：（1）这三个厂家的广告，分别利用了统计中的哪一个特征数（平均数、中位数、众数）进行宣传？（2）如果三种产品的售价一样，作为顾客的你选购哪个厂家的产品？请说明理由．Ⅳ（本题满分8分）BED CFab A22．如图， 已知等边三角形ABC 中，点D ，E ，F 分别为边AB ，AC ，BC 的中点，M 为直线BC 上一动点，△DMN 为等边三角形（点M 的位置改变时， △DMN 也随之整体移动） ． （1）如图①，当点M 在点B 左侧时，请你判断EN 与MF 有怎样的数量关系？点F 是否在直线NE 上？都请直接．．．．写出结论，不必证明或说明理由； （2）如图②，当点M 在BC 上时，其它条件不变，（1）的结论中EN 与MF 的数量关系是否仍然成立?若成立，请利用图②证明；若不成立，请说明理由；（3）若点M 在点C 右侧时，请你在图③中画出相应的图形，并判断（1）的结论中EN 与MF 的数量关系是否仍然成立?若成立?请直接写出结论，不必证明或说明理由．Ⅴ（本题满分14分）图① 图② 图③A·BCD EF··N MFEDCB ANMF EDCBA·23．如图，在平面直角坐标系中，以点(11)C ，为圆心，2为半径作圆，交x 轴于A B ，两点，开口向下的抛物线经过点A B ，，且其顶点P 在C 上．（1）求ACB 的大小；（2）写出A B ，两点的坐标； （3）试确定此抛物线的解析式；（4）在该抛物线上是否存在一点D ，使线段OP 与CD 互相平分？若存在，求出点D 的坐标；若不存在，请说明理由．2010年中考数学试题参考答案及评分标准二、填空题（本大题共6小题，每小题4分，共24分） 8．(00)，；9．152；10．210；11．4.8；12．23；13．4 三、解答题（本大题Ⅰ—Ⅴ题，共10小题，共98分） Ⅰ．（本题满分12分，第14题6分，第15题6分） 14．解：原式＝9－16÷（－8）＋1－23×23……………………2分 ＝9＋2＋1－3.……………………………………4分 ＝9 ………………………………6分15．解：原式211(1)1(1)(1)1x x x x x -=-++-+······································································ 2分 2211(1)(1)1(1)(1)x x x x x x -+--=-=+++ ······························································· 4分 22(1)x =+ ········································································································ 5分当1x =时，原式23== ··································································· 6分 Ⅱ．（本题满分28分，第16题7分，第17题10分，第18题11分）16．（1）连结OC ，则 OC AB ⊥． …………………………………………………1分∵OA OB =，∴1122AC BC AB ===⨯ ………………………………………2分在Rt AOC △中，3OC ===．∴ ⊙O 的半径为3． …………………………………………………………3分 （2）∵ OC =12OB , ∴ ∠B =30o , ∠COD =60o ． ……………………………………5分 ∴扇形OCD 的面积为OCD S 扇形=260π3360⨯⨯=32π． …………………………………5分阴影部分的面积为：Rt Δ=OBC OCD S S S -阴影扇形=12OC CB ⋅－3π2－3π2．…………………………7分 17．解：（1）设购买乙种电冰箱x 台，则购买甲种电冰箱2x 台，丙种电冰箱(803)x -台，根据题意，列不等式： ································································ 1分120021600(803)2000132000x x x ⨯++-⨯≤． ···························································· 3分解这个不等式，得14x ≥． ·································································································· 4分 ∴至少购进乙种电冰箱14台． ····························································································· 5分 （2）根据题意，得2803x x -≤． ····················································································· 6分 解这个不等式，得16x ≤． ·································································································· 7分 由（1）知14x ≥． 1416x ∴≤≤． 又x 为正整数， 141516x ∴=，，． ···················································································································· 8分 所以，有三种购买方案：方案一：甲种电冰箱为28台，乙种电冰箱为14台，丙种电冰箱为38台； 方案二：甲种电冰箱为30台，乙种电冰箱为15台，丙种电冰箱为35台； 方案三：甲种电冰箱为32台，乙种电冰箱为16台，丙种电冰箱为32台． ··················· 10分 18．解：（1）5000…………………………………2分甲 ………………………………4分（2）设所求直线的解析式为：y =kx +b (0≤x ≤20)， ………5分由图象可知：b =5000，当x =20时，y =0， ∴0=20k +5000，解得k = -250. …7分即y = -250x +5000 (0≤x ≤20) ……………7分（3）当x =15时，y = -250x +5000= -250×15+5000=5000-3750=1250. ………8分 两人相距：(5000 -1250)-(5000-2000)=750（米）………………9分 两人速度之差:750÷(20-15)=150（米/分）……………11分Ⅲ．（本题满分36分，第19题12分，第20题12分，第21题12分） 19解：（1）P （抽到牌面数字是4）13=； ········································································ 2分（2）游戏规则对双方不公平． ················································································· 5分 理由如下：由上述树状图或表格知：所有可能出现的结果共有9种． P （抽到牌面数字相同）=3193=， P （抽到牌面数字不相同）=6293=．∵1233<，∴此游戏不公平，小李赢的可能性大． ············································ 12分 （说明：答题时只需用树状图或列表法进行分析即可）20．解：过点C 作CE AD ∥，交AB 于E CD AE ∥，CE AD ∥ ····································································································· 2分∴四边形AECD 是平行四边形 ······························································································ 4分 50AE CD ∴==m ，50EB AB AE =-=m ，30CEB DAB ∠=∠= ···························· 6分又60CBF ∠=，故30ECB ∠=，50CB EB ∴==m ···················································· 8分∴在Rt CFB △中，sin 50sin 6043CF CB CBF =∠=≈m ········································ 11分 答：河流的宽度CF 的值为43m ． ······················································································ 12分21．答：（1）甲厂的广告利用了统计中的平均数． ····························································· 2分乙厂的广告利用了统计中的众数． ············································································ 4分 丙厂的广告利用了统计中的中位数． ············································································ 7分分…………………………8分11F B C （2） 选用甲厂的产品． 因为它的平均数较真实地反映灯管的使用寿命 ······················· 10分 或选用丙厂的产品．因为丙厂有一半以上的灯管使用寿命超过12个月 ··························· 10分Ⅳ．（本题满分8分）22．（1）判断：EN 与MF 相等 （或EN=MF ），点F 在直线NE 上， ········ 2分（2）成立． ······························ 3分 证明：法一：连结DE ，DF ．∵△ABC 是等边三角形， ∴AB =AC =BC ．又∵D ，E ，F 是三边的中点，∴DE ，DF ，EF 为三角形的中位线．∴DE =DF =EF ，∠FDE =60°．又∠MDF +∠FDN =60°， ∠NDE +∠FDN =60°，∴∠MDF =∠NDE ．在△DMF 和△DNE 中，DF =DE ，DM =DN ， ∠MDF =∠NDE ，∴△DMF ≌△DNE ． 8∴MF =NE ． ·························· 6分法二：延长EN ，则EN 过点F ．∵△ABC 是等边三角形， ∴AB =AC =BC ．又∵D ，E ，F 是三边的中点， ∴EF =DF =BF ．∵∠BDM +∠MDF =60°， ∠FDN +∠MDF =60°，∴∠BDM =∠FDN ．又∵DM =DN ， ∠ABM =∠DFN =60°，∴△DBM ≌△DFN ．∴BM =FN ．∵BF =EF ， ∴MF =EN ． ·························· 6分（3）画出图形（连出线段NE ）， 6MF 与EN 相等的结论仍然成立（或MF =NE 成立）． ·············· 8分Ⅴ．（本题满分14分）23．解：（1）作CHN C A B F M D E NC A B F MD E12 1CH = ，半径2CB = ·························································· 1分60BCH ∠= ，120ACB ∴∠= ········································· 3分（2）1CH = ，半径2CB =HB ∴=(1A ，················································ 5分(1B ··············································································· 6分 （3）由圆与抛物线的对称性可知抛物线的顶点P 的坐标为(13)， ······································· 7分 设抛物线解析式2(1)3y a x =-+ ·························································································· 8分把点(1B 代入上式，解得1a =- ·············································································· 9分 222y x x ∴=-++ ·············································································································· 10分 （4）假设存在点D 使线段OP 与CD 互相平分，则四边形OCPD 是平行四边形 ·········· 11分 PC OD ∴∥且PC OD =．PC y ∥轴，∴点D 在y 轴上． ····················································································· 12分又2PC = ，2OD ∴=，即(02)D ，． 又(02)D ，满足222y x x =-++， ∴点D 在抛物线上 ··············································································································· 13分 所以存在(02)D ，使线段OP 与CD 互相平分． ·································································· 14分。

1 / 42010年部分省市中考数学试题分类汇编 尺规作图1．（2010年某某某某）如图，有一块三角形材料（△ABC ），请你画出一个圆，使其与△ABC的各边都相切. 解：结论： 【关键词】尺规作图【答案】正确画出两条角平分线，确定圆心；确定半径；正确画出圆并写出结论．2．（2010年门头沟区）如图（1），凸四边形ABCD ，如果点P 满足APD APB α∠=∠=，且BPC CPD β∠=∠=，则称点P 为四边形ABCD 的一个半等角点．（1）在图（2）正方形ABCD 内画一个半等角点P ，且满足αβ≠； （2）在图（3）四边形ABCD 中画出一个半等角点P ， 保留画图痕迹（不需写出画法）．【关键词】四边形、对称、尺规作图 【答案】解 ：ABCB'图（2）图（3）ACPDABCDP2 / 43.（2010年某某市潼南县）画一个等腰△ABC ，使底边长BC=a ，底边上的高为h （要求：用尺规作图，保留作图痕迹，写出已知，求作，不写作法和证明）. 已知：求作：【关键词】尺规作图 【答案】已知：线段a 、h求作：一个等腰△ABC 使底边BC=a ，底边BC 上的高为h ----------------------------------------------1分 画图（保留作图痕迹图略）--------------------------6分4.（2010年某某某某）已知△ABC ，利用直尺和圆规，根据下列要求作图（保留作图痕迹，不要求写作法），并根据要求填空： (1)作∠ABC 的平分线BD 交AC 于点D ；(2)作线段BD 的垂直平分线交AB 于点E ，交BC 于点F ． 由⑴、⑵可得：线段EF 与线段BD 的关系为【答案】⑴、⑵题作图如下：由作图可知线段EF 与线段BD 的关系为：互相垂直平分．ah3 / 4．【关键词】尺规作图 作角的平分线 作线段的垂直平分线.5.（2010年某某某某）如图，在梯形ABCD 中，AB ∥CD（1）用尺规作图方法，作∠DAB 的角平分线AF （只保留作图痕迹，不写作法和证明） （2）若AF 交CD 边于点E ，判断△ADE 的形状（只写结果） 解：(1)所以射线AF 即为所求 (2)△ADE 是等腰三角形.6．(2010年某某)尺规作图：请在原图上作一个∠AOC ，使其是已知∠AOB 的23倍．（要求：写出已知、求作，保留作图痕迹，在所作图中标上必要的字母，不写作法和结论） 已知： 求作：【答案】已知：∠AOB.求作：∠AOC=23∠AOB.作图如下：OA6题图B19题答图CDBAO4 / 4。

四边形训练题1、如图，EF 过矩形ABCD 的对角线的交点O ，且分别交AB 、CD 于E 、F ，那么阴影部分的面积是 矩形ABCD 的面积的（ ） A 51B 41C 31D 1032、已知点E 、F 是矩形ABCD 的边BC 、CD 的中点，且BF 与DE 交于点G ，则ABCDABGD S S 矩形四边形的值为3、已知点E 是ABCD 的CD 边的中点，且BE 交对角线AC 于点G ；如果S △CEG ＝1，则ABCD 的 面积为4、已知点E 、F 是ABCD 的BC 、CD 边的中点，AE 、AF 与对角线BD 相交。

记图中阴影部分面积为S 1，非阴影部分面积为S 2，则21S S ＝ 5、如图，已知P 是矩形ABCD 的内的一点.求证：PA 2＋PC 2＝PB 2＋PD 26、已知点P 是边长为1的正方形ABCD 内一点，如果∠DPC ＝90°，PA 2－PB 2＝21。

求∠PCB 的度数。

7、已知点P 是正方形ABCD 内一点，且PA ＝PB ＝10，并且点P 到CD 边的距离也是10， 求正方形ABCD 的面积。

8、如图，点E 、F 是矩形ABCD 边BC 、CD 上的点，如果S △CEF ＝3，S △ABE ＝4，S △ADF ＝5；求S △AEF9、（江阴）如图，点E 、F 是ABCD 边AB 、BC 上的点，⑴如果AB ＝10，AB 与CD 的距离为8，且点E 、F 分别是AB 、BC 的中点，求S △DEF ⑵若△ADE 、△BEF 、△CDF 的面积分别为5、3、4，求△DEF 的面积。

A BCD E FOBECFDACFD CDPABCDPBAECD GFB ACD GE BACDFEPCDBA第1题图第2题图第3题图第4题图10、平行四边形ABCD 中，E 是CD 边上任意一点。

求证：S △ABE ＝S △BCE ＋S △ADE ＝21S ABCD11、在梯形ABCD 中，AB ∥DC ，点E 是腰CD 的中点。

2010年部分省市中考数学试题分类汇编压轴题(四)23．(安徽省)如图，已知111ABC A B C △∽△，相似比为k （k >1），且ABC △的三边长分别为a 、b 、c （a>b>c ），111A B C △的三边长分别为1a 、1b 、1c .（1）若c=a 1，求证：a=kc ；[证]（2）若c=a 1，试给出符合条件的一对111ABC A B C △和△，使得a 、b 、c 和1a 、1b 、1c 都是正整数，并加以说明；[解]（3）若b=a 1，c=b 1，是否存在111ABC A B C △和△使得k =2？请说明理由.[解]解:（1）证：111ABC A B C △∽△，且相似比为11(1).ak k k a ka a >∴=∴=，， 又1.c a a kc =∴=， ··········································································· （3分） （2）解：取11186443 2.a b c a b c ======，，，同时取，， ··············· （8分） 此时1111112a b cABC A B C a b c ===∴，△∽△且1.c a = ······························ （10分） 注：本题也是开放型的，只要给出的ABC △和111A B C △符合要求就相应赋分. （3）解：不存在这样的ABC △和111A B C △.理由如下： 若2k =，则111222.a a b b c c ===，， 又1b a =，1c b =，第23题图112244a a b b c ∴====，2.b c ∴= ························································································ （12分）24b c c c c a ∴+=+<=，而b c a +>，故不存在这样的ABC △和111A B C △，使得 2.k = ··································· （14分） 注：本题不要求学生严格按反证法的证明格式推理，只要能说明在题设要求下2k =的情况不可能即可. 24．（芜湖市 本小题满分14分）如图，在平面直角坐标系中放置一矩形ABCO ，其顶点为A （0，1）、B （－33，1）、C （－33，0）、O （0，0）．将此矩形沿着过E （－3，1）、F （－433，0）的直线EF 向右下方翻折，B 、C 的对应点分别为B ′、C ′． （1）求折痕所在直线EF 的解析式；（2）一抛物线经过B 、E 、B ′三点，求此二次函数解析式；（3）能否在直线EF 上求一点P ，使得△PBC 周长最小？如能，求出点P 的坐标；若不能，说明理由．解：（2）设矩形沿直线EF 向右下方翻折后，B 、C 的对应点为1122()()B x y C x y B B A AE AE A ''''''⊥，，，．过作交所在直线于点. 2360B E BE B EF BEF ''==∠=∠=︒，， 6033B EA A E B A '''''∴∠=︒∴=，，.1102(02)A A B y x y B '''∴∴==--与重合，在轴上．，即，.[此时需说明()11B x y y '，在轴上]. ······································································ 6分设二次函数解析式为：2y ax bx c =++抛物线经过()33B -，1、()3E -，1、()0-2B '，.得到233127331c a b c a b c -=⎧⎪-+=⎨⎪-+=⎩解得134332a b c ⎧=-⎪⎪⎪=-⎨⎪=-⎪⎪⎩2143233y x x ∴=---该二次函数解析式. ····················································· 9分（3）能，可以在直线EF 上找到P 点，连接B C EF P BP '交于点，再连接.由于B P BP P C '=，此时点到、B '在一条直线上，故BP PC B P PC '+=+的和最小， 由于BC 为定长，所以满足PBC ∆周长最小. ······················································ 10分 设直线B C '的解析式为：y kx b =+2033bk b-=⎧⎪⎨=-+⎪⎩23:29B C y x '∴=--直线的解析式为. ·································· 12分 182332119103411x y x P B C EF y y x ⎧⎧=-⎪=--⎪⎪'∴⎨⎨⎪⎪=-=+⎩⎪⎩又为直线和直线的交点，解得 18311P ⎛⎫∴- ⎪⎝⎭10点的坐标为，-11. ··································································· 14分 [注：对于以上各大题的不同解法，解答正确可参照评分！]26.( 重庆市綦江县) 已知：抛物线y=ax 2+bx+c(a ＞0)的图象经过点B(12,0)和C(0，-6），对称轴为x=2.(1)求该抛物线的解析式； (2)点D 在线段AB 上且AD=AC ，若动点P 从A 出发沿线段AB 以每秒1个单位长度的速度匀速运动，同时另一动点Q 以某一速度从C 出发沿线段CB 匀速运动，问是否存在某一时刻，使线段PQ 被直线CD 垂直平分？若存在，请求出此时的时间t （秒）和点Q 的运动速度；若不存在，请说明理由；(3)在（2）的结论下，直线x=1上是否存在点M ，使△MPQ 为等腰三角形？若存在，请求出所有点M 的坐标；若不存在请说明理由. 解：方法一：∵抛物线过C(0,-6) ∴c=－6, 即y=ax 2+bx －6由⎪⎩⎪⎨⎧=-+=-061214422b a a b解得：a=161 ,b=－41∴该抛物线的解析式为y=161x 2－41x －6 -----------------3分 方法二：∵A 、B 关于x=2对称∴A （－8，0） 设y=a(x ＋8)(x －12)C 在抛物线上 ∴－6=a ×8×(－12) 即a=161 ∴该抛物线的解析式为：y=161x 2－41x －6 --------3分（2）存在，设直线CD 垂直平分PQ,在Rt △AOC 中，AC=2268+=10=AD∴点D 在对称轴上，连结DQ 显然∠PDC=∠QDC ，-----------4分 由已知∠PDC=∠ACD∴∠QDC=∠ACD ∴DQ ∥AC -----------------------------5分 DB=AB －AD=20-10=10∴DQ 为△ABC 的中位线 ∴DQ=21AC=5 -----------------6分 AP=AD-PD=AD-DQ=10-5=5 ∴t=5÷1=5(秒)∴存在t=5(秒)时，线段PQ 被直线CD 垂直平分-----------7分 在Rt △BOC 中, BC=22126+=65 ∴CQ=35∴点Q 的运动速度为每秒553单位长度.------------------8分 （3）存在 过点Q 作QH ⊥x 轴于H ，则QH=3，PH=9在Rt △PQH 中，PQ=2239+=310 --------------------9分 ①当MP=MQ ，即M 为顶点，设直线CD 的直线方程为：y=kx+b(k ≠0),则：⎩⎨⎧+==-b k b 206 解得：⎩⎨⎧=-=36k b ∴y=3x-6当x=1时，y=－3 ∴M 1(1, －3) ------------------------10分 ②当PQ 为等腰△MPQ 的腰时，且P 为顶点. 设直线x=1上存在点M(1,y) ,由勾股定理得： 42+y 2=90 即y=±74∴M 2（1，74） M 3（1，－74） -----------------------11分 ③当PQ 为等腰△MPQ 的腰时，且Q 为顶点.过点Q 作QE ⊥y 轴于E ，交直线x=1于F ，则F(1, －3) 设直线x=1存在点M(1,y), 由勾股定理得： (y ＋3)2+52=90 即y=－3±65∴M 4(1, －3＋65) M 5((1, －3－65) --------------------12分 综上所述：存在这样的五点：M 1(1, －3), M 2（1，74）, M 3（1，－74）, M 4(1, －3＋65), M 5((1, －3－65).25．（山东省滨州市 本题满分l0分）如图，四边形ABCD 是菱形，点D 的坐标是（0，3），以点C 为顶点的抛物线c bx ax y ++=2恰好经过x 轴上A 、B 两点．（1）求A 、B 、C 三点的坐标；（2）求过A 、B 、C 三点的抛物线的解析式；（3）若将上述抛物线沿其对称轴向上平移后恰好过D 点，求平移后抛物线的解析式，并指出平移了多少个单位?解：①由抛物线的对称性可知AM=BM在Rt△AOD和Rt△BMC中，∵OD=MC，AD=BC，∴△AOD≌△BMC．∴OA=MB=MA．………………………………………l分设菱形的边长为2m，在Rt△AOD中，2)22m=+)32((m解得m=1．∴DC=2，OA=1，OB=3．∴A、B、C三点的坐标分别为（1，0）、（3，0）、（2，3）………………… 4分②设抛物线的解析式为y=a（x—2）2+3代入A点坐标可得a=—3抛物线的解析式为y=—3（x—2）2+3……………………………………7分③设抛物线的解析式为y=—3（x一2）2+k代入D（0，3）可得k=53所以平移后的抛物线的解析式为y=—3（x一2）2+53..............................9分平移了53一3=43个单位． 026.（山东省烟台市本题满分14分）如图，已知抛物线y=x2+bx－3a过点A（1，0），B（0，－3），与x轴交于另一点C.（1）求抛物线的解析式；（2）若在第三象限的抛物线上存在点P，使△PBC为以点B为直角顶点的直角三角形，求点P的坐标；（3）在（2）的条件下，在抛物线上是否存在一点Q，使以P，Q，B，C为顶点的四边形为直角梯形？若存在，请求出点Q的坐标；若不存在，请说明理由.解：（1）把A（1，0），B（0，－3）代入y=x2+bx－3a中，得1+b－3a=0－3a=－3a=1解得b=2∴抛物线的解析式为y=x2+2x－3………………………………………4分（2）令y=0，得x2+2x－3=0，解得x1=－3，x2=1∴点C（－3，0） (5)分∵B（0，－3）∴△BOC为等腰直角三角形.∴∠CBO=45°……………………………………………………6分过点P作PD⊥y轴，垂足为D，∵PB⊥BC，∴∠PBD=45°∴PD=BD……………………………8分所以可设点P（x，－3+x）则有－3+x=x2+2x－3，∴x=－1，所以P点坐标为（－1，－4）………………………10分（3）由（2）知，BC⊥BP当BP为直角梯形一底时，由图象可知点Q不可能在抛物线上.若BC为直角梯形一底，BP为直角梯形腰时，∵B（0，－3），C（－3，0），∴直线BC的解析式为y=－x－3…………………………11分∵直线PQ∥BC，且P（－1，－4），∴直线PQ的解析式为y=－（x+1）－3－1即y=－x－5…………………………………………………12分xy OA B CD EP y =－x －5联立方程组得y =x 2+2x －3解得x 1=－1，x 2=－2…………………………………………………………………………13分 ∴x =－2，y =－3，即点Q （－2，－3）∴符合条件的点Q 的坐标为（－2，－3）………………………………………………14分28．(四川省成都市)在平面直角坐标系xOy 中，抛物线2y ax bx c =++与x 轴交于A B 、两点（点A 在点B 的左侧），与y 轴交于点C ，点A 的坐标为(30)-，，若将经过A C 、两点的直线1y kx b =+沿y 轴向下平移3个单位后恰好经过原点，且抛物线的对称轴是直线2x =-．（1）求直线AC 及抛物线的函数表达式；（2）如果P 是线段AC 上一点，设ABP ∆、BPC ∆的面积分别为ABP S ∆、BPC S ∆，且:2:3ABP BPC S S ∆∆=，求点P 的坐标；（3）设Q 的半径为l ，圆心Q 在抛物线上运动，则在运动过程中是否存在Q 与坐标轴相切的情况？若存在，求出圆心Q 的坐标；若不存在，请说明理由．并探究：若设⊙Q 的半径为r ，圆心Q 在抛物线上运动，则当r 取何值时，⊙Q 与两坐轴同时相切？解：（1）∵y kx b =+沿y 轴向下平移3个单位后恰好经过原点，∴3b =，(0 3)C ，。