【开题报告】非线性Hammerstein模型的辨识
- 格式:pdf
- 大小:696.63 KB
- 文档页数:8

基于Hammerstein模型的执行机构非线性参数辨识陈艺文;刘鑫屏;董子健【期刊名称】《华北电力大学学报(自然科学版)》【年(卷),期】2024(51)1【摘要】针对火电机组中流过执行机构的介质流量难以测量,导致执行机构的非线性特性无法直接求取这一问题,提出用构建Hammerstein模型代替直接测量介质流量的间接测量法,进而求取执行机构的非线性特性,然后分别使用粒子群算法(PSO)和樽海鞘群算法(SSA),辨识所构建的Hammerstein模型的参数。
另外,针对PSO 算法和SSA算法辨识Hammerstein模型参数精度不高以及收敛速度慢的问题,提出了一种改进的粒子群-樽海鞘群的混合算法(IPS)。
最后基于烟道挡板的指令数据与再热器出口温度数据对模型进行了仿真。
仿真结果表明,提出的IPS算法能改善PSO算法的过早收敛问题,提高SSA算法的辨识速度。
因此通过建立Hammerstein模型能够解决介质流量难以测量的执行机构非线性参数辨识问题,并且提出的IPS算法能准确且快速的辨识Hammerstein模型的各项参数。
【总页数】8页(P135-142)【作者】陈艺文;刘鑫屏;董子健【作者单位】华北电力大学控制与计算机工程学院【正文语种】中文【中图分类】TP273【相关文献】1.基于Hammerstein模型的非线性气动弹性系统辨识2.伺服系统Hammerstein 非线性模型及参数辨识方法研究3.基于Hammerstein模型描述的非线性系统辨识新方法4.基于Hammerstein模型的非线性系统辨识方法研究5.基于Hammerstein模型的非线性系统参数辨识算法研究因版权原因,仅展示原文概要,查看原文内容请购买。


一种辨识Wiener-Hammerstein模型的新方法
徐小平;钱富才;王峰
【期刊名称】《控制与决策》
【年(卷),期】2008(23)8
【摘要】针对非线性Wiener-Hammerstein模型,提出利用粒子群优化算法对非线性模型进行辨识的新方法.该方法的基本思想是将非线性系统的辨识问题转化为参数空间上的优化问题;然后采用粒子群优化算法获得该优化问题的解.为了进一步增强粒子群优化算法的辨识性能,提出利用一种混合粒子群优化算法.最后,仿真结果验证了该方法的有效性和可行性.
【总页数】6页(P929-934)
【关键词】辨识;混合;粒子群优化;Wiener-Hammerstein模型
【作者】徐小平;钱富才;王峰
【作者单位】西安理工大学自动化与信息工程学院,西安710048;西安交通大学理学院,西安710049
【正文语种】中文
【中图分类】TP27
【相关文献】
1.一种用于模型结构辨识的新方法 [J], 吴晓燕;周延延;张双选
2.一种P ol SAR图像统计模型辨识新方法 [J], 崔浩贵;刘涛;单鸿昌;蒋宇中;高俊
3.一种辨识 Hammerstein 模型的新方法 [J], 李文江;林思建;王璇
4.基于Wiener-Hammerstein模型的一种系统辨识方法 [J], 白克强
5.一种基于数据挖掘的模糊模型辨识及参数调整新方法 [J], 张立权;邵诚
因版权原因,仅展示原文概要,查看原文内容请购买。

辨识Hammerstein模型的两步法
黄正良; 万百五
【期刊名称】《《控制理论与应用》》
【年(卷),期】1995(012)001
【摘要】本文利用稳态和动态信息提出了一种辨识Hammerstein模型的新方法─—两步法.该方法利用稳态信息获取非线性增益的强一致性估计;利用动态信息获取线性子系统未知参数的强一致性估计.该方法具有计算简单和辨识精度高等优点.最后的仿真结果说明了该方法的有效性和实用性.
【总页数】6页(P34-39)
【作者】黄正良; 万百五
【作者单位】不详
【正文语种】中文
【中图分类】TP271
【相关文献】
1.基于函数连接神经网络的传感器Hammerstein模型辨识研究 [J], 刘滔;韩华亭;马婧;雷超
2.基于伪Hammerstein模型的速率依赖迟滞辨识 [J], 邓亮;杨平;程启明;杨旭红
3.含有色噪声的神经模糊Hammerstein模型分离辨识 [J], 方甜莲;贾立
4.针对Hammerstein模型的典型系统辨识方法 [J], 翟江涛;赫赤;姚志军;戴跃伟
5.基于Hammerstein模型的双闭环直流调速系统建模及参数辨识 [J], 李翠翠
因版权原因,仅展示原文概要,查看原文内容请购买。
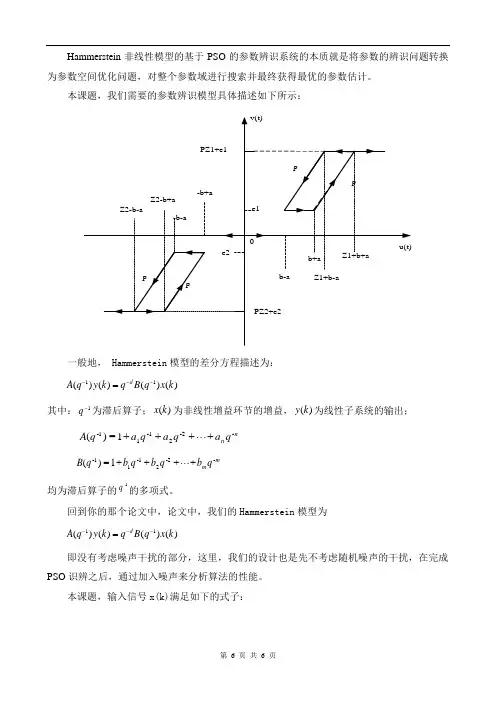
Hammerstein 非线性模型的基于PSO 的参数辨识系统的本质就是将参数的辨识问题转换为参数空间优化问题,对整个参数域进行搜索并最终获得最优的参数估计。
本课题,我们需要的参数辨识模型具体描述如下所示:一般地, Hammerstein 模型的差分方程描述为:11()()()()d A q y k q B q x k ---=其中:1-q 为滞后算子;)(k x 为非线性增益环节的增益,)(k y 为线性子系统的输出; nn q a q a q a q A -2-21-11-++++1=)(mm q b q b q b q B -2-21-11-++++1=)(均为滞后算子的1-q 的多项式。
回到你的那个论文中,论文中,我们的Hammerstein 模型为11()()()()d A q y k q B q x k ---=即没有考虑噪声干扰的部分,这里,我们的设计也是先不考虑随机噪声的干扰,在完成PSO 识辨之后,通过加入噪声来分析算法的性能。
本课题,输入信号x(k)满足如下的式子:1111111221122()()0()()0(())()()0(())()()0(())()()0()(())pZ e u t Z b aand u t orZ b a u t Z b aand u t p u t a b e b a u t Z b aand u t p u t a b e Z b a u t b aand u t p u t a b e b a u t Z b aand u t v t p u t a b e Z b a +>++∆>+-<<++∆<--++≤≤++∆>-++-+≤≤-+∆>+-+-≤≤+-∆<=+++--2222212()()0()()0()()0()()0()()00()()u t b aand u t pZ e u t Z b aand u t orZ b a u t Z b aand u t e b a u t b aand u t e b a u t b aand u t b a u t b aand u t ⎧⎫⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪≤≤--∆<⎨⎬⎪⎪+<--∆<--<<-+∆>⎪⎪-<<+∆>⎪⎪⎪⎪--<<-+∆<⎪⎪⎪⎪-+≤≤-∀∆⎩⎭这里,将V 改写为如下的式子:12311221122()()()()()()()()()pr pr v t pu t f t paf t pbf t pZ h t pZ h t e h t e h t =--++++其中:12311221122()()()()()()()()()pr pr v t pu t f t paf t pbf t pZ h t pZ h t e h t e h t =--++++11212()[(1([()()][(())]))(1([()()][()()]))](1)[(1([()()][()()]))(1([()()][()()]))]f t h u t Z b a h b a u t h Z b a u t h u t b a h u t Z b a h b a u t h Z b a u t h u t b a αα=--++++-+--+-+--++---+++--+----+--+21212()[(1([()()][(())]))(1([()()][()()]))](1)[(1([()()][()()]))(1([()()][()()]))]f t h u t Z b a h b a u t h Z b a u t h u t b a h u t Z b a h b a u t h Z b a u t h u t b a αα=--++++-+--+-+--+----+++--+----+--+31212()[(1([()()][(())]))(1([()()][()()]))](1)[(1([()()][()()]))(1([()()][()()]))]f t h u t Z b a h b a u t h Z b a u t h u t b a h u t Z b a h b a u t h Z b a u t h u t b a αα=--++++----+-+--++---+++-------+--+111222()[()()](1)[()()]()[()()](1)[()()]h t h u t Z b a h u t Z b a h t h Z b a u t h Z b a u t αααα=-+++--+-=-+-+----12()[()()]()[()()]pr pr h t h u t b a h t h b a u t =--=-+-本系统,需要识辨的系统为:121()(1)(2)()(1)y t a y t a y t v t b v t =----++-1212()(1)0.15(2)0.2(1)0.35(2)2,0.5,1, 1.2,1, 1.5, 1.2y t v t v t y t y t p a b Z Z e e =-+-+---=====-==-需要辨识的参数1212112[,,,,,,,,,]p pa pb pZ pZ e e b a a下面为代码的仿真说明部分:根据论文中的理论,我们首先需要将Hammerstein非线性模型进行分离,得到8个不同的模型,逐个对其参数进行识辨。



基于组合式信号的Hammerstein OE模型辨识引言随着工业自动化和智能化的不断发展,对于系统建模和控制算法的需求也在不断增加。
在系统辨识领域,Hammerstein模型是一种常用的非线性系统建模方法,它将系统分为非线性静态部分和线性动态部分,并将二者组合起来进行建模。
而对于Hammerstein模型的参数辨识,则是实际应用中的一个重要问题。
本文将讨论基于组合式信号的Hammerstein OE(Output Error)模型的辨识方法,旨在为相关领域的研究者提供参考和借鉴。
一、Hammerstein模型简介Hammerstein模型是一种将非线性静态部分和线性动态部分组合在一起进行建模的系统模型。
它通常由两部分组成:非线性静态函数和线性动态系统。
1. 非线性静态部分非线性静态部分通常由一个非线性函数表示,其输出只与输入相关,而与时间无关。
非线性部分可以是各种不同的函数,如幂函数、指数函数、对数函数等,常用的非线性函数包括Sigmoid函数、Tanh函数等。
线性动态部分通常由差分方程或传递函数表示,描述系统的动态响应。
Hammerstein模型的建模和辨识可以用于描述许多实际系统,如电机系统、水泵系统、飞机系统等。
在实际应用中,对于Hammerstein模型的参数辨识是非常重要的,因为只有辨识到准确的模型参数,才能够进行有效的控制和优化。
在Hammerstein模型的辨识过程中,需要收集系统的输入输出数据,并通过合适的辨识算法来估计模型的参数。
而对于Hammerstein模型的辨识,OE模型是一种常用的形式,其中O代表输出,E代表误差。
1. 组合式信号的设计组合式信号通常由多个不同频率、不同幅值的正弦波信号组合而成,可以采用正弦波叠加的方式进行设计。
通过合理选择正弦波信号的频率和幅值,可以使得系统在不同频率处产生较大的输出响应,从而更好地估计系统的频率响应特性。
2. 数据采集使用设计好的组合式信号对待辨识系统进行激励,并采集系统的输入输出数据。

(LSE —SVD),仅需假设输入为持续激励,并可获得在有噪声情况下系统的有效辨识,但这种算法只在被控对象可无误差的分解为非线性和线性环节且非线性部分的基先验已知时,且最小二乘所得参数矩阵的秩为l ,才能保证辨识误差在额定范围内,否则辨识误差将受到参数矩阵其他特征值干扰,无法保证辨识落入允许范围;第四类是参]5[数过度化法,是使Hamerstein 系统过度参数化,从而在未知参数下过度参数化的系]7,6[统就线性化了,然后就可以使用线性估计算法进行辨识,这种方法的难点在于所得到的线性系统维数可能很大,因此系统的收敛性和鲁棒性就可能成问题;第五类子空间辨识法,通常适用于多输入、多输出的非线性系统的辨识。
]9,8[在近年来的研究中,基于群集智能方法的发展,越来越多演化计算技术被应用到复杂系统辨识当中。
如蚁群算法(ACO ),粒子群优化(PSO )算法和细菌觅食(BFO )优化算法等在Hammerstein 模型的辨识中得到了广泛的发展和应用,其理论也在不断地改进和完善。
下面简要介绍下粒子群优化(PSO )算法和细菌觅食(BFO )优化算法。
1. 粒子群优化PSO 算法1995年,Kennedy 和Eberhar 提出一种较为新颖的优化算法—— 粒子群优化算]11,10[法(ParticleSwarm Optimization ,PSO)。
该算法与蚁群算法(AntColony Optimization ,ACO)相似,也是一种基于群体智能(Swarm Intelligence ,SI)的优化算法,即模拟鸟群觅食的过程,而其功能与遗传算法(Genetic Algorithm ,GA)非常相似。
PSO 优化算法起源于对简单社会系统的模拟,PSO 算法是一种有效的解决优化问题的群集智能算法,它的突出特点是算法中需要选择的参数少,程序实现简单,并在种群数量、寻优速度等方面较其他进化算法具有一定的优势,尤其是在高噪信比情况下,也收到较满意的结果。


基于Hsia算法的Hammerstein模型辨识
沈同全;孙逢春;程夕明
【期刊名称】《系统仿真学报》
【年(卷),期】2007(19)23
【摘要】针对采用广义最小二乘法(GLS)辨识Hammerstein模型时反复滤波,计算效率不高的问题,提出了利用Hsia算法进行Hammerstein模型辨识的策略。
该法不需滤波,克服最小二乘解有偏性的同时,消除了Hammerstein模型中非线性增益的阶次对计算效率降低的作用,编程简单,计算快速。
仿真及试验研究证明该法省时明显,值得推广。
【总页数】3页(P5373-5375)
【关键词】非线性动态过程;Hammerstein模型;Hsia算法;系统辨识
【作者】沈同全;孙逢春;程夕明
【作者单位】北京理工大学机械与车辆工程学院
【正文语种】中文
【中图分类】TP391.9
【相关文献】
1.基于Hammerstein-Wiener模型的非线性系统盲辨识算法及仿真 [J], 席宏光;李昇;于帅涛
2.基于混合粒子群优化算法辨识Hammerstein模型 [J], 徐小平;钱富才;王峰
3.基于量子遗传算法的循环流化床锅炉Hammerstein模型辨识 [J], 王东风;任燕
燕;刘长良;韩璞;
4.基于APSO_WLSSV M算法的Hammerstein ARMAX模型参数辨识 [J], 郭伟;李明家;李涛;乔东东;魏妙
5.基于APSO_WLSSVM算法的Hammerstein ARMAX模型参数辨识 [J], 郭伟;李明家;李涛;乔东东;魏妙;;;;;;;
因版权原因,仅展示原文概要,查看原文内容请购买。
基于函数连接神经网络的传感器Hammerstein模型辨识研究传感器Hammerstein模型是一种用于建模非线性系统的重要工具,通过将线性动力学系统与非线性静态模块相连接,实现对非线性系统的建模与辨识。
在传感器领域,准确的模型辨识对于系统的设计和性能优化至关重要。
本文将介绍使用基于函数连接神经网络的方法来进行传感器Hammerstein模型的辨识研究。
1. 引言传感器是现代工业控制和监测系统中不可或缺的组成部分。
然而,由于传感器本身的非线性特性,常导致模型辨识的困难。
因此,传感器模型的建立与辨识成为热门研究领域。
Hammerstein模型作为一种常用的非线性模型,具有较好的适应性和表达能力。
2. 传感器Hammerstein模型的特点传感器Hammerstein模型由线性动力学系统和非线性静态模块连接而成。
线性动力学系统通常用差分方程或微分方程表示,而非线性静态模块则可以通过函数连接神经网络来表示。
传感器Hammerstein模型的特点在于其具有复杂的非线性映射特性,能够很好地描述传感器的非线性动态行为。
3. 函数连接神经网络函数连接神经网络(Functionally Connected Neural Networks,简称FCNN)是一种通过将多个神经网络连接在一起构成一个整体网络,来实现复杂非线性函数逼近的方法。
FCNN能够通过学习样本数据集中的非线性映射关系,从而实现对传感器Hammerstein模型的辨识。
4. 传感器Hammerstein模型辨识方法传感器Hammerstein模型辨识的关键在于寻找合适的训练样本集和优化算法。
在这里,我们采用了基于函数连接神经网络的方法。
具体的模型辨识步骤如下:a) 收集传感器输入和输出数据,构建样本数据集。
b) 构建函数连接神经网络架构,确定神经网络的层数和节点数。
c) 使用样本数据集对函数连接神经网络进行训练。
d) 通过优化算法对函数连接神经网络进行参数调整,使得模型的输出与实际输出之间的误差最小化。
基于合作协同进化算法的非线性系统辨识研究針对Hammerstein模型中的非线性环节,传统算法不易辨识,导致辨识精度低等问题。
应采用合作协同进化算法利用异构双种群搜索的方式,对Hammerstein 模型的线性环节和非线性环节分开辨识,在邻域模型中彼此合作构成完整解,根据适应度函数值寻求最优解。
实验证明,改进算法比传统算法具有更高的精度、稳定性以及快速性,从而验证了此算法在非线性系统辨识方面的优越性。
标签:协同进化算法;粒子群;Hammerstein模型;系统辨识1引言所谓的系统辨识问题就是根据工业过程中的过程输入和输出观测数据,按照某种规则建立生产过程中的一种较为实用的模型的理论和方法。
Hammerstein模型是典型的非线性系统模型,应用广泛,结构复杂,众多学者采用传统的群智能算法对该模型进行辨识,但这些算法均存在对非线性环节不易辨识问题,导致辨识精度低等缺点。
针对该问题,本文提出异构双种群合作协同算法对Hammerstein模型进行辨识,其思想为采用不同机制的双种群在解空间中并行搜索,每个种群个体均为解的一部分,在邻域模型中合作构成完整解,根据适应度函数选出最优值。
仿真实验证明,这一算法有效的解决了传统算法在非线性系统辨识中的瓶颈问题,这对非线性系统辨识领域的研究具有非常重要的意义。
2Hammerstein模型的原理Hammerstein模型由增益环节和动态线性环节构成,结构图型如图1所示。
Hammerstein模型的方程表达式为:A(q-1)y(k)=B(q-1)x(k)+C(q-1)ξ(k)x(k)=r1u(k)+r2u2(k)+r3u3(k)+…+rpup(k)A(q-1)=1+a1q-1+a2q-2+…+amq-mB(q-1)=b1q-1+b2q-2+…+bnq-nC(q-1)=1+c1q-1+c2q-2+…+crq-r (1)其中,q-1为滞后算子,SymbolxA@ (k)是均值为零,方差为σ2的高斯白噪声序列,u(k)和y (k)分别为系统的输入和输出,SymbolxA@ (k)和u(k)相互无关。
一种辨识 Hammerstein 模型的新方法
李文江;林思建;王璇
【期刊名称】《计量学报》
【年(卷),期】2015(000)004
【摘要】为了提高非线性 Hammerstein 模型的辨识精度,提出一种利用混合优化算法对非线性模型进行辨识的新方法。
该算法的基本思想是把非线性系统的参数辨识问题转化为参数空间上的函数优化问题,然后利用遗传算法和改进的粒子群优化算法相结合寻求并获得参数问题的最优解。
最后通过仿真研究表明,该方法对于非线性辨识具有较好的有效性和鲁棒性,获得了良好的辨识效果,是一种可行的解决非线性辨识问题的方法。
【总页数】5页(P418-422)
【作者】李文江;林思建;王璇
【作者单位】辽宁工程技术大学电气与控制工程学院,辽宁葫芦岛 125105;辽宁工程技术大学电气与控制工程学院,辽宁葫芦岛 125105;辽宁工程技术大学电气与控制工程学院,辽宁葫芦岛 125105
【正文语种】中文
【中图分类】TB973
【相关文献】
1.一种P ol SAR图像统计模型辨识新方法 [J], 崔浩贵;刘涛;单鸿昌;蒋宇中;高俊
2.基于Wiener-Hammerstein模型的一种系统辨识方法 [J], 白克强
3.基于Hammerstein模型描述的非线性系统辨识新方法 [J], 向微;陈宗海
4.一种辨识Hammerstein模型的新方法 [J], 郎自强
5.一种辨识Wiener-Hammerstein模型的新方法 [J], 徐小平;钱富才;王峰
因版权原因,仅展示原文概要,查看原文内容请购买。
开题报告
电气工程与自动化
非线性Hammerstein模型的辨识
一、选题的背景与意义
系统辨识是是现代控制理论中的一个重要分支。
通过辨识建立数学模型的目的是估计表征系统行为的重要参数,建立一个能模仿真实系统行为的模型,用当前可测量的系统的输入和输出预测系统输出的未来演变,以及控制器的设计。
非线性系统辨识是系统辨识的一个重要的发展方向,一直是现代辨识领域中的一个主要课题,对其研究有十分重要的理论和实际意义。
非线性问题的主要困难之一是一直缺乏描述各种非线性系统特性的统一的数学模型。
为此,人们提出了多种类型的模型,如块联模型]1[
、神经网络模型、双线性模型、非线性参数模型等等。
]2[]3[
Hammerstein模型属于块联模型,由一个线性动态系统跟随一个非线性静态模块构成。
自从Narendra& Gallman 1966年提出了Hammerstein模型后,由于模型结构简
]4[
单且能有效地描述常见的非线性动态系统特性,所以许多学者相继研究了Hammerstein 模型参数的估计方法,近年来Hammerstein模型被广泛地应用于非线性系统辨识。
辨识Hammerstein模型的意义在于:利用辨识结果获得中间层输出,选择合适的性能指标,就可以把原非线性系统的控制问题分解为线性模块的动态优化问题和非线性模块的静态求根问题,因此可以有效结合线性模型预测控制的成熟理论解决这类非线性对象的控制问题,避免传统非线性控制方法计算量大,收敛性和闭环稳定性不能得到保证等诸多问题。
二、研究的基本内容与模拟解决的主要问题:
针对Hammerstein模型的辨识问题,可以归结为线性模块的动态优化问题和非线性模块的静态求根问题。
因此研究的重点就是如何运用比较新颖的优化算法得到Hammerstein模型的参数解集,并能通过和传统算法的比较论证阐述采用方法的合理性,可行性及有效性。
具体需要解决的问题包括以下几点:
1.什么是Hammerstein模型,它的基本结构式怎么样的;
2.确定Hammerstein非线性系统辨识的思想和实现方法;
3.熟悉PSO/BFO优化算法和熟悉最小二乘法估计方法;。