[推荐学习]2018届高三数学一轮复习第八章立体几何第三节直线平面平行的判定与性质夯基提能

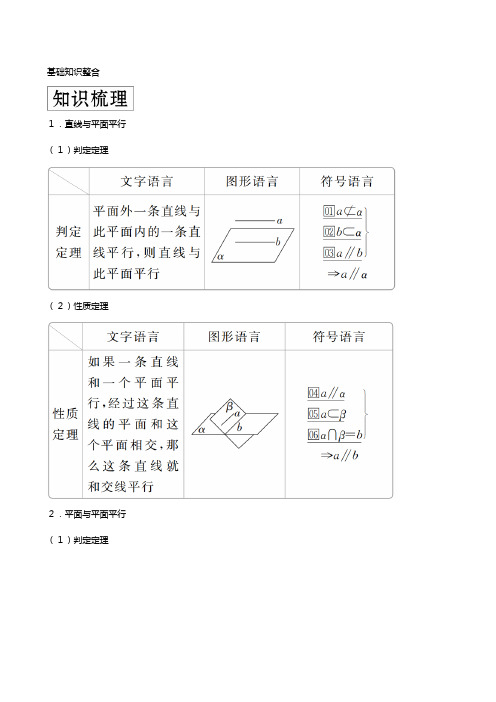
基础知识整合１．直线与平面平行（１）判定定理（２）性质定理２．平面与平面平行（１）判定定理（２）性质定理１．垂直于同一条直线的两个平面平行，即若a⊥α，a⊥β，则α∥β.２．垂直于同一个平面的两条直线平行，即若a⊥α，b⊥α，则a∥Ｂ．３．平行于同一个平面的两个平面平行，即若α∥β，β∥γ，则α∥γ.１．已知直线l和平面α，若l∥α，P∈α，则过点P且平行于l的直线（）Ａ．只有一条，不在平面α内Ｂ．只有一条，且在平面α内Ｃ．有无数条，一定在平面α内Ｄ．有无数条，不一定在平面α内答案B解析过直线外一点作该直线的平行线有且只有一条，因为点P在平面α内，所以这条直线也应该在平面α内．２．（２0１9·吉林普通中学模拟）已知α，β表示两个不同的平面，直线m是α内一条直线，则“α∥β ”是“m∥β ”的（）Ａ．充分不必要条件Ｂ．必要不充分条件Ｃ．充要条件Ｄ．既不充分也不必要条件答案A解析由α∥β，m⊂α，可得m∥β；反过来，由m∥β，m⊂α，不能推出α∥β.综上，“α∥β ”是“m∥β ”的充分不必要条件．３．若空间四边形ABCD的两条对角线AC，BD的长分别是8,１２，过AB的中点E且平行于BD，AC 的截面四边形的周长为（）Ａ．１0 Ｂ．２0Ｃ．8 Ｄ．４答案B解析设截面四边形为EFGH，F，G，H分别是BC，CD，DA的中点，∴EF＝GH＝４，FG＝HE＝6．∴周长为２×（４＋6）＝２0．４．如图所示，P为矩形ABCD所在平面外一点，矩形对角线交点为O，M为PB的中点，给出下列五个结论：１PD∥平面AMC；２OM∥平面PCD；３OM∥平面PDA；４OM∥平面PBA；５OM∥平面PBＣ．其中正确的个数是（）Ａ．１Ｂ．２Ｃ．３Ｄ．４答案C解析矩形ABCD的对角线AC与BD交于点O，所以O为BD的中点．在△PBD中，M是PB的中点，所以OM是△PBD的中位线，OM∥PD，则PD∥平面AMC，OM∥平面PCD，且OM∥平面PDＡ．因为M∈PB，所以OM与平面PBA，平面PBC相交．５．（２0１9·南通模拟）如图，四棱锥P—ABCD的底面是一直角梯形，AB∥CD，BA⊥AD，CD＝２AB，PA⊥底面ABCD，E为PC的中点，则BE与平面PAD的位置关系为________．答案平行解析取PD的中点F，连接EF，AF，在△PCD中，EF綊错误!CＤ．又∵AB∥CD且CD＝２AB，∴EF綊AB，∴四边形ABEF是平行四边形，∴EB∥AF.又∵EB⊄平面PAD，AF⊂平面PAD，∴BE∥平面PAＤ．6．如图所示，ABCD—A１B１C１D１是棱长为a的正方体，M，N分别是下底面的棱A１B１，B１C１的中点，P是上底面的棱AD上的一点，AP＝错误!，过P，M，N的平面交上底面于PQ，Q在CD上，则PQ＝________.答案错误!a解析如图所示，连接AC，易知MN∥平面ABCＤ．∴MN∥PQ.又∵MN∥AC，∴PQ∥AＣ．又∵AP＝错误!，∴错误!＝错误!＝错误!＝错误!.∴PQ＝错误!AC＝错误!×错误!a＝错误!Ａ．核心考向突破考向一有关平行关系的判断例１（１）（２0１9·湖南联考）已知m，n是两条不同的直线，α，β，γ是三个不同的平面，下列命题中正确的是（）Ａ．若m∥α，n∥α，则m∥nＢ．若m∥α，m∥β，则α∥βＣ．若α⊥γ，β⊥γ，则α∥βＤ．若m⊥α，n⊥α，则m∥n答案D解析A中，两直线可能平行、相交或异面；B中，两平面可能平行或相交；C中，两平面可能平行或相交；D中，由线面垂直的性质定理可知结论正确，故选Ｄ．（２）（２0１9·四川成都模拟）已知直线a，b和平面α，下列说法中正确的是（）Ａ．若a∥α，b⊂α，则a∥bＢ．若a⊥α，b⊂α，则a⊥bＣ．若a，b与α所成的角相等，则a∥bＤ．若a∥α，b∥α，则a∥b答案B解析对于A，若a∥α，b⊂α，则a∥b或a与b异面，故A错误；对于B，利用线面垂直的性质，可知若a⊥α，b⊂α，则a⊥b，故B正确；对于C，若a，b与α所成的角相等，则a与b相交、平行或异面，故C错误；对于D，由a∥α，b∥α，得a，b之间的位置关系可以是相交、平行或异面，故D错误．触类旁通解决有关线面平行、面面平行的基本问题的注意点（１）判定定理与性质定理中易忽视的条件，如线面平行的判定定理中，条件“线在面外”易忽视．（２）结合题意构造或绘制图形，结合图形作出判断．（３）举反例否定结论或用反证法推断命题是否正确．即时训练１．（２0１9·潍坊模拟）已知m，n，l１，l２表示直线，α，β表示平面．若m⊂α，n⊂α，l１⊂β，l２⊂β，l１∩l２＝M，则α∥β的一个充分条件是（）Ａ．m∥β且l１∥α Ｂ．m∥β且n∥βＣ．m∥β且n∥l２Ｄ．m∥l１且n∥l２答案D解析由定理“如果一个平面内有两条相交直线分别与另一个平面平行，那么这两个平面平行”可得，由选项D可推知α∥β.故选Ｄ．２．已知m，n表示两条不同的直线，α表示平面，则下列说法正确的是（）Ａ．若m∥α，n∥α，则m∥nＢ．若m⊥α，n⊂α，则m⊥nＣ．若m⊥α，m⊥n，则n∥αＤ．若m∥α，m⊥n，则n⊥α答案B解析由题可知，若m∥α，n∥α，则m与n平行、相交或异面，所以A错误；若m⊥α，n⊂α，则m ⊥n，故B正确；若m⊥α，m⊥n，则n∥α或n⊂α，故C错误；若m∥α，m⊥n，则n∥α或n⊥α或n 与α相交，故D错误．考向二直线与平面平行的判定与性质角度错误!用线线平行证明线面平行例２（１）在四棱锥O—ABCD中，底面ABCD是平行四边形，M为OA的中点，N为BC的中点，证明：直线MN∥平面OCＤ．证明证法一：取OB的中点E，连接ME，NE，如图１，则ME∥AB，又AB∥CD，所以ME∥CD，又NE∥OC，且ME∩NE＝E，OC∩CD＝C，所以平面MNE∥平面OCD，所以MN∥平面OCＤ．证法二：取OD的中点F，连接MF，CF，如图２，则MF綊错误!AD，又底面ABCD是平行四边形，则NC綊错误!AD，所以MF綊NC，所以四边形MNCF是平行四边形，所以MN∥FC，又MN⊄平面OCD，FC⊂平面OCD，根据直线与平面平行的判定定理可知，直线MN∥平面OCＤ．（２）（２0１9·山东模拟）如图，在三棱台DEF—ABC中，AB＝２DE，G，H分别为AC，BC的中点．求证：BD∥平面FGH.证明证法一：连接DG，CD，设CD∩GF＝M，连接MH.在三棱台DEF—ABC中，AB＝２DE，G为AC的中点，可得DF∥GC，DF＝GC，所以四边形DFCG为平行四边形，则M为CD的中点，又H为BC的中点，所以HM∥BＤ．又HM⊂平面FGH，BD⊄平面FGH，所以BD∥平面FGH.证法二：在三棱台DEF—ABC中，由BC＝２EF，H为BC的中点，可得BH∥EF，BH＝EF，所以四边形HBEF为平行四边形，BE∥HF.在△ABC中，G为AC的中点，H为BC的中点，所以GH∥AＢ．又GH∩HF＝H，所以平面FGH∥平面ABEＤ．因为BD⊂平面ABED，所以BD∥平面FGH.角度错误!用线面平行证明线线平行例３如图，在多面体ABCDEF中，DE⊥平面ABCD，AD∥BC，平面BCEF∩平面ADEF＝EF，∠BAD＝60°，AB＝２，DE＝EF＝１．（１）求证：BC∥EF；（２）求三棱锥B—DEF的体积．解（１）证明：∵AD∥BC，AD⊂平面ADEF，BC⊄平面ADEF，∴BC∥平面ADEF.又BC⊂平面BCEF，平面BCEF∩平面ADEF＝EF，∴BC∥EF.（２）过点B作BH⊥AD于点H.∵DE⊥平面ABCD，BH⊂平面ABCD，∴DE⊥BH.∵AD⊂平面ADEF，DE⊂平面ADEF，AD∩DE＝D，∴BH⊥平面ADEF.∴BH是三棱锥B—DEF的高．在Rt△ABH中，∠BAD＝60°，AB＝２，故BH＝错误!.∵DE⊥平面ABCD，AD⊂平面ABCD，∴DE⊥AＤ．由（１）知BC∥EF，且AD∥BC，∴AD∥EF，∴DE⊥EF.∴三棱锥B—DEF的体积V＝错误!×S△DEF×BH＝错误!×错误!×１×１×错误!＝错误!.触类旁通判断或证明线面平行的常用方法（１）利用线面平行的定义（无公共点）．（２）利用线面平行的判定定理（a⊄α，b⊂α，a∥b⇒a∥α）．错误!（４）利用面面平行的性质（α∥β，a⊄α，a⊄β，a∥α⇒a∥β）．即时训练３．（２0１9·长春一调）如图所示，E是以AB为直径的半圆弧上异于A，B的点，矩形ABCD 所在平面垂直于该半圆所在的平面．（１）求证：EA⊥EC；（２）设平面ECD与半圆弧的另一个交点为F.求证：EF∥AＢ．证明（１）∵E是半圆上异于A，B的点，∴AE⊥EＢ．又∵平面ABCD⊥平面ABE，平面ABCD∩平面ABE＝AB，CB⊥AB，∴CB⊥平面ABE.又∵AE⊂平面ABE，∴CB⊥AE.∵BC∩BE＝B，∴AE⊥平面CBE.又∵EC⊂平面CBE.∴AE⊥EＣ．（２）∵CD∥AB，AB⊂平面ABE，CD⊄平面ABE，∴CD∥平面ABE.又∵平面CDE∩平面ABE＝EF.∴CD∥EF.又∵CD∥AＢ．∴EF∥AＢ．考向三面面平行的判定与性质例４（２0１8·云南模拟）如图所示的几何体ABCDFE中，△ABC，△DFE都是等边三角形，且所在平面平行，四边形BCED是边长为２的正方形，且所在平面垂直于平面ABＣ．（１）求几何体ABCDFE的体积；（２）证明：平面ADE∥平面BCF.解（１）取BC的中点O，ED的中点G，连接AO，OF，FG，AG.∵AO⊥BC，AO⊂平面ABC，平面BCED⊥平面ABC，∴AO⊥平面BCEＤ．同理FG⊥平面BCEＤ．∵AO＝FG＝错误!，∴VABCDFE＝错误!×４×错误!×２＝错误!.（２）证明：由（１）知AO∥FG，AO＝FG，∴四边形AOFG为平行四边形，∴AG∥OF，又∵DE∥BC，DE∩AG＝G，DE⊂平面ADE，AG⊂平面ADE，FO∩BC＝O，FO⊂平面BCF，BC⊂平面BCF，∴平面ADE∥平面BCF.触类旁通判定面面平行的方法（１）利用定义：即证两个平面没有公共点（不常用）．错误!错误!４利用平面平行的传递性，即两个平面同时平行于第三个平面，则这两个平面平行客观题可用.即时训练４．如图，在四棱锥P—ABCD中，∠ABC＝∠ACD＝90°，∠BAC＝∠CAD＝60°，PA⊥平面ABCD，PA＝２，AB＝１．设M，N分别为PD，AD的中点．（１）求证：平面CMN∥平面PAB；（２）求三棱锥P—ABM的体积．解（１）证明：∵M，N分别为PD，AD的中点，∴MN∥PA，又MN⊄平面PAB，PA⊂平面PAB，∴MN∥平面PAＢ．在Rt△ACD中，∠CAD＝60°，CN＝AN，∴∠ACN＝60°.又∠BAC＝60°，∴CN∥AＢ．∵CN⊄平面PAB，AB⊂平面PAB，∴CN∥平面PAＢ．又CN∩MN＝N，∴平面CMN∥平面PAＢ．（２）由（１）知，平面CMN∥平面PAB，∴点M到平面PAB的距离等于点C到平面PAB的距离．∵AB＝１，∠ABC＝90°，∠BAC＝60°，∴BC＝错误!，∴三棱锥P—ABM的体积V＝VM—PAB＝VC—PAB＝VP—ABC＝错误!×错误!×１×错误!×２＝错误!.。

2018高考数学异构异模复习考案 第八章 立体几何 8.3 直线、平面平行的判定与性质撬题 理1.已知m ，n 是两条不同直线，α，β是两个不同平面，则下列命题正确的是( ) A ．若α，β垂直于同一平面，则α与β平行 B ．若m ，n 平行于同一平面，则m 与n 平行C ．若α，β不平行，则在α内不存在与β平行的直线D ．若m ，n 不平行，则m 与n 不可能垂直于同一平面 答案 D解析 A 中，垂直于同一个平面的两个平面可能相交也可能平行，故A 错误；B 中，平行于同一个平面的两条直线可能平行、相交或异面，故B 错误；C 中，若两个平面相交，则一个平面内与交线平行的直线一定和另一个平面平行，故C 错误；D 中，若两条直线垂直于同一个平面，则这两条直线平行，所以若两条直线不平行，则它们不可能垂直于同一个平面，故D 正确．2．如图所示，在多面体A 1B 1D 1DCBA 中，四边形AA 1B 1B ，ADD 1A 1，ABCD 均为正方形，E 为B 1D 1的中点，过A 1，D ，E 的平面交CD 1于F .(1)证明：EF ∥B 1C ；(2)求二面角E －A 1D －B 1的余弦值．解 (1)证明：由正方形的性质可知A 1B 1∥AB ∥DC ，且A 1B 1＝AB ＝DC ，所以四边形A 1B 1CD 为平行四边形，从而B 1C ∥A 1D ，又A 1D ⊂面A 1DE ，B 1C ⊄面A 1DE ，于是B 1C ∥面A 1DE .又B 1C ⊂面B 1CD 1，面A 1DE ∩面B 1CD 1＝EF ，所以EF ∥B 1C .(2)因为四边形AA 1B 1B ，ADD 1A 1，ABCD 均为正方形，所以AA 1⊥AB ，AA 1⊥AD ，AB ⊥AD 且AA 1＝AB ＝AD ，以A 为原点，分别以AB →，AD →，AA 1→为x 轴，y 轴和z 轴单位正向量建立如图所示的空间直角坐标系，可得点的坐标A (0,0,0)，B (1,0,0)，D (0,1,0)，A 1(0,0,1)，B 1(1,0,1)，D 1(0,1,1)，而E 点为B 1D 1的中点，所以E 点的坐标为(0.5,0.5,1)．设面A 1DE 的法向量n 1＝(r 1，s 1，t 1)，而该面上向量A 1E →＝(0.5,0.5,0)，A 1D →＝(0,1，－1)，由n 1⊥A 1E →，n 1⊥A 1D →得⎩⎪⎨⎪⎧0.5r 1＋0.5s 1＝0，s 1－t 1＝0，(－1,1,1)为其一组解，所以可取n 1＝(－1,1,1)．设面A 1B 1CD 的法向量n 2＝(r 2，s 2，t 2)，而该面上向量A 1B 1→＝(1,0,0)，A 1D →＝(0,1，－1)，由此同理可得n 2＝(0,1,1)．所以结合图形知二面角E －A 1D －B 1的余弦值为|n 1·n 2||n 1|·|n 2|＝23×2＝63.3．如图，在几何体ABCDE 中，四边形ABCD 是矩形，AB ⊥平面BEC ，BE ⊥EC ，AB ＝BE ＝EC ＝2，G ，F 分别是线段BE ，DC 的中点．(1)求证：GF ∥平面ADE ；(2)求平面AEF 与平面BEC 所成锐二面角的余弦值． 解法一 (1)证明：如图，取AE 的中点H ，连接HG ，HD ，又G 是BE 的中点， 所以GH ∥AB ，且GH ＝12AB .又F 是CD 的中点， 所以DF ＝12CD .由四边形ABCD 是矩形得，AB ∥CD ，AB ＝CD ，所以GH ∥DF ，且GH ＝DF ，从而四边形HGFD 是平行四边形，所以GF ∥DH . 又DH ⊂平面ADE ，GF ⊄平面ADE ， 所以GF ∥平面ADE .(2)如图，在平面BEC 内，过B 点作BQ ∥EC .因为BE ⊥CE ，所以BQ ⊥BE .又因为AB ⊥平面BEC ，所以AB ⊥BE ，AB ⊥BQ .以B 为原点，分别以BE →，BQ →，BA →的方向为x 轴，y 轴，z 轴的正方向建立空间直角坐标系，则A (0,0,2)，B (0,0,0)，E (2,0,0)，F (2,2,1)．因为AB ⊥平面BEC ，所以BA →＝(0,0,2)为平面BEC 的法向量． 设n ＝(x ，y ，z )为平面AEF 的法向量． 又AE →＝(2,0，－2)，AF →＝(2,2，－1)，由⎩⎪⎨⎪⎧n ·AE →＝0，n ·AF →＝0，得⎩⎪⎨⎪⎧2x －2z ＝0，2x ＋2y －z ＝0，取z ＝2，得n ＝(2，－1,2)．从而cos 〈n ，BA →〉＝n ·BA→|n |·|BA →|＝43×2＝23， 所以平面AEF 与平面BEC 所成锐二面角的余弦值为23.解法二 (1)证明：如下图，取AB 中点M ，连接MG ，MF .又G 是BE 的中点，可知GM ∥AE . 又AE ⊂平面ADE ，GM ⊄平面ADE ， 所以GM ∥平面ADE .在矩形ABCD中，由M，F分别是AB，CD的中点得MF∥AD.又AD⊂平面ADE，MF⊄平面ADE，所以MF∥平面ADE.又因为GM∩MF＝M，GM⊂平面GMF，MF⊂平面GMF，所以平面GMF∥平面ADE.因为GF⊂平面GMF，所以GF∥平面ADE.(2)同解法一．4．一个正方体的平面展开图及该正方体的直观图的示意图如图所示．在正方体中，设BC的中点为M，GH的中点为N.(1)请将字母F，G，H标记在正方体相应的顶点处(不需说明理由)；(2)证明：直线MN∥平面BDH；(3)求二面角A－EG－M的余弦值．解(1)点F，G，H的位置如下图所示．(2)证明：连接BD，设O为BD的中点，连接OM，OH.因为M，N分别是BC，GH的中点，所以OM ∥CD ，且OM ＝12CD ，HN ∥CD ，且HN ＝12CD .所以OM ∥HN ，OM ＝HN .所以MNHO 是平行四边形，从而MN ∥OH . 又MN ⊄平面BDH ，OH ⊂平面BDH ， 所以MN ∥平面BDH .(3)解法一：连接AC ，过M 作MP ⊥AC 于P . 在正方体ABCD －EFGH 中，AC ∥EG ，所以MP ⊥EG . 过P 作PK ⊥EG 于K ，连接KM . 所以EG ⊥平面PKM ，从而KM ⊥EG . 所以∠PKM 是二面角A －EG －M 的平面角． 设AD ＝2，则CM ＝1，PK ＝2. 在Rt △CMP 中，PM ＝CM sin45°＝22. 在Rt △PKM 中，KM ＝PK 2＋PM 2＝322.所以cos ∠PKM ＝PK KM ＝223.即二面角A －EG －M 的余弦值为223.解法二：如下图，以D 为坐标原点，分别以DA →，DC →，DH →的方向为x ，y ，z 轴的正方向，建立空间直角坐标系D －xyz .设AD ＝2，则M (1,2,0)，G (0,2,2)，E (2,0,2)，O (1,1,0)，所以GE →＝(2，－2,0)，MG →＝(－1,0,2)． 设平面EGM 的一个法向量为n 1＝(x ，y ，z )， 由⎩⎪⎨⎪⎧n 1·GE →＝0，n 1·MG →＝0，得⎩⎪⎨⎪⎧2x －2y ＝0，－x ＋2z ＝0，取x ＝2，得n 1＝(2,2,1)．在正方体ABCD －EFGH 中，DO ⊥平面AEGC ，则可取平面AEG 的一个法向量为n 2＝DO →＝(1,1,0)．所以cos 〈n 1，n 2〉＝n 1·n 2|n 1|·|n 2|＝2＋2＋04＋4＋1×1＋1＋0＝223，故二面角A －EG －M 的余弦值为223.5．如图，在三棱台DEF －ABC 中，AB ＝2DE ，G ，H 分别为AC ，BC 的中点．(1)求证：BD ∥平面FGH ；(2)若CF ⊥平面ABC ，AB ⊥BC ，CF ＝DE ，∠BAC ＝45°，求平面FGH 与平面ACFD 所成的角(锐角)的大小．解 (1)证法一：连接DG ，CD ，设CD ∩GF ＝O ，连接OH . 在三棱台DEF －ABC 中，AB ＝2DE ，G 为AC 的中点，可得DF ∥GC ，DF ＝GC ，所以四边形DFCG 为平行四边形． 则O 为CD 的中点， 又H 为BC 的中点， 所以OH ∥BD .又OH ⊂平面FGH ，BD ⊄平面FGH ， 所以BD ∥平面FGH .证法二：在三棱台DEF －ABC 中， 由BC ＝2EF ，H 为BC 的中点， 可得BH ∥EF ，BH ＝EF ，所以四边形BHFE 为平行四边形， 可得BE ∥HF .在△ABC 中，G 为AC 的中点，H 为BC 的中点， 所以GH ∥AB .又GH ∩HF ＝H ，所以平面FGH ∥平面ABED . 因为BD ⊂平面ABED ， 所以BD ∥平面FGH .(2)解法一：设AB ＝2，则CF ＝1. 在三棱台DEF －ABC 中，G 为AC 的中点，由DF ＝12AC ＝GC ，可得四边形DGCF 为平行四边形， 因此DG ∥FC .又FC ⊥平面ABC ，所以DG ⊥平面ABC .连接GB ，在△ABC 中，由AB ⊥BC ，∠BAC ＝45°，G 是AC 中点， 所以AB ＝BC ，GB ⊥GC ， 因此GB ，GC ，GD 两两垂直．以G 为坐标原点，建立如图所示的空间直角坐标系G －xyz . 所以G (0,0,0)，B (2，0,0)，C (0，2，0)，D (0,0,1)．可得H ⎝ ⎛⎭⎪⎫22，22，0，F (0，2，1)． 故GH →＝⎝⎛⎭⎪⎫22，22，0，GF →＝(0，2，1)设n ＝(x ，y ，z )是平面FGH 的法向量，则 由⎩⎪⎨⎪⎧n ·GH →＝0，n ·GF →＝0，可得⎩⎨⎧x ＋y ＝0，2y ＋z ＝0.可得平面FGH 的一个法向量n ＝(1，－1，2)．因为GB →是平面ACFD 的一个法向量，GB →＝(2，0,0)，所以cos 〈GB →，n 〉＝GB →·n|GB →|·|n |＝222＝12.所以平面FGH 与平面ACFD 所成角(锐角)的大小为60°. 解法二：作HM ⊥AC 于点M ，作MN ⊥GF 于点N ，连接NH ，BG .由FC ⊥平面ABC ，得HM ⊥FC . 又FC ∩AC ＝C ， 所以HM ⊥平面ACFD ， 因此GF ⊥NH ，所以∠MNH 即为所求的角．设AB ＝2，在△BGC 中，MH ∥BG ，MH ＝12BG ＝22，由△GNM ∽△GCF ， 可得MN FC ＝GMGF，从而MN ＝66. 由HM ⊥平面ACFD ，MN ⊂平面ACFD ， 得HM ⊥MN ，因此tan ∠MNH ＝HM MN＝3， 所以∠MNH ＝60°.所以平面FGH 与平面ACFD 所成角(锐角)的大小为60°.6．如图，四棱锥P －ABCD 中，底面ABCD 为矩形，PA ⊥平面ABCD ，E 为PD 的中点．(1)证明：PB ∥平面AEC ；(2)设二面角D －AE －C 为60°，AP ＝1，AD ＝3，求三棱锥E －ACD 的体积． 解 (1)证明：连接BD 交AC 于点O ，连接EO . 因为ABCD 为矩形，所以O 为BD 的中点． 又E 为PD 的中点，所以EO ∥PB .EO ⊂平面AEC ，PB ⊄平面AEC ，所以PB ∥平面AEC .(2)因为PA ⊥平面ABCD ，ABCD 为矩形，所以AB ，AD ，AP 两两垂直．如图，以A 为坐标原点，AB →的方向为x 轴的正方向，|AP →|为单位长，建立空间直角坐标系A －xyz .则D (0，3，0)，P (0,0,1)，E ⎝ ⎛⎭⎪⎫0，32，12，AE →＝⎝⎛⎭⎪⎫0，32，12.设B (m,0,0)(m >0)，则C (m ，3，0)，AC →＝(m ，3，0)， 设n 1＝(x ，y ，z )为平面ACE 的法向量，则⎩⎪⎨⎪⎧n 1·AC →＝0，n 1·AE →＝0，即⎩⎪⎨⎪⎧mx ＋3y ＝0，32y ＋12z ＝0，可取n 1＝⎝⎛⎭⎪⎫3m ，－1，3. 又n 2＝(1,0,0)为平面DAE 的法向量， 由题设|cos 〈n 1，n 2〉|＝12，即33＋4m 2＝12， 解得m ＝32.因为E 为PD 的中点，所以三棱锥E －ACD 的高为12.三棱锥E －ACD 的体积V ＝13×12×3×32×12＝38. 7．如图，在四棱柱ABCD －A 1B 1C 1D 1中，底面ABCD 是等腰梯形，∠DAB ＝60°，AB ＝2CD ＝2，M 是线段AB 的中点．(1)求证：C 1M ∥平面A 1ADD 1；(2)若CD 1垂直于平面ABCD 且CD 1＝3，求平面C 1D 1M 和平面ABCD 所成的角(锐角)的余弦值．解 (1)证明：因为四边形ABCD 是等腰梯形，且AB ＝2CD ，所以AB ∥DC .又由M 是AB 的中点，因此CD ∥MA 且CD ＝MA .连接AD 1，在四棱柱ABCD －A 1B 1C 1D 1中，因为CD ∥C 1D 1，CD ＝C 1D 1， 可得C 1D 1∥MA ，C 1D 1＝MA ， 所以四边形AMC 1D 1为平行四边形．因此C 1M ∥D 1A ，又C 1M ⊄平面A 1ADD 1，D 1A ⊂平面A 1ADD 1， 所以C 1M ∥平面A 1ADD 1.(2)解法一：连接AC ，MC ，由(1)知，CD ∥AM 且CD ＝AM ， 所以四边形AMCD 为平行四边形．可得BC ＝AD ＝MC ，由题意∠ABC ＝∠DAB ＝60°，所以△MBC 为正三角形，因此AB ＝2BC ＝2，CA ＝3，因此CA ⊥CB .以C 为坐标原点，建立如图所示空间直角坐标系C －xyz .所以A (3，0,0)，B (0,1,0)，D 1(0,0，3)．因此M ⎝⎛⎭⎪⎫32，12，0， 所以MD 1→＝⎝ ⎛⎭⎪⎫－32，－12，3，D 1C 1→＝MB →＝( －32，12，0 ).设平面C 1D 1M 的一个法向量n ＝(x ，y ，z )， 由⎩⎪⎨⎪⎧n ·D 1C 1→＝0，n ·MD 1→＝0，得⎩⎨⎧3x －y ＝0，3x ＋y －23z ＝0，可得平面C 1D 1M 的一个法向量n ＝(1，3，1)．又CD 1→＝(0,0，3)为平面ABCD 的一个法向量．因此cos 〈CD 1→，n 〉＝CD 1→·n|CD 1→||n |＝55. 所以平面C 1D 1M 和平面ABCD 所成的角(锐角)的余弦值为55. 解法二：由(1)知平面D 1C 1M ∩平面ABCD ＝AB ，过C 向AB 引垂线交AB 于N ，连接D 1N . 由CD 1⊥平面ABCD ，可得D 1N ⊥AB ， 因此∠D 1NC 为二面角C 1－AB －C 的平面角． 在Rt △BNC 中，BC ＝1，∠NBC ＝60°， 可得＝32. 所以ND 1＝CD 21＋2＝152. 在Rt △D 1中，cos ∠D 1NC ＝D 1N＝32152＝55. 所以平面C 1D 1M 和平面ABCD 所成的角(锐角)的余弦值为55. 8．如图，在三棱锥P －ABC 中，D ，E ，F 分别为棱PC ，AC ，AB 的中点．已知PA ⊥AC ，PA ＝6，BC ＝8，DF ＝5.求证：(1)直线PA ∥平面DEF ； (2)平面BDE ⊥平面ABC .证明 (1)因为D ，E 分别为棱PC ，AC 的中点，所以DE ∥PA . 又因为PA ⊄平面DEF ，DE ⊂平面DEF ，所以直线PA ∥平面DEF . (2)因为D ，E ，F 分别为棱PC ，AC ，AB 的中点，PA ＝6，BC ＝8， 所以DE ∥PA ，DE ＝12PA ＝3，EF ＝12BC ＝4.又因为DF ＝5，故DF 2＝DE 2＋EF 2，所以∠DEF ＝90°，即DE ⊥EF . 又PA ⊥AC ，DE ∥PA ，所以DE ⊥AC .因为AC ∩EF ＝E ，AC ⊂平面ABC ，EF ⊂平面ABC ， 所以DE ⊥平面ABC .又DE ⊂平面BDE ，所以平面BDE ⊥平面ABC .。