物理中求极值的常用方法
- 格式:doc
- 大小:234.50 KB
- 文档页数:9


用“配方法”求物理极值例析山东省沂源四中(256104)任会常用“配方法”求极值是高中数学中最基本、最常用且最简单的一种方法。
也是我们求解高中物理极值问题常用的方法之一。
有些物理极值问题,若运用“配方法”求解,简捷明快,一目了然。
现举两例解析如下:例1、两物体沿着成a 角的两条直线作匀速运动,速度大小都是v 。
起初它们的位置分别在P 、Q 两点,如图1所示。
已知l PQ =。
问,经过多少时间两物体间的距离最近?最近距离是多少?解析:设两物体分别运动到MN 时,它们相距最近(用S 表示最近距离)。
在ΔQMN 中,vt l QN -=,根据余弦定理得: αcos )(2)()(222vt l vt vt l vt S ---+= 将上式整理配方得:2sin 22cos 2222ααl l vt l S +⎪⎭⎫ ⎝⎛-= 由此式可知,当v l t l vt 2,02==-即时,S 有最小值,其值为2sin min αl S =。
例2、在图2的电路中,电池的电动势ε=5V ,内电阻r=10Ω,固定电阻R=90Ω,R 0是可变电阻。
R 0在由零增加到400Ω的过程中,求可变电阻R 0上消耗热功率最大的条件和最大热功率。
解析:根据闭合电路的欧姆定律得:r R R I ++=0ε①又 ∵ 02R I P ⋅= ② ∴2002)(r R R R P ++=ε ③ 将③式整理配方得:[])(4)(0202r R R r R R P +++-=ε ④ 由④式可知,当R 0=R+r=90Ω+10Ω=100Ω时, R 0上消耗热功率最大,其最大值为: 2图1图PW W r R P m 161)1090(45)(422=+=+=ε 上述两例,也可以用其他多种方法求解,但配方法是较为简捷的一种方法。
同学们不妨作一比较。
练习题:1、一辆汽车在十字路口等候绿灯,当绿灯亮时,汽车以2m/s 2 的加速度开始行驶。
恰在这时,一辆自行车以8m/s 的速度匀速驶来,从后面超过汽车。

拉格朗日乘数法求极值例题拉格朗日乘数法是求解多元函数极值问题的一种常用方法,它被广泛应用于经济学、物理学等领域。
本文将通过一个例题来详细介绍拉格朗日乘数法的应用。
例题:求函数 $f(x,y)=x^2+y^2$ 在约束条件$g(x,y)=x+y-1=0$ 下的最小值。
解析:首先,我们需要确定拉格朗日乘数法的基本思路。
其核心是将约束条件与目标函数合并成一个函数,再通过求导的方式求得该函数的极值点。
具体步骤如下:1.建立拉格朗日函数设 $L(x,y,lambda)=f(x,y)+lambda g(x,y)$,其中$lambda$ 为拉格朗日乘数。
2.求解拉格朗日函数的偏导数$$begin{cases}frac{partial L}{partial x}=2x+lambda =0frac{partial L}{partial y}=2y+lambda =0frac{partial L}{partial lambda}=x+y-1=0end{cases}$$3.解方程组由上面的方程组可以解得 $x=frac{1}{2}$,$y=frac{1}{2}$,$lambda=-1$。
4.判断极值通过二阶导数判断可得,此时为函数 $f(x,y)=x^2+y^2$ 的最小值。
因此,该例题的最小值为$f(frac{1}{2},frac{1}{2})=frac{1}{2}$。
通过这个例题,我们可以看到拉格朗日乘数法的应用非常灵活,不仅可以求解二元函数的最值问题,还可以处理多元函数的极值问题。
而且,在实际问题中,拉格朗日乘数法常常被用于约束条件较为复杂的情况下,例如非线性约束条件或多个约束条件等。
总之,拉格朗日乘数法是一种非常实用的数学工具,在解决实际问题中具有广泛的应用价值。

Vo万能公式 基本不等式 物理极值湖北利川一中 邓国庆 445400问题1:一条宽度为L 的河,水流速度为V o ,船在静水中速度为V ,若V o >V ,船怎样航行位移最小?最小位移是多少?解:设船头指向与河岸成 α角,建立如图所示坐标。
则 c o s s i n V x V o V V y V αα=+⎧⎨=⎩由于V o >V ,船不可能到正对岸。
设船实际航向与河岸成θ角,则 sin tan cos V Vo V αθα=+ θ越大,实际位移越小。
由万能公式 22tan2sin 1tan 2ααα=+ 221t a n2c o s 1t a n 2ααα-=+ 并设tan 2x α=得: s i nt a n c o s V V o V αθα=+=222()()()V V Vo VVo V Vo V x Vo V x x x=+++-+-由于()Vo V Vo V x x ++-≥=()Vo VVo V x x+=- 即tan 2x α==tan θ最大,θ最大。
此时 cos α=-V Vo 即船头指向与河岸下游成arccos(-VVo )时船位移最小。
此时 tan θ=sin V Vo θ=最小位移S=sin L θ=LVoV实际的运动情况如图问题2:湖中有一小岛A ,A 与直湖岸的距离为d ,湖岸边有一点B ,B 沿湖岸方向与A 点的距B离为L。
一人自A点出发,要达到B点。
已知他在水中游泳的速度为v1,在岸上行走的速度为v2,且v1‹v2,要求他由A至B所用时间最短,问此人应当如何选择其运动路线?解:设人先与湖岸成α角游泳,然后上岸行走,则运动时间t=12212coscossinsin sin sindLd L d dv v v v vαααααα-+=+-由于22tan2sin1tan2ααα=+221t a n2c o s1t a n2ααα-=+并设tan2xα=得:t=2121212()2v vL dv v xv v v x⎧-⎫+++⎨⎬⎭⎩2122L dv v v≥+当2121()v vv v xx-=+即 x=tan2α=时t最小此时12cosvvα=设实际情况AB与湖岸夹角为θ则cosθ=L可得当θ≥α即cosθcosα≤L≤人应选择由A到B直接游向B的路径时间最短。



专题8 临界极值问题1. 力学“临界极值问题”的一般方法:(1)临界条件相当于是题目中的隐含条件,是物体从一个状态到另一个状态转折的一个中间状态;(2)常见的有5种临界,需要熟练掌握出现这些临界状态时,对应的临界条件是那些。
2. 常见的五种临界点 (1)共速临界:①在相遇追及问题中,涉及能否追上、相距最远、最近时,临界条件即为二者速度相等; ②传送带、滑块木板问题中,摩擦力发生突变的时刻也是共速的时刻。
(2)变速临界:①变加速运动中,a=0,速度最大或者最小; ②变速运动中,v=0,位移最大。
(3)松断临界: ①绳子松弛T=0; ②断裂T=Tmax 。
(4)分离临界:①分离瞬间:相互0F N (隔离法); ②分离瞬间:各自a 相同。
(5)滑动临界:①刚好滑动瞬间,相互之间的静摩擦达到最大静摩擦即:f=fm 。
拓展:(1)整体法与隔离法;将AB 之间的摩擦为最大静摩擦作为已知条件,利用整体法与隔离法列方程求解;(2)外力分配公式:AB 仍然看成相对静止,求出f 静,再利用f 静的范围f 静≤fmax ,进行求解;常用外力分配公式大大简化计算。
小结论:滑块木板模型中 1μ< 2μ,达到共速后不会相对滑动,无论在水平面还是斜面都适用( 1μ表示地面与木板之间的摩擦因数, 2μ表示滑块与木板之间的摩擦因数)。
3. 力学极值问题①物理方法:临界状态法,图解法;②数学方法:三角函数法、二次函数法、不等式法、图像法等;()ϕθθθ++=+sin b a bcos asin 22 (其中abtan =ϕ) ;由sc+cs 推导 ③逻辑方法:极限法、极值法、特殊值法。
例1. 倾角为θ=45°、外表面光滑的楔形滑块M 放在水平面AB 上,滑块M 的顶端O 处固定一细线,细线的另一端拴一小球,已知小球的质量为m =55kg ,当滑块M 以a =2g 的加速度向右运动时,则细线拉力的大小为(取g =10 m/s 2)( )A .10 NB .5 N C. 5 ND .10 N例2. 如图所示,木块A的质量为m,木块B的质量为M,叠放在光滑的水平面上,A、B 之间的滑动摩擦因数为μ,若最大静摩擦力等于滑动摩擦力,重力加速度为g.现用水平力F作用于A,则保持A、B相对静止的条件是F不超过() A.μmg B.μMg C.μmg(1+ m/M ) D.μMg(1+ M/m )变式:若地面摩擦因素为μ',在F的作用下AB一起匀加速运动,求F的最大值?例3. 如图所示,梯形物体的质量分别为M和m,斜面的倾角为θ,接触面都光滑。

“数学极值法”在物理问题中的妙用应用数学知识处理物理问题的能力,是物理教学培养学生五个方面能力中的重要一个.其中,数学求极值的方法在解决物理问题时被广泛应用.现就高中物理解题过程中常遇到的几种数学求极值的方法归纳如下,以期同广大同仁进行交流. 1.关于 θθcos sin b a Y += 的应用 )sin(cos sin 22ϕθθθ++=+=b a b a Y 且ϕtg =ab.要使Y 有最大值,需1)sin(=+ϕθ, 即︒=+90ϕθ.例1.如图1所示,质量为m 的物块放置在水平地面上,物块与地面的动摩擦因数为μ,要使小物块沿水平面匀速运动,θ为何值时,F 有最小值?是多少?解:以m 为研究对象, 受力分析如右图: m 匀速运动时:mgF F F F N N =+=θμθsin cos)sin(1mgsin cos mg 2ϕθμμθμθμ++=+=F ,μϕ1=tg . 当 2min 1mgF 1arctan 22μμμπϕπθ+=-=-=时,.2.关于c bx axY ++=2的应用根据二次函数的特点:0>a 时, 图象开口向上,Y 有最小值; 0<a 时,图象开口向下,Y 有最大值.且当abx 2-=时,Y 有最值. 例2.一辆汽车在十字路口等候绿灯,当绿灯亮时汽车汽车以2/3s m 的速度开始行驶,恰在这时一辆自行车以s m /6的速度匀速驶来,从后面赶过汽车.试求:汽车从路口开动后,在追上自行车之前经过多长时间两车相距最远?此距离是多少?解析:设汽车在追上自行车之前经t 秒两车相距最远,则有:6)2(2323621222+--=-=-=∆t t t at t v s 自由二次函数的极值条件知:s t 2=时,s ∆最大,最大值为m 6图 1F NF3.关于判别式0≥∆的应用要使方程02=++c bx ax 有解,须满足0≥∆.例3 质点从A 点由静止出发沿直线运动到B 点停止,在这段时间内,物体可以做匀速运动,也可以做加速度为a 的匀变速运动,要使质点从A 到B 运动的时间最短,质点应如何运动已知?最短时间是多少?已知A 、B 间的距离为s .解析:质点从A 到B 最简单的运动形式为:先做匀加速,再做匀速,最后做匀减速. 设质点从A 到B 运动的总时间为t ,做匀加速的时间为1t ,做匀减速运动的时间为3t ,则做匀速直线运动的时间为31t t t --根据题意有:31t t = ①)(21213112321t t t at at at s --++=② 由①②两式得: 0121=+-s att at ③要使③式有解,须满足0≥∆ 即 04)(2≥-as at 得as t 2≥ 即t 的最小值为:a st 2= 带入③得ast t ==31 即物体先做匀加速直线运动后做匀 减速直线运动.4.关于定和求积原理的应用两数和为常数,当两数相等时其乘积最大.由)0,0(,2)(2>>+≤y x y x xy ,若P y x =+(定值),则当y x =时:x 、y 的乘积有极大值. 例5.已知Ω=21R ,Ω=32R ,Ω=53R 电源电动势V 6=ε,电源内阻 Ω=5.0γ.问:变阻器滑动片在何处时,电源发热功率最小?解析:设电源发热功率为P ,干路电流为I 据γ⋅=2I P , 可知:I 最小时,P 最小.外R I +=γε ①32132x 1)()R R R R R R R R R x ++-+⋅+=(外 ②根据定和求积原理可知:当x x R R R R R -+=+321时,I 有最小值. 即Ω=-+=32132R R R R x 时,I 的最小值为A I 2min =得:W P 2min = 5.关于定积求和原理的应用两数乘积为常数时,两数相等时,其和值最小. 由xy y x 2≥+, 若常数)(k xy =, 则x y =时,x 与y 的和最小.例6:一个连同装备总质量为M 的宇航员,在距离飞船S 处与飞船处于相对静止状态,他准备对太空中的哈勃望远镜进行维修.宇航员背着装有质量为0m 的2O 贮气筒,筒内有一个可以使2O 以速度v 喷出的喷嘴,宇航员维修完毕后,必须向反方向释放2O ,才能回到飞船,同时又必须保留一部分2O 供途中呼吸之用,宇航员的耗氧率为Q (kg/s).若不考虑喷出2O 对质量的影响,求:为了使总耗氧量最低,应该一次喷出多少氧气?解析:以飞船为参照物,设喷出质量m 的氧气时,宇航员获得'v 的速度,则由动量守 恒可知:0)('=--mv v m M因不考虑喷出2O 对质量的影响,所以有:Mmvv ='宇航员返回时间: mv Msvs t =='宇航员返回过程中呼吸用氧mvQMsQt m =='故总耗氧量为mvQMsm m m +=+'因: 定值)(v QMs mv QMs m=,故当mvQMsm =时耗氧量最少 则总耗氧量最少为vQMs26.关于求导法求函数极限的应用一般地,当函数)(x f y =在0x 连续时,判别)(0x f 是极大(小)值的方法是:(1)如果在0x 附近的左侧0)('>x f ,右侧0)('<x f ,那么,)(0x f 是极大值. (2)如果在0x 附近的左侧0)('<x f ,右侧0)('>x f ,那么,)(0x f 是极小值. 例7 如图所示.一根不可伸长的轻绳两端各系一个小球a 和b ,跨在两根固定在同一高度的光滑水平细杆上,质量为3m 的a 球置于地面上,质量为m 的b 球从水平位置静止释放.当a 球对地面压力刚好为零时,b 球摆过的角度为θ.下列结论正确的是 ( ) A .θ=90° B .θ=45°C .b 球摆动到最低点的过程中,重力对小球做功的功率先增大后减小D .b 球摆动到最低点的过程中,重力对小球做功的功率一直增大解析:由机械能守恒以及圆周运动的相关知识可求得:当a 球对地面压力刚好为零时,b 球摆过的角度θ为090.设b 球的摆动半径为R ,当摆过角度θ时的速度为v ,对b 球由动能定理:221mv sin mgR =θ① 此时重力的瞬时功率为: θcos mgv p = ② 由① ②得: θθ2322cos sin 2R g m p = ③对于函数θθ2cos sin =y 其一阶导数为:)sin 31(cos cos sin 3cos 22'θθθθθ-=-=y33arcsin0<<θ 0'>y 原函数单调递增 233arcsinπθ<< 0'<y 原函数单调递减 故当33arcsin =θ y 取极大值.即b 球摆动到最低点的过程中,重力对小球做功的功率先增大后减小.。


物理学中的极值问题与极端法【高考展望】物理学中的临界和极值问题牵涉到一定条件下寻求最佳结果或讨论其物理过程范围的问题,此类问题通常难度较大技巧性强,所涉及的内容往往与运动学、动力学、电磁学密切相关,综合性强。
在高考命题中经常以压轴题的形式出现,临界和极值问题是每年高考必考的内容之一。
【知识升华】物理极值问题,就是求某物理量在某过程中的极大值或极小值。
物理极值问题是物理学中的一个重要内容,涉及的知识面广,综合性强。
在科学领域中,数学因为其众所周知的准确而成为研究者们最广泛用于交流的语言。
如果在解决这些问题时能与数学知识灵活地整合,运用适合的方法,将会拓展解决物理问题的思路,提高运用数学知识解决物理问题的能力。
所谓临界问题是指当某种物理现象(或物理状态)变为另一种物理现象(或另一物理状态)的转折状态叫临界状态.可理解成“恰好出现”或“恰好不出现”.某种物理现象转化为另一种物理现象的转折状态称为临界状态。
至于是“出现”还是“不出现”,需视具体问题而定。
临界问题往往是和极值问题联系在一起的。
【方法点拨】求解极值问题的方法可分为物理方法和数学方法.物理方法包括:(1)利用临界条件求极值;(2)利用问题的边界条件求极值;(3)利用矢量图求极值;(4)用图像法求极值。
数学方法包括:(1)用三角函数求极值;(2)用二次方程的判别式求极值;(3)用不等式的性质求极值;(4)利用二次函数极值公式求极值。
一般而言,物理方法直观、形象,对构建模型及动态分析等能力要求较高,而用数学方法求极值思路严谨,对数学能力要求较高。
多数极值问题,并不直截了当地把极值或临界值作为题设条件给出,而是隐含在题目中,要求学生在对物理概念、规律全面理解的基础上,仔细审题,深入细致地分析问题,将隐含的题设条件——极值挖掘出来,把极值问题变成解题的中间环节。
【典型例题】类型一、利用二次函数极值公式(或配方法)求极值二次函数2y ax bx c =++有如下知识:(1)若0a >、2bx a =-时,y 有极小值2min 44ac b y a -=;(2)若0a <、2bx a=-时,y 有极大值2max 44ac b y a -=。
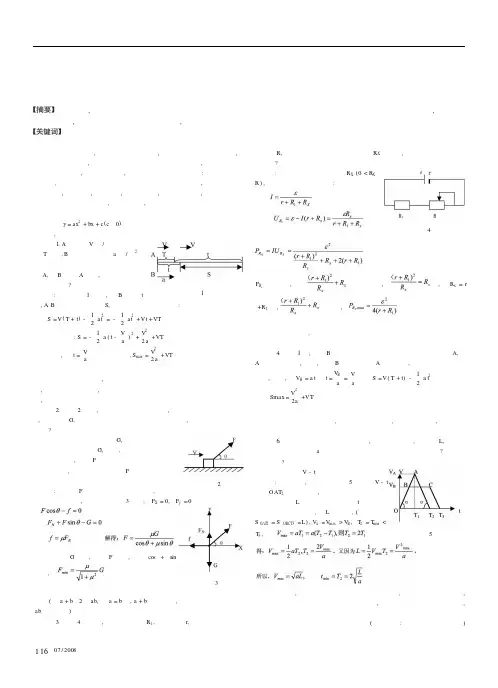
高中物理极值问题求解的一般规律◆陈 兴极值问题,就是求某物理量在某过程中的极大值或极小值。
极值问题在高中物理的力学、热学、电学等部分均有出现,且解题方法变化多样,是考查学生能力的重要题型之一,也是学生普遍感到困难的题型之一。
高中物理教学极值问题物理规律中学物理习题中,遇求极值的问题很多,且多为思维难度大的习题,由于数学知识的制约,无法用高等数学求极值的方法求极值,只能用初等数学的方法求极值,根据不同问题,通常涉及到的数学知识有:点到直线的距离最短,两数的几何平均值小于或等于它们的算术平均值,二次函数求极值的方法,因式分解,三角函数,几何作图法,有关圆的知识,等等。
下面就物理极值问题,以问题为例,粗谈求解的一般规律。
一、利用二次函数规律求物理极值的问题函数y =ax 2+bx +c (c ≠0)存在有极值。
若列出的物理方程满足二次函形式,则可由求二次函数极值的方法求解物理极值。
图1例1.A 物体以V 米/秒做匀速直线运动T 秒后,B 物体以加速度a 米/秒2从同一地点由静止开始做匀加速直线运动追赶A,求B 追到A 之前,它们之间的最大距离为多少?解:分析如图1所示,设B 出发t 秒时,A 、B 物体间的距离为S,据题意可列物理方程为:S =V (T +t )-12at 2=-12at 2+Vt +VT经配方有:S =-12a (t -V a)2+V 22a+VT可见,当t =V a时有最大距离,S m ax =V 22a+VT二、利用三角函数规律求物理极值的问题在物理极值问题中,有许多题目里的物理量变化关系与角度变化有关,于是对这一类问题,我们只要着眼于列出被求物理量与角度的物理方程,再利用三角函数的有关规律即可求解物理极值。
例2.如图2所示,物体放置在水平地面上,它们之间的动摩擦因数为μ,物体重为G,欲使物体沿水平地面做匀速直线运动,所用的最小拉力为多大?图2 该题的已知量只有μ和G,说明最小拉力的表达式中最多只含有μ和G,但是,物体沿水平地面做匀速直线运动时,拉力F 可由夹角的不同值而有不同的取值。
极值知识点总结一、极大值和极小值在数学中,极大值和极小值是极值的两种形式。
在一个给定的函数上,极大值指函数在某个点上的最大值,而极小值指函数在某个点上的最小值。
1.1 极大值一个函数在某个点上的极大值是指在这个点的邻域内,函数值最大的值。
如果存在一个点x0,对于任意满足|x-x0|<δ的x,f(x)≤f(x0),那么f(x0)就是函数f(x)在x0处的极大值。
1.2 极小值同样地,一个函数在某个点上的极小值是指在这个点的邻域内,函数值最小的值。
如果存在一个点x0,对于任意满足|x-x0|<δ的x,f(x)≥f(x0),那么f(x0)就是函数f(x)在x0处的极小值。
1.3 区间极值定理对于一个连续函数f(x),如果函数在一个闭区间[a, b]上连续,在内部开区间(a, b)上可导,那么函数在[a, b]上至少有一个极大值和一个极小值。
1.4 极值的必要条件如果一个函数在某一点上的极值,那么该点一定是一个驻点。
这是因为一个函数在极值点上的导数一定为零,所以导数为零是函数极值的必要条件。
1.5 极值的充分条件如果一个函数在某一点上的二阶导数存在,并且在该点的二阶导数为正,那么该点为极小值点;如果二阶导数为负,则为极大值点。
1.6 极值的判定方法判断一个函数在某一点上的极值,可以通过求导数来进行判定。
求得导数后,把导数等于零的点称为临界点。
在临界点上求得的函数值即为该点的极值。
二、求解极值的方法2.1 开闭区间法对于一个函数在一个区间[a, b]上的极值,可以先求得在区间内部的导数和端点的函数值,然后通过比较得到极值的位置。
2.2 二次函数法对于一个二次函数,可以通过求导得到导函数,然后通过导函数的判定方法求得极值点的位置。
2.3 拐点法对于一个函数,如果在某点的导数从正变为负,或者从负变为正,那么该点就是函数的极值点。
这就叫做拐点法。
2.4 点与切线法对于一个函数,在某一点的切线斜率为零时,该点为极值点。
拉格朗日公式求极值
拉格朗日公式,作为数学领域中一个重要的公式,广泛应用于物理学、工程学等众多学科。
它能帮助我们求解许多极值问题,具有重要的理论和实际意义。
一、拉格朗日公式的推导
1.拉格朗日公式的基本形式拉格朗日公式可以表示为:L = L(x, y, z, ...) = L(x) + L(y) + L(z) + ...,其中x, y, z, ...为各个变量的函数。
2.拉格朗日公式的推导过程拉格朗日公式的推导过程较为复杂,涉及微积分、偏导数等概念。
具体推导过程可参考相关数学教材。
二、拉格朗日公式的性质
1.拉格朗日公式的极值性质当拉格朗日公式的导数为零时,即L"(x) = L"(y) = L"(z) = ...= 0,可以得到各个变量的极值。
2.拉格朗日公式的优化性质拉格朗日公式具有优化性质,可以通过求解拉格朗日公式的极值问题,得到原问题的最优解。
三、拉格朗日公式的应用
1.求解极值问题
拉格朗日公式可以用于求解各种极值问题,如求解函数的极大值、极小值等。
2.优化问题
拉格朗日公式在优化问题中具有广泛应用,如求解凸优化问题、约束优化问题等。
四、结论
拉格朗日公式作为数学领域中的一个重要公式,具有重要的理论和实际意义。
物理解题中求极值的常用方法运用数学工具处理物理问题的能力是高考重点考查的五种能力之一,其中极值的计算在教学中频繁出现。
因为极值问题围广、习题多,会考、高考又经常考查,应该得到足够重视。
另外很多学生数、理结合能力差,这里正是加强数理结合的“切人点”。
学生求极值,方法较少,教师应该在高考专题复习中提供多种求极值的方法。
求解物理极值问题可以从物理过程的分析着手,也可以从数学方法角度思考,下面重点对数学方法求解物理极值问题作些说明。
1、利用顶点坐标法求极值对于典型的一元二次函数y=ax 2+bx+c,若a>0,则当x=-a b 2时,y 有极小值,为y min =a b ac 442-;若a<0,则当x=-ab2时,y 有极大值,为y max =a b ac 442-;2、利用一元二次函数判别式求极值 对于二次函数y=ax 2+bx+c ,用判别式法 利用Δ=b 2-4ac ≥0。
(式中含y) 若y ≥A ,则y min =A 。
若y ≤A ,则y max =A 。
3、利用配方法求极值对于二次函数y=ax 2+bx+c ,函数解析式经配方可变为y=(x-A)2+常数:(1)当x =A 时,常数为极小值;或者函数解析式经配方可变为y = -( x -A )2+常数。
(2)当x =A 时,常数为极大值。
4、利用均值定理法求极值 均值定理可表述为≥+2ba ab ,式中a 、b 可以是单个变量,也可以是多项式。
当a =b 时, (a+b)min =2ab 。
当a =b 时, (a+b) max =2)(2b a +。
5、利用三角函数求极值如果所求物理量表达式中含有三角函数,可利用三角函数的极值求解。
若所求物理量表达式可化为“y=Asin ααcos ”的形式,则y=21Asin2α,在α=45º时,y 有极值2A 。
对于复杂的三角函数,例如y=asin θ+bcos θ,要求极值时先需要把不同名的三角函数sin θ和cosθ,变成同名的三角函数,比如sin(θ+ф) 。
这个工作叫做“化一”。
首先应作辅助角如所示。
考虑asin θ+bcos θ= (θθcos sin 2222ba b ba a +++)=22b a + (cos фsin θ+sin фcos θ)=22b a +sin(θ+ф) 其最大值为22b a +。
6、用图象法求极值通过分析物理过程遵循的物理规律,找到变量之间的函数关系,作出其图象,由图象可求得极值。
7、用分析法求极值分析物理过程,根据物理规律确定临界条件求解极值。
下面针对上述7种方法做举例说明。
例1:如图2所示的电路中。
电源的电动势ε=12伏,阻r =0.5欧,外电阻R 1=2欧,R 2=3欧,滑动变阻器R 3=5欧。
求滑动变阻器的滑动头P 滑到什么位置,电路中的伏特计的示数有最大值?最大值是多少?分析:设aP 间电阻为x ,外电路总电阻为R. 则:R 1R 3ap bVr 、εR 2图2φa b 图110)8)(2(532)53)(2())((321321X X X X R R R X R R X R R -+=++-++=++-++=先求出外电阻的最大值R max 再求出伏特计示数的最大值U max 。
本题的关键是求R max ,下面用四种方法求解R max 。
[方法一] 用顶点坐标法求解抛物线方程可表示为y =ax 2+bx+c 。
考虑R =10)8)(2(x x -+=101662++-x x ,设y =-x 2+6x+16,当x =ab2-= —)1(26-=3时,R max (3)=101636)3(2+⨯+- =2.5Ω。
[方法二] 用配方法求解考虑R =10)8)(2(x x -+ =101662++-x x =1025)3(2+--x 。
即x =3Ω时,R max =5.21025=Ω。
[方法三] 用判别式法求解考虑R =101662++-x x ,则有-x 2+6x+16-10R =0,Δ=b 2-4ac =36-4(-1)(16-10R)>0,即:100-40R ≥0, R ≤2.5Ω,即R max =2.5Ω。
[方法四] 用均值定理法求解 考虑R =10)8)(2(x x -+,设a =2+x ;b =8-x 。
当a =b 时,即2+x =8-x , 即x =3Ω时,R max (3)=10)38)(32(-+ =2.5Ω。
也可以用上面公式(a+b)max =2)]8)(2[(2x x -+=25,R max =10)(max b a +=1025=2.5Ω。
以上用四种方法求出R max =2.5Ω,下边求伏特计的最大读数。
I min =rR +m ax ε=5.05.212+=4(A)。
U max =ε- I min r =12-4⨯0.5=10(V)。
即变阻器的滑动头P 滑到R 3的中点2.5Ω处,伏特计有最大值,最大值为10伏。
例2:如图3所示。
光滑轨道竖直放置,半圆部分的半径为R ,在水平轨道上停着一个质量为M =0.99kg 的木块,一颗质量为m =0.01Kg 的子弹,以V 0=400m/s 的水平速度射入木块中,然后一起运动到轨道最高点水平抛出,试分析:当圆半径R 多大时,平抛的水平位移是最大?且最大值为多少?[解析]子弹与木块发生碰撞的过程,动量守恒,设共同速度为V 1,则: mV 0=(m+M)V 1, 所以:V 1=0V M m m +=s m s m /4/40099.001.001.0=⨯+设在轨道最高点平抛时物块的速度为V 2,由于轨道光滑,故机械能守恒:2221)(21)(2)(21V M m gR M m V m M +++=+ 所以:V 2=)/(])(4)[(21M m gR m M V M m ++-+=R R Rg V 401610444221-=⨯-=-则平抛后的位移可以表示为:图3s =V 2t =V 2104)4016(4RR g R ⨯-=⨯=4R R 4.02+-。
因为a=-1<0,所以水平位移S 应该存在最大值。
当R=)1(24.02-⨯-=-a b =0.2m 时, S max =0.8m例3:在一平直较窄的公路上,一辆汽车正以22m/s 的速度匀速行驶,正前方有一辆自行车以4m/s 的速度同向匀速行驶,汽车刹车的最大加速度为6m /s 2,试分析两车不相撞的条件。
[解析]要使二者不相撞,则二者在任一时间的位移关系应满足 V 0t-S Vt at +<221 (式中S 为汽车刹车时与自行车间距) 代入数据整理得:3t 2-18t+S>0, 显然,当满足∆=b 2-4ac ≥0,即∆=182-4⨯3S ≥0得:S ≤27m ,S min =27m 。
当汽车刹车时与自行车间距为27米时是汽车不与自行车相撞的条件。
例4:如图4所示。
一辆四分之一圆弧小车停在不光滑水平地面上,质量为m 的小球从静止开始由车顶无摩擦滑下,且小车始终保持静止状态,试分析:当小球运动到什么位置时,地面对小车的摩擦力最大?最大值是多少?[解析]:设圆弧半径为R ,当小球运动到重力mg 与半径夹角为θ时,速度为V ,根据机械能守恒定律和牛顿第二定律有:图4RVmmg N mgR mV 22cos cos 21=-=θθ 解得小球对小车的压力为:N=3mgcos θ,其水平分量为:N x =3mgsin θcos θ=θ2sin 23mg 根据平衡条件,地面对小车的静摩擦力水平向右,大小为:f= N x =θ2sin 23mg 可以看出:当sin2θ=1,即θ=45º时,地面对小车的静摩擦力最大,其值为:f max =mg 23。
例5:如图5所示。
质量为m 的物体由力F 牵引而在地面上匀速直线运动。
物体与地面间的滑动摩擦系数为μ,求力F 最小时的牵引角θ。
(F 的方向是随θ变化的。
)[解析]:因物体匀速直线运动,所以有: Fcos θ-f =0 ①f =μN =μ(mg-Fsin θ) ② ②代人①得:Fcos θ-μmg+μFsin θ=0 即:F =θμθμsin cos +mg。
分母为两项不同名的三角函数,需要转化成同名的三角函数,也就是需要“化一”。
由前面的“化一”结论得:a sin θ+b cos θ=22b a +sin(θ+ф) 考虑本题分母:μsin θ+cos θ与a sin θ+b cos θ用比较法,得:a =μ;b =1。
于是tg ф=μ1=a b ,则ф=arc tg μ1。
所以,μsin θ+cos θ=12+μsin(θ+arc tg μ1)。
要使F 最小,则分母μsin θ+cos θ需最大,因此,θ+arc tgμ1=2π。
所以有:θ=2π-arc tg μ1=2π-arc ctg μ=arc tg μ。
即:θ=arc tg μ时,F 最小。
作为教师,运用“求导数”对本题验算非常简便。
F =θμθμsin cos +mg 。
考虑0=θd dF,则有μcos θ-sin θ=0则θ=arc tg μ,即当F 最小时,牵引角θ=arc tg μ。
例6:甲、乙两物体同时、同地、同向由静止出发,甲做匀加速直线运动,加速度为4米/秒2,4秒后改为匀速直线运动;乙做匀加速直线运动,加速度为2米/秒2,10秒后改为匀速直线运动,求乙追上甲之前它们之间的最大距离。
分析:运用物理规律和图形相结合求极值.是常用的一种比较直观的方法。
由题意可知,4秒后甲做匀速直线运动的速度为:V 甲=a 甲t 甲=4⨯4=16(m /s)。
乙10秒后做匀速运动的速度为:V 乙=a 乙t 乙=2⨯10=20(m /s)。
可画出v —t 如上图6所示。
图线在A(8,16)点相交,这表明在t =8秒时,两物体的速度相等,因此.在t =8秒时,两者间的距离最大。
此时两图线所围观积之差,就是两者间的最大距离。
即S max =21⨯4⨯16 + 4⨯16 — 21⨯8⨯16=32(m)。
用分析法求极值在物理计算中较常见。
经过对物理状态或过程分析后求极值,不一定要用繁难的数学,关键是确定临界状态和过程的最值。
例7:如图7所示。
AB 、CD 是两条足够长的固定平行金属导轨,两条导轨间的距离为L ,导轨平面与平面的夹角是θ,在整个导轨平面部有垂直于导轨平面斜向上方的匀强磁场,磁感应强度为B 。
在导轨的AC 端连接一个阻值为R 的电阻,一根垂直于导轨放置的金属棒ab ,质量为m ,从静止开始沿导轨下滑。
已知ab 与导轨间的滑动摩擦系数为μ,导轨和金属棒的电阻不计。
求ab 棒的最大速度。
[解析]:采用分析法要注意抓三个环节,即分析物理过程;确定极值状态;运用物理规律求解。