§14.1 圆锥曲线及其生成

数学圆锥曲线
数学圆锥曲线是一种极其重要的数学曲线，它出现在物理、力学、天文学以及
其他多个领域，许多重要的物理定律都可以用它来表示。

圆锥曲线由旋转椭圆构成，其中椭圆的长轴是它的主轴，由一系列的椭圆弧构成，形成一个圆锥形。

它可以用来描述物体发生微小变形时产生的轨迹，例如弹簧的振动、圆周运动等等。

此外，由于它的许多特性，如简单的半径、角速度、坐标系的建立等，它被广泛应用于机械设计、数学建模以及航天技术等多个方面。

第1章 圓錐曲線 3
母線
L 0L
V αα(一點
)L 0
V
E
(兩相交直線)
1-1 圓錐曲線名詞的由來
▲ 圓錐與圓錐曲線
1. 圓錐：
取兩條相交於定點 V 的直線 L 0 與 L ，假設它們的夾角為
α( 0°＜α＜90° )。

固定 L 0 為軸，而將 L 繞著 L 0 旋轉一周，且使其
夾角α保持不變，那麼直線 L 所掃出的曲面，稱為錐面。

此時交點
V 稱為圓錐的頂點，α稱為半頂角，動直線 L 稱為母線，定直線 L 0
稱為圓錐的中心軸。

配合課本P. 2
2. 圓錐曲線：
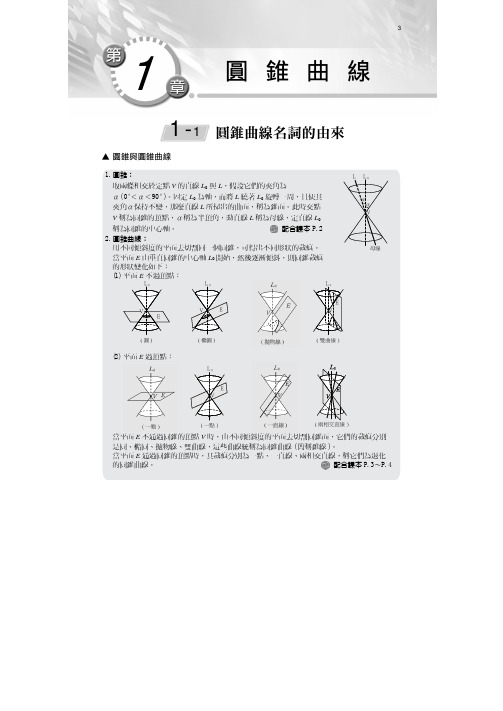
用不同傾斜度的平面去切割同一個圓錐，可得出不同形狀的截痕。

當平面E 由垂直圓錐的中心軸L 0開始，然後逐漸傾斜，則圓錐截痕
的形狀變化如下：
(1) 平面E 不過頂點：
(圓)L 0V
E (橢圓)L 0V E (雙曲線)L 0
V
E
(2) 平面E 過頂點： 當平面 E 不通過圓錐的頂點 V 時，由不同傾斜度的平面去切割圓錐面，它們的截痕分別 是圓、橢圓、拋物線、雙曲線，這些曲線統稱為圓錐曲線 ( 簡稱錐線 )。

當平面 E 通過圓錐的頂點時，其截痕分別為一點、一直線、兩相交直線，稱它們為退化 的圓錐曲線。

配合課本P. 3～P. 4 3圓 錐 曲 線 1。

圆锥曲线与其方程圆锥曲线是数学中一个非常有趣且重要的概念，它是由一个平面与一个圆锥相交而形成的曲线。

圆锥曲线包括圆、椭圆、双曲线和抛物线四种类型，每种类型都有其独特的特点和方程。

首先，让我们来了解一下圆锥曲线中最简单的一种类型——圆。

圆可以被描述为一个平面上与一个圆心和半径相关联的点的集合。

其方程可以表示为(x-a)²+(y-b)²=r²，其中(a,b)是圆心的坐标，r是半径的长度。

圆的方程可以用来确定圆上的任意一点的坐标，从而使我们能够对圆进行研究和分析。

接下来，我们来讨论椭圆。

椭圆是圆锥曲线中另一种常见的类型，它具有两个焦点和一个长轴和短轴。

椭圆的方程可以表示为(x-h)²/a²+(y-k)²/b²=1，其中(h,k)是椭圆的中心坐标，a和b分别是长轴和短轴的长度。

椭圆的方程可以帮助我们确定椭圆上的点，并且可以用来计算椭圆的周长和面积。

双曲线是另一种重要的圆锥曲线类型。

它有两个分离的曲线分支，并且具有两个焦点和一个虚线的对称轴。

双曲线的方程可以表示为(x-h)²/a²-(y-k)²/b²=1，其中(h,k)是双曲线的中心坐标，a和b分别是曲线分支的长度。

双曲线的方程可以帮助我们确定双曲线上的点，并且可以用来研究双曲线的性质和特征。

最后，我们来谈谈抛物线。

抛物线是圆锥曲线中最具有特色的一种类型，它具有一个焦点和一条对称轴。

抛物线的方程可以表示为y=ax²+bx+c，其中a、b和c 是常数。

抛物线的方程可以帮助我们确定抛物线上的点，并且可以用来研究抛物线的形状和性质。

通过了解圆锥曲线和它们的方程，我们可以更好地理解和应用这些曲线。

圆锥曲线在几何学、物理学、工程学和计算机图形学等领域都有广泛的应用。

例如，在物理学中，椭圆轨道被用来描述行星的运动；在工程学中，抛物线被用来设计抛物面反射器；在计算机图形学中，圆锥曲线被用来生成二维和三维图形。

平面几何中的圆锥曲线圆锥曲线，是平面几何中的一类特殊曲线，由圆生成的曲线。

圆锥曲线包括椭圆、双曲线和抛物线三种类型，它们在数学、物理、工程等领域都有广泛的应用。

本文将分别介绍椭圆、双曲线和抛物线的性质与应用。

一、椭圆椭圆是圆锥曲线中的一种，其定义是平面上到两个定点的距离之和等于常数的点的集合。

这两个定点称为焦点，连接两个焦点的线段称为主轴。

椭圆还有一根辅助轴，垂直于主轴并通过椭圆的中心。

椭圆具有许多重要的性质和特点。

首先，椭圆是一个闭合曲线，即椭圆上的点是有限的。

其次，椭圆上的任意点到两个焦点的距离之和等于常数，这被称为椭圆的焦点距离定律。

另外，椭圆还具有对称性，即关于主轴和辅助轴都具有对称性。

在实际应用中，椭圆广泛用于椭圆轨道的描述，如行星绕太阳的轨道。

此外，椭圆还用于数学、物理和工程等领域，如天体力学、椭圆积分等。

二、双曲线双曲线也是圆锥曲线的一种，其定义是平面上到两个定点的距离之差等于常数的点的集合。

与椭圆不同，双曲线有两条渐近线，且曲线上的点数是无限的。

双曲线也有主轴和辅助轴，分别与椭圆相似。

双曲线的性质与椭圆有一些相似之处，如焦点距离定律和对称性。

同时，双曲线还有许多特有的性质。

例如，当点离两个焦点的距离之差等于零时，曲线上的点就变成了双曲线的渐近线。

此外，双曲线还具有合成结构，即由两个分离的曲线组成。

双曲线在物理学中有重要的应用，例如描述光的折射、电场的分布等。

此外，双曲线还出现在几何光学、热力学、电磁学等领域。

三、抛物线抛物线是圆锥曲线的最后一种类型，其定义是平面上到一个定点的距离等于到一条直线的距离的点的集合。

抛物线是一个开口朝上或朝下的曲线，具有对称性。

抛物线的特点之一是其焦点和直线的关系。

焦点位于抛物线的对称轴上，并且到对称轴的距离等于到准线的距离。

此外，抛物线还具有反射性质，即任意一条从焦点发射的光线，折射后都会通过抛物线的焦点。

抛物线在物理学和工程学中都有广泛的应用。

例如，抛物线形状的水流可用于喷泉设计，抛物线镜实现了广角成像，还有抛物线伞等。

圆锥曲线知识点知识点一：圆锥曲线的统一定义椭圆、双曲线、抛物线统称圆锥曲线。

平面内，到一定点的距离与它到一条定直线（不经过定点）的距离之比是常数e的点的轨迹叫做圆锥曲线。

定点叫做焦点，定直线叫做准线、常数叫做离心率。

①e∈（0，1）时轨迹是椭圆；②e=1时轨迹是抛物线；③e∈（1，+∞）时轨迹是双曲线。

知识点二：圆锥曲线的标准方程和几何性质1．椭圆：(1)定义：平面内到两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫椭圆，这两个定点叫焦点．(2)标准方程当焦点在轴上时，椭圆的标准方程：，其中；当焦点在轴上时，椭圆的标准方程：，其中；(3)椭圆的的简单几何性质:范围：，，焦点，顶点、，长轴长= ，短轴长= ，焦距＝，2．双曲线(1)定义：平面内与两个定点F1、F2的距离的差的绝对值等于常数(小于|F1F2|)的点的轨迹叫做双曲线,这两个定点叫双曲线的焦点．(2)标准方程当焦点在轴上时，双曲线的标准方程：，其中；当焦点在轴上时，双曲线的标准方程：，其中 .(3)双曲线的简单几何性质范围：，；焦点，顶点，实轴长= ，虚轴长= ，焦距＝；离心率是，准线方程是；渐近线： .3．抛物线(1)定义:平面内与一个定点F和一条定直线l的距离相等的点的轨迹叫做抛物线，定点F叫做抛物线的焦点，定直线l叫做抛物线的准线．(2)标准方程四种形式：，，，。

(3)抛物线标准方程的几何性质范围：，，对称性：关于x轴对称顶点：坐标原点离心率： .知识点三：直线和圆锥曲线的位置关系1．直线Ax+By+C＝0和椭圆的位置关系：将直线方程代入椭圆后化简为一元二次方程，其判别式为Δ。

(1)若Δ＞0，则直线和椭圆相交，有两个交点(或两个公共点)；(2)若Δ＝0，则直线和椭圆相切，有一个切点(或一个公共点)；(3)若Δ＜0，则直线和椭圆相离，无公共点．2．直线Ax+By+C＝0和双曲线的位置关系：将直线方程代入双曲线方程后化简方程①若为一元一次方程，则直线和双曲线的渐近线平行，直线和双曲线只有一个交点，但不相切不是切点；②若为一元二次方程，则(1)若Δ＞0，则直线和双曲线相交，有两个交点(或两个公共点)；(2)若Δ＝0，则直线和双曲线相切，有一个切点；(3)若Δ＜0，则直线和双曲线相离，无公共点．注意：如说直线和双曲线有一个公共点，则要考虑两种情况：一个切点和一个交点3．直线Ax+By+C＝0和抛物线y2＝2px(p＞0)的位置关系：将直线方程代入抛物线方程后化简后方程：①若为一元一次方程，则直线和抛物线的对称轴平行，直线和抛物线有一个交点，但不相切不是切点；②若为一元二次方程，则(1)若Δ＞0，则直线和抛物线相交，有两个交点(或两个公共点)；(2)若Δ＝0，则直线和抛物线相切，有一个切点；(3)若Δ＜0，则直线和抛物线相离，无公共点。

圆锥曲线基本公式圆锥曲线是数学中重要的几何概念之一，它由圆锥与一个平面相交而形成。

圆锥曲线的基本公式包括椭圆、双曲线和抛物线。

首先，我们来看椭圆。

椭圆是圆锥和平面相交时，平面与圆锥轴线之间的夹角小于圆锥的母线夹角的情况。

椭圆的基本公式可以表示为：（x-h）^2/a^2 +（y-k）^2/b^2 = 1其中，（h，k）为椭圆的中心点坐标，a为椭圆长轴的半长，b为椭圆短轴的半长。

这个公式是椭圆的标准方程，通过改变参数a和b的值可以调整椭圆的形状和大小。

其次，我们来看双曲线。

双曲线是圆锥与平面相交时，平面与圆锥轴线之间的夹角大于圆锥的母线夹角的情况。

双曲线的基本公式可以表示为：（x-h）^2/a^2 -（y-k）^2/b^2 = 1或（y-k）^2/b^2 -（x-h）^2/a^2 = 1其中，（h，k）为双曲线的中心点坐标，a和b分别为双曲线的长轴半长和短轴半长。

这两个公式分别对应于双曲线的横轴和纵轴方向，通过改变参数a和b的值可以调整双曲线的形状和大小。

最后，我们来看抛物线。

抛物线是圆锥与平面相交时，平面与圆锥轴线之间的夹角等于圆锥的母线夹角的情况。

抛物线的基本公式可以表示为：y = ax^2 + bx + c其中，a、b和c为常数，通过改变这些常数的值可以调整抛物线的形状，例如改变a的正负可以使抛物线开口朝上或朝下。

除了基本公式，圆锥曲线还有许多性质和特点值得研究。

例如，椭圆的离心率小于1，而双曲线的离心率大于1。

离心率是描述圆锥曲线形状的一个重要指标，它是与圆锥曲线焦点之间的距离比上椭圆长轴或双曲线的实际距离的比值。

离心率越接近于0，圆锥曲线越接近于圆形；离心率越大，圆锥曲线的形状越扁平。

此外，圆锥曲线还有许多重要的性质和应用，例如在天文学中描述行星轨道、在物理学中描述抛物线运动等。

总之，圆锥曲线是数学中重要且有趣的概念，它的基本公式包括椭圆、双曲线和抛物线。

通过这些公式及其性质，我们可以研究和描述各种各样的曲线形状和特点。

平面几何中的圆锥曲线圆锥曲线是平面几何中的一类重要曲线，它们具有独特的性质和应用。

本文将对圆锥曲线的定义、特点以及其在科学和工程领域的应用进行探讨。

一、圆锥曲线的定义圆锥曲线是指在平面几何中由一个固定点F（焦点）和一条固定线段L（准线）确定的曲线。

圆锥曲线分为三类：椭圆、双曲线和抛物线。

它们的定义和性质可以通过几何方法和代数方法加以描述。

二、椭圆椭圆是圆锥曲线中最简单的一种形式。

椭圆曲线可以通过以下几种方式来定义：1. 平面上到两个给定点F1和F2的距离之和等于常数2a（椭圆的长轴），则该点的轨迹为椭圆；2. 平面上到一个给定中心点O的距离和到椭圆焦点F的距离之和等于常数a，则该点的轨迹为椭圆。

椭圆具有以下特点：1. 对称性：椭圆关于其长轴和短轴的中点具有对称性；2. 焦点和准线：椭圆的焦点在长轴上，准线与短轴平行；3. 离心率：椭圆的离心率在0到1之间，离心率越大，椭圆越扁平；4. 圆形特例：当椭圆的两焦点重合时，其为一个圆。

椭圆在科学和工程领域有广泛的应用，例如天体力学中的行星轨道计算、通信技术中的调制解调、地理测量中的椭球体建模等。

三、双曲线双曲线是圆锥曲线中另一种重要的曲线形式。

双曲线曲线可以通过以下几种方式来定义：1. 平面上到两个给定点F1和F2的距离之差等于常数2a（双曲线的距离），则该点的轨迹为双曲线；2. 平面上到一个给定中心点O的距离和到双曲焦点F的距离之差等于常数a，则该点的轨迹为双曲线。

双曲线具有以下特点：1. 对称性：双曲线关于其长轴和短轴的中点具有对称性；2. 焦点和准线：双曲线的焦点在长轴上，准线与短轴平行；3. 两支分离：双曲线由两支构成，相互分离；4. 离心率：双曲线的离心率大于1，越接近1，双曲线越扁平。

双曲线在科学和工程领域也有广泛的应用，例如天体力学中的行星摄动计算、电磁学中的电荷分布建模等。

四、抛物线抛物线是圆锥曲线中最后一种形式。

抛物线可以通过以下几种方式来定义：1. 平面上到一个给定焦点F的距离和到一条给定直线L（准线）的距离相等，则该点的轨迹为抛物线；2. 平面上到一个给定中心点O的距离和到抛物焦点F的距离相等，则该点的轨迹为抛物线。

圆锥曲线的分类及基本方程圆锥曲线是解析几何中最为重要的一类曲线，不仅在数学领域有广泛应用，在物理、化学、工程等多个领域中也有着重要的作用。

本文将围绕圆锥曲线的分类及基本方程展开讨论。

一、圆锥曲线的定义圆锥曲线是指由一个固定点F（焦点）和一个固定直线L（直角母线）所确定的点P（动点）的轨迹。

如果点P在直线L同侧与焦点F的距离大于点P到直线L的距离，则称此为椭圆；如果点P在直线L同侧与焦点F的距离等于点P到直线L的距离，则称此为双曲线；如果点P在直线L的另一侧，且距离相等，则称此为圆。

二、圆锥曲线的分类根据圆锥曲线的定义，可以将它们分为三类：椭圆、双曲线和圆。

下面分别进行讲解。

1. 椭圆椭圆是指在平面直角坐标系中，到空间内两个定点F1、F2距离之和为定值2a、固定数e小于1的点P所形成的轨迹。

其中，a为椭圆的半长轴，b为椭圆的半短轴，c为椭圆的焦距，e为椭圆的离心率，有以下基本方程：(x^2 / a^2) + (y^2 / b^2) = 1其中，如果椭圆的中心在坐标系原点上，则方程为：x^2 / a^2 + y^2 / b^2 = 12. 双曲线双曲线是指在平面直角坐标系中，到空间内两个定点F1、F2距离之差为定值2a、固定数e大于1的点P所形成的轨迹。

其中，a为双曲线的半轴，b为双曲线的次轴，c为双曲线的焦距，e为双曲线的离心率，有以下基本方程：(x^2 / a^2) - (y^2 / b^2) = 1其中，如果双曲线的中心在坐标系原点上，则方程为：x^2 / a^2 - y^2 / b^2 = 13. 圆圆是指在平面直角坐标系中离空间内一个固定点O距离相等的点P所组成的轨迹，该固定点称为圆心，离圆心最远的点称为圆的周围。

圆的方程为：(x - a)^2 + (y - b)^2 = r^2其中，（a，b）为圆心坐标，r为圆的半径。

三、圆锥曲线的性质1. 椭圆的离心率小于1，且对称轴平行于 y 轴，故对称于 x 轴的部分也是椭圆。

圆锥曲线过程
圆锥曲线是代数几何学中的一个重要领域，它研究的是三维空间中圆锥与平面的交点集合。

这个集合可以是直线、椭圆、抛物线或双曲线。

圆锥曲线的研究始于希腊数学家阿波罗尼奥斯的《圆锥曲线论》。

他将圆锥与平面的交点集合分为三类：直线、椭圆和双曲线。

后来，笛卡尔将这些曲线用代数方程描述，从而开启了代数几何学的新篇章。

圆锥曲线的研究涉及到许多数学工具和方法，如解析几何、微积分、矩阵论等。

它不仅在数学中有重要的应用，还在物理学、工程学、计算机图形学等领域中起着重要作用。

圆锥曲线的研究过程中，人们发现了许多有趣的性质和定理。

比如，任何一条椭圆或双曲线的两个焦点之和是一个常数；任何一条抛物线都可以看作是一个点和一条直线的轨迹；直线是一种特殊的圆锥曲线，其方程可以表示成一次方程等等。

总之，圆锥曲线是数学中一个非常有趣而又重要的领域，它的研究涉及到许多数学工具和方法，有着广泛的应用价值。

- 1 -。

圆锥曲线的性质及分类圆锥曲线是数学中重要的曲线形状之一，由圆锥与平面相交形成。

它们具有独特的性质和分类。

本文将探讨圆锥曲线的性质及其分类。

一、圆锥曲线的定义圆锥曲线即是平面和圆锥交叠后形成的曲线。

圆锥曲线可以分为三种类型：椭圆、抛物线和双曲线。

它们的性质和特点不尽相同。

二、椭圆的性质及分类椭圆是一种闭合曲线，其定义为平面上离定点F1、F2的距离之和为常数2a的点构成的轨迹。

椭圆具有以下性质：1. 定义性质：椭圆的离心率e满足0<e<1，焦点之间的距离为2ae。

2. 对称性质：椭圆具有关于两个坐标轴对称的性质。

3. 切线性质：椭圆上任一点处的切线与该点到两焦点的连线垂直。

三、抛物线的性质及分类抛物线是一种开放的曲线，其定义为平面上点到定点F的距离与其到直线L的距离相等的点构成的轨迹。

抛物线具有以下性质：1. 定义性质：抛物线的离心率e等于1，焦点为定点F，准线为直线L。

2. 对称性质：抛物线具有关于纵轴对称的性质。

3. 切线性质：抛物线上任一点处的切线与该点到焦点的连线垂直。

四、双曲线的性质及分类双曲线是一种开放的曲线，其定义为平面上离定点F1、F2的距离之差为常数2a的点构成的轨迹。

双曲线具有以下性质：1. 定义性质：双曲线的离心率e大于1，焦点之间的距离为2ae。

2. 对称性质：双曲线具有关于两个坐标轴的对称性质。

3. 切线性质：双曲线上任一点处的切线与该点到两焦点的连线的夹角等于一个定值。

五、圆锥曲线的分类根据离心率的不同，圆锥曲线可以分为三类：椭圆（离心率e<1）、抛物线（离心率e=1）和双曲线（离心率e>1）。

通过调整焦点之间的距离和离心率的大小，可以得到不同类型的圆锥曲线。

六、结论圆锥曲线是一类重要的数学曲线，包括椭圆、抛物线和双曲线。

它们具有各自独特的性质和分类，通过调整焦点位置和离心率的值，可以得到不同类型的圆锥曲线。

对于圆锥曲线的研究和应用，有助于深入理解曲线的几何性质和数学规律，拓宽数学相关领域的研究和应用范围。