广东省广州市2012年数学中考模拟试卷(1)

2012年广州市西关外国语学校初三第一次模拟考试数 学 试 卷本试卷共三大题25小题，共4页，满分150分．考试时间120分钟．注意事项:1．答卷前，考生务必在答题卡上用黑色字迹的钢笔或签字笔填写自己的考号、姓名；再用2B 铅笔把对应考号的标号涂黑．2．选择题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；不能答在试卷上． 3．填空题和解答题必须用黑色字迹的钢笔或签字笔作答，涉及作图的题目，用2B 铅笔画图．答案必须写在答题卡各题目指定区域内的相应位置上；改动的答案也不能超出指定的区域．不准使用铅笔、圆珠笔和涂改液．不按以上要求作答的答案无效．4．考生可以．．使用计算器．必须保持答题卡的整洁． 第一部分 选择题（共30分）一、选择题（本大题共10小题，每小题3分，满分30分）1．计算：2-=（ ）A ．-1B ．-3C ．3D ．52．用科学记数法表示0.0000210，结果是（ ）A ．2.10×10－4B ．2.10×10－5C ． 2.1×10－4D ．2.1×10－53．点P （－2，1）关于x 轴对称的点的坐标是（ ）A ．（－2，－1）B ．（2，－1）C ．（1，－2）D ．（2，1） 4．计算232(3)x x ⋅-的结果是（ ）A ．56x -B ．56xC ．62x -D ．62x 5．为了解某班学生每天使用零花钱的情况，小明随机调查了15名同学，结果如下表：A ．众数是5元B ．平均数是2.5元C ．极差是4元D ．中位数是3元 6．两个大小不同的球在水平面上靠在一起，组成如图所示的几何体，则该几何体的左视图是（ ）A ．两个外离的圆B ．两个外切的圆C ．两个相交的圆D ．两个内切的圆7．甲、乙两名同学在一次用频率去估计概率的实验中，统计了某一结果出（第6题）现的频率绘出的统计图如图所示，符合这一结果的实验可能是（ ） A.掷一枚正六面体的骰子，出现1点的概率 B. 任意写一个正整数，它能被3整除的概率 C.抛一枚硬币，出现正面的概率D. 从一个装有2个白球和1个红球的袋子中任取一球，取到白球的概率8．如图，AB 为⊙O 的直径，PD 切⊙O 于点C ，交AB 的延长线于D ，且CO ＝CD ，则∠PCA ＝（ ）A ．30°B ．45°C ．60°D ．67.5°9．如图，在平行四边形ABCD 中，E 是BC 的中点，且∠AEC =∠DCE ，则下列结论不正确的是（ ）A ．S △AFD =2S △EFB B ．BF =21DFC ．四边形AECD 是等腰梯形 D ．∠AEB =∠ABC 10．如图，是反比例函数1k y x=和2k y x=（12k k <）在第一象限的图象，直线AB ∥x 轴，并分别交两条曲线于A 、B 两点，若2AO B S ∆=，则21k k -的值是（ ） A ．1 B ．2 C ．4 D ．8、（第8题）（第7题）（第9题）（第10题）第二部分非选择题（共120分）二、填空题（本大题共6小题，每小题3分，满分18分）11.分解因式：228x-=．12.如图,D EF△是由A B C△绕着某点旋转得到的,则这点的坐标是．13．如图，现有一个圆心角为90°，半径为16cm的扇形纸片，用它恰好围成一个圆锥的侧面（接缝忽略不计），则该圆锥底面圆的半径为cm.14.已知方程2520x x-+=的两个解分别为1x、2x，则1212x x x x+-⋅的值为.15.以数轴上的原点O为圆心，3为半径的扇形中，圆心角∠AOB＝90°，另一个扇形是以点P为圆心，5为半径，圆心角∠CPD＝60°，点P在数轴上表示实数a，如图，如果两个扇形的圆弧部分( AB和C D)相交，那么实数a的取值范围是．16．如图，45AOB∠= ，过O A上到点O的距离分别为1,3,5,7,9,11…的点作O A的垂线与OB相交，得到并标出一组黑色梯形，它们的面积分别为1234S S S S，，，，,则第一个黑色梯形的面积=1S；观察图中的规律，第n(n为正整数)个黑色梯形的面积=nS．三、解答题（本大题共9小题，满分102分）17.（本题满分9分）解分式方程：22125=---xx（第13题）（第15题）（第16题）18.（本题满分9分）先化简，再请你用喜爱的数代入求值.xx x x x x xx x 42)44122(322-+÷+----+19.（本题满分10分）今年“五一”假期，某数学活动小组组织一次登山活动.他们从山脚下A 点出发沿斜坡AB 到达B 点，再从B 点沿斜坡BC 到达山顶C 点，路线如图所示.斜坡AB 的长为1040米，斜坡BC 的长为400米，在C 点测得B 点的俯角为30°,已知A 点海拔121米，C 点海拔721米. （1）求B 点的海拔；（2）求斜坡AB 的坡度.20.（本题满分10分）某商场为了吸引顾客，设计了一种促销活动：在一个不透明的箱子里放有4个相同的小球，球上分别标有“0元”、“10元”、“20元”和“30元”的字样．规定：顾客在本商场同一日内，每消费满200元，就可以在箱子里先后摸出两个球（第一次摸出后不放回），商场根据两小球所标金额的和返还相应价格的购物券，可以重新在本商场消费，某顾客刚好消费200元． （1）该顾客至少可得到_____元购物券，至多可得到_______元购物券；（2）请你用画树状图或列表的方法，求出该顾客所获得购物券的金额不低于30元的概率．21.（本题满分12分）已知，AB 是⊙O 的直径，AB =8，点C 在⊙O 的半径OA 上运动，PC ⊥AB ，垂足为C ，PC =5，PT 为⊙O 的切线，切点为T . ⑴ 如图⑴，当C 点运动到O 点时，求PT 的长;⑵ 如图⑵，当C 点运动到A 点时，连结PO 、BT ，求证：PO ∥BT ; ⑶ 如图⑶，设y PT =2，x AC =，求y 与x 的函数关系式及y 的最小值.图(1)22.（本题满分12分）随着人们经济收入的不断提高及汽车产业的快速发展，汽车已越来越多地进入普通家庭．据某市交通部门统计，2008年底该市汽车拥有量为75万辆，而截止到2010年底，该市的汽车拥有量已达108万辆．⑴求2008年底至2010年底该市汽车拥有量的年平均增长率；⑵为了保护城市环境，缓解汽车拥堵状况，该市交通部门拟控制汽车总量，要求到2012年底全市汽车拥有量不超过125.48万辆；另据统计，从2011年初起，该市此后每年报废的汽车数量是上年底汽车拥有量的10%假设每年新增汽车数量相同，请你估算出该市从2011年初起每年新增汽车数量最多不超过多少万辆．23．（本题满分12分）如图，在梯形ABCD中，AB∥DC，∠BCD＝90°，且AB＝1，BC＝2，tan∠ADC ＝2．⑴求证：DC＝BC；＝BF，试判断△ECF的形状，并证明你的结论；⑶在⑵的条件下，当BE：CE＝1：2，∠BEC＝135°时，求sin∠BFE的值．24．（本题满分14分）已知：m 、n 是方程2650x x -+=的两个实数根，且m <n ，抛物线2y x bx c=-++的图像经过点A (m ，0)、B (0，n )． （1）求这个抛物线的解析式；（2）设（1）中抛物线与x 轴的另一交点为C ，抛物线的顶点为D ，试求出点C 、D 的坐标和△BCD 的面积；（3）P 是线段OC 上的一点，过点P 作PH ⊥x 轴，与抛物线交于H点，若直线BC 把△PCH 分成面积之比为2：3的两部分，请求出P 点的坐标．25.（本题满分14分）在□ABCD 中，∠BAD 的平分线交直线BC 于点E ，交直线DC 于点F 。

2012年广州市初中毕业生学业考试数 学第一部分 选择题（共30分）一、选择题（本大题共10小题，每小题3分，满分30分。

在每小题给出的4个选项中只有一项是符合题目要求的） 1．实数3的倒数是（ ）。

（A ）、31-（B ）、31（C ）、3- （D ）、32．将二次函数2x y =的图象向下平移1个单位，则平移后的二次函数的解析式为（ ）。

（A ）、12-=x y（B ）、 12+=x y （C ）、2)1(-=x y（D ）、2)1(+=x y3．一个几何体的三视图如图1所示，则这个几何体是（ ）。

（A ）、四棱锥 （B ）、 四棱柱 （C ）、三棱锥 （D ）、三棱柱4．下面的计算正确的是( ) 。

（A ）、156=-a a （B ）、 223a a a =+（C ）、b a b a +-=--)(（D ）、b a b a +=+2)(25．如图2，在等腰梯形ABCD 中，BC ∥AD ,AD =5,DC =4,DE ∥AB 交BC 于点E ，且EC =3，则梯形ABCD 的周长是（ ） （A ）、26 （B ）、25 （C ）、21（D ）、206．.已知,071=++-b a 则=+b a ( ) 。

（A ）、-8 （B ）、 -6 （C ）、6（D ）、87. Rt ABC △中，∠C=900，AC =9,BC =12,则点C 到AB 的距离是( )。

（A ）、536 （B ）、2512 （C ）、49 （D ）、433 8.已知a >b .若c 是任意实数，则下列不等式中总是成立的是（ ）。

（A ）、a+c <b+c （B ）、 a-c >b-c （C ）、ac <bc （D ）、ac >bc9.在平面中，下列命题为真命题的是（ ）。

（A ）、四边相等的四边形是正方形 （B ）、对角线相等的四边形是菱形 （C ）、四个角相等的四边形是矩形（D ）、对角线互相垂直的四边形是平行四边形 10.如图3，正比例函数x ky 11=和反比例函数xky 22=的图象交于A(-1,2)、B （1，-2）两点。

绝密★启用前2012年广州市初中毕业生学业考试综合训练数 学本试卷分选择题和非选择题两部分，共三大题25小题，共4页，满分150分．考试用时120分钟．第一部分（选择题 共30分）一、选择题（本大题共10小题，每小题3分，满分30分，在每小题给出的四个选项中，只有一项是符合题目要求的．）1.下列计算正确的是（ ）A. 632a a a =• B.()()2222b a b a b a -=-+ C.()6223b a ab = D. 325=-a a2.将叶片图案旋转180°后，得到的图形是（ ）A ．B ．C ．D ．3.方程组⎩⎨⎧=+=-422y x y x 的解是（ ）A ．⎩⎨⎧==21y xB ．⎩⎨⎧==13y xC ．⎩⎨⎧-==2y xD ．⎩⎨⎧==02y x4.当x 为满足什么条件时，分式21+-x x 无意义（ ） A ．x =1 B ．x =－1 C ．x =2 D ．x =－2 5. 长方体的主视图与左视图如图所示（单位：cm ），则这个长方体的体积是（ ）A ．24cm 3B ．12cm 3C ．8cm 3D ．4cm 36.在一个不透明的口袋中，装有5个红球3个白球，它们除颜色外都相同，从中任意摸出一个球，摸到红球的概率为（ ）A ．15 B ．13 C ．58 D ．387.如图，DE 是△ABC 的中位线，若BC 的长是3cm ，则DE 的长是（ ）A ．1.5cmB ．2cmC ．3cmD ．6cm第5题图左视图主视图2342E A BCD8.实数a在数轴上的位置如图所示，则22(4)(11)a a -+- 化简后为（ ） A ． 7 B ． －7 C ． 2a －15 D ． 无法确定9. 抛物线221y x x =-+的顶点坐标是（ ）A ．（1，0）B ．（－1，0）C ．（－2，1）D ．（2，－1） 10. 如图，在Rt △ABC 中，∠ACB=90°，CD ⊥AB ，垂足为D.若AC=5，BC=2，则sin ∠ACD 的值为( ) A.53 B.255 C. 52 D. 23第二部分（非选择题 共120分）二、填空题（本大题共6小题，每小题3分，满分18分．） 11. —12的倒数是 12．因式分解：224a a -= ．13．不等式23x x >-的解集为 ．14．圆锥的底面半径为8，母线长为9，则该圆锥的侧面积为 15．二次函数y=2x ²-6与x 轴的交点是___________________． 16．观察下列图形（每幅图中最小．．的三角形都是全等的），请写出第n 个图中最小．．的三角形的个数有 个． 三、解答题（本大题共9小题，满分102分，解答应写出文字说明、证明过程或演算步骤）17．（本小题满分9分）解方程：2311-=+x x 18．（本小题满分9分）如图：在四边形ABCD 中，AD ∥BC ，AB =CD ，E 是BC 上一点，DE =AB 。

2012年广东省中考数学模拟试卷（七）一．选择题（本大题共5小题，每小题3分，共15分）在每小题给出的四个选项中，只有一个是正确的，请将正确选项的字母写在答题卷相应的答题位置上．C3．（3分）（2009•金华）一个几何体及它的主视图和俯视图如图所示，那么它的左视图正确的是（）．C D．4．（3分）玉树地震后，各界爱心如潮，4月20日搜索“玉树捐款”获得约7945000条结果，其中7945000用科学记二、填空题（4&#215;5=20分）6．（4分）（2011•昭通）分解因式：3a2﹣27=_________．7．（4分）（2007•义乌市）如图，在△ABC中，点D、E分别是边AB、AC的中点，已知DE=6cm，则BC=_________ cm．8．（4分）（2009•湛江）一件衬衣标价是132元，若以9折降价出售，仍可获利10%，则这件衬衣的进价是_________元．9．（4分）（2011•南漳县模拟）为了测量一个圆铁环的半径，某同学用了如下方法，将铁环平放在水平桌面上，用有一个角为30°的直角三角板和刻度尺按如图所示的方法得到相关数据，进而求出铁环半径，若测得PA=5cm，则铁环的半径是_________cm．10．（4分）（2009•金华）“赵爽弦图”是由四个全等的直角三角形与一个小正方形拼成的一个大正方形．如果小正方形的面积为4，大正方形的面积为100，直角三角形中较小的锐角为α，则tanα的值等于_________．三、解答题（本大题5小题，每小题6分，共30分）11．（6分）（2009•张家界）计算：．12．（6分）（2009•兰州）如图，要在一块形状为直角三角形（∠C为直角）的铁皮上裁出一个半圆形的铁皮，需先在这块铁皮上画出一个半圆，使它的圆心在线段AC上，且与AB、BC都相切．请你用直尺和圆规画出来（要求用尺规作图，保留作图痕迹，不要求写作法）．13．（6分）如图，在▱ABCD的各边AB、BC、CD、DA上，分别取点K、L、M、N，使AK=CM、BL=DN，则四边形KLMN为平行四边形吗？说明理由．14．（6分）（2009•庆阳）如图1，一扇窗户打开后用窗钩AB可将其固定．（1）这里所运用的几何原理是（）（A）三角形的稳定性（B）两点之间线段最短；（C）两点确定一条直线（D）垂线段最短；（2）图2是图1中窗子开到一定位置时的平面图，若∠AOB=45°，∠OAB=30°，OA=60cm，求点B到OA边的距离．（≈1.7，结果精确到整数）15．（6分）（2011•鼎湖区模拟）如图所示，⊙O的直径AB为10cm，弦AC为6cm，∠ACB的平分线交⊙O于D，求BC，AD，BD的长．四．解答题（本大题4小题，每小题7分，共28分）16．（7分）某商场为了吸引顾客，设计了一个摸球获奖的箱子，箱子中共有20个球，其中红球2个，兰球3个，黄球5个，白球10个，并规定购买100元的商品，就有一次摸球的机会，摸到红、兰、黄、白球的（一次只能摸一个），顾客就可以分别得到80元、30元、10元、0元购物卷，凭购物卷仍然可以在商场购买，如果顾客不愿意摸球，那么可以直接获得购物卷10元．（1）每摸一次球所获购物卷金额的平均值是多少？（2）你若在此商场购买100元的货物，两种方式中你应选择哪种方式？为什么？17．（7分）（2010•海门市二模）某地有一人患了流感，经过两轮传染后共有121人患了流感，每轮传染中平均一个人传染了几个人？18．（7分）（2013•武侯区一模）已知二次函数y=x2﹣kx+k﹣5（1）求证：无论k取何实数，此二次函数的图象与x轴都有两个交点；（2）若此二次函数图象的对称轴为x=1，求它的解析式．19．（7分）如图，过点P（2，）作x轴的平行线交y轴于点A，交双曲线（x＞0）于点N，作PM⊥AN交双曲线（x＞0）于点M，连接AM．已知PN=4．（1）求k的值；（2）设直线MN解析式为y=ax+b，求不等式≥ax+b的解集．五．解答题（本大题3小题，每小题9分，共27分）20．（9分）（2012•陵县二模）在我们学习过的数学教科书中，有一个数学活动，其具体操作过程是：第一步：对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展开（如图1）；第二步：再一次折叠纸片，使点A落在EF上，并使折痕经过点B，得到折痕BM，同时得到线段BN（如图2）．请解答以下问题：（1）如图2，若延长MN交BC于P，△BMP是什么三角形？请证明你的结论；（2）在图2中，若AB=a，BC=b，a、b满足什么关系，才能在矩形纸片ABCD上剪出符合（1）中结论的三角形纸片BMP？21．（9分）（2009•黑河）某电脑公司经销甲种型号电脑，受经济危机影响，电脑价格不断下降．今年三月份的电脑售价比去年同期每台降价1000元，如果卖出相同数量的电脑，去年销售额为10万元，今年销售额只有8万元．（1）今年三月份甲种电脑每台售价多少元？（2）为了增加收入，电脑公司决定再经销乙种型号电脑，已知甲种电脑每台进价为3500元，乙种电脑每台进价为3000元，公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台，有几种进货方案？（3）如果乙种电脑每台售价为3800元，为打开乙种电脑的销路，公司决定每售出一台乙种电脑，返还顾客现金a 元，要使（2）中所有方案获利相同，a值应是多少此时，哪种方案对公司更有利？22．（9分）（2009•湘潭）如图，在平面直角坐标系中，四边形OABC为矩形，OA=3，OC=4，P为直线AB上一动点，将直线OP绕点P逆时针方向旋转90°交直线BC于点Q．（1）当点P在线段AB上运动（不与A，B重合）时，求证：OA•BQ=AP•BP；（2）在（1）成立的条件下，设点P的横坐标为m，线段CQ的长度为l，求出l关于m的函数解析式，并判断l 是否存在最小值？若存在，请求出最小值；若不存在，请说明理由；（3）直线AB上是否存在点P，使△POQ为等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由．2012年广东省中考数学模拟试卷（七）参考答案与试题解析一．选择题（本大题共5小题，每小题3分，共15分）在每小题给出的四个选项中，只有一个是正确的，请将正确选项的字母写在答题卷相应的答题位置上．C3．（3分）（2009•金华）一个几何体及它的主视图和俯视图如图所示，那么它的左视图正确的是（）．C D．4．（3分）玉树地震后，各界爱心如潮，4月20日搜索“玉树捐款”获得约7945000条结果，其中7945000用科学记二、填空题（4&#215;5=20分）6．（4分）（2011•昭通）分解因式：3a2﹣27=3（a+3）（a﹣3）．7．（4分）（2007•义乌市）如图，在△ABC中，点D、E分别是边AB、AC的中点，已知DE=6cm，则BC=12 cm．8．（4分）（2009•湛江）一件衬衣标价是132元，若以9折降价出售，仍可获利10%，则这件衬衣的进价是108元．9．（4分）（2011•南漳县模拟）为了测量一个圆铁环的半径，某同学用了如下方法，将铁环平放在水平桌面上，用有一个角为30°的直角三角板和刻度尺按如图所示的方法得到相关数据，进而求出铁环半径，若测得PA=5cm，则铁环的半径是5cm．=510．（4分）（2009•金华）“赵爽弦图”是由四个全等的直角三角形与一个小正方形拼成的一个大正方形．如果小正方形的面积为4，大正方形的面积为100，直角三角形中较小的锐角为α，则tanα的值等于．8=三、解答题（本大题5小题，每小题6分，共30分）11．（6分）（2009•张家界）计算：．12．（6分）（2009•兰州）如图，要在一块形状为直角三角形（∠C为直角）的铁皮上裁出一个半圆形的铁皮，需先在这块铁皮上画出一个半圆，使它的圆心在线段AC上，且与AB、BC都相切．请你用直尺和圆规画出来（要求用尺规作图，保留作图痕迹，不要求写作法）．13．（6分）如图，在▱ABCD的各边AB、BC、CD、DA上，分别取点K、L、M、N，使AK=CM、BL=DN，则四边形KLMN为平行四边形吗？说明理由．14．（6分）（2009•庆阳）如图1，一扇窗户打开后用窗钩AB可将其固定．（1）这里所运用的几何原理是（）（A）三角形的稳定性（B）两点之间线段最短；（C）两点确定一条直线（D）垂线段最短；（2）图2是图1中窗子开到一定位置时的平面图，若∠AOB=45°，∠OAB=30°，OA=60cm，求点B到OA边的距离．（≈1.7，结果精确到整数）x=3015．（6分）（2011•鼎湖区模拟）如图所示，⊙O的直径AB为10cm，弦AC为6cm，∠ACB的平分线交⊙O于D，求BC，AD，BD的长．=5（四．解答题（本大题4小题，每小题7分，共28分）16．（7分）某商场为了吸引顾客，设计了一个摸球获奖的箱子，箱子中共有20个球，其中红球2个，兰球3个，黄球5个，白球10个，并规定购买100元的商品，就有一次摸球的机会，摸到红、兰、黄、白球的（一次只能摸一个），顾客就可以分别得到80元、30元、10元、0元购物卷，凭购物卷仍然可以在商场购买，如果顾客不愿意摸球，那么可以直接获得购物卷10元．（1）每摸一次球所获购物卷金额的平均值是多少？（2）你若在此商场购买100元的货物，两种方式中你应选择哪种方式？为什么？，，，×××=1517．（7分）（2010•海门市二模）某地有一人患了流感，经过两轮传染后共有121人患了流感，每轮传染中平均一个人传染了几个人？18．（7分）（2013•武侯区一模）已知二次函数y=x2﹣kx+k﹣5（1）求证：无论k取何实数，此二次函数的图象与x轴都有两个交点；（2）若此二次函数图象的对称轴为x=1，求它的解析式．，19．（7分）如图，过点P（2，）作x轴的平行线交y轴于点A，交双曲线（x＞0）于点N，作PM⊥AN交双曲线（x＞0）于点M，连接AM．已知PN=4．（1）求k的值；（2）设直线MN解析式为y=ax+b，求不等式≥ax+b的解集．））代入y=，））∴由图象知，不等式五．解答题（本大题3小题，每小题9分，共27分）20．（9分）（2012•陵县二模）在我们学习过的数学教科书中，有一个数学活动，其具体操作过程是：第一步：对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展开（如图1）；第二步：再一次折叠纸片，使点A落在EF上，并使折痕经过点B，得到折痕BM，同时得到线段BN（如图2）．请解答以下问题：（1）如图2，若延长MN交BC于P，△BMP是什么三角形？请证明你的结论；（2）在图2中，若AB=a，BC=b，a、b满足什么关系，才能在矩形纸片ABCD上剪出符合（1）中结论的三角形纸片BMP？BP=．b21．（9分）（2009•黑河）某电脑公司经销甲种型号电脑，受经济危机影响，电脑价格不断下降．今年三月份的电脑售价比去年同期每台降价1000元，如果卖出相同数量的电脑，去年销售额为10万元，今年销售额只有8万元．（1）今年三月份甲种电脑每台售价多少元？（2）为了增加收入，电脑公司决定再经销乙种型号电脑，已知甲种电脑每台进价为3500元，乙种电脑每台进价为3000元，公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台，有几种进货方案？（3）如果乙种电脑每台售价为3800元，为打开乙种电脑的销路，公司决定每售出一台乙种电脑，返还顾客现金a 元，要使（2）中所有方案获利相同，a值应是多少此时，哪种方案对公司更有利？22．（9分）（2009•湘潭）如图，在平面直角坐标系中，四边形OABC为矩形，OA=3，OC=4，P为直线AB上一动点，将直线OP绕点P逆时针方向旋转90°交直线BC于点Q．（1）当点P在线段AB上运动（不与A，B重合）时，求证：OA•BQ=AP•BP；（2）在（1）成立的条件下，设点P的横坐标为m，线段CQ的长度为l，求出l关于m的函数解析式，并判断l 是否存在最小值？若存在，请求出最小值；若不存在，请说明理由；（3）直线AB上是否存在点P，使△POQ为等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由．有最小值；，则，有最小值．。

2012年广州市初中毕业生学业考试数 学本试卷分选择题和非选择题两部分，共三大题25小题，共4页，满分150分，考试用时120分钟注意事项：1．答卷前，考生务必在答题卡第1面、第3面、第5面上用黑色字迹的钢笔或签字笔填写自已的考生号、姓名；填写考场试室号、座位号，再用2B 铅笔把对应这两个号码的标号涂黑。

2．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号，不能答在试卷上。

3．非选择题必须用黑色字迹的钢笔或签字笔作答，涉及作图的题目，用2B 铅笔画图，答案必须写在答题卡各题目指定区域内的相应位置上，如需改动，先划掉原来的答案，然后再写上新的答案，改动的答案也不能超出指定的区域，不准使用铅笔，圆珠笔和涂改液，不按以上要求作答的答案无效。

4．考生必须保持答题卡的整洁，考试结束后，将本试卷和答题卡一并交回。

第一部分 选择题 （共30分）一、选择题（本大题共10小题，每小题3分，满分30分，在每小题给出的四个选项中，只有一项是符合题目要求的。

） 1． 实数3的倒数是（ ）A ．31-B ．31C ．3-D ．32． 将二次函数2x y =的图像向下平移1个单位，则平移后的二次函数的解析式为（ ）A ．12-=x yB ．12+=x yC ．2)1(-=x yD ．2)1(+=x y3． 一个几何体的三视图如图1所示，则这个几何体是（ ）A ． 四棱锥B ．四棱柱C ．三棱锥D ．四棱柱4．下面的计算正确的是（ ）A ．156=-a aB ．3233a a a =+C ．b a b a +-=--)(D ．b a b a +=+22）（5．如图2，在等腰梯形ABCD 中，BC ∥AD ，AD=5, DC=4, DE ∥AB 交BC 于点E ，且EC=3.则梯形ABCD 的周长是（ ）A ．26B ．25C ．21D ．206． 已知071=-+-ba ，则=+b a （ ）A ．8-B ．6-C ．6D ．87．在Rt △ABC 中，∠C=90°, AC=9 , BC=12.则点C 到AB 的距离是（ ）A ．536B ．2512C ．49D ．4338．已知b a >，若c 是任意实数，则下列不等式总是成立的是（ ）A ．c b c a +<+B ．c b c a ->-C ．bc ac <D ．bc ac >9．在平面中，下列命题为真命题的是（ ）A ．四边相等的四边形是正方形B ．对角线相等的四边形是菱形C ．四个角相等的四边形是矩形D ．对角线互相垂直的四边形是平行四边形10．如图3，正比例函数x k y 11=和反比例函数xk y 22=的图象交于)2,1(-A 、），（21-B 两点，若21y y <，则x 的取值范围是 （ ）A ．1-<x 或1>xB ．1-<x 或10<<xC ．01<<-x 或10<<xD ．01<<-x 或1>x图2ED CBA第二部分 非选择题 （共120分）二、填空题（本大题共6小题，每小题3分，满分18分.）11．已知∠ABC=30°, BD 是∠ABC 的平分线，则∠ABD=_______度．12．不等式101≤-x 的解集是_______．13．分解因式：a a 83-=_______．14．如图4，在等边△ABC 中，AB=6，D 是BC 上一点.且BC=3BD ，△ABD 绕点A 旋转后的得到△ACE. 则CE 的长为_______．EB A15．已知关于x 的一元二次方程0322=--k x x 有两各项等的实数根，则k 的值为_______． 16．如图5，在标有刻度的直线l 上，从点A 开始. 以AB=1为直径画半圆，记为第1个半圆 以BC=2为直径画半圆，记为第2个半圆 以CD=4为直径画半圆，记为第3个半圆 以DE=8为直径画半圆，记为第4个半圆……,按此规律，继续画半圆，则第4个半圆的面积是第3个半圆面积的_______倍,第n 个半圆的面积为_______． （结果保留π）三、解答题（本大题共9小题，满分102分，解答应写出文字说明、证明过程或演算步骤）17．（本小题满分9分） 解方程组：⎩⎨⎧=+=-1238y x y x18．（本小题满分9分）如图6，点D 在AB 上，点E 在AC 上，AB=AC ，∠B=∠C.求证：BE=CDEDCBA19．（本小题满分10分）广州市努力改善空气质量，近年来空气质量明显好转，根据广州市环境局公布的2006～2010这五年的全年空气质量优良的天数，绘制折线图如图7，根据图中信息回答：（1）这五年的全年空气质量是优良的天数的中位数是_______ ；极差是_______ ； （2） 这五年的全年空气质量优良天数与它的前一年相比较，增加最多的是______年（填写年份）； （3）求这五年的全年空气质量优良天数的平均数.20．（本小题满分10分）已知511=+b a )(b a ≠，求)()(b a a b b a b a ---的值.21．（本小题满分12分）甲、乙两个袋中均装有三张除所标数值外完全相同的卡片，甲袋中的三张卡片上的所标的数值分别为7-、1-、3,乙袋中的三张卡片上所标的数值分别为2-、1、6 ，先从甲袋中随机取一张卡片，用x 表示取出的卡片上标的数值，再从乙袋从随机取出一张卡片，用y 表示取出的卡片上标的数值.把x 、y 分别作为点A 的横坐标、纵坐标.（1）用适当的方法写出点）（y x A ,的所有情况； （2）求点A 落在第三象限的概率 .22．（本小题满分12分）如图8，⊙P 的圆心为）（2,3-P ，半径为3，直线MN 过点）（0,5M 且平行于y 轴，点N 在点M 的上方.（1）在图中作出⊙P 关于y 轴的对称的⊙P ’，根据作图直接写出⊙P ’与直线MN 的位置关系 ；（2）若点N 在（1）中的⊙P ’上，求PN 的长.23．（本小题满分12分）某城市居民用水实施阶梯收费.每户每月用水量如果未超过20吨，按每吨1.9元收费：每户每月用水量如果超过20吨，未超过的部分仍按每吨1.9元收费，超过的部分则按每吨2.8元收费.设某户每月用水量为x 吨，应收水费为y 元。

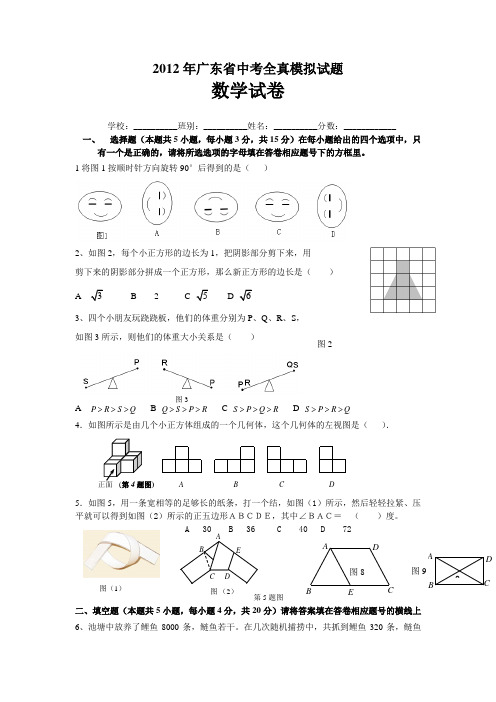
2012年广东省中考全真模拟试题数学试卷学校：__________班别：__________姓名：__________分数：____________一、 选择题（本题共5小题，每小题3分，共15分）在每小题给出的四个选项中，只有一个是正确的，请将所选选项的字母填在答卷相应题号下的方框里。

1将图1按顺时针方向旋转90°后得到的是（ ）2、如图2，每个小正方形的边长为1，把阴影部分剪下来，用 剪下来的阴影部分拼成一个正方形，那么新正方形的边长是（ ） AB 2CD 3、四个小朋友玩跷跷板，他们的体重分别为P 、Q 、R 、S ， 如图3所示，则他们的体重大小关系是（ ）A P R S Q >>>B Q S P R >>>C S P Q R >>>D S P R Q >>>4．如图所示是由几个小正方体组成的一个几何体，这个几何体的左视图是（ ）．5．如图5，用一条宽相等的足够长的纸条，打一个结，如图（1）所示，然后轻轻拉紧、压平就可以得到如图（2）所示的正五边形ＡＢＣＤＥ，其中∠ＢＡＣ＝ （ ）度。

A 30B 36C 40D 72二、填空题（本题共5小题，每小题4分，共20分）请将答案填在答卷相应题号的横线上 6、池塘中放养了鲤鱼8000条，鲢鱼若干。

在几次随机捕捞中，共抓到鲤鱼320条，鲢鱼图3A B C 图8 E D 图2A )BCD 图9 A B DO图（1） 第5题图 图 （2）400条。

估计池塘中原来放养了鲢鱼__________条。

7．据国务院权威发布，截至6月15日12时，汶地震灾区共接受国内外社会各界捐赠款物约4570000万元，用科学计数法表示为 万元.8 .如图8，在等腰梯形ABCD 中，AD ∥BC ，AE ∥DC ，AB=6cm ，则AE= cm. 9 如图9，在矩形ABCD 中，对角线AC ，BD 交于点O ，已知∠AOD=120°,AB=2.5, 则AC 的长为 ．10.用同样大小的黑色棋子按图6所示的方式摆图形，按照这样的规律摆下去，则第n 个图形需棋子 枚（用含n 的代数式表示）.三、解答题。

12354A B CDEF第2题图2012年花都区初中毕业班数学综合练习（一）一、选择题（每小题3分，共30分） 1．3-的绝对值是（ ▲ ） A ．3B ．3-C ．13 D ．13- 2．如图，直线AB 、CD 被直线EF 所截，则∠3的同旁内角是 （ ▲ ） A ．∠1 B ．∠2 C ．∠4 D ．∠53．股市有风险，投资需谨慎。

截至今年五月底，我国股市开户总数约95000000，正向1亿挺进，95000000用科学计数法表示为（▲ ）×106×107×108×10910页，其中语文2页、数学3页、英语5页，他随机地从讲义夹中抽出1页，抽出的试卷恰好是数学试卷的概率为（ ▲ ） A.21B.103C.52D.101 5．抛物线2(2)3y x =-+的对称轴是（ ▲ ）x = -2x =2 C.直线x =x =36．下列运算中，结果正确的是 （ ▲）A ．a a a 34=-B ．5210a a a =÷C ．532a a a =+D ．1243a a a =⋅ 7.有一组数据3,4,2,1,9,4，则下列说法正确的是（ ▲ ） A ．众数和平均数都是4 B ．中位数和平均数都是4 C ．极差是8,中位数是3.5 D ．众数和中位数都是48.如图所示的物体由两个紧靠在一起的圆柱组成，小刚准备画出它的三视图， 那么他所画的三视图中的俯视图应该是（ ▲） A ．两个相交的圆 B ．两个内切的圆 C ．两个外切的圆D ．两个外离的圆9．已知C B A ,,是⊙O 上不同的三个点，︒=∠50AOB ，则ACB ∠=（ ▲） A ．︒50B ．︒25 C ．︒50或︒130D ．︒25或︒155第8题图主视方向A D HGCFBE 第15题图10、如图所示，函数y 1＝|x |和y 2＝13x ＋43的图象相交于(－1,1)，(2,2)两点，当y 1>y 2时，x 的取值X 围是( )A ．x <－1B ．－1<x <2C ．x >2D ．x <－1或x >2二、填空题：（每小题3分，共18分）11．分解因式：2xy x -=___▲_______.12. 已知三角形的两边长分别为3和6，那么第三边长的取值X 围是___▲_______. 13、函数x y -=2的自变量的取值X 围是 ▲。

广州市中考数学模拟试卷(一)问 卷一、选择题（本大题共10小题，每小题3分，满分30分，在每小题给出的四个选项中，只有一项是符合题目要求的。

）1. 下列各数中既不是正数也不是负数的是 ( ) A ．—1 B ．0 C ．2 D ．π2. 某班抽取6名同学参加体能测试，成绩如下：85，95，85，80，80，85. 下列表述错误的是 ( )A ． 众数是85B ． 平均数是85C ． 中位数是80D ．极差是15 3. 如果,0,>>c b a 那么下列不等式中不成立的是( ) A ．c b b a +>+ B ．a c b c ->- C ．bc ac > D ．cb c a > 4. 下列各式中计算正确的是( )A ．222)(y x y x +=+B ．226)3(x x = C ．623)(x x = D ．422a a a =+5. 如图，△ABC 中，AB =AC =15，D 在BC 边上，DE ∥BA 于 点E ，DF ∥CA 交AB 于点F ，那么四边形AFDE 的周长 是( ) A ． 30 B ． 25 C ． 20 D ． 15 7. 在平面直角坐标系中，已知线段AB 的两个端点分别是A （-4，-1），B （1，1），将线 段AB 平移后得到线段A ′B ′，若点A ′的坐标为（-2，2），则B ′的坐标为 ( ) A ．（4，3） B ．（3，4） C ．（1，-2） D ．（-2，-1） 8.已知圆锥的底面半径为5cm ，侧面积为65πcm 2，则圆锥的母线长为( ) A ．11cm B ．12cm C ．13cm D ．14cm 9.下列函数的图象关于y 轴成轴对称的函数是( ) A ．x y 2= B ．13--=x y C ．xy 6=D ．12+=x y 10．如图，填在各方格中的三个数之间均具有相同的规律，根据此规律，n 的值是( ) 1 3 5 m 2 3 4 15 6 35 8 nA ． 48B ． 56C ． 63D ． 74. 第二部分（非选择题 共120分）二、填空题（本大题共6小题，每小题3分，满分18分.）11. 当实数x 的取值使得x -2有意义时，函数13-=x y 中，y 的取值范围是_________12. 如图，将△OAB 绕点O 按逆时针方向旋转至△OA ′B ′， 这时点B 在边A ′B ′上，已知AB =5cm ，BB ′= 2cm ， 则A ′B 的长是 _______CD E BF A OBAB 'A '13. 分解因式=-a a 5463____________14. 已知关于x 的方程2440ax x -+=有两个相等的实根，则代数式22(2)3aa a ++-的值为 ___________15.已知二次函数21y x mx =--，当x <4时，函数值y 随x 的增大而减小，则m 的取值范围是_________16. 如图，已知正方形纸片ABCD 的边长为8，⊙O 的半径为2，圆心在正方形的中心上，将纸片按图示方式折 叠，使EA ′恰好与⊙O 相切于点A ′（△EFA ′与⊙0 除切点外无重叠部分），延长FA ′交CD 边于点G ， 则A ′G 的长是 ___________三、解答题（本大题共9小题，满分102分，解答应写出文字说明、证明过程或演算步骤） 17．（本小题满分9分）解不等式组523132x x x +⎧⎪+⎨⎪⎩≥＞，并写出不等式组的整数解．18．（本小题满分9分）如图，在Rt △ABC 中，90C ∠=︒，点D 是AC 的中点， 且90A CDB ∠+∠=︒，过点,A D 作⊙O ，使圆心O 在AB 上，⊙O 与AB 交于点E .求证：直线BD 与⊙O 相切；19. （本小题满分10分）某文化用品商店用2 000元购进一批学生书包，上市后发现供不应求，商店又购进第二批同样的书包，所购数量是第一批购进数量的3倍，但单价贵了4元，结果第二批用了6 300元．(1)求第一批购进书包的单价是多少元？ (2)若商店销售这两批书包时，每个售价都是120元，全都售出后，商店共盈利多少元？OFEDGCB AA '20．（本小题满分10分）如图，小明在大楼30米高（即PH＝30米）的窗口P处进行观测，测得山坡上A处的俯角为15°，山脚B处的俯角为60°，已知该山坡的坡度i（即tan∠ABC）为1：3，点P、H、B、C、A在同一个平面上．点H、B、C在同一条直线上，且PH⊥HC．（1）山坡坡角（即∠ABC）的度数等于_______度；（2）求A、B两点间的距离（结果精确到0.1米）．21．（本小题满分12分）某公司组织部分员工到一博览会的A、B、C、D、E五个展馆参观，公司所购门票种类、数量绘制成的条形和扇形统计图如图所示．请根据统计图回答下列问题：（1）将条形统计图和扇形统计图在图中补充完整；（2）若A馆门票仅剩下一张，而员工小明和小华都想要，他们决定采用抽扑克牌的方法来确定，规则是：“将同一副牌中正面分别标有数字1，2，3，4的四张牌洗匀后，背面朝上放置在桌面上，每人随机抽一次且一次只抽一张；一人抽后记下数字，将牌放回洗匀后背面朝上放置在桌面上，再由另一人抽．若小明抽得的数字比小华抽得的数字大，门票给小明，否则给小华．”请用画树状图或列表的方法计算出小明和小华获得门票的概率，并说明这个规则对双方是否公平．A B DF CE22．（本小题满分12分）为了增强居民节水意识，某市自来水公司对居民用水采用 以户为单位分段计费的方法收费，每个月收取水费y （元） 与用水量x （吨）之间的函数关系如图，按上述分段收费标 准，小明家三、四月份分别交水费26元和18元，求小明家 四月份比三月份少用水多少吨？23．（本小题满分12分）如图，在梯形ABCD 中，AD //BC ，AB ＝DC ， 过点D 作DE ⊥BC ，垂足为E ，并延长DE 至F ， 使EF ＝DE ．联结BF 、CD 、AC ．（1）求证：四边形ABFC 是平行四边形； （2）如果DE 2＝BE ·CE ，求证：四边形ABFC 是矩形24．（本小题满分14分）如图1，在等腰梯形ABCD 中，AD BC ∥，E 是AB 的中点，过点E 作EF BC ∥交CD 于点F ．46AB BC ==，，60B =︒∠. （1）求点E 到BC 的距离；（2）点P 为线段EF 上的一个动点，过P 作PM EF ⊥交BC 于点M ，过M 作MN AB ∥交折线ADC 于点N ，连结PN ，设EP x =.① 当点N 在线段AD 上时（如图2），PMN △的形状是否发生改变？ 若不变，求出PMN △的周长；若改变，请说明理由；② 当点N 在线段DC 上时（如图3），是否存在点P ，使PMN △为等腰三角形？ 若存在，请求出所有满足要求的x 的值；若不存在，请说明理由.图1A D E BFCPNM图2A DE BFCPN M图3AD E BFCY （元）5020O 10 20 X （吨）25．（本小题满分14分）平面直角坐标系中，平行四边形ABOC如图放置，点A、C的，0)，将此平行四边形绕点0顺时针坐标分别为(0，3)、(1A B OC。

2012年初中毕业班综合模拟测试数 学 试 题本试卷分选择题和非选择题两部分，共三大题25小题，满分150分．考试时间为120分钟．注意事项：1.答卷前，考生务必在答题卡第1页上用黑色字迹的钢笔或签字笔填写自己的考生号、姓名；填写考场试室号、座位号，再用2B 铅笔把对应这两个号码的标号涂黑．2.选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号；不能答在试卷上．3.非选择题必须用黑色字迹的钢笔或签字笔作答，涉及作图的题目，用2B 铅笔画图．答案必须写在答题卡各题目指定区域内的相应位置上；如需要改动，先划掉原来的答案，然后再写上新的答案；改动的答案也不能超出指定的区域．不准使用铅笔、圆珠笔和涂改液．不按以上要求作答的答案无效．4.考生必须保持答题卡的整洁，考试结束后，将本试卷和答题卡一并交回．第一部分 选择题（共30分）一、选择题（本大题共10小题，每小题3分，满分30分．在每小题给出的四个选项中，只有一项是符合题目要求的.）1．3-的结果为（ * ）（A ）3 （B ）±3 （C ）－3 （D ）无法确定2．在函数x y 23-=中，自变量x 的取值范围是（ * ）（A ）23>x （B ）23≥x （C ）23<x（D ）23≤x 3．计算223)3(a a ÷的结果是（ * ）（A ）46a（B ）49a（C ）49a -（D ）39a4．下面各整式能直接运用完全平方公式分解因式的是（ * ） （A ）92-x（B ）962-+x x（C ）962++x x （D ）9642++x x5．如图，BD 为⊙O 的直径，点A 、C 均在⊙O 上，∠CBD ＝60°，则∠A 的度数为（ * ）（A ）60° （B ）30°（C ）45° （D ）20°6．如图，在□ABCD 中，已知AD ＝8㎝， AB ＝6㎝， DE 平分∠ADC 交BC 边于点E ，则BE 等于 （ ） （A ）2cm（B ）4cm（C ）6cm（D ）8cm第5题 第6题DCAB7．某制衣厂要确定一种衬衫不同号码的生产数量，在做市场调查时，该向商家侧重了解这种衬衫不同号码的销售数量的（ * ） （A ）平均数（B ）中位数 （C ）众数（D ）极差8．抛物线322++-=x x y 与两坐标轴的交点个数为（ * ） （A ）0（B ）1（C ）2（D ）39. 把半径为10，面积为π60的扇形做成圆锥的侧面，则圆锥的高是（ * ）（A ）10（B ）8（C ）6（D ）410.如图，直角梯形ABCD 中，∠BCD ＝90°，AD ∥BC ，BC ＝CD ，E 为梯形内一点，且∠BEC ＝90°，将△BEC 绕C 点旋转90°使BC 与DC 重合，得到△DCF ，连EF 交CD 于M ．已知BC ＝5，CF ＝3，则DM:MC 的值为（ * ）（A ）5:3 （B ）3:5 （C ）4:3 （D ）3:4第二部分 非选择题（共120分）二、填空题（本大题共6小题，每小题3分，满分18分．）11．当5=x 时，12-x 的值为 ．12．若关于x 的一元二次方程082=-+kx x 的一个根是2，则另一个根是__________． 13．若点)1,3(-P 是反比例函数上的一点，则这个反比例函数的解析式为___________． 14．已知两圆的半径分别为6㎝和2㎝，圆心距为4㎝，则这两个圆的位置关系为 ． 15．已知点)0,2(A 、)2,0(B 、),1(m C -在同一条直线上，则m 的值为 ． 16．如图，在等腰梯形ABCD 中，AD ∥BC ，AB ＝5，AD ＝6，BC ＝12，点E 在AD 边上，且AE ：ED ＝1：2，点P 是AB 边上的一个动点，（P 不与A ，B 重合）过点P 作PQ ∥CE 交BC 于点Q ，设AP=x ，CQ=y ，则y 与x 之间的函数关系是_________________.三、解答题（本大题共9小题，满分102分．解答应写出文字说明、证明过程或演算步骤）17．（本小题满分9分）计算 2933x x x --- 第16题F第10题如图7，点A 、E 、B 、D 在一条直线上，AE ＝DB ，AC ＝DF ，AC ∥DF ． 求证：BC ＝EF19．（本小题满分10分）广安市某楼盘准备以每平方米6000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望，房地产开发商为了加快资金周转，对价格经过两次下调后，决定以每平方米4860元的均价开盘销售。

2012年广东省广州市海珠区中考数学一模试卷一、选择题（本大题共10小题，每小题3分，满分30分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．计算（﹣1）3=（）A．1 B．﹣1 C．3 D．﹣32．下列各图中，不是中心对称图形的是（）A． B． C． D．3．4的平方根是（）A．2 B．﹣2 C．±2 D．±44．如图，∠1与∠2是同位角，若∠2=65°，则∠1的大小是（）第4题图A．25° B．65° C．115° D．不能确定5．下列运算正确的是（）A．a2•a3=a6 B．x4÷x=x3 C．（x2）3=x5 D．2a•3a=6a6．下列三视图所对应的直观图是（）第6题图A． B． C． D．7．在某市初中学业水平考试体育学科的800米耐力测试中，某考点同时起跑的甲和乙所跑的路程S（米）与所用时间t（秒）之间的函数图象分别为线段OA和折线OBCD．则下列说法正确的是（）第7题图A．在起跑后 180 秒时，甲乙两人相遇B．甲的速度随时间的增加而增大C．起跑后400米内，甲始终在乙的前面D．甲比乙先到终点8．在共有15人参加的“我爱祖国”演讲比赛中，参赛选手要想知道自己是否能进入前8名，只需要了解自己的成绩以及全部成绩的（）A．平均数 B．众数 C．中位数 D．方差9．若二次函数的解析式为y=2x2﹣4x+3，则其函数图象与x轴交点的情况是（）A．没有交点 B．有一个交点 C．有两个交点 D．无法确定10．如图所示，已知在三角形纸片ABC中，BC=3，AB=6，∠BCA=90°．在AC上取一点E，以BE为折痕，使AB的一部分与BC重合，A与BC延长线上的点D重合，则DE的长度为（）第10题图A．6 B．3 C．32D．3二、填空题（本大题共6小题，每小题3分，满分18分．）11．分解因式：2x2﹣4x+2= ．12．函数y=中，自变量x的取值范围是．13．如图，AB为⊙O的直径，点C在⊙O上，若∠C=20°，则∠BOC= ．第13题图第14题图14．如图，D、E分别是△ABC的边AB、AC的中点，若DE的长是3，则BC的长是．15．方程组的解是．16．a是不为1的有理数，我们把称为a的差倒数，如：2的差倒数是，﹣1的差倒数是．已知，是a1的差倒数，a3是的差倒数，a4是a3的差倒数，…，以此类推，则a2012= ．三、解答题（本大题共9小题，满分102分．解答应写出文字说明、证明过程或演算步骤．）17．（10分）（1）解方程：；（2）先化简，再求值：，其中，．18．（10分）如图，在平面直角坐标系xoy中，直角梯形OABC，BC∥AO，A（﹣2，0），B（﹣1，1），将直角梯．形OABC绕点O顺时针旋转90°后，点A、B、C分别落在点A′、B′、C′处．请你解答下列问题：（1）在如图直角坐标系xOy中画出旋转后的梯形O′A′B′C′；（2）求点A旋转到A′所经过的弧形路线长．第18题图19．（10分）“戒烟一小时，健康亿人行”．今年国际无烟日，小华就公众对在餐厅吸烟的态度进行了随机抽样调查，主要有四种态度：A．顾客出面制止；B．劝说进吸烟室；C．餐厅老板出面制止；D．无所谓．他将调查结果绘制了两幅不完整的统计图．请你根据图中的信息回答下列问题：第19题图（1）求这次抽样的公众有多少人？（2）请将统计图①补充完整；（3）在统计图②中，求“无所谓”部分所对应的圆心角是多少度？（4）若城区人口有20万人，估计赞成“餐厅老板出面制止”的有多少万人？（5）小华在城区中心地带随机对路人进行调查，请你根据以上信息，求赞成“餐厅老板出面制止”的概率是多少？20．（10分）如图所示，在平行四边形ABCD的对角线上AC上取两点E和F，若AE=CF．求证：∠AFD=∠CEB．第20题图21．（10分）甲、乙两船同时从港口A出发，甲船以60海里/时的速度沿北偏东30°方向航行，乙船沿北偏西45°方向航行，1小时后甲船到达B点，乙船正好到达甲船正西方向的C点，问甲、乙船之间的距离是多少海里？（结果精确到0.1米）第21题图22．（12分）已知：如图，在直角坐标系xOy中，Rt△OCD的一边OC在x轴上．∠C=90°，点D在第一象限，OC=3，DC=4，反比例函数的图象经过OD的中点A．（1）求该反比例函数的解析式；（2）若该反比例函数的图象与Rt△OCD的另一边DC交于点B，求过A、B两点的直线的解析式．第22题图24．（14分）如图1，在△ABC中，AB=BC=5，AC=6，△ECD是△ABC沿BC方向平移得到的，连接AE、AC、BE，且AC和BE相交于点O．（1）求证：四边形ABCE是菱形；（2）如图2，P是线段BC上一动点（不与B、C重合），连接PO并延长交线段AE于点Q，过Q作QR⊥BD交BD于R．①四边形PQED的面积是否为定值？若是，请求出其值；若不是，请说明理由；②以点P、Q、R为顶点的三角形与以点B、C、O为顶点的三角形是否可能相似？若可能，请求出线段BP的长；若不可能，请说明理由．第24题图25．（14分）如图，在直角坐标系xOy中，已知点P（2，），过P作PA⊥y轴交y轴于点A，以点P为圆心PA为半径作⊙P，交x轴于点B，C，抛物线y=ax2+bx+c经过A，B，C三点．（1）求点A，B，C的坐标；（2）求出该抛物线的解析式；（3）抛物线上是否存在点Q，使得四边形ABCP的面积是△BPQ面积的2倍？若存在，请求出所有满足条件的点；若不存在，请说明理由．第25题图。