唐山市2018-2019学年度高三年级第二次模拟考试理科数学答案
- 格式:docx
- 大小:131.63 KB
- 文档页数:8


唐山市2018—2019学年度高三年级第二次模拟考试文科数学参考答案一.选择题:A卷:BDCAA CBDCC ADB卷:BDCCA CBDCA AD二.填空题:13.7 14.-51315.2n-1 16.55三.解答题:17.解:(1)因为2c=3a+2b cos A,所以由正弦定理可得:2sin C=3sin A+2sin B cos A,所以2sin C=2(sin A cos B+cos A sin B)=3sin A+2sin B cos A,即2sin A cos B=3sin A,因为sin A≠0,所以cos B=3 2.又0<B<π,故B=6.…6分(2)因为S△ABC=12ac sin B=14a=32,所以a=23,由余弦定理可得,b2=a2+c2-2ac cos B=7,所以b=7.…12分18.解:(1)连接AC,交BD于点O,连接OA1,因为四边形ABCD为菱形,所以AC⊥BD,从而OA1⊥BD,OC⊥BD,又因为OA1∩OC=O,所以BD⊥平面A1OC,因为A 1C 平面A 1OC ,所以A 1C ⊥BD . …5分(2)在菱形ABCD 中,OA =OC =3,又A 1C =3,所以△A 1OC 为等边三角形且S △A 1OC =334. 由(1)可知,BD ⊥平面A 1OC ,所以V A 1-BCD = 13S △A 1OC ·BD =32. 在△A 1DC 中,A 1D =CD =2,A 1C =3,S △A 1DC =394, 设点B 到平面A 1DC 的距离为d ,由V B -A 1DC =V A 1-BCD 得, 13S △A 1DC ·d =32, 所以d =61313, 即点B 到平面A 1DC 的距离为61313. …12分 19.解:(1)-x =62.5×5×0.03+67.5×5×0.05+72.5×5×0.06+77.5×5×0.04+82.5×5×0.02=71.75.因为抽取的样本中,果径在[60,65),[65,70),[70,75),[75,80),[80,85]的频率分别为0.15,0.25,0.3,0.2,0.1,所以样本的中位数为70+ 1 3×5≈71.67. …5分(2)由图2可知,果径在80以上的苹果中,特级果、一级果、二级果所占比例约 1 5, 1 2, 310, 所以按方案一进行收购,则1kg 的收购价X ≈12× 1 5+10× 1 2+9× 310=10.1>10. 故果园种植户应选择第一种收购方案. …12分(比较两种方案收购总额的大小,同样给分.)20.解:(1)由已知可得,|PN |=|PM |,即点P 到定点N 的距离等于到直线l 1的距离,故P 点的轨迹是以N 为焦点,l 1为准线的抛物线,所以曲线C 的方程为y 2=4x . …4分(2)设A (x 1,y 1),B (x 2,y 2),D (x 0,y 0),直线l 2斜率为k ,显然k ≠0, 由⎩⎨⎧y =kx +m ,y 2=4x 得,k 2x 2+(2km -4)x +m 2=0,x 1+x 2=4-2kmk 2.所以x 0=x 1+x 22=2-km k 2,y 0=kx 0+m = 2 k ,即D (2-km k 2, 2 k ).因为直线l 2与圆E :(x -3)2+y 2=6相切于点D ,所以|DE |2=6;DE ⊥l 2,从而(2-km k 2-3)2+( 2 k )2=6;2-kmk 2-3=-2,整理可得( 2 k )2=2,即k =±2.所以m =0,故l 2的方程为y =2x 或y =-2x . …12分21.解:(1)f '(x )=e x +a e -x -(a +1)=e -x (e x -1)(e x -a ). …1分 当a ≤0时,e x -a >0,x ∈(-∞,0)时,f '(x )<0,f (x )单调递减;x ∈(0,+∞)时,f '(x )>0,f (x )单调递增. …2分 当0<a <1时,x ∈(-∞,ln a )和(0,+∞)时,f '(x )>0,f (x )单调递增;x ∈(ln a ,0)时,f '(x )<0,f (x )单调递减. …4分 当a =1时,f '(x )≥0,f (x )单调递增. …5分 当a >1时,x ∈(-∞,0)和(ln a ,+∞)时,f '(x )>0,f (x )单调递增;x ∈(0,ln a )时,f '(x )<0,f (x )单调递减.…7分(2)由(1)得,当a =1时,f (x )=e x -e -x -2x ,因为f(0)=0,所以f(x)仅有一个零点0.且x>0时,f(x)>f(0)=0,即e x>e-x+2x>2x.…8分当0<a<1时,因为f(0)=1-a>0,所以f(x)在(ln a,+∞)内没有零点,且f(ln a)>0.由x>0时e x>2x,得e2x>4x2,x>ln x.所以x=-4a时,ex<1,e-x>16a2,从而-a e-x<-16a,所以f(-4a)<1-16a-(a+1)(-4a)=5-12a<0,又ln a=-ln 1a>-1a>-4a,所以f(x)在(-4a,ln a)内有一个零点,所以当0<a<1时,f(x)仅在(-4a,ln a)内有一个零点.…10分当a>1时,当x=4a时,-a e-x>-a,e x=e4a>16a2,从而f(4a)>16a2-a-(a+1)(4a)=a(12a-5)>0,又ln a<a<4a,所以f(x)在(ln a,4a)内有一个零点,所以当a>1时,f(x)仅在(ln a,4a)内有一个零点.综上,a>0时,f(x)有且仅有一个零点.…12分22.解:(1)依题意可得,圆C 1:(x -1)2+y 2=1;圆C 2:(x +2)2+y 2=4.所以C 1:x 2+y 2=2x ;C 2:x 2+y 2=-4x ,因为x 2+y 2=ρ2,x =ρcos θ,所以C 1:ρ=2cos θ;C 2:ρ=-4cos θ. …4分(2)因为C 1,C 2都关于x 轴对称,△OAB 为等边三角形,所以不妨设A (ρA ,θ),B (ρB ,θ+ π 3),0<θ< π 2. 依题意可得,ρA =2cos θ,ρB =-4cos (θ+π 3). 从而2cos θ=-4cos (θ+ π 3), 整理得,2cos θ=3sin θ,所以tan θ=233, 又因为0<θ< π 2,所以cos θ=217, |AB |=|OA |=ρA =2217. …10分23.解: (1)因为|ax +1|+|ax -1|≥|(ax +1)-(ax -1)|=2,等号当且仅当(ax +1)(ax -1)≤0时成立,所以f (x )的最小值为2-2a -4=-2a -2.依题意可得,-2a -2≥0,所以a ≤-1. …4分(2)因为a >0,f (x )=|ax +1|+|ax -1|-2a -4,所以f (x )=⎩⎨⎧-2ax -2a -4,x ≤- 1 a ,-2a -2,- 1 a <x < 1 a ,2ax -2a -4,x ≥ 1 a . 所以y =f (x )的图像与x 轴围成的封闭图形为等腰梯形ABCD , 且顶点为A (-1- 2 a ,0),B (1+ 2 a ,0),C ( 1 a ,-2a -2),D (- 1 a ,-2a -2)从而S=2(1+3a)(a+1)=2(a+3a)+8.因为a+3a≥23,等号当且仅当a=3时成立,所以当a=3时,S取得最小值43+8.…10分。

唐山市2018—2018学年度高三年级第二次模拟考试文科数学参考答案一、选择题A 卷:BDCCB BABAD CA B 卷:DABBC ACBDD BC 二、填空题(13)54 (14)6 (15)100π (16)100三、解答题 (17)解:(Ⅰ)由余弦定理知c 2-a 2-b 2=-2ab cos C ,又△ABC 的面积S = 1 2ab sin C =3 4(c 2-a 2-b 2),所以 1 2ab sin C =34(-2ab cos C ),得tan C =-3.因为0<C <π,所以C =2π3.…6分(Ⅱ)由正弦定理可知a sin A =b sin B =csin C=2,所以有a +b =2sin A +2sin B =2,sin A +sin ( π3-A )=1,展开整理得,sin ( π 3+A )=1,且 π 3< π 3+A <2π 3,所以A = π6.…12分 (18)解:因为K 2=160×640×200×600=16.667>10.828.所以能在犯错概率不超过0.001的前提下认为该校学生母语对于学习和掌握一门外语有关系. …6分2种,所以学生甲负责收集成绩且学生乙负责数据处理的概率是P = 2 6= 13. (12)分(19)解:(Ⅰ)连接B 1C 交BC 1于点P ,连接PD .由于BB 1C 1C 是平行四边形,所以P 为为B 1C 的中点 因为D 为AC 的中点,所以直线PD ∥B 1A , 又PD ⊂平面B 1CD ,B 1A ⊄平面BC 1D ,所以AB 1∥平面BC 1D .…6分(Ⅱ)直三棱柱ABC -A 1B 1C 1的体积V 1= 12×2×2×2=4.三棱锥C 1-BDC 的体积V 2与三棱锥A 1-BDA 的体积V 3相等,V 2=V 3= 1 3× 1 2× 1 2×2×2×2= 23.所以几何体BDA 1B 1C 1的体积V =V 1-V 2-V 3= 83.…12分(20)解:(Ⅰ)f '(x )= 1 x - m x 2=x -mx2. 则f '(2)=2-m4,f (2)=ln 2+ m2. 则曲线y =f (x )在(2,f (2))处的切线为y =2-m 4(x -2)+ln 2+ m2,即y =2-m 4x +m -1+ln 2. …3分依题意,m -1+ln 2=ln 2,所以m =1.故f (x )=ln x + 1x. (5)分(Ⅱ)由(Ⅰ)知,f (x )=ln x + 1 x ,f '(x )=x -1x.当x ∈[ 12,1]时,f '(x )≤0,f (x )单调递减,此时,f (x )∈[1,2-ln 2];当x ∈[1,5]时,f '(x )≥0,f (x )单调递增,此时,f (x )∈[1,ln 5+ 15]. (10)分ABCDA 1B 1C 1P因为(ln 5+ 1 5)-(2-ln 2)=ln 10- 9 5>ln e 2- 9 5= 1 5,所以ln 5+ 15>2-ln 2.因此,f (x )的取值范围是[1,ln 5+ 15]. (12)分(21)解:(Ⅰ)设圆C 的圆心坐标为(x ,y ),则其半径r =x 2+(y -1)2.依题意,r 2-y 2=1,即x 2+(y -1)2-y 2=1,整理得曲线E 的方程为x 2=2y .…4分(Ⅱ)设A (x 1,y 1),B (x 2,y 2),则y 1= 1 2x 21,y 2= 1 2x 22.设直线m 方程为y =kx + 12,代入曲线E 方程,得x 2-2kx -1=0,则x 1+x 2=2k .…6分对y = 1 2x 2求导,得y '=x .于是过点A 的切线为y =x 1(x -x 1)+ 1 2x 21,即y =x 1x - 1 2x 21.① 由①同理得过点B 的切线为y =x 2x - 1 2x 22.②设C (x 0,y 0),由①、②及直线m 方程得x 0=x 1+x 22=k ,y 0=x 1x 0- 1 2x 21=- 1 2.…8分M 为抛物线的焦点,y =- 12为抛物线的准线,由抛物线的定义,得|AB |=y 1+ 1 2+y 2+ 1 2=k (x 1+x 2)+2=2(k 2+1).点C 到直线m 的距离d =|kx 0-y 0+ 12|k 2+1=k 2+1. …10分所以△ABC 的面积S = 1 2|AB |·d =(k 2+1)k 2+1.由已知(k 2+1)k 2+1=22,有且仅有k =±1.故直线m 的方程为y =±x + 12.…12分(22)证明:(Ⅰ)连接BD ,因为D 为BC ︵的中点,所以BD =DC . 因为E 为BC 的中点,所以DE ⊥BC . 因为AC 为圆的直径,所以∠ABC =90︒,所以AB ∥DE .…5分(Ⅱ)因为D 为BC ︵的中点,所以∠BAD =∠DAC , 又∠BAD =∠DCB ,则∠DAC =∠DCB .又因为AD ⊥DC ,DE ⊥CE ,所以△DAC ∽△ECD .所以AC CD =ADCE,AD ·CD =AC ·CE ,2AD ·CD =AC ·2CE , 因此2AD ·CD =AC ·BC .…10分(23)解:(Ⅰ)将椭圆C 的参数方程化为普通方程,得x 24+y 23=1.a =2,b =3,c =1,则点F 坐标为(-1,0).l 是经过点(m ,0)的直线,故m =-1. …4分(Ⅱ)将l 的参数方程代入椭圆C 的普通方程,并整理,得(3cos 2α+4sin 2α)t 2-6t cos α-9=0.设点A ,B 在直线参数方程中对应的参数分别为t 1,t 2,则|FA |·|FB |=|t 1t 2|=93cos 2α+4sin 2α=93+sin 2α. 当sin α=0时,|FA |·|FB |取最大值3;当sin α=±1时,|FA |·|FB |取最小值 94. (10)分(24)解:(Ⅰ)当a =2时,f (x )=2(|x -2|-|x +4|)=⎩⎪⎨⎪⎧12,x <-4,-4x -4,-4≤x ≤2,-12,x >2.当x <-4时,不等式不成立;当-4≤x ≤2时,由-4x -4<2,得- 32<x ≤2;当x >2时,不等式必成立.综上,不等式f (x )<2的解集为{x |x >- 32}.…6分(Ⅱ)因为f (x )=|ax -4|-|ax +8|≤|(ax -4)-(ax +8)|=12, 当且仅当ax ≤-8时取等号. 所以f (x )的最大值为12.故k 的取值范围是[12,+∞).…10分。

唐山市2018—2019学年度高三年级第二次模拟考试文科数学参考答案一.选择题:A 卷:BDCAA CBDCC ADB 卷:BDCCA CBDCA AD 二.填空题: 13.714.-51315.2n -1 16.55三.解答题: 17.解:(1)因为2c =3a +2b cos A ,所以由正弦定理可得:2sin C =3sin A +2sin B cos A ,所以2sin C =2(sin A cos B +cos A sin B )=3sin A +2sin B cos A , 即2sin A cos B =3sin A ,因为sin A ≠0,所以cos B =32. 又0<B <π,故B =π6.…6分(2)因为S △ABC =12ac sin B =14a =32,所以a =23,由余弦定理可得,b 2=a 2+c 2-2ac cos B =7, 所以b =7. …12分18.解:(1)连接AC ,交BD 于点O ,连接OA 1, 因为四边形ABCD 为菱形, 所以AC ⊥BD ,从而OA 1⊥BD ,OC ⊥BD , 又因为OA 1∩OC =O , 所以BD ⊥平面A 1OC , 因为A 1C ⊂平面A 1OC , 所以A 1C ⊥BD . …5分(2)在菱形ABCD 中,OA =OC =3,又A 1C =3,所以△A 1OC 为等边三角形且S △A 1OC =334.由(1)可知,BD ⊥平面A 1OC , 所以V A 1-BCD =13S △A 1OC ·BD =32.ABCA 1DO在△A 1DC 中,A 1D =CD =2,A 1C =3,S △A 1DC =394, 设点B 到平面A 1DC 的距离为d ,由V B -A 1DC =V A 1-BCD 得,13S △A 1DC ·d =32,所以d =61313,即点B 到平面A 1DC 的距离为61313. …12分19.解: (1)-x =62.5×5×0.03+67.5×5×0.05+72.5×5×0.06+77.5×5×0.04+82.5×5×0.02=71.75.因为抽取的样本中,果径在[60,65),[65,70),[70,75),[75,80),[80,85]的频率分别为0.15,0.25,0.3,0.2,0.1,所以样本的中位数为70+13×5≈71.67. …5分(2)由图2可知,果径在80以上的苹果中,特级果、一级果、二级果所占比例约15,12,310, 所以按方案一进行收购,则1kg 的收购价X ≈12×15+10×12+9×310=10.1>10.故果园种植户应选择第一种收购方案. …12分 (比较两种方案收购总额的大小,同样给分.) 20.解:(1)由已知可得,|PN |=|PM |,即点P 到定点N 的距离等于到直线l 1的距离, 故P 点的轨迹是以N 为焦点,l 1为准线的抛物线, 所以曲线C 的方程为y 2=4x . …4分 (2)设A (x 1,y 1),B (x 2,y 2),D (x 0,y 0),直线l 2斜率为k ,显然k ≠0,由⎩⎨⎧y =kx +m ,y 2=4x得,k 2x 2+(2km -4)x +m 2=0, x 1+x 2=4-2kmk 2.所以x 0=x 1+x 22=2-km k 2,y 0=kx 0+m =2k ,即D (2-km k 2, 2k).因为直线l 2与圆E :(x -3)2+y 2=6相切于点D , 所以|DE |2=6;DE ⊥l 2,从而(2-km k 2-3)2+(2k )2=6;2-km k2-3=-2, 整理可得(2k)2=2,即k =±2.所以m =0,故l 2的方程为y =2x 或y =-2x . …12分(1)f'(x)=e x+a e-x-(a+1)=e-x(e x-1)(e x-a).…1分当a≤0时,e x-a>0,x∈(-∞,0)时,f'(x)<0,f(x)单调递减;x∈(0,+∞)时,f'(x)>0,f(x)单调递增.…2分当0<a<1时,x∈(-∞,ln a)和(0,+∞)时,f'(x)>0,f(x)单调递增;x∈(ln a,0)时,f'(x)<0,f(x)单调递减.…4分当a=1时,f'(x)≥0,f(x)单调递增.…5分当a>1时,x∈(-∞,0)和(ln a,+∞)时,f'(x)>0,f(x)单调递增;x∈(0,ln a)时,f'(x)<0,f(x)单调递减.…7分(2)由(1)得,当a=1时,f(x)=e x-e-x-2x,因为f(0)=0,所以f(x)仅有一个零点0.且x>0时,f(x)>f(0)=0,即e x>e-x+2x>2x.…8分当0<a<1时,因为f(0)=1-a>0,所以f(x)在(ln a,+∞)内没有零点,且f(ln a)>0.由x>0时e x>2x,得e2x>4x2,x>ln x.所以x=-4a时,ex<1,e-x>16a2,从而-a e-x<-16a,所以f(-4a)<1-16a-(a+1)(-4a)=5-12a<0,又ln a=-ln 1a>-1a>-4a,所以f(x)在(-4a,ln a)内有一个零点,所以当0<a<1时,f(x)仅在(-4a,ln a)内有一个零点.…10分当a>1时,当x=4a时,-a e-x>-a,e x=e4a>16a2,从而f(4a)>16a2-a-(a+1)(4a)=a(12a-5)>0,又ln a<a<4a,所以f(x)在(ln a,4a)内有一个零点,所以当a>1时,f(x)仅在(ln a,4a)内有一个零点.综上,a>0时,f(x)有且仅有一个零点.…12分(1)依题意可得,圆C 1:(x -1)2+y 2=1;圆C 2:(x +2)2+y 2=4. 所以C 1:x 2+y 2=2x ;C 2:x 2+y 2=-4x , 因为x 2+y 2=ρ2,x =ρcos θ,所以C 1:ρ=2cos θ;C 2:ρ=-4cos θ. …4分(2)因为C 1,C 2都关于x 轴对称,△OAB 为等边三角形,所以不妨设A (ρA ,θ),B (ρB ,θ+ π 3),0<θ< π2.依题意可得,ρA =2cos θ,ρB =-4cos (θ+π3). 从而2cos θ=-4cos (θ+π3), 整理得,2cos θ=3sin θ,所以tan θ=233,又因为0<θ< π 2,所以cos θ=217,|AB |=|OA |=ρA =2217.…10分23.解:(1)因为|ax +1|+|ax -1|≥|(ax +1)-(ax -1)|=2, 等号当且仅当(ax +1)(ax -1)≤0时成立, 所以f (x )的最小值为2-2a -4=-2a -2. 依题意可得,-2a -2≥0, 所以a ≤-1. …4分(2)因为a >0,f (x )=|ax +1|+|ax -1|-2a -4,所以f (x )=⎩⎨⎧-2ax -2a -4,x ≤- 1a ,-2a -2,- 1 a <x < 1a,2ax -2a -4,x ≥ 1a.所以y =f (x )的图像与x 轴围成的封闭图形为等腰梯形ABCD ,且顶点为A (-1-2a ,0),B (1+ 2a ,0),C (1a ,-2a -2),D (- 1a,-2a -2)从而S =2(1+3a )(a +1)=2(a + 3a)+8. 因为a +3a ≥23,等号当且仅当a =3时成立,所以当a =3时,S 取得最小值43+8.…10分。

唐山市2018—2019学年度高三年级第一次模拟考试理科数学参考答案一.选择题:A 卷:CDBAA CDBAC BCB 卷:CDCAA CDBABBC二.填空题: (13)-4(14)7(15)2π(16)332三.解答题: (17)解:(1)令n =1,得a 1+a 1=2,(a 1+2)(a 1-1)=0,得a 1=1, 所以S n =n ,即S n =n 2.当n ≥2时,a n =S n -S n -1=2n -1, 当n =1时,a 1=1适合上式, 所以a n =2n -1. …6分(2)b n =(-1)n -1•a n +1S n +n =(-1)n -1•2n +1n 2+n=(-1)n -1•(1n +1n +1)…8分当n 为偶数时,T n =b 1+b 2+…+b n=(1 1+ 1 2)-( 1 2+ 1 3)+( 1 3+ 1 4)-( 1 4+ 1 5)+…-(1n +1n +1)=1-1n +1=nn +1当n 为奇数时,T n =b 1+b 2+…+b n=(1 1+ 1 2)-( 1 2+ 1 3)+( 1 3+ 1 4)-( 1 4+ 1 5)+…+(1n +1n +1)=1+1n +1=n +2n +1综上所述,T n =错误! …12分 另解:T n =b 1+b 2+…+b n=(1 1+ 1 2)-(1 2+ 1 3)+( 1 3+ 1 4)-( 1 4+ 1 5)+…+(-1)n -1•(1n +1n +1)=1+(-1)n -1•1n +1=n +1+(-1)n -1n +1…12分(18)解:(1)因为E ,F 分别为AB ,AC 边的中点, 所以EF ∥BC , 因为∠ABC =90°,所以EF ⊥BE ,EF ⊥PE , 又因为BE ∩PE =E , 所以EF ⊥平面PBE , 所以BC ⊥平面PBE . …5分 (2)取BE 的中点O ,连接PO ,由(1)知BC ⊥平面PBE ,BC ⊂平面BCFE , 所以平面PBE ⊥平面BCFE ,因为PB =BE =PE ,所以PO ⊥BE ,又因为PO ⊂平面PBE ,平面PBE ∩平面BCFE =BE , 所以PO ⊥平面BCFE . …7分 分别以OB ,OP 所在直线为x ,z 轴,过O 且平行BC 的直线为y 轴建立空间直角坐标系,则P (0,0,3) ,C (1,4,0), F (-1,2,0).PC →=(1,4,-3),PF →=(-1,2,-3)设平面PCF 的法向量为m =(x ,y ,z ),则⎩⎪⎨⎪⎧PC →·m =0,PF →·m =0,即⎩⎪⎨⎪⎧x +4y -3z =0,-x +2y -3z =0,则m =(-1,1,3),易知n =(0,1,0)为平面PBE 的一个法向量, cos 〈m ,n 〉=-1⨯0+1⨯1+3⨯0(-1)2+12+(3) 2=1 5=55, 所以平面PBE 与平面PCF 所成锐二面角的余弦值55.…12分(19)解:(1)当k =1 2时,直线l :y = 12(x +4)即x -2y +4=0.此时,直线l 与抛物线C 相切,由⎩⎨⎧x -2y +4=0y 2=2px得y 2-4py +8p =0,由∆=0即16p 2-32p =0,得p =2, 所以C 的方程为y 2=4x . …5分(2)直线l :y =k (x +4),其中k ≠0,设A (x 1,y 1),B (x 2,y 2),联立⎩⎨⎧y =k (x +4)y 2=4x得:ky 2-4y +16k =0,由∆=16-64k 2>0知:k 2<14.根据韦达定理得:⎩⎪⎨⎪⎧y 1+y 2=4 k ,y 1y 2=16, …① 又A 为PB 的中点,得:y 1=12y 2,…②由①②得:k 2=29,符合∆>0,所以|AB |=(1+1k 2)[(y 1+y 2)2-4y 1y 2]=4(1+k 2)(1-4k 2)k 2=211. …12分 (20)解:(1)分层抽样.…2分 (2)将列联表中的数据代入公式计算得K 2=n (ad -bc )2(a +b )(c +d )(a +c )(b +d )=200(40×50-100×10)2140×60×50×150≈3.175>2.706,所以有90%的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”. …6分 (3)以频率作为概率,从该小区随机选择1家企事业单位作为普查对象,入户登记顺利的概率为 4 5,随机选择1家个体经营户作为普查对象,入户登记顺利的概率为 23.X 可取0,1,2,3,4.P (X =0)=1 5×(1 3)3= 1135,P (X =1)=4 5×(1 3)3+1 5×C 13×2 3×(1 3)2= 10135, P (X =2)=4 5×C 13× 2 3×(1 3)2+1 5×C 23×(2 3)2×1 3= 36 135, P (X =3)=4 5×C 23×( 2 3)2×1 3+1 5×(2 3)3= 56 135, P (X =4)=4 5×( 2 3)3= 32 135.X E (X )=0× 1 135+1× 10 135+2× 36 135+3× 56 135+4× 32 135=145.…12分(21)解:(1)由f (x )≥0得ax -ln xx≥0,从而ax ≥ln x x ,即a ≥ln xx2.…2分设g (x )=ln xx 2,则g '(x )=1-2ln x x 3,(x >0)所以0<x <e 时,g '(x )>0,g (x )单调递增; x >e 时,g '(x )<0,g (x )单调递减,所以当x =e 时,g (x )取得最大值g (e)=12e,故a 的取值范围是a ≥12e.…6分(2)设y =f (x )的图像与y =a 相切于点(t ,a ),依题意可得⎩⎨⎧f (t )=a ,f '(t )=0.因为f '(x )=a -1-ln xx 2,所以⎩⎨⎧at -ln tt=a ,a -1-ln tt2=0,消去a 可得t -1-(2t -1)ln t =0. …9分令h (t )=t -1-(2t -1)ln t ,则h '(t )=1-(2t -1)·1t -2ln t =1t-2ln t -1,显然h '(t )在(0,+∞)上单调递减,且h '(1)=0, 所以0<t <1时,h '(t )>0,h (t )单调递增; t >1时,h '(t )<0,h (t )单调递减, 所以当且仅当t =1时h (t )=0. 故a =1. …12分(22)解:(1)当α= π2时,l :x =1;当α≠ π2时,l :y =tan α(x -1).由ρsin 2θ=4cos θ得,ρ2sin 2θ=4ρcos θ, 因为x =ρcos θ,y =ρsin θ,所以曲线C 的直角坐标方程y 2=4x . …5分(2)将直线l 的参数方程代入曲线C 的直角坐标方程得: (sin 2α)t 2-(4cos α)t -4=0,则t 1+t 2=4cos αsin 2α,t 1t 2=-4sin 2α,因为|AB |=|t 1-t 2|=(t 1+t 2)2-4t 1t 2=4sin 2α=8,所以sin α=22或-22,因为0<α<π,所以sin α=22,故α= π4或3π4.…10分(23)解:(1)∵a ,b 是正实数,∴a +b ≥2ab , ∴ab ≤1,∴(a +b )2=a +b +2ab ≤4, ∴a +b ≤2,当且仅当a =b =1时,取“=”. …5分(2)∵a 2+b 2≥2ab ,∴2(a 2+b 2)≥a 2+b 2+2ab =(a +b ) 2=4, ∴a 2+b 2≥2,∴(a +b 3)(a 3+b )=a 4+b 4+a 3b 3+ab ≥a 4+b 4+2a 2b 2=(a 2+b 2) 2≥4,当且仅当⎩⎨⎧ a =b ,a 2b 2=1,即a =b =1时,取“=”.…10分。
河北省唐山市2018-2019学年高三下学期理数第三次模拟考试试卷(B卷)一、选择题:本题共12小题,每小题5分,共60分.1.已知集合M={x|x>3},N={xlx2-7x+10≤0},则MUN=()A.[2,3)B.(3,5]C.(-∞,5]D.[2,+∞)2.已知复数:满足(2+i)z=i2019,则:在复平面上对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限3.中国古代数学名著《九章算术》卷“商功”篇章中有这样的问题:“今有方锥,下方二丈七尺,高二丈九尺。
问积几何?”(注:一丈等于十尺)。
若此方锥的三视图如图所示(其中俯视图为正方形),则方锥的体积为()(单位:立方尺)A.7047B.21141C.7569D.227074.已知sinα+ √3cosα=2,则tanα=()A.- √3B.√3C.- √33D.√335.设函数y=f(x)的定义域为I.则“f(x)在I上的最大为M”是“ x∈I,f(x)≤M”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6.设双曲线C:x2a2−y2b2=1(a>b>0)的两条渐近线的夹角为α.且cosα= 13,则C的离心率为()A.√52B.√62C.√72D.27.函数f(x)=tanx-x3的部分图象大致为()A .B .C .D .8.一个袋子中装有大小形状完全相同的4个白球和3个黑球,从中一次摸出3个球,已知摸出球的颜色不全相同,则摸出白球个数多于黑球个数的概率为( ) A .1835B .35C .2235D .11159.将函数f (x )=sin(ωx+ π3 )(0>0)的图象向右平移 π6个单位长度,得到的图象关于y 轴对称,则ω的最小值为( ) A .7B .6C .5D .410.设椭圆C : x 2a 2+y 2b2=1 (a>b>0)的左,右焦点分别为F 1,F 2,离心率为 √53 ,以F 1F 2为直径的圆与C 在第一象限的交点为P ,则直线PF 1的斜率为( ) A .13B .12C .√33D .√3211.在△ABC 中,AB=AC , BD⃗⃗⃗⃗⃗⃗ =3DC ⃗⃗⃗⃗⃗⃗ ,AD=2,△ABC 的面积为2 √3 ,则∠ADB=( ) A .30° B .45° C .60° D .30°或60°12.已知e 是自然对数的底数,不等式x[(e x-1+1)(e 1-x +1)-(e -1+e )2]>0的解集为( )A .(-1,0)U (3,+∞)B .(-1,0)U (0,3)C .(-∞,-1)U (3,+∞)D .(-∞,-1)U (0,3)二、填空题:本题共4小题,每小题5分,共20分。
绝密★启用前 试卷类型:A2018---2019年汕头市高三年级第二次模拟考试考试数学(理科) 2019.5本试卷共6页,21小题,满分150分.考试用时120分钟.注意事项:1.答卷前,考生首先检查答题卡是否整洁无缺损,监考教师分发的考生信息条形码是否正确;之后务必用0.5毫米黑色字迹的签字笔在答题卡指定位置填写自己的学校、姓名和考生号,同时,将监考教师发放的条形码正向准确粘贴在答题卡的贴条形码区,请保持条形码整洁、不污损.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,答案不能答在试卷上.不按要求填涂的,答案无效.3.非选择题必须用0.5毫米黑色字迹的签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上,请注意每题答题空间,预先合理安排;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.作答选做题时,请先用2B 铅笔填涂选做题的题号对应的信息点,再做答.漏涂、错涂、多涂的答案无效 5.考生必须保持答题卡的整洁,考试结束后,将答题卡交回.参考公式:① 体积公式:13V S h V S h =⋅=⋅柱体锥体,,其中,,V S h 分别是体积、底面积 和高;② 平面上两点),(),,(2211y x B y x A 的距离公式:212212)()(||y y x x AB -+-= 一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知函数lg y x =的定义域为A , {}01B x x =≤≤,则AB =( )A .()0,+∞B .[]0,1C .[)0,1D .(]0,12. 如图是根据某班学生在一次数学考试中的成绩画出的频率分布直方图,若80分以上为优秀,根据 图形信息可知:这次考试的优秀率为 ( ) A .25% B .30% C .35% D .40%3. 已知向量(3,1)=a ,(,2)x =-b ,(0,2)=c ,若()⊥-a b c ,则实数x 的值为 ( )A .43 B .34 C .34- D .43- 4.将函数y =2cos2x 的图象向右平移2π个单位长度,再将所得图象的所有点的横坐标缩短到原来的21倍(纵坐标不变),得到的函数解析式为( ) A .y =cos2xB .y =-2cos xC .y =-2sin4xD .y =-2cos4x5. 已知圆C :222)()(r b y a x =-+-的圆心为抛物线x y 42=的焦点,直线3x +4y +2=0与圆C 相切,则该圆的方程为 ( )A .2564)1(22=+-y xB .2564)1(22=-+y x C .1)1(22=+-y xD .1)1(22=-+y x6.如图,在由x =0,y =0,x =2π及y =x cos 围成区 域内任取一点,则该点落在x =0,y =sinx 及y =cosx 围成的区域内(阴影部分)的概率为( )A 、1B-1 CD 、3-7.把边长为1的正方形ABCD 沿对角线BD 折起, 形成的三棱锥A BCD -的正视图与俯视图如图所示, 则其侧视图的面积为( )A8.已知在平面直角坐标系中有一个点列:()12220,1,(,)P P x y ,……()*(,)n n n P x y n ∈N .若点(,)n n n P x y 到点()111,n n n P x y +++的变化关系为:⎩⎨⎧+=-=++nn n nn n x y y x y x 11()*n ∈N ,则||20142013P P 等于 ( ) A.10042 B .10052 C .10062 D .10072二、填空题:本题共7小题,考生作答6小题,每小题5分,共30分 (一)必做题(9~13题)9.若C x ∈,则关于x 的一元二次方程012=+-x x 的根为 .10. 命题“2,11x x ∀∈+≥R ”的否定是 .11.若关于x 、y 的不等式组5002x y y a x -+≥⎧⎪≥⎨⎪≤≤⎩表示的平面区域 是一个三角形,则a 的取值范围是 .12.执行如右图所示的程序框图,若输入n 的值为常数)3,(≥∈*m N m m ,则输出的s 的值为 (用m 表示) .13.关于x 的不等式),(1+∈>+R b a b ax 的解集为),1(+∞,那么ba 11+的取值范围是 .(二)选做题(14、15题,考生只能从中选做一题,两题全答的,只计前一题的得分)14. (坐标系与参数方程选做题) 已知直线L:1()42x tt R y t=+⎧∈⎨=-⎩与圆M:2cos 2([0,2]2sin x y θθπθ=+⎧∈⎨=⎩相交于AB ,则以AB 为直径的圆的面积为 。
河北省唐山市2019学年度高三年级 第二次模拟考试数学(理)试题说明:一、本试卷共4页,包括三道大题,24道小题,共150分,其中1.~(21)小题为必做题,(22)~(24)小题为选做题.二、答题前请仔细阅读答题卡上的“注意事项”,按照“注意事项”的规定答题.三、做选择题时,每小题选出答案后,用2B 铅笔把答题卡上对应题目的标号涂黑.如需改动,用橡皮将原选涂答案擦干净后,再选涂其他答案, 四、考试结束后,将本试卷与原答题卡一并交回, 参考公式: 样本数据n x x x ,,,21 的标准差;x x x x x x x n s n 其中],)()()[(122221-+-+-=为样本平均数;柱体体积公式:为底面面积其中S Sh V ,=、h 为高;锥体体积公式:h S Sh V ,,31为底面面积其中=为高;球的表面积、体积公式:,34,432R V R S ππ==其中R 为球的半径。
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,有且只有一项符合题目要求.1.已知1zi -=2+i ,则复数z 的共轭复数为A .-3-iB .-3+iC .3+iD .3-i2.261()x x -的展开式中的常数项为A .-15B .15C .-20D .203.己知命题p :“a>b”是“2a>2b”的充要条件;q :x ∃∈R ,lx+l l≤x,则 A .⌝p ∨q 为真命题 B .p ∧⌝q 为假命题 C .p ∧q 为真命题D . p ∨q 为真命题4.已知α是第三象限的角,且tan α=2,则sin (α+4π)= A.10-B.10C.10-D .105.设变量x 、y 满足1,0,220,x y x y x y +≥⎧⎪-≥⎨⎪--≥⎩则目标函数z=2x+y 的最小值为A .6B .4C .2D .326.把函数y=sin (2x-6π)的图象向左平移6π个单位后,所得函数图象的一条对称轴为A .x=0B .x=6πC .x=—12πD .x=2π7.执行如图所示的算法,若输出的结果y≥2,则输入的x 满足A .x≤一l 或x≥4B .x≤-lC.-1≤x≤4 D.x≥4 8.已知某几何体的三视图如图所示,则其体积为A.1 B.43C.53D.29.奇函数f(x)、偶函数g(x)的图象分别如图1、2所示,方程f(g(x))=0、g(f(x))=0 的实根个数分别为a、b,则a+b=A.14 B.10 C.7 D.310.直线l与双曲线C:22221(0,)x ya ba b-=>>交于A、B两点,M是线段AB的中点,若l与OM (O是原点)的斜率的乘积等于1,则此双曲线的离心率为ABC.2 D. 311.曲线y=11xx-+与其在点(0,一1)处的切线及直线x=1所围成的封闭图形的面积为A.1-ln2 B.2-2n2 C. ln2 D.2ln2-112.把一个皮球放入如图所示的由8根长均为20 cm的铁丝接成的四棱锥形骨架内,使皮球的表面与8根铁丝都有接触点,则皮球的半径为A.B.10 cmC.D.30cm二、填空题:本大题共4小题,每小题5分,共20分13.函数的定义域为 。
--- 唐山市 2018— 2019 学年度高三年级第二次模拟考试 理科数学参考答案
一.选择题: A 卷: DACAD CBBCB DB
B 卷: DBCAD
CBAC
B DA
二.填空题: 2
13. 9 14. 3 15. 660 16. 27 三.解答题: 17.解: ( 1)由已知及正弦定理可得: 2sin C= 3sinA+2sin Bcos A, 所以 2(sin Acos B+ sin BcosA)= 3sin A+ 2sin Bcos A, 即 2sin Acos B= 3sin A, 3
因为 sin A≠0,所以 cosB =
2 . 又 0<B< π,故 B= . ⋯ 6 分
6 ( 2)在△ ABC 中,由正弦定理可得 a = b ,
sin A sin B 所以 asin B= bsin A= 3,
由( 1)知 B= 6 , 所以 a= 2 3, b2= a2+ c2- 2accos B=
19, 由余弦定理可
得,
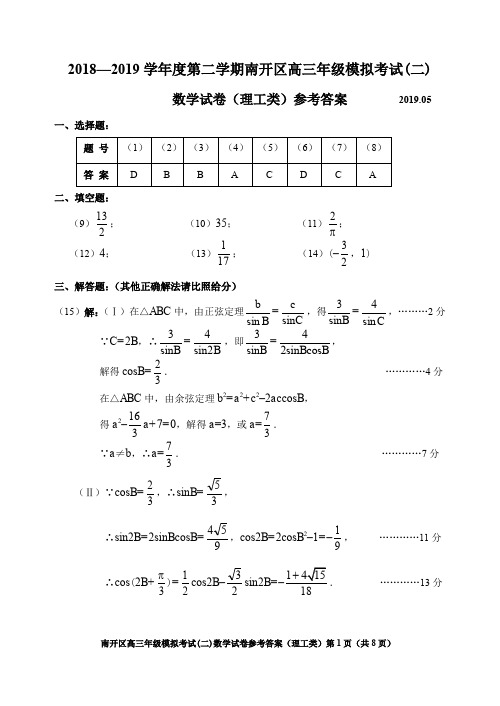
所以 b= 19. ⋯ 12 分 18.解: ( 1)连接 AC,交 BD 于点 O,连接 OA1, z A1 --- 因为四边形 ABCD 为菱形, 所以 AC ⊥BD , E 从而 OA 1⊥ BD, OC⊥ BD ,
D 又因为 OA1 ∩OC= O, C y 所以 BD ⊥平面 A1 OC,
A O 因为 A1C 平面 A1OC, B x 所以 BD ⊥A1C, 所以异面直线 A1C 与 BD 所成角的大小为 90°. ⋯ 5 分
( 2)由( 1)可知,∠ A1OC 即为二面角 A1- BD - C 的平面角,所以∠ A1OC=
60°.
→ → O- xyz,
则 以 O 为坐标原点, OB , OC 为 x, y 轴正方向,建立空间直
角坐标系 B(4, 0, 0), D(- 4, 0, 0), C(0, 4 3, 0), A1 (0, 2 3, 6), E(0, 3 3, 3).
高三理科数学参考答案第 1 页 --- → → → 所以 BE = ( -4, 3 3, 3), DA1 =(4, 2 3, 6), DC = (4, 4 3, 0).
设平面 A1DC 的法向量为 n= (x, y,z),
→ 4x+2 3y+ 6z=
0, DA1· n= 0,
则 即 → 4x+ 4 3y= 0,
DC · n= 0,
取 x= 3,则 n= ( 3,- 3,- 1) , → - 24 12 cos BE , n = =- ,
13· 2 13 13
所以直线 BE 与平面 A1DC 所成角的正弦值为 12. ⋯ 12 分 13
19.解: - + 72.5× 5× 0.06+ 77.5× 5× 0.04
+ 82.5× 5× ( 1) x= 62.5× 5× 0.03+
67.5× 5× 0.05
0.02=71.75. 所以 M 服从正态分布 N (71.75, 35.4).
从而有 P (59.85< M< 77.7)= P ( μ- 2σ< Z< μ+σ) = 1 [P ( μ- 2σ< Z< μ+ 2σ)+ P( μ- 2 σ< Z< μ+σ) ] = 0.818 6, 故采摘的 10 000 个苹果中,果径位于区间 (59.85, 77.7) 的苹果个数约为 10 000×
0.818 6= 8 186(个). ⋯ 5 分
( 2)由图 2 可知,果径在 80 以上的苹果中,特级果、一级果、二级果的概率分别
为 1 , 1 , 3 , 5 2 10 设出售 1kg 果径在 80 以上苹果的收入为 Y,则 Y 的分布列为:
Y 12 10 9
P 1 1 3 5 2 10 故 E(Y)= 12× 1 +10× 1 + 9× 3 =10.1, --- 5 2 10 所以 E(X) =800E(Y)= 8 080 元. ⋯ 12 分
20.解: (1)设 M (0, m), N (n, 0), P (x, y), 由 | MN| =1 得 m2 +n2 =1. 由→ = → 得 , - = ,- , MP 3 MN (x y m) 3(n m) 从而 x= 3n,y- m=- 3m, 所以 n= x , m=- y , 3 2 所以曲线 x2 y2 ⋯ 6 分 E 的方程为 + = 1.
9 4 (2) MN : y= kx+m,所以 n=- m .① k 设 P ( x1, y1), Q (x2, y2), 将 MN 代入到 E 的方程并整理,可得(4+ 9k2)x2+18kmx+ 9m2- 36= 0,
高三理科数学参考答案第 2 页 --- - 18km 所以 x1+ x2= 4+
9k2 . 因为 | PN| = | MQ| ,所以 MN 和 PQ 的中点重合,
所以 - 9km= n ,② 4+
9k2 2
联立①②可得 k2= 4 ,故 k=± 2 . ⋯ 12 分 9 3 21.解: (1) f (x)= 4ex+2e- 2x- a, 令 g ( x)=4ex+ 2e- 2x- a,则 g (x)= 4ex- 4e- 2x, 显然 g (x)在 (-∞,+∞ )单调递增,且 g (0)= 0,所以当 x∈ (-∞, 0)时, g (x)< 0,g ( x)单调递减; 当 x∈ (0,+∞ ) 时, g (x)> 0, g (x)单调递增. 所以 g (x)的最小值为 g (0) = 6- a,即 f (x)的最小值为 6- a,要使 f (x)为单调增函数,则有 f (x)≥ 0, 所以 6- a≥ 0,故 a≤ 6. ⋯ 4 分 ( 2)证明: (ⅰ)由( 1)得 g (x)的两个零点为 x1, x2, x1< 0<x2,且 a> 6.
f (x)在 (-∞, x1)和 (x2 ,+∞ )上单调递增,在 ( x1, x2)上单调递减.令 h ( x)=g ( x)- g (-x), 则 h (x) =g (x)+g (- x) = 4ex- 4e-2 x+ 4e- x- 4e2 x = 4[- (ex+e- x)2+ (ex+ e- x)+ 2] = 4[2- (ex+e- x)][1 + (ex+e- x)] <0, 所以 h (x)在 (0,+∞ )上单调递减, 当 x> 0 时, h (x)< h (0) = 0. 所以 g (x2)-g (-x2)< 0,从而 g (x2)< g (- x2),又 g ( x2)= g (x1)= 0, 所以 g (x1)<g (-x2), 因为 g (x)在 (-∞, 0)上单调递减, x1,- x2 ∈(-∞, 0),
所以 x1>- x2,故 x1+ x2>0. ⋯ 9 分 (ⅱ) f (x)+ f (- x)= 4ex- e-2 x+ 4e- x- e2x, =- (ex+ e- x)2+ 4(ex+ e-x)+ 2 =- (ex+ e- x- 2)2+ 6 ≤ 6. 由(ⅰ)得 x1 +x2>0,所以 x2>- x1> 0, --- 由 f (x)在 (x1, x2)上单调递减,可得 f (x2)< f (- x1),
从而有 f (x1 )+ f (x2 )< f (x1)+f (- x1)≤ 6,
所以 f (x1)+ f ( x2)< 6. ⋯ 12 分
高三理科数学参考答案第 3 页 --- 22.解: (1)依题意可得,圆 C1: (x-1) 2+y2= 1;圆 C2 :(x+ 2)2+ y2=4.所以 C1: x2+ y2= 2x; C2: x2+ y2=- 4x,
2 2 2 因为 x + y = ρ, x= ρcos θ,
所以 C1: ρ=2cos θ; C2: ρ=- 4cos θ. ⋯ 4
分
( 2)因为 C1,C2 都关于 x 轴对称,△ OAB 为等边三角形, 所以不妨设 A (ρ, θ), B ρ, θ+ π π. A ( B 3 ), 0< θ< 2 A B ( 3 ).
依题意可得, ρ=2cos θ, ρ=- 4cos θ+ π
从而 2cosθ=- 4cos (θ+ 3π),
整理得, 2cos θ= 3sin θ,所以 tan θ=2 3 3,
又因为
0< θ< π,所以 cos
θ= 21, 2 7
| AB| = | OA| = ρ=2 21. ⋯ 10 分
A 7 23.解: (1)因为 | ax+ 1| + | ax- 1| ≥| (ax+1)- (ax- 1)| = 2,
等号当且仅当 (ax+ 1)(ax-1)≤ 0 时成立,所以 f (x)的最小值为 2- 2a- 4=- 2a- 2.依题意可得,- 2a- 2≥ 0, 所以 a≤- 1. ⋯ 4 分 (2)因为 a> 0, f (x)= | ax+ 1| + | ax- 1| - 2a- 4, - 2ax- 2a- 4,x≤- 1 , a
所以 f (x)= - 2a- 2, - 1 < x< 1 , a a 1