2014年普通高等学校招生全国统一考试(浙江文科地理综合)

2014年普通高等学校招生全国统一考试（浙江卷）数学（理科）一．选择题：本大题共10小题，每小题5分，共50分. 在每小题给出的四个选项中，只有一项是符合题目要求的.（1）设全集{}2|≥∈=x N x U ，集合{}5|2≥∈=x N x A ，则=A C U （ ）A. ∅B. }2{C. }5{D. }5,2{（2）已知i 是虚数单位，R b a ∈,,则“1==b a ”是“i bi a 2)(2=+”的（ ）A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件（3）某几何体的三视图（单位：cm ）如图所示，则此几何体的表面积是A. 902cmB. 1292cmC. 1322cmD. 1382cm4.为了得到函数x x y 3cos 3sin +=的图像，可以将函数x y 3sin 2=的图像（ ）A.向右平移4π个单位 B.向左平移4π个单位 C.向右平移12π个单位 D.向左平移12π个单位 5.在46)1()1(y x ++的展开式中，记n m y x 项的系数为),(n m f ，则=+++)3,0(2,1()1,2()0,3(f f f f ）（ ）A.45B.60C.120D. 2106.已知函数则且,3)3()2()1(0,)(23≤-=-=-≤+++=f f f c bx ax x x f （ ）A.3≤cB.63≤<cC.96≤<cD. 9>c7.在同意直角坐标系中，函数x x g x x x f a a log )(),0()(=≥=的图像可能是（ ）8.记,max{,},x x y x y y x y ≥⎧=⎨<⎩，,min{,},y x y x y x x y ≥⎧=⎨<⎩，设,a b 为平面向量，则（ ） A.min{||,||}min{||,||}a b a b a b +-≤B.min{||,||}min{||,||}a b a b a b +-≥C.2222min{||,||}||||a b a b a b +-≥+D.2222min{||,||}||||a b a b a b +-≤+ 9.已知甲盒中仅有1个球且为红球，乙盒中有m 个红球和n 个篮球()3,3m n ≥≥，从乙盒中随机抽取()1,2i i =个球放入甲盒中.（a ）放入i 个球后，甲盒中含有红球的个数记为()1,2i i ξ=；（b ）放入i 个球后，从甲盒中取1个球是红球的概率记为()1,2i p i =.则A.()()1212,p p E E ξξ><B.()()1212,p p E E ξξ<>C.()()1212,p p E E ξξ>>D.()()1212,p p E E ξξ<<10.设函数21)(x x f =，),(2)(22x x x f -=|2sin |31)(3x x f π=，99,,2,1,0,99==i i a i ，记|)()(||)()(||)()(|98991201a f a f a f a f a f a f I k k k k k k k -++-+-= ，.3,2,1=k 则A.321I I I <<B. 312I I I <<C. 231I I I <<D. 123I I I <<二、填空题：本大题共7小题，每小题4分，共28分.11.若某程序框图如图所示，当输入50时，则该程序运算后输出的结果是________.12.随机变量ξ的取值为0,1,2，若()105P ξ==，()1E ξ=，则()D ξ=________. 13.当实数x ，y 满足240,10,1,x y x y x +-≤⎧⎪--≤⎨⎪≥⎩时，14ax y ≤+≤恒成立，则实数a 的取值范围是________.14.在8张奖券中有一、二、三等奖各1张，其余5张无奖.将这8张奖券分配给4个人，每人2张，不同的获奖情况有_____种（用数字作答）.15.设函数()⎪⎩⎪⎨⎧≥-<+=0,0,22x x x x x x f 若()()2≤a f f ，则实数a 的取值范围是______ 16.设直线)0(03≠=+-m m y x 与双曲线12222=-by a x （0a b >>）两条渐近线分别交于点B A ,，若点)0,(m P 满足PB PA =,则该双曲线的离心率是__________17、如图，某人在垂直于水平地面的墙面前的点处进行射击训练. 已知点到墙面的距离为，某目标点沿墙面的射击线移动，此人为了准确瞄准目标点，需计算由点观察点的仰角的大小.若则的最大值19（本题满分14分）已知数列{}n a 和{}n b 满足()()*∈=N n a a a n b n 221 .若{}n a 为等比数列，且.6,2231b b a +== （1）求n a 与n b ；（2）设()*∈-=N n b a c n n n 11。

绝密★启用前2014年全国普通高等学校招生统一考试文科综合能力测试地理（广东卷带解析）试卷副标题考试范围：xxx ；考试时间：22分钟；命题人：xxx学校:___________姓名：___________班级：___________考号：___________注意事项．1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上第I 卷（选择题）一、选择题（题型注释）1、近年来，我国南方沿海出现“填海造房风”，所建“海景房”将吸引居民居住在海岸线附近。

“海景房”面临的灾害风险最小的是 A ．台风引发风暴潮 B ．寒潮造成冰冻 C ．海岸受侵蚀后退D ．地表下沉塌陷2、沙漠中植被的出现可对沙丘产生一定的影响。

其主要作用机制是 A ．降低风速进而增加风沙流对地表的侵蚀 B ．增加风沙流中颗粒物的含量而减少堆积 C ．促进风沙流携沙能力的增强而增大侵蚀 D ．拦截风沙流中的悬浮颗粒物并形成沉降图2、图3分别为我国某地不同海拔、不同坡度的乡村聚落数量统计图。

读图并结合所学知识，完成4-5题。

A．在各海拔段中，海拔1250-1400m的区域聚落数量最少B．在各海拔段中，坡度﹤2°的区域聚落数量最多C．在各海拔段中，海拔1550-1700m的区域聚落数量最多D．在各海拔段中，坡度15-20°的区域聚落数量最少4、该地最有可能位于我国A．黄土高原B．三江平原C．塔里木盆地D．江南丘陵5、近年来，随着我国内地的企业不断增加，原在沿海工作的务工人员出现大量返乡就业的现象。

这种现象总体上不利于A．推进家乡城镇化进程B．促进家乡经济发展C．增加春运长途客运量D．促进区域文化交流6、随着我国南方地区部分江河水库主要功能的退化，大坝将被拆除。

当河流生态系统稳定之后，与拆坝前相比，将会出现的变化有A．坝址上游枯水期平均水位上升B．坝址上游汛期出现的季节提前C．坝址下游径流量年际变化减小D．坝址下游的汛期洪峰流量增大7、北半球春分日，当某地（30°N，120°E）刚进入白昼这一时刻，东半球（20°W向东至160°E）处于白昼的范围约占全球面积的A．1/2B．1/3 C．1/6 D．1/98、热红外遥感影像亮度可反映地物表面温度，地物的表面温度越高，在影像中就越亮。

最新浙江省高三五校联考锁定命题范围针对性冲刺文科综合试题注意事项：1.本试卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分。

2.考生领到试卷后，须按规定在试卷上填写姓名、准考证号，并在答题卡上填涂对应的试卷类型信息点。

3.所有答案必须在答题卡上指定区域内作答。

考试结束后，将本试卷和答题卡一并交回。

第I卷（选择题）单项选择题（本题共35个小题，每小题4分，共140分。

在每小题给出的四个选项中，只有一个正确选项。

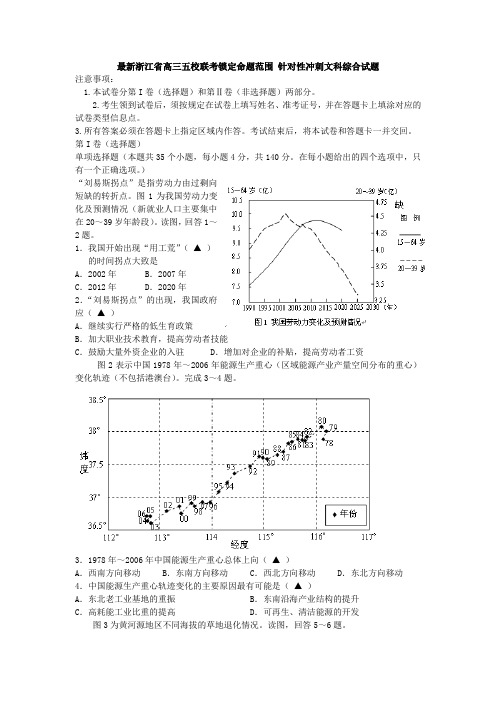
）“刘易斯拐点”是指劳动力由过剩向短缺的转折点。

图1为我国劳动力变化及预测情况（新就业人口主要集中在20～39岁年龄段）。

读图，回答1～2题。

1．我国开始出现“用工荒”（▲）的时间拐点大致是A．2002年B．2007年C．2012年D．2020年2．“刘易斯拐点”的出现，我国政府应（▲）A．继续实行严格的低生育政策B．加大职业技术教育，提高劳动者技能C．鼓励大量外资企业的入驻 D．增加对企业的补贴，提高劳动者工资图2表示中国1978年～2006年能源生产重心（区域能源产业产量空间分布的重心）变化轨迹（不包括港澳台）。

完成3～4题。

3．1978年～2006年中国能源生产重心总体上向（▲）A．西南方向移动B．东南方向移动C．西北方向移动D．东北方向移动4．中国能源生产重心轨迹变化的主要原因最有可能是（▲）A．东北老工业基地的重振B．东南沿海产业结构的提升C．高耗能工业比重的提高D．可再生、清洁能源的开发图3为黄河源地区不同海拔的草地退化情况。

读图，回答5～6题。

5．黄河源地区草地退化的特点是（▲）A．居民点密度越大草地退化率越高B．海拔4500～4600米的草地退化率最小C．居民点密度越大草地退化面积越大D．海拔4300～4400米的草地退化面积最大6．影响黄河源地区不同海拔草地面积大小的主要因素是（▲）A．土壤水分气温B．土壤水分坡度 C．气温光照D．光照坡度7．四城市中，夏半年盛行风风向基本相同的城市是（▲）A．甲、乙B．乙、丙 C．甲、丁D．丙、丁8．影响丙地7月降水日数多的主要原因是（▲）A．副热带高压控制 B．气流受地形抬升 C．受海洋西风控制 D．受海洋信风控制下图为世界局部地区某节气的海平面等压线分布图。

2014年普通高等学校招生全国统一考试（浙江卷）数学（文科）一、选择题：本大题共10小题，每小题5分，共50分. 在每小题给出的四个选项中，只有一项是符合题目要求的.1设集合S={x/x>=2}，T={x/x<=5},则=ST （ ）.A ．(],5-∞B ．[)2+∞，C ．()2,5D ．[]2,5 2.设四边形ABCD 的两条对角线,AC BD ，则“四边形ABCD 为菱形”是“AC BD ⊥”的（ ）.A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 3.某几何体的三视图（单位：cm ）如图所示，则该几何体的的体积是（ ）.俯视图侧视图正视图A ．372cm B.390cm C ．3108cm D.3138cm 4.（2014浙江文4）为了得到函数x x y 3cos 3sin +=的图像，可以将函数y x 的图像（ ）. A ．向右平移π12个单位 B ．向右平移π4个单位 C ．向左平移π12个单位 D ．向左平移π4个单位5.已知圆22220x y x y a ++-+=截直线20x y ++=所得弦的长度为4，则实数a 的值是（ ）.A ．2-B ．4-C ．6-D ．8-6.（2014浙江文6）设,m n 是两条不同的直线，,αβ是两个不同的平面（ ）. A ．若m n ⊥，//n α，则m α⊥ B ．若//m β，βα⊥，则m α⊥ C ．若,,m n n ββα⊥⊥⊥，则m α⊥ D ．若m n ⊥，n β⊥，βα⊥，则m α⊥7. （2014浙江文7）已知函数()32f x x ax bx c =+++，且()()()01233f f f <-=-=-…，则（ ）. A.3c …B.36c <…C.69c <…D. 9c >8.（2014浙江文8）在同一直角坐标系中，函数()()0a f x x x =>，()log a g x x =的图像可能是（ ）.PMCBAA. B. C. D. 9.（2014浙江文9）设θ为两个非零向量,a b 的夹角，已知对任意实数t ，t +b a 的最小值为1.（ ）.A ．若θ确定，则a 唯一确定B ．若θ确定，则b唯一确定C ．若a 确定，则θ唯一确定 D ．若b 确定，则θ唯一确定10.（2014浙江文10）如图所示，某人在垂直于水平地面ABC 的墙面前的点A 处进行射击训练. 已知点A到墙面的距离为AB ，某目标点P 沿墙面上的射线CM移动，此人为了准确瞄准目标点P ，需计算由点A 观察点P 的仰角θ的大小（仰角θ为直线AP 与平面ABC 所成角）.若15m,25m,30AB AC BCM ==∠=，则tan θ的最大值是（ ）.ABCD二、填空题：本大题共7小题，每小题4分，共28分.11.已知i 是虚数单位，计算()21i=1+i -____________.12.若实数,x y 满足240101x y x y x +-⎧⎪--⎨⎪⎩………，则x y +的取值范围是_____________.13.若某程序框图如图所示，当输入50时，则该程序运行后输出的结果是__________.14.在3张奖券中有一、二等奖各1张，另1张无奖，甲、乙两人各抽取1张，两人都中奖的概率是______________.15.设函数()2222, 0, 0x x x f x x x ⎧++⎪=⎨->⎪⎩…，若()()2f f a =，则a =_________.16.已知实数,,a b c 满足0a b c ++=，2221a b c ++=，则a 的最大值是____________.17.（2014浙江文17）设直线()300x y m m -+=≠与双曲线()2222100x y a b a b-=>>，的两条渐近线分别交于点,A B ，若点(),0Pm 满足PA PB =，则该双曲线的离心率是______________.三．解答题：本大题共5小题，共72分。

2014年普通高等学校招生全国统一考试（浙江卷）文科数学试题答案与解析1.解析[)2,S =+∞，(],5T =-∞，[]2,5S T = .故选D.2. 解析若四边形ABCD 为菱形，则AC BD ⊥，反之，若AC BD ⊥，则四边形ABCD 不一定是菱形，故选A.3. 解析由三视图可知，该几何体是由一个长方体和一个直三棱柱构成的组合体，如图，其体积为1643433902⨯⨯+⨯⨯⨯=3cm ，故选B.4. 解析因为ππs i n 3c o s 2c o s 2c o s 3412y x x x x ⎡⎤⎛⎫⎛⎫=+=-=-⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，所以将c o s 3y x =的图像向右平移π12个单位即可得到πcos 312y x ⎡⎤⎛⎫=- ⎪⎢⎥⎝⎭⎣⎦的图像，故选A.5. 解析将圆的方程化为标准方程为()()22112x y a ++-=-，所以圆心为()1,1-，半径r =20x y ++=的距离d ==，故224r d -=，即224a --=，所以4a =-，故选B.6. 解析对于选项A 、B 、D ，均能举出//m α的反例；对于选项C ，若m β⊥，n β⊥，则//m n ，又n α⊥，所以m α⊥，故选C.7. 解析 由 ()()()01233f f f <=-=-…，得 0184227933a b c a b c a b c <-+-+=-+-+=-+-+…，由1842a b c a b c -+-+=-+-+得370a b --=， ①由12793a b c a b c -+-+=-+-+，得4130a b --=， ② 由①②，解得6a =，11b =，所以063c <-…，即69c <…，故选C.8. 解析因为0a >，且1a ≠，所以()a f x x =在()0,+∞上单调递增，所以排除A ；当01a <<或1a >时，B 、C 中()f x 与()g x 的图像矛盾，故选D.9.解析22222222cos t t t t θ+=+⋅⋅+=+⋅+b a a a b b a a b b ，设()2222cos f t t θ=+⋅+a a b b ，则二次函数()f t 的最小值为1，即22222244cos 14θ-=a b a b a，化简得22sin 1θ=b .因为0>b ，0πθ剟，所以sin 1θ=b ，若θ确定，则b 唯一确定，而b 确定，θ不确定，故选B.10. 解析如图，过P 作PQ BC ⊥于Q ，则PQ ⊥平面ABC ，所以PAQ θ∠=， 设PQ x =m，则=CQ m，20BC =m，()20BQ =m ，所以AQ ==m ，所以tan =θ=.设25t x=，则22262527335525t t x x ⎛-+=-+=-+ ⎝⎭，所以当5t=，即12512x =时，26253x +取得最小值2725，即tan θ=，故选D.11. 解析()()()()()21i i 1i1i 1i 11i 2i 2i i 2221i -⋅-----====--⋅-+. 12. 解析画出可行域如图，可行域为ABC △的内部及其边界，设x y t +=，则y x t =-+，t 的几何意义为直线y x t =-+在y 轴上的截距，当直线通过点A ，B 时，t 取得最小值与最大值，可求得A ，B 两点的坐标分别为()1,0和()2,1，所以13t 剟，即x y +的取值范围是[]1,3.QM CB AP13. 解析第一步：1i =，1S =，此时2i =；第二步：2i =，2124S =⨯+=，此时3i =；第三步：3i =，24311S =⨯+=，此时4i =；第四步：4i =，211426S =⨯+=，此时5i =；第五步：5i =，22655750S =⨯+=>，此时6i =；符合条件，所以输出6. 14. 解析设A 为一等奖奖券，B 为二等奖卷，C 为无奖奖卷，则甲、乙两人抽取的所有可能结果为AB 、BA 、AC 、CA 、BC 、CB ，共6种，而甲、乙两人都中奖的情况有AB 、BA ，共2种，故所求概率为2163=. 15. 解析若0a >，则()20f a a =-<，所以()()4222f f a aa =-+，由()()2f f a=，得42222a a -+=，解得a =.若0a …，则()()2222110f a a a a =++=++>，所以()()()22202ff a aa =-++<≠.综上，a =16. 解析 因为222b a bc +…，即()()2222222b cbc bc b c +++=+…，所以()2222b c b c ++…，由0a b c ++=，得b c a +=-，由2221a b c ++=，得()22222122b c a a b c +-=+=…，所以223a …，所以33a -剟故a17. 解析 由30x y m b y x a -+=⎧⎪⎨=⎪⎩得点A 的坐标为,33ambm b a b a ⎛⎫ ⎪--⎝⎭，由30x y m b y x a -+=⎧⎪⎨=-⎪⎩得点B 的坐标为，则AB 的中点C 的坐标为22223,99a m b m b a b a ⎛⎫ ⎪--⎝⎭，因为13AB k =，所以22223939CPb mb a k a m m b a-==---，即()2222339b a b a =---，化简得224a b =， 即()2224a c a =-，所以2245c a =，所以254e =，所以2e =18. 解析（I ）由已知得()21cos 4sin sin 2A B A B --+=+⎡⎤⎣⎦，化简得2cos cos 2sin sin A B A B -+=，故()cos 2A B +=-，所以3π4A B +=，从而π4C =. （II ）因为1sin 2ABC S ab C =△，由6ABC S =△，4b =，π4C =，得a =.由余弦定理,33am bm b a b a -⎛⎫⎪++⎝⎭2222cos c a b ab C =+-，得c 评注 本题主要考查两角和与差的余弦公式、二倍角公式、余弦定理、三角形面积公式等基础知识，同时考查运算求解能力.19. 解析（I ）由题意知()()1123336a d a d ++=，将11a =代入上式解得2d =或5d =-.因为0d >，所以2d =.从而21n a n =-，()2*n S n n =∈N .（II ）由（I ）得()()12211m m m m k a a a a m k k +++++++=+-+ ，所以()()21165m k k +-+=.由*,m k ∈N ，知2111m k k +-+>…，故211315m k k +-=⎧⎨+=⎩，所以54m k =⎧⎨=⎩.评注 本题主要考查等差数列的概念、通项公式、求和公式等基础知识，同时考查运算求解能力.20. 解析（I ）连接BD ，在直角梯形BCDE 中，由1D E B E ==，2CD =，得B D B C ==由AC ，2AB =，得222AB AC B C =+，即A C B C ⊥.又平面ABC ⊥平面BCDE ，从而AC ⊥平面BCDE .（II ）在直角梯形BCDE中，由BD BC ==2DC =，得BD BC ⊥.又平面ABC ⊥平面BCDE ，所以BD ⊥平面ABC .作//EF BD ，与CB 延长线交于F ，连接AF ，则EF ⊥平面ABC .所以EAF ∠是直线AE 与平面ABC 所成的角.在Rt BEF △中，由1EB =，π4EBF ∠=，得2EF =，2BF =；在Rt ACF △中，由AC，2CF =2AF =. 在Rt AEF △中，由2EF =，AF =，得tan EAF ∠=.所以，直线AE 与平FED CBA面ABC所成的角的正切值是13. 评注本题主要考查直线与平面的位置关系、线面所成的角等基础知识，同时考查空间想象能力和推理论证能力.21. 解析 （I ）因为0a >，11x -剟，所以（i ）当01a <<时，若[]1,x a ∈-，则()333f x x x a =-+，则()2330f x x '=-<，故()f x 在()1,a -上是减函数；若[]1,x a ∈-，则()333f x x x a =-+，()2330f x x '=-<，故()f x 在(),1a 上是增函数.所以()()3g a f a a ==.（ii ）当1a …时，有x a …，则()333f x x x a =-+，()2330f x x '=-<，故()f x 在()1,1-上是减函数，所以()()123g a f a ==-+.综上，（II ）令()()()h x f x g a =-.（i ）当01a <<时，()3g a a =，若[],1x a ∈，()3333h x x x a a =+--，得()233h x x '=+，则()h x 在(),1a 上是增函数.所以，()h x 在[],1a 上的最大值是()3143h a a =--，且01a <<，所以()14h ….故()()4f x g a +…；若[]1,x a ∈-，()3333h x x x a a =-+-，得()233h x x '=-，则()h x 在()1,a -上是减函数，所以()h x 在[]1,a -上的最大值是()3123h a a -=+-.令()223t a a a =+-，()2330t x a '=->，知()t a 在()0,1上是增函数.所以，()()14t a t <=，即()14h -<.故()()4f x g a +….（ii ）当1a …时，()23g a a =-+，故()332h x x x =-+，得()233h x x '=-，此时()h x 在()1,1-上是减函数，因此()h x 在[]1,1-上的最大值是()14h -=.故()()4f x g a x +….综上，当[]1,1x ∈-时，恒有()()4f x g a +….评注本题主要考查函数最大（小）值的概念、利用导数研究函数的单调性等基础知识，同时考查推理论证、分类讨论、分析问题和解决问题等综合解题能力.22.解析 （I ）由题意知焦点()0,1F ，准线方程为1y =-.设()00,P x y ，由抛物线定义知01PF y =+，得到02y =，所以()2P或()2P -.由3PF FM =，分别得23M ⎛⎫ ⎪ ⎪⎝⎭或23M ⎫⎪⎪⎝⎭. ()3,01,=23, 1.a a g a a a ⎧<<⎨-+⎩…（II ）设直线AB 的方程为y kx m =+，点()11,A x y ，点()22,B x y ，()00,P x y .由2,4y kx m x y=+⎧⎨=⎩得2440x kx m --=，于是216160k m ∆=+>，124x x k +=，124x x m =-，所以AB 的中点M 的坐标为()22,2k k m +.由3PF FM =得()()200,132,21x y k k m --=+-，所以0206,463,x k y k m =-⎧⎪⎨=--⎪⎩由2004x y = 得214515k m =-+.由0∆>，20k …，得1433m -<….又因为AB =，点()0,1F 到直线AB的距离为d =所以48ABP ABF S S m ==-=△△. 记()321435133f m m m m m ⎛⎫=-++-< ⎪⎝⎭….令()291010f m m m '=-+=，解得119m =，21m =. 可得()f m 在11,39⎛⎫- ⎪⎝⎭上是增函数，在1,19⎛⎫ ⎪⎝⎭上是减函数，在41,3⎛⎫ ⎪⎝⎭上是增函数.又1256492433f f ⎛⎫⎛⎫=> ⎪ ⎪⎝⎭⎝⎭，所以当19m =时，()f m 取到最大值256243，此时k =所以，ABP △. 评注 本题主要考查抛物线的几何性质、直线与抛物线的位置关系、三角形面积公式、平面向量等基础知识，同时考查解析几何的基本思想方法和运算求解能力.。

数学试卷 第1页（共6页） 数学试卷 第2页（共6页） 数学试卷 第3页（共6页）绝密★启用前2014年普通高等学校招生全国统一考试（浙江卷）数学(文科)本试题卷分选择题和非选择题两部分.全卷共6页,选择题部分1至3页,非选择题部分4至6页.满分150分,考试时间120分钟. 考生注意：1.答题前,请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填写在试题卷和答题纸规定的位置上.2.答题时,请按照答题纸上“注意事项”的要求,在答题纸相应的位置上规范作答,在本试题卷上作答一律无效. 参考公式：球的表面积公式 柱体的体积公式24πS R = V Sh =球的体积公式其中S 表示柱体的底面积,h 表示柱体的高 33π4V R =台体的体积公式其中R 表示球的半径 11221(S )3V h S S S =++锥体的体积公式其中1S ,2S 分别表示台体的上、下底面积, 13V Sh =h 表示台体的高其中S 表示锥体的底面积,如果事件A ,B 互斥,那么h 表示锥体的高()()()P A B P A P B +=+选择题部分（共50分）一、选择题：本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{|2}S x x =≥,{|5}T x x =≤,则S T =I( )A .(,5]-∞B .[2,)+∞C .(2,5)D .[2,5]2.设四边形ABCD 的两条对角线为AC ,BD ,则“四边形ABCD 为菱形”是“AC BD ⊥”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件3.某几何体的三视图（单位：cm ）如图所示,则该几何体的体积是( )A .372cmB .390cmC .3108cmD .3138cm4.为了得到函数sin3cos3y x x =+的图象,可以将函数2cos3y x =的图象( )A .向右平移π12个单位B .向右平移π4个单位C .向左平移π12个单位D .向左平移π4个单位5.已知圆22220x y x y a ++-+=截直线20x y ++=所得弦的长度为4,则实数a 的值是( )A .2-B .4-C .6-D .8- 6.设m ,n 是两条不同的直线,α,β是两个不同的平面( )A .若m n ⊥,n αP ,则m α⊥B .若m βP ,βα⊥,则m α⊥C .若m β⊥,n β⊥,n α⊥,则m α⊥D .若m n ⊥,n β⊥,βα⊥,则m α⊥7.已知函数32()f x x ax bx c =+++,且0(1)(2)(3)3f f f -=-=-＜≤,则( )A .3c ≤B .36c ＜≤C .69c ＜≤D .9c ＞8.在同一直角坐标系中,函数()(0)a f x x x =>,()log a g x x =的图象可能是( )ABCD9.设θ为两个非零向量a ,b 的夹角.已知对任意实数t ,|b t +a |是最小值为1 ( )A .若θ确定,则| a |唯一确定B .若θ确定,则| b |唯一确定C .若| a |确定,则θ唯一确定D .若| b |确定,则θ唯一确定10.如图,某人在垂直于水平地面ABC 的墙面前的点A 处进行射击训练.已知点A 到墙面的距离为AB ,某目标点P 沿墙面的射线CM 移动,此人为了准确瞄准目标点P ,需计算由点A 观察点P 的仰角θ的大小（仰角θ为直线AP 与平面ABC 所成角）.若15m AB =,25m AC =,30BCM ∠=o ,则tan θ的最大值是( )A .30B .30 C .43D .53-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------姓名________________ 准考证号_____________数学试卷 第4页（共6页） 数学试卷 第5页（共6页） 数学试卷 第6页（共6页）非选择题部分（共100分）二、填空题：本大题共7小题,每小题4分,共28分.11.已知i 是虚数单位,计算21i(1i)-=+ . 12.若实数x ,y 满足240,10,1,x y x y x +-⎧⎪--⎨⎪⎩≤≤≥则x y +的取值范围是 .13.若某程序框图如图所示,当输入50时,则该程序运行后输出的结果是 .14.在3张奖券中有一、二等奖各1张,另1张无奖.甲、乙两人各抽取1张,两人都中奖的概率是 .15.设函数2222, 0,(), 0,x x x f x x x ⎧++⎪=⎨-⎪⎩≤＞若(())2f f a =,则a = .16.已知实数a ,b ,c 满足0a b c ++=,2221a b c ++=,则a 的最大值是 .17.设直线30(0)x y m m -+=≠与双曲线22221(0,0)x y a b a b -=>>的两条渐近线分别交于点A ,B .若点(,0)P m 满足||||PA PB =,则该双曲线的离心率是 .三、解答题：本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤. 18.（本题满分14分）在ABC △中,内角A ,B ,C 所对的边分别为a ,b ,c .已知24sin 4sin sin 2A BA B -+22=+.（Ⅰ）求角C 的大小；（Ⅱ）已知4b =,ABC △的面积为6,求边长c 的值.19.（本题满分14分）已知等差数列{}n a 的公差0d >,设{}n a 的前n 项和为n S ,2336S S =g . （Ⅰ）求d 及n S ；（Ⅱ）求m ,k （*,m k ∈Ν）的值,使得1265m m m m k a a a a +++++++=L .20.（本题满分15分）如图,在四棱锥A BCDE -中,平面ABC ⊥平面BCDE ,90CDE BED ∠=∠=o ,2AB CD ==,1DE BE ==,2AC =.（Ⅰ）证明：AC ⊥平面BCDE ；（Ⅱ）求直线AE 与平面ABC 所成角的正切值.21.（本题满分15分）已知函数3()3||(0)f x x x a a =+->.若()f x 在[]1,1-上的最小值记为()g a . （Ⅰ）求()g a ；（Ⅱ）证明：当[]1,1x ∈-时,恒有()()4f x g x +≤.22.（本题满分14分）已知ABP △的三个顶点在抛物线C ：24x y =上,F 为抛物线C 的焦点,点M 为AB 的中点,3PF FM =u u u r u u u u r .（Ⅰ）若||3PF =,求点M 的坐标； （Ⅱ）求ABP △面积的最大值.PBA M FyxOAD EBC。

数学试卷 第1页（共18页） 数学试卷 第2页（共18页） 数学试卷 第3页（共18页）绝密★启用前2014年普通高等学校招生全国统一考试（浙江卷）数学(文科)本试题卷分选择题和非选择题两部分.全卷共6页,选择题部分1至3页,非选择题部分4至6页.满分150分,考试时间120分钟. 考生注意：1.答题前,请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填写在试题卷和答题纸规定的位置上.2.答题时,请按照答题纸上“注意事项”的要求,在答题纸相应的位置上规范作答,在本试题卷上作答一律无效. 参考公式：球的表面积公式 柱体的体积公式24πS R =V Sh =球的体积公式其中S 表示柱体的底面积,h 表示柱体的高 33π4V R = 台体的体积公式其中R 表示球的半径121(S )3V h S = 锥体的体积公式其中1S ,2S 分别表示台体的上、下底面积,13V Sh = h 表示台体的高其中S 表示锥体的底面积, 如果事件A ,B 互斥,那么 h 表示锥体的高 ()()()P A B P A P B +=+选择题部分（共50分）一、选择题：本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{|2}S x x =≥,{|5}T x x =≤,则S T =( ) A .(,5]-∞ B .[2,)+∞ C .(2,5) D .[2,5]2.设四边形ABCD 的两条对角线为AC ,BD ,则“四边形ABCD 为菱形”是“AC BD ⊥”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件3.某几何体的三视图（单位：cm ）如图所示,则该几何体的体积是( )A .372cmB .390cmC .3108cmD .3138cm4.为了得到函数sin3cos3y x x =+的图象,可以将函数y x =的图象( )A .向右平移π12个单位 B .向右平移π4个单位C .向左平移π12个单位D .向左平移π4个单位5.已知圆22220x y x y a ++-+=截直线20x y ++=所得弦的长度为4,则实数a 的值是 ( )A .2-B .4-C .6-D .8-6.设m ,n 是两条不同的直线,α,β是两个不同的平面( ) A .若m n ⊥,n α,则m α⊥ B .若m β,βα⊥,则m α⊥ C .若m β⊥,n β⊥,n α⊥,则m α⊥D .若m n⊥,n β⊥,βα⊥,则m α⊥7.已知函数32()f x x ax bx c =+++,且0(1)(2)(3)3f f f -=-=-＜≤,则 ( ) A .3c ≤ B .36c ＜≤ C .69c ＜≤ D .9c ＞8.在同一直角坐标系中,函数()(0)a f x x x =>,()log a g x x =的图象可能是( )ABCD9.设θ为两个非零向量a ,b 的夹角.已知对任意实数t ,|b t +a |是最小值为1 ( ) A .若θ确定,则| a |唯一确定-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------姓名________________ 准考证号_____________数学试卷 第4页（共18页） 数学试卷 第5页（共18页） 数学试卷 第6页（共18页）B .若θ确定,则| b |唯一确定C .若| a |确定,则θ唯一确定D .若| b |确定,则θ唯一确定10.如图,某人在垂直于水平地面ABC 的墙面前的点A 处进行射击训练.已知点A 到墙面的距离为AB ,某目标点P 沿墙面的射线CM 移动,此人为了准确瞄准目标点P ,需计算由点A 观察点P 的仰角θ的大小（仰角θ为直线AP 与平面ABC 所成角）.若15m AB =,25m AC =,30BCM ∠=,则tan θ的最大值是( )ABC D非选择题部分（共100分）二、填空题：本大题共7小题,每小题4分,共28分. 11.已知i 是虚数单位,计算21i(1i)-=+ .12.若实数x ,y 满足240,10,1,x y x y x +-⎧⎪--⎨⎪⎩≤≤≥则x y +的取值范围是 .13.若某程序框图如图所示,当输入50时,则该程序运行后输出的结果是 .14.在3张奖券中有一、二等奖各1张,另1张无奖.甲、乙两人各抽取1张,两人都中奖的概率是 . 15.设函数2222, 0,(), 0,x x x f x x x ⎧++⎪=⎨-⎪⎩≤＞若(())2f f a =,则a = .16.已知实数a ,b ,c 满足0a b c ++=,2221a b c ++=,则a 的最大值是 .17.设直线30(0)x y m m -+=≠与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A ,B .若点(,0)P m 满足||||PA PB =,则该双曲线的离心率是 .三、解答题：本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤.18.（本题满分14分）在ABC △中,内角A ,B ,C 所对的边分别为a ,b ,c .已知24si n 4s i n si n 2A B A B -+2=+（Ⅰ）求角C 的大小；（Ⅱ）已知4b =,ABC △的面积为6,求边长c 的值.19.（本题满分14分）已知等差数列{}n a 的公差0d >,设{}n a 的前n 项和为n S ,2336S S =. （Ⅰ）求d 及n S ；（Ⅱ）求m ,k （*,m k ∈Ν）的值,使得1265m m m m k a a a a +++++++=.20.（本题满分15分）如图,在四棱锥A BCDE -中,平面ABC ⊥平面B C D E ,90CDE BED∠=∠=,2AB CD ==,1DE BE ==,AC =（Ⅰ）证明：AC ⊥平面BCDE ； （Ⅱ）求直线AE 与平面ABC 所成角的正切值.21.（本题满分15分）已知函数3()3||(0)f x x x a a =+->.若()f x 在[]1,1-上的最小值记为()g a .（Ⅰ）求()g a ；（Ⅱ）证明：当[]1,1x ∈-时,恒有()()4f x g x +≤.A D EB C数学试卷 第7页（共18页） 数学试卷 第8页（共18页） 数学试卷 第9页（共18页）22.（本题满分14分）已知ABP △的三个顶点在抛物线C ：24x y =上,F 为抛物线C 的焦点,点M 为AB 的中点,3PF FM =. （Ⅰ）若||3PF =,求点M 的坐标； （Ⅱ）求ABP △面积的最大值.2014年普通高等学校招生全国统一考试（浙江卷）数学（文科）答案解析选择题部分一、选择题 1.【答案】D[2,5]S T =数学试卷 第10页（共18页） 数学试卷 第11页（共18页） 数学试卷 第12页（共18页）析】依题意，对任||1b at +≥恒成立，22)2||||cos 1ta b t a b θ++≥恒成立，||b 为定值时二次函数才有最小值.故选示】由题意可得对||1b at +≥恒成立，22)2||||c o s t a b t a b θ++≥恒成立，综合选项可得结论.【考点】平面向量数量积的运算，零向量，数量积表示两个向量的320225m m -+的最大值为4333⨯【提示】由条件利用两个复数代数形式的乘除法，虚数单位i 的幂运算性质，计算求得结果. 【考点】复数代数形式的乘除运算 12.【答案】2【解析】不等式组表示的平面区域如图中ABC ∆，令z x y =+，解方程组24010x y x y +-≤⎧⎨--≤⎩得(2,1)C ，解方程组101x y x --≤⎧⎨≥⎩得(1,0)B ，平移直线z x y =+经过点C 使得z 取得最大值，即max 213z =+=，当直线z x y=+经过点(1,0)B 使得z 取得最小值，即min 101z =+=，故x y +的取值范围是[1,3].【提示】作出不等式组对应的平面区域，利用目标函数的几何意义，求目标函数z x y =+的最小值. 【考点】简单线性规划 13.【答案】6【解析】当0S =，i 1=，则第一次运行2011S =⨯+=，i 112=+=； 第二次运行2114S =⨯+=，i 213=+=； 第三次运行24311S =⨯+=，i 314=+=； 第四次运行211426S =⨯+=，i 415=+=；第五次运行22655750S =⨯+=>，i 516=+=终止循环，故输出i 6=. 【提示】根据框图的流程模拟运行程序，直到满足条件50S >，跳出循环体，确定输出的i 的值. 【考点】程序框图24s i n222A-1cos(A42--2cos cosA B∴-cos18ab C=ABC△中由条件利用二倍角的余弦公式、两角和的余cosab C的值【考点】二倍角的余弦，两角和与差的正弦函数，余弦定理（Ⅰ）2d=，所以2336S=得0=，解得)*∈Ν.265m ka+=∈Ν，265m ka+=进行分类讨论，求出符合条件的CDE∠=BF ED=在ACB△中，2AB=，ABC⊥平面BCDE，AC∴（Ⅰ）01a>，-时，若1,[]x a∈﹣上是减数学试卷第13页（共18页）数学试卷第14页（共18页）数学试卷第15页（共18页）数学试卷 第16页（共18页）数学试卷 第17页（共18页） 数学试卷 第18页（共18页），由3PF FM =，得kx m +，11)(,A x y 3PF FM =，得04y =，得2241AB k k m =++，点F 2481||ABP ABF S S m k m ∴==+=△△﹣，13⎛-< ⎝PBA M FyxO。

绝密★启用前2014年全国普通高等学校招生统一考试文科综合能力测试地理（福建卷带解析）试卷副标题考试范围：xxx ；考试时间：30分钟；命题人：xxx学校:___________姓名：___________班级：___________考号：___________注意事项．1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上第I 卷（选择题）一、选择题（题型注释）人口抚养比是指非劳动人口与劳动年龄（15～64岁）人口数之比。

图3示意1980～2030年我国少儿抚养比和老年抚养比的变化趋势。

读图回答下列小题。

1、2015年前后我国老年抚养比变化明显，主要的影响因素是 A ．性别比例B ．医疗水平C ．教育程度D ．年龄结构2、随着我国人口抚养比的变化，2025年后可能出现A ．人口迁移加剧B ．劳动力渐不足C ．人口分布不均D ．社会负担减轻我国第四个南极科学考察站—泰山站（73°51'S ，76°58'E ）于2014年2月8日正式建成开站。

图6示意某科考队员当日拍摄的一天太阳运动轨迹合成图。

读图回答下列小题。

3、该日太阳位于图示F 位置时A.泰山（36°N ，117°E ）旭日东升B.东京（36°N ，141°E ）夕阳西斜C.纽约（41°N ，74°E ）烈日当空 开普敦（34°S ，18°E ）夜色深沉 4、次日泰山站 A ．日出正南 B ．太阳高度变大 C ．白昼变短D ．极昼即将开始图5示意1月、7月北半球纬向风的平均风向及风速（单位：m/s ）随纬度和高度的变化。

读图回答下列小题。

5、图中风向和风速季节变化最大的是 A ．①B ．②C ．③D ．④6、下列地理现象与图中风向、风速纬度分布规律相似的是 A ．气温分布B ．降水分布C ．地势起伏D ．洋流分布图4示意1992年～2010年中国对非洲农产品进出口的变化。

2014年普通高等学校招生全国统一考试数学试卷（浙江卷）一．选择题：本大题共10小题，每小题5分，共50分. 在每小题给出的四个选项中，只有一项是符合题目要求的。

1.设集合 {}|2S x x =≥，{}|5T x x =≤，则S T =（ ）（A ）(],5-∞ （B ）[)2,+∞ （C ）()2,5 （D ）[]2,52.设四边形ABCD 的两条对角线为AC 、BD ，则“四边形ABCD 为菱形”是“BD AC ⊥”的（ ）（A ）充分不必要条件 （B ）必要不充分条件（C ）充分必要条件 （D ）既不充分也不必要条件3. 某几何体的三视图（单位：cm ）如图所示，则该几何体的体积是（ ）（A ）372cm （B ）390cm（C ）3108cm （D ）3138cm4.为了得到函数x x y 3cos 3sin +=的图象，可以将函数x y 3cos 2=的图象（ ） （A ）向右平移12π个单位长 （B ）向右平移4π个单位长 （C ）向左平移12π个单位长 （D ）向左平移4π个单位长 5.已知圆02222=+-++a y x y x 截直线02=++y x 所得弦的长度为4，则实数a 的值为（ ） （A ）2- （B ）4- （C ）6- （D ）8-6.设m 、n 是两条不同的直线，α、β是两个不同的平面，则（ ）（A ）若n m ⊥，α//n ，则α⊥m （B ）若β//m ，αβ⊥，则α⊥m（C ）若β⊥m ，β⊥n ，α⊥n ，则α⊥m （D ）若n m ⊥，β⊥n ，αβ⊥，则α⊥m7. 已知函数()32f x x ax bx c =+++，且()()()01233f f f <-=-=-≤，则（ ）（A ）3≤c （B ）63≤<c （C ）96≤<c （D ）9>c8.在同一坐标系中，函数()()0a f x x x =≥，()log a g x x =的图象可能是（ ）9.设θ为两个非零向量,a b 的夹角，已知对任意实数t ，||b ta +的最小值为1。