浅谈初中数学线段之和最值问题讲课稿
- 格式:doc
- 大小:332.50 KB
- 文档页数:5

浅谈初中数学线段之和最值问题近年来,在全国各地出现的中考试题的平面几何最值问题中,呈现出变化多、涉及面广、形式灵活的 景象,对学生来讲是个难点;如果深入思考,可以发现:这类试题的命制都是立足于教材,解决途径都是 运用转化的思想“化折为直”。
本文中,笔者根据近几年的中考试题,结合浙教版教材和自己的教学体会, 谈谈初中数学中求线段之和最值的求解策略。
1.直接应用定(公)理求最值平面几何解决最短线路问题时常用的公理(定理):①两点之间线段最短•②三角形的两边之和大于第三边,两边之差小于第三边(②是由①得出) ;③直线外一点到直线的所有线段中垂线段最短•1.1应用两点之间线段最短教材链接:七上7.3线段的长短作业题:D如图,A 、B 、C D 表示4个村庄.村民们准备合打一口水井,(1)略(2)你能给出一 中使水井到各村庄的距离之和最小的方案吗?若能,请标出水井的位置,并说明理由 A口 解题分析:u B教材作业题中,因点 D 与点B 、点A 与点C 是定点,当水井打在 AC 与BD 的交点时,水 井到各村庄的距离之和最小,直接利用“两点之间线段最短”的原理。
中考链接:(2009山东潍坊)已知边长为 a 的正三角形 ABC 一象限),两顶点 A,B 分别在平面直角坐标系的 x 轴,y 轴的正半轴上滑动,点C 在第一象限,连接OC, 求OC 的长的最大值.解题分析:潍坊的这一试题对教材进行了拓展:点 C 为动点,直接相联不可能解决,但因为直角三角形斜边上的中线长和等边三角形边上的中线也是定值,所以设AB 中点为P,在一般情况下 OP+P O OC 当OP 、C 三点一线时 OC=OP+P 最大. 求解策略:教材的模型是在两定点之间求最小值,根据“两点之间线段最短” 连,对无法或较难量化的两点间距离则可以利用几何图形的性质转化为“折线和” 系或两点间线段最短可得出最值 .1.2应用垂线段最短教材链接:七上7.7相交线(2)作业题如图,直线I 表示一段河道,点A 表示集镇,图上距离与实际距离之 比为1 : 2000 000.现要从河I 向集镇A 引水,问沿怎样的路线开挖水渠, 才能使水渠的长度最短?……解题分析:教材作业题解决思路是过点A 向垂直于水渠的方向开挖水渠,水渠长最短•直接利用“直线外一点到直线的所有线中垂线段最 短”的原理.试题链接:2010台湾如图,△ ABC 中,有一点 P 在AC 上移动.若AB=AC=5,BC=6 的最小值为何?(A ) 8 (B ) 8.8 (C ) 9.8 (D ) 10解题分析:台湾此题AP*PC=AC 为定值5,从而三线段和转化 值,因为B 为定点,P 为AC 上一动点,所以BP 最小值就是定点 B求解策略:教材的模型是已知一定点和一定直线求最小值 .解答此类试题只要透过问题找到本质,剔T\7*,只要把两定点直接相 ,再利用三角形三边关到AC 的垂线A則 APBPCP为求BP 最小除一些不变的线段(和)转化为一定点到一定直线的距离,再利用“直线外一点到直线的所有线中垂线段 最短”即可得出最小值•在平面几何求最值这类问题中,应用轴对称变换、平移变换和旋转变换这三种图形变换及性质,可以 将那些分散、远离的条件转移到适当的位置上,得以相对集中后,再应用上述定(公)理,便可迎刃而解2.结合图形变换求最值' 2. 1应用轴对称变换把直线同侧的线段和转化为异侧线段之和 ”2.1.1 —定直线+两定点+ —动点教材链接:浙教版科学七下1.5光的反射和折射—基本模型1:(将军饮马问题)白日登山望烽火,黄昏饮马傍交河。




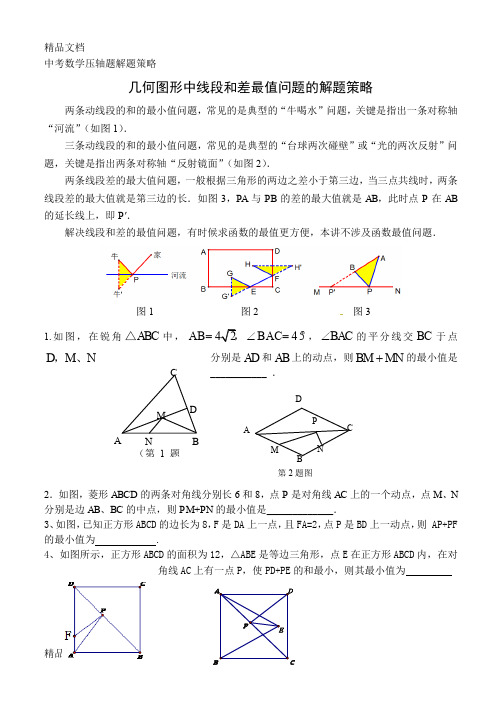
中考数学压轴题解题策略几何图形中线段和差最值问题的解题策略两条动线段的和的最小值问题,常见的是典型的“牛喝水”问题,关键是指出一条对称轴“河流”(如图1).三条动线段的和的最小值问题,常见的是典型的“台球两次碰壁”或“光的两次反射”问题,关键是指出两条对称轴“反射镜面”(如图2).两条线段差的最大值问题,一般根据三角形的两边之差小于第三边,当三点共线时,两条线段差的最大值就是第三边的长.如图3,P A 与PB 的差的最大值就是AB ,此时点P 在AB 的延长线上,即P ′.解决线段和差的最值问题,有时候求函数的最值更方便,本讲不涉及函数最值问题.图1 图2 图31.如图,在锐角ABC △中,45AB BAC =∠=°,BAC ∠的平分线交BC 于点分别是AD 和AB 上的动点,则BM MN +的最小值是D M N,、___________ .2.如图,菱形ABCD 的两条对角线分别长6和8,点P 是对角线AC 上的一个动点,点M 、N分别是边AB 、BC 的中点,则PM +PN 的最小值是_____________.3、如图,已知正方形ABCD 的边长为8,F 是DA 上一点,且FA=2,点P 是BD 上一动点,则 AP+PF 的最小值为 .4、如图所示,正方形ABCD 的面积为12,△ABE 是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P ,使PD+PE 的和最小,则其最小值为A B C D N M (第1题第2题图 D A B C P M N5.如图,菱形ABCD中,AB=2,∠A=120°,点P、Q、K分别为线段BC、CD、BD上的任意一点,求PK+QK的最小值.6.如图,菱形ABCD中,∠A=60°,AB=3,⊙A、⊙B的半径分别为2和1,P、E、F分别是边CD、⊙B和⊙A上的动点,求PE+PF的最小值.7.如图,在平行四边形ABCD中,∠BCD=30°,BC=4,CD=3,M是AD边的中点,N 是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C 长度的最小值是.8.如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,将△EBF 沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的小值是()A.B.6 C.D.49.如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C. 则A′C长度的最小值是 .10.如图,矩形ABCD中,AB=2,BC=3,以A为圆心,1为半径画圆,E是⊙A上一动点,P 是BC上的一动点,则PE+PD的最小值是.11.如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为____12.如图,已知A(0, 2)、B(6, 4)、E(a, 0)、F(a+1, 0),求a为何值时,四边形ABEF周长最小?请说明理由.13.如图,△ABC中,∠ACB=90°,AC=2,BC=1.点A、C分别在x轴和y轴的正半轴上,当点A在x轴上运动时,点C也随之在y轴上运动.在整个运动过程中,求点B到原点的最大距离.14.如图,已知A(-2,0)、B(4, 0)、(D .设F为线段BD上一点(不含端点),连结AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止.当点F的坐标是多少时,点M在整个运动过程中用时最少?15.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.点E是BC边上的点,连结AE,过点E作AE的垂线交AB边于点F,求AF的最小值.16.如图,抛物线21442y x x =-+与y 轴交于点A ,B 是OA 的中点.一个动点G 从点B 出发,先经过x 轴上的点M ,再经过抛物线对称轴上的点N ,然后返回到点A .如果动点G 走过的路程最短,请找出点M 、N 的位置,并求最短路程.如图,在△ABC 中,∠ABC =90°,AB =6,BC =8,O 为17.的中点,过O 作OE ⊥OF ,OE ,OF 分别交射线AB ,AC于E ,F ,连接EF ,则EF 长度的最小值为_______. BC18.如图,在Rt AOB ∆中,OA OB ==,⊙O 的半径为1,点P 是AB 边上的动点,过点P 作⊙O 的一条切线PQ (点Q 为切点),则切线长PQ 的最小值为 .19、在三角形ABC 中,AB=AC=2,∠ABC=30°,点M,N 分别在边AB,AC 上,将三角形AMN 沿MN 翻折,点A 落到点A ’处,则线段BA ’长度的最小值是AMA'N BCO F EA20.如图,线段AB的长为2,C为AB上一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCE,那么DE长的最小值是.。
求两条线段和的最大值的方法1. 开篇引子嘿,朋友们,今天我们来聊聊一个有趣的话题——两条线段的和,听起来是不是有点像数学课上那些枯燥的理论?但是,等等,别急着翻白眼哦!其实,这个话题不仅让人思考,还可以应用在我们的生活中,真的是“千条线,万条线,还是得看咋连”嘛!就像咱们日常生活中的那些选择,选择怎么做才能得到最好的结果。
这可真是个值得思考的问题,说不定你也能从中找到一些启发!2. 理论基础2.1 线段的定义首先,咱们得明白“线段”到底是什么东西。
想象一下,两根绳子,头一头系着你最爱的小猫,另一头则是你的好朋友,兄弟齐心,其利断金,怎么拉都不会散,是吧?这就是线段的力量。
简单来说,线段就是两点之间的最短距离,但它却有无穷的可能性和变数。
2.2 计算方式那么,我们怎么计算这两条线段的和呢?其实很简单,跟你吃了两个汉堡饱饱的感觉一样,线段的和就是把它们的长度加在一起。
记住这个公式,和=线段1+线段2。
这就跟咱们在超市买东西一样,收银员那张小票上的总价,简简单单!不过,不要小看这几个数字,里面的奥妙可大了去了,值得我们好好琢磨。
3. 最大值的探讨3.1 选择的智慧接下来,我们来聊聊如何让这两条线段的和达到最大值。
选择,可以说是人生的一个大课题。
比如,你去自助餐厅,总是得先看一下菜品,再决定自己要哪几个,才能让你的美食之旅达到峰值嘛。
为了最大化线段的和,你要从可选的线段里面做出最佳选择。
3.2 实际应用就拿实际生活来举个例子吧!想象你准备去海边度假,选了两条随机的沙滩椅。
你当然希望这两条椅子之间的间距适中,既不太远让你觉得孤独,也不太近让你觉得尴尬。
就跟人生的“黄金比例”一样,适中最为可贵!如果时间允许,可以对不同的线段长度进行试探,比如说,走一走看看,直到你找到那条让你“哇哦”的完美组合。
4. 实践中的小秘诀4.1 直觉与经验再告诉你个小秘诀,很多时候,我们的直觉和经验能帮我们达到意想不到的效果。
比如说,作为老法师的我,虽然我不是什么数学天才,但我在遇到类似的线段和问题时,总是先大致估算一下,然后用最简单的方法去算一算。
浅谈初中数学线段之和最值问题近年来,在全国各地出现的中考试题的平面几何最值问题中,呈现出变化多、涉及面广、形式灵活的景象,对学生来讲是个难点;如果深入思考,可以发现:这类试题的命制都是立足于教材,解决途径都是运用转化的思想“化折为直”。
本文中,笔者根据近几年的中考试题,结合浙教版教材和自己的教学体会,谈谈初中数学中求线段之和最值的求解策略。
1.直接应用定(公)理求最值平面几何解决最短线路问题时常用的公理(定理):①两点之间线段最短.②三角形的两边之和大于第三边, 两边之差小于第三边(②是由①得出);③直线外一点到直线的所有线段中垂线段最短.1.1应用两点之间线段最短教材链接:七上7.3线段的长短作业题: 如图,A 、B 、C 、D 表示4个村庄.村民们准备合打一口水井,(1)略(2)你能给出一中使水井到各村庄的距离之和最小的方案吗?若能,请标出水井的位置,并说明理由. 解题分析: 教材作业题中,因点D 与点B 、点A 与点C 是定点,当水井打在AC 与BD 的交点时,水井到各村庄的距离之和最小,直接利用“两点之间线段最短”的原理。
中考链接:(2009山东潍坊)已知边长为a 的正三角形ABC(一象限),两顶点A,B 分别在平面直角坐标系的x 轴,y 轴的正半轴上滑动,点C 在第一象限,连接OC,求OC 的长的最大值.解题分析:潍坊的这一试题对教材进行了拓展:点C 为动点,直接相联不可能解决,但因为直角三角形斜边上的中线长和等边三角形边上的中线也是定值,所以设AB 中点为P ,在一般情况下OP+PC >OC ,当O 、P 、C 三点一线时OC=OP+PC 最大.求解策略:教材的模型是在两定点之间求最小值,根据“两点之间线段最短”,只要把两定点直接相连,对无法或较难量化的两点间距离则可以利用几何图形的性质转化为“折线和”,再利用三角形三边关系或两点间线段最短可得出最值.1.2应用垂线段最短教材链接:七上7.7相交线(2)作业题如图,直线l 表示一段河道,点A 表示集镇,图上距离与实际距离之比为1︰2000 000.现要从河l 向集镇A 引水,问沿怎样的路线开挖水渠,才能使水渠的长度最短?……解题分析:教材作业题解决思路是过点A 向垂直于水渠的方向开挖水渠,水渠长最短. 直接利用“直线外一点到直线的所有线中垂线段最短”的原理.试题链接:2010台湾如图,△ABC 中,有一点P 在AC 上移动.若AB=AC=5,BC=6,則AP +BP +CP的最小值为何?(A) 8 (B) 8.8 (C) 9.8 (D) 10解题分析:台湾此题AP +PC=AC 为定值5,从而三线段和转化为求BP 最小值,因为B 为定点,P 为AC 上一动点,所以BP 最小值就是定点B 到AC 的垂线段.求解策略:教材的模型是已知一定点和一定直线求最小值.解答此类试题只要透过问题找到本质,剔ACDA B C P除一些不变的线段(和)转化为一定点到一定直线的距离,再利用“直线外一点到直线的所有线中垂线段最短” 即可得出最小值.在平面几何求最值这类问题中,应用轴对称变换、平移变换和旋转变换这三种图形变换及性质,可以将那些分散、远离的条件转移到适当的位置上,得以相对集中后,再应用上述定(公)理,便可迎刃而解.2.结合图形变换求最值2. 1应用轴对称变换把直线同侧的线段和转化为异侧线段之和 2.1.1一定直线+两定点+一动点教材链接:浙教版科学七下1.5光的反射和折射 基本模型1:(将军饮马问题)白日登山望烽火,黄昏饮马傍交河。
诗中隐含着一个有趣的数学问题:诗中将军在观望烽火之后从山脚上的A 点出发,奔向交河旁边的P 点饮马,饮马后再到B 点宿营,试问怎样走,才能使总的路程最短?如图,在定直线l 同侧有两个定点A 、B,在定直线l 上有一动点P ,请找到使PA+PB 最短的点P 位置. 思路分析:如图2作A 关于直线l 的对称点'A ,连接'A B 交l 于p ,则p 点即为所求使AP+BP 为最短的距离(此题过B 作关于l 的对称点'B 也可,方法都是一样的.中考链接: 2010湖北鄂州市如图所示,四边形OABC 为正方形,边长为6,点C 、A 分别在x 轴,y 轴的正半轴上,点D 在OA 上,且D 点的坐标为)0,2(,P 是OB 上的一动点,试求PA PD +和的最小值是 A .102 B. 10 C. 4 D. 6解题分析:由已知得点P 为定直线OB 上的动点,点D 和点A 为两个定点,符合模型;用正方形的轴对称性可知点A 关于OB 的对称点就是点C,因此PA PD +和的最小值就是PC PD +的最小值,而点A和点C 都是定点,根据“两点之间线段最短”可得DC 即为所求.求解策略:此类试题往往把背景变换成角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等,但都有一个 “轴对称性”的图形共同点,解题时只要从变换的背景中提取“一定直线+两定点+一动点”的数学模型,再通过找定直线的对称点把同侧线段和转化为异侧线段和,利用“两点间线段最短”,实现“折”转“直”即可解决.若设问是求三角形周长或四边形周长最值,则必含有定长线段,依然可以转化为两线段和的最值.2.1.2两定直线+一定点+一动点基本模型2:如图1,已知两定直线a 和l ,其中在定直线l 上有一个定点A,在定直线a 上有一动点P ,请找到使PA 和点P 到直线l 距离之和的最小值的点P 位置.思路分析:如图2作A关于直线a 的对称点'A ,过'A 作'A H 垂直l 于点H ,则p 点即为所求使AP 和P 到直线l 距离和为最短的点.中考链接:2009绍兴定义一种变换:平移抛物线1F 得到抛物线2F ,使2F 经过1F 的顶点A .设2F 的对称轴分别交21F ,F y O D A x PB C于点B ,D ,点C 是点A 关于直线BD 的对称点.(1)、(2)略(3)如图3,若1F :3732312+-=x xy ,经过变换后,32=AC ,点P 是直线AC 上的动点,求点P 到点D 的距离和到直线AD 的距离之和的最小值.解题分析: 容易证得菱形ABCD ,由菱形对称性可知PB PD =.如图1,作AD PH ⊥交AD 于点H , 则PH PB PH PD +=+. 要使PH PD +最小, 只要使PH PB +最小,此最小值是点B 到AD 的距离, 即ABD ∆边AD 上的高h .(∵1=DN ,3=AN ,AC DB ⊥,∴︒=∠30DAN ,故ABD ∆是等边三角形. ∴323==AD h ∴ 最小值为3. (C 在点A 的右侧和左侧同理).求解策略:解决此类题的关键是在轴对称背景中提取模型条件,通过找定直线的对称点把同侧线段和转化为异侧线段和,利用“点到直线垂线段最短”,实现“折”转“直”时,最小值就得到。
2.1.2两定直线+一定点+两动点基本模型3:如图,已知∠AOB=45°,其中有一定点P ,在AO,BO 的边上有两动点MN ,是否存在点MN ,使得△PMN 的周长最小o A B PMNoABPMNP 1P 2解题分析:要求△PMN 周长的最小值,其实就是求PM+PN+MN 的最小值,根据基本模型2,作P 关于OA 的对称点P 1,作P 关于OB 的对称点P 2,连接P 1 P 2交OA,OB 于点M,N ,则PM+PN+MN 最小,即△PMN 的周长最小。
2. 2.应用平移变换将无交点的两线段之和转化为“将军饮马问题” 中的两线段之和 教材链接:浙教版七下2.6图形变换的简单应用作业题:B DC A PO y x F 1F 2 (第24题图3)B D C O y x F 1A P 图2 N BD C Oy x F 1F 2 A P 图1 HN“要在一条河上架一座桥(桥通常与河岸垂直),小聪小明小慧分别提供了一种方案,哪一种方案能使从A 地到B 地的路程最短?请说明理由.” (建桥问题)思路分析:小明的方案能使从A 到B 地的路程最短.方法是:将B 点向下平移到M ,使B M 的长等于桥长;连结A 、M 交b 于点D,过点D 作a 的垂线,交a 于点C,则CD 是桥所在的位置.基本模型4;两定点+一定直线+同侧两定点如图1,已知两定点A 、B 和定直线L ,其中在定直线上有两个定距离的动点A,B 请在直线L 上找到使AC+BD 值最小的点C 和点D 的位置.思路分析:如图2,作点B 的对称点'B ,过点A 作'AA ∥L,且'AA =CD,连结'B A ‘与直线L 交点即为所求的点D 位置,点C 位置随之也就确定. 该模型是教材的变式。
中考链接: 2010天津:在平面直角坐标系中,矩形OACB 的顶点O 在坐标原点,顶点A 、B 分别在x 轴、y 轴的正半轴上,3=OA ,4=OB ,D 为边OB 的中点.(Ⅰ)略(Ⅱ)若E 、F 为边OA 上的两个动点,且2=EF ,当四边形CDEF 的周长最小时,求点E 、F 的坐标.解题思路: 如图,由于CD 和EF 是两定长线段,因此,四边形CDEF 的周长最小值其实就是DE+CF 的最小值.作点D 关于x 轴的对称点D ',在CB 边上截取2=CG ,连接D G '与x 轴交于点E ,在EA 上截取2EF =.∵ GC ∥EF ,GC EF =,∴ 四边形GEFC 为平行四边形,有CF GE =.又 DC 、EF 的长为定值,∴ 此时得到的点E 、F 使四边形CDEF 的周长最小.∵ 由 Rt OE D '∆∽Rt BG D '∆,可得31=OE .∴ 37231=+=+=EF OE OF .∴ 点E 的坐标为(31,0),点F 的坐标为(37,0).天津试题是模型的变式,区别在于把定直线异侧不“聚头”的两线段变化成定直线同侧不“聚头”的两线段.解决过程中多了一次轴对称变换.求解策略:此类题是求定直线同侧未连接两线段和的最小值,首先需要用轴对称变换转化成“建桥问题”模型后,再用平移变换将未连接的两线段在定直线上“聚头”,等量转化为折线,利用“两点间线段最短”,实现“折”转“直”找到其中一个点的位置,另一点位置也随之找到.2.3应用旋转变换将交于同一点的三线段之和改变位置等量转化为两定点间的折线之和 教材链接:浙教版八下课本第82页:你听说过费马点吗?……费马点有许多有趣并且有意义的性质……把你的探究结果写成一篇小论文,并通过与同学交流来修改完善你的小论文.中考链接: 2010福建宁德如图,四边形ABCD 是正方形,△ABE 是等边三角形,M 为对角线BD (不含B 点)上任意一点,将BM 绕点B 逆时针旋转60°得到BN ,连接EN 、AM 、CM.⑴略⑵ ①略②当M 点在何处时,AM +BM +CM 的值最小,并说明理由;⑶ 略解题分析:根据旋转变换的性质可得:EN=AM,△BNM 为等边三角形推的MN=BN,此时AM +BM +CM 的最小值转化为求“三折线”EN+NM+MC 的最小值.根据“两点之间线段最短” EN+NM+MC 等于CE 时最小.所以,当M 位于BD 与CE 交点时,AM +BM +CM 的值最小,即等于EC 的长.求解策略:此类试题的模型是:三条聚在一起的线段,求线段和的最小值;解决策略是利用旋转变换,把如图1所求的“相聚于同一点的三条线段”转化为如图2“两定点间的三折线”;根据“两点之间线段最短”可知两定点的连线长即为所求的线段和最小值.中考试题依托的是教材.试题命制往往有从教材中提取模型、类比模型、变式模型三类.作为教师,不管在平时教学还是在中考复习中,应立足教材,深挖教材,拓展例、习题及重视学生的探究;作为学生,解题不在多,真正掌握方法就行!所以,找到变幻万千的试题背后最本质的原理或模型,才能发展思维,提升能力;因此,重视解题后的反思及整理才是学习之根本.EA BN M。