完美版河北工程大学土木施工2013-2012学年线代试卷--科信(A)

A 卷 第 1 页 共 5 页昆明理工大学考试试卷参考答案及评分标准（ 2012 / 2013 学年 上 学期）工程力学B （ A 卷）专业年级： 出题教师签名一. 是非题 （每题2分，共10分。

正确用√，错误用×，填入括号内。

） 1 ×；2 ×；3 √；4 ×；5 √二. 填空题 (每空1分，共15分。

请将简要答案填入划线内。

)1. 抵抗破坏的能力；抵抗变形的能力；保持原有平衡形态的能力；2. 弹性阶段；屈服阶段；硬化阶段；缩颈阶段；3. 伸长率；断面收缩率；4. 4个；=0,=0A A ωθ；C C =,=c c ωωθθ右右左左；5. 点面对应；转向一致；夹角两倍。

三. 选择题 （每题3分，共15分。

请将答案的序号填入划线内。

） 1 B； 2 C； 3 A； 4 C ； 5 DA 卷 第 2 页 共 5 页四、画受力图（本题10分）（1）整体受力图（3分） （2）吊车（2分）（3）AC 杆（3分） (4)CD 杆（2分）五. 计算题（本题10分）（1）以圆球、AB 杆为研究对象画受力图。

（4分）（2）列平衡方程。

（4分）圆球：'10:cos 600Y N P =-=∑AB 杆：10:cos30-0Ax B X FN T =+=∑ 10:-sin 300Ay Y FN ==∑ 10:-/2cos300A B M N l T l =⨯+⨯⨯=∑（3）求解。

（2分）=-3AX F ；=Ay F P；=3B TA 卷 第 3 页 共 5 页答案：（1）画轴力图（4）；F N1 = -100 kN ，F N2 = -260 kN（2）计算横截面应力（4分）311-1-10010==-2.50.20.2N F MPa A σ⨯=⨯； 322-2-26010==-6.50.20.2N F MPa Aσ⨯=⨯ （3）计算A 点相对于C 点位移（2分） 3-51910010 1.5===3.7510100100.20.2N AC AC F l l m EA⨯⨯∆⨯⨯⨯⨯A 卷 第 4 页 共 5 页答案：（1）画扭矩图（4分）；T 图：max T =-14 kN.m（2）计算切应力（7分）： E 点：3414100.0228.50.132E PT MPa I ρτπ⨯⨯===⨯ 最大切应力：3max max 3141071.30.116tT MPa W τπ⨯===⨯ 所以max τ=71.3MPa ，发生在横截面的边缘处。

内蒙古电力通讯职业技术学校2012-2013学年度第二学期《电工仪表与测量》期末考试试卷（A）考试时间90分钟，满分100分姓名班级评卷人石春丹一、填空题（每题1分共40分）1、磁电系测量机构中游丝的作用有两个：一是二是。

2、电工指示仪表按工作原理分类，主要分为系仪表、系仪表、仪表和系仪表四大类。

3．磁电系电流表由与两者组成。

4电工测量的对象主要指、、、电能、电功率、频率，电感、电容等。

5．电压互感器二次侧的额定电压规定为V，电流互感器二次侧的额定电流规定为A。

6．分流电阻一般采用电阻率较，电阻温度系数很的制成。

7、根据误差产生原因不同电测量指示仪表分为误差和误差，误差大小可以用绝对误差、相对误差和三种形式表示。

8、普通单相功率表有三个量程，它们是、、。

9、使功率表正向偏转的流入端称为功率表“发电机端”，接线时应将“发电机端”接至使得电流方向对于一致。

10、万用表由表头、转换开关组成。

11、兆欧表必须水平放置于的地方，以免在摇动时因抖动忽然倾斜产生测量误差。

12、摇动手柄的转速要均匀，一般规定为转／分钟，允许有20%的变化选择13、工程中，通常将电阻按阻值大小分为电阻、电阻、电阻。

按获取测量结果的方式来分类，测量电阻的方法有、和类。

14．接地的目的是为了保证和的安全以及，如果接地电阻不符合要求，不但，而且会造成严重的。

15、单相功率变送器由电压互感器、、磁饱和方波振荡器、和板式开关电路等构成。

二、选择题（每题2分共30分）1．直流电压表的分压电阻必须与其测量机构。

A，断开B．串联C．并联D．短路2．磁电系检流计常用来。

A．判定电流的有无B．测量电流的大小C．精密测量电流的大D．精密测量电压的大小4．钳形电流表的优点是。

A．准确度高B．灵敏度高 C.可以交、直流两用D．可以不切断电路测电流5．伏安法测电阻属于。

A．直接法B．间接法C．前接法D．比较法6．用直流单臂电桥测量一估算值为几欧的电阻时，比例臂应选。

试卷代号：1129（1884）中央广播电视大学2011—2012学年度第一学期“开放本科”期末考试(半开卷)土木工程力学（本）试题2012年1月一、单项选择题（每小题3分，共30分）在所列备选项中，选一项正确的或最好的作为答案，将选项号填入各题的括号A. 质点的质量B. 自振频率C. 振幅D. 干扰力的大小6. 用力矩分配法计算超静定结构时，刚结点的不平衡力矩等于（ B ）。

A. 外力矩B.附加刚臂中的约束反力矩C.杆端固端弯矩D.杆端的传递弯矩7. 影响线的纵坐标是（ D ）。

A. 固定荷载的数值B. 移动荷载的数值C.不同截面的某一量值D.指定截面的某一量值8. 受弯杆件截面内力有（ D ）。

A. 弯矩B.剪力3））15. 图(a)对称结构受对称荷载作用，利用对称性可简化为图(b) 来计算。

（√）16. 结构的自振频率与干扰力无关。

（√）17. 位移法的基本结构不是唯一的。

（×）18. 由于支座位移超静定结构产生的内力与刚度的绝对值有关。

（√）19. 实际桁架结构的杆件只有轴力产生。

（ × ）20. 结构的自振频率与结构中某杆件的刚度有关。

（√ ）三、（10分）21.作图示静定结构的弯矩图。

四、（16分）)1.（A ．0,0,0==≠N Q F F MB ．0,0,0=≠=N Q F F M 0,0,0≠==N Q F F MD ．0,0,0===N Q F F M2.机动法作静定梁弯矩影响线应用的原理是( C )。

A.变形体虚功原理B.叠加原理C.刚体虚功原理D.互等原理3．结构不考虑阻尼时的自振频率为ω，考虑阻尼时的自振频率为D ω，则( C )478．用位移法求解图示结构时，基本未知量的个数是（ B ）。

A ．2B ．3C ．4D ．59．简支梁A 支座竖向反力yA F 影响线纵坐标k y 的物理意义是 ( D )。

A ．A 支座竖向反力B ．P=1在截面K 的位置C ．P=1在截面A 的位置D ．A 、B 同时满足10．力法典型方程中的系数项∆表示基本结构在( A )。

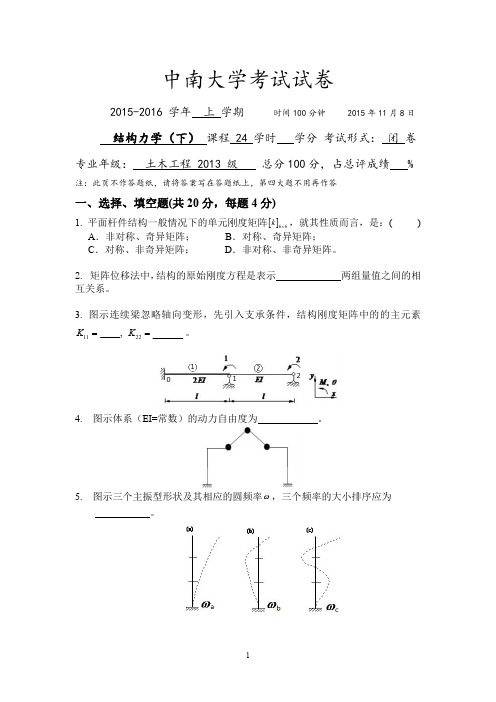
中南大学考试试卷2015-2016学年上学期时间100分钟2015年11月8日结构力学（下）课程24学时学分考试形式：闭卷专业年级：土木工程2013级总分100分，占总评成绩%注：此页不作答题纸，请将答案写在答题纸上，第四大题不用再作答一、选择、填空题(共20分，每题4分)1.平面杆件结构一般情况下的单元刚度矩阵[]k66⨯，就其性质而言，是：() A．非对称、奇异矩阵；B．对称、奇异矩阵；C．对称、非奇异矩阵；D．非对称、非奇异矩阵。

2.矩阵位移法中，结构的原始刚度方程是表示两组量值之间的相互关系。

3.图示连续梁忽略轴向变形，先引入支承条件，结构刚度矩阵中的的主元素11____,K=22K=。

4.图示体系（EI=常数）的动力自由度为。

5.图示三个主振型形状及其相应的圆频率ω，三个频率的大小排序应为。

二、计算题（共50分）1.计算图示结构(a)和(b)两种离散方式的最大带宽，并对图（a ）以单刚的子块形式写出原始刚度矩阵中的子块[12K ]、[66K ]、[78K ]。

（8分）（a ）（b ）2.图示平面结构用矩阵位移法计算，求结点2和结点3的综合结点荷载列阵。

（10分）3.求图示结构的自振频率，略去杆件自重和阻尼的影响。

（8分）4.求图示体系的自振频率和主振型。

已知：m m m 12==。

EI =常数。

（12分）提示：两自由度结构自由振动振幅方程为：2111112222211122221()01()0m A m A m A m A δδωδδω⎧-+=⎪⎨+-=⎪⎩5.图示体系52210EI kN m =⨯⋅,120S θ-=,20W kN =,10P kN =。

求质点处最大位移和最大弯矩。

（12分）三、根据电算结果作弯矩图（共10分）某刚梁，结构离散情况如下图所示，已利用PF 程序求出计算结果，根据计算结果作出其弯矩图M （单位：kN .m ）。

（各单元始端i <末端j ；E ，I 取为常数1，A 取为13e ）The Terminal ForcesmemberN F (first)S F (first)M(first)N F (end)S F (end)M(end)1-8.313-9.551-12.7968.31319.551-45.40728.31340.634-10.036-8.31379.366-67.426360.185-16.626-44.557-60.18516.626-21.946四、上机题（20分，此题不用再作）1．作图示刚架的M、F、N F图，已知各杆截面均为矩形，柱截面宽S0.5m,高0.5m,梁截面宽0.4m,高0.5m，各杆E=3.65×104MPa。

东 北 大 学秦 皇 岛 分 校课程名称： 工程力学 试卷： (A ) 考试形式： 闭卷 授课专业： 相关专业 考试日期：2013年12 月31日 试卷：共3页题号 一 二 三 四 五 六 七 八 总分得分 阅卷人一、选择题：（每题3分，共30分） [1] 二力平衡公理适用于（ ）。

A 、任何物体B 、固体C 、弹性体D 、刚体 [2] 某平面任意力系向O 点简化，得到如图所示的一个力F 和一个力偶矩为M 的力偶，则该力系的最后合成结果为 ( ) A 、作用在O 点的一个合力； B 、合力偶；C 、作用在O 点上边某点的一个合力；D 、作用在O 点下边某点的一个合力。

[3] 其他条件不变时，如果轴向拉伸杆件的长度增大一倍，那么横截面的正应力将 ( )A 、增大B 、减少C 、不变D 、以上都不对 [4] 两根材料和柔度都相同的压杆（ ）A 、临界应力一定相等，临界压力不一定相等；B 、临界应力不一定相等，临界压力一定相等C 、临界应力和临界压力不一定相等D 、临界应力和临界压力一定相等[5] 铸铁试件扭转破坏是 ( )A 、沿横截面拉断B 、沿横截面剪断C 、沿45螺旋面拉断D 、沿45螺旋面剪断[6] 低碳钢材料发生弯扭组合变形，对其进行强度计算时，应该采用（ ）A 、第一或第二强度理论B 、第二或第三强度理论C 、第一或第四强度理论D 、第三或第四强度理论[7] 某瞬时平面图形上任意两点A 、B 的速度分别为A υ和B υ。

则此时该两点连线中点C 的速度为 ( )A 、B AC υυυ+= B 、)(21B AC υυυ+=C 、)(21B A C υυυ-=D 、)(21A B C υυυ-=[8] 简支梁上作用均布载荷q 和集中力偶M 0，当M 0在梁上任意移动时，梁的 ( )。

A 、Q(剪力图)，M （弯矩）图都变化 B 、Q ，M 图都不变化 C 、Q 图不变，M 图变化 D 、Q 图变化，M图不变[9] 支撑情况不同的圆截面细长杆，各杆直径和材料相同，临界应力最大的是（ ）A 、杆AB 、杆BC 、杆CD 、以上都不对装订线装 订 线 内 不 要 答 题学 号姓 名班 级MOF5m7m9mABCFFF[10]为使全梁不出现正弯矩，则m ≥____________。

中国矿业大学2012～2013学年第 1 学期《矿井通风与安全》试卷（A ）卷考试时间：100 分钟 考试方式：闭卷一、名词解释（每题3分，共24分）1、空气的相对湿度；2、通风机工况点3、等积孔；4、均压防灭火；5、输送倍线；6、自然发火期；7、呼吸性粉尘；8、高瓦斯矿井； 二、简述题（每题8分，共32分）9、矿井通风风量的调节方法有哪几种？简述降阻调节的主要措施有哪些?10、请简述如何计算掘进工作面的配风量？ 11、煤尘爆炸的条件是什么？ 12、试述煤炭自燃的充要条件？ 三、计算题（共34分） 13．如图1，用皮托管和压差计测得A 、B 两风筒的压力分别为h 1＝-600，h 2＝100，h 4=700，h 5＝100 Pa 。

求h 3、h 6的压力各为多少？各压差计测得的是什么压力？（8分）图114．如图2所示的并联风网，已知各分支风阻：R1＝1.10，R2＝0.57 N·s2/m8，总风量Q＝40 m3/s，巷道面积S1＝6 m2，S2＝8 m2，求：（1）分支1和2中的自然分配风量Q1和Q2；（2）若分支1需风量为10 m3/s，分支2需风量为30 m3/s，采用风窗调节，风窗应设置在哪个分支？风窗风阻和开口面积为多少？（8分）图215. 在下图中1是扇风机的个体风压曲线，2是夏天反向的自然风压与1串联后的联合风压曲线，4是冬天的正向自然风压与1串联后的联合风压曲线，3是矿井的风阻曲线，试标注出夏天与冬天扇风机的实际工况点？(8分)16.如下图所示的通风网络，已知各巷道的阻力h1＝80，h2＝100，h3＝30，h5＝140，h6=100Pa，求巷道4、7、8的阻力及巷道4、7、8的风流方向。

（8分）17、什么是煤与瓦斯突出，论述突出发生的一般规律？中国矿业大学2012～2013学年第 1 学期《矿井通风与安全》试卷（A）卷答案考试时间：100 分钟考试方式：闭卷一、名词解释1、空气的相对湿度；表示。

2012～2013 学年度第 一 学期《高等数学(理工)A1》试卷（ A 卷）适用年级专业：2012级材料科学与工程、材料成型与控制工程、冶金工程、机械设计制造及其自动化、工业工程、工业设计、电气工程与自动化、电子信息工程、自动化、测控技术与仪器、化学工程与工艺、环境工程、生物工程、土木工程 考 试 形 式：（ ）开卷、（ V ）闭卷二级学院： 行政班级： 学 号： 教 学 班： 任课教师： 姓 名： 注：学生在答题前，请将以上内容完整、准确填写，填写不清者，成绩不计。

一、单项选择题.（每小题 3分，共 15 分）1、设函数()ln(1)f x x x =-，2()tan g x arc x =-,则0x →时，()f x 是()g x 的（ ）.A.等价无穷小B.同阶但非等价无穷小C.高阶无穷小D.低阶无穷小 2. 若1lim ()2x f x +→=，以下结论正确的是（ ）.A.函数在1x =处有定义，且(1)2f =B. 函数在1x =处某去心领域内有定义C.函数在1x =处左侧某领域内有定义D. 函数在1x =处右侧某领域内有定义 3.数列{}n x 收敛是它的子数列{}kn x 收敛的（ ）.A.充要条件B.充分非必要条件C.必要非充分条件D.既非充分又非必要 4.设函数ln(3)()(1)x t dt f x x x +=-⎰，则0x =是()f x 的（ ）．A.无法确定B.无穷间断点C. 可去间断点D.跳跃间断点 5.下列说法正确的是（ ）.A.若0x x =是()f x 的极值点，则0()0f x '= B.若0()0f x '=，则若0x x =是()f x 的极值点C.若()0f x ''=，则0x x =是函数()f x 的拐点D.以上说法都不正确.二、填空题.（每题 3 分，共 15分）1. 211dxx+∞-∞+⎰＝ .……………………………………………线………………………………………订………………………………………装………………2.设函数,0()21,0ax e x f x x x ⎧>=⎨+≤⎩，()f x 在点0x =可导，则a =3. 函数2()23f x x x =--在区间[1,3]-上满足罗尔定理条件的ξ的值是__________.4.曲线2ln y x x =+在1x =处的切线方程为 ．14ln(x dxx += ．.（每题 5分，共15分）1. 2lim 1sin cos x x xx x→-+-. 2. 202(e )lim sin xtx dt x x→⎰．3. 1sin 0lim (12)xx x →-.四、求下列函数的导数或微分.（每题 5分，共 15分）1．设arcsin ln 5ln(sec tan )x e y x x +++=+，求dy ．2.函数()=y f x 由方程yxx y =所确定的隐函数，求d d y x.3.设ln(1)arctan x t y t t=+⎧⎨=-⎩,求22d d y x.五、求下列不定积分和定积分.（每题6分，共18分）1. ⎰.2. sinx xdx ⎰3.. 222(1)xdx x +⎰六、求函数3(1)(1)y x x =-+的单调区间,并求极值．（8分）七、求由曲线y y x==所围成的图形的面积，并求其围成的平面图形绕x 轴旋转一周所成的旋转体的体积. （8 分）八、设()f x 在[]0,1上连续，在()0,1内可导，且(1)0f =，证明：在()0,1内至少存在一ξ，使3()()0f f ξξξ'+=．（6分）。