一种BP神经网络气象预测中的应用研究

人工神经网络在青草沙水库库外潮位预测中的应用研究作者：程诚祝一欣王静雅来源：《科协论坛·下半月》2013年第12期摘要：介绍利用Matlab神经网络工具箱，通过各类网络参数的整定，设计出能够准确预测青草沙水库库外潮位变化的BP神经网络。

计算结果表明，设计的BP神经网络模型能够准确地预测出潮位的变化情况，有着良好的精度及泛化能力。

关键词：人工神经网络青草沙潮位预测中图分类号：TV675 文献标识码：A 文章编号：1007-3973（2013）012-035-02青草沙水库是我国最大的河口江心水库，相比黄浦江上游、陈行水库及东风西沙水源地，青草沙水库有着库容大（有效库容达4.35亿立方米）、供水量大（设计供水规模719万立方米/日）、水质好（总体水质达到地表水Ⅱ类标准），在水库蓄满时，可在不取水的情况下连续供应68天。

若能够提前预知库外潮位变化情况，水库管理者就能准确制定每日的闸门运行调度计划，使水库总体蓄水量始终保持在合理的范围内，确保1300万上海市民的饮用水安全。

针对这一情况，本文提出了一种利用BP神经网络的方法对青草沙库外潮位进行分析和预测的方法。

1 BP神经网络基本原理BP（Back Propagation）网络是1986年由Rumelhart和McCelland为首的科学家小组提出，是一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。

典型的含有一个隐含层的BP网络模型，在模型的运行过程中，经过反复学习训练，确定与最小误差相对应的网络参数（权值和阈值），训练即告停止。

此时经过训练的神经网络即能对类似样本的输入信息，自行处理输出误差最小的经过非线形转换的信息。

具体算法如下：第一步：初始化，赋给Wij和Wjk各一个较小的随机非零值。

第三步：计算样本的误差项对所有样本重复第二步和第三步。

第四步：按权值修正公式修改权值第五步：按新的权值计算输出Yk，考察误差是否达到规定的要求。

LSTM神经网络在气象数据时间序列预测中的应用气象数据的时间序列预测一直是气象学领域的重要研究方向。

随着人工智能技术的快速发展，深度学习模型被广泛应用于气象数据的预测和分析。

其中，LSTM（Long Short-Term Memory）神经网络作为一种特殊的循环神经网络模型，在气象数据时间序列预测中展现出了强大的能力。

LSTM神经网络是一种具有记忆单元和门控机制的循环神经网络模型。

相较于传统的循环神经网络，LSTM能够更好地解决长期依赖问题，具有较强的记忆能力。

这使得它在处理时间序列数据时具有优势。

在气象学中，时间序列数据通常包含多个变量，如温度、湿度、风速等。

这些变量之间存在复杂而非线性的关系，在传统方法中很难进行准确预测。

而LSTM神经网络通过其强大的非线性建模能力，可以更好地捕捉这些变量之间复杂关系，并进行准确预测。

首先，在应用LSTM神经网络进行气象数据时间序列预测之前，需要对数据进行预处理和特征提取。

这包括数据清洗、缺失值处理、数据平滑等步骤。

同时，还需要对时间序列数据进行特征提取，如滑动窗口法、傅里叶变换等方法，以便将其转化为适合LSTM模型输入的格式。

其次，在构建LSTM模型时，需要确定模型的结构和参数。

LSTM模型包含输入层、隐藏层和输出层。

隐藏层中的记忆单元和门控机制是LSTM的核心组成部分。

通过调整隐藏层数量、记忆单元个数以及门控机制参数等，可以优化模型性能。

然后，在训练过程中，需要选择适当的损失函数和优化算法来对模型进行训练和更新参数。

常用的损失函数包括均方误差（MSE）、平均绝对误差（MAE）等，常用的优化算法包括梯度下降法、Adam优化算法等。

在训练完成后，可以使用已经训练好的LSTM神经网络对未来气象数据进行预测。

通过将历史时间序列数据输入到已经训练好的模型中，并结合之前学习到的权重和偏置信息，可以得到未来一段时间内气象变量值的预测结果。

除了单一变量的预测，LSTM神经网络还可以用于多变量的联合预测。

bp神经网络的应用综述近年来，人工神经网络（ANN）作为一种神经网络形式在不断发展，因其计算能力强，对现实世界较好地识别和适应能力，已得到越来越广泛的应用，其中，BP神经网络是最典型的人工神经网络之一。

BP神经网络是指以马尔可夫随机过程为基础的反向传播算法，具有自组织学习、泛化、模糊推理的特点，具有非常广泛的应用场景。

它可以用来解决实际问题。

首先，BP神经网络可以用来解决分类问题。

它可以根据给定的输入向量和输出向量，训练模型以分类相关的输入特征。

这种模型可以用来解决工业控制问题、专家系统任务等。

例如，BP神经网络可以用来识别照片中的面孔，帮助改进自动门的判断等。

此外，BP神经网络还可以用于计算机视觉，即以计算机图像识别的形式进行图像处理。

通常，计算机视觉技术需要两个步骤，即识别和分析。

在识别步骤中，BP神经网络可以被用来识别图片中的特征，例如物体的形状、大小、颜色等；在分析步骤中，BP神经网络可以用来分析和判断图片中的特征是否满足要求。

此外，BP神经网络还可以用于机器人技术。

它可以用来识别机器人环境中的物体，从而帮助机器人做出正确的动作。

例如，利用BP神经网络，机器人可以识别障碍物并做出正确的行动。

最后，BP神经网络还可以用于未来的驾驶辅助系统中。

这种系统可以利用各种传感器和摄像机，搜集周围环境的信息，经过BP神经网络分析，判断当前环境的安全程度，及时采取措施，以达到更好的安全驾驶作用。

综上所述，BP神经网络具有自组织学习、泛化、模糊推理的特点，拥有非常广泛的应用场景，可以用于分类问题、计算机视觉、机器人技术和驾驶辅助系统等。

然而，BP神经网络也存在一些问题，例如训练时间长，需要大量的训练数据，容易受到噪声攻击等。

因此，研究人员正在积极改进BP神经网络，使其能够更好地解决各种问题。

第１３卷㊀第９期Ｖｏｌ．１３Ｎｏ．９㊀㊀智㊀能㊀计㊀算㊀机㊀与㊀应㊀用ＩｎｔｅｌｌｉｇｅｎｔＣｏｍｐｕｔｅｒａｎｄＡｐｐｌｉｃａｔｉｏｎｓ㊀㊀２０２３年９月㊀Ｓｅｐ．２０２３㊀㊀㊀㊀㊀㊀文章编号：２０９５－２１６３（２０２３）０９－０１６８－０４中图分类号：Ｓ６２５；ＴＰ１８３文献标志码：Ａ基于ＧＡ－ＢＰ神经网络的温室温度预测研究李其操，董自健（江苏海洋大学电子工程学院，江苏连云港２２２００５）摘㊀要：温度对于温室内作物的生长起着重要的作用，为了更精准的管理和控制温室内的温度，提出了基于遗传算法优化的ＢＰ神经网络预测模型（ＧＡ－ＢＰ），对温室内温度进行预测㊂本文利用遗传算法对ＢＰ神经网络的权值和阈值进行优化，使模型避免出现局部最优，有效改善了传统ＢＰ神经网络预测模型的性能，使预测出的温度更加精准㊂实验证明，选择隐藏层节点数为７时，ＧＡ－ＢＰ神经网络预测模型的预测结果最佳，平均绝对误差（ＭＡＥ）㊁均方误差（ＭＳＥ）和平均绝对百分比误差（ＭＡＰＥ）分别为０．４４１㊁０．２７６㊁０．５２５㊂与传统ＢＰ神经网络预测模型相比分别提升了１３．２％㊁３８．４％㊁２１．５％㊂关键词：遗传算法；ＢＰ神经网络；温室温度；预测模型ＧｒｅｅｎｈｏｕｓｅｔｅｍｐｅｒａｔｕｒｅｐｒｅｄｉｃｔｉｏｎｂａｓｅｄｏｎＧＡ－ＢＰｎｅｕｒａｌｎｅｔｗｏｒｋＬＩＱｉｃａｏ，ＤＯＮＧＺｉｊｉａｎ（ＳｃｈｏｏｌｏｆＥｌｅｃｔｒｏｎｉｃＥｎｇｉｎｅｅｒｉｎｇ，ＪｉａｎｇｓｕＯｃｅａｎＵｎｉｖｅｒｓｉｔｙ，ＬｉａｎｙｕｎｇａｎｇＪｉａｎｇｓｕ２２２００５，Ｃｈｉｎａ）ʌＡｂｓｔｒａｃｔɔＴｅｍｐｅｒａｔｕｒｅｐｌａｙｓａｎｉｍｐｏｒｔａｎｔｒｏｌｅｉｎｔｈｅｇｒｏｗｔｈｏｆｃｒｏｐｓｉｎｔｈｅｇｒｅｅｎｈｏｕｓｅ．Ｉｎｏｒｄｅｒｔｏｍａｎａｇｅａｎｄｃｏｎｔｒｏｌｔｈｅｔｅｍｐｅｒａｔｕｒｅｉｎｔｈｅｇｒｅｅｎｈｏｕｓｅｍｏｒｅａｃｃｕｒａｔｅｌｙ，ａｇｅｎｅｔｉｃａｌｇｏｒｉｔｈｍ－ｏｐｔｉｍｉｚｅｄＢＰｎｅｕｒａｌｎｅｔｗｏｒｋｐｒｅｄｉｃｔｉｏｎｍｏｄｅｌ（ＧＡ－ＢＰ）ｗａｓｐｒｏｐｏｓｅｄｔｏｐｒｅｄｉｃｔｔｈｅｔｅｍｐｅｒａｔｕｒｅｉｎｔｈｅｇｒｅｅｎｈｏｕｓｅ．Ｉｎｔｈｉｓｐａｐｅｒ，ｔｈｅｇｅｎｅｔｉｃａｌｇｏｒｉｔｈｍｉｓｕｓｅｄｔｏｏｐｔｉｍｉｚｅｔｈｅｗｅｉｇｈｔｓａｎｄｔｈｒｅｓｈｏｌｄｓｏｆｔｈｅＢＰｎｅｕｒａｌｎｅｔｗｏｒｋ，ｓｏｔｈａｔｔｈｅｍｏｄｅｌａｖｏｉｄｓｌｏｃａｌｏｐｔｉｍｉｚａｔｉｏｎ，ｅｆｆｅｃｔｉｖｅｌｙｉｍｐｒｏｖｅｓｔｈｅｐｅｒｆｏｒｍａｎｃｅｏｆｔｈｅｔｒａｄｉｔｉｏｎａｌＢＰｎｅｕｒａｌｎｅｔｗｏｒｋｐｒｅｄｉｃｔｉｏｎｍｏｄｅｌ，ａｎｄｍａｋｅｓｔｈｅｐｒｅｄｉｃｔｅｄｔｅｍｐｅｒａｔｕｒｅｍｏｒｅａｃｃｕｒａｔｅ．Ｅｘｐｅｒｉｍｅｎｔｓｓｈｏｗｔｈａｔｗｈｅｎｔｈｅｎｕｍｂｅｒｏｆｈｉｄｄｅｎｌａｙｅｒｎｏｄｅｓｉｓｓｅｌｅｃｔｅｄｔｏｂｅ７，ｔｈｅｐｒｅｄｉｃｔｉｏｎｒｅｓｕｌｔｏｆｔｈｅＧＡ－ＢＰｎｅｕｒａｌｎｅｔｗｏｒｋｐｒｅｄｉｃｔｉｏｎｍｏｄｅｌｉｓｔｈｅｂｅｓｔ，ａｎｄｔｈｅｍｅａｎａｂｓｏｌｕｔｅｅｒｒｏｒ（ＭＡＥ），ｍｅａｎｓｑｕａｒｅｅｒｒｏｒ（ＭＳＥ）ａｎｄｍｅａｎａｂｓｏｌｕｔｅｐｅｒｃｅｎｔａｇｅｅｒｒｏｒ（ＭＡＰＥ）ａｒｅ０．４４１，０．２７６，ａｎｄ０．５２５ｒｅｓｐｅｃｔｉｖｅｌｙ．ＣｏｍｐａｒｅｄｗｉｔｈｔｈｅｔｒａｄｉｔｉｏｎａｌＢＰｎｅｕｒａｌｎｅｔｗｏｒｋｐｒｅｄｉｃｔｉｏｎｍｏｄｅｌ，ｉｔｈａｓｉｎｃｒｅａｓｅｄｂｙ１３．２％，３８．４％，ａｎｄ２１．５％ｒｅｓｐｅｃｔｉｖｅｌｙ．ʌＫｅｙｗｏｒｄｓɔｇｅｎｅｔｉｃａｌｇｏｒｉｔｈｍ；ＢＰｎｅｕｒａｌｎｅｔｗｏｒｋ；ｇｒｅｅｎｈｏｕｓｅｔｅｍｐｅｒａｔｕｒｅ；ｐｒｅｄｉｃｔｉｏｎｍｏｄｅｌ作者简介：李其操（１９９７－），男，硕士研究生，主要研究方向：农业物联网；董自健（１９７３－），男，博士，教授，主要研究方向：检测与控制㊁通信技术㊂通讯作者：董自健㊀㊀Ｅｍａｉｌ：ｄｚｊｉａｎ＠１２６．ｃｏｍ收稿日期：２０２２－１０－２００㊀引㊀言中国是排在世界前列的农业生产大国，温室的面积占据着世界首位㊂温室内的环境因素对于作物的生长有着至关重要的影响［１－２］㊂目前，温室的调控方式大多是凭借工人的生产经验，通过获得的传感器数据，进行预判性的调控㊂因此，能够精准的预测出温室内的温度情况，对温室调控系统有很大的帮助㊂近年来，许多学者提出了针对温度预测的方法㊂如：左志宇［３］提出采用时序分析法建立温度预测模型的方法；徐意［４］构建了基于ＲＢＦ神经网络的温室温度预测模型；徐宇［５］构建了基于复数神经网络的温室温度预测模型；王红君［６］利用贝叶斯正则化算法对ＢＰ神经网络进行改进，降低了影响温度的因子之间的耦合度等㊂但是，上述预测模型都容易出现陷入局部最优的情况㊂因此，本文利用遗传算法，对ＢＰ神经网络的初始权值和阈值进行优化，使预测模型避免出现局部最优的情况，从而对温室内温度进行更精准的预测㊂１㊀ＧＡ－ＢＰ神经网络预测模型的构建１．１㊀ＢＰ神经网络ＢＰ神经网络的主要思想是：训练数据通过前馈网络训练后得到输出数据，将输出数据与期望数据进行对比得到误差，反向传播网络将得到的误差反向输入输出层，对网络的连接权值和阈值进行反复训练，缩小网络输出和期望输出之间的误差㊂输入㊁输出层为单层结构，而隐藏层可以是单层或多层㊂输入层㊁隐藏层㊁输出层之间的神经元都是相互连接的，为全连接㊂ＢＰ神经网络结构如图１所示㊂uy输入层节点隐藏层节点输出层节点图１㊀ＢＰ神经网络结构图Ｆｉｇ．１㊀ＳｔｒｕｃｔｕｒｅｏｆＢＰｎｅｕｒａｌｎｅｔｗｏｒｋ㊀㊀假设输入层节点数为ｎ，隐藏层节点数为ｌ，输出层节点数为ｍ，输入层到隐藏层的权重为ωｉｊ，隐藏层到输出层的权重为ωｊｋ，输入层到隐藏层的阈值为ａｊ，隐藏层到输出层的阈值为ｂｋ，学习速率为η，激励函数为ｇ（ｘ）㊂其中，激励函数为ｇ（ｘ）取ｓｉｇｍｏｉｄ函数㊂形式如式（１）所示：ｇｘ()＝１１＋ｅ－ｘ（１）㊀㊀隐藏层的输出如式（２）所示：Ｈｊ＝ｇðｎｉ＝１ωｉｊｘｉ＋ａｊ()（２）㊀㊀输出层的输出如式（３）所示：Ｏｋ＝ðｌｊ＝１Ｈｊωｊｋ＋ｂｋ（３）㊀㊀网络误差如式（４）所示：ｅｋ＝Ｙｋ－Ｏｋ（４）㊀㊀其中，Ｙｋ为期望输出㊂输入层到隐藏层权值的更新公式如式（５）所示：㊀㊀ωｉｊ＝ωｉｊ＋ηＨｊ１－Ｈｊ()ｘｉðｍｋ＝１ωｊｋｅｋ（５）隐藏层到输出层权值的更新公式如式（６）所示：ωｊｋ＝ωｊｋ＋ηＨｊｅｋ（６）㊀㊀隐藏层节点阈值的更新公式如式（７）所示：ａｊ＝ａｊ＋ηＨｊ１－Ｈｊ()ðｍｋ＝１ωｊｋｅｋ（７）㊀㊀输出层节点阈值的更新公式如式（８）所示：ｂｋ＝ｂｋ＋ηｅｋ（８）㊀㊀由于ＢＰ神经网络的初始连接权值和阈值是随机选定，可能会使网络陷入局部极值，权值收敛到局部最小值，从而出现网络训练失败，模型的预测精度不高的结果㊂因此，本文采用遗传算法对ＢＰ神经网络进行优化，得到权值和阈值的最优解，使模型能够更高效的训练和更精准的预测㊂１．２㊀遗传算法（１）初始化种群㊂种群中的个体由ＢＰ神经网络中输入层到隐藏层的权值㊁隐藏层的阈值㊁隐藏层到输出层的权值和输出层的阈值编码而成㊂（２）适应度函数㊂适应度函数用于表明ＢＰ神经网络中权值和阈值的优劣性，个体适应度值为训练数据预测误差绝对值之和㊂适应度函数的计算公式如式（９）所示：Ｆｉ＝ｋðｎｉ＝１ａｂｓｙｉ－ｏｉ()()（９）式中：ｋ为系数，ｎ为神经网络输出节点数量，ｙｉ为神经网络第ｉ个节点的期望输出，ｏｉ为神经网络第ｉ个节点的预测输出㊂（３）选择操作㊂选择操作从旧群体中以一定概率选择优良个体组成新的种群，以繁殖得到下一代个体，本文采用轮盘赌法，每个个体ｉ被选择的概率ｐｉ如式（１０）所示：ｐｉ＝ＦｉðＮｊ＝１Ｆｉ（１０）式中：Ｎ为种群规模，Ｆｉ为第ｉ个个体适应度值㊂（４）交叉操作㊂交叉操作是指从种群中随机选择两个个体，通过两个染色体的交换组合，把父串的优秀特征遗传给子串，从而产生新的优秀个体，由于个体采用实数编码，所以交叉操作采用实数交叉法［７］㊂第ｊ个个体Ｓｊ和ｋ个个体Ｓｋ在ｉ位的交叉过程如式（１１）所示：Ｓｊ，ｉ＝Ｓｊ，ｉ１－ｂ()＋Ｓｋ，ｉ㊃ｂＳｋ，ｉ＝Ｓｋ，ｉ１－ｂ()＋Ｓｊ，ｉ㊃ｂ{（１１）式中ｂ为［０，１］区间内的随机数㊂（５）变异操作㊂为了防止遗传算法在优化过程中陷入局部最优解，在搜索过程中，需要对个体进行变异㊂经过交叉操作后得到新的染色体后，随机选择染色体上的若干个基因，将这若干个基因的值进行随机修改，从而更新了染色体的基因，突破了搜索的限制，更有利于获取全局最优解［８］㊂选择第ｉ个９６１第９期李其操，等：基于ＧＡ－ＢＰ神经网络的温室温度预测研究个体的第ｊ个基因ａｉｊ进行变异，操作过程如式（１２）㊁式（１３）所示：ａｉｊ＝ａｉｊ＋ａｍａｘ－ａｉｊ()㊃ｆｓ()ｒ＞０．５ａｉｊ－ａｉｊ－ａｍｉｎ()㊃ｆｓ()ｒɤ０．５{（１２）ｆｓ()＝ｒ１－ｓＧｍａｘæèçöø÷（１３）式中：ａｍａｘ㊁ａｍｉｎ分别是个体ｉ的最大值和最小值，ｓ是迭代次数，Ｇｍａｘ是最大进化次数，ｒ为［０，１］区间内的随机数㊂１．３㊀ＧＡ－ＢＰ神经网络预测模型ＧＡ－ＢＰ神经网络预测模型由遗传算法（ＧｅｎｅｔｉｃＡｌｇｏｒｉｔｈｍｓ，ＧＡ）优化部分和ＢＰ神经网络两部分组成㊂由于种群中的每个个体都包含了ＢＰ神经网络的初始权值和阈值，遗传算法部分的作用是优化ＢＰ神经网络的权值和阈值㊂通过计算ＢＰ神经网络的误差，得到个体适应度值㊂经过遗传算法的选择㊁交叉和变异操作找到最优适应度值的个体㊂对最优个体进行解码，得到权值和阈值，赋值给ＢＰ神经网络，再使用反向传播进行训练㊂ＧＡ－ＢＰ神经网络预测模型的执行过程如图２所示㊂输出预测结果满足终止条件更新权值和阈值计算误差获取最优权值和阈值确定B P 神经网络初始权值和阈值满足终止条件选择、交叉、变异计算适应度值初始化种群对权值和阈值编码YNNY图２㊀遗传算法优化ＢＰ神经网络流程图Ｆｉｇ．２㊀ＦｌｏｗｃｈａｒｔｏｆｇｅｎｅｔｉｃａｌｇｏｒｉｔｈｍｔｏｏｐｔｉｍｉｚｅＢＰｎｅｕｒａｌｎｅｔｗｏｒｋ２㊀实验与结果分析２．１㊀样本数据采集本文实验数据采集自连云港赣榆葡萄园第６号温室，选用温度㊁湿度㊁二氧化碳浓度㊁土壤氮含量㊁土壤磷含量和土壤钾含量作为样本数据㊂每１５ｍｉｎ采集一次数据，共采集了２２９２组样本数据㊂为了实验测试更方便，本文选用其中２０００组数据，并将前８０％的样本数据作为训练样本，剩余的２０％样本数据作为测试样本㊂部分样本数据见表１㊂表１㊀部分样本数据Ｔａｂ．１㊀Ｐａｒｔｉａｌｓａｍｐｌｅｄａｔａ日期时间温度／ħ湿度／％二氧化碳浓度／（ｐｐｍ）土壤氮含量／％土壤磷含量／％土壤钾含量／％２０２２／８／２１１８：４０：３８２８．２８７３６１２５．２２６７０２０２２／８／２１１９：１９：４１２７．８８６３５９２５．２２５７０２０２２／８／２１１９：３４：５５２７．８８６３６０２５．１２６７０２０２２／８／２１１９：５０：１０２７．６８６３５９２５．２２５７０２０２２／８／２１２０：０５：２４２７．６８６３５８２５．２２５７０２０２２／８／２１２０：２０：３９２７．５８６３５８２５．２２５６８２．２㊀模型参数设定２．２．１㊀ＢＰ神经网络结构根据所获得的样本数据，将输入层节点设定为５，即５个特征，分别为湿度㊁二氧化碳浓度㊁土壤氮含量㊁土壤磷含量和土壤钾含量数据；输出层节点为１个，特征为温度数据；通过试凑法确定隐藏层节点为７个㊂因此，ＢＰ神经网络的结构为５－７－１㊂２．２．２㊀遗传算法参数设定由于过多的迭代次数会影响模型的训练效率，且适应度曲线在迭代５０次后的变化幅度不大，因此本实验将进化迭代次数设定为５０次，种群规模为３０，交叉概率为０．３，变异概率为０．１㊂图３为遗传算法的适应度曲线㊂10410310210110099980102030405060进化代数适应度平均适应度适应度曲线终止代数=50图３㊀遗传算法适应度曲线Ｆｉｇ．３㊀Ｇｅｎｅｔｉｃａｌｇｏｒｉｔｈｍｆｉｔｎｅｓｓｃｕｒｖｅ０７１智㊀能㊀计㊀算㊀机㊀与㊀应㊀用㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀第１３卷㊀２．３㊀模型评价标准为了评定预测模型的性能，本文以平均绝对误差（ＭＡＥ）㊁均方误差（ＭＳＥ）和平均绝对百分比误差（ＭＡＰＥ）作为评判预测模型性能优劣的标准㊂各评估误差指标的计算公式如式（１４） 式（１６）所示：ＭＡＥ＝１ｎðｎｉ＝１ｙ＾ｉ－ｙｉ（１４）ＭＳＥ＝１ｎðｎｉ＝１ｙ＾ｉ－ｙｉ()２（１５）ＭＡＰＥ＝１ｎðｎｉ＝１ｙ＾ｉ－ｙｉｙｉ（１６）式中：ｙ＾ｉ为模型的预测值，ｙｉ为真实值，ｎ为样本数㊂所得的值越小，则模型的性能越优异㊂２．４㊀预测结果及分析通过ＭＡＴＬＡＢ软件对ＧＡ－ＢＰ神经网络预测模型和传统ＢＰ神经网络预测模型进行验证，得到的预测对比结果如图４所示㊂预测结果实际值282726252423222120050100150200250300350400样本编号温度（ａ）ＧＡ－ＢＰ网络预测输出预测结果实际值282726252423222120050100150200250300350400样本编号温度（ｂ）ＢＰ网络预测输出图４㊀ＧＡ－ＢＰ与ＢＰ训练效果对比图Ｆｉｇ．４㊀ＣｏｍｐａｒｉｓｏｎｏｆＧＡ－ＢＰａｎｄＢＰｔｒａｉｎｉｎｇｅｆｆｅｃｔｓ㊀㊀由图４可知，ＧＡ－ＢＰ神经网络预测模型与传统ＢＰ神经网络预测模型相比，ＧＡ－ＢＰ的预测效果更优，预测结果更贴近实际值㊂评价结果见表２㊂可以看出，ＧＡ－ＢＰ预测模型的各项误差指标均小于传统ＢＰ预测模型㊂实验证明，ＧＡ－ＢＰ神经网络预测模型具有更好的预测效果㊂表２㊀模型的评价指标对比Ｔａｂ．２㊀Ｃｏｍｐａｒｉｓｏｎｏｆｅｖａｌｕａｔｉｏｎｉｎｄｉｃａｔｏｒｓｏｆｔｈｅｍｏｄｅｌｓ评价指标ＧＡ－ＢＰＢＰＭＡＥ０．４４１０．５０８ＭＳＥ０．２７６０．４４８ＲＭＳＥ０．５２５０．６６９３㊀结束语本文以温室内湿度㊁二氧化碳浓度和土壤氮磷钾含量与温度有关的影响因子作为输入量，以温度作为输出量，通过遗传算法优化ＢＰ神经网络的权值和阈值，构建了ＧＡ－ＢＰ神经网络预测模型㊂实验证明，ＧＡ－ＢＰ神经网络预测模型能够更精准的进行温室内温度预测，对于温室管理有一定的参考价值㊂参考文献［１］王军伟．苏北地区日光温室构型优化㊁室内温湿度分析及应用效果初探［Ｄ］．南京：南京农业大学，２０１５．［２］王克安，李絮花，吕晓惠，等．不同结构日光温室温湿度变化规律及其对番茄产量和病害的影响［Ｊ］．山东农业科学，２０１１，２３５（３）：３３－３６．［３］左志宇，毛罕平，张晓东，等．基于时序分析法的温室温度预测模型［Ｊ］．农业机械学报，２０１０，４１（１１）：１７３－１７７，１８２．［４］徐意，项美晶．基于ＲＢＦ神经网络的温室温度调控研究［Ｊ］．农机化研究，２０１０，３２（３）：７４－７６．［５］徐宇，冀荣华．基于复数神经网络的智能温室温度预测研究［Ｊ］．中国农机化学报，２０１９，４０（４）：１７４－１７８．［６］王红君，史丽荣，赵辉，等．基于贝叶斯正则化ＢＰ神经网络的日光温室温度预测模型［Ｊ］．湖北农业科学，２０１５，５４（１７）：４３００－４３０３．［７］曹雪丽．配送中心订单分批处理随机服务系统模型与优化研究［Ｄ］．北京：北京物资学院，２０１２．［８］高基旭，王珺．一种基于遗传算法的多边缘协同计算卸载方案［Ｊ］．计算机科学，２０２１，４８（１）：７２－８０．１７１第９期李其操，等：基于ＧＡ－ＢＰ神经网络的温室温度预测研究。

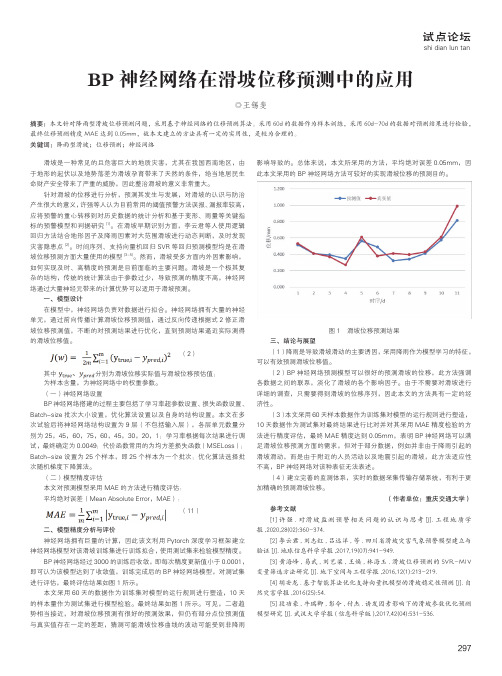
试点论坛shi dian lun tan297BP 神经网络在滑坡位移预测中的应用◎王锡斐摘要：本文针对降雨型滑坡位移预测问题，采用基于神经网络的位移预测算法。

采用60d 的数据作为样本训练，采用60d-70d 的数据对预测结果进行检验，最终位移预测精度MAE 达到0.05mm，故本文建立的方法具有一定的实用性，是较为合理的。

关键词：降雨型滑坡；位移预测；神经网络滑坡是一种常见的且危害巨大的地质灾害，尤其在我国西南地区，由于地形的起伏以及地势落差为滑坡孕育带来了天然的条件，给当地居民生命财产安全带来了严重的威胁，因此整治滑坡的意义非常重大。

针对滑坡的位移进行分析，预测其发生与发展，对滑坡的认识与防治产生很大的意义，许强等人认为目前常用的阈值预警方法误报、漏报率较高，应将预警的重心转移到对历史数据的统计分析和基于变形、雨量等关键指标的预警模型和判据研究[1]。

在滑坡早期识别方面，李云君等人使用逻辑回归方法结合地形因子及降雨因素对大范围滑坡进行动态判断，及时发现灾害隐患点[2]。

时间序列、支持向量机回归SVR 等回归预测模型均是在滑坡位移预测方面大量使用的模型[3-5]。

然而，滑坡受多方面内外因素影响，如何实现及时、高精度的预测是目前面临的主要问题。

滑坡是一个极其复杂的结构，传统的统计算法由于参数过少，导致预测的精度不高，神经网络通过大量神经元带来的计算优势可以适用于滑坡预测。

一、模型设计在模型中，神经网络负责对数据进行拟合。

神经网络拥有大量的神经单元，通过前向传播计算滑坡位移预测值，通过反向传递根据式2修正滑坡位移预测值，不断的对预测结果进行优化，直到预测结果逼近实际测得的滑坡位移值。

（2）其中分别为滑坡位移实际值与滑坡位移预估值；为样本含量，为神经网络中的权重参数。

（一）神经网络设置BP 神经网络搭建的过程主要包括了学习率超参数设置、损失函数设置、Batch-size 批次大小设置，优化算法设置以及自身的结构设置。

BP神经网络模型第1节基本原理简介近年来全球性的神经网络研究热潮的再度兴起，不仅仅是因为神经科学本身取得了巨大的进展．更主要的原因在于发展新型计算机和人工智能新途径的迫切需要．迄今为止在需要人工智能解决的许多问题中，人脑远比计算机聪明的多，要开创具有智能的新一代计算机，就必须了解人脑，研究人脑神经网络系统信息处理的机制．另一方面，基于神经科学研究成果基础上发展出来的人工神经网络模型，反映了人脑功能的若干基本特性，开拓了神经网络用于计算机的新途径．它对传统的计算机结构和人工智能是一个有力的挑战，引起了各方面专家的极大关注．目前，已发展了几十种神经网络，例如Hopficld模型，Feldmann等的连接型网络模型，Hinton等的玻尔茨曼机模型，以及Rumelhart等的多层感知机模型和Kohonen的自组织网络模型等等。

在这众多神经网络模型中，应用最广泛的是多层感知机神经网络。

多层感知机神经网络的研究始于50年代，但一直进展不大。

直到1985年，Rumelhart等人提出了误差反向传递学习算法（即BP算），实现了Minsky的多层网络设想，如图34-1所示。

BP 算法不仅有输入层节点、输出层节点，还可有1个或多个隐含层节点。

对于输入信号，要先向前传播到隐含层节点，经作用函数后，再把隐节点的输出信号传播到输出节点，最后给出输出结果。

节点的作用的激励函数通常选取S 型函数，如Qx e x f /11)(-+=式中Q 为调整激励函数形式的Sigmoid 参数。

该算法的学习过程由正向传播和反向传播组成。

在正向传播过程中，输入信息从输入层经隐含层逐层处理，并传向输出层。

每一层神经元的状态只影响下一层神经输入层 中间层 输出层 图34-1 BP 神经网络模型元的状态。

如果输出层得不到期望的输出，则转入反向传播，将误差信号沿原来的连接通道返回，通过修改各层神经元的权值，使得误差信号最小。

社含有n 个节点的任意网络，各节点之特性为Sigmoid 型。

《基于深度学习的气象预测研究》篇一一、引言随着科技的飞速发展，深度学习在各个领域的应用越来越广泛。

在气象预测领域，传统的预测方法已经难以满足人们对于准确性和精细度的需求。

因此，本文旨在探讨基于深度学习的气象预测研究，以提高预测的准确性和效率。

二、深度学习在气象预测中的应用深度学习是一种模拟人脑神经网络的工作方式的机器学习方法。

在气象预测中，深度学习可以通过学习大量的历史气象数据，发现数据之间的复杂关系和规律，从而实现对未来气象情况的预测。

1. 数据预处理在进行深度学习气象预测之前，需要对原始的气象数据进行预处理。

这包括数据清洗、特征提取、数据归一化等步骤。

通过这些预处理步骤，可以将原始数据转化为适合深度学习模型输入的格式。

2. 模型构建深度学习模型是气象预测的核心。

常用的深度学习模型包括卷积神经网络（CNN）、循环神经网络（RNN）和长短期记忆网络（LSTM）等。

这些模型可以有效地处理气象数据中的时空相关性，提高预测的准确性。

3. 训练与优化在构建好模型后，需要使用大量的历史气象数据进行训练。

通过不断地调整模型的参数，优化模型的性能，使模型能够更好地适应不同的气象情况。

同时，还需要对模型进行验证和测试，确保模型的可靠性和泛化能力。

三、基于深度学习的气象预测的优势与挑战1. 优势基于深度学习的气象预测具有以下优势：（1）准确性高：深度学习可以通过学习大量的历史数据，发现数据之间的复杂关系和规律，提高预测的准确性。

（2）适应性强：深度学习模型可以适应不同的气象情况和地域特点，具有较好的泛化能力。

（3）预测时间短：深度学习模型可以在短时间内对大量的数据进行处理和预测，提高工作效率。

2. 挑战虽然基于深度学习的气象预测具有很多优势，但也面临着一些挑战：（1）数据量大：气象数据量大且复杂，需要进行大量的数据预处理工作。

（2）模型复杂：深度学习模型的构建和训练需要较高的技术水平和计算资源。

（3）不确定性：气象预测本身就存在不确定性，如何提高预测的稳定性和可靠性是一个重要的挑战。

电力需求预测基于BP神经网络模型引言在当今社会中，电力需求预测对于能源供应商和电力系统运营商来说是一个关键的任务。

准确地预测电力需求可以帮助电力系统更好地规划资源分配，提高能源利用效率，降低能源浪费，并确保电力系统的稳定运行。

本文将介绍一种基于BP神经网络模型的电力需求预测方法，并探讨其在实际应用中的优势和局限性。

1. 研究背景和意义：随着工业化和城市化的快速发展，电力需求规模呈现出快速增长的趋势。

然而，电力供应的能力与电力需求的匹配程度却难以保持一致。

因此，准确地预测电力需求对于电力系统运营商和能源供应商来说具有重要意义。

2. 电力需求预测方法：BP神经网络模型是一种常用的基于历史数据的预测方法。

它通过训练神经网络来学习历史数据中的模式和趋势，并用于预测未来的电力需求。

BP神经网络模型具有多层结构，包括输入层、隐藏层和输出层。

输入层将历史数据作为输入，隐藏层通过学习历史数据的模式来预测未来的需求。

输出层给出了对未来电力需求的预测结果。

3. BP神经网络模型的优势：（1）灵活性：BP神经网络模型可以适应各种类型的电力需求预测问题，包括小时、日或年度的需求预测。

它可以根据需求数据的特征自动调整网络的参数和结构，并产生准确的预测结果。

（2）非线性建模：BP神经网络模型可以处理非线性关系，这在电力需求预测中非常重要。

电力需求往往受多种因素的影响，如天气、经济状况和人口增长等，这些因素之间存在复杂的非线性关系。

BP神经网络模型能够捕捉这些关系，并进行准确的预测。

（3）自适应性：BP神经网络模型可以通过不断训练来提高预测的准确性。

随着新的数据不断到来，模型可以自动地更新参数和结构，以适应新的需求模式。

4. BP神经网络模型的局限性：（1）数据需求：BP神经网络模型需要大量的历史数据来进行训练。

如果历史数据不足或质量不高，模型的预测准确性将受到限制。

（2）超参数选择：BP神经网络模型有许多超参数需要人工选择，如网络的层数、节点数和学习速率等。