2019-2020年初中数学六年级下册第9章 几何图形初步9.1 几何图形人教五四学制版拔高训练第八十二篇

2019年精选数学六年级下册[第9章几何图形初步9.1 几何图形]人教五四学制版习题精选[含答案解析]第七十五篇第1题【单选题】如图，图中共有三角形( )A、30个B、32个C、34个D、35个【答案】：【解析】：第2题【单选题】下列说法不正确的是( )A、长方体与正方体都有六个面B、圆锥的底面是圆C、棱柱的上下底面是完全相同的图形D、五棱柱有五个面，五条棱【答案】：【解析】：第3题【单选题】正多面体的面数、棱数、顶点数三在之间存在一个奇特的关系，若用F，E，V分别表示正多面体的面数、棱数、顶点数，则有F+V-E=2，现有一个正多面体共有12条棱，6个顶点，则它的面数F等于( )A、6B、8C、12D、20【答案】：【解析】：第4题【填空题】如图是由______、长方体、圆柱三种几何体组成的物体．A、三棱柱【答案】：【解析】：第5题【填空题】如图所示为8个立体图形．其中，柱体的序号为______，锥体的序号为______，有曲面的序号为______．【答案】：【解析】：第6题【解答题】将一个半径为2cm的圆分成3个扇形，其圆心角的比1：2：3，求：（1）各个扇形的圆心角的度数．（2）其中最大一个扇形的面积．【答案】：【解析】：第7题【解答题】如图，将下列图形与对应的图形名称用线连接起来：【答案】：【解析】：第8题【综合题】已知长方形的长为4 cm．宽为3 cm，将其绕它的一边所在的直线旋转一周，得到一个几何体．求此几何体的体积；求此几何体的表面积．（结果保留π）【答案】：【解析】：第9题【综合题】推导猜测三棱锥有______条棱，四棱锥有______条棱，五棱锥有______条棱．______棱锥有30条棱．一个棱锥的棱数是100，则这个棱锥是______棱锥，面数是______．【答案】：【解析】：第10题【综合题】如图，纸上有五个边长为1的小正方形组成的图形纸，我们可以把它剪开拼成一个正方形。

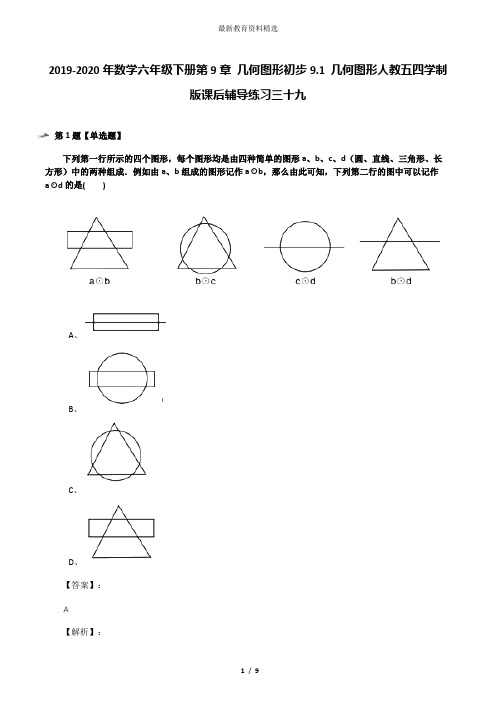
2019-2020年数学六年级下册第9章几何图形初步9.1 几何图形人教五四学制版课后辅导练习三十九第1题【单选题】下列第一行所示的四个图形，每个图形均是由四种简单的图形a、b、c、d（圆、直线、三角形、长方形）中的两种组成．例如由a、b组成的图形记作a⊙b，那么由此可知，下列第二行的图中可以记作a⊙d 的是( )A、B、C、D、【答案】：【解析】：第2题【单选题】在长方形、长方体、三角形、球、直线、圆中，有( )个平面图形．A、3B、4C、5D、6【答案】：【解析】：第3题【单选题】一个三棱柱的侧面数，顶点数分别是( )．A、3，6B、4，10C、5，15D、6，15【答案】：【解析】：第4题【单选题】下列图形属于平面图形的是( )A、长方体B、圆锥体C、圆柱体【答案】：【解析】：第5题【单选题】下列说法错误的是( )A、长方体、正方体都是棱柱B、球体的三种视图均为同样大小的图形C、三棱柱的侧面是三角形D、六棱柱有六条棱、六个侧面、侧面为长方形【答案】：【解析】：第6题【单选题】如图中，三角形的个数为( )?B、30个C、28个D、16个【答案】：【解析】：第7题【单选题】经过圆锥顶点的截面的形状可能是( ) A、B、C、D、【答案】：【解析】：第8题【单选题】下列几何体中，属于锥体的有( )AB、CD【答案】：【解析】：第9题【填空题】确定一个圆有两要素，一是______，二是______．【答案】：第10题【填空题】如图，在长方体ABCD﹣EFGH中，与面ABFE平行的面是______．?【答案】：【解析】：第11题【填空题】如图中，共有______个三角形的个数，______个平行四边形，______个梯形．【答案】：第12题【填空题】如图，是一个几何体从正面、左面、上面看得到的平面图形，判断下面说法的正误（正确的在括号内划△，错误的在括号内划▲）（1）这是一个棱锥______．（2）这个几何体有4个面______ ．（3）这个几何体有5个顶点______（4）这个几何体有8条棱______（5）请你再说出一个正确的结论______【答案】：【解析】：第13题【填空题】一只小蚂蚁从如图所示的正方体的顶点A沿着棱爬向有蜜糖的点B，它只能经过三条棱，请你数一数，小蚂蚁有______种爬行路线．【答案】：【解析】：第14题【解答题】如图，甲、乙、丙、丁四个扇形的圆心角度数比为1：2：4：5，请完成下面问题：（1）求出扇形丁的圆心角度数；（2）如果圆的半径r为2，请求出扇形乙的面积．【答案】：【解析】：第15题【解答题】图中有多少个三角形？【答案】：【解析】：。

几何图形（复习课）
一．这是一节复习课，复习的内容是，小学阶段学过的所有几何图形。

二．教学目标：
1.归纳总结所学过的几何图形，有简单到复杂。

直线到平面
到立体图形。

2.掌握图形的求面积或体积（容积）的计算方法，并总结出
公式。

3.熟练掌握面积，体积的单位换算。

三．授课过程：
1.结合教学目标，分小组归纳总结。

2.各小组派代表到讲台上给大家展示自己的总结结果。

3.教师做系统的总结并补充。

4.结合课本做一些这方面的练习（求面积和体积）。

四．布置作业：
总结出所有图形求面积或体积的计算公式，用字母表示。

专题13几何图形初步目录一览知识目标（新课程标准提炼）中考解密（分析考察方向，精准把握重难点）重点考向（以真题为例，探究中考命题方向）►考向一认识立体图形►考向二几何体的展开与折叠►考向三有关角的计算问题►考向四余角、补角与对顶角、邻补角►考向五平行线的性质与判定最新真题荟萃（精选最新典型真题，强化知识运用，优化解题技巧）1. 掌握五个基本事实；2. 会比较线段的长短，理解线段的和、差，以及线段中点的意义；3. 理解角的概念，能比较角的大小．认识度、分、秒，会对度、分、秒进行简单的换算，并会计算角的和、差；4. 理解对顶角、余角、补角等概念，探索并掌握对顶角相等、同角（等角）的余角相等、同角（等角）的补角相等的性质；识别同位角、内错角、同旁内角；5. 理解垂线、垂线段的概念，能用三角尺或量角器过一点画已知直线的垂线；6. 理解平行线的概念；掌握平行线的性质定理；探索并证明平行线的判定定理和性质定理；7. 了解平行于同一条直线的两条直线平行；8. 通过具体实例，了解定义、命题、定理、推论的意义．结合具体实例，会区分命题的条件和结论，了解原命题及其逆命题的概念．会识别两个互逆的命题，知道原命题成立其逆命题不一定成立；9. 了解反例的作用，知道利用反例可以判断一个命题是错误的．通过实例体会反证法的含义．该版块内容是初中几何的基础，是非常基础也是非常重要的，年年都会考查，分值为8分左右，预计2023年各地中考还将出现，大部分地区在选填题中考察可能性较大，主要考察平行线的性质和判定、方位角、角度的大小等知识，这些知识点考查较容易，另外平行线的性质可能在综合题中出现，考查学生能力，比如：作平行的辅助线，构造特殊四边形，此类题目有一定难度，需要学生灵活掌握．►考向一 认识立体图形（2023•乐山）1．下面几何体中，是圆柱的是（ ）A ．B ．C ．D ． （2023•娄底）2．一个长方体物体的一顶点所在A 、B 、C 三个面的面积比是3:2:1，如果分别按A 、B 、C 面朝上将此物体放在水平地面上，地面所受的压力产生的压强分别为A P 、B P 、C P （压强的计算公式为F P S =），则::A B C P P P =（ ）A ．2:3:6B ．6:3:2C ．1:2:3D ．3:2:1（2023•巴中）3．下列图形中为圆柱的是（ ）A ． B ． C ． D ．►考向二 几何体的展开与折叠（2023•达州）4．下列图形中，是长方体表面展开图的是（）A．B．C．D．（2023•威海）5．如图是一正方体的表面展开图．将其折叠成正方体后，与顶点K距离最远的顶点是（ ）A．A点B．B点C．C点D．D点（2023•青岛）6．一个不透明小立方块的六个面上分别标有数字1，2，3，4，5，6，其展开图如图①所示．在一张不透明的桌子上，按图②方式将三个这样的小立方块搭成一个几何体，则该几何体能看得到的面上数字之和最小是（ ）A．31B．32C．33D．34►考向三有关角的计算问题（2022•烟台）7．如图，某海域中有A ，B ，C 三个小岛，其中A 在B 的南偏西40°方向，C 在B 的南偏东35°方向，且B ，C 到A 的距离相等，则小岛C 相对于小岛A 的方向是（ ）A ．北偏东70°B ．北偏东75°C ．南偏西70°D ．南偏西20°（2022•湘潭）8．如图，一束光沿CD 方向，先后经过平面镜OB 、OA 反射后，沿EF 方向射出，已知120AOB ∠=︒，20CDB ∠=︒，则∠=AEF ．（2019•烟台）9．小明将一张正方形纸片按如图所示顺序折叠成纸飞机，当机翼展开在同一平面时(机翼间无缝隙)，AOB ∠的度数是 .►考向四 余角、补角与对顶角、邻补角解题技巧/易错易混1.识别对顶角时，要抓住两个关键要素：一是顶点，二是边．先看两个角是否有公共顶点，再看两个角的两边是否分别互为反向延长线．两条直线相交形成两对对顶角．2.互为邻补角的两个角一定互补，但互补的两个角不一定是邻补角；一个角的邻补角有两个，但一个角的补角可以有很多个（2023•北京）10．如图，90AOC BOD ∠=∠=︒，126AOD ∠=︒，则BOC ∠的大小为（ ）A ．36︒B ．44︒C ．54︒D ．63︒（2023•河南）11．如图，直线AB ，CD 相交于点O ，若180∠=︒，230∠=︒，则AOE ∠的度数为（ ）A ．30︒B ．50︒C ．60︒D ．80︒（2022•桂林）12．如图，直线l 1，l 2相交于点O ，∠1＝70°，则∠2＝ °．►考向五 平行线的性质与判定（2023•绵阳）13．光线在不同介质中的传播速度是不同的，因此当光线从水中射向空气时，要发生折射，由于折射率相同，所以在水中平行的光线，在空气中也是平行的．如图，1122,2∠=︒∠的度数为（ ）A ．32︒B ．58︒C ．68︒D ．78︒（2023•重庆）14．如图，,⊥∥AB CD AD AC ，若155∠=︒，则2∠的度数为（ ）A ．35︒B ．45︒C ．50︒D ．55︒（2023•金华）15．如图，已知12350∠=∠=∠=︒，则4∠的度数是（ ）A ．120︒B ．125︒C ．130︒D ．135︒（2022•自贡）16．如图，直线,AB CD 相交于点O ，若130∠= ，则2∠的度数是（ ）A ．30°B ．40°C ．60°D ．150°（2022•河北）17．①~④是由相同的小正方体粘在一起的几何体，若组合其中的两个，恰是由6个小正方体构成的长方体，则应选择（ ）A ．①③B ．②③C ．③④D ．①④（2023•临沂）18．下图中用量角器测得ABC ∠的度数是（ ）A ．50︒B ．80︒C ．130︒D ．150︒（2023•河北）19．淇淇一家要到革命圣地西柏坡参观．如图，西柏坡位于淇淇家南偏西70︒的方向，则淇淇家位于西柏坡的（ ）A ．南偏西70︒方向B ．南偏东20︒方向C ．北偏西20︒方向D ．北偏东70︒方向（2022•甘肃）20．若40A ∠=︒，则A ∠的余角的大小是（ ）A ．50°B ．60°C ．140°D ．160°（2023•金昌）21．如图1，汉代初期的《淮南万毕术》是中国古代有关物理、化学的重要文献，书中记载了我国古代学者在科学领域做过的一些探索及成就．其中所记载的“取大镜高悬，置水盆于其下，则见四邻矣”，是古人利用光的反射定律改变光路的方法，即“反射光线与入射光线、法线在同一平面上；反射光线和入射光线位于法线的两侧；反射角等于入射角”．为了探清一口深井的底部情况，运用此原理，如图在井口放置一面平面镜可改变光路，当太阳光线AB 与地面CD 所成夹角50ABC ∠=︒时，要使太阳光线经反射后刚好垂直于地面射入深井底部，则需要调整平面镜EF 与地面的夹角EBC ∠=（ ）A ．60︒B ．70︒C ．80︒D ．85︒（2023•临沂）22．在同一平面内，过直线l 外一点P 作l 的垂线m ，再过P 作m 的垂线n ，则直线l 与n 的位置关系是（ ）A ．相交B ．相交且垂直C ．平行D ．不能确定（2022•泸州）23．如图，直线a b ，直线c 分别交a ，b 于点A ，C ，点B 在直线b 上，AB AC ⊥，若1130∠=︒，则2∠的度数是（ ）A ．30︒B ．40︒C ．50︒D ．70︒（2022•贺州）24．如图，直线a ，b 被直线c 所截，下列各组角是同位角的是（ ）A ．1∠与2∠B ．1∠与3∠C ．2∠与3∠D ．3∠与4∠（2022•台州）25．如图，已知190∠=︒，为保证两条铁轨平行，添加的下列条件中，正确的是（ ）A ．290∠=︒B ．390∠=︒C ．490∠=︒D ．590∠=︒（2022•吉林）26．如图，如果12∠=∠，那么AB CD ∥，其依据可以简单说成（ ）A ．两直线平行，内错角相等B ．内错角相等，两直线平行C ．两直线平行，同位角相等D ．同位角相等，两直线平行（2021•铜仁市）27．直线AB 、BC 、CD 、EG 如图所示，1280∠=∠=︒，340∠=︒，则下列结论错误的是（ ）A ．//AB CDB ．40EBF ∠=︒C ．32FCG ∠+∠=∠D ．EF BE>（2023•内蒙古）28．将一副直角三角板按如图所示的方式摆放，点C 在FD 的延长线上，且AB FC ，则CBD ∠的度数为（ ）A ．10︒B ．15︒C ．20︒D ．25︒（2023•荆州）29．如图所示的“箭头”图形中，AB CD ∥，80B D ∠=∠= ，47E F ∠=∠= ，则图中G ∠的度数是（ ）A ．80B ．76C ．66D ．56（2023•常州）30．若圆柱的底面半径和高均为a ，则它的体积是 （用含a 的代数式表示）．（2023•无锡）31．若直三棱柱的上下底面为正三角形，侧面展开图是边长为6的正方形，则该直三棱柱的表面积为 ．（2022•百色）32．如图摆放一副三角板，直角顶点重合，直角边所在直线分别重合，那么∠BAC 的大小为（2022•玉林）33．已知∠α=60°，则∠α的余角等于 度．（2022•连云港）34．已知∠A 的补角是60°，则A ∠= ︒．（2022•西藏）35．如图，依下列步骤尺规作图，并保留作图痕迹：（1）分别以点A，B为圆心，大于12AB的长为半径作弧，两弧相交于E，F两点，作直线EF；（2）以点A为圆心，适当长为半径画弧，分别交AB，AC于点G，H，再分别以点G，H为圆心，大于12GH的长为半径画弧，两弧在∠BAC的内部相交于点O，画射线AO，交直线EF于点M．已知线段AB＝6，∠BAC＝60°，则点M到射线AC的距离为．（2023•镇江）36．如图，一条公路经两次转弯后，方向未变．第一次的拐角ABC∠是140︒，第二次的拐角BCD∠是°．（2021•兰州）37．将一副三角板如图摆放，则∥，理由是．（2023•台州）38．用一张等宽的纸条折成如图所示的图案，若120∠=︒，则∠2的度数为．（2023•武汉）39．如图，在四边形ABCD 中，,AD BC B D ∠=∠∥，点E 在BA 的延长线上，连接CE ．(1)求证：E ECD ∠=∠；(2)若60,∠=︒E CE 平分BCD ∠，直接写出BCE 的形状．（2022•武汉）40．如图，在四边形ABCD 中，AD BC ∥，80B ∠=︒．(1)求BAD ∠的度数；(2)AE 平分BAD ∠交BC 于点E ，50BCD ∠=︒．求证：AE DC ∥．参考答案：1．B【分析】根据圆柱的特征，即可解答．【详解】解：A.是正方体，故不符合题意；B.是圆柱，故符合题意；C.是圆锥，故不符合题意；D.是球体，故不符合题意，故选：B．【点睛】本题考查了认识立体图形，熟练掌握每个几何体的特征是解题的关键．2．A【分析】首先根据长方体的性质，得出相对面的面积相等，再根据物体的压力不变，结合反比例函数的性质进行分析，即可得出答案．【详解】解：∵长方体物体的一顶点所在A、B、C三个面的面积比是3:2:1，∴长方体物体的A、B、C三面所对的与水平地面接触的面积比也为3:2:1，∵FPS=，0F>，且F一定，∴P随S的增大而减小，∴111::::2:3:6321A B CP P P==．故选：A．【点睛】本题考查了反比例函数的性质，解本题的关键在熟练掌握反比例函数的性质．3．B【分析】圆柱是由上下两个平行且大小一样的圆面和一个侧面（曲面）组成的立体图形，直接根据圆柱体的几何特点解答即可．【详解】根据圆柱的特点可知选项B中的图形是圆柱．故选：B．【点睛】此题考查认识立体图形，熟记常见的立体图形的几何特点是解题的关键．4．C【分析】根据长方体有六个面，以及Z字型进行判断即可．【详解】解：A中展开图有7个面，不符合要求；B中展开图无法还原成长方体，不符合要求；C正确，故符合要求；D中展开图有5个面，不符合要求，故选：C．【点睛】本题考查了长方体的展开图．解题的关键在于对知识的熟练掌握．5．D【分析】根据题意画出立体图形，即可求解．【详解】解：折叠之后如图所示，则K与点D的距离最远，故选D．【点睛】本题考查了正方体的展开与折叠，学生需要有一定的空间想象能力．6．B【分析】根据正方体展开图的特征，得出相对面上的数字，再结合正方体摆放方式，得出使该几何体能看得到的面上数字之和最小，则看不见的面数字之和要最大，即可解答．【详解】解：由图①可知：1的相对面是3，2的相对面是4，5的相对面是6，由图2可知：要使该几何体能看得到的面上数字之和最小，则看不见的面数字之和要最大，上面的正方体有一个面被遮住，则这个面数字为6，++++=；能看见的面数字之和为：1234515左下的正方体有3个面被遮住，其中两个为相对面，则这三个面数字分别为4，5，6，++=；能看见的面数字之和为：1236右下的正方体有2个面被遮住，这两个面不是相对面，则这两个面数字为4，6，+++=；能看见的面数字之和为：123511++=，∴能看得到的面上数字之和最小为：1561132故选：B．【点睛】本题主要考查了正方体的相对面，掌握正方体展开图中“相间一行是相对面”，是解题的关键．7．A【分析】根据题意可得∠ABC ＝75°，AD ∥BE ，AB ＝AC ，再根据等腰三角形的性质可得∠ABC ＝∠C ＝75°，从而求出∠BAC 的度数，然后利用平行线的性质可得∠DAB ＝∠ABE ＝40°，从而求出∠DAC 的度数，即可解答．【详解】解：如图：由题意得：∠ABC ＝∠ABE +∠CBE ＝40°+35°＝75°，AD ∥BE ，AB ＝AC ，∴∠ABC ＝∠C ＝75°，∴∠BAC ＝180°﹣∠ABC ﹣∠C ＝30°，∵AD ∥BE ，∴∠DAB ＝∠ABE ＝40°，∴∠DAC ＝∠DAB +∠BAC ＝40°+30°＝70°，∴小岛C 相对于小岛A 的方向是北偏东70°，故选：A ．．【点睛】本题考查了方向角，等腰三角形的性质，熟练掌握等腰三角形的性质是解题的关键．8．40°##40度【分析】根据入射角等于反射角，可得,CDB EDO DEO AEF ∠=∠∠=∠，根据三角形内角和定理求得40OED ∠=︒，进而即可求解．【详解】解：依题意，,CDB EDO DEO AEF ∠=∠∠=∠，∵120AOB ∠=︒，20CDB ∠=︒，20CDB EDO ∴∠=∠=︒，∴18040OED ODE AOB ∠=-∠-∠=︒，∴40AEF DEO ∠=∠=︒．故答案为：40°．【点睛】本题考查了轴对称的性质，三角形内角和定理的应用，掌握轴对称的性质是解题的关键．9．45°【分析】根据折叠过程可知，在折叠过程中角一直是轴对称的折叠.【详解】在折叠过程中角一直是轴对称的折叠，22.5245AOB ︒︒∠=⨯=故答案为45°【点睛】考核知识点：轴对称.理解折叠的本质是关键.10．C【分析】由90AOC BOD ∠=∠=︒，126AOD ∠︒=，可求出COD ∠的度数，再根据角与角之间的关系求解．【详解】∵=90AOC ∠︒，126AOD ∠︒=，∴36COD AOD AOC ∠=∠-∠=︒，∵90BOD ∠=︒，∴903654BOC BOD COD ∠=∠-∠=︒-︒=︒．故选：C ．【点睛】本题考查的知识点是角的计算，注意此题的解题技巧：两个直角相加和AOD ∠相比，多加了BOC ∠．11．B【分析】根据对顶角相等可得180AOD ∠=∠=︒，再根据角的和差关系可得答案．【详解】解：∵180∠=︒，∴180AOD ∠=∠=︒，∵230∠=︒，∴2803050AOE AOD ∠=∠-∠=︒-︒=︒，故选：B【点睛】本题主要考查了对顶角的性质，解题的关键是掌握对顶角相等．12．70【分析】根据对顶角的性质解答即可．【详解】解：∵∠1和∠2是对顶角，∴∠2＝∠1＝70°，故答案为：70．【点睛】本题主要考查了对顶角，熟练掌握对顶角相等是解答本题的关键．13．B【分析】本题主要考查了平行线的性质．根据平行线的性质解答，即可求解．【详解】解：如图，根据题意得：a b ，c d ∥，∴13180∠+∠=︒，32∠=∠，∵1122∠=︒，∴258∠=︒．故选：B ．14．A【分析】根据两直线平行，同旁内角互补可得CAB ∠的度数，根据垂直的定义可得90CAD ∠=︒，然后根据2CAB CAD Ð=Ð-Ð即可得出答案．【详解】解：∵AB CD ∥，155∠=︒，∴18055125CAB Ð=°-°=°，∵AD AC ⊥，∴90CAD ∠=︒，∴21259035CAB CAD Ð=Ð-Ð=°-°=°，故选：A ．【点睛】本题考查了平行线的性质以及垂线的定义，熟知两直线平行同旁内角互补是解本题的关键．15．C【分析】由1350∠=∠=︒可得a b ∥，可得2550∠=∠=︒，再利用邻补角的含义可得答案．【详解】解：如图，标记角，∵1350∠=∠=︒，∴a b ∥，而250∠=︒，∴2550∠=∠=︒，∴41805130∠=︒-∠=︒；故选C【点睛】本题考查的是平行线的判定与性质，邻补角的含义，熟记平行线的判定与性质是解本题的关键．16．A【分析】根据对顶角相等可得2=1=30∠∠︒．【详解】解：∵130∠= ，1∠与2∠是对顶角，∴2=1=30∠∠︒．故选：A ．【点睛】本题考查了对顶角，解题的关键是熟练掌握对顶角的性质：对顶角相等．17．D【分析】观察图形可知，①~④的小正方体的个数分别为4，3，3，2，其中②③组合不能 构成长方体，①④组合符合题意【详解】解：观察图形可知，①~④的小正方体的个数分别为4，3，3，2，其中②③组合不能构成长方体，①④组合符合题意故选D【点睛】本题考查了立体图形，应用空间想象能力是解题的关键．18．C【分析】由图形可直接得出．【详解】解：由题意，可得130ABC ∠=︒，故选：C ．【点睛】本题考查角的度量，量角器的使用方法，正确使用量角器是解题的关键．19．D【分析】根据方向角的定义可得答案．【详解】解：如图：∵西柏坡位于淇淇家南偏西70︒的方向，∴淇淇家位于西柏坡的北偏东70︒方向．故选D ．【点睛】本题主要考查方向角，理解方向角的定义是正确解答的关键．20．A【分析】用90°减去40°即可求解．【详解】解：∵40A ∠=︒，∴A ∠的余角=904050︒-︒=︒，故选A【点睛】本题考查了求一个角的余角，掌握和为90° 的两角互为余角是解题的关键．21．B【分析】如图，过B 作BQ ⊥平面镜EF ，可得90QBE QBF ∠=∠=︒，ABC CBQ ABQ MBQ ∠+∠=∠=∠，而90CBQ QBM CBM ∠+∠=∠=︒，再建立方程5090CBQ CBQ ︒+∠=︒-∠，可得20CBQ ∠=︒，从而可得答案．【详解】解：如图，过B 作BQ ⊥平面镜EF ，∴90QBE QBF ∠=∠=︒，ABC CBQ ABQ MBQ ∠+∠=∠=∠，而90CBQ QBM CBM ∠+∠=∠=︒，∴5090CBQ CBQ ︒+∠=︒-∠，∴20CBQ ∠=︒，∴902070EBC ∠=︒-︒=︒，故选B ．【点睛】本题考查的是垂直的定义，角的和差运算，角平分线的含义，属于跨学科题，熟记基础概念是解本题的关键．22．C【分析】本题考查了垂线和平行线，熟练掌握同一平面内，垂直于同一条直线的两条直线平行是关键．根据同一平面内，垂直于同一条直线的两条直线平行，即可得出答案．【详解】解：∵l m ⊥，n m ⊥，∴l n ∥．故选：C ．23．B【分析】本题考查平行线的性质，解答本题的关键是明确平行线的性质．首先利用平行线的性质得到1DAC ∠∠=，然后利用AB AC ⊥得到90BAC ∠=︒，最后利用角的和差关系求解．【详解】解：如图所示，∵直线a b ，∴1DAC ∠∠=，∵1130∠=︒，∴130DAC ∠=︒，又∵AB AC ⊥，∴90BAC ∠=︒，∴21309040DAC BAC ∠∠∠=-=︒-︒=︒．故选：B ．24．B【分析】两条线a 、b 被第三条直线c 所截，在截线的同旁，被截两直线的同一方，把这种位置关系的角称为同位角，据此作答即可．【详解】解：∠1与∠2是对顶角，选项A 不符合题意；∠1与∠3是同位角，选项B 符合题意；∠2与∠3是内错角，选项C 不符合题意；∠3与∠4是邻补角，选项D 不符合题意；故选：B ．【点睛】此题考查了同位角、内错角、同旁内角，熟记同位角、内错角、同旁内角的定义是解题的关键．25．C【分析】根据平行线的判定方法进行判断即可．【详解】解：A.∠1与∠2是邻补角，无法判断两条铁轨平行，故此选项不符合题意；B. ∠1与∠3与两条铁轨平行没有关系，故此选项不符合题意；C. ∠1与∠4是同位角，且∠1=∠4=90°，故两条铁轨平行，所以该选项正确；D. ∠1与∠5与两条铁轨平行没有关系，故此选项不符合题意；故选：C ．【点睛】本题主要考查了平行线的判定，熟练掌握平行线的判定是解答本题的关键．26．D【分析】根据“同位角相等，两直线平行”即可得．【详解】解：因为1∠与2∠是一对相等的同位角，得出结论是AB CD ，所以其依据可以简单说成同位角相等，两直线平行，故选：D ．【点睛】本题考查了平行线的判定，熟练掌握平行线的判定方法是解题关键．27．D【分析】根据平行线的判定定理、三角形的外角定理以及等腰三角形的等角对等边的性质依次判断．【详解】解：∵1280∠=∠=︒，∴//AB CD ，故A 选项正确；∵180∠=︒，∴80EBF EFB ∠+∠=︒,∵340EFB ∠=∠=︒,∴40EBF ∠=︒,故B 选项正确；32FCG ∠+∠=∠，故C 选项正确；∵40EFB EBF ∠=∠=︒，∴EF=BE ，故D 选项错误，故选：D ．【点睛】此题考查平行线的判定定理、三角形的外角定理以及等腰三角形的等角对等边的性质，熟记各定理是解题的关键．28．B【分析】平行线的性质，得到ABD FDE ∠=∠，再利用CBD ABD ABC ∠=∠-∠，进行求解即可．【详解】解：由题意，得：4530EDF ABC ∠=︒∠=︒，，∵AB FC ，∴45ABD FDE ∠=∠=︒，∴15CBD ABD ABC ∠=∠-∠=︒；故选B ．【点睛】本题考查平行线的性质，三角板中角度的计算．正确的识图，掌握平行线的性质，是解题的关键．29．C【分析】延长AB 交EG 于点M ，延长CD 交GF 于点N ，过点G 作AB 的平行线GH ，根据平行线的性质即可解答．【详解】解：如图，延长AB 交EG 于点M ，延长CD 交GF 于点N ，过点G 作AB 的平行线GH ，4780,E F EBA FDC ∠=∠=∠=∠= ，33EMA EBA E ∴∠=∠-∠=︒，33FNC FDC F ∠=∠-∠=︒，,AB CD AB HG ∥∥ ，HG CD ∴∥，33MGH EMA ∴∠=∠=︒，33NGH FND ∠=∠=︒，333366EGF ∴∠=︒+︒=︒，故选：C ．【点睛】本题考查了平行线的判定及性质，三角形外角的定义和性质，作出正确的辅助线是解题的关键．30．3πa 【详解】根据圆柱的体积=圆柱的底面积⨯圆柱的高，可得23ππV a a a == ．故答案为：3πa ．【点睛】本题主要考查代数式和整式的乘法运算，牢记整式乘法的运算性质是解题的关键．31．36+##36+【分析】根据题意得出正三角形的边长为2，进而根据表面积等于两个底面积加上侧面正方形的面积即可求解．【详解】解：∵侧面展开图是边长为6的正方形，∴底面周长为6，∵底面为正三角形，∴正三角形的边长为2作CD AB ⊥，ABC 是等边三角形，2AB BC AC ===，1AD ∴=，∴在直角ADC ∆中，CD ==，122ABC S ∴=⨯=∴该直三棱柱的表面积为6636⨯+=+故答案为：36+．【点睛】本题考查了三棱柱的侧面展开图的面积，等边三角形的性质，正方形的性质，熟练掌握以上知识是解题的关键．32．135°##135度【分析】根据三角板及其摆放位置可得180,45BAO BAC OAC OAC ∠=︒=∠+∠∠=︒，求解即可．【详解】180,45BAO BAC OAC OAC ∠=︒=∠+∠∠=︒ ，18045135BAC ∴∠=︒-︒=︒，故答案为：135°．【点睛】本题考查了求一个角的补角，即两个角的和为180度时，这两个角互为补角，熟练掌握知识点是解题的关键．33．30【详解】∵互余两角的和等于90°，∴α的余角为：90°-60°=30°.故答案为：3034．120【分析】如果两个角的和等于180°，就说这两个角互为补角．由此定义即可求解．【详解】解：∵∠A 的补角是60°，∴∠A =180°-60°=120°，故答案为：120．【点睛】本题考查补角的定义，熟练掌握两个角互为补角的定义是解题的关键．35【分析】根据线段的垂直平分线和角平分线的作法可知：EF 是线段AB 的垂直平分线，AO 是∠AOB 的平分线，利用线段的垂直平分线的性质和角平分线的性质的求解即可．【详解】解：如图所示：根据题意可知：EF 是线段AB 的垂直平分线，AO 是∠BAC 的平分线，∵AB =6，∠BAC =60°，∴∠BAO =∠CAO =12∠BAC =30°，AD =12AB =3，∴AM =2MD ，在Rt △ADM 中，222(2)MD MD AD =+，即22243MD MD =+，∴MD ∵AM 是∠AOB 的平分线，MD ⊥AB ，∴点M 到射线AC【点睛】本题考查作图-基本作图，线段的垂直平分线的性质，角平分线的性质等知识，解题的关键是理解题意灵活运用基本作图的知识解决问题．36．140【分析】根据两次转弯后方向不变得到AB CD ，即可得到140BCD ABC ∠=∠=︒．【详解】解：∵一条公路经两次转弯后，方向未变，∴转弯前后两条道路平行，即AB CD ，∴140BCD ABC ∠=∠=︒．故答案为：140．【点睛】此题考查了平行线的性质，由题意得到AB CD 是解题的关键．37． BC DE 内错角相等，两直线平行【分析】根据三角板的角度可知90BCA DEF ∠=∠=︒，根据内错角相等，两直线平行判断即可．【详解】解：一副三角板如图摆放，∴90BCA DEF ∠=∠=︒，∴//BC DE （内错角相等，两直线平行），故答案为：BC ；DE ；内错角相等，两直线平行．【点睛】本题考查了平行线的判定，熟知平行线的判定定理是解本题的关键．38．140︒##140度【分析】如图，先标注点与角，由对折可得：1420∠=∠=︒，求解3180220140∠=︒-⨯︒=︒，利用AB CD ∥，从而可得答案．【详解】解：如图，先标注点与角，由对折可得：1420∠=∠=︒，∴3180220140∠=︒-⨯︒=︒，∵AB CD ∥，∴23140∠=∠=︒；故答案为：140︒【点睛】本题考查的是折叠的性质，平行线的性质，熟记两直线平行，同位角相等是解本题的关键．39．(1)见解析(2)等边三角形【分析】（1）由平行线的性质得到EAD B ∠=∠，已知,B D ∠=∠则EAD D ∠=∠，可判定,BE CD ∥即可得到E ECD ∠=∠；（2）由60E ∠=︒，E ECD ∠=∠得到60ECD E ∠=∠=︒，由CE 平分BCD ∠，得到60BCE ECD ∠=∠=︒，进一步可得BCE E BEC ∠=∠=∠，即可证明BCE 是等边三角形．【详解】（1）证明：AD BC ，∴EAD B ∠=∠，,B D ∠=∠ EAD D ∴∠=∠，,BE CD ∴∥E ECD ∴∠=∠．（2）∵60E ∠=︒，E ECD ∠=∠，∴60ECD E ∠=∠=︒，∵CE 平分BCD ∠，∴60BCE ECD ∠=∠=︒，∴60BCE E ∠=∠=︒，∴18060B BCE E ∠=︒-∠-∠=︒，∴BCE E B ∠=∠=∠，∴BCE 是等边三角形【点睛】此题考查了平行线的判定和性质、等边三角形的判定、三角形内角和定理、角平分线的定义等知识，熟练掌握平行线的判定和性质是解题的关键．40．(1)100BAD ∠=︒(2)证明见解析【分析】本题主要考查了平行线的判定和性质．（1）根据两直线平行，同旁内角互补，即可求解；（2）根据AE 平分BAD ∠，可得50DAE ∠=︒．再由AD BC ∥，可得50AEB DAE ∠=∠=︒．即可求证．【详解】（1）解：∵AD BC ∥，∴180B BAD ∠+∠=°，∵80B ∠=︒，∴100BAD ∠=︒．（2）证明：∵AE 平分BAD ∠，∴1502DAE BAD ∠=∠=︒．∵AD BC ∥，∴50AEB DAE ∠=∠=︒．∵50BCD ∠=︒，∴BCD AEB ∠=∠．∴AE DC ∥．。

精选2019-2020年数学六年级下册第9章几何图形初步9.1 几何图形人教五四学制版课后辅导练习-含答案解析第三十篇第1题【单选题】有3块积木，每一块的各面都涂上不同的颜色，3块的涂法完全相同，现把它们摆放成不同的位置（如图），请你根据图形判断涂成绿色一面的对面的颜色是( )A、白B、红C、黄D、黑【答案】：【解析】：第2题【单选题】下面的图形中，不是平面图形的是( )A、角B、圆柱C、直线D、圆【答案】：【解析】：第3题【单选题】将一个直角三角形绕它的最长边（斜边）旋转一周得到的几何体是图中的( ) A、B、C、D、【答案】：【解析】：第4题【单选题】一个直棱柱有12个顶点，则它的棱的条数是( )A、12B、6C、18D、20【答案】：【解析】：第5题【单选题】以下图形中，不是平面图形的是( )A、线段B、角C、圆锥D、圆【答案】：【解析】：第6题【单选题】一个六棱柱的顶点个数、棱的条数、面的个数分别是( )A、6、12、6B、12、18、8C、18、12、6D、18、18、24【答案】：【解析】：第7题【解答题】观察图中的立体图形，分别写出它们的名称．【答案】：【解析】：第8题【解答题】如图①、②、③、④四个图形都是平面图形，观察图②和表中对应数值，探究计数的方法并解答下面的问题．（1）数一数每个图各有多少顶点、多少条边、这些边围成多少区域，将结果填入下表：（2）根据表中的数值，写出平面图的顶点数、边数、区域数之间的关系；（3）如果一个平面图形有20个顶点和11个区域，求这个平面图形的边数．【答案】：【解析】：第9题【解答题】人人争当小小设计师．一个工程队为建设一项重点工程，要在一块长方形荒地上建造几套简易住房，每一套简易住房的平面是由长4y、宽4x构成，要求建成：两室、一厅、一厨、一卫．其中客厅面积为6xy；两个卧室的面积和为8xy；厨房面积为xy；卫生间面积为xy．请你根据所学知识，在所给图中设计其中一套住房的平面结构示意图．【答案】：【解析】：第10题【解答题】张先生前年在美美家园住宅小区订购了一套住房，图纸如图所示。

2019-2020年人教五四学制版初中数学六年级下册第9章几何图形初步9.2 直线、射线、线段复习巩固五十九第1题【单选题】如图中的线段，直线或射线，能相交的是( )A、B、C、D、【答案】：【解析】：第2题【单选题】下列说法中正确的有( )①过两点有且只有一条直线．②连接两点的线段叫做两点间的距离．③两点之间，线段最短．④若AB=BC，则点B是AC的中点．⑤射线AC和射线CA是同一条射线．A、1个B、2个C、3个D、4个【答案】：【解析】：第3题【单选题】下列说法：①过两点有且只有一条直线；②连接两点的线段叫做两点的距离；③两点之间，线段最短；④如果AB=BC，那么B是线段AC的中点。

其中正确的有( )A、1个B、2个C、3个D、4个【答案】：【解析】：第4题【单选题】如图中的线段，直线或射线，能相交的是( ) AB、CD【答案】：【解析】：第5题【单选题】延长线段AB到点C，下列说法中正确的是( )A、点C在线段AB上B、点C在直线AB上C、点C不在直线AB上D、点C在直线AB的延长线上【答案】：【解析】：第6题【单选题】已知A、B两点之间的距离是10cm，C是线段AB上的任意一点，则AC中点与BC中点间距离是( )A、3cmB、4cmC、5cmD、不能计算【答案】：【解析】：第7题【填空题】已知线段AB=20cm，直线AB上有一点C，且BC=6cm，点M是线段AB的中点，点N是线段BC的中点，则MN=______cm．【答案】：【解析】：第8题【填空题】如图，线段AB=BC=CD=DE=1cm，图中所有线段的长度之和为______cm．【答案】：【解析】：第9题【填空题】两点的所有连线中，______最短．连接______的______叫做两点间的距离．【答案】：【解析】：第10题【填空题】如图，要从B点到C点，有三条路线：①从B到A再到C；②从B到D再到C；③线段BC．要使距离最近，你选择路线______（填序号），理由是______【答案】：【解析】：第11题【填空题】木匠师傅锯木料时，一般先在木板上画出两个点，然后过这两点得出一条墨线，这是根据数学原理______.【答案】：【解析】：第12题【解答题】如图所示，点A在线段CB上，AC=有误AB，点D是线段BC的中点．若CD=3，求线段AD的长．【答案】：【解析】：第13题【综合题】探究题：如图①，已知线段AB=14cm，点C为AB上的一个动点，点D、E分别是AC和BC的中点．若点C恰好是AB中点，则DE=______cm；若AC=4cm，求DE的长；试利用“字母代替数”的方法，设AC=a cm请说明不论a取何值（a不超过14cm），DE的长不变；知识迁移：如图②，已知∠AOB=120°，过角的内部任一点C画射线OC，若OD、OE分别平分∠AOC 和∠BOC，试说明∠DOE=60°与射线OC的位置无关．【答案】：无【解析】：第14题【综合题】按下列要求画图并填空：画图：① 过点A画AD⊥BC，垂足为D② 过点C画CE⊥AB，垂足为E③ 过点B画BF⊥AC，垂足为F填空：① 点B、C两点的距离是线段______的长度，AD的长度表示点A到直线______的距离.② 点B到直线AC的距离是线段______的长度.③点E到直线AB的距离是______.【答案】：【解析】：第15题【综合题】如图，公路上依次有A、B、C三站，上午8时，甲骑自行车从A、B之间离A站18km的P点出发，向C站匀速前进，15分钟到达距离A站22km的某处．设x小时后，甲离A站ykm，用含x的代数表示y；若A、B和B、C间的距离分别是30km和20km，则上午______到______的时间内，甲在B、C两站之间（不包括B、C两站）．【答案】：【解析】：。

第 9单元总复习第3课时图形与几何(1)【教学内容】课本第116页的第2题，课本第119～120页的练习二十八第11～16题。

【教学目标】1.通过一视图和三视图摆放小正方体，进一步培养学生空间想象力。

2.进一步明确长方体、正方体的特征，理解长方体、正方体表面积和体积的含义，并正确计算。

3.能运用长方体、正方体的知识解决简单的问题。

【教学过程】一、知识梳理1.摆一摆。

（1）只给一个正面看到的正方体小木块堆成的图形，怎样摆？有多种摆法?（2）给出从正面、上面、左边看到的正方体小木块堆成的图形，怎样摆？有多种摆法吗?2.长方体和正方体。

（1）说一说长方体和正方体的特征。

将学生的回答填在空格中。

①长方体有个面。

②每个面是什么形状？③哪些面是完全相同的？④长方体有条棱。

⑤哪些棱长度相等？⑥长方体有个顶点。

⑦还有什么发现？（2）表面积。

学生看图解答：①上、下每个面是形，长，宽，面积是，两个面积和是。

②前、后每个面是形，长，宽，面积是，两个面积和是。

③左、右每个面是形，长，宽，面积是，两个面积和是。

④这个长方体的表面积是：。

⑤如果这个长方体箱子没有盖子，那么要扣除哪个面的面积？需要材料面积是多少？⑥如果要在这个箱子的四周贴上一圈包装纸，包装纸的面积是多少？扣除哪些面的面积？（3）体积。

学生看图回答问题。

（以上面的图为例）①这个箱子的容积是多少？可以怎么求？②长方体、正方体的体积公式是什么？（4）体积单位。

①常用的体积单位有哪些？②一般情况下升、毫升是用于什么单位？③说一说，你所了解的体积单位间的进率。

二、巩固练习完成课本第116页第2题。

完成课本117页第3题。

1.完成课本第120页的第16题。

此题是图形变换的习题，练习时，让学生在小组内说说图一是怎样变换得到图二的。

2.完成课本第119页的第11题。

练习时，由学生独立填写，然后全班反馈，反馈时，让学生再次说说表面积和体积的区别。

3.完成课本第119页的第12题。

六年级数学下册第九章几何图形初步重点解析考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I 卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I 卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、已知C 是线段AB 的中点，则BC AB 的值为（ ）． A ．13 B ．12 C ．1 D ．22、如图，将一副直角三角尺按不同方式摆放，则图中α∠与β∠互余的是（ ）A ．B ．C ．D ．3、某同学从A 地出发沿北偏东30°的方向步行5分钟到达B 地，再由B 地沿南偏西40°的方向步行到达C 地，则∠ABC 的大小为（ ）A ．10°B ．20°C ．35°D ．70°4、将一副三角板按如图所示拼接，若∠ADE 、∠CBE 均小于平角，则∠ADE +∠CBE 等于（ ）A ．300°B ．285°C ．270°D ．265°5、已知点D 是线段AB 的中点，C 是线段AD 的中点，若CD ＝1，则AB ＝（ ）A ．1B ．2C ．3D ．46、下列立体图形中，各面不都是．．．平面图形的是（ ） A ． B ． C ． D ．7、如果A 、B 、C 三点在同一直线上，线段4cm AB =，2cm BC =，那么A 、C 两点之间的距离为（ ）A ．2cmB ．6cmC ．2cm 或6cmD ．无法确定8、如图，下列说法正确的是（ ）A ．线段AB 与线段BA 是不同的两条线段B ．射线BC 与射线BA 是同一条射线C ．射线AB 与射线AC 是两条不同的射线D ．直线AB 与直线BC 是同一条直线9、如图，将一副直角三角尺按不同方式摆放，则图中α∠与β∠互余的是（ ）A．B．C．D．10、已知∠AOB＝100°，过点O作射线OC、OM，使∠AOC＝20°，OM是∠BOC的平分线，则∠BOM的度数为（）A．60°B．60°或40°C．120°或80°D．40°第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、若∠α＝53°18′，则∠α的余角的度数为 _____．2、如图，两根木条的长度分别为7cm和12cm．在它们的中点处各打一个小孔M、N（木条的厚度，宽度以及小孔大小均忽略不计）．将这两根木条的一端重合并放置在同一条直线上，则两小孔间的距离MN=______cm．3、若小明从A处沿北偏东40︒方向行走至点B处，又从B处沿东偏南20︒方向行走至点C处，则∠_______．ABC=4、如图，已知O 是直线AB 上一点，OC 平分∠BOD ，OE 平分∠AOD ，则与∠DOE 互余的角有___个．5、已知4018B '∠=︒，则∠B 的补角的度数为______．三、解答题（5小题，每小题10分，共计50分）1、如图，线段8AB =，点C 是AB 的中点，D 是BC 的中点，E 是AD 的中点．(1)求线段BD 的长；(2)求线段EC 的长．2、已知：如图，点A 、B 、C 、D 四点共线，AC ＝2BC ，BC ＝3，D 为AB 中点，求CD 的长．3、如图，ON 平分AOC ∠，OM 平分BOC ∠．(1)计算求值：若90AOB ∠=︒，60AOC ∠=︒，求MON ∠的度数；(2)拓展探究：若90AOB ∠=︒，则MON ∠=______°；(3)问题解决：若AOB x ∠=︒，MON y ∠=︒，①用含x 的代数式表示y =______；②如果156AOB MON ∠+∠=︒，试求MON ∠的度数．4、如图，∠AOB 是直角，∠BOC ＝40°，OD 是∠AOC 的平分线，求∠BOD 的度数．5、已知线段AB a （如图），延长BA 至点C ，使2AC AB =，延长AB 至点D ，使12BD AB =．(1)请按上述要求画全图形；(2)求线段CD 的长（用含a 的代数式表示）；(3)若E 是CD 的中点, 3AE =，求a 的值．-参考答案-一、单选题1、B【解析】【分析】 根据线段中点的定义可知12AC BC AB ==，由此求解即可． 【详解】解：∵C是AB的中点，∴12AC BC AB==，∴12 BCAB=，故选B．【点睛】本题主要考查了与线段中点有关的计算，熟知线段中点的定义是解题的关键．2、A【解析】【分析】A项根据平角的意义即可判断；B根据同角的余角相等即可判断；C根据等角的补角相等即可判断；D 根据角度的关系求出两角的角度再进一步判断即可．【详解】解：A、图中∠α+∠β=180︒-90︒=90︒，∠α与∠β互余，故本选项符合题意；B、图中∠α=∠β，不一定互余，故本选项不符合题意；C、图中∠α=∠β=135︒，不是互余关系，故本选不符合题意；D、图中∠α=45︒，∠β=60︒，不是互余关系，故本选不符合题意；故选：A．【点睛】本题考查了余角和补角，是基础题，熟记余角的概念是解题的关键．3、A【解析】【分析】根据方向角的意义以及角的和差关系进行计算即可.【详解】解：由题意得，30NAB ABS ∠︒∠＝＝，40SBC ∠︒＝，ABC SBC ABS ∴∠∠-∠＝4030︒-︒＝10︒＝.故选：A .【点睛】本题考查方向角，理解方向角的意义，掌握角的和差关系是解决问题的关键.4、B【解析】【分析】根据求邻补角以及几何图形中角度的计算求解即可【详解】解：∠ADE +∠CBE 180BDE CBA DBE =︒-∠+∠+∠180456090=︒-︒+︒+︒135150=︒+︒285=︒故选B【点睛】本题考查了求一个角的补角，以及三角尺中角度的计算，数形结合是解题的关键．5、D【解析】【分析】根据线段的中点性质先求出AD，再求出AB即可．【详解】解：如图：C是线段AD的中点，1CD=，∴==，AD CD22点D是线段AB的中点，∴==，24AB AD故选：D．【点睛】本题考查了两点间距离，解题的关键是根据题目的已知条件画出图形．6、B【解析】【分析】根据立体图形的基本性质即可求解．【详解】解：A.四棱锥是由平面围成，B. 圆锥是由2个面围成，底面是平面，侧面是曲面，不都是由平面图形围成，C. 六棱柱是由平面围成，D. 三棱柱是由平面围成，故选：B．【点睛】本题考查了立体图形的基本性质，逐个判断即可得出答案．7、C【解析】【分析】根据题意，利用分类讨论的数学思想可以求得A、C两点间的距离．【详解】解：∵A、B、C三点在同一条直线上，线段AB=4cm，BC=2cm，∴当点C在点B左侧时，A、C两点间的距离为：4-2=2（cm），当点C在点B右侧时，A、C两点间的距离为：4+2=6（cm），故选C．【点睛】本题考查两点间的距离，解答本题的关键是明确题意，利用分类讨论的数学思想解答．8、D【解析】【分析】根据直线、线段、射线的区别进行判断即可．【详解】解：A、线段AB与线段BA端点相同，顺序不同，属于一条线段，故错误；B、射线BC与射线BA端点与方向均不同，不是同一射线，故错误；C、射线AB与射线AC端点相同，方向相同，属于同一射线，故错误；D、直线AB与直线BC属于同一直线，故正确．故选：D．【点睛】本题考查的是直线、线段、射线的定义，熟练掌握之间的区别即可进行解题．9、A【解析】【分析】A项根据平角的意义即可判断；B根据同角的余角相等即可判断；C根据等角的补角相等即可判断；D 根据角度的关系求出两角的角度再进一步判断即可．【详解】解：A、图中∠α+∠β=180︒-90︒=90︒，∠α与∠β互余，故本选项符合题意；B、图中∠α=∠β，不一定互余，故本选项不符合题意；C、图中∠α=∠β=135︒，不是互余关系，故本选不符合题意；D、图中∠α=45︒，∠β=60︒，不是互余关系，故本选不符合题意；故选：A．【点睛】本题考查了余角和补角，是基础题，熟记余角的概念是解题的关键．10、B【解析】【分析】分两种情况求解：①当OC在∠AOB内部时，②当OC在∠AOB外部时；分别求出∠BOM的度数即可．【详解】解：如图1，当OC在∠AOB内部时，∵∠AOB＝100°，∠AOC＝20°，∴∠BOC＝80°，∵OM是∠BOC的平分线，∴∠BOM＝40°；如图，当OC在∠AOB外部时，∵∠AOB＝100°，∠AOC＝20°，∴∠BOC＝120°，∵OM是∠BOC的平分线，∴∠BOM＝60°；综上所述：∠BOM的度数为40°或60°，故选：B．【点睛】本题考察了角的计算，熟练掌握角平分线的性质，分两种情况画出图形是解题的关键．二、填空题︒1、3642'【解析】【分析】相加为90°的两个角互为余角，根据定义解答．【详解】︒，解：90°-∠α＝90°-53°18′=3642'︒．故答案为：3642'【点睛】此题考查了余角的定义，熟记定义并正确运算是解题的关键．2、2.5或9.5##9.5或2.5【解析】【分析】本题没有给出图形，在画图时，应考虑到A、B、M、N四点之间的位置关系的多种可能，再根据题意正确地画出图形解题．【详解】解：本题有两种情形：（1）当A、C（或B、D）重合，且剩余两端点在重合点同侧时，MN=CN-AM=12CD-12AB=6-3.5=2.5（厘米）；（2）当B、C（或A、C）重合，且剩余两端点在重合点两侧时，MN=CN+BM=12CD+12AB，=6+3.5=9.5（厘米）．故两根木条的小圆孔之间的距离MN是2.5cm或9.5cm，故答案为：2.5或9.5．【点睛】本题考查两点之间的距离问题，在未画图类问题中，正确画图很重要，本题渗透了分类讨论的思想，体现了思维的严密性，在今后解决类似的问题时，要防止漏解．【解析】【分析】根据题意可得40BAD ∠=︒，20FBC ∠=︒，得出40ABE ∠=︒，70CBE ∠=︒，根据各角之间的数量关系求解即可得．【详解】解：如图所示：根据题意可得40BAD ∠=︒，20FBC ∠=︒，∴40ABE ∠=︒，902070CBE ∠=︒-︒=︒，∴110ABC ABE CBE ∠=∠+∠=︒，故答案为：110︒．【点睛】题目主要考查方位角的计算，理解题意，找准各角之间的关系是解题关键．4、2【解析】【分析】根据OC 平分∠BOD ，OE 平分∠AOD ，可得∠AOE ＝∠DOE ＝12∠AOD ，∠BOC ＝∠DOC ＝12∠BOD ，从而得到∠DOC +∠DOE ＝90°，∠BOC +∠DOE ＝90°，即可求解．解：∵∠AOD +∠BOD ＝180°，OC 、OE 分别平分∠BOD 和∠AOD ，∴∠AOE ＝∠DOE ＝12∠AOD ，∠BOC ＝∠DOC ＝12∠BOD ，∴∠DOC +∠DOE ＝90°，∠BOC +∠DOE ＝90°，∴与∠DOE 互余的角有∠DOC 和∠BOC ．故答案为：2【点睛】本题主要考查了有关角平分线的计算，余角的性质，邻补角的性质，熟练掌握余角的性质，邻补角的性质是解题的关键．5、4942'︒【解析】【分析】根据补角的性质，即可求解．【详解】解：∵4018B '∠=︒，∴∠B 的补角的度数为9040184942''︒-︒=︒．故答案为：4942'︒【点睛】本题主要考查了补角的性质，熟练掌握互为补角的两个角的和等于180°是解题的关键．三、解答题1、 (1)2(2)1【分析】（1）由点C 是AB 的中点可得AC ＝BC ＝4，由点D 是BC 的中点可得BD ＝CD ＝2即可；（2）由（1）可知AE 、AD 的长，再根据EC ＝AC −AE ，即可得出线段EC 的长．(1)解：因为点C 是AB 的中点，8AB =， 所以142AC BC AB ===， 又因为点D 是BC 的中点， 所以122BD CD BC ===．(2)解：由（1）得4AC =，6AD AC CD =+=，因为E 是AD 的中点， 所以132AE ED AD ===， 所以431EC AC AE =-=-=．【点睛】本题考查了两点间的距离以及线段中点的定义，利用线段的和差是解题关键．2、1.5【解析】【分析】由题意易得AC ＝6，然后可得AB ＝9，进而根据线段中点的性质及线段和差关系可求解．【详解】解：∵AC＝2BC，BC＝3，∴AC＝6，∴AB＝AC＋BC＝9，∵D为AB中点，∴DB＝12AB＝4.5，∴DC＝DB﹣BC＝1.5．【点睛】本题主要考查线段的和差关系及中点的性质，熟练掌握线段的和差关系及中点的性质是解题的关键．3、(1)45°(2)45(3)①12x；②52°【解析】【分析】（1）先求出∠BOC的度数，再根据角平分线的定义求出∠MOC与∠NOC的度数，然后相减即可得解；（2）仿照（1）的步骤求解即可；（3）①先求出∠BOC的度数，再根据角平分线的定义求出∠MOC与∠NOC，然后根据∠MON=∠MOC-∠NOC列式整理即可；②根据（2）①的规律，∠MON的度数等于∠AOB的一半，进行求解即可．(1)解：∵∠AOB＝90°，∠AOC＝60°，∴∠BOC＝∠AOB＋∠AOC＝90°＋60°＝150°，∵ON平分∠AOC，OM平分∠BOC，∴111507522COM BOC∠=∠==︒⨯︒，11603022CON AOC∠=∠==︒⨯︒，∴∠MON＝∠COM－∠CON＝75°－30°=45°；(2)∵∠AOB＝90°∴∠BOC＝∠AOB＋∠AOC＝90°＋∠AOC，∵ON平分∠AOC，OM平分∠BOC，∴1145+22COM BOC AOC∠=∠=∠，12CON AOC∠=∠，∴∠MON＝∠COM－∠CON＝1145+22AOC AOC∠-∠=45°；(3)①∵∠AOB=x°，∴∠BOC=∠AOB+∠AOC=x°+∠AOC，∵ON平分∠AOC，OM平分∠BOC．∴∠MOC=12∠BOC=12x+12∠AOC，∠NOC=12∠AOC，∴∠MON=∠MOC-∠NOC=12x，即y=12x；②由题意可得x+12x=156，解得：x=104，从而y=12x=52即∠MON=52°．【点睛】本题考查了角的计算，主要利用了角的平分线的定义，准确识图是解题的关键．4、25°【解析】【分析】根据∠AOB是直角，∠BOC＝40°，可得∠AOC=130°，再由OD是∠AOC的平分线，可得∠COD=65°，即可求解．【详解】解：∵∠AOB是直角，∴∠AOB=90°，∵∠BOC＝40°，∴∠AOC=∠AOB+∠BOC=130°，∵OD是∠AOC的平分线，∴1652COD AOC∠=∠=︒，∴∠BOD=∠COD-∠BOC=25°．【点睛】本题主要考查了有关角平分线的计算，角的和与差，根据题意，准确得到角与角间数量关系是解题的关键．5、 (1)见解析(2)72 CD a=(3)12a=【解析】【分析】（1）根据题意，画出图形，即可求解；（2）根据2AC AB =，12BD AB =可得AC =2a ，12BD a =，即可求解； （3）根据E 是CD 的中点，可得1724CE CD a ==，从而得到14AE AC CE a =-=，即可求解． (1)解：如图所示：(2)解：∵AC =2AB =2a ，1122BD AB a ==， ∴17222CD AC AB BD a a a a =++=++=； (3)解：如图，∵E 是CD 的中点， ∴1724CE CD a ==， ∴71244AE AC CE a a a =-=-=， ∵AE =3，即134a =，a ．∴12【点睛】本题主要考查了线段的和与差，有关线段中点的计算，根据题意，准确画出图形是解题的关键．。