分形混沌实验报告2

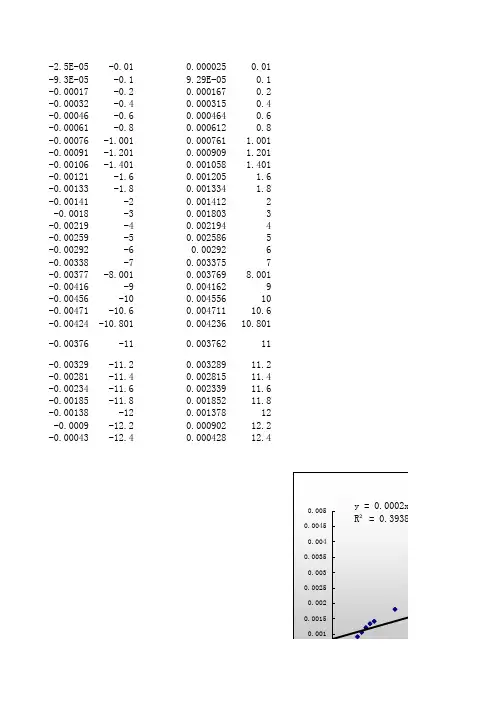
-2.5E-05-0.010.0000250.01-9.3E-05-0.19.29E-050.1-0.00017-0.20.0001670.2-0.00032-0.40.0003150.4-0.00046-0.60.0004640.6-0.00061-0.80.0006120.8-0.00076-1.0010.000761 1.001-0.00091-1.2010.000909 1.201-0.00106-1.4010.001058 1.401-0.00121-1.60.001205 1.6-0.00133-1.80.001334 1.8-0.00141-20.0014122-0.0018-30.0018033-0.00219-40.0021944-0.00259-50.0025865-0.00292-60.002926-0.00338-70.0033757-0.00377-8.0010.0037698.001-0.00416-90.0041629-0.00456-100.00455610-0.00471-10.60.00471110.6-0.00424-10.8010.00423610.801-0.00376-110.00376211-0.00329-11.20.00328911.2-0.00281-11.40.00281511.4-0.00234-11.60.00233911.6-0.00185-11.80.00185211.8-0.00138-120.00137812-0.0009-12.20.00090212.2-0.00043-12.40.00042812.40.000428325个6sigma品质网：http://wwY X预测值残差预测区间下限预测区间上限0.0000250.010.00083956-0.00081456-0.0016441940.003323313 9.29368E-050.10.000856892-0.000763956-0.0016250370.003338822 0.0001670840.20.000876151-0.000709067-0.0016037820.003356085 0.0003153830.40.000914669-0.000599286-0.0015613720.003390709 0.0004636790.60.000953186-0.000489507-0.0015190940.003425466 0.0006119480.80.000991703-0.000379755-0.0014769490.003460356 0.000760985 1.0010.001030413-0.000269428-0.0014347280.003495555 0.000909297 1.2010.001068931-0.000159633-0.0013928510.003530713 0.001057598 1.4010.001107448-4.98503E-05-0.0013511090.003566005 0.001205182 1.60.001145773 5.94092E-05-0.001309710.003601256 0.001333827 1.80.001184290.000149537-0.0012682380.003636819 0.00141193120.0012228080.000189123-0.0012269020.003672517 0.00180310130.0014153950.000387706-0.001022280.00385307 0.00219442640.0016079820.000586444-0.0008211240.004037088 0.00258611850.0018005690.000785549-0.0006234690.004224607 0.00292007960.0019931560.000926923-0.0004293390.004415651 0.00337512170.0021857430.001189377-0.0002387390.004610225 0.0037685468.0010.0023785230.001390023-5.14752E-050.004808521 0.0041618590.0025709170.0015909320.0001319190.005009915 0.004555809100.0027635040.0017923040.000312040.005214969 0.00471111110.60.0028790570.0018320540.0004184730.005339641 0.00423568610.8010.0029177670.001317920.0004538560.005381678 0.00376197110.0029560910.0008058780.0004887530.00542343 0.0032892811.20.0029946090.0002946720.0005236920.005465525 0.00281481511.40.003033126-0.0002183120.0005584990.005507754 0.0023387111.60.003071644-0.0007329340.0005931720.005550115 0.00185243311.80.003110161-0.0012577280.0006277140.005592608 0.001377727120.003148679-0.0017709520.0006621250.0056352320.000901712.20.003187196-0.0022854960.0006964040.005677987 0.00042832512.40.003225713-0.0027973890.0007305540.005720872个人免费版：仅授权个人学习使用，企业使用必须购买授权，否则为盗版！6sigma品质网：一元线性回归分析数据回归系数置信水平0.05统计量变量数据个数均值自变量30 5.937166667因变量300.001981055回归统计量回归平方和 2.46186E-05误差平方和 3.78973E-05X平方和663.7564642回归系数R0.62753267回归系数R平方0.393797252调整了的R平方0.372147154标准误差0.001163389截距0.000837634斜率0.000192587回归方程Y=0.000837633729593507+0.00019258706951633X回归系数t检验R t统计量t临界值p值显著性0.62753267 4.264875973 2.0484071150.000205781显著方差分析和斜率的F检验自由度平方和平均平方和F统计量回归1 2.46186E-05 2.46186E-0518.18916706剩余28 3.78973E-05 1.35347E-06总计29 6.25159E-05斜率的t检验系数标准误差t统计量t临界值斜率0.000192587 4.51565E-05 4.264875973 2.048407115斜率的置信区间置信区间下限0.000100088置信区间上限0.000285086自回归的检验杜宾-沃森统计量0.074181158杜宾-沃森下临界值 1.35杜宾-沃森上临界值 1.49结果正相关置信区间估计请输入X的值 5.937166667 h统计量0.033333333区间估计置信水平0.05 t临界值 2.048407115 Y预测值的均值0.001981055 Y预测值的均值估计：区间半宽0.000435092 置信区间下限0.001545964 置信区间上限0.002416147单个X对Y的影响：区间半宽0.002422488 预测区间下限-0.000441433 预测区间上限0.004403543F临界值p值显著性4.1959717070.000205781显著p值显著性0.000205781显著。

混沌与分形（二）：分形的奇迹——分数维的曲线混沌的秘密，不可思议地隐藏在分形的世界里。

分形（fractal），该术语最早是由美国数学家曼德勃罗（Mandelbrot）于1973年提出。

曼德勃罗（1924-2010）（图片来源网络）在其名著《大自然的分形几何学》中，曼德勃罗开创了分形几何学。

分形几何以及与其相关的非线性理论，很快就显示出强大的生命力，其影响迅速遍及科学和社会的每个角落。

许多学科中的难题，因为分形的介入而焕然一新。

如梦初醒的科学家才发现，原来分形的身影已经在世界上默默存在了数亿年，从地球诞生始就向大自然昭示其深邃的奥秘。

植物的分形（图片来源：网络）生活中常见的花菜、雷雨过后的闪电、凛冬漫天飞舞的雪花、贝壳身上的螺旋图案，小至各种植物的结构及形态，遍布人体全身纵横交错的血管，大到天空中聚散不定的白云、连绵起伏的群山，它们都或多或少表现出分形的特征。

乍看起来杂乱无章的分形，原来是大自然的基本存在形式，无处不在，随处可见。

分形如此广泛地分布在自然界中，却又与千百年来的智者擦肩而过。

它的发现，正式揭开了大自然最迷人和动人的奥义之一。

早在两千多年前的古希腊时代，人们最杰出的成就来自数论与几何，特别是欧几里得几何的建立，更使得几何学成为最严格和易于把握的公理化体系。

几何研究的对象是图形。

为了研究不同的几何对象，人们倾向于把它们进行归类。

从点、线、面到立体，人们的思维逐渐扩展开来。

渐渐地，人们意识到区别几何图形的重要分水岭：维度。

直线和曲线是一维的图形，平面则是二维的图形，立体则属于三维的空间。

一切都是那么的直观，历史在平静地流淌。

直到有一天，一件匪夷所思的事打破了人们对维度的信念。

1890年，意大利数学家皮亚诺（Piano）构造了一种奇怪的曲线，该曲线自身并不相交，但是它却能通过一个正方形内部所有的点。

换句话说，这条曲线就是正方形本身，进而应该拥有和正方形一样的面积！这个怪异的结论让当时的数学家大吃一惊，更让数学界感到深切的不安：如此一来，我们拿什么来区分曲线和平面？这条曲线究竟是一维，还是二维？经典的几何在它面前束手无策。

实验二：混沌波形发生实验
实验发生过程中，依次观察到的非线性电路的振荡周期分岔现象和混沌现象：
a.单周期分岔；
b.双周期分岔；
c.四周期分岔；
d.多周期分岔；
e.单吸引子；
f. 双吸引
子。

a.单周期分岔
b. 双周期分岔
c. 四周期分岔
d. 多周期分岔
e.单吸引子
f. 双吸引子
实验三：混沌电路的同步实验
图一图二
理论上，两路波形完全相等时，图片上的这条线将是一条45度的非常干净的直线。

45度表示两路波形的幅度基本一致，线的长度表达了波形的振幅，线的粗细代表两路波形的幅度和相位在细节上的差异。

故而这条线表达出了两路波形的同步程度。

由图一可以看出，这条线的45度角度并不明显，而且非常粗糙，可以判断在实验中两路波形并不完全相等，也就是说，两路波形的同步程度还有待提高。

经过调试，示波器上图片的直线形成了一条45度的非常干净的直线，如图二所示，即两路波形达到了同步状态。

用非线性电路研究混沌现象一． 实验目的掌握用示波器观察正弦波形的周期分岔及混沌现象的方法。

学会自己设计和制作一个实用电感器以及测量非线性器件伏安特性的方法。

二． 实验原理1.非线性电路与非线性动力学实验电路如图1所示，图1中只有一个非线性元件R ，它是一个有源非线性负阻器件。

电感器L 和电容C 2组成一个损耗可以忽略的谐振回路；可变电阻R V 和电容器C 1串联将振荡器产生的正弦信号移相输出。

本实验中所用的非线性元件R 是一个三段分段线性元件。

图2所示的是该电阻的伏安特性曲线，从特性曲线显示中加在此非线性元件上电压与通过它的电流极性是相反的。

由于加在此元件上的电压增加时，通过它的电流却减小，因而将此元件称为非线性负阻元件。

图1非线性电路原理图 图2非线性元件伏安特性 图1电路的非线性动力学方程为：1121)(1C C C C U g U U G dtdU C ⋅--⋅= L C C C i U U G dt dU C +-⋅=)(21122 (1)2C L U dt di L -=式中，导纳V R G /1=，1C U 和2C U 分别为表示加在电容器C 1和C 2上的电压，L i 表示流过电感器L 的电流，G 表示非线性电阻的导纳。

2.有源非线性负阻元件的实现有源非线性负阻元件实现的方法有多种，这里使用的是一种较简单的电路，采用两个运算放大器和六个配置电阻来实现其电路如图4所示，实验所要研究的是该非线性元件对整个电路的影响，而非线性负阻元件的作用是使振动周期产生分岔和混沌等一系列非线性现象。

图3有源非线性器件图4双运放非线性元件的伏安特性实际非线性混沌实验电路如图5所示。

图5非线性电路混沌实验电路图三．实验步骤测量一个铁氧体电感器的电感量，观测倍周期分岔和混沌现象。

1.按图5所示电路接线，其中电感器L由实验者用漆包铜线手工缠绕。

可在线框上绕70-75圈，然后装上铁氧体磁心，并把引出漆包线端点上的绝缘漆用刀片刮去，使两端点导电性能良好。

第1篇一、实验目的1. 理解混沌现象的基本特征。

2. 掌握混沌系统的基本理论和方法。

3. 通过实验验证混沌现象的存在。

4. 培养学生的科学实验能力和分析问题能力。

二、实验原理混沌现象是自然界、人类社会和科学技术中普遍存在的一种复杂现象。

混沌系统具有以下基本特征：对初始条件的敏感依赖性、长期行为的不可预测性、分岔和混沌吸引子等。

本实验通过计算机模拟混沌现象，验证混沌系统的基本特征。

三、实验设备与材料1. 计算机2. 混沌原理实验软件3. 数据记录表格四、实验步骤1. 打开混沌原理实验软件，选择合适的混沌模型（如洛伦兹系统、双摆系统等）。

2. 设置初始参数，如初始速度、初始位置等。

3. 运行实验，观察混沌现象的表现。

4. 记录实验数据，包括时间、初始参数、混沌现象等。

5. 分析实验数据，验证混沌现象的基本特征。

五、实验结果与分析1. 实验结果显示，混沌现象在洛伦兹系统中表现得尤为明显。

当系统参数达到一定范围时，系统表现出混沌行为，如分岔和混沌吸引子等。

2. 通过对实验数据的分析，得出以下结论：（1）混沌现象对初始条件具有敏感依赖性。

在实验中，当初始参数发生微小变化时，系统行为会发生显著变化，从而验证了混沌现象的敏感性。

（2）混沌现象具有长期行为的不可预测性。

在实验中，尽管系统参数保持不变，但随着时间的推移，系统行为逐渐变得复杂，最终进入混沌状态，验证了混沌现象的不可预测性。

（3）混沌现象存在分岔现象。

在实验中，当系统参数逐渐变化时，系统状态会经历从有序到混沌的过程，验证了混沌现象的分岔特性。

（4）混沌现象具有混沌吸引子。

在实验中，系统最终会收敛到一个稳定的混沌吸引子，验证了混沌现象的吸引子特性。

六、实验结论1. 混沌现象是自然界、人类社会和科学技术中普遍存在的一种复杂现象，具有对初始条件的敏感依赖性、长期行为的不可预测性、分岔和混沌吸引子等基本特征。

2. 通过实验验证了混沌现象的存在，有助于我们更好地理解混沌现象的本质。

第1篇一、实验目的1. 理解混沌现象的基本概念和特性。

2. 掌握混沌波形的产生机制。

3. 通过实验观察和分析混沌波形的动力学行为。

4. 研究混沌波形在不同参数条件下的变化规律。

二、实验原理混沌现象是自然界和工程领域中普遍存在的一种非线性动力学现象。

它表现为系统在确定性条件下呈现出复杂的、不可预测的行为。

混沌波形的产生通常与非线性动力学方程有关，其中典型的混沌系统包括洛伦茨系统、蔡氏电路等。

本实验采用蔡氏电路作为混沌波形的产生模型。

蔡氏电路由三个非线性元件（电阻、电容和运算放大器）和一个线性元件（电阻）组成。

通过改变电路中的电阻和电容值，可以调节电路的参数，从而产生混沌波形。

三、实验仪器与设备1. 蔡氏电路实验板2. 数字示波器3. 函数信号发生器4. 万用表5. 计算机及数据采集软件四、实验步骤1. 搭建蔡氏电路：根据实验板上的电路图，将电阻、电容和运算放大器等元件按照电路图连接好。

2. 调节电路参数：使用万用表测量电路中各个元件的参数值，并记录下来。

3. 输入信号：使用函数信号发生器输出正弦波信号，作为蔡氏电路的输入信号。

4. 观察混沌波形：打开数字示波器，观察电路输出端的混沌波形。

调整电路参数，观察混沌波形的变化规律。

5. 数据采集：使用数据采集软件，记录混沌波形的时域和频域特性。

6. 分析结果：对采集到的数据进行处理和分析，研究混沌波形的动力学行为。

五、实验结果与分析1. 混沌波形的产生：当电路参数满足一定条件时，蔡氏电路可以产生混沌波形。

混沌波形具有以下特点：- 复杂性：混沌波形呈现出复杂的非线性结构，难以用简单的数学公式描述。

- 敏感性：混沌波形对初始条件和参数变化非常敏感，微小变化可能导致完全不同的波形。

- 自相似性：混沌波形具有自相似结构，局部结构类似于整体。

2. 混沌波形的参数调节：通过调节电路参数，可以改变混沌波形的特性。

例如，改变电容值可以改变混沌波形的周期和频率；改变电阻值可以改变混沌波形的幅度和形状。

竭诚为您提供优质文档/双击可除非线性电路中的混沌现象实验报告篇一：非线性电路混沌实验报告近代物理实验报告指导教师：得分：实验时间：20XX年11月8日，第十一周，周一，第5-8节实验者：班级材料0705学号20XX67025姓名童凌炜同组者：班级材料0705学号20XX67007姓名车宏龙实验地点：综合楼404实验条件：室内温度℃，相对湿度%，室内气压实验题目：非线性电路混沌实验仪器：（注明规格和型号）1.约结电子模拟器约结电子模拟器的主要电路包括:1.1,一个压控震荡电路,根据约瑟夫方程,用以模拟理想的约结1.2,一个加法电路器,更具电路方程9-1-10,用以模拟结电阻、结电容和理想的约结三者相并联的关系1.3，100khz正弦波振荡波作为参考信号2.低频信号发生器用以输出正弦波信号，提供给约结作为交流信号3.数字示波器用以测量结电压、超流、混沌特性和参考信号等各个物理量的波形实验目的：1.了解混沌的产生和特点2.掌握吸引子。

倍周期和分岔等概念3.观察非线性电路的混沌现象实验原理简述：混沌不是具有周期性和对称性的有序，也不是绝对的无序，而是可以用奇怪吸引子等来描述的复杂有序——混沌而呈现非周期性的有序。

混沌的最本质特征是对初始条件极为敏感。

1.非线性线性和非线性，首先区别于对于函数y=f(x)与其自变量x的依赖关系。

除此之外，非线性关系还具有某些不同于线性关系的共性：1.1线性关系是简单的比例关系，而非线性是对这种关系的偏移1.3线性关系保持信号的频率成分不变，而非线性使得频率结构发生变化1.4非线性是引起行为突变的原因2.倍周期，分岔，吸引子，混沌借用T.R.malthas的人口和虫口理论，以说明非线性关系中的最基本概念。

虫口方程如下：xn?1xn(1?xn)μ是与虫口增长率有关的控制参数，当1 1?，这个值就叫做周期或者不动点。

在通过迭代法解方程的过程中，最终会得到一个不随时间变化的固定值。

大学混沌实验报告大学混沌实验报告引言：大学生活是一个充满了各种可能性和挑战的阶段。

在这个阶段，我们面临着来自学业、社交和个人发展的各种压力和选择。

为了更好地了解大学生活中的混沌现象，我们进行了一项混沌实验，以探索混沌现象对大学生活的影响和应对策略。

实验设计：为了模拟大学生活中的混沌现象，我们选择了一个具有多个变量的实验场景。

我们邀请了一组志愿者参与实验，并将他们置于一个充满不确定性和挑战的环境中。

实验持续了一个学期，我们记录了志愿者在实验期间的种种体验和反应。

实验结果：在实验过程中，我们观察到了一系列混沌现象。

首先，志愿者们在面对学业压力时表现出了不同的应对策略。

有些人选择积极主动地面对挑战，主动寻求帮助和解决方案。

而另一些人则表现出了消极应对的态度，选择逃避和放弃。

这种差异性导致了志愿者们在学业上的成绩和表现上的差异。

其次，社交关系也是混沌现象的一个重要方面。

在实验中，我们观察到志愿者们之间的友谊和人际关系的发展过程中存在着不确定性和波动。

有时，一些志愿者之间的友谊会因为误解和冲突而受到影响，而另一些人则能够通过沟通和理解来解决问题。

这种不确定性和波动给志愿者们的情绪和心理健康带来了一定的影响。

最后，个人发展也是混沌现象的一个重要方面。

在实验中，我们观察到志愿者们在个人发展过程中面临着各种选择和困惑。

有些人在探索自己的兴趣和激情时表现得游刃有余，而另一些人则感到迷茫和无助。

这种不确定性和挑战性给志愿者们的未来规划和职业发展带来了一定的影响。

讨论与总结：通过这个混沌实验，我们深入了解了大学生活中的混沌现象对个人和社会的影响。

混沌现象不仅存在于大学生活中，也存在于我们的日常生活中。

在面对混沌现象时，我们需要具备一定的适应能力和解决问题的能力。

积极主动地面对挑战，寻求帮助和解决方案，是应对混沌现象的有效策略。

此外，建立良好的社交关系和培养健康的心理状态也是应对混沌现象的重要因素。

在大学生活中，我们应该充分认识到混沌现象的存在，并学会应对和处理。

混沌实验报告混沌实验报告引言：混沌，这个词充满了神秘和魅力，它是一种看似无序却又包含着某种规律的现象。

混沌理论的提出，为我们解开了一些自然界中看似混乱的现象背后隐藏的规律。

为了更好地了解混沌现象，我们进行了一系列混沌实验。

实验一：双摆实验我们首先进行了双摆实验，这是一种经典的混沌系统。

通过调整摆的初始条件，我们观察到了摆的运动呈现出了混沌现象。

在初始条件微小变化的情况下，摆的运动轨迹产生了巨大的差异。

这说明了混沌系统对初始条件的极端敏感性。

实验二：洛伦兹系统实验接下来，我们进行了洛伦兹系统实验。

洛伦兹系统是混沌理论的经典案例之一。

通过调整系统的参数，我们观察到了系统状态的变化。

当参数处于某个特定范围时，系统呈现出混沌状态。

这种混沌状态的特点是系统状态在相空间中呈现出复杂的轨迹，即“蝴蝶效应”。

实验三：分形实验分形是混沌理论的重要组成部分。

我们进行了一系列分形实验，包括分形图形的绘制和分形维度的计算。

通过这些实验，我们发现分形具有自相似性和无穷细节的特点。

无论是在自然界中的山脉、云朵，还是在人造的分形图形中，我们都能够看到这种无穷细节的美妙。

实验四：混沌与控制混沌现象的存在给控制系统设计带来了挑战，但同时也为我们提供了新的思路。

我们进行了一系列混沌与控制相关的实验，探索如何利用混沌现象来设计更有效的控制系统。

通过混沌系统的反馈和调节，我们成功地实现了对系统状态的控制。

结论：通过一系列混沌实验，我们深入了解了混沌现象的特点和规律。

混沌系统对初始条件的敏感性、复杂的轨迹和无穷细节的特点给我们带来了许多启示。

混沌现象不仅存在于自然界中，也可以在人工系统中得到应用。

混沌理论的研究对于我们认识世界的深入，以及在控制系统设计中的创新具有重要意义。

未来，我们将继续深入研究混沌现象，探索更多的应用领域，为科学和技术的发展做出贡献。

参考文献：1. Strogatz, S. H. (2014). Nonlinear dynamics and chaos: with applications to physics, biology, chemistry, and engineering. CRC press.2. Ott, E., Grebogi, C., & Yorke, J. A. (1990). Controlling chaos. Physical review letters, 64(11), 1196-1199.3. Mandelbrot, B. B. (1982). The fractal geometry of nature. WH freeman.。

试验十二 分形、混沌——迭代一、试验目的：1、Koch 曲线、Sierpinski 三角形、Cantor 集的计算机实现2、掌握用迭代、递归生成分形3、用Matlab 观察分岔与混沌现象二、分形相关程序：1、从一条直线段开始，将线段中间的三分之一部分用一个等边三角形的两边代替，形成山丘形图形如下在新的图形中，又将图中每一直线段中间的三分之一部分都用一个等边三角形的两条边代替，再次形成新的图形如此迭代，形成Koch 分形曲线。

算法分析：考虑由直线段（2个点）产生第一个图形（5个点）的过程。

图1中，设1P 和5P 分别为原始直线段的两个端点，现需要在直线段的中间依次插入三个点2P ，3P ，4P 。

显然2P 位于线段三分之一处，4P 位于线段三分之二处，3P 点的位置可看成是由4P 点以2P 点为轴心，逆时针旋转600而得。

旋转由正交矩阵 ⎪⎪⎪⎪⎭⎫ ⎝⎛-=)3cos()3sin()3sin()3cos(ππππA 实现。

算法根据初始数据（1P 和5P 点的坐标），产生图1中5个结点的坐标。

结点的坐标数组形成一个25⨯矩阵，矩阵的第一行为1P 的坐标，第二行为2P 的坐标……，第五行为5P 的坐标。

矩阵的第一列元素分别为5个结点的x 坐标，第二列元素分别为5个结点的y 坐标。

进一步考虑Koch 曲线形成过程中结点数目的变化规律。

设第k 次迭代产生的结点数为k n ，第1+k 次迭代产生的结点数为1+k n ，则k n 和1+k n 中间的递推关系为341-=+k k n n 。

实验程序及注释：p=[0 0;10 0]; %P 为初始两个点的坐标,第一列为x 坐标,第二列为y 坐标 n=2; %n 为结点数A=[cos(pi/3) -sin(pi/3);sin(pi/3) cos(pi/3)]; %旋转矩阵for k=1:4d=diff(p)/3; %diff 计算相邻两个点的坐标之差,得到相邻两点确定的向量%则d 就计算出每个向量长度的三分之一,与题中将线段三等分对应m=4*n-3; %迭代公式q=p(1:n-1,:); %以原点为起点,前n-1个点的坐标为终点形成向量p(5:4:m,:)=p(2:n,:); %迭代后处于4k+1位置上的点的坐标为迭代前的相应坐标p(2:4:m,:)=q+d; %用向量方法计算迭代后处于4k+2位置上的点的坐标p(3:4:m,:)=q+d+d*A'; %用向量方法计算迭代后处于4k+3位置上的点的坐标p(4:4:m,:)=q+2*d; %用向量方法计算迭代后处于4k 位置上的点的坐标 n=m; %迭代后新的结点数目endplot(p(:,1),p(:,2)) %绘出每相邻两个点的连线axis([0 10 0 10])实验数据记录：由上面的程序，可得到如下的Koch 分形曲线：2、由四边形的四个初始点出发，对于四边形的每条边，生成元如下：可得到火焰般的图形。

混沌现象研究实验报告混沌现象是一种复杂的动力学现象，它展现了一种看似随机但又有序的行为。

混沌现象在物理学、数学、生物学等多个领域都得到了广泛的研究和应用。

在本实验中，我们将使用一个简单的混沌系统模型进行研究，探究混沌现象的基本特征和产生机制。

首先，我们介绍实验所使用的混沌系统模型，这是一个基于离散映射的模型。

模型的动力学方程如下：x(n+1) = r*x(n)*(1-x(n))其中，x(n)是系统在第n个时间步的状态变量，r是一个控制参数，决定了系统的行为。

该方程描述了一个种群数量的变化规律，可以用来研究种群的动态演化。

为了观察混沌现象，我们在模型中引入了一个初始条件x0。

我们会通过调节参数r和初始条件x0的值，观察系统的演化过程。

在实验中，我们将选择不同的参数r值和初始条件x0，观察系统的行为。

例如，我们可以选择r=2.5和x0=0.5作为初始条件。

我们将通过迭代计算x(n)的值，并绘制出x(n)随时间的变化图像。

实验结果显示，当r取不同的值时，系统的行为也会发生明显的变化。

当r小于3时，系统的行为相对简单，呈现出周期性和收敛性；当r大于3时，系统的行为变得复杂，呈现出混沌现象。

我们可以通过统计混沌系统产生的时间序列数据的特征，如Lyapunov指数、分岔图、功率谱等来定量描述混沌现象。

此外，我们还可以通过系统的相图来观察混沌现象。

相图描述了系统状态变量的轨迹，可以直观地展示系统的复杂行为。

我们将绘制x(n)和x(n+1)的关系图像，以及x(n+1)和x(n+2)的关系图像，通过观察图像的形状和分布情况，可以发现混沌现象的特征。

通过实验的观察和分析，我们可以得出以下结论：1. 混沌现象具有确定性，但是在初值和参数微小变化的情况下表现出不可预测的特点；2. 混沌系统的行为对参数和初值条件非常敏感，微小的变化可以导致完全不同的演化结果；3. 混沌系统的行为可以通过一些统计特征来描述，如Lyapunov指数、分岔图、功率谱等；4. 混沌现象具有普适性，可以在不同的领域中观察到。

实验四函数的迭代、混沌与分形解读实验四函数的迭代、混沌与分形[实验目的]1. 认识函数的迭代；2. 了解混沌和分形.迭代在数值计算中占有很重要的地位,了解和掌握它是很有必要的.本实验将讨论用Newton迭代求方程根的问题,以及迭代本身一些有趣的现象.§1 基本理论1.1 迭代的概念给定某个初值,反复作用以同一个函数的过程称为迭代.函数f(x)的迭代过程如下:x0,x1=f(x0),x2=f(x1),……..,xn=f(xn-1)….., 它生成了一个序列{xn}迭代序列.许多由递推关系给出的数列,都是递推序列.例如数列. X0=1,xn=1+1/(1+xn-1)(n=1,2,…………..)是由函数f(x)=1+1/(1+x)=(2+x)/(1+x)取初值为1所得的迭代序列. 1.2 迭代序列的收敛性定理设函数f(x)满足: (1) 对任意x?(a,b),f(x)?(a,b); (2) f(x)在(a,b)内可导,且存在常数L使得|f(x)'|=L<1, 则当初值x0? (a,b)时,由f(x)生成的迭代序列收敛.在迭代函数f(x)连续的条件下,如果迭代数列收敛,则它一定收敛于方程x=f(x)的根.该方程的根也称函数f(x)的不动点.设x*为f(x)的不动点,f(x)'在x*的附近连续,若|f(x*)'|<1,则称不动点x*是稳定的;若f(x*)'=0,则称不动点x*是超稳定的.在超稳定点x*附近,迭代过程xn+1=f(xn)收敛到x*的速度是非常快的. 1.3 Newton迭代法设函数g(x)具有一阶导数,且g(x)'?0,则函数f(x)=x-g(x)/g(x)'的迭代称为Newton 迭代,若函数f(x)存在不动点,则它一定是方程g(x)=0的根,故Newton迭代法可用来求方程g(x)=0的根.§2 实验内容与练习2.1 迭代的收敛对于函数迭代,最重要的问题是迭代序列的收敛性.一般说,迭代序列是否收敛取决于迭代函数与初值.表4.1 Newton 法求方程的根所得的迭代序列迭代次数n 1 2 3 4 5 6 7 迭代序列xn 6.17647 7.5641 9.85437 12.5529 14.7125 15.9668 16.5642 f'(xn) 1.900071.43369 0.968319 0.661453 0.509988 0.444765 0.418018 迭代次数n 11 12 13 14 15 16 17 迭代序列xn 16.9884 16.9954 16.9981 16.9993 16.9997 16.9999 17 f'(xn)0.400463 0.400185 0.400074 0.400030 0.400012 0.100005 0.400002 8 9 10 16.8218 16.9281 16.9711 0.407224 0.402892 0.401157 18 19 20 17 17 17 0.400001 0.4 0.4 作为一个例子，我们用来讨论用Newton迭代法求函数g（x）=（x-17）5/3（x-5）-2/3的根，其Mathematica程序为： Clear[g，x]；g[x_]：=（x-17）^(5/3)*(x-5)^(-2/3); f[x_]=Factor[x-g(x)]/D[g[x],x]]; x0=5.5;n=20; For[i=1,i<=n,i++,x0=N[f[x0]];Print[i,” “,x0,” “,D[f[x],x]/.x->x0] ]执行结果见表4.1.表4.1的结果说明迭代序列收敛于g(x)的零点17.我们注意到程序中取的迭代处值为5.5,如果其它的数作为初值,所得的迭代序列是否收敛于17呢?我们可以取其它初值做实验,结果得到表4.2(表中第三列是迭代序列的前6位有效数字首次为17.0000的步数).表4.2 取不同初值的收敛情况初值 -40000 -500 -20 0 4 4.9 收敛性收敛于17 收敛于17 收敛于17 收敛于17 收敛于17 收敛于17 收敛到17的步数 16 16 16 17 17 19 初值 5 5.1 6 20 100 1000 收敛性收敛于5 收敛于17 收敛于17 收敛于17 收敛于17 收敛于17 收敛到17的步数 19 17 12 12 14 14 从表4.2中可看出,只要初值不取5,迭代序列都收敛于17,且收敛速度与初值的选取关系不大.前面程序中使用的f(x)为g(x)的化简过的Newton迭代函数,用Mathematica命令可检查出它为(25x-85)/(x+3)(注意,这个式子扩充了原迭代函数在x=5,x=17处的定义),解方程f(x)=x.得到x=17,与x=5.即17和5是f(x)的两个不动点,有前面的讨论知这两个不动点是有区别的:对于17,不管初值取为多少(只要不为5),迭代序列总是收敛于它;而对于5,只要初值取为5时,迭代序列才以它为极限,这样一种现象在函数的迭代中普遍存在,为方便区分起见,我们给这样两种点各一个名称:像17这样的所有附近的点在迭代过程中都趋向于它的不动点,称为吸引点;而像5这样的所有附近的点在迭代过程中都远离它的不动点,称为排斥点.上面的f(x)=(25x-85)/(x+3)是一个分式线性函数,对于一般的分式线性函数,迭代序列是否总是收敛呢?练习1 编程判断函数f(x)=(x-1)/(x+1)的迭代序列是否收敛.在上节我们已经指出,如果迭代序列收敛,一定收敛到函数的某个不动点,这就是说,迭代函数存在不动点是迭代序列收敛的必要条件.那么如果迭代函数存在不动点,迭代序列是否一定收敛呢?练习2 先分别求出分式线性函数f1(x)=(x-1)/(x+3),f2(x)=(-x+15)/(x+1)的不动点,再编程判断它们的迭代序列是否收敛.运用上节的收敛定理可以证明:如果迭代函数在某不动点处具有连续的导数且导数值介于-1与1之间,那么取该不动点附近的点为初值所得到的迭代序列一定收敛到该不动点.练习3 你能否说明为什么17是f(x)=(25x-85)/(x+3)的吸引点,而5是f(x)的排斥点?尽量多找些理由支持这个结论.练习4 能否找到一个分式线性函数(ax+b)/(cx+d),使它产生的迭代序列收敛到给定的数?用这种办法计算2.2.2迭代的”蜘蛛图”对函数的迭代过程,我们可以用几何图象来直观地显示它.在xoy平面上,先作出函数y=f(x)与y=x的图象,对初值x0,在曲线y=f(x)上可确定一点p0,它以x0为横坐标,过p0引平行x轴的直线,设该直线与y=x交与点Ｑ1作平行于y轴的直线它与曲线y=f(x)的交点记为p1,重复上面的过程,就在曲线y=f(x)上得到点列p1,p2,??，如图４.１，不难知道，这些点的横坐标构成的序列x0,x1,x2,??，xn??就是迭代序列.若迭代序列收敛,则点列p1,p2,??趋向于y=f（x）与y=x的交点p*，因此迭代序列是否收敛，可以在图上观查出来，这种图因其形状像蜘蛛网而被称为“蜘蛛网”图。

大学物理实验混沌实验报告大学物理实验混沌实验报告引言：混沌理论是近几十年来在物理学领域中引起了广泛关注的一个重要研究方向。

混沌现象的出现使得我们对于自然界中的复杂系统的行为有了更深入的认识。

本次实验旨在通过具体实例，探索混沌现象的产生和特征，并通过数据分析和模型建立来解释混沌现象的本质。

实验目的：1. 了解混沌现象的基本概念和特征；2. 掌握混沌实验的基本方法和数据处理技巧；3. 通过实验数据分析和模型建立，探索混沌现象的本质。

实验装置和方法：实验装置主要由一个简单的双摆系统组成。

通过调整摆的初始条件和参数，观察双摆系统的运动状态，并记录相应的数据。

实验过程中，我们采用了以下方法：1. 调整初始条件：通过改变摆的初始角度和角速度，探索不同初始条件下双摆系统的运动情况；2. 调整参数：改变摆的长度、质量和重力加速度等参数，观察对双摆系统运动的影响；3. 数据记录：使用传感器记录摆的角度和角速度随时间的变化，并将数据保存下来。

实验结果与数据分析：通过实验观察和数据记录，我们得到了大量的实验数据。

首先，我们通过绘制摆的角度随时间的变化曲线，发现双摆系统呈现出复杂的非周期性运动。

进一步分析数据，我们发现摆的角度随时间的变化呈现出明显的不规则性，即混沌现象。

具体来说，摆的角度在一定范围内波动，但并不呈现出明确的周期性，而是呈现出一种看似无序的、随机的运动状态。

接下来，我们对实验数据进行了进一步的分析。

通过计算摆的角速度随时间的变化率，我们发现角速度也呈现出类似的混沌现象。

摆的角速度在一定范围内变化，但并没有明显的周期性规律，而是表现出一种看似无序的、随机的变化趋势。

模型建立与混沌现象解释：为了解释这种混沌现象，我们引入了混沌理论中的一个重要概念——“敏感依赖于初始条件”。

简单来说，这个概念指的是在某些复杂系统中，微小的初始条件变化可能会导致系统的演化结果产生巨大的差异。

在双摆系统中，由于摆的运动受到多个因素的影响，如摆的长度、质量、重力加速度等，微小的初始条件变化可能会导致摆的运动轨迹发生巨大的变化，从而呈现出混沌现象。

混沌系统实验报告混沌系统实验报告引言：混沌系统是一种具有极其复杂行为的动力学系统，其特征是对初始条件极其敏感，微小的初始差异会导致系统的巨大变化。

混沌系统的研究对于理解自然界中的复杂现象和应用于实际问题具有重要意义。

本实验旨在通过构建一个简单的混沌系统模型，观察和分析其行为，并对其进行定性和定量的描述。

实验设计：在本实验中，我们选择了一个经典的混沌系统模型——Logistic映射模型。

该模型的迭代公式为：Xn+1 = r*Xn*(1-Xn)，其中Xn为第n次迭代的值，r为系统的参数，取值范围为0到4。

我们将通过改变参数r的值，观察系统的演化过程，并分析其混沌特性。

实验过程与结果：1. 参数r在0到1之间时，系统呈现简单的周期行为。

当初始条件在一定范围内变化时，系统会收敛到一个稳定的周期轨道上，如图1所示。

2. 当参数r在1到3之间时，系统开始表现出混沌行为。

初始条件的微小变化会导致系统轨迹的巨大差异，如图2所示。

此时系统的演化呈现出无规律的、看似随机的行为。

3. 参数r在3到3.57之间时，系统出现周期倍增的现象。

初始条件微小变化会导致系统周期的倍增，如图3所示。

这种倍增现象最终导致系统进入混沌状态。

4. 当参数r超过3.57时，系统进一步加剧了混沌行为。

此时系统的轨迹呈现出分形结构，即自相似的形态重复出现，如图4所示。

分形结构的出现是混沌系统的典型特征之一。

实验分析：通过实验观察和结果分析，我们可以得出以下结论：1. 混沌系统的行为对初始条件极其敏感，微小的差异会导致系统的巨大变化。

这种敏感性使得混沌系统的行为难以预测和控制。

2. 混沌系统的行为具有一定的规律性，如周期倍增和分形结构等。

这些规律性的出现使得我们可以对混沌系统进行定性和定量的描述。

3. 混沌系统的研究对于理解自然界中的复杂现象具有重要意义。

例如，气象学中的天气预测、经济学中的市场波动等都可以通过混沌系统的理论和方法进行分析和预测。

混沌原理实验报告篇一：混沌上机实验报告混沌上机实验报告学院：课程名称：混沌学生姓名：许亮亮学号：1106440513 实验一一、上机题目：在VC中自制调色板二、上机目的与要求1.熟悉一种编程语言环境及相关图形功能，能够灵活使用画笔，画刷等绘图工具。

2.利用相关编程语言的图形功能，制作20色以上调色板。

3.理解平面与屏幕的对应关系，掌握吸引子的构造原理与色带的制作方法，为下一个实验做准备工作。

三、思路及步骤1.在MFC中，创建一个对话框窗口。

在主窗体中添加一个textbox 控件，作为调色板的产生区域。

在其属性中的样式里，将“凹陷”和“边框”选上。

2.为了使调色板的长宽可变，在text区域的右部添加两个编辑框，分别控制产生色块的行列数量。

在ClassWizard里为其添加成员变量，变量名分别为m_length和m_width，并设置变量值区域，长在1和7之间，宽在1和5之间。

另外，添加一个控制时间间隔的编辑框，命名为m_elapse，以毫秒为单位。

类型均为int。

3.添加两个按钮，“绘图”和“退出”。

界面效果如下。

4.为绘图按钮添加消息映射函数。

在text的区域绘制一个矩形，坐标为(15,615),(20,425)，用白色画刷填充。

产生的每个色块为边长为80单位的正方形，行列数量由输入的m_length和m_width决定。

每产生一个，调用Sleep(m_elpase)函数，等待m_elpase个间隔后再产生下一个。

此调色板的颜色全部由随机数控制，即用random()函数产生RGB三种颜色。

部分代码如下：四、所作图形7*5的调色板5*4的调色板，时间间隔较大，颜色差别也较大，并过渡了一个色调可以看到，时间间隔为500ms时，每两个色块的颜色相同五，实验部分代码// Set the icon for this dialog. The framework does this automatically // when the application’s main window is not a dialog SetIcon(m_hIcon, TRUE); SetIcon(m_hIcon, FALSE);// TODO: Add extra initialization here// Set big icon // Set small iconreturn TRUE; // return TRUE unless you set the focus to a control}void CTiaosebanDlg::OnSysCommand(UINT nID, LPARAM lParam) { if ((nID 0xFFF0) == IDM_ABOUTBOX) {CAboutDlg dlgAbout;dlgAbout.DoModal(); } else {CDialog::OnSysCommand(nID, lParam); }}// If you add a minimize button to your dialog, you will need the code below // to draw the icon. For MFC applications using the document/view model, // this is automatically done for you by the framework.void CTiaosebanDlg::OnPaint() { if (IsIconic()) {CPaintDC dc(this); // device context for paintingSendMessage(WM_ICONERASEBKGND, (WPARAM) dc.GetSafeHdc(), 0); // Center icon in client rectangleint cxIcon = GetSystemMetrics(SM_CXICON);int cyIcon = GetSystemMetrics(SM_CYICON);CRect rect;GetClientRect(rect);int x = (rect.Width() cxIcon + 1) / 2;int y = (rect.Height() cyIcon + 1) / 2; // Draw the icon dc.DrawIcon(x, y, m_hIcon); } else {CDialog::OnPaint();}篇二：混沌通讯实验报告篇一：近代物理实验混沌通信实验报告近代物理实验——混沌电路及其在加密通信中的应用预习报告：蔡氏电路虽然简单，但具有丰富而复杂的混沌动力学特性，而且它的理论分析、数值模拟和实验演示三者能很好地符合，因此受到人们广泛深入的研究。

第1篇一、实验背景混沌现象是自然界和人类社会中普遍存在的一种复杂现象，它具有对初始条件的敏感依赖性、长期行为的不可预测性和丰富多样的动力学行为等特点。

近年来，混沌理论在工程、物理、生物、经济等领域得到了广泛的应用。

为了深入理解混沌现象，我们进行了混沌原理实验，以下是实验总结。

二、实验目的1. 了解混沌现象的产生原因和特点；2. 掌握混沌系统的基本动力学行为；3. 研究混沌现象在工程领域的应用。

三、实验原理混沌现象的产生与非线性动力学系统密切相关。

在非线性系统中，系统状态的变化往往受到初始条件、参数选择等因素的影响，从而导致系统呈现出复杂的行为。

混沌现象具有以下特点：1. 对初始条件的敏感依赖性：系统状态的微小差异会导致长期行为的巨大差异；2. 长期行为的不可预测性：混沌系统在长期演化过程中表现出随机性；3. 动力学行为的丰富多样性：混沌系统具有多种动力学行为，如周期运动、倍周期运动、分岔、吸引子等。

四、实验内容1. 搭建混沌电路实验平台；2. 观察混沌现象的产生过程；3. 研究混沌系统的动力学行为；4. 分析混沌现象在工程领域的应用。

五、实验结果与分析1. 混沌现象的产生过程：通过实验观察到，在混沌电路中，当电路参数达到一定范围时，系统状态将呈现混沌行为。

此时，电路输出信号呈现出复杂、无规律的变化，表现出混沌现象。

2. 混沌系统的动力学行为：实验过程中，我们观察到混沌系统具有以下动力学行为：（1）周期运动：当电路参数在某一范围内变化时，系统状态呈现周期性变化；（2）倍周期运动：当电路参数进一步变化时，系统状态呈现倍周期性变化；（3）分岔：当电路参数继续变化时，系统状态发生分岔，产生新的混沌吸引子；（4）吸引子：混沌系统在长期演化过程中，最终趋于某一稳定状态，称为吸引子。

3. 混沌现象在工程领域的应用：混沌现象在工程领域具有广泛的应用，如：（1）混沌加密：利用混沌系统对信息进行加密，提高信息安全性；（2）混沌通信：利用混沌信号进行通信，提高通信质量；（3）混沌控制：利用混沌系统进行控制，实现精确控制目标。

第1篇一、实验目的1. 了解混沌现象的产生及其特点。

2. 通过实验观察混沌摆的动力学行为，分析混沌摆的运动规律。

3. 掌握混沌摆实验的基本操作方法，提高实验技能。

二、实验原理混沌现象是指在确定性系统中，由于初始条件的微小差异，导致系统演化过程出现长期不可预测的行为。

混沌摆是一种典型的混沌系统，其运动状态受初始条件、摆长、摆锤质量等因素的影响。

本实验采用单摆模型，利用混沌摆的运动特性，观察其混沌现象。

实验原理如下：1. 摆的运动方程：根据牛顿第二定律，单摆的运动方程可表示为：$$ \ddot{\theta} + \frac{g}{l} \sin \theta = 0 $$其中，$\theta$ 为摆角，$g$ 为重力加速度，$l$ 为摆长。

2. 混沌现象的产生：当摆长和摆锤质量满足一定条件时，混沌现象会出现。

混沌摆的混沌现象表现为摆角和摆角速度的长期不可预测性。

三、实验器材1. 混沌摆装置：包括摆长可调的单摆、摆锤、支架等。

2. 数字示波器：用于测量摆角和摆角速度。

3. 摆长测量尺：用于测量摆长。

4. 计时器：用于测量摆的运动周期。

四、实验步骤1. 调整混沌摆装置，确保摆长、摆锤质量和支架稳固。

2. 使用数字示波器测量摆角和摆角速度，记录初始条件。

3. 改变摆长，观察摆的运动状态，记录摆角和摆角速度。

4. 改变摆锤质量，观察摆的运动状态，记录摆角和摆角速度。

5. 对比不同初始条件下的摆的运动状态，分析混沌现象。

五、实验数据记录与处理1. 记录不同摆长和摆锤质量下的摆角和摆角速度。

2. 计算摆的运动周期。

3. 分析摆的运动状态，观察混沌现象。

六、实验结果与分析1. 实验结果显示，当摆长和摆锤质量满足一定条件时，混沌现象会出现。

摆角和摆角速度的长期不可预测性表现为摆的运动轨迹复杂、运动周期无规律等。

2. 通过对比不同初始条件下的摆的运动状态，可以发现，混沌现象的产生与初始条件的微小差异密切相关。

当初始条件接近时，摆的运动状态也接近，而当初始条件相差较大时，摆的运动状态差异明显。