八年级下第十五章 15.1.4 整式的乘法(二)——单项式乘多项式导学案

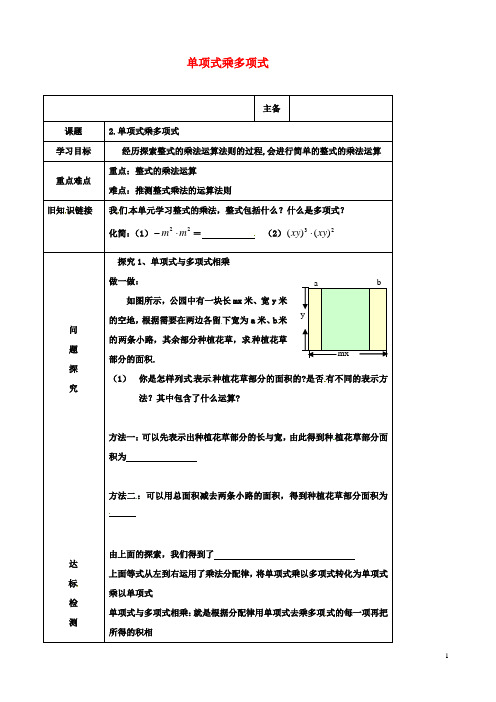
单项式乘多项式 主备课题 2.单项式乘多项式学习目标 经历探索整式的乘法运算法则的过程,会进行简单的整式的乘法运算重点难点重点：整式的乘法运算难点：推测整式乘法的运算法则旧知识链接 我们本单元学习整式的乘法，整式包括什么？什么是多项式？化简：（1）22m m ⋅-＝ （2）23)()(xy xy ⋅问题探究达标检测探究1、单项式与多项式相乘做一做：如图所示，公园中有一块长mx 米、宽y 米的空地，根据需要在两边各留下宽为a 米、b 米的两条小路，其余部分种植花草，求种植花草部分的面积. （1） 你是怎样列式表示种植花草部分的面积的?是否有不同的表示方法？其中包含了什么运算?方法一：可以先表示出种植花草部分的长与宽，由此得到种植花草部分面积为方法二：可以用总面积减去两条小路的面积，得到种植花草部分面积为由上面的探索，我们得到了上面等式从左到右运用了乘法分配律，将单项式乘以多项式转化为单项式乘以单项式单项式与多项式相乘：就是根据分配律用单项式去乘多项式的每一项再把所得的积相a bymx探究2计算：（1）)6)(211012(3322xy y y x xy -+--（2）)(5)()2(2222ab b a a b ab a --+⋅-练习：1．判断题：(1) 3a 3·5a 3=15a 3 （ ）(2)ab ab ab 4276=⋅ ( )(3)12832466)22(3a a a a a -=-⋅ ( )(4) －x 2(2y 2－xy)=－2xy 2－x 3y ( )2．计算题：(1) )261(2a a a + (2) )21(22y y y -(3) －3x(－y －xyz) (4) 3x 2(－y －xy 2＋x 2)(5) （x 3）2―2x 3[x 3―x （2x 2―1）] (6) x n （2x n+2－3x n-1+1）拓展：1． 已知有理数a 、b 、c 满足 |a ―b ―3|+（b+1）2+|c －1|=0，求（－3ab ）·（a 2c －6b 2c ）的值。

品名单价（元）数量笔记本 5.2015钢笔3.4015贺卡0.7015⑴有几种算法计算共花了多14.1.4 整式的乘法第 1 课时单项式与单项式、多项式相乘学习目标1．能熟练、正确地运用法则进行单项式与单项式单项式与多项式的乘法运算.3．经历探索乘法运算法则的过程，让学生体验从“特殊”到“一般”的分析问题的方法，感受“转化思想”、“数形结合思想”，发展观察、归纳、猜测、验证等能力.4．初步学会从数学角度提出问题，运用所学知识解决问题，发展应用意识. 通过反思, 获得解决问题的经验.发展有条理的思考及语言表达能力.学习重点：在经历法则的探究过程中，深刻理解法则从而熟练地运用法则. 学习难点：正确判断单项式与多项式相乘的积的符号.学习过程：一、联系生活设境激趣问题一： 1.在一次绿色环保活动中购买奖品如下表,请列式：方法1: ; 方法2：.联系⋯⋯ ①2．将等式15（5.20+3.40+0.70） =15 5.2×0+15 ×3.40+15×0.70 中的数字用字母代替也可得到等式：m（a+b+c）=ma+mb+mc；⋯⋯②⑵各种算法之间有什么问题二：如图长方形操场,计算操场面积？方法1: .3．讨论解决：（1）单项式与多项式相乘,运用的数同号相乘，异号相乘4. 抢答 :下列各题的解法是否正确，1 2 1 3 1 21a(a 2+a+2)= 1 a 3+ 1 a 2+1正确的请打∨错的请打 × ，并说明原因 (1)22 23 3(2)3a 2b(1-ab 2c)=-3a 3b 33）23 5x(2x 2-y)=10x 3-5xy (24) (-2x).(ax+b-3)=-2ax 2-2bx-6x5．计算： ⑴ （5a 2－·（）⑵ 2a 2(1ab b 2) 5a(a 2b ab 2)2方法 2：.可得到等式 （乘法分配律）； 二、探究学习，获取新知 .1．等式②左右两边有什么特点 ? 2．提炼法则：3．符号语言： a （b+c ）=ab+ac 或 m （ a+b+c ）=ma+mb+mc 4．思想方法：剖析法则 m （a+b+c ） =ma+mb+mc ，得出： 转化 单项式 ×多项式 —— → 单项式 ×单项式 乘法分配律 三、理解运用，巩固提高问 题 三 ： 1.计 算 ： ⑴ （ 2a 2） （3ab 2 5ab 3） ⑵ （ 2 ab 2-2ab ） ?ab⑶ 2（-2a ）.（2a 2-3a+1） 2．单项式与多项式相乘的步骤：①按乘法分配律把乘积写 成；②单项式的乘法运算 .思想是2）单项式乘多项式的结果仍是多项式，积的项数与原多项式的项3）单项式分别与多项式的每一项相乘时，要注意积的各项符号的确定：四. 题型探索中考链接问题四：(2011中考题)先化简，再求值.2a3b2(2ab3-1)-(- 2 a2b2)(3a- 9 a2b3)其中a= 1 ,b=-3.3 2 3归纳小结：1．用单项式乘多项式法则去括号和单项式乘单项式法则进行计2．合并同类项化简. 3．把已知数代入化简式，计算求值.五、联系现实升华思维问题五：1. 某长方形足球场的面积为(2x2+500)平方米，长为(2x+10) 米和宽为x米，这个足球场的长与宽分别是多少米？2.你能用几种方法计算下面图形的面积S？五、总结反思，归纳升华知识梳理：六、达标检测，体验成功 (时间 6 分钟，满分100 分)1、填空：(每小题7 分，共28分)(1) a (2 a 2一3a+1)= _________ ；(2)3 a b(2a 2b－ a b+1) = ____________ ；3 2 1 1(3) _____________________________ (3a b2+3a b一2b)(1a b)= _________ ；(4)(一2 x2)( x2－1 x一1) = ______________ ．4 3 2 2当你的才华还撑不起你的野心时，那你就应该静下心来学习。

徐闻县和安中学 数学教研组 ◆八年级数学导学案 ◆◆我们的约定：我的课堂 我作主！执笔：林朝清 校审：第 周 星期 第 节 本学期学案累计: 59 课时 姓名：________课题：15.1.4 整式的乘法（第2课时）学习目标 我的目标 我实现1、总结单项式与多项式的乘法运算法则；2、能灵活运用单项式与多项式的运算法则进行运算。

3、经历探索乘法运算法则的过程，体会乘法分配律的作用和转化思想。

学习过程 我的学习 我作主☆☆☆导学活动1 我探索 我快乐 一、学习准备：1、什么叫多项式？例说出多项式的项和各项系数.2、计算：(1)、)4()25.0(2x x -⋅-= (2)、)2()3(22xy x ⋅-=☆☆☆导学活动2我尝试 我成功通过阅读教材P145-146,思考后，回答下面的问题：1、乘法的分配律：m(a+b+c)= 总结：单项式乘以多项式的法则： 单项式与多项式相乘，就是用 去 乘 的 ，再把所得的积相 。

☆☆☆导学活动3：我挑战 我自信探究一：运用单项式乘以多项式的的法则： 1、2(4)(31)x x -⋅+= 2、221(2)32ab ab a -⋅= 3、1(31)4m mx x m -+-=4、2(3)(21)a a a -⋅-+= 合作讨论：单项式乘以多项式积的项数 与 相同，并注意每项的符号。

探究二：单项式乘以多项式法则进行混合运算：5、)(5))(2(2222ab b a a b ab a -++-6、22(1)2(1)3(25)x x x x x x -++--7、完成P146练习。

探究三：化简求值： 8、()()xxx x x x x ------22322121023，其中x =-122011年上学期◆八年级（ ）班级 设计时间 2011年11月12日☆☆☆限时训练（8分钟 ）我自信 我进取1、()x x y -3562、()a ab ab --+2232351 3、x xy y ⎛⎫-+ ⎪⎝⎭221224、22(1)2(1)3(25)x x x x x x -++--， 其中x =15、要使x(x 2+a )+3x-2b=x 3+5x+4成立，则a ,b 的值分别为多少☆☆☆导学活动4：我的小结 我分享单项式与多项式相乘，就是用 去乘 的 ，再把所得的积相。

人教版数学八年级上册《第三课时 15.1.4单项式乘单项式、单项式乘多项式》教案一. 教材分析《第三课时 15.1.4 单项式乘单项式、单项式乘多项式》是人教版数学八年级上册的一节重要内容。

这一节内容主要介绍了单项式乘单项式和单项式乘多项式的运算法则，是学生学习多项式乘法的基础。

通过本节课的学习，学生能够理解和掌握单项式乘单项式和单项式乘多项式的计算方法，并为后续的多项式乘法学习打下基础。

二. 学情分析八年级的学生已经掌握了实数运算、整式乘法等相关知识，具备了一定的数学基础。

但是，对于单项式乘单项式和单项式乘多项式的计算方法，部分学生可能还比较陌生，需要通过例题和练习来进一步理解和掌握。

此外，学生对于数学概念的理解和运用能力各有差异，需要教师在教学过程中给予关注和引导。

三. 教学目标1.理解单项式乘单项式和单项式乘多项式的运算法则。

2.能够运用运算法则正确计算单项式乘单项式和单项式乘多项式的运算。

3.培养学生的数学思维能力和解决问题的能力。

四. 教学重难点1.单项式乘单项式和单项式乘多项式的运算法则的理解和运用。

2.学生对于数学概念的理解和运用能力的提升。

五. 教学方法1.采用问题驱动法，引导学生通过思考和讨论来理解和掌握单项式乘单项式和单项式乘多项式的运算法则。

2.使用示例讲解法，通过具体的例题来展示和解释单项式乘单项式和单项式乘多项式的计算方法。

3.运用练习法，通过大量的练习题来巩固和提高学生的计算能力。

六. 教学准备1.准备相关的教学PPT和教学素材。

2.准备相关的练习题和答案。

3.准备黑板和粉笔。

七. 教学过程1.导入（5分钟）教师通过提问方式引导学生回顾实数运算、整式乘法等相关知识，为新课的学习做好铺垫。

2.呈现（10分钟）教师通过PPT展示单项式乘单项式和单项式乘多项式的运算法则，并进行解释和讲解。

3.操练（10分钟）教师给出一些单项式乘单项式和单项式乘多项式的例子，让学生分组讨论并进行计算。

§15.1.4 整式的乘法导学案——单项式乘多项式学习目标：理解单项式乘多项式的法则；能熟练地运用单项式乘多项式的运算法则进行计算。

学习重点：理解单项式乘多项式的法则，并运用这个法则进行计算。

学习难点：理解单项式乘多项式法则。

学习过程：学习内容导学设计学习笔记复习准备1、①同底数幂相乘,底数______,指数______用式子表示为:_____________________②幂的乘方，底数______,指数_______用式子表示为: ____________________③积的乘方等于____________________用式子表示为: _____________________注意：上述各式中，a、b可代表任何有意义的。

2、计算：(1) x·x2 ·x3 ·x4 =_____ (2) (-a)(-a3 )(-a)2 = _____ (3) (-a3)2 = _____ (4) y12=( )3 =( )6(5) （-2xy2）= _____ (6) 已知a m =3,a n =2,则a2m+3n = _____ (7) 2a3 ·a4 –3a · a2 ·a4＋4a · a6 =__ __3、叙述单项式乘单项式的法则4、计算)3()2(2xyxy-⋅知识探究与１．如下图，学校有一块长为a米，宽为b米的矩形操场，现在要割出一块边长分别为2c、b米的矩形场地作篮球场，试用不同的方法表示余下的场地的面积。

从不同的表示方法中，你能得到什么结论？２．三家连锁店以相同的价格m销售某种商品，他们在一个月内的销售量分别是a,b,c.你能用不同的方法计算他们在这个月内销售这种商品的总收入吗？。

《14.1.4整式的乘法——单项式乘多项式》导学案班级_______姓名 _____小组____ 小组评价_____教师评价一、学习目标1、探索并了解单项式与多项式相乘的法则，并运用它进行运算；2、会利用法则进行单项式与多项式的乘法运算；3、积极投入，激情展示，做最佳自己。

二、自主学习（一）知识回顾：1、幂的三个运算性质（用符号表示）_2、单项式乘以单项式的运算法则:3、计算22231(0.5)(2)2ab c ab bc ⋅-⋅-4、整式包括 和 ；多项式221x x --的项是 ，它是 次 项式。

5、用式子表示乘法分配律：单项式与多项式相乘 用式子可以表示为：p(a+b+c)=______________（读三遍）三、合作探究1、计算并指出每一步的依据 (- 2a) ⋅(2a 2 - 3a + 1)2、下面的图说明了一个什么数学问题例1 计算：（1） (-4x 2) ·(3x+1)（2） ab ab ab 21)232(2∙-（3）)227(6)5)(3-(2222y xy x y x xy -+四、练习A 组1、(-5a 2b)(-3a)=2、(2x)3(-5xy 2)=3、3x 2•5x 3=4、4y •(-2xy 2)=5、(3x 2y)3•(-4x)=6、（-2a ）3•(-3a)2=7、(4a-b 2)(-2b)=8、(-4x 2) •(3x+1)=9、3a(5a-2b) =10、计算(3a 2b)2+(-2ab)(-4a 3b)11、计算2524(-)(2)233xy xy xy y ⋅-+13、计算：)227(6)5)(3-(2222y xy x y x xy -+B 组先化简，后求值：1、)232()(32222a ab a ab ab ab b a ab -+--+，其中2,3a b ==2、解不等式222(1)(32)21x x x x x x+--+>-3、解方程0.5x(x+2)=1-x(3-0.5x)C组1、若(-5a m+1b2n-1)(2a n b m)=-10a4b4，则m-n的值为______2、已知A=2223a ab b+-，B=12ab-，C=33241184a b a b-，求22A B C⋅-.。

八年级数学导学案课题：15.1.4 整式的乘法——单项式乘单项式【学习目标】1、熟练运用单项式乘单项式法则进行运算；2、经过单项式乘单项式法则的运用。

3、体验运用法则的价值；培养学生观察、比较、归纳及运算的能力。

【学习重点和难点】1、重点：单项式乘单项式2、难点：归纳概括单项式乘单项式的方法【问题导读单】阅读P144—145页（练习完成）回答下列问题1、仔细研读144页“问题与思考”（1）（3×105）×（5×102）=所用到的运算律：（2）类似3x 2·4xy=（3×4）·（x 2·x ）·y=（5a 2b ）（-3ac ）=结合以上分析总结出“单项式乘以单项式法则”（自己理解记忆）：说明法则中 相乘，其余作为积中一因式抄下。

2、仔细研读145页例4，说明解题中每个等号都做些什么？解题中是如何运用法则的？（与同组同学交流）3、完成145页练习，写出详细解题过程。

4、计算下面各式，并说明理由：(先定积的符号)（1）)3(522ab b a -∙ （2）21ab ·(32ab 2－2ab ) 解：原式=__(5⨯___)(_____)2∙a (_____∙b ) 解：原式= 21ab · －21ab · = = +（3）)6)(3x y x --（ 解：原式=注意：（1） 你能说出每一步计算的依据吗？（2） 单项式与单项式相乘的结果是什么？【问题训练单】1、计算（1）（-3x ）2= （2）（-b 2）3=(3)a 3·a = (4)(y 2)2 ·y 3 =2、提空：（1）像3a ，xy 2这样，数字和字母乘积的式子叫做 式（2）像2x-3，x+4y 2这样，几个单项式的和叫做 式（3）单项式与多项式统称 式3、判断正误（1）-4x 是单项式（ ） （2）-4x+1是单项式（ ）（3）2xy 2是多项式（ ） （4）x 2-2x+1是多项式（ ）（5）单项式-3ab 的系数是-3（ ） （6）单项式a2b 的系数是0（ ）4、计算 （1）3x 2 ·5x 3= （2）4y ·（-2xy 2）=（3）（2m 2n ）·（mn ）= （4）（-a 2b ）·（5b 2）=（5）（3x 2y ）2 ·（-4x ）= （6）（-2a ）3 ·（-3a ）2=5、判断正误（1）3a 2 ·2a 3=6a 6 （ ） （2）2x 2 ·3x 2=6x 4 （ ）（3）3x 2 ·4x 2=12x 2 （ ） （4）5y 3 ·3y 5=15y 15 （ ）6、思维拓展计算 (1) 25)(35)(109b a b a +⋅+ （2） [3(x-y)2]·[-2(x-y)3]·[4(x-y)] 提示：可以把a+b 、x-y 看作一个字母。

学校塘坊初中章节13. 2,.1编号005编制：向辉审核：陈元海审批：时间2010/9/13整式的乘法（二）单项式乘以多项式导学案一、学习目标(一)知识目标1.经历探索单项式与多项式乘法的运算法则的过程，会进行简单的单项式与多项式的乘法运算.2.理解单项式与多项式相乘的算理，体会乘法分配律及转化思想的作用.(二)能力目标1.发展有条理思考和语言表达能力.2.培养学生转化的数学思想.(三)情感目标在探索单项式与多项式乘法运算法则的过程中，获得成就感，建立学习数学的信心和勇气.二、教学重难点（一）教学重点：单项式与多项式相乘的乘法法则及应用.（二）教学难点：灵活运用单项式与多项式相乘的乘法法则.四、教学过程Ⅰ.提出问题，引入新课整式包括什么？整式的乘法，我们上一节课学习了其中的一部分——单项式与单项式相乘.你认为整式的乘法还应学习哪些内容呢？很好！我们这节课就接着来学习整式的乘法——单项式与多项式相乘. Ⅱ.探究新知（１）算一算6×（2）利用面积的不同表示方式或乘法分配律转化为单项式与单项式相乘，探索单项式与多项式相乘的乘法法则乘法分配律对于含有字母的代数也同样适用，因为代数式中的字母所表示的也是数，即m(a+b+c)＝ma+mb+mc这一结论还可以用长方形的面积给以说明（１）用不同的方法表示下面长方形的面积ma b c看图回答：①大长方形的长是___________,面积是___________②Ⅰ、Ⅱ、Ⅲ三个小长方形的面积分别是____________③由(1)、(2)得出等式__________根据以上方法，请同学们计算2ab·(a2b-2ab2+3)解：2ab·(a2b-2ab2+3)＝2ab·a2b +2ab·(-2ab2)+ 2ab×3 (乘法分配律)＝2a3b2-4a2 b3+6ab (单项式与单项式相乘)同学们考虑，怎样叙述单项式与多项式相乘的法则?其实，单项式与多项式相乘，就是利用乘法分配律转化为单项式与单项式相乘，这样新知识就转化成了我们学过的知识.这种“转化”的思想是我们学习数学非常重要的一种思想.我们在处理一些问题时经常用到它，例如新知识学习转化为我们学过的、熟悉的知识；复杂的知识转化为几个简单的知识等.我们通过画面面积的不同表达方法和乘法分配律，得出了单项式乘以多项式的运算法则：单项式与多项式相乘，就是根据分配律用单项式去乘多项式的每一项，再把所得的积相加，下面我们来看它的具体运用.Ⅲ、应用举例 例1 计算明确单项式乘多项式每一步的算理，体会由单项式与多项式相乘的方法(1) 2ab (5a 2b+3ab 2)； (2)-2a(2a 2-3a-1)(3)(32ab 2-2ab) 21ab (4)(-12xy 2-10xy 2+21y 3)(-6xy 3) 例2 计算-2a 2·(ab+b 2)-5a(a 2b-ab 2)解法1： -2a 2·(ab+b 2)-5a(a 2b-ab 2)＝-2a 3b-2a 2b 2-5a 3b+5a 2b 2＝-7a 3b+3a 2b 2解法2： -2a 2·(ab+b 2)-5a(a 2b-ab 2)＝-(2a 3b+2a 2b 2)-(5a 3b-5a 2b 2)＝-2a 3b-2a 2b 2-5a 3b+5a 2b 2＝-7a 3b+3a 2b 2先由学生讨论解题方法，然后由教师指定两人板演，并根据学生的板演情况指出：解法1将2a 2与5a 前面的“-”看成性质符号，解法2将2a 2与5a 前面的“-”看成运算符号。

15.1.4整式的乘法（第二课时）学习目标：（1）探索多项式乘法法则的过程，理解多项式乘法法则；（2）灵活运用多项式乘以多项式的运算法则。

学习重点：多项式与多项式相乘的法则学习难点：理解法则并可以灵活应用一、学习过程：（一）、复习巩固：1、导学前测：（1）单项式×单项式运算法则：___________________________________________________________________ （2）单项式×多项式运算法则：2、计算下列各题：（1）2ab3x (-5a2by4) (2) - x2y3z(6xy2-18xyz3)3、整式的乘法：单项式×单项式单项式×多项式4、张伯伯准备把长为m米、宽为a米的长方形鱼塘进行扩建，使得长再增加n米，宽再增加b米，求扩建后鱼塘的面积.一起探究：1．求扩建后鱼塘的面积有哪些方法？将计算过程和结果写出来（二）探索法则与应用。

根据乘法分配律，我们也能得到下面等式：把（m+n）看作一个整体：(m+n)(a+b)=(m+n)a+(m+n)b= 或把（a+b）看作一个整体：(m+n)(n+b)= = 提问：多项式与多项式相乘是怎样化为单项式与单项式相乘的？____________体会法则的理论依据：_____________________________________________ 多项式乘以多项式的法则：（三）例题讲解例1、计算：x+px+q 练习：1、计算（1）)1)(2(+-χχ（2）)2a3(2a31-⎪⎭⎫⎝⎛-（3）)y2)(3y(-+χχ；（4）)4b2)(2b3(-+-χχ.2、计算，思考你能发现什么规律？①(x+2)(x+3)；②(x-1)(x+2)；③(x+2)(x-2)；④(x-5)(x-6)；⑤(x+5)(x+5)；⑥(x-5)(x-5)；（四）、当堂检测：1、计算下列各题：（1）（m+3n）(m-3n) （2）(a－4)(a＋1)（3）（2x2-3y）(3x2+2y) (4)(3x-y)(3x+y)(9x2+y2)2、先化简，再求值（3x-2y）（y-3x）－（2x-y）（3x+y），其中x=3,y=2.3、如图，在一块长为50米、宽为30米的长方形场地上建造一个露天游泳池，使四周人行道的宽都是x米，请你用含x的式子表示游泳池的面积.。