黄金分割同步练习及答案 (4)

27.1.2 黄金分割基础训练知识点1 比例中项1.若x是2,18的比例中项,则x=___________.2.若线段a=6 cm,b=3 cm,且c是a,b的比例中项,则线段c的长度为( )A.3错误!未找到引用源。

cmB.±3错误!未找到引用源。

cmC.±18 cmD.18 cm3.如果a∶b=3∶2,且b是a,c的比例中项,那么b∶c等于( )A.4∶3B.3∶2C.2∶3D.3∶44.如图,有三个直角三角形,其中OA=AB=BC=CD=1,则线段OA,OD的比例中项线段的长度为( )A.错误!未找到引用源。

B.错误!未找到引用源。

C.±错误!未找到引用源。

D.错误!未找到引用源。

知识点2 黄金分割5.如果点C是线段AB的黄金分割点(AC>BC),则下列比例式正确的是( )A.AB∶AC=AC∶BCB.AB∶BC=BC∶ACC.AC∶BC=BC∶ABD.AC∶AB=AB∶BC6.若点C为线段AB的黄金分割点,且AC>BC,则①AB=错误!未找到引用源。

AC;②AC=错误!未找到引用源。

AB;③AB∶AC=AC∶CB;④AC≈0.618AB.其中正确的有( )A.1个B.2个C.3个D.4个7.从美学角度来说,人的上身长与下身长之比为黄金比例,可以给人一种协调的美感.某女老师上身长约61.80 cm,下身长约93.00 cm,她要穿约___________cm的高跟鞋才能达到黄金比的美感效果(精确到1 cm).提升训练考查角度1 利用比例性质求解比例中项问题8.已知线段a,b,c满足错误!未找到引用源。

=错误!未找到引用源。

=错误!未找到引用源。

,且a+2b+c=26.(1)求a,b,c的值;(2)若线段x是线段a,b的比例中项,求x.考查角度2 利用黄金分割的定义找黄金分割点(计算法、定义法)9.以长为2的线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.(1)求MA,DM的长;(2)求证:AM2=AD·DM.(3)根据(2)的结论你能找出图中的一个黄金分割点吗?考查角度3 利用黄金分割的定义证明黄金矩形(计算法、定义法)10.宽与长的比是错误!未找到引用源。

6.2黄金分割A组题1、点C是线段AB的黄金分割点，且AC＞BC，若AB=2cm，则BC ≈cm。

（精确到0.1cm）≈2、顶角为的等腰三角形称为黄金三角形，等腰△ABC中，若∠A=360，则BCAB3、研究表明：标准人体的黄金分割点是人的肚脐，请你计算身高180cm的人，如果肚脐是黄金分割点，那头顶到肚脐的长度约为cm。

（精确到1c m）4、已知点C是线段AB的黄金分割点(AC＞BC)，那么AC是线段与的比例中项，若AC=10cm，则BC约为cm。

（精确到0.1cm）5、已知点C是线段的黄金分割点，且AC＞BC，则下列等式中成立的是（）A、2AB AC BCCB AC AB=•=•B、2C、2=•AC AB BCAC BC AB=•D、226、如图，点C是线段AB的黄金分割点，矩形ABFD的宽与长的比等于黄金比，则下列结论中错误的是DA（）A、四边形ACED是正方形B、矩形CBFE是黄金矩形C、EC与EF之比是黄金比D、EC与DF之比是黄金比7、下列说法中正确的是（）A、如果一条线段是另两条线段的比例中项，那么这三条线段构成黄金比；B、一条线段上的黄金分割点只有一个；；C、黄金分割比是512D、黄金分割比就是我们看上去舒服的比。

8、科学研究表明：当人的下肢长度与身高的比约为0.618时，看起来最美。

若某成年女士身高为153cm，下肢长为92cm，则该女士穿的高跟鞋鞋跟的最佳高度约为多少cm？（精确到0.1cm）9、如图，电视节目主持人在主持节目时，站在舞台的黄金分割点处最自然得体，若舞台AB长为20米，试计算主持人应走到离A点至少多少米处是最自然得体的位置？（结果精确到0.1米）10、如图，梯形ABCD中，AD∥BC，AB=AD=DC，AC=BD=BC。

①求∠ABC的度数；②图中有多少个黄金三角形？把它们一一写出来。

11、如图，△ABC中，AB=AC，AC的垂直平分线交AC于D，交AB于E，且AE=BC。

第4课时 黄金分割知识点 对黄金分割的理解1.已知点C 把线段AB 分成两条线段AC ,BC ,下列说法错误的是( )A .如图果AC AB =BC AC ,那么线段AB 被点C 黄金分割 B .如图果AC 2=AB ·BC ,那么线段AB 被点C 黄金分割C .如图果线段AB 被点C 黄金分割,那么AC 与AB 的比叫做黄金比D .一条线段有两个黄金分割点2.已知点C 是线段AB 的黄金分割点,且AC>BC ,AB=2,则AC 的长为 ( )A .√5-1B .3-√5C .√5-12D .0.6183.人体的正常体温是37 ℃左右,根据有关测定,当气温处于人体正常体温的黄金比值时,人体感觉最舒适,这个气温的度数约为 (精确到1 ℃).4.世界上有名的建筑物中几乎都包含“黄金分割”,如图广播电视塔同样蕴含着“黄金分割”,如图,塔高AB 为339米,观光区P 为塔AB 的黄金分割点(AP>PB ),求观光区的高度.(结果精确到1米)5.美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感.如图,某女士的身高为160 cm,下半身长x 与身高l 的比值是0.60,为尽可能达到好的效果,她应穿的高跟鞋的高度大约为( )A .6 cmB .10 cmC .4 cmD .8 cm6.C 是线段AB 的黄金分割点,且AB=6 cm,则BC 的长为( )A.(3√5-3)cmB.(9-3√5)cmC.(3√5-3)cm或(9-3√5)cmD.(9-3√5)cm或(6√5-6)cm7.[教材习题4.8第1题变式题]如图,乐器上的一根弦AB=80 cm,两个端点A,B固定在乐器板面上,支撑点C是靠近点B的黄金分割点,支撑点D是靠近点A的黄金分割点,求支撑点C,D 之间的距离.∶1的矩形叫做黄金矩形,黄金矩形令人赏心悦目,它给我们以协调匀称的8.宽与长之比为√5-12美感.如图,如图果在一个黄金矩形里面画一个正方形,那么留下的矩形CDFE还是黄金矩形吗?请证明你的结论.答案1.C2.A ∵C 是线段AB 的黄金分割点,且AC>BC ,∴AC=√5-12AB. 又∵AB=2,∴AC=√5-1.3.23 ℃ 37×√5-12≈23(℃).4.解:∵塔高AB 为339米,观光区P 为塔AB 的黄金分割点(AP>PB ), ∴AP=√5-12AB=√5-12×339≈210(米). 故观光区的高度约为210米.5.D6.C ∵C 是线段AB 的黄金分割点,且AB=6 cm,∴BC=√5-12AB=(3√5-3)cm 或BC=3-√52AB=(9-3√5)cm .7.解:∵支撑点C 是靠近点B 的黄金分割点,支撑点D 是靠近点A 的黄金分割点, ∴AC=BD=80×√5-12=(40√5-40)cm, ∴CD=BD-(AB-AC )=BD+AC-AB=(80√5-160)cm .8.解:留下的矩形CDFE 还是黄金矩形.证明:∵四边形ABEF 是正方形,四边形ABCD 是矩形,∴AB=DC=AF .又∵AB AD =√5-12, ∴AF AD =√5-12, 即F 是线段AD 的黄金分割点,∴FD AF =AF AD =√5-12, ∴FD DC =√5-12, ∴矩形CDFE 是黄金矩形.。

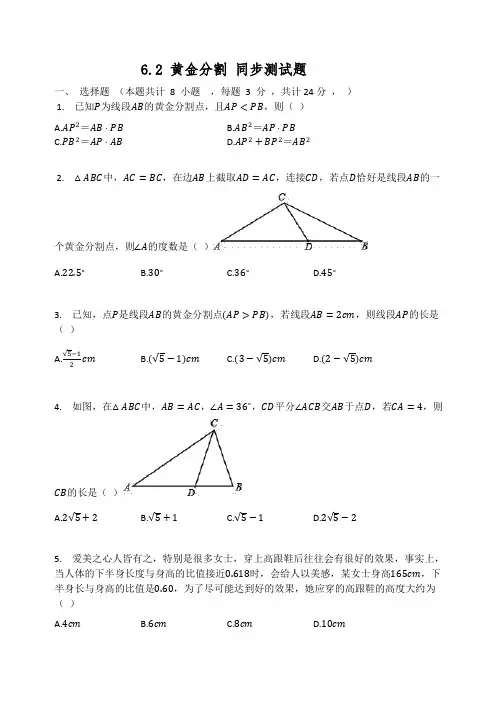
6.2 黄金分割同步测试题一、选择题（本题共计8 小题，每题3 分，共计24分，）1. 已知P为线段AB的黄金分割点，且AP<PB，则（）A.AP2＝AB⋅PBB.AB2＝AP⋅PBC.PB2＝AP⋅ABD.AP2+BP2＝AB22. △ABC中，AC=BC，在边AB上截取AD=AC，连接CD，若点D恰好是线段AB的一个黄金分割点，则∠A的度数是（）A.22.5∘B.30∘C.36∘D.45∘3. 已知，点P是线段AB的黄金分割点(AP>PB)，若线段AB=2cm，则线段AP的长是（）cm B.(√5−1)cm C.(3−√5)cm D.(2−√5)cmA.√5−124. 如图，在△ABC中，AB=AC，∠A=36∘，CD平分∠ACB交AB于点D，若CA=4，则CB的长是（）A.2√5+2B.√5+1C.√5−1D.2√5−25. 爱美之心人皆有之，特别是很多女士，穿上高跟鞋后往往会有很好的效果，事实上，当人体的下半身长度与身高的比值接近0.618时，会给人以美感，某女士身高165cm，下半身长与身高的比值是0.60，为了尽可能达到好的效果，她应穿的高跟鞋的高度大约为（）A.4cmB.6cmC.8cmD.10cm6. 如图，P是线段AB的黄金分割点(PB>PA)，四边形ABCD、四边形PBEF都是正方形，且面积分别为S1、S2，四边形APMD、四边形APFN都是矩形，且面积分别为S3、S4，下列说法正确的是（）A.s2=√5−12s1 B.s2=s3 C.s3=√5−12s4 D.s4=√5−127. 美术专家认为：如果人的下身长与自己的身高之比是黄金分割数(√5−12≈0.618)，那么就非常美丽，已知一个女孩身高为155cm，下半身为94cm，请你们替她选一个高度最理想的高跟鞋，则高度应为（）A.2∼3cmB.3∼4cmC.4∼5cmD.5∼6cm8. 如图，在△ABC中，AB=AC=1，∠A=36∘，BD平分∠ABC，则BC的长为（）A.1 2B.−1+√52C.1−√52D.−1+√52二、填空题（本题共计10 小题，每题3 分，共计30分，）9. 已知点P是线段AB上的黄金分割点，AP>PB，AB=4厘米，则线段AP=________厘米．10. 我们知道，下身长与身高的比等于黄金数的人身材比较协调．某女士身高1.50米，其下身长90厘米，则她应该穿________厘米高的高跟鞋比较合适（精确到1厘米）．11. 点C是线段AB上的一个黄金分割点，且AC>BC，若AB=5cm，则AC=________cm，BC=________cm．12. 已知线段AB的长度为2，点C为线段AB上的黄金分割点(AC>BC)，则AC的长度为________．13. 为了美观起见，通常把一本书的宽与长之比设计成黄金比．已知这本书的宽为15cm，则它的长为________cm（精确到0.1cm）．14. 已知线段AB＝4厘米，点P是线段AB的黄金分割点(AP>BP)，那么线段AP＝________厘米．（结果保留根号）15. 如果点P是线段AB的黄金分割点，且AP>PB，已知AB=4，则AP=________（结果保留根号）．16. 已知线段AB=4dm，点C是线段AB上一点，AC>BC，若C点是线段AB的黄金分割点，则AC=________dm．（保留根号）17. 科学研究表明，当人的下肢长与身高之比成0.618时，看起来最美，某成年女士身高为160cm，下肢长96cm，该女士穿的高跟鞋鞋跟的最佳高度应约为________cm（精确到0.1cm）18. 在人体躯干和身高的比例上，肚脐是理想的黄金分割点，即比例越接近0.618越给人以美感．张女士的身高为1.60米，身体躯干（脚底到肚脐的高度）与身高的比为0.60，那么她应选择约________厘米的高跟鞋看起来更美．（精确到十分位）三、解答题（本题共计6 小题，共计60分，）19. 已知M是线段AB的黄金分割点，且AM>BM．（1）写出AB、AM、BM之间的比例式；（2）若AB=12cm，求AM与BM的长．20. 已知线段AB=a，点C为AB的黄金分割点，求AC的长．21. 中国民间乐器二胡的“千斤钩”钩在弦长的黄金分割点处音质最好，一把二胡的弦长为68cm，求“千金钩”上、下两部分弦长．22. 一般认为，如果一个人的肚脐以上的高度与肚脐以下的高度符合黄金分割，则这个人好看．如图，是一个参加空姐选拔活动的选手情况，那么她应该穿多高的鞋子好看？,√5≈2.236）（精确到1cm）（参考数据：黄金分割数：√5−1223. 已知线段AB，按照如下的方法作图：以AB为边作正方形ABCD，取AD的中点E，连接EB，延长DA到F，使EF=EB，以线段AF为边，作正方形AFGH，那么点H是线段AB的黄金分割点吗？请说明理由．24. 电视节目主持人在主持节目时，站在舞台的黄金分割点处最自然得体．如图，若舞台AB长为20米，主持人现站在A处，请问主持人应走到离A点至少多少米处才最自然得体？（结果精确到0.1米）参考答案一、选择题（本题共计8 小题，每题 3 分，共计24分）1.【答案】C【解答】∵ P为线段AB的黄金分割点，且AP<PB，∵ PB2＝AP⋅AB．2.【答案】C【解答】解：∵ 点D是线段AB的一个黄金分割点，∵ AD2=BD⋅AB，∵ AD=AC=BC，∵ BC2=BD⋅AB，即BC:BD=AB:BC，而∠ABC=∠CBD，∵ △BCD∽△BAC，∵ ∠A=∠BCD，设∠A=x，则∠B=x，∠BCD=x，∵ ∠ADC=∠BCD+∠B=2x，而AC=AD，∵ ∠ACD=∠ADC=2x，∵ x+2x+x+x=180∘，解得x=36∘，即∠A=36∘．故选：C．3.【答案】B【解答】解：由于P为线段AB=8cm的黄金分割点，且AP是较长线段；=√5−1．则AP=2×√5−12故选B．4.【答案】D【解答】解：∵ △ABC中，AB=AC，∠A=36∘，∵ △ABC是黄金三角形，∵ BC=√5−12AC=2√5−2，故选：D．5.【答案】C【解答】解：根据已知条件得下半身长是160×0.6=96cm，设需要穿的高跟鞋是ycm，则根据黄金分割的定义得：96+y160+y=0.618，解得：y≈8cm．故选C．6.【答案】B【解答】解：根据黄金分割得出：PB=√5−12AB，设AB=x，PB=√5−12x，PA=(1−√5−12)x，∵ S1=x2，S2=√5−12x⋅√5−12x，S3=(1−√5−12)x⋅x，S4=(1−√5−12)x⋅√5−12x，∵ S1S2=3−√5，故A错误；S2S3=1，即S2=S3，故B正确；S3 S4=√52√5−4，故C错误；S4S1=√5−2，故D错误；故选B．7.【答案】C【解答】解：设高跟鞋的高度是xcm ，则 94+x 155+x =0.618，解得：x ≈4.69，即高跟鞋的高度应为4∼5cm ．故选C ．8.【答案】B【解答】解：∵ AB =AC ，∠A =36∘，∵ ∠ABC =∠ACB =12×(180∘−36∘)=72∘，∵ BD 平分∠ABC ，∵ ∠ABD =∠CBD =12×72∘=36∘， ∵ ∠A =∠ABD ，∵ AD =BD ，又∵ ∠ACB =∠BCD ，∵ △ABC ∽△BCD ，∵ BC CD =AC BC ，设BC =x ，则x 1−x =1x ， 整理得，x 2+x −1=0，解得x 1=−1+√52，x 2=−1−√52（舍去）， 即BC 的长为−1+√52． 故选B ．二、 填空题 （本题共计 10 小题 ，每题 3 分 ，共计30分 ）9.【答案】 2√5−2【解答】解：由于P 为线段AB =4厘米的黄金分割点，且AP 是较长线段；则AP =4×√5−12=2√5−2（厘米）．故答案为：2√5−2．10.【答案】7【解答】答：设高跟鞋鞋跟的高度为x ，根据题意列方程得：(90+x)÷(150+x)≈0.618，解得x ≈7．故答案为：7．11.【答案】5√5−52,15−5√52 【解答】解：∵ C 为线段AB 上的一个的黄金分割点，且AC >BC ，∵ AC =√5−12AB ，BC =AB −AC =3−√52AB ，∵ AB =5cm ，∵ AC =√5−12×5=5√5−52(cm)，BC =3−√52×5=15−5√52(cm)． 故答案为：5√5−52，15−5√52． 12.【答案】 √5−1【解答】∵ C 为线段AB 上的黄金分割点，AC >BC ，∵ AC =√5−12AB =√5−1， 13.【答案】24.3【解答】解：根据题意得这本书的长=√5−12≈150.618≈24.3(cm)．故答案为24.3．14.【答案】2√5−2【解答】∵ 点P 是线段AB 的黄金分割点，AP >BP ，AB＝2√5−2，∵ AP=√5−1215.【答案】6−2√5【解答】解：∵ 点P是线段AB的黄金分割点，且AP>PB，AB=4，=6−2√5，∵ AP=4×3−√52故答案为：6−2√5．16.【答案】(2√5−2)【解答】解：由于C为线段AB=4dm的黄金分割点，且AC>BC，AC为较长线段；=2√5−2(dm)．则AC=4×√5−12故答案为：(2√5−2)．17.【答案】7.5【解答】解：设该女士穿的鞋跟高度约为xcm，由题意得(96+x)：(160+x)=0.618，解得x≈7.5．故答案为：7.5．18.【答案】7.5【解答】解：设应选择xcm的高跟鞋，∵ 张女士的身高为1.60米，身体躯干（脚底到肚脐的高度）与身高的比为0.60，∵ 其身高为1.60米=160厘米，身体躯干高为160×0.60=96厘米，≈0.618，则有96+x160+x解得：x≈7.5．故本题答案为：7.5．三、解答题（本题共计6 小题，每题10 分，共计60分）19.【答案】解：（1）∵ M是线段AB的黄金分割点，且AM>BM，∵ AM:AB=BM:AM，∵ AM2=BM⋅AB；（2）AM=√5−12AB=√5−12×12=6√5−6，BM=AB−AM=12−6√5+6=18−6√5．【解答】解：（1）∵ M是线段AB的黄金分割点，且AM>BM，∵ AM:AB=BM:AM，∵ AM2=BM⋅AB；（2）AM=√5−12AB=√5−12×12=6√5−6，BM=AB−AM=12−6√5+6=18−6√5．20.【答案】解：根据题意得当AC为较长线段时，AC=√5−12AB=√5−12a；当AC为较短线段时，AC=AB−√5−12AB=3−√52a．【解答】解：根据题意得当AC为较长线段时，AC=√5−12AB=√5−12a；当AC为较短线段时，AC=AB−√5−12AB=3−√52a．21.【答案】解：“千金钩”上部分弦长=68×√5−12=34√5−34cm，下两部分弦长=68−(34√5−34)=102−34√5cm．【解答】解：“千金钩”上部分弦长=68×√5−12=34√5−34cm，下两部分弦长=68−(34√5−34)=102−34√5cm．22.【答案】她应该穿约10cm高的鞋好看【解答】设她应该穿xcm的鞋子，依题意得：65 95+x =√5−12，解得x≈10，经检验，x≈10是原方程的解．23.【答案】解：设正方形ABCD的边长为2a，在Rt△AEB中，依题意，得AE=a，AB=2a，由勾股定理知EB=√AB2+AE2=√5a，∵ AH=AF=EF−AE=EB−AE=(√5−1)a，HB=AB−AH=(3−√5)a；∵ AH2=(6−2√5)a2，AB⋅HB=2a×(3−√5)a=(6−2√5)a2，∵ AH2=AB⋅HB，所以点H是线段AB的黄金分割点．【解答】解：设正方形ABCD的边长为2a，在Rt△AEB中，依题意，得AE=a，AB=2a，由勾股定理知EB=√AB2+AE2=√5a，∵ AH=AF=EF−AE=EB−AE=(√5−1)a，HB=AB−AH=(3−√5)a；∵ AH2=(6−2√5)a2，AB⋅HB=2a×(3−√5)a=(6−2√5)a2，∵ AH2=AB⋅HB，所以点H是线段AB的黄金分割点．24.【答案】主持人应走到离A点至少7.6米处才最自然得体．【解答】解：根据黄金比得：20×(1−0.618)≈7.6米，∵ 黄金分割点有2个，∵ 20−7.6=12.4，由于7.6<12.4米。

北师大版九年级数学上册第四章4.4.4黄金分割 同步测试题一、选择题1．已知点C 把线段AB 分成两条线段AC ，BC ，下列说法错误的是( )A ．如果AC AB ＝BCAC ，那么线段AB 被点C 黄金分割B ．如果AC 2＝AB ·BC ，那么线段AB 被点C 黄金分割C ．如果线段AB 被点C 黄金分割，那么AC 与AB 的比叫做黄金比D ．一条线段有两个黄金分割点2．已知点C 是线段AB 的黄金分割点，且AC ＞BC ，则下列各式中正确的是( )A ．AB 2＝AC ·BC B ．BC 2＝AC ·AB C ．AC 2＝BC ·ABD ．AC 2＝2AB ·BC3．已知AB ＝2 cm ，C 为AB 上的黄金分割点，且AC ＞BC ，则AC 的值为( )A ．(5－1)cmB ．0.618 cmC ．(3－5)cmD.3－52cm4．若点C 是线段AB 的黄金分割点，且AC ＞BC ，则下列说法正确的有( )①AB ＝5＋12AC ；②AC ＝3－52AB ；③AB ∶AC ＝AC ∶BC ；④AC ≈0.618AB. A ．1个B ．2个C ．3个D ．4个5.我们把宽与长的比值等于黄金比5－12的矩形称为黄金矩形．如图，在黄金矩形ABCD(AB ＞BC)的边AB 上取一点E ，使得BE ＝BC ，连接DE ，则AEAD等于( )A.22B.5－12C.3－52D.5＋12二、填空题6.已知线段AB，点P是它的黄金分割点，AP＞BP，设以AP为边的正方形的面积为S1，以PB，AB为边的矩形的面积为S1与S2的关系是S1＝S2．7．相邻两边长的比值是黄金分割数的矩形，叫做黄金矩形，从外形看，它最具美感．现在想要制作一张“黄金矩形”的贺年卡，如果较长的一条边长等于20 cm，那么相邻一条边的边长等于(105－10)cm.8．已知线段AB＝4 cm，C为AB的黄金分割点，则AC的长为(25－2)cm或(6－25)cm．9．宽与长的比是5－12(约为0.618)的矩形叫做黄金矩形．黄金矩形蕴藏着丰富的美学价值，给我们以协调和匀称的美感．我们可以用这样的方法画出黄金矩形：如图，作正方形ABCD，分别取AD，BC的中点E，F，连接EF；以点F为圆心，FD的长为半径画弧，交BC的延长线于点G；作GH⊥AD，交AD的延长线于点H，则图中是黄金矩形的是矩形DCGH．10．如图，△ABC是顶角为36°的等腰三角形，若△ABC，△BDC，△DEC都是黄金三角形(底与腰的比为5－12的三角形是黄金三角形)．已知AB＝4，则DE＝6－25．11．乐器上一根弦AB长80 cm，两个端点A，B固定在乐器板上，支撑点C是靠近点B的黄金分割点，支撑点D是靠近点A的黄金分割点，则CD的长为(805－160)cm.9．如图，连接正五边形ABCDE的各条对角线围成一个新的五边形MNPQR.图中有很多顶角为36°的等腰三角形，我们把这种三角形称为“黄金三角形”，黄金三角形的底与腰之比为5－1 2.若AB＝5－12，则MN＝5－2．三、解答题12．如图，正方形ABCD的边长为2，点E是BC的中点，点F在BC的延长线上，且EF＝DE，以CF为边作正方形CFGH，点H在CD边上．试说明点H是线段CD的黄金分割点．13.如图，以长为2 cm的线段AB为边作正方形ABCD，取AB的中点P，在BA的延长线上取点F，使PF＝PD，以AF为边作正方形AFEM，点M落在AD上．(1)试求AM，DM的长；(2)点M是线段AD的黄金分割点吗？请说明理由．14．如图，在△ABC中，AC＝BC，在边AB上截取AD＝AC，连接CD，若点D恰好是线段AB 的一个黄金分割点，且有AD＞BD，求∠A的度数．15．如图，在△ABC中，AB＝AC，AC的垂直平分线交AC于点D，交AB于点E.若AE＝BC，则点E是线段AB的黄金分割点吗？说明你的理由．参考答案1-5、CCACB6、S1＝S2．7、(105－10)cm.8、(25－2)cm或(6－25)cm．9、矩形DCGH．10、6－25．11、5－2．12、解：∵点E是BC的中点，∴EC＝1.∴EF＝DE＝22＋12＝ 5. ∴CF＝5－1.∵四边形CFGH是正方形，∴CH＝CF＝5－1.∴CHCD＝5－12.∴点H是线段CD的黄金分割点．13、解：(1)在Rt△APD中，AP＝1 cm，AD＝2 cm，由勾股定理，得PD＝AD2＋AP2＝ 5 cm.∴AM＝AF＝PF－AP＝PD－AP＝(5－1)cm.∴DM＝AD－AM＝(3－5)cm.(2)点M是线段AD的黄金分割点，理由如下：∵AM2＝(5－1)2＝6－25，AD·DM＝2×(3－5)＝6－25，∴AM2＝AD·DM.∴点M是线段AD的黄金分割点．14、解：∵点D是线段AB的一个黄金分割点，且AD＞BD，∴AD2＝BD·AB.∵AD＝AC＝BC，∴BC2＝BD·AB，即BC∶BD＝AB∶BC.∵∠CBD＝∠ABC，∴△BCD∽△BAC.∴∠A＝∠BCD.设∠A＝x，则∠B＝x，∠BCD＝x，∴∠ADC＝∠BCD＋∠B＝2x.∵AC＝AD，∴∠ACD＝∠ADC＝2x.在△ABC中，x＋(2x＋x)＋x＝180°，解得x＝36°，∴∠A＝36°.15、解：点E是线段AB的黄金分割点．理由如下：连接EC.∵DE是AC的垂直平分线，∴EA＝EC.又∵AE＝BC，∴EC＝BC.∴∠BEC＝∠B.∵AB＝AC，∴∠ACB＝∠B.∴∠BEC＝∠ACB.又∵∠B＝∠B，∴△CEB∽△ACB.∴BEBC＝BCAB，即BC2＝BE·AB，又∵AE＝BC，∴AE2＝BE·AB.∴点E是线段AB的黄金分割点1、在最软入的时候，你会想起谁。

18.2 黄金分割点C 把线段AB 分成两条线段AC 和BC ,如果AC AB =BCAC ,那么称线段AB 被点C 黄金分割,点C 叫做线段AB 的黄金分割点,AC 与AB 的比叫做黄金比.注意:(1)一条线段有两个黄金分割点; (2)黄金比k=√5-12≈0.618. 1.[2020·泰安泰山区期末] 已知点P 是线段AB 的黄金分割点(AP>PB ),AB=10,那么AP 的长是 ( ) A .5√5-5 B .5-√5C .5√5-1D .√5-122.[2020·金昌] 生活中到处可见黄金分割的美.如在设计人体雕像时,使雕像的腰部以下a 与全身b 的高度比值接近0.618,可以增加视觉美感.若中b 为2米,则a 约为 ( )A .1.24米B .1.38米C .1.42米D .1.62米3.若点C 是线段AB 的黄金分割点,且AC>BC ,则下列说法正确的有 ( )①AB=√5+12AC ;②AC=3-√52AB ; ③AB∶AC=AC∶BC ; ④AC ≈0.618AB. A .1个 B .2个C .3个D .4个4.如若点C 是线段AB 的黄金分割点(AC>BC ),AB=1,则AC= ,BC= .5.一个主持人站在舞台的黄金分割点处最自然得体,若舞台AB 的长为20米,主持人现在站在A 处,则他应至少再走 米才最自然得体.(结果精确到0.1米)6.如求作线段AB 的黄金分割点.(作出一个即可)7.“黄金分割”是一条举世公认的美学定律.例如在摄影中,人们常依据黄金分割进行构,使画面整体和谐.目前,照相机和手机自带的九宫格就是黄金分割的简化版.要拍摄草坪上的小狗,按照黄金分割的原则,应该使小狗置于画面(如中的位置()A.①B.②C.③D.④8.已知点C是线段AB的黄金分割点,且AB=2,则AC等于()A.√5-1B.3-√5D.√5-1或3-√5C.√5-129.如已知线段AB,点P是它的黄金分割点,AP>BP,设以AP为边的正方形的面积为S1,以BP,AB 长为边的矩形的面积为S2,则S1与S2的关系是()A.S1>S2B.S1<S2C.S1=S2D.S1≥S210.五角星是我们常见的形,如五角形外围的各个边都相等.其中,点C,D是线段AB的黄金分割点,AB=20 cm.求EC+CD的长.答案1.A2.A3.C解：∵ABAC =√5-1=2×(√5+1)4=√5+12,∴AB=√5+12AC,①正确;AC=√5-12AB,②错误;AB∶AC=AC∶BC,③正确;AC=√5-12AB≈0.618AB,④正确.4.√5-123-√525.7.66.略7.B8.D9.C10.解:∵EC=AC,∴EC+CD=AC+CD=AD.∵点D是线段AB的黄金分割点(AD>BD),∴AD=√5-12·AB=(10 √5-10)cm.即EC+CD=(10√5-10)cm.。

黄金分割专项练习30题（有答案）1．定义：如图1，点C在线段AB上，若满足AC2=BC?AB，则称点C为线段AB的黄金分割点．如图2，△ABC 中，AB=AC=1，∠A=36°，BD平分∠ABC交AC于点D．（1）求证：点D是线段AC的黄金分割点；（2）求出线段AD的长．2．如图，用长为40cm的细铁丝围成一个矩形ABCD（AB＞AD）．（1）若这个矩形的面积等于99cm2，求AB的长度；（2）这个矩形的面积可能等于101cm2吗？若能，求出AB的长度，若不能，说明理由；（3）若这个矩形为黄金矩形（AD与AB之比等于黄金比），求该矩形的面积．（结果保留根号）3．定义：如图1，点C在线段AB上，若满足AC2=BC?AB，则称点C为线段AB的黄金分割点．如图2，△ABC中，AB=AC=2，∠A=36°，BD平分∠ABC交AC于点D．（1）求证：点D是线段AC的黄金分割点；（2）求出线段AD的长．4．作一个等腰三角形，使得腰与底之比为黄金比．（1）尺规作图并保留作图痕迹；（2）写出你的作法；（3）证明：腰与底之比为黄金比．5．（1）已知线段AB的长为2，P是AB的黄金分割点，求AP的长；（2）求作线段AB的黄金分割点P，要求尺规作图，且使AP＞PB．6．如图，线段AB的长度为1．（1）线段AB上的点C满足系式AC2=BC?AB，求线段AC的长度；（选做）（2）线段AC上的点D满足关系式AD2=CD?AC，求线段AD的长度；（选做）（3）线段AD上的点E满足关系式AE2=DE?AD，求线段AE的长度；上面各题的结果反映了什么规律？（提示：在每一小题中设x和l）7．如图，在△ABC中，AB=AC，∠A=36°，∠1=∠2，请问点D是不是线段AC的黄金分割点．请说明理由．8．在△ABC中，AB=AC=2，BC=﹣1，∠A=36°，BD平分∠ABC，交于AC于D．试说明点D是线段AC的黄金分割点．9．在数学上称长与宽之比为黄金分割比的矩形为黄金矩形，如在矩形ABCD中，当时，称矩形ABCD为黄金矩形ABCD．请你证明黄金矩形是由一个正方形和一个更小的黄金矩形构成．10．如图，设AB是已知线段，在AB上作正方形ABCD；取AD的中点E，连接EB；延长DA至F，使EF=EB；以线段AF为边作正方形AFGH．则点H是AB的黄金分割点．为什么说上述的方法作出的点H是这条线段的黄金分割点，你能说出其中的道理吗？请试一试，说一说．11．如图，已知△ABC中，D是AC边上一点，∠A=36°，∠C=72°，∠ADB=108°．求证：（1）AD=BD=BC；（2）点D是线段AC的黄金分割点．12．已知AB=2，点C是AB的黄金分割线，点D在AB上，且AD2=BD?AB，求的值．13．如果一个矩形ABCD（AB＜BC）中，≈0.618，那么这个矩形称为黄金矩形，黄金矩形给人以美感．在黄金矩形ABCD内作正方形CDEF，得到一个小矩形ABFE（如图），请问矩形ABFE是否是黄金矩形？请说明你的结论的正确性．14．五角星是我们常见的图形，如图所示，其中，点C，D分别是线段AB的黄金分割点，AB=20cm，求EC+CD的长．15．人的肚脐是人的身高的黄金分割点，一般来讲，当肚脐到脚底的长度与身高的比为0.618时，是比较好看的黄金身段．一个身高1.70m的人，他的肚脐到脚底的长度为多少时才是黄金身段（保留两位小数）？16．如图所示，以长为2的定线段AB为边作正方形ABCD，取AB的中点P，连接PD，在BA的延长线上取点F，使PF=PD，以AF为边作正方形AMEF，点M在AD上．（1）求AM，DM的长；（2）点M是AD的黄金分割点吗？为什么？17．如图，点P是线段AB的黄金分割点，且AP＞BP，设以AP为边长的正方形面积为S1，以PB为宽和以AB为长的矩形面积为S2，试比较S1与S2的大小．18．如图，在平行四边形ABCD中，E为边AD延长线上的一点，且D为AE的黄金分割点，即，BE交DC于点F，已知，求CF的长．19．图1是一张宽与长之比为的矩形纸片，我们称这样的矩形为黄金矩形．同学们都知道按图2所示的折叠方法进行折叠，折叠后再展开，可以得到一个正方形ABEF和一个矩形EFDC，那么EFDC这个矩形还是黄金矩形吗？若是，请根据图2证明你的结论；若不是，请说明理由．20．（如图1），点P将线段AB分成一条较小线段AP和一条较大线段BP，如果，那么称点P为线段AB的黄金分割点，设=k，则k就是黄金比，并且k≈0.618．（1）以图1中的AP为底，BP为腰得到等腰△APB（如图2），等腰△APB即为黄金三角形，黄金三角形的定义为：满足≈0.618的等腰三角形是黄金三角形；类似地，请你给出黄金矩形的定义：；（2）如图1，设AB=1，请你说明为什么k约为0.618；（3）由线段的黄金分割点联想到图形的“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成面积为S1和面积为S2的两部分（设S1＜S2），如果，那么称直线l为该图形的黄金分割线．（如图3），点P是线段AB的黄金分割点，那么直线CP是△ABC的黄金分割线吗？请说明理由；（4）图3中的△ABC的黄金分割线有几条？21．在人体躯干（脚底到肚脐的长度）与身高的比例上，肚脐是理想的黄金分割点，即比例越接近0.618，越给人以美感．张女士原来脚底到肚脐的长度与身高的比为0.60，她的身高为1.60m，她应该选择多高的高跟鞋穿上看起来更美？（精确到十分位）22．已知线段AB，按照如下的方法作图：以AB为边作正方形ABCD，取AD的中点E，连接EB，延长DA到F，使EF=EB，以线段AF为边，作正方形AFGH，那么点H是线段AB的黄金分割点吗？请说明理由．23．如图，用纸折出黄金分割点：裁一张正方的纸片ABCD，先折出BC的中点E，再折出线段AE，然后通过折叠使EB落到线段EA上，折出点B的新位置B′，因而EB′=EB．类似地，在AB上折出点B″使AB″=AB′．这时B″就是AB的黄金分割点．请你证明这个结论．24．如图，用纸折出黄金分割点：裁一张边长为2的正方形纸片ABCD，先折出BC的中点E，再折出线段AE，然后通过折叠使EB落在线段EA上，折出点B的新位置F，因而EF=EB．类似的，在AB上折出点M使AM=AF．则M是AB的黄金分割点吗？若是请你证明，若不是请说明理由．25．如图，在△ABC中，点D在边AB上，且DB=DC=AC，已知∠ACE=108°，BC=2．（1）求∠B的度数；（2）我们把有一个内角等于36°的等腰三角形称为黄金三角形．它的腰长与底边长的比（或者底边长与腰长的比）等于黄金比．①写出图中所有的黄金三角形，选一个说明理由；②求AD的长；③在直线AB或BC上是否存在点P（点A、B除外），使△PDC是黄金三角形？若存在，在备用图中画出点P，简要说明画出点P的方法（不要求证明）；若不存在，说明理由．26．宽与长的比是的矩形叫黄金矩形．心理测试表明：黄金矩形令人赏心悦目，它给我们以协调，匀称的美感．现将小波同学在数学活动课中，折叠黄金矩形的方法归纳如下（如图所示）：第一步：作一个正方形ABCD；第二步：分别取AD，BC的中点M，N，连接MN；第三步：以N为圆心，ND长为半径画弧，交BC的延长线于E；第四步：过E作EF⊥AD，交AD的延长线于F．请你根据以上作法，证明矩形DCEF为黄金矩形．27．在△ABC中，AB=AC，∠A=36°，把像这样的三角形叫做黄金三角形．（1）请你设计三种不同的分法，将黄金三角形ABC分割成三个等腰三角形，使得分割成的三角形中含有两个黄金三角形（画图工具不限，要求画出分割线段；标出能够说明不同分法所得三角形的内角度数，不要求写画法，不要求证明．分别画在图1，图2，图3中）注：两种分法只要有一条分割线段位置不同，就认为是两种不同的分法．（2）如图4中，BF平分∠ABC交AC于F，取AB的中点E，连接EF并延长交BC的延长线于M．试判断CM 与AB之间的数量关系？只需说明结果，不用证明．答：CM与AB之间的数量关系是．28．折纸与证明﹣﹣﹣用纸折出黄金分割点：第一步：如图（1），先将一张正方形纸片ABCD对折，得到折痕EF；再折出矩形BCFE的对角线BF．第二步：如图（2），将AB边折到BF上，得到折痕BG，试说明点G为线段AD的黄金分割点（AG＞GD）29．三角形中，顶角等于36°的等腰三角形称为黄金三角形，如图1，在△ABC中，已知：AB=AC，且∠A=36°．（1）在图1中，用尺规作AB的垂直平分线交AC于D，并连接BD（保留作图痕迹，不写作法）；（2）△BCD是不是黄金三角形？如果是，请给出证明；如果不是，请说明理由；（3）设，试求k的值；（4）如图2，在△A1B1C1中，已知A1B1=A1C1，∠A1=108°，且A1B1=AB，请直接写出的值．30．如图1，点C将线段AB分成两部分，如果，那么称点C为线段AB的黄金分割点．某研究小组在进行课题学习时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成两部分，这两部分的面积分别为S1，S2，如果，那么称直线l为该图形的黄金分割线．（1）研究小组猜想：在△ABC中，若点D为AB边上的黄金分割点（如图2），则直线CD是△ABC的黄金分割线．你认为对吗？为什么？（2）请你说明：三角形的中线是否也是该三角形的黄金分割线？（3）研究小组在进一步探究中发现：过点C任作一条直线交AB于点E，再过点D作直线DF∥CE，交AC于点F，连接EF（如图3），则直线EF也是△ABC的黄金分割线．请你说明理由．（4）如图4，点E是平行四边形ABCD的边AB的黄金分割点，过点E作EF∥AD，交DC于点F，显然直线EF是平行四边形ABCD的黄金分割线．请你画一条平行四边形ABCD的黄金分割线，使它不经过平行四边形ABCD各边黄金分割点．黄金分割专项练习30题参考答案: 1．（1）证明：∵AB=AC=1，∴∠ABC=∠C=（180°﹣∠A）=（180°﹣36°）=72°，∵BD平分∠ABC交AC于点D，∴∠ABD=∠CBD=∠ABC=36°，∴∠BDC=180°﹣36°﹣72°=72°，∴DA=DB，BD=BC，∴AD=BD=BC，易得△BDC∽△ABC，∴BC：AC=CD：BC，即BC2=CD?AC，∴AD2=CD?AC，∴点D是线段AC的黄金分割点；（2）设AD=x，则CD=AC﹣AD=1﹣x，∵AD2=CD?AC，∴x2=1﹣x，解得x1=，x2=，即AD的长为2．解：（1）设AB=xcm，则AD=（20﹣x）cm，根据题意得x（20﹣x）=99，整理得x2﹣20x+99=0，解得x1=9，x2=11，当x=9时，20﹣x=11；当x=11时，20﹣11=9，而AB＞AD，所以x=11，即AB的长为11cm；（2）不能．理由如下：设AB=xcm，则AD=（20﹣x）cm，根据题意得x（20﹣x）=101，整理得x2﹣20x+101=0，因为△=202﹣4×101=﹣4＜0，所以方程没有实数解，所以这个矩形的面积可能等于101cm2；（3）设AB=xcm，则AD=（20﹣x）cm，根据题意得20﹣x=x，解得x=10（﹣1），则20﹣x=10（3﹣），所以矩形的面积=10（﹣1）?10（3﹣）=（400﹣800）cm2．3．解：（1）∵∠A=36°，AB=AC，∴∠ABC=∠ACB=72°，∵BD平分∠ABC，∴∠CBD=∠ABD=36°，∠BDC=72°，∴AD=BD，BC=BD，∴△ABC∽△BDC，∴=，即=， ∴AD 2=AC?CD ．∴点D 是线段AC 的黄金分割点．（2）∵点D 是线段AC 的黄金分割点，∴AD=AC ，∵AC=2，∴AD=﹣14．解：（1）腰与底之比为黄金比为黄金比如图，（2）作法：①画线段AB 作为三角形底边；②取AB 的一半作AB 的垂线AC ，连接BC ，在BC 上取CD=CA ．③分别以A 点和B 点为圆心、以BD 为半径划弧，交点为E ；④分别连接EA 、EB ，则△ABE 即是所求的三角形．（3）证明：设AB=2，则AC=1，BC=，AE=BE=BD=BC ﹣CD=﹣1，=． 5．解：（1）由于P 为线段AB=2的黄金分割点，则AP=2×=﹣1，或AP=2﹣（﹣1）=3﹣； （2）如图，点P 是线段AB 的一个黄金分割点．6．解：（1）设AC=x ，则BC=AB ﹣AC=1﹣x ，∵AC 2=BC?AB ，∴x 2=1×（1﹣x ），整理得x 2+x ﹣1=0，解得x 1=，x 2=（舍去），所以线段AC 的长度为； （2）设线段AD 的长度为x ，AC=l ，∵AD 2=CD?AC ，∴x 2=l×（l ﹣x ），∴x 1=，x 2=（舍去），∴线段AD 的长度AC ；（3）同理得到线段AE 的长度AD ； 上面各题的结果反映：若线段AB 分成两条线段AC 和BC （AC ＞BC ），且使AC 是AB 和BC 的比例中项（即AB ：AC=AC ：BC ），则C 点为AB 的黄金分割点7．解：D 是AC 的黄金分割点．理由如下：∵在△ABC 中，AB=AC ，∠A=36°，∴∠ABC=∠ACB==72°．∵∠1=∠2，∴∠1=∠2=∠ABC=36°．∴在△BDC中，∠BDC=180°﹣∠2﹣∠C=72°，∴∠C=∠BDC，∴BC=BD．∵∠A=∠1，∴AD=BC．∵△ABC和△BDC中，∠2=∠A，∠C=∠C，∴△ABC∽△BDC，∴，又∵AB=AC，AD=BC=BD，∴，∴AD2=AC?CD，即D是AC的黄金分割点8．证明：∵AB=AC，∠A=36°，∴∠ABC=（180°﹣36°）=72°，∵BD平分∠ABC，交于AC于D，∴∠DBC=×∠ABC=×72°=36°，∴∠A=∠DBC，又∵∠C=∠C，∴△BCD∽△ABC，∴∵AB=AC，∴=，∵AB=AC=2，BC=﹣1，∴（﹣1）2=2×（2﹣AD），解得AD=，AD：AC=（）：2．∴点D是线段AC的黄金分割点．9．证明：在AB上截取AE=BC，DF=BC，连接EF．∵AE=BC，DF=BC，∴AE=DF=BC=AD，又∵∠ADF=90°，∴四边形AEFD是正方形．BE=，∴，∴矩形BCFE的宽与长的比是黄金分割比，矩形BCFE是黄金矩形．∴黄金矩形是由一个正方形和一个更小的黄金矩形构成．10．解：设正方形ABCD的边长为2，在Rt△AEB中，依题意，得AE=1，AB=2，由勾股定理知EB===，∴AH=AF=EF﹣AE=EB﹣AE=﹣1，HB=AB﹣AH=3﹣；∴AH2=（）2=6﹣2，AB?HB=2×（3﹣）=6﹣2，∴AH2=AB?HB，所以点H是线段AB的黄金分割点．11．证明：（1）∵∠A=36°，∠C=72°，∴∠ABC=180°﹣36°﹣72°=72°，∵∠ADB=108°，∴∠ABD=180°﹣36°﹣108°=36°，∴△ADB是等腰三角形，∵∠BDC=180°﹣∠ADC=180°﹣108°=72°，∴△BDC是等腰三角形，∴AD=BD=BC．（2）∵∠DBC=∠A=36°，∠C=∠C，∴△ABC∽△BDC，∴BC：AC=CD：BC，∴BC2=AC?DC，∵BC=AD，∴AD2=AC?DC，∴点D是线段AC的黄金分割点．12．解：∵D在AB上，且AD2=BD?AB，∴点D是AB的黄金分割点而点C是AB的黄金分割点，∴AC=AB=﹣1，AD=AB﹣AB=AB=3﹣或AD=﹣1，AC=3﹣，∴CD=﹣1﹣（3﹣）=2﹣4，∴==或==．13．解：矩形ABFE是黄金矩形．∵AD=BC，DE=AB，∴==﹣1==．∴矩形ABFE是黄金矩形．14．解：∵D为AB的黄金分割点（AD＞BD），∴AD=AB=10﹣10，∵EC+CD=AC+CD=AD，∴EC+CD=（10﹣10）cm．15．解：设他的肚脐到脚底的长度为xm时才是黄金身段，根据题意得x：1.70=0.618，即x=1.70×0.618≈1.1（m）．答：他的肚脐到脚底的长度为1.1m时才是黄金身段．16．解：（1）在Rt△APD中，AP=1，AD=2，由勾股定理知PD===，∴AM=AF=PF﹣AP=PD﹣AP=﹣1，DM=AD﹣AM=3﹣．故AM的长为﹣1，DM的长为3﹣；（2）点M是AD的黄金分割点．由于=，∴点M是AD的黄金分割点．17．解：∵点P是线段AB的黄金分割点，且AP＞BP，∴AP2=BP×AB，又∵S1=AP2，S2=PB×AB，∴S1=S2．18．解：∵四边形ABCD为平行四边形，∴∠CBF=∠AEB，∠BCF=∠BAE，∴△BCF∽△EAB，∴，即，把AD=，AB=+1代入得，=，解得：CF=2．故答案为：2．19．解：矩形EFDC是黄金矩形，证明：∵四边形ABEF是正方形，∴AB=DC=AF，又∵，∴，即点F是线段AD的黄金分割点．∴，∴，∴矩形CDFE是黄金矩形．20．解：（1）满足≈0.618的矩形是黄金矩形；（2）由=k得，BP=1×k=k，从而AP=1﹣k，由得，BP2=AP×AB，即k2=（1﹣k）×1，解得k=，∵k＞0，∴k=≈0.618；（3）因为点P是线段AB的黄金分割点，所以，设△ABC的AB上的高为h，则，∴∴直线CP是△ABC的黄金分割线．（4）由（2）知，在BC边上也存在这样的黄金分割点Q，则AQ也是黄金分割线，设AQ与CP交于点W，则过点W的直线均是△ABC的黄金分割线，故黄金分割线有无数条．21．解：根据已知条件得下半身长是160×0.6=96cm，设选择的高跟鞋的高度是xcm，则根据黄金分割的定义得：=0.618，解得：x≈7.5cm．故她应该选择7.5cm左右的高跟鞋穿上看起来更美．22．解：设正方形ABCD的边长为2a，在Rt△AEB中，依题意，得AE=a，AB=2a，由勾股定理知EB==a，∴AH=AF=EF﹣AE=EB﹣AE=（﹣1）a，HB=AB﹣AH=（3﹣）a；∴AH2=（6﹣2）a2，AB?HB=2a×（3﹣）a=（6﹣2）a2，∴AH2=AB?HB，所以点H是线段AB的黄金分割点．23．证明：设正方形ABCD的边长为2，E为BC的中点，∴BE=1∴AE==，又∵B′E=BE=1，∴AB′=AE﹣B′E=﹣1，∴AB″∴点B″是线段AB的黄金分割点．24．证明：∵正方形ABCD的边长为2，E为BC的中点，∴BE=1∴AE==，∵EF=BE=1，∴AF=AE﹣EF=﹣1，∴AM=AF=﹣1，∴AM：AB=（﹣1）：2，∴点M是线段AB的黄金分割点．25．解：（1）∵BD=DC=AC．则∠B=∠DCB，∠CDA=∠A．设∠B=x，则∠DCB=x，∠CDA=∠A=2x．又∠BOC=108°，∴∠B+∠A=108°．∴x+2x=108，x=36°．∴∠B=36°；（2）①有三个：△BDC，△ADC，△BAC．∵DB=DC，∠B=36°，∴△DBC是黄金三角形，（或∵CD=CA，∠ACD=180°﹣∠CDA﹣∠A=36°．∴△CDA是黄金三角形．或∵∠ACE=108°，∴∠ACB=72°．又∠A=2x=72°，∴∠A=∠ACB．∴BA=BC．∴△BAC是黄金三角形．②△BAC是黄金三角形，∴，∵BC=2，∴AC=﹣1．∵BA=BC=2，BD=AC=﹣1，∴AD=BA﹣BD=2﹣（﹣1）=3﹣，③存在，有三个符合条件的点P1、P2、P3．ⅰ）以CD为底边的黄金三角形：作CD的垂直平分线分别交直线AB、BC得到点P1、P2．ⅱ）以CD为腰的黄金三角形：以点C为圆心，CD为半径作弧与BC的交点为点P3．26．证明：在正方形ABCD中，取AB=2a，∵N为BC的中点，∴NC=BC=a．在Rt△DNC中，．又∵NE=ND，∴CE=NE﹣NC=（﹣1）a．∴．故矩形DCEF为黄金矩形．27．解：（1）（2）CM=AB（4分）28．证明：如图，连接GF，设正方形ABCD的边长为1，则DF=．在Rt△BCF中，BF==，则A′F=BF﹣BA′=﹣1．设AG=A′G=x，则GD=1﹣x，在Rt△A′GF和Rt△DGF中，有A'F2+A'G2=DF2+DG2，即，解得x=，即点G是AD的黄金分割点（AG＞GD）．29．解：（1）如图所示；（2）△BCD是黄金三角形．证明如下：∵点D在AB的垂直平分线上，∴AD=BD，∴∠ABD=∠A．∵∠A=36°，AB=AC，∴∠ABC=∠C=72°，∴∠ABD=∠DBC=36°．又∵∠BDC=∠A+∠ABD=72°，∴∠BDC=∠C，∴BD=BC，∴△BCD是黄金三角形．（3）设BC=x，AC=y，由（2）知，AD=BD=BC=x．∵∠DBC=∠A，∠C=∠C，∴△BDC∽△ABC，∴，即，整理，得x2+xy﹣y2=0，解得．因为x、y均为正数，所以．（4）．理由：延长BC到E，使CE=AC，连接AE．∵∠A=36°，AB=AC，∴∠ACB=∠B=72°，∴∠ACE=180°﹣72°=108°，∴∠ACE=∠B1A1C1．∵A1B1=AB，∴AC=CE=A1B1=A1C1，∴△ACE≌△B1A1C1，∴AE=B1C1．由（3）知，∴，，∴．30．解：（1）直线CD是△ABC的黄金分割线．理由如下：设△ABC的边AB上的高为h．则，，，∴，．又∵点D为边AB的黄金分割点，∴，∴．故直线CD是△ABC的黄金分割线．（2）∵三角形的中线将三角形分成面积相等的两部分，∴，即，故三角形的中线不可能是该三角形的黄金分割线．（3）∵DF∥CE，∴△DFC和△DFE的公共边DF上的高也相等，∴S△DFC=S△DFE，∴S△ADC=S△ADF+S△DFC=S△ADF+S△DFE=S△AEF，S△BDC=S四边形BEFC．又∵，∴．因此，直线EF也是△ABC的黄金分割线．（7分）（4）画法不惟一，现提供两种画法；画法一：如答图1，取EF的中点G，再过点G作一条直线分别交AB，DC于M，N点，则直线MN就是平行四边形ABCD的黄金分割线．画法二：如答图2，在DF上取一点N，连接EN，再过点F作FM∥NE交AB于点M，连接MN，则直线MN 就是平行四边形ABCD的黄金分割线．（9分）。

6.2 黄金分割同步测试题（满分120分；时间：120分钟）一、选择题（本题共计10 小题，每题3 分，共计30分，）1. 已知P是线段AB的黄金分割点，且AP>PB，AB=10，则AP长约为（）A.0.618B.6.18C.3.82D.0.3822. △ABC中，AC=BC，在边AB上截取AD=AC，连接CD，若点D恰好是线段AB的一个黄金分割点，则∠A的度数是（）A.22.5∘B.30∘C.36∘D.45∘3. 如果点C为线段AB的黄金分割点，且AC>BC，则下列各式不正确的是（）A.AB:AC=AC:BCB.AC=√5−12ABC.AB=√5+12AC D.BC≈0.618AB4. 如图，△ABC中，AB=AC，∠A=36∘，CD是∠ACB的平分线，则△DBC的面积与△ADC的面积的比值是（）A.√5−12B.√5+12C.3−√52D.3+√525. 把2米长的线段进行黄金分割，则分成的较长线段的长为（）A.−1+√5B.3−√5C.3+√5D.1+√56. 现已知线段AB=10，点P是线段AB的黄金分割点，PA>PB，那么线段PA的长约为（）A.6.18B.0.382C.0.618D.3.287. 已知点P是线段AB的黄金分割点，AP>PB，若AB=2，则PB=()A.√5−12B.√5+12C.3−√5D.√5−18. 已知点P是线段AB的黄金分割点，且AP>PB，则下列各式的值不等于√5−12的是（）A.AP ABB.PBAPC.PBABD.√PBAB9. 顶角为36∘的等腰三角形称为黄金三角形，如图，五边形ABCDE的5条边相等，5个内角相等，则图中共有黄金三角形的个数是（）A.25B.10C.15D.2010. 如图所示，顶角为36∘的等腰三角形，其底边与腰之比等于k，这样的三角形叫做黄金三角形．已知AB=1，△ABC为第一个黄金三角形，△BCD为第二个黄金三角形，△CDE为第三个黄金三角形，以此类推，第2014个黄金三角形的周长为（）A.k2012B.k2013C.k2013(2+k)D.k20132+k二、填空题（本题共计10 小题，每题3 分，共计30分，）11. C是长为10cm的线段AB的黄金分割点(AC>BC)，则AC=________．12. 如图，△ABC中，D是AB的黄金分割点(AD<BD)，过点D作DE // BC交AC于E，若BC=3+√5，则DE=________．13. 美是一种感觉，当人体下半身长与身高的比值越接近0.618时，越给人一种美感．李老师身高165厘米，下半身长与身高的比值是0.6，为了尽可能达到好的效果，她应穿的高跟鞋的高度大约为________（结果精确到0.1）．14. 美是一种感觉，一矩形的长为6cm，宽为3cm，当矩形的宽与长的比值是黄金比值时，这样的矩形给人一种美感．试问长不变，宽增加________cm时，给人的美感效果最佳．15. 有些植物茎上，相邻两张叶子成137∘28′的角，这种角度使植物通风和采光的效果最佳，这一度数与________∘角成黄金比例．16. 要使点B是线段AC的黄金分割点(AB>BC)，那么线段AB、BC、AC应满足的数量关系是________．17. 若点P是AB的黄金分割点(AP<BP)，则线段AP、BP、AB满足关系式________．18. 如果点P是线段AB的黄金分割点，且AP<PB，那么PB的值为________．PA19. 已知线段AB，点C是靠近B点的AB的黄金分割点．点G是靠近点A的黄金分割点，则AG=________．BC20. 报幕员在台上时，若站在黄金分割点处，会显得活泼而生动，已知舞台长10米，那么报幕员要至少走________米报幕．三、解答题（本题共计6 小题，共计60分，）21. 如图，在五角星图形中，AD=BC，C，D两点都是AB的黄金分割点，AB=1，求CD的长．22.（1）已知线段AB的长为2，P是AB的黄金分割点，求AP的长；（2）求作线段AB的黄金分割点P，要求尺规作图，且使AP>PB．23. 在△ABC中，D为BC边上一点，过点D作DE//AB交AC与点E，连接BE.若BE= CD，∠C=∠ABE.(1)点D是线段BC的黄金分割点吗？请说明你的理由；(2)已知BC=1，计算黄金比.24. 如图，在线段AB上有一点C，若AC:CB=CB:AB，则称点C为AB的黄金分割点，现已知AB=1，点C是线段AB的黄金分割点(AC<BC)，求BC的长．25. 在△ABC中，AB=AC，∠A=36∘，把像这样的三角形叫做黄金三角形．（1）请你设计三种不同的分法，将黄金三角形ABC分割成三个等腰三角形，使得分割成的三角形中含有两个黄金三角形（画图工具不限，要求画出分割线段；标出能够说明不同分法所得三角形的内角度数，不要求写画法，不要求证明．分别画在图1，图2，图3中）注：两种分法只要有一条分割线段位置不同，就认为是两种不同的分法．（2）如图4中，BF平分∠ABC交AC于F，取AB的中点E，连接EF并延长交BC的延长线于M．试判断CM与AB之间的数量关系？只需说明结果，不用证明．答：CM与AB之间的数量关系是________．26. 如图，AB是⊙O的直径，点C在⊙O上，∠BOC=108∘，过点C作直线CD分别交直线AB，OD=2．AB和⊙O于点D、E，连接OE，DE=12（1）求∠CDB的度数；（2）我们把有一个内角等于36∘的等腰三角形称为黄金三角形．它的腰长与底边长的比．（或者底边长与腰长的比）等于黄金分割比√5−12①写出图中所有的黄金三角形，选一个说明理由；②求弦CE的长；③在直线AB或CD上是否存在点P（点C、D除外），使△POE是黄金三角形？若存在，画出点P，简要说明画出点P的方法（不要求证明）；若不存在，说明理由．参考答案一、选择题（本题共计10 小题，每题 3 分，共计30分）1.【答案】B【解答】解：由于P为线段AB=10的黄金分割点，且AP是较长线段；则AP=√5−12AB≈0.618AB=0.618×10=6.18．故选B．2.【答案】C【解答】解：∵ 点D是线段AB的一个黄金分割点，∵ AD2=BD⋅AB，∵ AD=AC=BC，∵ BC2=BD⋅AB，即BC:BD=AB:BC，而∠ABC=∠CBD，∵ △BCD∽△BAC，∵ ∠A=∠BCD，设∠A=x，则∠B=x，∠BCD=x，∵ ∠ADC=∠BCD+∠B=2x，而AC=AD，∵ ∠ACD=∠ADC=2x，∵ x+2x+x+x=180∘，解得x=36∘，即∠A=36∘．故选：C．3.【答案】D【解答】解：∵ AC>BC，∵ AC是较长的线段，根据黄金分割的定义可知：AB:AC=AC:BC，AC=√5−12AB，AB=√5+12AC，AC≈0.618AB．故选D．【答案】A【解答】解：设AB=x，BC=y．∵ △ABC中，AB=AC，∠A=36∘，∵ ∠ABC=∠ACB=72∘．∵ CD是角平分线，∵ ∠BCD=∠ACD=36∘．∵ AD=CD=BC=y，∵ BD=x−y．∵ ∠BCD=∠A=36∘，∠B=∠ACB=72∘，∵ △DBC∽△ABC．∵ ABBC =BCBD，即xy =yx−y，x2−xy−y2=0，x=1±√52y（负值舍去）．则yx =√5−12．∵ △DBC与△ADC底边分别为BD，AD时，高度相等，∵ △DBC的面积与△ADC的面积的比值是：ADBD =yx=√5−12．故选：A．5.【答案】A【解答】把2米长的线段进行黄金分割，分成的较长线段的长=√5−12×2=√5−1，【答案】A【解答】解：∵ 点P是线段AB的黄金分割点，∵ PA=0.618AB=6.18．故选：A．7.【答案】C【解答】解：当AP>BP时，AP=√5−12×2=√5−1，PB=2−(√5−1)=3−√5，故选C.8.【答案】C【解答】解：∵ 点P是线段AB的黄金分割点，且AP>PB，∵ AP=√5−12AB，设AB=2，则AP=√5−1，BP=2−(√5−1)=3−√5，∵ APAB =√5−12；PB AP =√5√5−1=√5−12；PB AB =3−√52≠√5−12；√PB AB =√3−√52=√5−12．故选C．9.【答案】D【解答】解：根据题意，得图中的黄金三角形有△BMN、△CNF、△DFG、△EHG、△AMH、△ABN、△CBM、△CDG、△EDF、△AGE、△ACD、△BDE、△CEA、△DBA、△EBC，△NCD，△HDE，△AME，△ABH，△BCF，共20个．故选D10.【答案】C【解答】解：∵ AB=AC=1，∵ △ABC的周长为2+k；△BCD的周长为k+k+k2=k(2+k)；△CDE的周长为k2+k2+k3=k2(2+k)；依此类推，第2014个黄金三角形的周长为k2013(2+k)；故选：C．二、填空题（本题共计10 小题，每题 3 分，共计30分）11.【答案】(5√5−5)cm【解答】解：∵ 点C是线段AB的黄金分割点(AC>BC)，∵ AC=√5−12AB，∵ AB=10cm，∵ AC=(5√5−5)cm．故答案为：(5√5−5)cm．12.【答案】2【解答】解：∵ DE // BC，∵ △ADE∽△ABC，∵ DEBC =ADAB，∵ D是AB的黄金分割点(AD<BD)，∵ BD=√5−12AB，∵ AD=AB−√5−12AB=3−√52AB，∵3+√5=3−√52，∵ DE=2．故答案为2．13.【答案】7.8cm 【解答】解：根据已知条件得下半身长是165×0.6=99cm，设需要穿的高跟鞋是ycm，则根据黄金分割的定义得：99+y165+y=0.618，解得：y≈7.8．故答案为7.8cm．14.【答案】(3√5−6)【解答】解：设宽增加xcm，根据题意得x+36=√5−12，解得x=3√5−6，即长不变，宽增加(3√5−6)cm时，给人的美感效果最佳．故答案为(3√5−6)．15.【答案】84.95∘或222.44【解答】解：137∘28′≈137.467∘，137.467∘×0.618=84.95∘，137.467∘÷0.618=222.44∘，所以137∘28′与84.95∘或222.44∘的角成黄金比例．故答案为84.95∘或222.44．16.【答案】AB2=BC⋅AC【解答】解：∵ 点B是线段AC的黄金分割点(AB>BC)，∵ AB2=BC⋅AC．故答案为AB2=BC⋅AC．17.【答案】BP2=AB⋅AP 【解答】解：∵ 点P是AB的黄金分割点(AP<BP)，∵ BP2=AB⋅AP．故答案为BP2=AB⋅AP．18.【答案】√5+12【解答】∵ 点P是线段AB的黄金分割点，且AP<PB，∵ PBPA =√5−13−√5=√5+12，19.【答案】1【解答】解：由题意得，AG=3−√52AB，BC=3−√52AB，∵ AGBC=1．故答案为：1．20.【答案】(15−5√5)【解答】解：报幕员要走的路程为：10×(1−√5−12)=15−5√5（米）．故答案为：(15−5√5)．三、解答题（本题共计6 小题，每题10 分，共计60分）21.【答案】解：∵ C、D两点都是AB的黄金分割点，∵ AC=BD=√5−12AB=√5−12，∵ AD=AC−CD=√5−12−CD，∵ AD=BC，∵ BC=√5−12−CD，而AC+BC=AB，∵ √5−12+√5−12−CD=1，∵ CD=√5−2．【解答】解：∵ C、D两点都是AB的黄金分割点，∵ AC=BD=√5−12AB=√5−12，∵ AD=AC−CD=√5−12−CD，∵ AD=BC，∵ BC=√5−12−CD，而AC+BC=AB，∵ √5−12+√5−12−CD=1，∵ CD=√5−2．22.【答案】解：（1）由于P为线段AB=2的黄金分割点，则AP=2×√5−12=√5−1，或AP=2−(√5−1)=3−√5；（2）如图，点P是线段AB的一个黄金分割点．【解答】解：（1）由于P为线段AB=2的黄金分割点，则AP=2×√5−12=√5−1，或AP=2−(√5−1)=3−√5；（2）如图，点P是线段AB的一个黄金分割点．23.【答案】解：(1)点D是线段BC的黄金分割点.证明：∵ ∠C=∠ABE，DE//AB，∵ ∠ABE=∠DEB，∵ ∠C=∠DEB.又∠EBD=∠CBE，∵ △EBD∼△CBE.∵ BEBC =BDBE，即BE2=BC⋅BD，又BE=CD，∵ CD2=BC⋅BD∵ D为线段BC的黄金分割点；(2)由(1)知，BDBC =CDBD，即BD2=BC⋅CD，∵ BD2=BC(BC−BD)，即BD2=BC2−BC⋅BD，BC2−BC⋅BD+14BD2=54BD2，BC BD =√5+12，BD=√5−12.所以黄金比为√5−12.【解答】解：(1)点D是线段BC的黄金分割点.证明：∵ ∠C=∠ABE，DE//AB，∵ ∠ABE=∠DEB，∵ ∠C=∠DEB.又∠EBD=∠CBE，∵ △EBD∼△CBE.∵ BEBC =BDBE，即BE2=BC⋅BD，又BE=CD，∵ CD2=BC⋅BD∵ D为线段BC的黄金分割点；(2)由(1)知，BDBC =CDBD，即BD2=BC⋅CD，∵ BD2=BC(BC−BD)，即BD2=BC2−BC⋅BD，BC2−BC⋅BD+14BD2=54BD2，BC BD =√5+12，BD=√5−12.所以黄金比为√5−12.24.【答案】解：∵ C为线段AB=1的黄金分割点，且AC<BC，BC为较长线段，∵ BC=√5−12AB=1×√5−12=√5−12．【解答】解：∵ C为线段AB=1的黄金分割点，且AC<BC，BC为较长线段，∵ BC=√5−12AB=1×√5−12=√5−12．25.【答案】解：（1）（2）CM=AB【解答】解：（1）（2）CM=AB26.【答案】AB，解：（1）∵ AB是⊙O的直径，DE=12∵ OA=OC=OE=DE，则∠EOD=∠CDB，∠OCE=∠OEC，设∠CDB=x，则∠EOD=x，∠OCE=∠OEC=2x，又∠BOC=108∘，∵ ∠CDB+∠OCD=108∘，∵ x+2x=108，x=36∘．∵ ∠CDB=36∘．（2）①有三个：△DOE，△COE，△COD．∵ OE=DE，∠CDB=36∘，∵ △DOE是黄金三角形；∵ OC=OE，∠COE=180∘−∠OCE−∠OEC=36∘．∵ △COE是黄金三角形；∵ ∠COB=108∘，∵ ∠COD=72∘；∵ ∠OCD=∠COD．∵ OD=CD，∵ △COD是黄金三角形；②∵ △COD是黄金三角形，∵ OCOD =√5−12，∵ OD=2，∵ OC=√5−1，∵ CD=OD=2，DE=OC=√5−1，∵ CE=CD−DE=2−(√5−1)=3−√5；③存在，有三个符合条件的点P1、P2、P3，如图所示，∵以OE为底边的黄金三角形：作OE的垂直平分线分别交直线AB、CD得到点P1、P2；∵以OE为腰的黄金三角形：点P3与点A重合．【解答】解：（1）∵ AB是⊙O的直径，DE=12AB，∵ OA=OC=OE=DE，则∠EOD=∠CDB，∠OCE=∠OEC，设∠CDB=x，则∠EOD=x，∠OCE=∠OEC=2x，又∠BOC=108∘，∵ ∠CDB+∠OCD=108∘，∵ x+2x=108，x=36∘．∵ ∠CDB=36∘．（2）①有三个：△DOE，△COE，△COD．∵ OE=DE，∠CDB=36∘，∵ △DOE是黄金三角形；∵ OC=OE，∠COE=180∘−∠OCE−∠OEC=36∘．∵ △COE是黄金三角形；∵ ∠COB=108∘，∵ ∠COD=72∘；∵ ∠OCD=∠COD．∵ OD=CD，∵ △COD是黄金三角形；②∵ △COD是黄金三角形，∵ OCOD =√5−12，∵ OD=2，∵ OC=√5−1，∵ CD=OD=2，DE=OC=√5−1，∵ CE=CD−DE=2−(√5−1)=3−√5；③存在，有三个符合条件的点P1、P2、P3，如图所示，∵以OE为底边的黄金三角形：作OE的垂直平分线分别交直线AB、CD得到点P1、P2；∵以OE为腰的黄金三角形：点P3与点A重合。