2019-2020学年徐州市铜山区八年级上期中数学试卷(有答案)

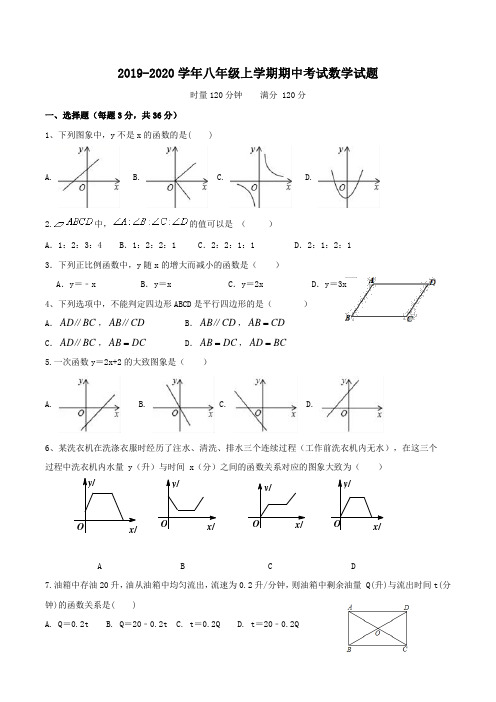
y /升 O x /分 y /O x /2019-2020学年八年级上学期期中考试数学试题时量120分钟 满分 120分一、选择题（每题3分，共36分）1、下列图象中，y 不是x 的函数的是( )A. B. C. D.2.中，的值可以是 （ ）A ．1：2：3：4B ．1：2：2：1C ．2：2：1：1D ．2：1：2：13．下列正比例函数中，y 随x 的增大而减小的函数是（ ）A ．y ＝﹣xB ．y ＝xC ．y ＝2xD ．y ＝3x4、下列选项中，不能判定四边形ABCD 是平行四边形的是（ ）A ．AD BC ∥，AB CD ∥B ．AB CD ∥，AB CD =C ．AD BC ∥，AB DC = D ．AB DC =，AD BC =5.一次函数y ＝2x+2的大致图象是（ ）A. B. C. D.6、某洗衣机在洗涤衣服时经历了注水、清洗、排水三个连续过程（工作前洗衣机内无水），在这三个过程中洗衣机内水量 y （升）与时间 x （分）之间的函数关系对应的图象大致为（ ）A B C D7.油箱中存油20升，油从油箱中均匀流出，流速为0.2升/分钟，则油箱中剩余油量 Q(升)与流出时间t(分钟)的函数关系是( )A. Q ＝0.2tB. Q ＝20﹣0.2tC. t ＝0.2QD. t ＝20﹣0.2Qy /O x /y /升 O x /分8.菱形的对角线长分别为3和4，则该菱形的面积是( )A．6 B．8 C．12 D．249.如图，矩形ABCD对角线相交于点O，∠AOB=60°，AB=4，则矩形的对角线AC为（）A.4B. 8C.D. 1010.如图，在菱形ABCD中，P、Q分别是AD、AC的中点，如果PQ=3，那么菱形ABCD的周长是（）A．30 B．24 C．18 D．611、某排球队12名队员的年龄情况如下表：年龄（岁）18 19 20 21 22人数 1 4 3 2 2（A）19，20 （B）19，19 （C）19，20.5 （D）20，1912、一组数据-1，-2，3，4，5，则该组数据的极差是（）A. 10B. 4C. 7D. 2二、填空题（每题3分，共18分）13、函数1-=xy的自变量 x 的取值范围是_____________．14、一组数据：3，5，5，6，7，7，8．则这组数据的中位数是 ______________.15、在中，两邻边的差为4cm，周长为32cm，则较长边长为__________．．16、已知直线y=kx与直线y=﹣3x﹣2平行，则k=________．17、如左下图所示，利用函数图象观察得方程组的解为_________.18.如图，在正方形ABCD中，对角线AC与BD相交于点O，E为BC上一点，CE=5，F为DE的中点．若△CEF的周长为18，则OF的长为____________．三、解答题：（共66分）19（6分）．体育课上，老师为了解女学生定点投篮的情况，随机抽取8名女生进行每人4次定点投篮的测试，进球数的统计如图所示．（1）求女生进球数的平均数、中位数；（2）投球4次，进球3个以上（含3个）为优秀，全校有女生1200人，估计为“优秀”等级的女生约为多少人？20（6分）.在平面直角坐标系中画出函数y=2x-4 的图象．并判断点 A(-3，-2)，B(3，2)是否在函数 y=2x-4 的图象上？21（6分）.某天早晨，小王从家出发步行前往学校，途中在路边一饭店吃早餐，如图所示是小王从家到学校这一过程中所走的路程 s（米）与时间t（分）之间的关系．（1）小王从家到学校的路程共米，从家出发到学校，小明共用了________分钟；（2）小王吃早餐用了分钟;（3）小王吃早餐以前和吃完早餐后的平均速度分别是多少米/分钟？21（8分）已知直线y=kx+b经过点A（3，7）和B（﹣8，-4）．（1）求直线的解析式；（2）求出该直线与x轴、y轴的交点坐标。

2020-2021学年江苏省徐州市市区部分初中八年级（上）期中数学试卷一、选择题（本大题共8小题，每小题3分，共24分．）1．（3分）自新冠肺炎疫情发生以来，全国人民共同抗疫，各地积极普及科学防控知识，下面是科学防控知识的图片，图片上有图案和文字说明，其中的图案是轴对称图形的是（）A．B．C．D．2．（3分）下列说法正确的是（）A．周长相等的两个三角形全等B．面积相等的两个三角形全等C．完全重合的两个三角形全等D．所有的等边三角形全等3．（3分）在以下列数值为边长的三角形中，不是直角三角形的是（）A．4，7，9B．5，12，13C．6，8，10D．9，40，414．（3分）如图，一根木棍斜靠在与地面（OM）垂直的墙（ON）上，设木棍中点为P，若木棍A端沿墙下滑，且B沿地面向右滑行．在此滑动过程中，点P到点O的距离（）A．变小B．不变C．变大D．无法判断5．（3分）在如图所示的若干个正方形拼成的图形中，与三角形ABC全等的三角形是（）A．△AEG B．△ADF C．△DFG D．△CEG6．（3分）在△ABC中，AB＝AC，D是BC边上的动点（点D与B，C不重合），△ABD和△ACD的面积分别表示S1和S2，下列条件不能说明AD是△ABC角平分线的是（）A．BD＝CD B．AD＝BC C．∠ADB＝∠ADC D．S1＝S27．（3分）如图，在△ACB的两边上分别取点A，B使得CA＝CB，将两个全等的直角三角板的直角顶点分别放在点A，B处，一条直角边分别落在∠ACB的两边上，另一条直角边交于点P，连接CP，则判定△ACP≌△BCP的依据是（）A．AAS B．ASA C．SSS D．HL8．（3分）在△ABC中，AB＝AC，设△ABC的面积为S，图1中，点E、F、M、N是中线AD上的点；图2中，三边的高AD、CF、BE交于点O；图3中，D为BC的中点，∠BAC＝∠MDN＝90°，这三幅图中，阴影部分面积为S的是（）A．①B．①②C．①③D．①②③二、填空题（本大题共8小题，每小题4分，共32分）9．（4分）如图，在△ABC和△ADC中，AB＝AD，BC＝DC，∠B＝130°，则∠D＝°．10．（4分）若等腰三角形的一个底角为70°，则此等腰三角形的顶角为．11．（4分）如图，已知直角△ABC中，CD是斜边AB上的高，AC＝4，BC＝3，则CD＝．12．（4分）将一个矩形纸片沿BC折叠成如图所示的图形，若∠ABC＝27°，则∠ACD的度数为．13．（4分）如图，等边△ABC中，D，E分别是AB、BC边上的一点，且AE＝BD，则∠DPC＝°．14．（4分）如图，在Rt△ABC中，∠ACB＝90°，分别以点B和点C为圆心，大于BC的长为半径作弧，两弧相交于D、E两点，作直线DE交AB于点F，交BC与点G，连接CF，若AC＝3，CG＝2，则CF的长为．15．（4分）如图，在△ABC中，AB＝5，BC＝12，AC＝13，三条角平分线相交于点P，则点P到AB的距离为．16．（4分）如图，正方形ABCD的边长为2，其面积标记为S1，以AD为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为S2，…按照此规律继续下去，则S2020的值为．三、解答题（本大题共9小题，共计84分）17．（8分）如图，已知AD平分∠EAC，且AD∥BC，求证AB＝AC．18．（8分）已知：如图，MS⊥PS，MN⊥SN，PQ⊥SN，垂足分别为S、N、Q，且MS＝PS．求证：△MNS≌△SQP．19．（12分）点A、B、C都在方格纸的格点上：（1）请在图①中再画出一个格点D，使与△ACD≌△CAB；（2）请在图②中再画出一个格点E，使△ABE为等腰三角形（画出所有正确答案）．20．（10分）国庆节期间小红外出游玩时看了鲜花拼成的“71”字样以及“7”内部的两个花坛M、N，抽象为数学图形具体位置如图所示，请用尺规作图帮小红找一处观赏位置P，满足观赏点P到AB和BC的距离相等，并且观赏点P到点M、N的距离也相等．（保留作图痕迹，并写出结论）结论为：即为所求作的点．21．（8分）勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，当两个全等的直角三角形如图摆放时，也可以用面积法来证明，请将下面说理过程补充完整：证明：连接DB，过点D作BC边上的高DF，交BC的延长线与点F，则四边形DFCE为长方形，所以DF＝EC＝．（用含字母的代数式表示）因为S四边形ABCD＝S△ACD+＝+；S四边形ABCD＝S△ADB+＝；所以；所以．22．（8分）如图，在△ABC中，CD是AB边上的高，BE是AC边上的中线，且BD＝CE．（1）求证：点D在BE的垂直平分线上；（2）若∠ABE＝20°，请求出∠BEC的度数．23．（8分）如图是实验室中的一种摆动装置，BC在地面上，△ABC是底边为BC的等腰直角三角形，摆动臂AD可绕点A旋转，摆动臂DM可绕点D旋转，AD＝30，DM＝10，在旋转过程中；（1）当A、D、M三点在同一直线上时，求AM的长；（2）当A、D、M三点为同一直角三角形的顶点时，求AM2的值．24．（8分）如图，把正方形纸片ABCD对折后再展开，折痕为EF，然后将点A翻折到EF上的点M处，折痕为BN，最后沿MC折叠，得△BMC，请你证明△BMC是等边三角形．25．（14分）如图，△ABC是等边三角形，AC＝2，点C关于AB对称的点为C′，点P是直线C′B上的一个动点．（1）若点P是线段C′B上任意一点（不与点C′，点B重合）①如图1，作∠P AE＝60°交BC于点E，AP与AE相等吗？请证明你的结论；②如图2，连接AP，作∠APD＝60°交射线BC于点D，PD与P A相等吗？请证明你的结论．（2）若点P在线段C′B的延长线上．①连接AP，作∠APD＝60°交射线BC于点D，依题意补全图3；②直接写出线段BD、AB、BP之间的数量关系．2020-2021学年江苏省徐州市市区部分初中八年级（上）期中数学试卷试题解析一、选择题（本大题共8小题，每小题3分，共24分．）1．解：A、不是轴对称图形；B、不是轴对称图形；C、不是轴对称图形；D、是轴对称图形．故选：D．2．解：A、全等三角形的周长相等，故本选项错误；B、全等三角形的面积相等，故本选项错误；C、正确；D、边长不相等的等边三角形不全等．故选：C．3．解：A、因为42+72≠98，所以不是直角三角形；B、因为52+128＝132，所以是直角三角形；C、因为63+82＝103，所以是直角三角形；D、因为92+404＝412，所以是直角三角形；故选：A．4．解：在木棍滑动的过程中，点P到点O的距离不发生变化，理由是：连接OP，∵∠AOB＝90°，P为AB中点，∴OP＝AB＝a，即在木棍滑动的过程中，点P到点O的距离不发生变化；故选：B．5．解：如图所示，BC＝DG＝＝＝，AB＝FD＝3，在△ABC和△FDG中，，∴△ABC≌△FDG（SSS），故选：C．6．解：若BD＝CD，AB＝AC，∴△ABD≌△ACD（SSS），∴∠BAD＝∠CAD，∴AD是△ABC角平分线；故A选项不符合题意；若∠ADB＝∠ADC，且∠ADB+∠ADC＝180°，∴∠ADB＝∠ADC＝90°，且AB＝AC，∴AD是△ABC角平分线；故C选项不符合题意；若S1＝S2，∴BD＝CD，且AB＝AC，∴AD是△ABC角平分线；故D选项不符合题意；若AD＝BC；故选：B．7．解：∵∠CAP＝∠CBP＝90°，∴在Rt△ACP与Rt△BCP中，，∴Rt△ACP≌Rt△BCP（HL）．故选：D．8．解：如图1，∵AB＝AC，∴BD＝CD，AD垂直平分BC，∴S△BDN＝S△DCN，S△BMN＝S△MNC，S△BFM＝S△CFM，S△EFB＝S△EFC，S△AEB＝S△AEC，∴阴影部分面积为S；如图2，∵AB＝AC，∴△ABC是等边三角形，且AD⊥BC，CF⊥AB，∴AD垂直平分BC，BE垂直平分AC，∴S△BDO＝S△CDO，S△AEO＝S△CEO，S△AFO＝S△BFO，∴阴影部分面积为S；如图3，连接AD，∵AB＝AC，∠BAC＝90°，∴AD＝BD，∠B＝∠DAC＝45°，∴∠ADM+∠BDM＝90°，且∠MDA+∠ADN＝90°，∴∠BDM＝∠ADN，且AD＝BD，∴△ADF≌△DBE（ASA）∴S△ADF＝S△DBE，∴阴影部分面积为S；故选：D．二、填空题（本大题共8小题，每小题4分，共32分）9．解：在△ADC和△ABC中，，∴△ABC≌△ADC（SSS），∴∠D＝∠B，∵∠B＝130°，∴∠D＝130°，故答案为：130．10．解：∵等腰三角形的一个底角为70°，∴顶角＝180°﹣（70°×2）＝40°，故答案为40°11．解：∵在Rt△ABC中，AC＝4，∴AB＝＝3，∴CD＝＝2.4．故答案为：5.4．12．解：∵AB∥CD，∴∠ABC＝∠1＝27°，由折叠得：∠1＝∠7＝27°，∴∠ACD＝180°﹣27°﹣27°＝126°，故答案为：126°．13．解：∵△ABC为等边三角形，∴∠CAE＝∠ABD＝60°，AC＝BA．在△ACE和△BAD中，，∴△ACE≌△BAD（SAS），∴∠ACE＝∠BAD．∵∠DPC＝∠CAP+ACP，∠BAD+∠CAP＝∠ACP+∠CAP＝60°，∴∠DPC＝60°．故答案为：60．14．解：由作图可知，DE垂直平分线段BC，∴CG＝GB＝2，FG⊥CB，∴∠FGB＝∠ACB＝90°，∴FG∥AC，∵CG＝GB，∴AF＝FB，∴FG＝AC＝，∵∠FGC＝90°，∴CF＝＝＝，故答案为．15．解：∵AB2+BC2＝32+122＝169＝AC4，∴△ABC是直角三角形，∵三条角平分线交于点P，∴点P到三边的距离相等，设为h，则S△ABC＝×（4+12+13）h＝，解得h＝2，即点P到AB的距离为2．故答案为：2．16．解：根据题意：第一个正方形的边长为2；第二个正方形的边长为：×2；第三个正方形的边长为：（）2×2，…第n个正方形的边长是（）n﹣1×5，所以S2020的值是（）2017即4﹣2017．故答案为2﹣2017．三、解答题（本大题共9小题，共计84分）17．证明：∵AD平分∠EAC，∴∠1＝∠2，∵AD∥BC，∴∠6＝∠B，∠2＝∠C，∴∠B＝∠C，∴AB＝AC．18．解：∵MS⊥PS，MN⊥SN，∴∠M+∠MSN＝∠MSN+∠PSQ，∴∠M＝∠PSQ；在△MNS与△SQP中，，∴△MNS≌△SQP（AAS）．19．解：（1）如图，△ACD即为所求．（2）如图，△ABE．20．解：如图，点P即为所求．故答案为：点P．21．证明：连接DB，过点D作BC边上的高DF，则四边形DFCE为长方形，所以DF＝EC＝b﹣a 因为S四边形ABCD＝S△ACD+S△ABC＝+；S四边形ABCD＝S△ADB+S△DCB＝；所以；所以a5+b2＝c2．故答案为：b﹣a；S△ABC；；S△DCB；；；；a2+b2＝c4．22．（1）证明：连接DE，∵CD是AB边上的高，∴∠ADC＝∠BDC＝90°，∵BE是AC边上的中线，∴AE＝CE，∴DE＝CE，∵BD＝CE，∴BD＝DE，∴点D在BE的垂直平分线上；（2）解：∵DE＝AE，∴∠A＝∠ADE，∵∠ADE＝∠DBE+∠DEB，∵BD＝DE，∴∠DBE＝∠DEB，∴∠A＝∠ADE＝2∠ABE，∵∠BEC＝∠A+∠ABE，∴∠BEC＝3∠ABE，∵∠ABE＝20°，∴∠BEC＝60°．23．解：（1）AM＝AD+DM＝40，或AM＝AD﹣DM＝20．（2）显然∠MAD不能为直角．当∠AMD为直角时，AM2＝AD2﹣DM8＝302﹣102＝800，∴AM＝20或﹣20．当∠ADM＝90°时，AM2＝AD6+DM2＝302+103＝1000，∴AM＝10或﹣10．综上所述，满足条件的AM的值为20．24．证明：∵四边形ABCD是正方形，∴AB＝BC，∵正方形纸片ABCD对折后再展开，折痕为EF，∴EF垂直平分BC，∴CM＝BM，∵将点A翻折到EF上的点M处，折痕为BN，∴AB＝MB，∴BM＝BC，∴BM＝BC＝CM，∴△BMC是等边三角形．25．解：（1）①AP＝AE，理由如下：∵△ABC是等边三角形，∴∠ABC＝60°＝∠BAC，AB＝AC，∵点C'与点C关于AB对称，∴∠C'BA＝∠CBA＝60°，∵∠P AE＝∠BAC＝60°，∴∠P AB＝∠EAC，∴△P AB≌△EAC（ASA），∴AP＝AE；②PD＝P A，理由如下：如图2中，作∠BPE＝60°交AB于点E，∵△ABC是等边三角形，∴∠ABC＝60°，∵点C'与点C关于AB对称，∴∠C'BA＝∠CBA＝60°＝∠BPE，∴∠PEB＝60°．∴△PBE是等边三角形，∴PB＝PE，AEP＝120°＝∠PBD．∵∠BPD+∠DPE＝60°，∠APE+∠DPE＝60°，∴∠BPD＝∠APE，在△PBD和△PEA中，，∴△PBD≌△PEA（ASA）．∴PD＝P A；（2）①解：补全图形，如图3所示：②解：结论：BD＝BP+AB，理由：如图5中，在BD上取一点E．∵∠EBP＝60°，BE＝BP，∴△EBP是等边三角形，∴∠BPE＝∠APD＝60°，∴∠APB＝∠EPD，∵PB＝PE，P A＝PD，∴△BP A≌△EPD（SAS），∴AB＝DE，∴BD＝BE+ED＝BP+AB．。

2019-2020学年八年级上学期期中考试数学试卷一、选择题（共12小题，每小题3分，共36分）1．（3分）如果一次函数y＝kx+b的图象经过一、二、三象限，那么k、b应满足的条件是（）A．k＞0，且b＞0B．k＜0，且b＜0C．k＞0，且b＜0D．k＜0，且b＞02．（3分）下列运算中，错误的有（）①＝；②＝±4；③＝＝﹣2；④＝+＝．A．1个B．2个C．3个D．4个3．（3分）的平方根是（）A．4B．﹣4C．±4D．±24．（3分）已知直线y＝﹣x+8与x轴、y轴分别交于点A和点B，M是OB上的一点，若将△ABM沿AM折叠，点B恰好落在x轴上的点B′处，则直线AM的函数解析式是（）A．y＝﹣x+8B．y＝﹣x+8C．y＝﹣x+3D．y＝﹣x+35．（3分）下列函数：①y＝﹣2x，②y＝﹣3x2+1，③y＝x﹣2，其中一次函数的个数有（）A．0个B．1个C．2个D．3个6．（3分）已知方程组，那么代数式8x﹣y﹣z的值是（）A．6B．7C．8D．97．（3分）已知，则＝（）A．B．C．1D．8．（3分）已知正比例函数y＝（2m﹣1）x的图象上两点A（x1，y1），B（x2，y2），当x1＜x2时，有y1＞y2，那么m的取值范围是（）A．m＜B．m＞C．m＜0D．m＞09．（3分）当a＜0，b＞0函数y＝ax+b与y＝bx+a在同一平面直角坐标系中的图象大致是（）A．B．C．D．10．（3分）下列实数中，1﹣，，3.14152，，0.，，﹣，0.2727727772…（两个2之间一次多一个7），其中无理数个数是（）A．2个B．3个C．4个D．5个11．（3分）对任意非零数m，直线y＝mx+2﹣5m，都经过一定点，则定点坐标为（）A．（0，2）B．（1，2）C．（5，2）D．（2，﹣2）12．（3分）已知x2++4＝4x，则代数式：的值为（）A．1.5B．2C．2.5D．3二、填空题（本题共4小题，每小题3分，共12分）13．（3分）若＝a+b，其中a是整数，0＜b＜1，则（4+）（a﹣b）＝．14．（3分）已知一次函数的图象经过点P（﹣3，0），且与两坐标轴截得的三角形面积为4，则此一次函数的解析式为．15．（3分）已知1＜a＜2，则|﹣|＝．16．（3分）已知a＜1，化简（a﹣1）＝．三、解答题（共52分）17．（4分）计算：|1﹣|+﹣（3.14﹣π）0﹣（﹣）﹣1．18．（8分）解方程组：（1）（2）19．（6分）在直角坐标系中，有四个点A（﹣8，3）、B（﹣4，5）、C（0，n）、D（m，0），当四边形ABCD的周长最短时，求的值．20．（6分）如图，两直线l1：y＝kx﹣2b+1和l2：y＝（1﹣k）x+b﹣1交于x轴上一点A，与y轴分别交于点B、C，若A的横坐标为2，（1）求这两条直线的解析式；（2）求△ABC的面积．21．（8分）如图所示，四边形OABC是矩形，点A、C的坐标分别为（3，0），（0，1），点D是线段BC上的动点（与端点B、C不重合），过点D作直线y＝﹣x+m交折线OAB 于点E．（1）请写出m的取值范围；（2）记△ODE的面积为S，求S与m的函数关系式．22．（8分）甲、乙两人从学校出发，沿相同的线路跑向公园．甲先跑一段路程后，乙开始出发，当乙超过甲150米时，乙停在此地等候甲，两人相遇后，乙和甲一起以甲原来的速度继续跑向公园．如图是甲、乙两人在跑步的全过程中经过的路程y（米）与甲出发的时间x（秒）之间函数关系的图象，根据题意填空：（1）在跑步的全过程中，甲共跑了米，甲的速度为米/秒；（2）乙最早出发时跑步的速度为米/秒，乙在途中等候甲的时间为秒；（3）乙出发秒后与甲第一次相遇．23．（12分）如图，一次函数的函数图象与x轴、y轴分别交于点A、B，以线段AB为直角边在第一象限内作Rt△ABC，且使∠ABC＝30°．（1）求△ABC的面积；（2）如果在第二象限内有一点P（m，），试用含m的代数式表示△APB的面积，并求当△APB与△ABC面积相等时m的值；（3）是否存在使△QAB是等腰三角形并且在坐标轴上的点Q？若存在，请写出点Q所有可能的坐标；若不存在，请说明理由．参考答案与试题解析一、选择题（共12小题，每小题3分，共36分）1．【解答】解：∵一次函数y＝kx+b的图象经过一、二、三象限，∴其图象如图所示，∴直线从左向右逐渐上升，∴k＞0，∵直线与y轴的交点在x轴的上方，∴b＞0，故选：A．2．【解答】解；①＝，故①错误；②＝4，故②错误；③负数没有平方根，故③错误；④＝＝，故④错误；故选：D．3．【解答】解：＝4，4的平方根是±2．故选：D．4．【解答】解：当x＝0时，y＝﹣x+8＝8，即B（0，8），当y＝0时，x＝6，即A（6，0），所以AB＝AB′＝10，即B′（﹣4，′0），设OM＝x，则B′M＝BM＝BO﹣MO＝8﹣x，B′O＝AB′﹣AO＝10﹣6＝4∴x2+42＝（8﹣x）2x＝3∴M（0，3）又A（6，0）直线AM的解析式为y＝﹣x+3．故选：C．5．【解答】解：①y＝﹣2x是正比例函数，也是一次函数，②y＝﹣3x2+1是二次函数，③y＝x﹣2是一次函数．故选：C．6．【解答】解：∵3x﹣y﹣2z＝1，∴﹣y﹣z＝1+z﹣3x，8x﹣y﹣z＝1+z﹣3x+8x＝5x+z+1，，①+②得：5x+z＝6，即8x﹣y﹣z＝6+1＝7，故选：B．7．【解答】解：解，得，x＝3z，y＝2z，把x＝3z，y＝2z代入得，原式＝＝，故选：A．8．【解答】解：∵正比例函数y＝（2m﹣1）x的图象经过点A（x1，y1）和点B（x2，y2），当x1＜x2时y1＞y2时，∴正比例函数y＝（2m﹣1）x的图象是y随x的增大而减小，∴2m﹣1＜0．解得m＜故选：A．9．【解答】解：∵a＜0，b＞0，∴函数y＝ax+b的图象经过第一、二、四象限，函数y＝bx+a的图象经过第一、三、四象限，观察图象，只有选项B符合题意．故选：B．10．【解答】解：1﹣，，0.2727727772…（两个2之间一次多一个7）是无理数，故选：B．11．【解答】解：∵y＝mx+2﹣5m＝m（x﹣5）+2，∴当x＝5时，y＝2．故选：C．12．【解答】解：∵x2++4＝4x，∴（x﹣2）2+＝0，则x﹣2＝0，y﹣1＝0，解得：x＝2，y＝1，∴＝+2＝2.5，故选：C．二、填空题（本题共4小题，每小题3分，共12分）13．【解答】解：∵＝a+b，其中a是整数，0＜b＜1，∴b＝﹣2，∴a＝2，∴（4+）（a﹣b）＝（4+）×（2﹣+2）＝（4+）×（4﹣）＝16﹣7＝9，故答案为：9．14．【解答】解：依照题意画出图形，如图所示．设一次函数图象与y轴交于点Q（0，m），则S△POQ＝×|﹣3|×|m|＝4，∴m＝±．设一次函数的解析式为y＝kx+b（k≠0）．当m＝时，将（﹣3，0），（0，）代入y＝kx+b，得：，解得：，∴一次函数的解析式为y＝x+．当m＝﹣时，同理可求出一次函数的解析式为y＝﹣x﹣．故答案为：y＝x+或y＝﹣x﹣．15．【解答】解：∵1＜a＜2，∴|﹣|＝a﹣（2﹣a）＝2a﹣2．故答案为：2a﹣2．16．【解答】解：∵a＜1，∴a﹣1＜0，∴（a﹣1）＝（a﹣1）＝（a﹣1）×[]＝﹣．故答案为：﹣．三、解答题（共52分）17．【解答】解：原式＝﹣1+2﹣1+2＝3．18．【解答】解：（1），把②代入①得：2x+15﹣4x＝11，解得：x＝2，把x＝2代入②得：y＝15﹣4×2＝7，方程组的解为：，（2）原方程组整理得：，②﹣①×10得：4y＝2，解得：y＝，把y＝代入①得：3x﹣1＝0，解得：x＝，故方程组的解为：．19．【解答】解：依题意画图得：作B关于Y轴的对称点B′，A关于X轴的对称点A′，连接A′B′，他们与X轴，Y轴的交点便为所求．如图所示，过A′与B′两点的直线的函数解析式可求．设过A′与B′两点的直线的函数解析式为y＝kx+b．依题意得：﹣8k+b＝﹣3，4k+b＝5解得，k＝，b＝，所以，（0，n）为（0，）．（m，0）为（﹣3.5，0）所以，＝﹣．故答案为﹣．20．【解答】解：（1）把A（2，0）分别代入y＝kx﹣2b+1和y＝（1﹣k）x+b﹣1得，解得，所以直线l1的解析式为y＝x﹣3，直线l2的解析式为y＝﹣x+1；（2）当x＝0时，y＝x﹣3＝﹣3，则B点坐标为（0，﹣3）；当x＝0时，y＝﹣x+1＝1，则C点坐标为（0，1），所以△ABC的面积＝×（1+3）×2＝4．21．【解答】解：（1）当y＝1时，有﹣x+m＝1，∴x＝2m﹣2，∴点D的坐标为（2m﹣2，1）．∵点D是线段BC上的动点（与端点B、C不重合），∴0＜2m﹣2＜3，∴1＜m＜2.5．故答案为：1＜m＜2.5．（2）①当点E在线段OA上时，如图1所示．当y＝0时，有﹣x+m＝0，∴x＝2m，∴点E的坐标为（2m，0），∴2m≤3，∴此时1＜m≤1.5，S＝OA•OC＝m；②当点E在线段AB上时（与端点A、B不重合），此时1.5＜m＜2.5，如图2所示．当x＝3时，y＝﹣x+m＝m﹣1.5，∴点E的坐标为（3，m﹣1.5）．∵点D的坐标为（2m﹣2，1），点B的坐标为（3，1），∴CD＝2m﹣2，BD＝5﹣2m，AE＝m﹣1.5，BE＝2.5﹣m，S＝S矩形OABC﹣S△OAE﹣S△OCD﹣S△BDE，＝OA•OC﹣OA•AE﹣OC•CD﹣BD•BE，＝3×1﹣×3（m﹣1.5）﹣（2m﹣2）﹣（5﹣2m）（2.5﹣m），＝﹣m2+2.5m．综上所述：S与m的函数关系式为S＝．22．【解答】解：（1）有函数图象可得，在跑步的全过程中，甲共跑了900米，甲的速度为：900÷600＝1.5米/秒，故答案为：900，1.5；（2）由图象可得，甲跑500秒的路程是：500×1.5＝750米，甲跑600米的时间是：（750﹣150）÷1.5＝400秒，乙跑步的速度是：750÷（400﹣100）＝2.5米/秒，乙在途中等候甲的时间是：500﹣400＝100秒，即乙跑步的速度是2.5米/秒，乙在途中等候甲的时间是100秒；（3）∵D（600，900），A（100，0），B（400，750），∴OD的函数关系式是y＝1.5x，AB的函数关系式是y＝2.5x﹣250，根据题意得，解得x＝250，250﹣100＝150（秒），即乙出发150秒时第一次与甲相遇．故答案为：（1）900；1.5；（2）2.5；100；（3）150．23．【解答】解：（1）∵一次函数的解析式为函数图象与x轴、y轴分别交于点A、B，∴A（1，0），B（0，），∴AB＝2，设AC＝x，则BC＝2x，由勾股定理得，4x2﹣x2＝4，解得x＝，S△ABC＝＝；（2）过P作PD⊥x轴，垂足为D，S△APB＝S梯形ODPB+S△AOB﹣S△APD＝•＝，﹣＝，解得m＝；（3）∵AB＝＝2，∴当AQ＝AB时，点Q1（3，0），Q2（﹣1，0），Q3（0，﹣）；当AB＝BQ时，点Q4（0，+2），Q5（0，﹣2），Q2（﹣1，0）；当AQ＝BQ时，点Q6（0，），Q2（﹣1，0），综上可得：（0，），（0，），（﹣1，0）（3，0），（0，），（0，）。

2019-2020学年度八年级数学上册期中考试卷（有答案）一、选择题（共10题；共20分）1.下列几何图形不一定是轴对称图形的是（）A. 线段B. 角C. 等腰三角形D. 直角三角形2.三角形一个外角小于与它相邻的内角，这个三角形是( )A. 直角三角形B. 锐角三角形C. 钝角三角形D. 属于哪一类不能确定3.（2017·金华）下列各组数中，不可能成为一个三角形三边长的是（ )A. 2，3，4B. 5，7，7C. 5，6，12D. 6，8，104.等腰三角形的两条边长分别为15cm和7cm，则它的周长为（）A. 37cmB. 29cmC. 37cm或29cmD. 无法确定5.如图，在△ABC中，AB=AC ，AD是BC边上的高，点E、F是AD的三等分点，若△ABC的面积为12,图中阴影部分的面积为( )．A. 6B. 10．5C. 11D. 15．56.如图，一副分别含有30°和45°角的两个直角三角板，拼成如图所示，其中∠C=90°，∠B=45°，∠E=30°，则∠BFD的度数是（）A. 10°B. 15°C. 25°D. 30°7.（2017•百色）多边形的外角和等于（）A. 180°B. 360°C. 720°D. （n﹣2）•180°8.如图，⊙C过原点，且与两坐标轴分别交于点A、点B，点A的坐标为（0，3），M是第三象限内上一点，∠BMO=120°，则⊙C的半径长为（）A. 6B. 5C. 3D. 39.能将三角形面积平分的是三角形的（）A. 角平分线B. 高C. 中线D. 外角平分线10.已知等腰三角形的周长为14,其腰长为4,则它的底边长为（）A. 4B. 5C. 6D. 4或6二、填空题（共5题；共18分）11.等腰三角形ABC中，顶角A为40°，点P在以A为圆心，BC长为半径的圆上，且BP=BA，则∠PBC的度数为________．12.如图示,点B在AE上,∠CBE=∠DBE,要使ΔABC≌ΔABD, 还需添加一个条件是________.（填上你认为适当的一个条件即可）13.十五边形的外角和等于________ ．14.已知点A（m，3）与点B（2，n）关于y轴对称，则m=________，n=________．15.如图，AC与BD交于点P，AP=CP，从以下四个论断①AB=CD，②BP=DP，③∠B=∠D，④∠A=∠C中选择一个论断作为条件，则不一定能使△APB≌△CPD的论断是________（限填序号）．三、解答题（共8题；共62分）16.如图，在△ABC中，点D、E分别为BC、AD的中点，若S△ABC=1，求S△ABE．17.已知：如图，PM⊥BD于BD中点M，PN⊥AD于AD中点N，PM=PN，试说明：OB=OA。

2019-2020年八年级数学上册期中测试卷 题 号 一 二 三 总 分 1～10 11～18 19 20 21 22 23 24 附加题

得 分

（A）①④ （B）②③ （C）③④15． 在4，3.5，π，7，9五个数中，无理数有 ········································· （ ）． （A）1个 （B）2个 （C）3个 （D）4个

16．某数的平方根等于它的立方根，则这个数 ··············································· （ ）． （A）1 （B）－1 （C）0 （D）以上都不对

17． 下列条件中，能说明四边形ABCD是平行四边形的是 ······························· （ ）． （A）∠A＝30°，∠B＝150°，∠C＝30°，∠D＝150° （B）∠A＝60°，∠B＝60°，∠C＝120°，∠D＝120° （C）∠A＝60°，∠B＝90°，∠C＝60°，∠D＝150° （D）∠A＝60°，∠B＝70°，∠C＝110°，∠D＝120°

18． 下列说法中，正确的是 ······································································· （ ）． （A）在成中心时称的图形中，连结对称点的线段不一定都经过对称中心 （B）在成中心对称的图形中，连结对称点的线段都被对称中心平分 （C）若两个图形的对应点连成的线段都经过某一点．那么这两个图形一定关于这一点成中心对称 （D）以上说法都正确

得 分 评卷人 得 分 评卷人 三、解答题：本大题共6小题，共76分．解答应写出文字说明或演算步骤． 19．（本小题满分16分）

计算：（1）2＋2－3（精确到百分位）；

（2）5＋π（保留2个有效数字）． 20．（本小题满分12分） 如图，一个长方形的运动场，有一个球落到了点C，小明要从点A走到点C捡球，至少要走多少米？